Unranking Small Combinations of a Large Set in Co-Lexicographic Order
Abstract
1. Introduction
- Listing is the process of generating all elements of a combinatorial set sequentially.
- Ranking is the process of getting the rank r of a combinatorial object a (the position of the object in their ordering).
- Unranking is the inverse process of ranking, and unranking algorithms allow to generate the object a that has a rank r.
- Random selection is the process of generating elements of a combinatorial set in a random order.
- UNRANKCOMB-A: decreasing lexicographical order, time complexity and space complexity;
- UNRANKCOMB-B: increasing lexicographical order, time complexity and space complexity;
- UNRANKCOMB-C: decreasing lexicographical order, time complexity and space complexity;
- UNRANKCOMB-D: decreasing lexicographical order, time complexity and space complexity.
2. Materials and Methods
2.1. Algorithms for Ranking and Unranking Combinations in Co-Lexicographic Order
| Algorithm 1: Algorithm for unranking combinations in colex order |
 |
- the number of iterations in the for-loop (Line 2 in Algorithm 1) is m;
- the minimum number of comparisons in the while-loop (Line 4 in Algorithm 1) is (when ) and the maximum number of comparisons is n (when );
- the computational complexity of calculating the value of a binomial coefficient is when and when .
2.2. Modification of Unranking Algorithm
| Algorithm 2: Modification of algorithm for unranking combinations in colex order |
 |
3. Results
| Algorithm 3: Preliminary search for the values of k for Algorithm 2 |
 |
- preliminary search for the value of k (Line 3 in Algorithm 2) by using Algorithm 3 that has time complexity;
- search for the true value of k by making iterations in the while-loop (Line 4 in Algorithm 2);
- calculation of the value of a binomial coefficient that has time complexity when .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kreher, D.L.; Stinson, D.R. Combinatorial Algorithms: Generation, Enumeration, and Search; ACM: New York, NY, USA, 1999. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1; Addison-Wesley Professional: Boston, MA, USA, 2011. [Google Scholar]
- Stojmenovic, I. Handbook of Applied Algorithms: Solving Scientific, Engineering and Practical Problems; Chapter Generating all and Random Instances of a Combinatorial Object; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 1–38. [Google Scholar] [CrossRef]
- Ruskey, F. Combinatorial Generation. Working Version (1j-CSC 425/520). Available online: http://page.math.tu-berlin.de/~felsner/SemWS17-18/Ruskey-Comb-Gen.pdf (accessed on 1 December 2021).
- Akl, S.G. A comparison of combination generation methods. ACM Trans. Math. Softw. 1981, 7, 42–45. [Google Scholar] [CrossRef]
- Mifsud, C.J. Algorithm 154: Combination in lexicographical order. Comm. ACM 1963, 6, 103. [Google Scholar] [CrossRef]
- Chan, B.; Akl, S.G. Generating combinations in parallel. BIT Numer. Math. 1986, 26, 1–6. [Google Scholar] [CrossRef]
- Chen, G.H.; Chern, M.S. Parallel generation of permutations and combinations. BIT Numer. Math. 1986, 26, 277–283. [Google Scholar] [CrossRef]
- Akl, S.G.; Gries, D.; Stojmenovic, I. An optimal parallel algorithm for generating combinations. Inform. Process. Lett. 1989, 33, 135–139. [Google Scholar] [CrossRef]
- Lin, C.-J. A parallel algorithm for generating combinations. Comput. Math. Appl. 1989, 17, 1523–1533. [Google Scholar] [CrossRef][Green Version]
- Tsay, J.C.; Lin, C.J. A systolic design for generating combinations in lexicographic order. Parallel Comput. 1990, 13, 119–125. [Google Scholar] [CrossRef]
- Stojmenovic, I. A simple systolic algorithm for generating combinations in lexicographic order. Comput. Math. Appl. 1992, 24, 61–64. [Google Scholar] [CrossRef][Green Version]
- Elhage, H.; Stojmenovic, I. Systolic generation of combinations from arbitrary elements. Parallel Process. Lett. 1992, 2, 241–248. [Google Scholar] [CrossRef]
- Kapralski, A. New methods for the generation of permutations, combinations, and other combinatorial objects in parallel. J. Parallel Distrib. Comput. 1993, 17, 315–326. [Google Scholar] [CrossRef]
- Xu, C.W.; Ma, X.; Shiue, W.K. A new parallel combination generator. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications, Sunnyvale, CA, USA, 9–11 August 1996; pp. 25–28. [Google Scholar]
- Kokosinski, Z. On parallel generation of combinations in associative processor architectures. In Proceedings of the IASTED International Conference on Parallel and Distributed Systems, Barcelona, Spain, 9–11 June 1997; pp. 283–289. [Google Scholar]
- Itai, A. Generating permutations and combinations in lexicographical order. J. Braz. Comput. Soc. 2001, 7, 65–68. [Google Scholar] [CrossRef][Green Version]
- Eades, P.; McKay, B. An algorithm for generating subsets of fixed size with a strong minimal change property. Inform. Process. Lett. 1984, 19, 131–133. [Google Scholar] [CrossRef]
- Xiang, L.; Ushijima, K. On O(1) time algorithms for combinatorial generation. Comput. J. 2001, 44, 292–302. [Google Scholar] [CrossRef]
- Torres-Jimenez, J.; Izquierdo-Marquez, I. A low spatial complexity algorithm to generate combinations with the strong minimal change property. Discret. Math. Algorithms Appl. 2019, 11, 1950060. [Google Scholar] [CrossRef]
- Ruskey, F.; Williams, A. The coolest way to generate combinations. Discret. Math. 2009, 309, 5305–5320. [Google Scholar] [CrossRef]
- Knott, G.D. A numbering system for combinations. Comm. ACM 1974, 17, 45–46. [Google Scholar] [CrossRef]
- Er, M.C. Lexicographic ordering, ranking and unranking of combinations. Int. J. Comput. Math. 1985, 17, 277–283. [Google Scholar] [CrossRef]
- Kokosinski, Z. Algorithms for unranking combinations and their applications. In Proceedings of the IASTED/ISMM International Conference on Parallel and Distributed Computing and Systems, Washington, DC, USA, 19–21 October 1995; pp. 216–224. [Google Scholar]
- Kokosinski, Z. Unranking combinations in parallel. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications, Sunnyvale, CA, USA, 9–11 August 1996; pp. 79–82. [Google Scholar]
- Ryabko, B.Y. Fast enumeration of combinatorial objects. Discret. Math. Appl. 1998, 8, 163–182. [Google Scholar] [CrossRef]
- Shablya, Y.; Kruchinin, D.; Kruchinin, V. Method for developing combinatorial generation algorithms based on AND/OR trees and its application. Mathematics 2020, 8, 962. [Google Scholar] [CrossRef]
- Genitrini, A.; Pepin, M. Lexicographic unranking of combinations revisited. Algorithms 2021, 14, 97. [Google Scholar] [CrossRef]
- Shimizu, T.; Fukunaga, T.; Nagamochi, H. Unranking of small combinations from large sets. J. Discret. Algorithms 2014, 29, 8–20. [Google Scholar] [CrossRef]
- Parque, V.; Miyashita, T. Towards the succinct representation of m out of n. In Proceedings of the Internet and Distributed Computing Systems, Tokyo, Japan, 11–13 October 2018; pp. 16–26. [Google Scholar] [CrossRef]
- Parque, V.; Miyashita, T. Unranking combinations using gradient-based optimization. In Proceedings of the International Conference on Tools with Artificial Intelligence, Volos, Greece, 5–7 November 2018; pp. 579–586. [Google Scholar] [CrossRef]
- Roberts, A.W.; Varberg, D.E. Convex Functions; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists; Elsevier Academic Press: Burlington, MA, USA, 2012. [Google Scholar] [CrossRef]
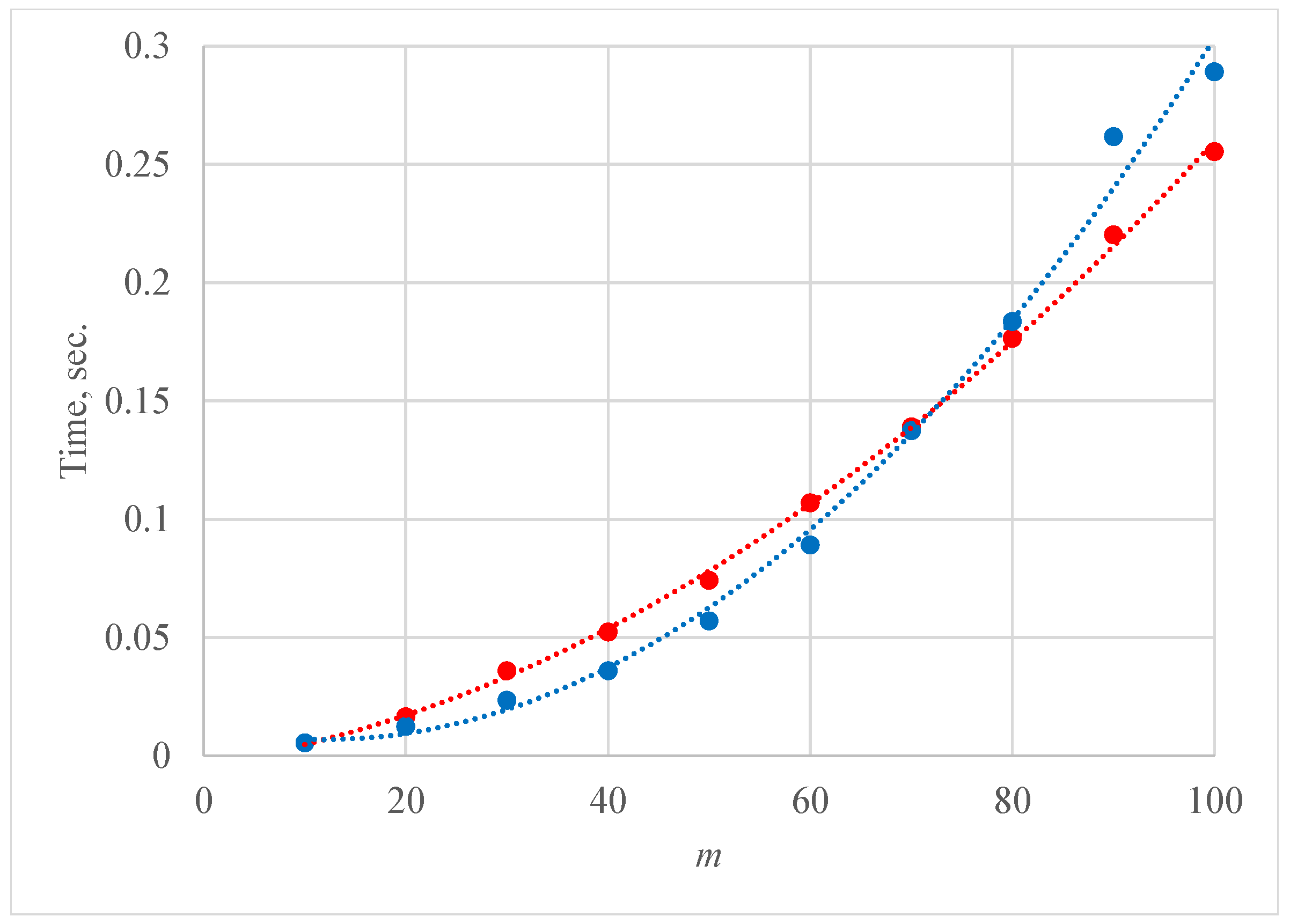
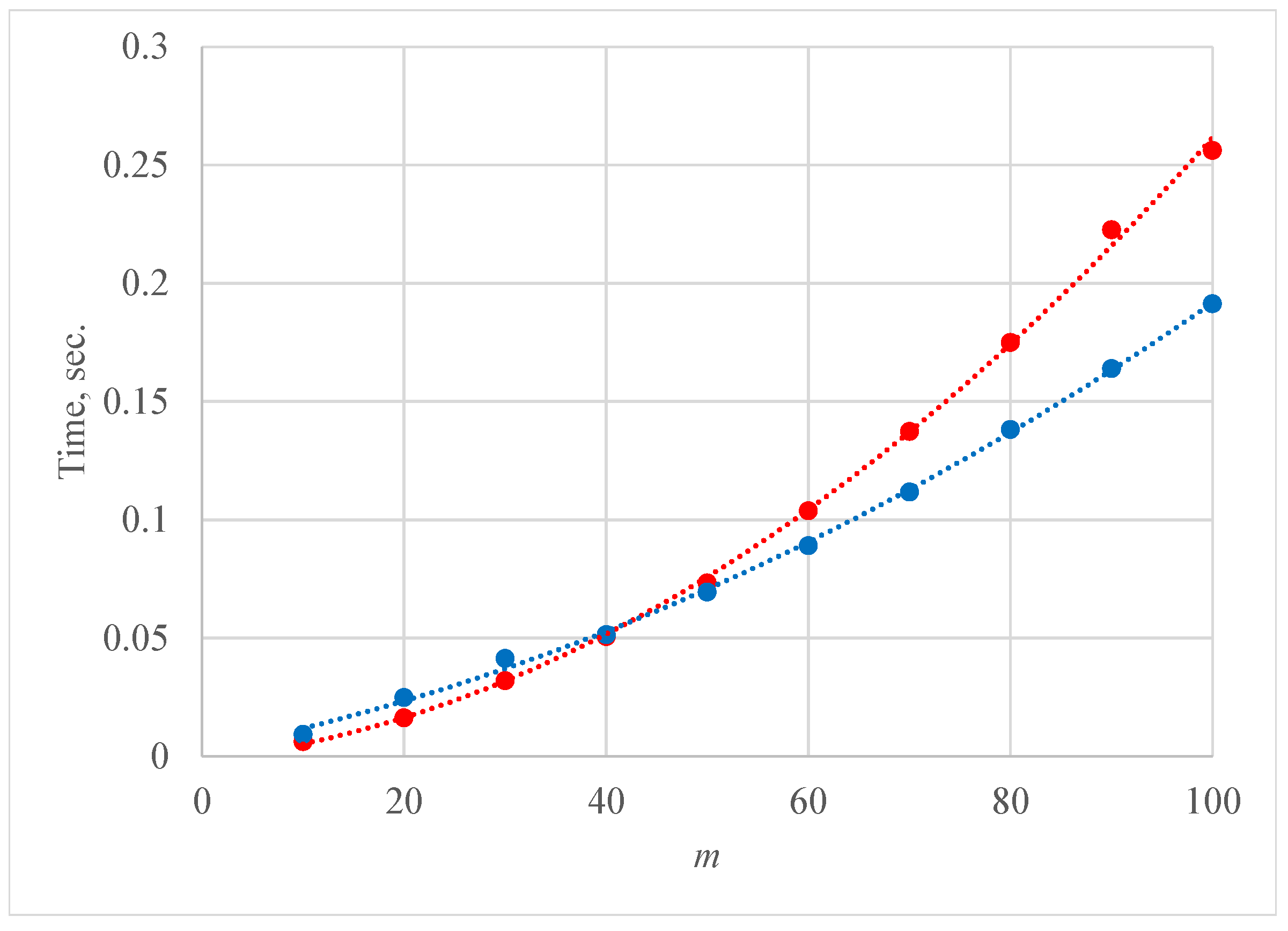
| r | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | ||||||||||||
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 60 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 70 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 80 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 90 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 100 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 110 | 2 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 120 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 130 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 140 | 3 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 150 | 4 | 3 | 3 | 3 | 2 | 1 | 2 | 2 | 1 | 1 | 1 | |
| 160 | 4 | 4 | 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | |
| 170 | 5 | 4 | 4 | 4 | 3 | 2 | 3 | 2 | 2 | 1 | 2 | |
| 180 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | |
| 190 | 7 | 6 | 5 | 5 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | |
| 200 | 7 | 6 | 6 | 5 | 5 | 4 | 3 | 3 | 3 | 2 | 2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruchinin, V.; Shablya, Y.; Kruchinin, D.; Rulevskiy, V. Unranking Small Combinations of a Large Set in Co-Lexicographic Order. Algorithms 2022, 15, 36. https://doi.org/10.3390/a15020036
Kruchinin V, Shablya Y, Kruchinin D, Rulevskiy V. Unranking Small Combinations of a Large Set in Co-Lexicographic Order. Algorithms. 2022; 15(2):36. https://doi.org/10.3390/a15020036
Chicago/Turabian StyleKruchinin, Vladimir, Yuriy Shablya, Dmitry Kruchinin, and Victor Rulevskiy. 2022. "Unranking Small Combinations of a Large Set in Co-Lexicographic Order" Algorithms 15, no. 2: 36. https://doi.org/10.3390/a15020036
APA StyleKruchinin, V., Shablya, Y., Kruchinin, D., & Rulevskiy, V. (2022). Unranking Small Combinations of a Large Set in Co-Lexicographic Order. Algorithms, 15(2), 36. https://doi.org/10.3390/a15020036






