Convex Neural Networks Based Reinforcement Learning for Load Frequency Control under Denial of Service Attacks
Abstract
:1. Introduction
- In this paper, we propose a load-frequency control strategy of convex neural network-based reinforcement learning that can resist DoS attacks and analyze the sufficient conditions for the stability of power grids as well as the convergence of convex neural network parameters during online learning.
- A long-term utility model of load-frequency control based on convex neural network approximation is proposed. Thus, the control output can be improved by the near global optimum obtained from the convex approximation. Additionally, the optimization speed is accelerated, and the efficiency of controllers is improved.
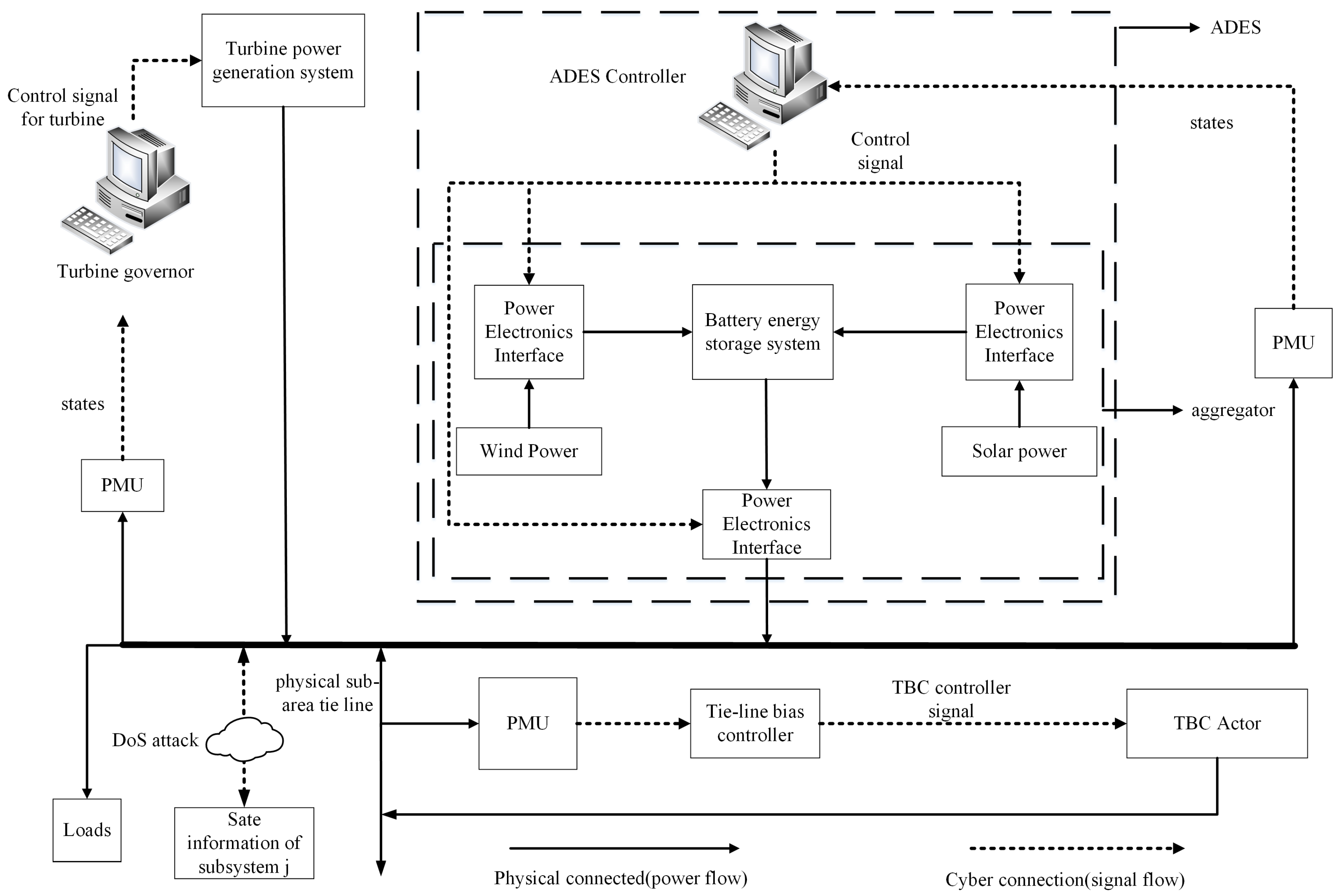
2. Load Frequency Control and DoS Attack Models Based on ADES
2.1. Load Frequency Control Model of Multi-Machine Power Grids
2.2. Dynamic Model of Load Frequency Control Considering DoS Attacks
3. Optimized Load Frequency Control with Convex Neural Network-Based Reinforcement Learning
3.1. Convex Neural Network Structure Design
3.2. Critic Networks for Long Term Future Cost Approximation under DoS Attacks
3.3. Actor Networks for Control Strategy under DoS Attacks
3.4. Critic-Actor Network Weight Learning
3.5. Analysis of Power Grid Stability and Convergence of Convex Neural Network Weights
- The expected control output designed in this paper and the gain term of the physical interconnection disturbances included in the subsystem model (1) are involved.
- The expected output of subsystem control and the calculation of actual control output including the variable set of information adjacent subsystems are involved.
- The modeling and estimation error term in model (9) include the estimation error relationships of physical and information interconnection disturbances between subsystems.
- When convex neural networks are used to approximate the critic networks and actor networks of reinforcement learning, the approximation errors and of convex neural networks are also considered. These two errors also include the estimation error relationships of physical and information interconnection disturbances between subsystems.
4. Experiment Environment
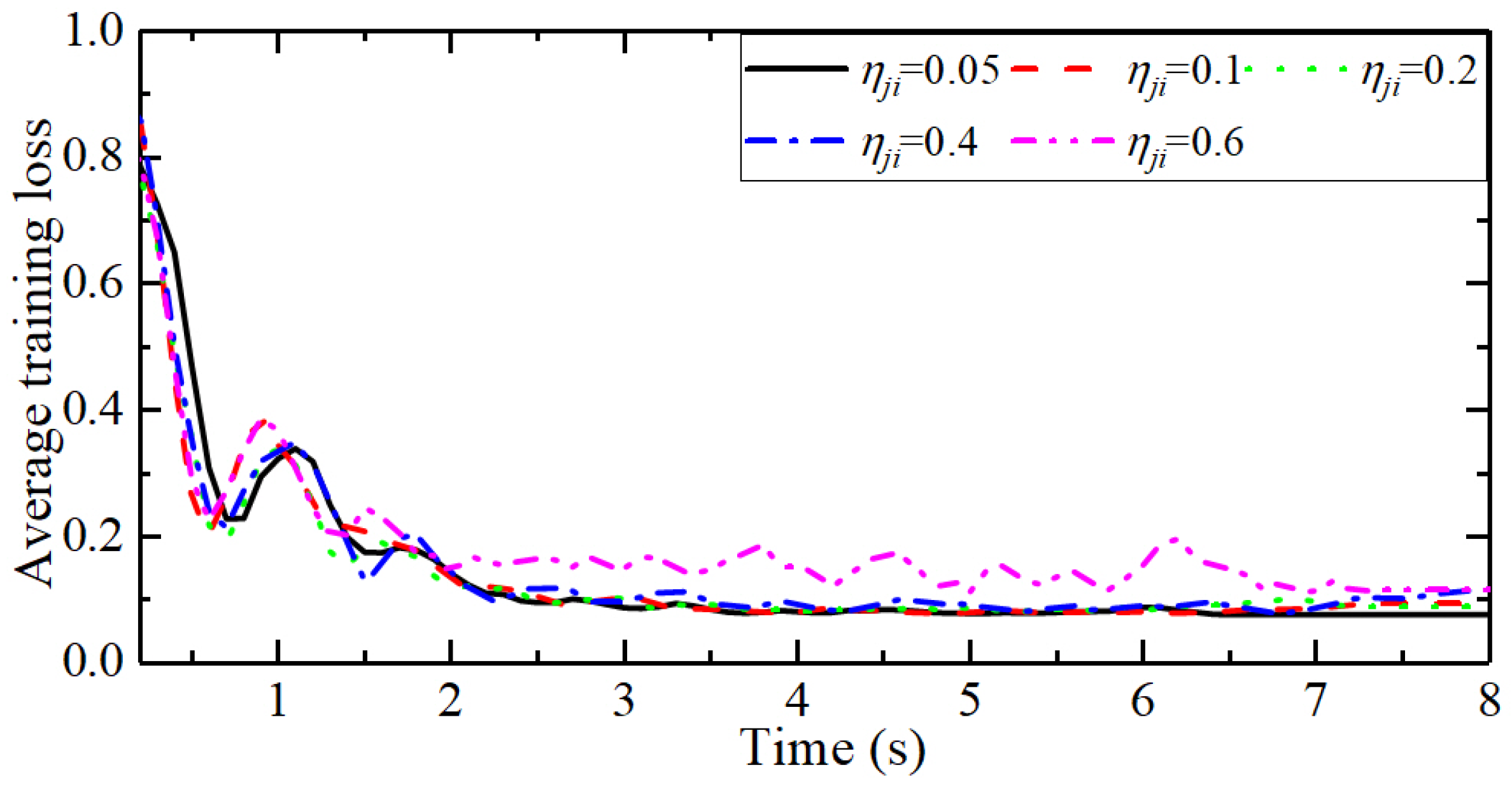
4.1. Configuration of System Model and Learning Parameters
4.2. Validation of the Strategy
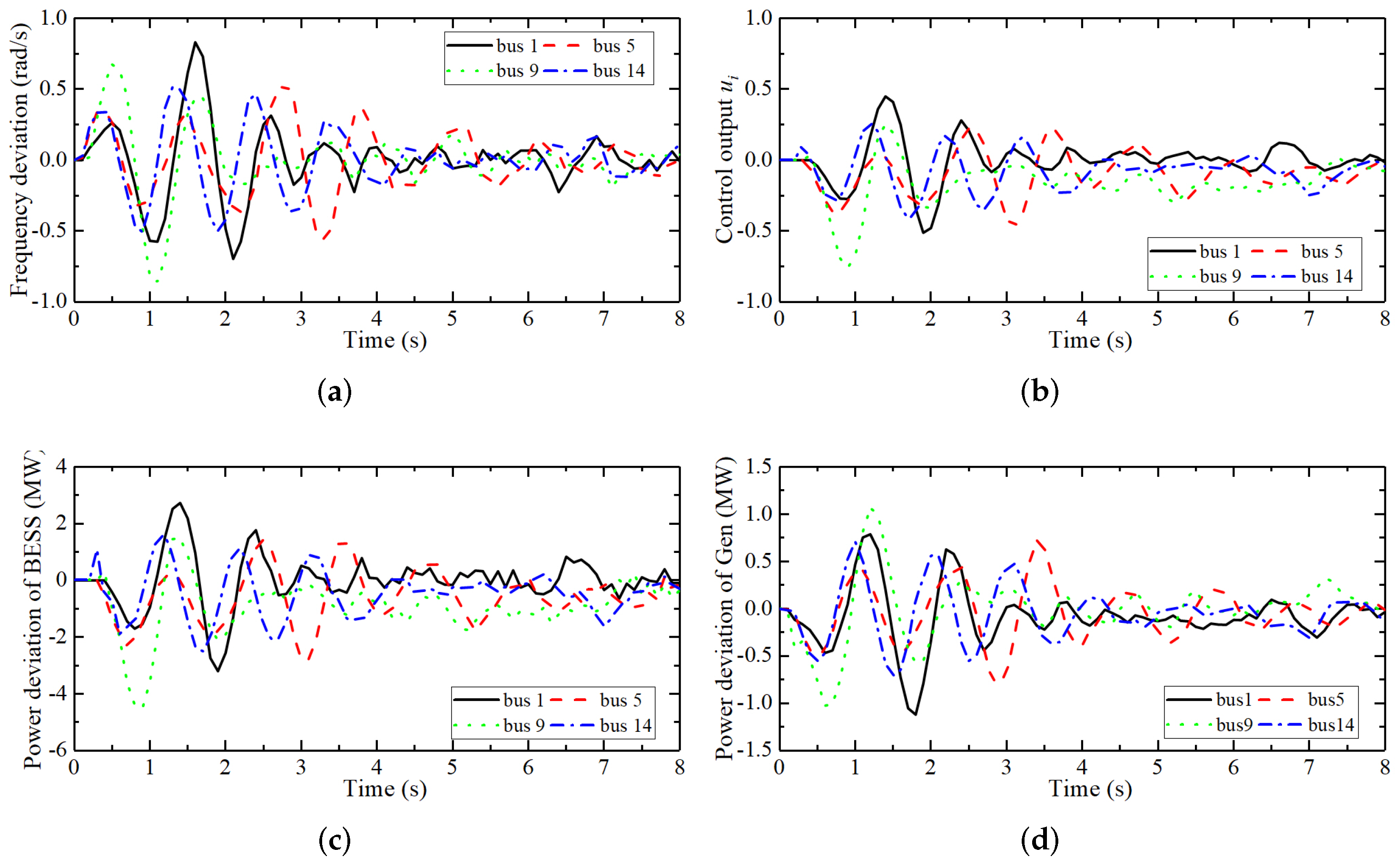
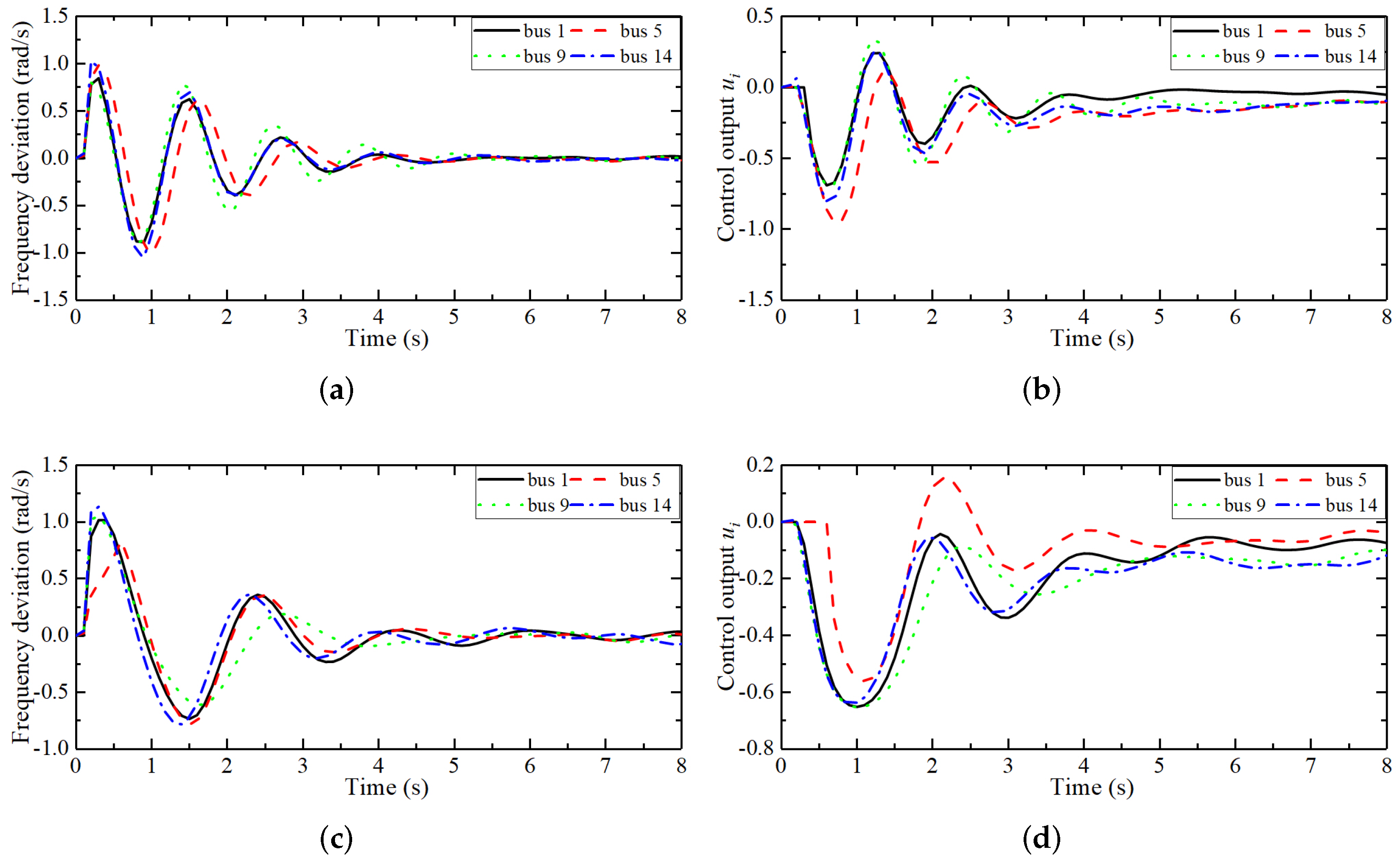
4.3. Case 1: Frequency Control of the IEEE 14-Bus Testing System under Different DoS Attack Intensities
4.4. Case 2: Comparative Analysis of Frequency Control Effects of Different Methods under DoS Attacks
4.5. Case 3: IEEE 118 Bus Testing System
4.6. Capacity Test of Battery Energy Storage System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Singh, A.K.; Singh, R.; Pal, B.C. Stability Analysis of Networked Control in Smart Grids. IEEE Trans. Smart Grid 2015, 6, 381–390. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Yang, Z.; Zhang, J.; Fei, Z.; Liu, W. Real-Time Compressive Sensing Based Control Strategy for a Multi-Area Power System. IEEE Trans. Smart Grid 2018, 9, 4293–4302. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, E.A. Exploiting the Operational Flexibility of Wind Integrated Hybrid AC/DC Power Systems. IEEE Trans. Power Syst. 2021, 36, 818–826. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary Frequency and Voltage Control of Islanded Microgrids via Distributed Averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Zhu, Z.; Sun, J.; Qi, G.; Chai, Y.; Chen, Y. Frequency Regulation of Power Systems with Self-Triggered Control under the Consideration of Communication Costs. Appl. Sci. 2017, 7, 688. [Google Scholar] [CrossRef]
- Chicco, G.; Riaz, S.; Mazza, A.; Mancarella, P. Flexibility from Distributed Multienergy Systems. Proc. IEEE 2020, 108, 1496–1517. [Google Scholar] [CrossRef]
- Sun, J.; Qi, G.; Mazur, N.; Zhu, Z. Structural Scheduling of Transient Control Under Energy Storage Systems by Sparse-Promoting Reinforcement Learning. IEEE Trans. Ind. Inf. 2022, 18, 744–756. [Google Scholar] [CrossRef]
- Gkatzikis, L.; Koutsopoulos, I.; Salonidis, T. The Role of Aggregators in Smart Grid Demand Response Markets. IEEE J. Sel. Areas Commun. 2013, 31, 1247–1257. [Google Scholar] [CrossRef]
- Meng, K.; Dong, Z.Y.; Xu, Z.; Zheng, Y.; Hill, D.J. Coordinated Dispatch of Virtual Energy Storage Systems in Smart Distribution Networks for Loading Management. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 776–786. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Huang, S.; Zhang, H.; Liu, Y.; Xue, Y. Hierarchical Control of Thermostatically Controlled Loads for Primary Frequency Support. IEEE Trans. Smart Grid 2018, 9, 2986–2998. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tang, Y.; Liao, K.; Syed, M.H.; Guillo-Sansano, E.; Burt, G.M. Aggregated Energy Storage for Power System Frequency Control: A Finite-Time Consensus Approach. IEEE Trans. Smart Grid 2019, 10, 3675–3686. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, Y.; Li, M. Dynamic Event-Based Model Predictive Load Frequency Control for Power Systems Under Cyber Attacks. IEEE Trans. Smart Grid 2021, 12, 715–725. [Google Scholar] [CrossRef]
- Liu, J.; Gu, Y.; Zha, L.; Liu, Y.; Cao, J. Event-Triggered Load Frequency Control for Multiarea Power Systems Under Hybrid Cyber Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1665–1678. [Google Scholar] [CrossRef]
- Wang, N.; Qian, W.; Xu, X. performance for load-frequency control systems with random delays. Syst. Sci. Control Eng. Open Access J. 2021, 9, 243–259. [Google Scholar] [CrossRef]
- Mohan, A.M.; Meskin, N.; Mehrjerdi, H. A Comprehensive Review of the Cyber-Attacks and Cyber-Security on Load Frequency Control of Power Systems. Energies 2020, 13, 3860. [Google Scholar] [CrossRef]
- Hu, S.; Yue, D.; Han, Q.L.; Xie, X.; Chen, X.; Dou, C. Observer-Based Event-Triggered Control for Networked Linear Systems Subject to Denial-of-Service Attacks. IEEE Trans. Cybern. 2020, 50, 1952–1964. [Google Scholar] [CrossRef]
- Dkhili, N.; Eynard, J.; Thil, S.; Grieu, S. A survey of modelling and smart management tools for power grids with prolific distributed generation. Sustain. Energy Grids Netw. 2020, 21, 100284. [Google Scholar] [CrossRef]
- Massoud Amin, S. Smart Grid: Overview, Issues and Opportunities. Advances and Challenges in Sensing, Modeling, Simulation, Optimization and Control. Eur. J. Control 2011, 17, 547–567. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef] [Green Version]
- Ning, C.; You, F. Data-Driven Adaptive Robust Unit Commitment Under Wind Power Uncertainty: A Bayesian Nonparametric Approach. IEEE Trans. Power Syst. 2019, 34, 2409–2418. [Google Scholar] [CrossRef]
- Wang, Q.; Li, F.; Tang, Y.; Xu, Y. Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 2019, 34, 4557–4568. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. Data-Driven Load Frequency Control for Stochastic Power Systems: A Deep Reinforcement Learning Method With Continuous Action Search. IEEE Trans. Power Syst. 2019, 34, 1653–1656. [Google Scholar] [CrossRef]
- Imthias Ahamed, T.; Nagendra Rao, P.; Sastry, P. A reinforcement learning approach to automatic generation control. Electr. Power Syst. Res. 2020, 63, 9–26. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Chen, X.; Fu, H.; Wu, M. Model-Free Distributed Consensus Control Based on Actor-Critic Framework for Discrete-Time Nonlinear Multiagent Systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4123–4134. [Google Scholar] [CrossRef]
- Daneshfar, F.; Bevrani, H. Load-frequency control: A GA-based multi-agent reinforcement learning. IET Gener. Transm. Distrib. 2010, 4, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.; Xu, Y. A Multi-Agent Deep Reinforcement Learning Method for Cooperative Load Frequency Control of a Multi-Area Power System. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.L.; Ge, X.; Wang, J. Secure State Estimation and Control of Cyber-Physical Systems: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 176–190. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, L.; Liu, N. Coordinated attacks on electric power systems in a cyber-physical environment. Electr. Power Syst. Res. 2017, 149, 156–168. [Google Scholar] [CrossRef]
- Chlela, M.; Mascarella, D.; Joos, G.; Kassouf, M. Fallback Control for Isochronous Energy Storage Systems in Autonomous Microgrids Under Denial-of-Service Cyber-Attacks. IEEE Trans. Smart Grid 2018, 9, 4702–4711. [Google Scholar] [CrossRef]
- Hahn, A.; Ashok, A.; Sridhar, S.; Govindarasu, M. Cyber-Physical Security Testbeds: Architecture, Application, and Evaluation for Smart Grid. IEEE Trans. Smart Grid 2013, 4, 847–855. [Google Scholar] [CrossRef]
- Chen, B.; Ho, D.W.C.; Zhang, W.A.; Yu, L. Distributed Dimensionality Reduction Fusion Estimation for Cyber-Physical Systems Under DoS Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 455–468. [Google Scholar] [CrossRef]
- Chen, W.; Ding, D.; Dong, H.; Wei, G. Distributed Resilient Filtering for Power Systems Subject to Denial-of-Service Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1688–1697. [Google Scholar] [CrossRef]
- Yang, F.S.; Wang, J.; Pan, Q.; Kang, P.P. Resilient Event-triggered Control of Grid Cyber-physical Systems Against Cyber Attack. Zidonghua Xuebao/Acta Autom. Sin. 2019, 45, 110–119. [Google Scholar]
- Feng, M.; Xu, H. Deep reinforecement learning based optimal defense for cyber-physical system in presence of unknown cyber-attack. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Liu, R.; Hao, F.; Yu, H. Optimal SINR-Based DoS Attack Scheduling for Remote State Estimation via Adaptive Dynamic Programming Approach. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7622–7632. [Google Scholar] [CrossRef]
- Niu, H.; Bhowmick, C.; Jagannathan, S. Attack Detection and Approximation in Nonlinear Networked Control Systems Using Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Kiumarsi, B.; Lewis, F.L. Actor-Critic-Based Optimal Tracking for Partially Unknown Nonlinear Discrete-Time Systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 140–151. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Zhu, Z.; Li, H.; Chai, Y.; Qi, G.; Wang, H.; Hu, Y.H. An integrated critic-actor neural network for reinforcement learning with application of DERs control in grid frequency regulation. Int. J. Electr. Power Energy Syst. 2019, 111, 286–299. [Google Scholar] [CrossRef]
- Xu, H.; Jagannathan, S. Neural Network-Based Finite Horizon Stochastic Optimal Control Design for Nonlinear Networked Control Systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 472–485. [Google Scholar] [CrossRef]
- Amos, B.; Xu, L.; Kolter, J.Z. Input Convex Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 46–155. [Google Scholar]
- Bach, F. Breaking the Curse of Dimensionality with Convex Neural Networks. Nihon Naika Gakkai Zasshi J. Jpn. Soc. Intern. Med. 2014, 100, 2574–2579. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2019, 518, 529–533. [Google Scholar] [CrossRef]
- Sun, J.; Li, P.; Wang, C. Optimise transient control against DoS attacks on ESS by input convex neural networks in a game. Sustain. Energy Grids Netw. 2021, 28, 100535. [Google Scholar] [CrossRef]
- Zhao-xia, X.; Mingke, Z.; Yu, H.; Guerrero, J.M.; Vasquez, J.C. Coordinated Primary and Secondary Frequency Support Between Microgrid and Weak Grid. IEEE Trans. Sustain. Energy 2019, 10, 1718–1730. [Google Scholar] [CrossRef] [Green Version]
- Sezer, N.; Muammer, E.A. Design and analysis of an integrated concentrated solar and wind energy system with storage. Int. J. Energy Res. 2019, 43, 3263–3283. [Google Scholar] [CrossRef]
- Reilly, J.T. From microgrids to aggregators of distributed energy resources. The microgrid controller and distributed energy management systems. Electr. J. 2019, 32, 30–34. [Google Scholar] [CrossRef]
- Zhu, Z.; Geng, G.; Jiang, Q. Power System Dynamic Model Reduction Based on Extended Krylov Subspace Method. IEEE Trans. Power Syst. 2016, 31, 4483–4494. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, K. Solving Power System Differential Algebraic Equations Using Differential Transformation. IEEE Trans. Power Syst. 2020, 35, 2289–2299. [Google Scholar] [CrossRef]
- Yuan, Y.; Yuan, H.; Guo, L.; Yang, H.; Sun, S. Resilient Control of Networked Control System Under DoS Attacks: A Unified Game Approach. IEEE Trans. Ind. Inf. 2016, 12, 1786–1794. [Google Scholar] [CrossRef]
- Qin, J.; Li, M.; Shi, L.; Yu, X. Optimal Denial-of-Service Attack Scheduling With Energy Constraint Over Packet-Dropping Networks. IEEE Trans. Autom. Control 2018, 63, 1648–1663. [Google Scholar] [CrossRef]
- Santhanam, V.; Davis, L.S. A Generic Improvement to Deep Residual Networks Based on Gradient Flow. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2490–2499. [Google Scholar] [CrossRef]
- Zheng, L.; Yang, L.; Liang, Y. A Modified Spectral Gradient Projection Method for Solving Non-Linear Monotone Equations with Convex Constraints and Its Application. IEEE Access 2020, 8, 92677–92686. [Google Scholar] [CrossRef]
- Amini, S.; Ghaemmaghami, S. Towards Improving Robustness of Deep Neural Networks to Adversarial Perturbations. IEEE Trans. Multimed. 2020, 22, 1889–1903. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Li, Y.; Cao, Y.; She, J.; Wu, M. A Two-Layer Active Disturbance Rejection Controller Design for Load Frequency Control of Interconnected Power System. IEEE Trans. Power Syst. 2016, 31, 3320–3321. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Guerrero, J.M.; Xu, Z.; Green, T.C. Multiple-Time-Scales Hierarchical Frequency Stability Control Strategy of Medium-Voltage Isolated Microgrid. IEEE Trans. Power Electron. 2016, 31, 5974–5991. [Google Scholar] [CrossRef]













| Parameter Name | Description | Value |
|---|---|---|
| inertia constant | 0.05 | |
| damping constant | 0.002 | |
| gas turbine constant | 0.2 | |
| governor constant | 5 | |
| regulation constant | 0.5 | |
| synchronizing constant | 0.5 | |
| Inertial time constant of BESS | 0.5 | |
| frequency bias gain | 1 | |
| tie-line bias control gain | 0.1 |
| Attack Time | Total Attack Time | |
|---|---|---|
| 0.05 | 1–1.3 s. | 0.3 s |
| 0.1 | 1–1.3 s, 7.2 s–7.4 s. | 0.5 s |
| 0.2 | 1–1.3 s, 2 s–2.2 s, | 1 s |
| 3 s–3.5 s. | ||
| 0.4 | 1–1.3 s, 1.6 s–2 s, | 1.1 s |
| 3 s–3.2 s, 7.2 s–7.4 s. | ||
| 0.6 | 1.3 s–1.5 s, 2 s–2.5 s, | 1.9 s |
| 3 s–4 s, 6.3 s–6.5 s, | ||
| 7.2 s–7.4 s. |
| Parameter Name | Description | Value |
|---|---|---|
| learning rate of critic networks | 0.001 | |
| learning rate of actor networks | 0.009 | |
| N | number of input neurons | 14 |
| sum of attack threshold | 6 | |
| number of network layers | 16 | |
| the maximum absolute value of | 0.4 | |
| the maximum value of | 0.015 | |
| Lipschitz constant | 1 | |
| the weight of | 0.7 | |
| the weight of | 0.3 | |
| damping factor | 0.8 | |
| S | long-term evaluation time windows | 10 |
| the maximum constraint of | 2.0 | |
| the maximum constraint of | 25 MW |
| Parameter Name | Description | Value |
|---|---|---|
| learning rate of critic networks | 0.0025 | |
| learning rate of actor networks | 0.0011 | |
| N | number of input neurons | 57 |
| sum of attack threshold | 22 | |
| number of network layers | 59 | |
| the maximum absolute value of | 0.4 | |
| the maximum value of | 0.015 | |
| Lipschitz constant | 1 | |
| the weight of | 0.7 | |
| the weight of | 0.3 | |
| damping factor | 0.8 | |
| S | long-term evaluation time windows | 10 |
| the maximum constraint of | 2.0 | |
| the maximum constraint of | 25 MW |
| Parameter Name | Description | Value |
|---|---|---|
| learning rate of critic networks | 0.0016 | |
| learning rate of actor networks | 0.0023 | |
| N | number of input neurons | 118 |
| sum of attack threshold | 5.2 | |
| number of network layers | 120 | |
| the maximum absolute value of | 0.4 | |
| the maximum value of | 0.015 | |
| Lipschitz constant | 1 | |
| the weight of | 0.7 | |
| the weight of | 0.3 | |
| damping factor | 0.8 | |
| S | long-term evaluation time windows | 10 |
| the maximum constraint of | 2.0 | |
| the maximum constraint of | 25 MW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, F.; Qi, G.; Zhu, Z.; Sun, J.; Hu, G.; Haner, M. Convex Neural Networks Based Reinforcement Learning for Load Frequency Control under Denial of Service Attacks. Algorithms 2022, 15, 34. https://doi.org/10.3390/a15020034
Zeng F, Qi G, Zhu Z, Sun J, Hu G, Haner M. Convex Neural Networks Based Reinforcement Learning for Load Frequency Control under Denial of Service Attacks. Algorithms. 2022; 15(2):34. https://doi.org/10.3390/a15020034
Chicago/Turabian StyleZeng, Fancheng, Guanqiu Qi, Zhiqin Zhu, Jian Sun, Gang Hu, and Matthew Haner. 2022. "Convex Neural Networks Based Reinforcement Learning for Load Frequency Control under Denial of Service Attacks" Algorithms 15, no. 2: 34. https://doi.org/10.3390/a15020034
APA StyleZeng, F., Qi, G., Zhu, Z., Sun, J., Hu, G., & Haner, M. (2022). Convex Neural Networks Based Reinforcement Learning for Load Frequency Control under Denial of Service Attacks. Algorithms, 15(2), 34. https://doi.org/10.3390/a15020034










