Abstract
A composition is a powerful tool for obtaining new numerical methods for solving differential equations. Composition ODE solvers are usually based on single-step basic methods applied with a certain set of step coefficients. However, multistep composition schemes are much less-known and investigated in the literature due to their complex nature. In this paper, we propose several novel schemes for solving ordinary differential equations based on the composition of adjoint multistep methods. Numerical stability, energy preservation, and performance of proposed schemes are investigated theoretically and experimentally using a set of differential problems. The applicability and efficiency of the proposed composition multistep methods are discussed.
1. Introduction
Ordinary differential equations (ODEs) are one of the most common mathematical models describing physical, biological, social, technical, and many other processes. A common tool for solving ODEs in digital computers is numerical integration methods. One of the most known examples of such algorithms is the well-known Runge-Kutta methods and linear multistep methods, which combine high computational efficiency and sufficient numerical stability. However, for some specific problems other properties of numerical integration methods are of great importance. Over the last 40 years, a new branch of numerical integration called geometric integration [1] has arisen. Geometric integration methods allow preserving the geometric properties of the original dynamical system like symplecticity, energy, or other first integrals. They also may possess symmetry, which helps to perform the simulation of physical systems more accurately and introduce the time-reversibility of the solution. Being initially applied mainly to Hamiltonian problems, geometric integration also showed its efficiency in solving non-Hamiltonian problems due to a smaller error constant in comparison with methods of the same order. Several symplectic modifications of Runge-Kutta [2,3,4] and linear multistep [5,6,7] methods were discovered recently. Two powerful approaches which are common in geometric integration are composition and splitting methods [8]. Yoshida [9] and Suzuki [10] developed a theoretical basis for a family of composition schemes that can be applied to an arbitrary symmetric basic method to increase its order of accuracy. Blanes et al. proposed several efficient composition and splitting schemes [11,12,13]. Recently some generalizations of the symplectic Euler method [14] over a broader class of ODEs were proposed, allowing the application of composition methods to some non-Hamiltonian problems.
Besides, in the case of the multistep methods, which are known for their low computational costs, the composition allows the breaking of the first and second Dahlquist barriers and obtaining strongly stable or even A-stable schemes. Examples of this sort are cyclic methods [15,16,17,18] in which multiple multistep methods are applied periodically. The multistep block methods [19] are another perfect example of such integrators.
It is known, that the composition of adjoint methods allows obtaining geometrical methods with higher accuracy order. The goal of the current study is to develop new numerical schemes by applying the composition technique to the linear multistep method and its adjoint, and the investigation of new integration methods in terms of key geometric properties and computational efficiency.
The rest of the paper is organized as follows. In Section 2, a brief introduction to the numerical integration of ODE, multistep methods and composition principle are given. In Section 3, a theory for the construction of numerical schemes by the composition of the multistep method and its adjoint is reported. In Section 4, two new composition schemes are proposed and some of their properties are described. Section 5 reports the results of a practical investigation of the properties of designed numerical composition schemes. Finally, Section 6 concludes the paper and discusses the obtained results.
2. Preliminary
2.1. Basic Definitions
Let us consider the initial value problem (IVP) as a system of first-order ordinary differential equations (ODE) with corresponding initial value:
where is a right-hand-side function, x is a independent variable often assumed as time, is an initial conditions (IC) and . The function satisfying (1) is called a solution of IVP.
By applying the numerical integration method one can obtain values of function in times with some accuracy. The simplest example of a numerical integration method is an explicit Euler method with a constant integration step:
where
and is a numerical approximation of .
The linear k-step numerical integration method can be described by the following formula:
where , and k is a number of steps. A linear multistep method is explicit if and implicit otherwise. In the latter case, there is dependence from which leads to the application of the Newton method, or another technique for resolving implicitness. There is another representation of multistep methods which is more common for software implementation:
where and . There is plenty of linear multistep methods, but the most common examples are explicit Adams-Bashforth methods and implicit Adams-Moulton methods which are often used within the common predictor-corrector scheme as well as implicit backward differentiation formulas. General forms and equations for coefficients of these methods are thoroughly given in [20]. Thus, we will further consider only some particular linear multistep methods.
To analyze linear multistep methods one can use the following generating polynomials:
According to the classical Dahlquist theory of stability, the linear multistep method is called stable or zero-stable if roots of lie on the unit circle and there should be no multiple roots of modulus one. Linear multistep method is called weakly stable if it is stable and have more than one root of modulus one, which leads to an empty stability region. Known examples of weakly stable methods are explicit midpoint rule and Milne-Simpson method. Linear multistep method is called strongly stable if it is stable and have a single root of modulus one. Examples of strongly stable method are Adams-Bashforth and Adams-Moulton method.
2.2. Composition of the Methods
Let us consider a single step of numerical integration method with step-size h as discrete map :
where . Then a composition of the methods is a composition of corresponding discrete maps and :
The adjoint of a discrete map is a discrete map for which the next equation is true:
where is an identity map. The numerical integration method is called symmetric if the corresponding discrete map is self-adjoint. Adjoint for simple numerical integration methods can be often found by the next rule of thumb:
- take step
- shift indices such that the term became the oldest
- express the term
The second step can be skipped and performed only for uniform representation. For example, the following is a process of finding the adjoint to Euler’s method (2):
The result is a well-known implicit Euler method:
The direct and reverse compositions of (2) and (5) with stepsize give a rise to midpoint rule:
and trapezoidal rule:
Both methods are symmetric, and the latter case is an example of a symmetric multistep method obtained by the composition of two adjoint methods one of which is the linear 0-step method and another is the linear 1-step method. Therefore, the question arises: can one obtain new efficient numerical schemes by the composition of linear multistep methods with ? Moreover, can the composition of adjoints be a stable basis for this operation?
3. Composition of Multistep Methods
Like single-step methods, multistep methods can be treated as discrete maps. Taking Let us consider a linear k-step method as the following discrete map:
The cyclic methods first described by Donelson et al. [15] were in fact the most general form of composition schemes consisting of m linear multistep methods:
which are applied cyclically.
Adjoint for Multistep Method
Adjoint for multistep method (3) can be derived in a similar way as for single step:
where .
Further, we will highlight one of the key problems in the successful construction of composition schemes. Let us consider the following implicit linear multistep method with non-zero coefficients :
The process of finding the adjoint equivalent to (7) is described in Figure 1. The resulting adjoint is the explicit linear multistep method:
Another case of the linear multistep method is:
Steps of obtaining the next adjoint method are depicted in Figure 2:
One can see that adjoint (10) is not a linear multistep method because it possesses single implicit dependence from , similarly to conventional implicit methods, and one additional implicitness from . Some researchers call such dependencies “super-future points” [21]. Methods of this type were firstly obtained by Cash to increase the stability region of backward differentiation formulas and are usually applied as predictor-corrector schemes with several predictors [22]. Of course, adjoints can be easily applied to ODE in a form and in that case can be indistinguishable from their counterpart due to their symmetric nature.
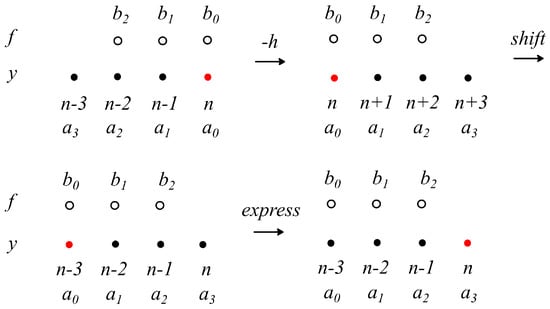
Figure 1.
Example of adjoint finding for (8).
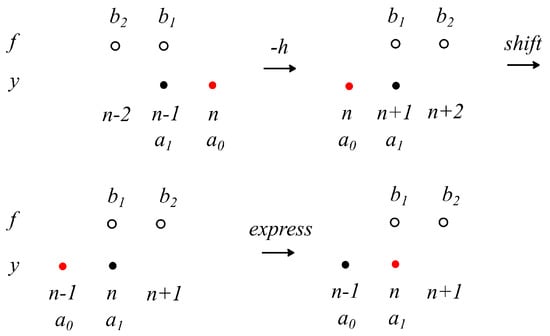
Figure 2.
Example of adjoint finding for (9).
The following theorems generalize our results in applying of adjoint methods.
Theorem 1.
The adjoint for the linear multistep method is a linear multistep method if and only if .
Proof.
Take the oldest non-zero . If there is non-zero with an index greater than l, then the adjoint has the term with and does not meet to (3). □
The adjoints which are not linear multistep methods have the same order of consistency [20]. Therefore for convergence of adjoint only stability is required. This leads us to the following theorems.
Theorem 2.
The adjoint of the stable linear multistep methods is stable if and only if all roots of are modulus one.
Proof.
If the generating polynomial of the linear multistep method have a root with modulus then the generating polynomial of its adjoint have a root with modulus . For stability of linear multistep method and its adjoint both and should be not larger than one. □
Theorem 3.
If then both linear multistep method and its adjoint can only be weakly stable in the best case. Otherwise at least one is unstable.
Proof.
If there is a non-zero coefficient with then generating polynomial have at least two roots. If some roots are out or in the unit circle then a linear multistep method or its adjoint is unstable. Otherwise, they both are weakly stable. □
The existence of stable composition schemes consisting of a stable multistep method and its unstable adjoint or unstable multistep method and its unstable adjoint is not proven yet. In addition, the presence of a strong stable composition scheme based on a weakly stable multistep method is an open question as well. We will follow the assumption that both linear multistep method adjoints must be strongly stable. Such limitation heavily restricts the list of suitable methods, because backward differentiation formulas produce unstable adjoints, and Adams-Bashforth and Adams-Moulton methods of higher orders have adjoints with multiple implicit dependencies. It should be noted, that the linear multistep methods which are already symmetric also are not appropriate for this task. Nevertheless, in the following section, we will show the possibility of constructing composition schemes based on the two-step Adams-Bashforth and Adams-Moulton methods.
4. The Proposed Composition Schemes
As was stated in Theorem 1 adjoints that are not linear multistep methods exist. Such adjoints are not directly applicable to solving IVP (1). In this research, we construct a composition method from the two-step Adams-Bashforth and Adams-Moulton methods and their adjoints. Despite the latter algorithm being “multi-implicit”, we will further show that such composition schemes can be obtained in practice. Moreover, one of these schemes demonstrates an interesting connection with the known multistep method.
4.1. Composition Scheme Based on Two-Step Adams-Bashforth Method
Let us consider the two-step Adams-Bashforth numerical integration method:
The adjoint for (11) is:
One can see that (12) have two implicit dependencies, which cannot be resolved by common techniques. However, we can construct the following composition scheme to obtain a single-step integration method:
Let us consider a linear ODE problem:
For linear ODE problem 13 can be easily reduced to single-step formulation:
First, (16) is substituted to (15):
Next, (17) is substituted to (16)
From (18) we can perform stability analysis the same way as for classical single-step methods. The stability function of the method (13) is:
In Figure 3 the stability domain corresponding to (19) is presented. One can see that the stability function is a rational function similar to the implicit midpoint rule and the obtained integration method is A-stable.
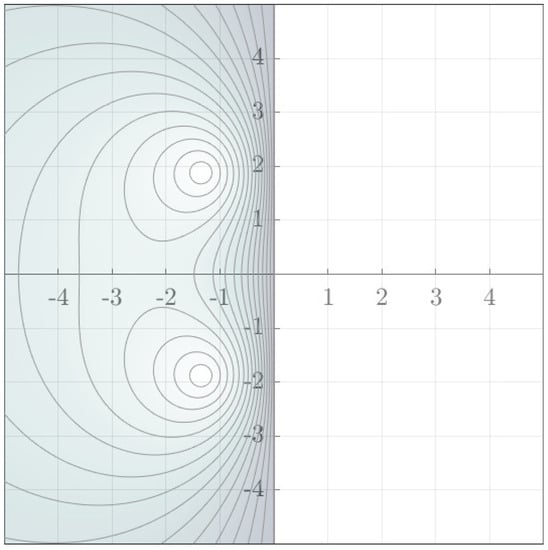
Figure 3.
Stability region of the composition scheme based on two-step Adams-Bashforth method.
4.2. Composition Scheme Based on Two-Step Adams-Moulton Method
The two-step Adams-Moulton method of the third order of accuracy can be described by the formula:
and its adjoint:
Similarly, as we did for the Adams-Bashforth method, one can obtain the following composition method:
For a linear problem it reduces to:
Stability function of the method (20) is:
In Figure 4 the stability domain corresponding to the stability function (21) is presented.
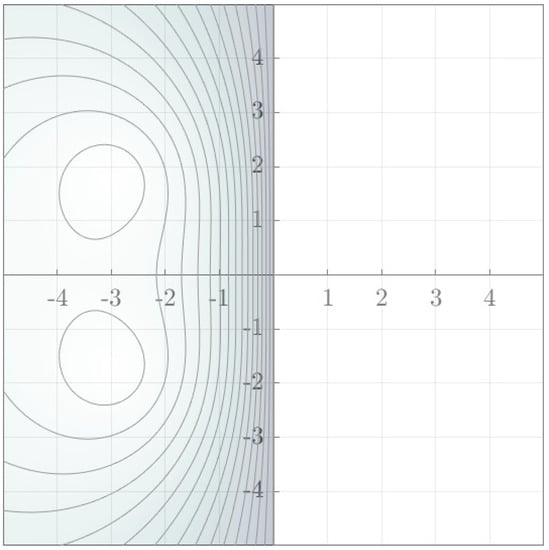
Figure 4.
Stability region of the composition scheme based on two-step Adams-Moulton method.
4.3. Error Growth and Order
The fastest-growing error term for a composition scheme based on the two-step Adams-Bashforth method is , and the fastest-growing error term for a composition scheme based on Adams-Moulton scheme is . The obtained schemes are of order two and four, correspondingly.
4.4. Linkage with Miln-Simpson Method
Next obvious step following from analyzing composition schemes based on two-step Adams-Bashforth and two-step Adams-Moulton methods consists of summarizing the corresponding equations. For (13) result is:
and for (20) result is:
It should be noted, that Equation (22) is a strict record of Simpson rule or, in sense of integration of IVP, is a Miln-Simpson method of fourth order taken with a half-step [20]:
Therefore, (20) can be assumed as the decomposition of the Miln-Simpson method. The closest example is a midpoint rule:
which has second order of accuracy but is weakly stable. The composition scheme obtained by decomposition midpoint rule into implicit and explicit Euler methods is as follows:
It possesses the second order of accuracy, is strongly stable, and is A-stable.
4.5. Implementation of Proposed Methods
Composition scheme (13) can be implemented using Newton iterations:
where are identity and zero-value matrices, and J is Jacobian of f.
The same stands for composition scheme (20):
One can see that for some extra memory costs, the overall computational costs of both schemes derive from two evaluation of right-hand-side function and two evaluation of Jacobian per Newton iteration.
5. Experimental Investigation
5.1. Computational Efficiency
The computational efficiency of the proposed methods was practically investigated using well-known nonlinear Rössler system, which exhibits chaotic behavior:
where parameters values are .
To investigate the efficiency of the proposed methods we used an efficiency plot tool, the maximal error is plotted along the x-axis and elapsed time is plotted along the y-axis. Since the absolute integration error of the method can’t be measured due to the absence of an analytical solution, relative integration error with respect to the eight-order Runge-Kutta method is found.
Proposed composition schemes were compared with methods-predecessors and the 3-step Adams-Moulton method of fourth order. With exception of the two-step Adams-Bashforth method, the Newton method was applied to resolve implicitness in all cases. In Figure 5 one can see that the composition scheme based on the two-step Adams-Bashforth method possesses very low efficiency in comparison to its predecessor despite better accuracy due to the Newton method’s extra computational costs. Nevertheless, the composition scheme based on the two-step Adams-Moulton method appears to be more efficient than the two-step Adams-Moulton method and has the same computational efficiency as a popular 3-step Adams-Moulton method, which makes it suitable for practical application.
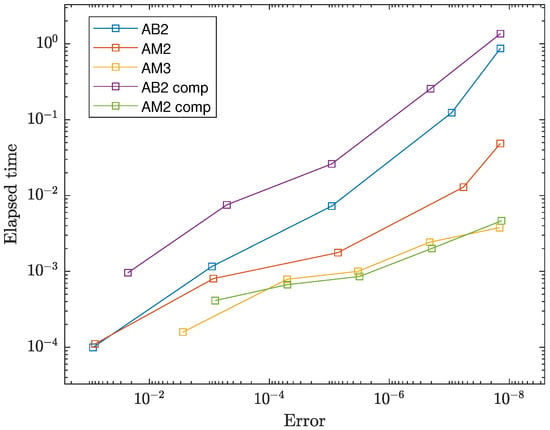
Figure 5.
Efficiency plot for two-step Adams-Bashforth method (AB2), two-step Adams-Moulton method (AM2), composition schemes based on them (AB2 comp and AM2 comp) and three-step Adams-Moulton method (AM3).
5.2. Energy Preservation
A numerical test for energy preservation was carried out for the following Hamiltonian system with non-separable Hamiltonian:
which leads to the following nonlinear ODE system:
In Figure 6 and Figure 7 the variations of Hamiltonian for test system solved by two-step Adams-Bashforth method, two-step Adams-Moulton and corresponding composition schemes are presented. Initial conditions were , integration step was set as . It can be clearly observed, that the composition version of the methods allows preserving Hamiltonian of the test system in both cases, which indicates the presence of desired geometrical properties of designed methods.
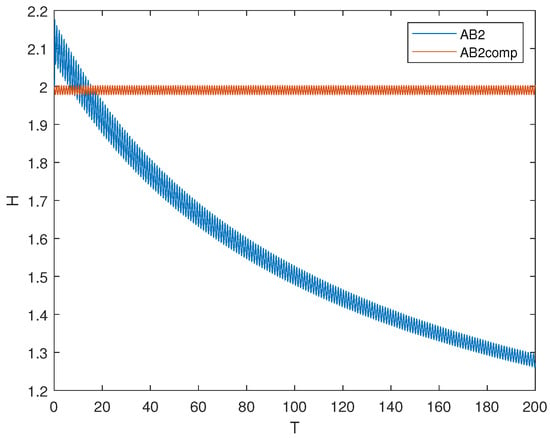
Figure 6.
Hamiltonian of system (24) solved by two-step Adams-Bashforth method (AB2) and composition scheme based on it (AB2comp).
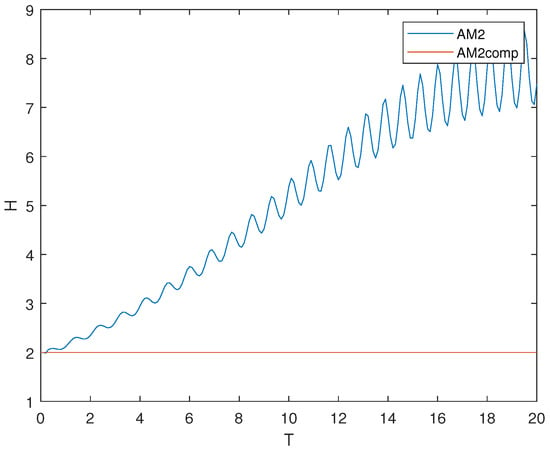
Figure 7.
Hamiltonian of system (24) solved by two-step Adams-Moulton method (AM2) and composition scheme based on it (AM2comp).
6. Conclusions
In the current study, we used the composition principle to construct several symplectic multistep numerical integration methods. As the main result, two numerical integration composition schemes of second and fourth order of accuracy based on two-step Adams-Bashforth and two-step Adams-Moulton methods were derived. The developed numerical schemes were investigated both theoretically and experimentally on a set of test initial value problems. The computational experiments show that the composition multistep methods allow preserving the geometrical properties of the continuous prototype and are A-stable. It should be noted, that developing composition schemes based on the two-step Adams-Bashforth method is more of theoretical interest due to high computational costs. Nevertheless, the second designed scheme, based on a two-step Adams-Moulton methods composition, is more promising for practical applications being as efficient as a popular 3-step Adams-Moulton method while possessing a much larger numerical stability. Our further studies will be devoted to the problem of the existence of a non-common linear multistep method that can lead to an efficient and stable composition scheme. The further evaluation of the computational efficiency of high-order multistep composition schemes is of great interest as well.
Author Contributions
Conceptualization, D.P. and D.B.; methodology, D.P.; software, D.P. and A.P.; validation, D.B. and E.N.; formal analysis, O.D. and A.P.; investigation, D.P. and O.D.; resources, E.N.; data curation, A.P.; writing—original draft preparation, D.P. and O.D.; writing—review and editing, D.B. and E.N.; visualization, O.D.; supervision, D.B., E.N. and A.P.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by Russian Science Foundation, project 22-19-00573.
Acknowledgments
The Authors are thankful to Artur Karimov for his useful suggestions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sanz-Serna, J.M. Symplectic integrators for Hamiltonian problems: An overview. Acta Numer. 1992, 1, 243–286. [Google Scholar] [CrossRef]
- Sun, G. A simple way constructing symplectic Runge-Kutta methods. J. Comput. Math. 2000, 18, 61–68. [Google Scholar]
- Monovasilis, T.; Kalogiratou, Z.; Simos, T. Exponentially fitted symplectic Runge–Kutta–Nyström methods. Appl. Math. Inf. Sci. 2013, 7, 81–85. [Google Scholar] [CrossRef]
- Quinlan, G.D.; Tremaine, S. Symmetric multistep methods for the numerical integration of planetary orbits. Astron. J. 1990, 100, 1694–1700. [Google Scholar] [CrossRef]
- Evans, N.W.; Tremaine, S. Linear multistep methods for integrating reversible differential equations. Astron. J. 1999, 118, 1888. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C. Symmetric multistep methods for charged-particle dynamics. SMAI J. Comput. Math. 2017, 3, 205–218. [Google Scholar] [CrossRef]
- McLachlan, R.I.; Quispel, G.R.W. Splitting methods. Acta Numer. 2002, 11, 341–434. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Suzuki, M. Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations. Phys. Lett. A 1990, 146, 319–323. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F. Raising the order of geometric numerical integrators by composition and extrapolation. Numer. Algorithms 2005, 38, 305–326. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F. Splitting methods for non-autonomous separable dynamical systems. J. Phys. A Math. Gen. 2006, 39, 5405. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F.; Murua, A. Splitting and composition methods in the numerical integration of differential equations. arXiv 2008, arXiv:0812.0377. [Google Scholar]
- Butusov, D.N.; Ostrovskii, V.Y.; Karimov, A.I.; Andreev, V.S. Semi-explicit composition methods in memcapacitor circuit simulation. Int. J. Embed. Real-Time Commun. Syst. (IJERTCS) 2019, 10, 37–52. [Google Scholar] [CrossRef]
- Donelson, J., III; Hansen, E. Cyclic composite multistep predictor-corrector methods. SIAM J. Numer. Anal. 1971, 8, 137–157. [Google Scholar] [CrossRef]
- Bickart, T.A.; Picel, Z. High order stiffly stable composite multistep methods for numerical integration of stiff differential equations. BIT Numer. Math. 1973, 13, 272–286. [Google Scholar] [CrossRef]
- Tendler, J.M.; Bickart, T.A.; Picel, Z. A stiffly stable integration process using cyclic composite methods. ACM Trans. Math. Softw. (TOMS) 1978, 4, 339–368. [Google Scholar] [CrossRef]
- Cash, J. On a class of cyclic methods for the numerical integration of stiff systems of ODEs. BIT Numer. Math. 1977, 17, 270–280. [Google Scholar] [CrossRef]
- Biala, T.; Jator, S.; Adeniyi, R.; Ndukum, P. Block Hybrid Simpson’s Method with Two Offgrid Points for Stiff System. Int. J. Nonlinear Sci. 2015, 20, 3–10. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Hojjati, G.; Ardabili, M.R.; Hosseini, S. New second derivative multistep methods for stiff systems. Appl. Math. Model. 2006, 30, 466–476. [Google Scholar] [CrossRef]
- Cash, J. On the integration of stiff systems of ODEs using extended backward differentiation formulae. Numer. Math. 1980, 34, 235–246. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).