On a Hypothetical Model with Second Kind Chebyshev’s Polynomial–Correction: Type of Limit Cycles, Simulations, and Possible Applications

Abstract

In this article, we explore a new extended Lienard-type planar system with “corrections” of the second kind Chebyshev’s polynomial $U_n$. The number and type of limit cycles are also studied. The discussion on the $y\left(t\right)$—component of the solution of the Lienard system is connected to searching for the solution of the synthesis of filters and electrical circuits. Numerical experiments, depicting our outcomes using CAS MATHEMATICA, are presented.

1. Introduction

Hilbert [1] proposed 23 mathematical problems, of which the second part of the 16th one is to find the maximal number of limit cycles and their relative locations for polynomial vector fields. A large part of the scientific articles is concerned with the Lienard system $x^{\prime }=y,y^{\prime }=g\left(x\right)+ϵf\left(x\right)$, where $ϵ$ is a small parameter and $f\left(x\right)$ and $g\left(x\right)$ are polynomials of degree m and n.

The Melnikov function [2] for the Lienard system [3]

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y-ϵ\left(a_{1}x+a_2{x}^2+\cdots +a_{2n+1}{x}^{2n+1}\right)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& -x\hfill \end{array}\right.$$

(1)

is defined as

$$M(\alpha ,\mu )=-2\pi {\alpha }^2\left(\frac{a_1}{2}+\frac{3}{8}{a}_3{\alpha }^2+\cdots +\left(\begin{array}{c}2n+2\\ n+1\end{array}\right)\frac{a_{2n+1}}{2^{2n+2}}{\alpha }^{2n}\right).$$

(2)

The Melnikov polynomial is defined as

$$P(r^2,n)=-\frac{1}{2\pi r^2}M(r,\mu ).$$

(3)

Perko and collaborators [4,5] ensure the needful information about radii and the number of limit cycles. More precisely, the system (1) for small enough $ϵ\ne 0$ has at most nlimit cycles asymptotic to circles of radii$r_j,j=1,2,\dots ,n$ as $ϵ\to 0$ if and only if then-th degree polynomial in $r^2$,

$$P(r^2,n)=\frac{a_1}{2}+\frac{3}{8}{a}_3{r}^2+\cdots +\left(\begin{array}{c}2n+2\\ n+1\end{array}\right)\frac{a_{2n+1}}{2^{2n+2}}{r}^{2n}$$

(4)

has n positive roots $r^2=r_j^2,j=1,2,\dots ,n$.

Denote by $U_n$ the second kind Chebyshev’s polynomial. The polynomials participate in the solution to some of the practical tasks [6]. In this article, we explore a new extended Lienard-type planar system with the polynomial $U_n$. The number and type of limit cycles is also investigated. The discussion (in Section 2.3) is on $y\left(t\right)$—the component of the solution of Lienard system that is connected to the solution of some practical issues such as the synthesis of “adaptive” filters and electrical circuits. Numerical examples, confirming the results we obtained through CAS MATHEMATICA, are received.

2. Main Results–Simulations

2.1. Extended Lienard-Type Planar System

The next model will be investigated:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y-ϵU_n\left(x\right)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& -x\hfill \end{array}\right.$$

(5)

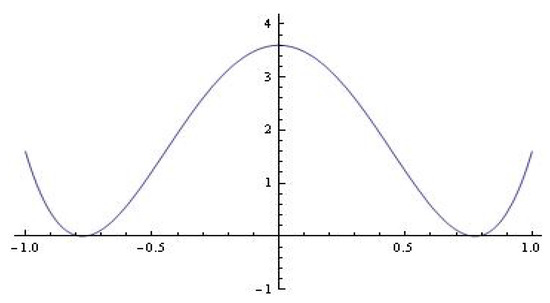
where $ϵ>0$ and $U_n\left(x\right)$ for $n=3,5,7,9,\dots$ is the Chebyshev’s polynomial of the second kind. For example, for $n=5,7,9,13$ we have (see Figure 1)

$$\begin{array}{ccc}{U}_5\left(x\right)\hfill & =& 32x^5-32x^3+6x\hfill \\ U_7\left(x\right)\hfill & =& 128x^7-192x^5+80x^3-8x\hfill \\ U_9\left(x\right)\hfill & =& 512x^9-1024x^7+672x^5-160x^3+10x\hfill \end{array}$$

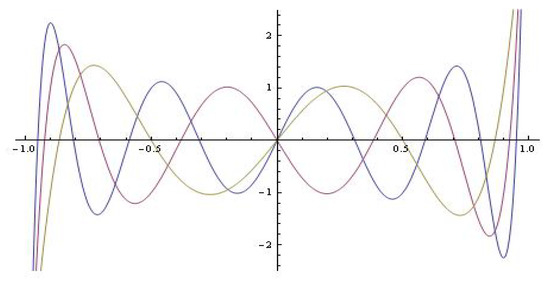
Figure 1. $U_n\left(x\right)$ for $n=5$, $n=7$ and $n=9$.

Under stated circumstances it can be indicated that the Lienard’s-type system (1) has a limit cycle. The proof of existence of the limit cycle is based on the check of the circumstances in Lienard’s theorem [3], and we will skip it. The process for user-initiated coefficient $ϵ=0.006$ and $n=5$, with the model (5) for $x_0=0.6$, $y_0=0.4$ is shown in Figure 2. For $ϵ=0.001$ and $n=5$ and $x_0=0.7$, $y_0=0.3$ see Figure 3. The simulation for $ϵ=0.006$ and $n=7$, with the model (5) for $x_0=0.6$, $y_0=0.4$, is shown in Figure 4. For $ϵ=0.003$ and $n=7$; $x_0=0.5$, $y_0=0.5$, see Figure 5.

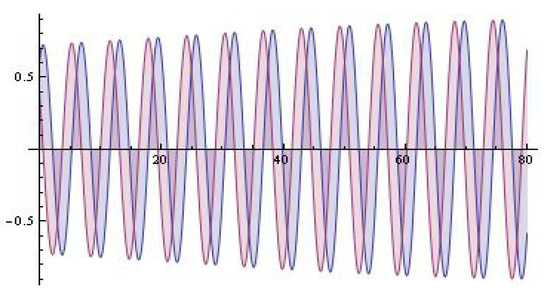
Figure 2. The system solutions ($ϵ=0.006$; $n=5$).

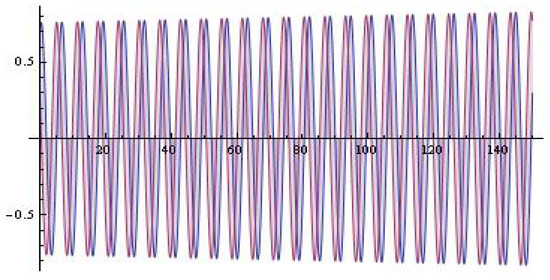
Figure 3. The system solutions ($ϵ=0.001$; $n=5$).

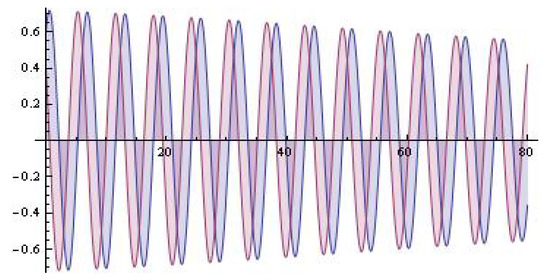
Figure 4. The system solutions ($ϵ=0.006$; $n=7$).

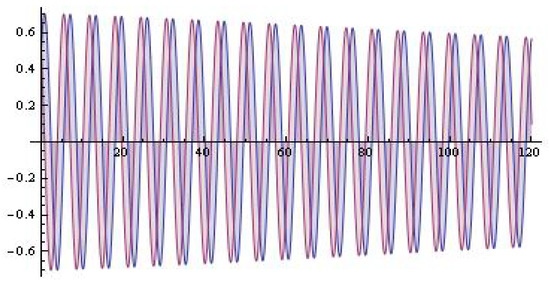
Figure 5. The system solutions ($ϵ=0.003$; $n=7$).

2.2. The New Model in the Light of Melnikov’s Considerations

The case $n=5$. Let us explore the model

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y-ϵ(32x^5-32x^3+\mu x)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& -x\hfill \end{array}\right.$$

(6)

where $\mu >0$, $ϵ>0$. The following is correct:

Proposition 1. 

The Lienard-type system (6) for $n=5$, and for all small enough $ϵ\ne 0$ for $\mu =7.2$ has a limit cycle with multiplicity–2.

Proof. 

For the Melnikov polynomial in $r^2$ (see Figure 6), we have:

$$P(r^2,2)=\frac{\mu }{2}-12r^2+10r^4.$$

(7)

Figure 6. $P(r^2,2)$ for $n=5$ and $\mu =7.2$.

□

The roots are

$$\frac{\sqrt{6-\sqrt{36-5\mu }}}{\sqrt{10}};\sqrt{\frac{3}{5}+\frac{1}{10}\sqrt{36-5\mu }}.$$

The radii $r_i;i=1,2$ for some values of $\mu$ are tabulated in Table 1.

Table 1. The radii $r_i;i=1,2$ for some values of $\mu$.

$\mathit{\mu }$	${\mathit{r}}_1$	${\mathit{r}}_2$
5	0.518013	0.965227
6	0.595862	0.919211
7	0.707107	0.83666
7.2	0.774597	0.774597

Evidently, for example $\mu =7.2$ we obtain a limit cycle with multiplicity–2 (see Table 1). This ends the proof of the proposition. The solution of the system (6) for $ϵ=0.001$, $n=5$, $\mu =7.2$ with $x_0=0.7$, $y_0=0.3$ is visualized on Figure 7.

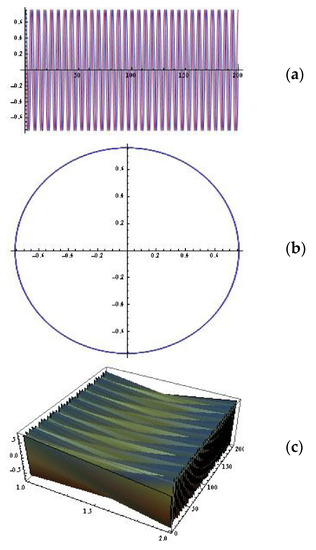
Figure 7. (a) The solutions of the system (6) ($ϵ=0.001$; $n=5$; $\mu =7.2$); (b) the portrait $(x,y)$; (c) 3D plot.

The case $n=7$. Let us explore the model

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y-ϵ(128x^7-192x^5+80x^3-\mu x)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& -x\hfill \end{array}\right.$$

(8)

where $\mu >0$, $ϵ>0$. The following is correct:

Proposition 2. 

The Lienard-type system (8) for $n=7$, and for all small enough $ϵ\ne 0$ for $\mu =7.00805257\dots$ has a simple limit cycle and limit cycle with multiplicity–2.

Proof. 

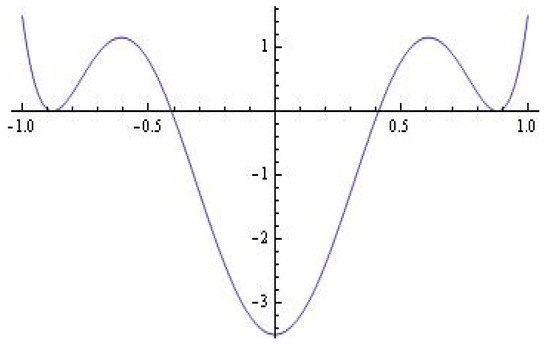
The Melnikov polynomial in $r^2$ (see Figure 8) gives:

$$P(r^2,3)=-\frac{\mu }{2}+30r^2-60r^4+35r^6.$$

(9)

Figure 8. $P(r^2,3)$ for $n=7$ and $\mu =7.00805257$. The roots are: $0.409106$—simple and $0.879462$—with multiplicity 2.

□

The radii $r_i;i=1,2,3$ for some values of $\mu$ are tabulated in Table 2.

Table 2. The values of $\mu$ that proceed in 3 positive zeros of the Melnikov polynomial (Theorem 2); for $\mu =7.00487909525$: a simple limit cycle and limit cycle with multiplicity–2.

$\mathit{\mu }$	${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$
7.5	0.433391	0.808263	0.934435
7.3	0.423255	0.826862	0.922735
7.1	0.413469	0.851545	0.904544
7.008805257	0.409106	0.878462	0.879469

For an proper choice of the parameter $\mu$ (for example $\mu =7.00805257$), we have a limit cycle and limit cycle with multiplicity 2 (see Table 2). The solution of the system (8) for $ϵ=0.001$, $n=7$, $\mu =7.00805257$ with $x_0=0.6$, $y_0=0.4$ is visualized in Figure 9.

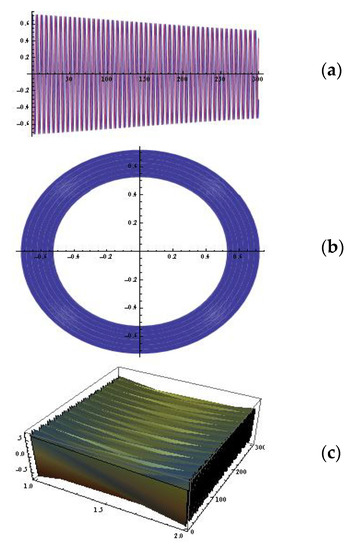
Figure 9. (a) The solutions of the system (8) ($ϵ=0.001$; $n=7$; $\mu =7.00805257$); (b) the portrait $(x,y)$; (c) 3D plot.

The case $n=9$. Consider the model

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y-ϵ(512x^9-1024x^7+672x^5-160x^3+{\mu }_{1}x)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& -x\hfill \end{array}\right.$$

(10)

where ${\mu }_1>0$, $ϵ>0$. The following is correct:

Proposition 3. 

The Lienard-type system (10) for $n=9$, and for all small enough $ϵ\ne 0$ for ${\mu }_1=9.0482691\dots$, has 2 simple limit cycles and limit cycle with multiplicity–2.

The proof of existence of limit cycles is based on the ideas given in Propositions 1 and 2, and we will omit it here.

We note that for the Melnikov polynomial in $r^2$ (see Figure 10) we obtain:

$$P(r^2,4)=\frac{\mu }{2}-60r^2+210r^4-280r^6+126r^8.$$

(11)

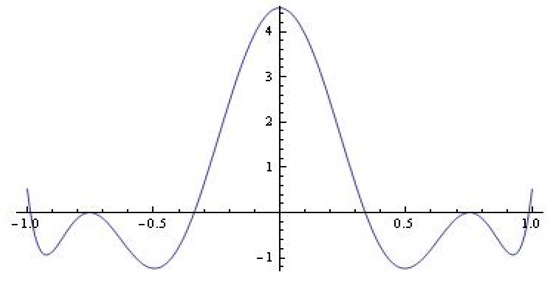
Figure 10. $P(r^2,4)$ for $n=9$ and ${\mu }_1=9.0482691\dots$. The simple roots are $0.338954$, $0.987437$ and root $0.75243$—with multiplicity 2.

The solution of the system (10) for $ϵ=0.001$, $n=9$, ${\mu }_1=9.0482691$ with $x_0=0.5$, $y_0=0.5$ is visualized in Figure 11.

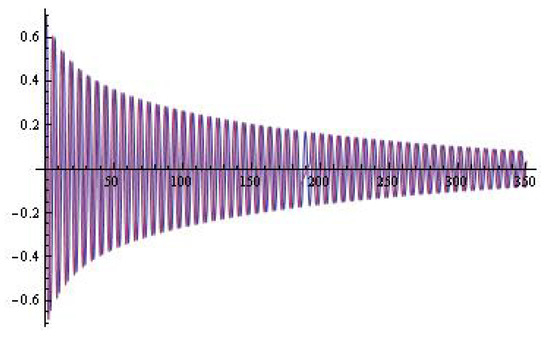
Figure 11. The solutions of the system (10) ($ϵ=0.001$; $n=9$; ${\mu }_1=9.0482691$).

2.3. Related Problems and Possible Applications

Let us explore the following Lienard system:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& g\left(x\right)+ϵf\left(x\right)y\hfill \end{array}\right.$$

(12)

where $0\le ϵ\le 1$.

Numerical examples

Example 1. 

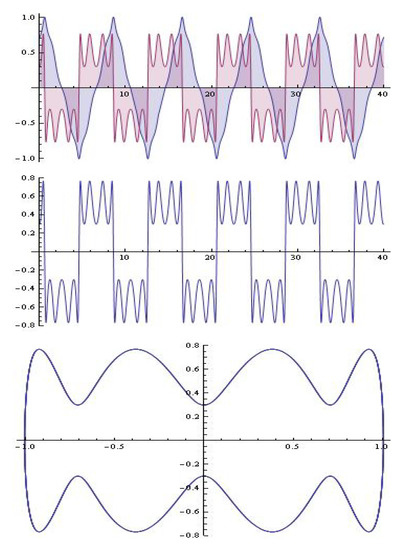
The solution of the system (12) for $ϵ=0.001$, $g\left(x\right)=U_7\left(x\right)$, $f\left(x\right)=x-x^3+x^5-\frac{1}{7}{x}^7$ (see oscillator model considered in [7]) is visualized in Figure 12.

Figure 12. The solutions of the system (12) (Example 1).

Example 2. 

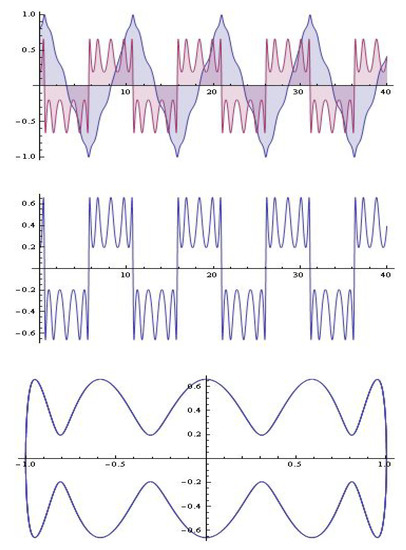
The solution of the system (12) for $ϵ=0.001$, $g\left(x\right)=U_9\left(x\right)$, $f\left(x\right)=x-x^3+x^5-\frac{1}{7}{x}^7$ is visualized on Figure 13.

Figure 13. The solutions of the system (12) (Example 2).

We will explicitly note that the $y\left(t\right)$-components of the differential systems discussed above can be used successfully in modeling and approximating functions and point sets in the field of signal theory, filters, and other characteristics.

Applications

We will consider 2 typical examples.

(A) Example 1 shows that the component $y\left(t\right)$ of the solution of system (12) (with $x_0=1.1$, $y_0=0.1$) can be used for the modeling and synthesis of electric circuits of the type shown in Figure 14 at an appropriately selected interval.

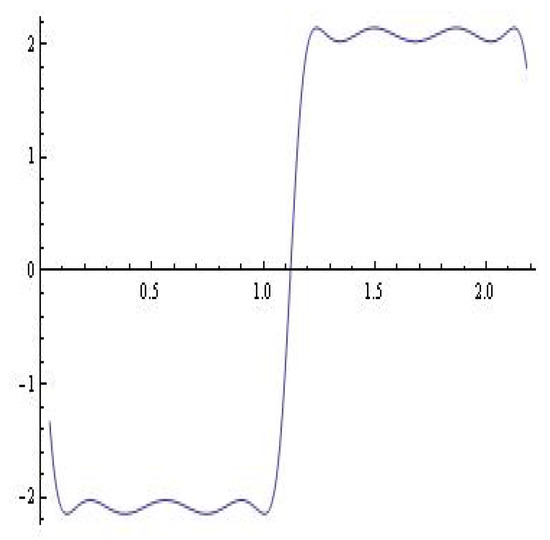
Figure 14. Application for modeling and analysis of electrical circuits and signal processes.

(B) A number of studies are known on the design of in some sense optimal filters, such as the exponential optimal filters of Tadmore and Tanner [8,9] (for the intrinsic properties of these filters concerning Hausdorff metrics, see [10]).

It is easy to take into account that the alteration of the variable t with $t=acos\theta$ in the y-component of the solution of the system (12) leads to a diagram characteristic of a filter.

By varying the parameter a, a variety of interesting models are obtained (see Figure 15).

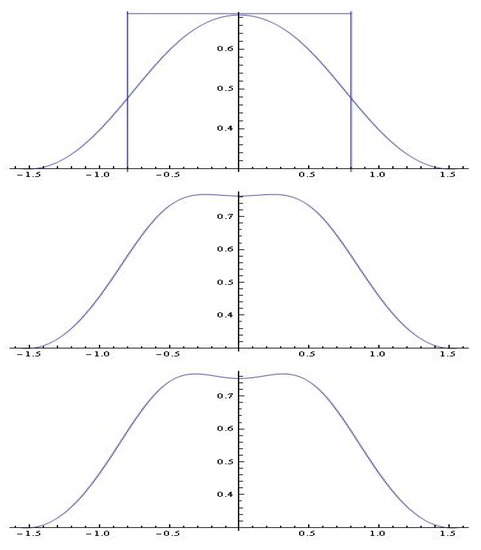
Figure 15. The model $y\left(\theta \right)$ for $x_0=0.7$, $y_0=0.3$ in $(-\frac{\pi }{2},\frac{\pi }{2})$ for (a) $a=0.4$; (b) $a=0.49$; and (c) $a=0.5$.

3. Concluding Remarks

The reader can pin down the adequate approximation results for some n. For example, for fixed $U_{13}\left(x\right)$ the Lienard system through Melnikov’s approach is defined as

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y-ϵ\left(\mu x-448x^3+4032x^5-15360x^7+28160x^9-24576x^{11}+8192x^{13}\right)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& -x\hfill \end{array}\right.$$

The Melnikov polynomial is of the form (see Figure 16):

$$P(r^2,6)=\frac{\mu }{2}-168r^2+1260r^4-4200r^6+6930r^8-5544r^{10}+1716r^{12}$$

and the following statement is valid:

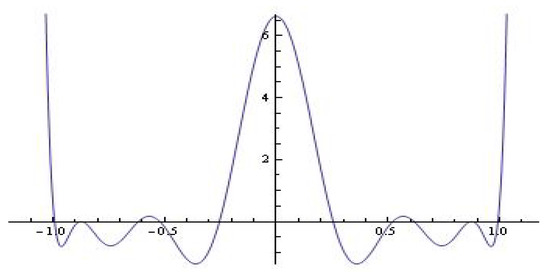
Figure 16. The Melnikov polynomial $P(r^2,6)$.

Proposition 4. 

The Lienard-type system for $\mu =13.25125164$ has four simple limit cycles: $0.254682$, $0.521069$, $0.61736$, and $0.992178$ and limit cycle $0.874307$ with multiplicity–2.

The topics in this paper are connected to solving some practical issues such as the synthesis of antennas and electrical circuits. For example, a simple circuit for testing the memristor model and corresponding current–voltage characteristics is given in [11], see Figure 17. For other results, see [11,12,13,14,15,16].

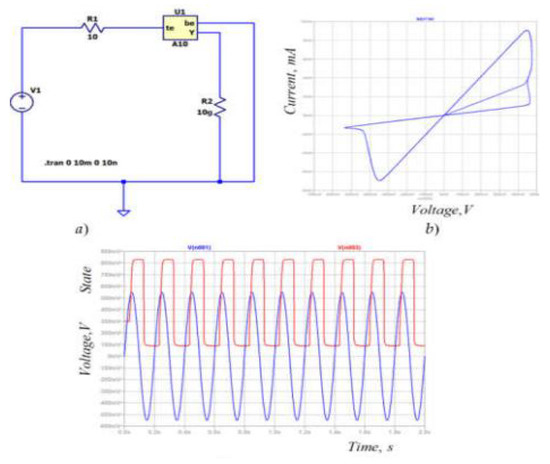
Figure 17. A simple circuit for testing the memristor model and corresponding current–voltage characteristics [11].

Intriguing radiation diagrams can be received with a proper selection of the functions $f\left(x\right)$ and $g\left(x\right)$ arising in the Lienard system. Interesting outcomes are obtained in [7,17,18,19,20].

Remark 1. 

The study of dynamical systems includes bifurcation theory with branch catastrophe theory [21]. Arnold [22] discussed the catastrophes of the ADE classification, because of their relation with the Lie groups. Consider the following model in the light of Zeeman’s approach [23]:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& c\left(F\right(x)-y)\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& \frac{1}{c}x\hfill \end{array}\right.$$

(13)

with $c>0$ and

$$F\left(x\right)=px-448x^3+4032x^5-15360x^7+28160x^9-24576x^{11}+8192x^{13}.$$

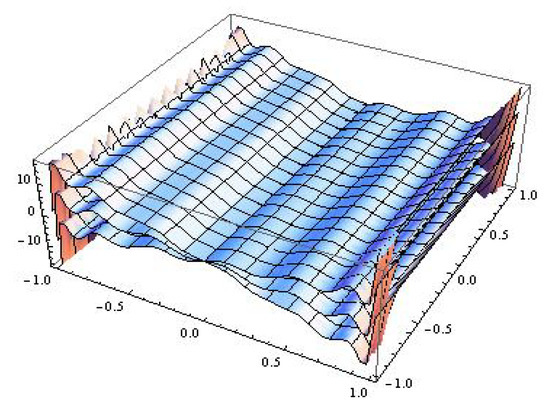
For the model the catastrophe surface $(x,y,p)=F\left(x\right)-y$ is depicted in Figure 18.

Figure 18. The catastrophe surface $(x,y,p)=F\left(x\right)-y$; $p=0.1,10,20$.

3.1. Numerical Issues Connected to the Investigation of the Roots of the Melnikov Polynomial

Let $D\left(\lambda \right)$ be the polynomial with real and multiple roots ${\lambda }_1,\dots ,{\lambda }_m$ with the multiplicities $s_i,i=1,\dots ,m$, where ${\displaystyle \sum _{i=1}^m}{s}_i=n$, i.e.,

$$D\left(\lambda \right)=\prod _{j=1}^m{(\lambda -{\lambda }_j)}^{s_j}.$$

The next iteration process can be used [24]:

$${\lambda }_i^{k+1}={\lambda }_i^k-\frac{s_i}{H\left({\lambda }_i^k\right)-{\displaystyle \sum _{l\ne i}^m}\frac{s_l}{{\lambda }_i^k-{\lambda }_l^k-{\Delta }_l^{R,k}}},i=1,\dots ,m;k=0,1,2,\dots .$$

where

$$\begin{array}{ccc}H\left({\lambda }_i^k\right)\hfill & =& \frac{D^{{}^{\prime }}\left({\lambda }_i^k\right)}{D\left({\lambda }_i^k\right)}\hfill \\ {\Delta }_t^{R,k}\hfill & =& -s_i{\left(H\left({\lambda }_i^k\right)-{\displaystyle \sum _{q\ne t}^m}\frac{s_q}{{\lambda }_t^k-{\lambda }_q^k-{\Delta }_q^{R-1,k}}\right)}^{-1},t=1,2,\dots ,m\hfill \\ {\Delta }_t^{0,k}\hfill & =& 0,t=1,2,\dots ,m;k=0,1,2,\dots .\hfill \end{array}$$

The next theorem is fulfilled

Theorem 1 

([24]). Let $0<q<1$, $d={\displaystyle \underset{i\ne j}{min}}|{\lambda }_i-{\lambda }_j|$ and $c>0$ be numbers such that

$$\begin{array}{c}d>c(2+3qn/s),\hfill \\ c^2(n-s^{{}^{\prime }}){\left((d-c)(d-2c-sqn/s)\left(1-\frac{(n/s+1)(n/s^{{}^{\prime }}-1)c^2{q}^2}{(d-c)(d-2c-sqn/s)}\right)\right)}^{-1}<1,\hfill \\ s={\displaystyle \underset{1\le j\le m}{max}}{s}_j;s^{{}^{\prime }}={\displaystyle \underset{1\le j\le m}{min}}{s}_j.\hfill \end{array}$$

If the initial approximations $\left\{{\lambda }_i^0\right\},i=1,2,\dots ,m$ of the zeros $\left\{{\lambda }_i\right\};i=1,2,\dots ,m$ satisfy the inequalities $|{\lambda }_i^0-{\lambda }_i|\le cq,i=1,2,\dots ,m$, then the inequalities

$$|{\lambda }_i^k-{\lambda }_i|\le c{q}^{{(2R+3)}^k},i=1,2,\dots ,m;k=0,1,2,\dots$$

hold true.

For other results see [25,26,27,28,29].

3.2. The Level Curves

For more details of the existing important results on the generalized polynomial Lienard differential systems and the limit-cycle bifurcations of some generalized polynomial Lienard systems, see [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47].

Consider the class of Lienard polynomial systems of the type

$$\left\{\begin{array}{ccc}{\displaystyle \frac{dx}{dt}}\hfill & =& y\hfill \\ {\displaystyle \frac{dy}{dt}}\hfill & =& U_7\left(x\right)+ϵ(ax+b{x}^2+c{x}^4+d{x}^6)y\hfill \end{array}\right.$$

(14)

where $0\le ϵ<1$; (a) $U_7\left(x\right)=128x^7-192x^5+80x^3-8x$ is the Chebyshev polynomial of the second kind and $a,b,c,d$ are bounded parameters. Without going into details, we will note some interesting level curves. For $ϵ=0$, system (14) is a Hamiltonian system with Hamiltonian

$$H(x,y)=\frac{y^2}{2}-16x^8+32x^6-20x^4+4x^2.$$

The level curves $L_{h_i}=\{H(x,y)=h_i\}$ are depicted in Figure 19. The case b) $U_9\left(x\right)=512x^9-1024x^7+672x^5-160x^3+10x$. The Hamiltonian of system (14) ($ϵ=0$) is

$$H(x,y)=\frac{y^2}{2}-5x^2+40x^4-112x^6+128x^8-\frac{256x^{10}}{5}.$$

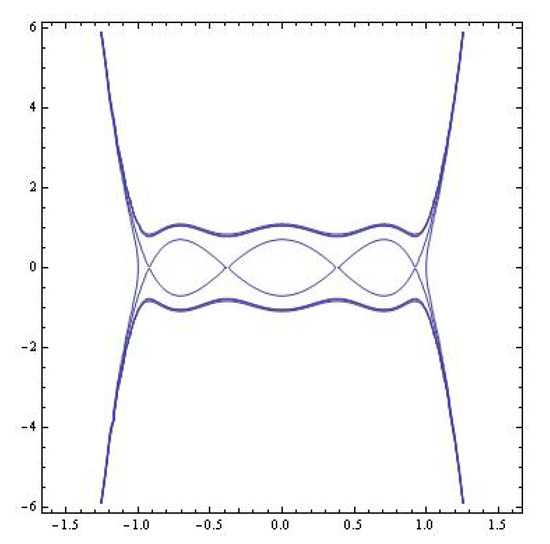
Figure 19. The level curves (the case a).

The level curves $L_{h_i}=\{H(x,y)=h_i\}$ are depicted in Figure 20.

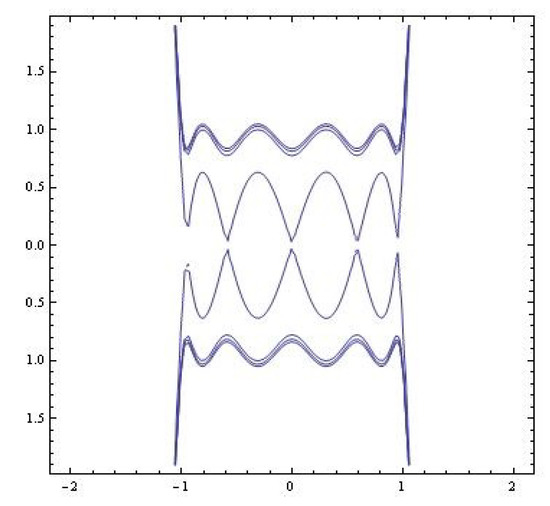
Figure 20. Level curves (the case b).

The outcomes received in this paper are based on the following algorithms:

(i) For the arbitrary order n fixed by the user—the production of the extended oscillator;

(ii) For the existence of the boundary cycle—the automatic checking of the rules in Lienard’s theorem;

(iii) For determining their number and type—receiving sure evaluations for the roots of the polynomial and the high-order Melnikov polynomials $P(r^2,n)$;

(iv) For embedding polynomial-type rectification factors—generating dynamic models.

Software for study and depiction have also been produced, written in CAS Mathematica. These modules are improving similar ones realized in computer algebraic systems designed for scientific calculations. The offered modules are only part of the more general project for investigating nonlinear models.