A Mask-Based Adversarial Defense Scheme
Abstract
1. Introduction
- We introduce a new adversarial defense method, MAD. Our method applies randomized masking at both training phase and test phase, which makes it resistant to adversarial attacks.
- Our method seems easily applicable to many existing DNNs. Compared with other adversarial defense methods, we do not need special treatment for the structures of DNNs, redesign of loss functions, or any (autoencoder-based) input filtering.
- The experiment on a variety of models (LeNet, VGG, and ResNet) has shown the effectiveness of our method with a significant improvement in defense (up to precision gain) when facing various adversarial samples, compared to models not trained with MAD.
2. Related Work
2.1. Adversarial Attack
2.2. Adversarial Defense
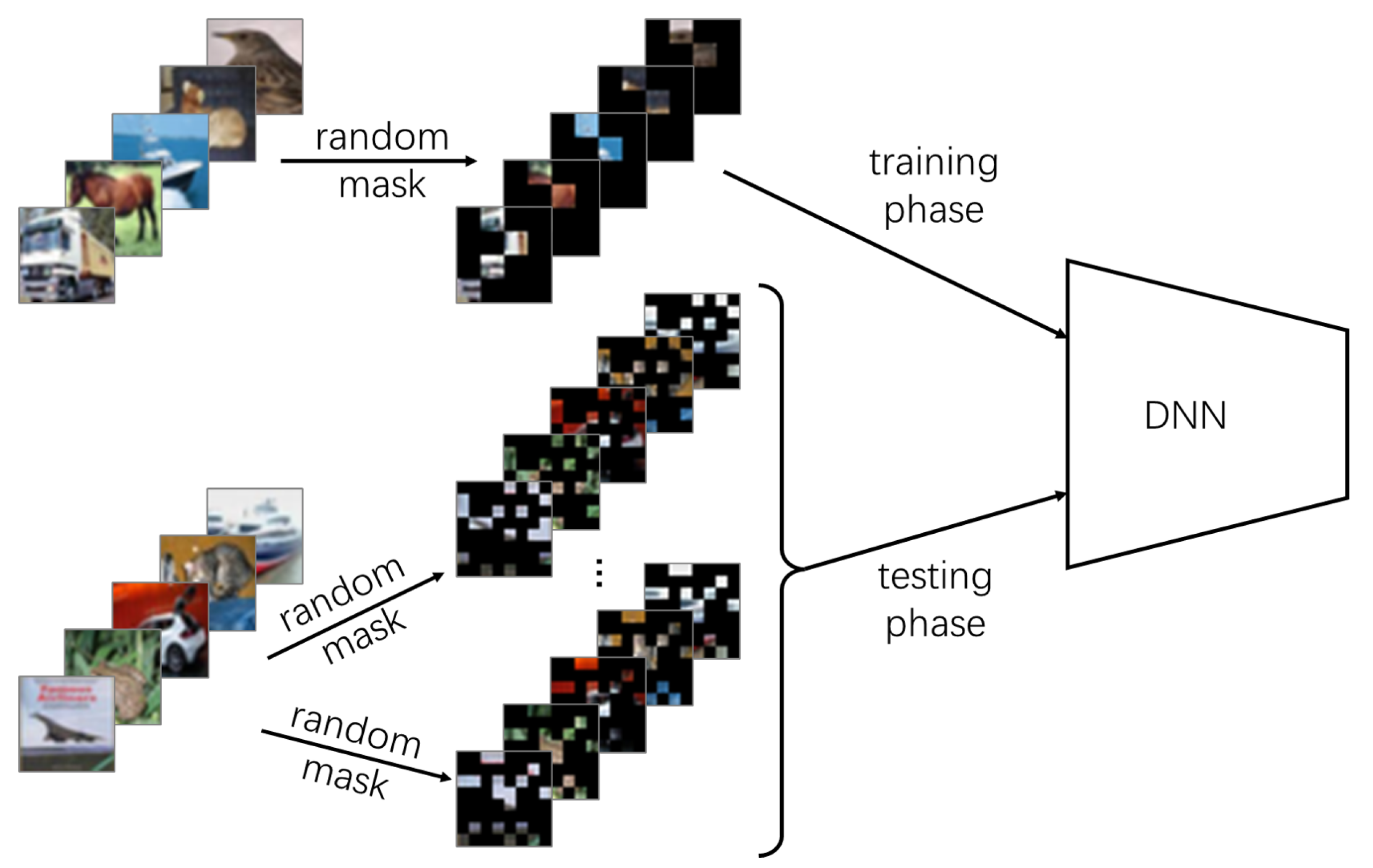
3. Materials and Methods
3.1. Training a Classifier for Masked Images
3.2. Mitigating Adversarial Attacks
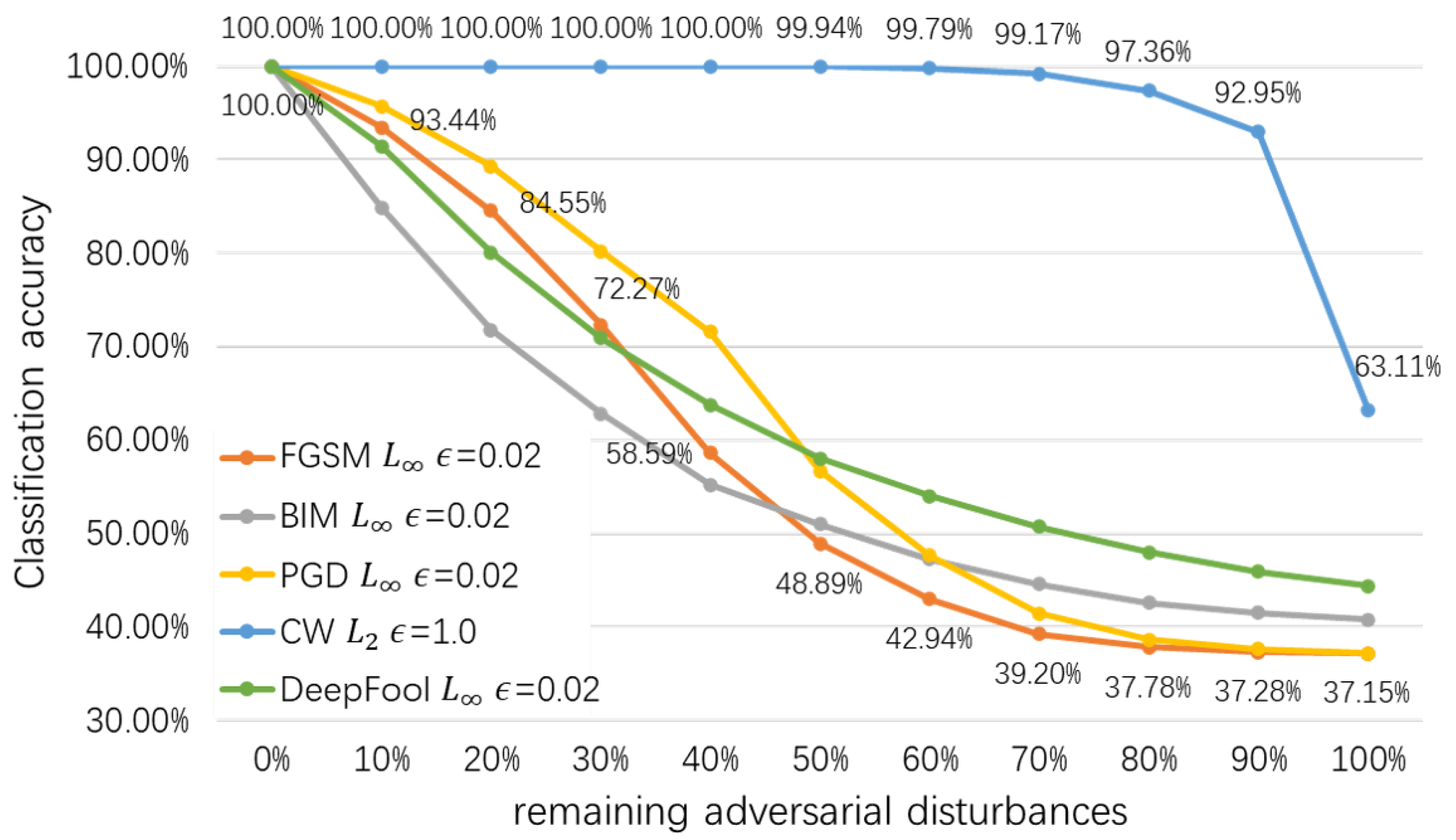
3.3. Basic Settings for Adversarial Attack and Defense
4. Results
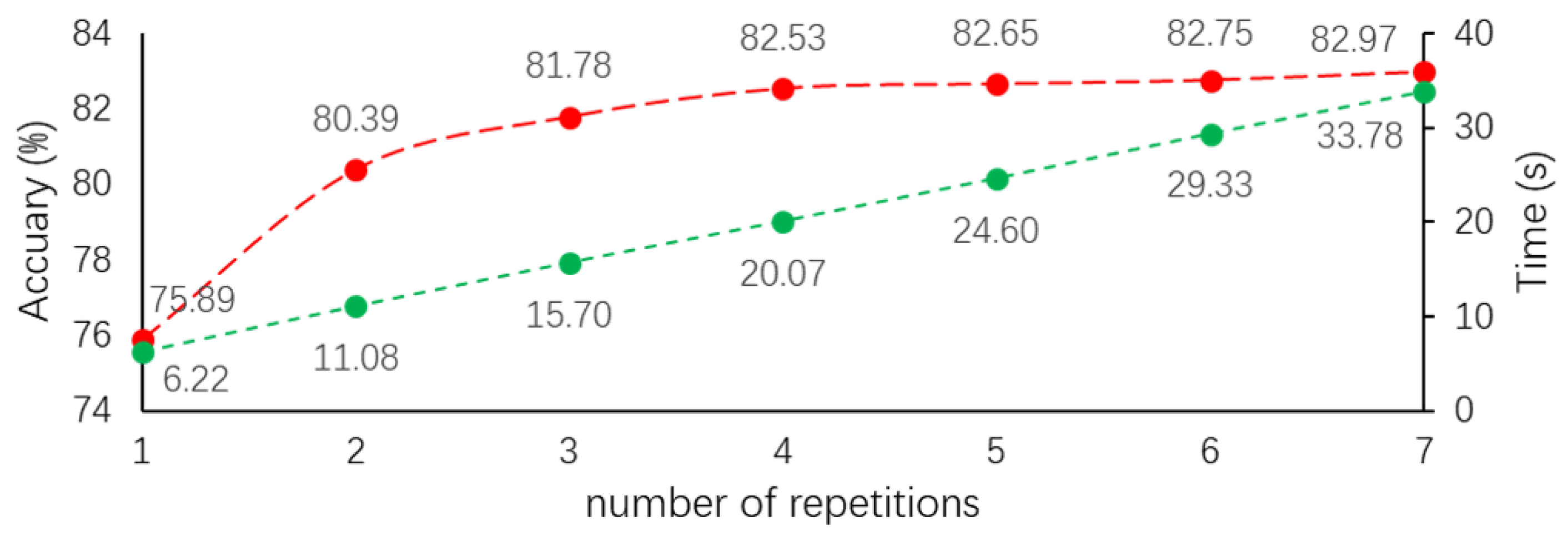
4.1. Ablation Study
4.2. On Mask Rates and Grid Sizes
4.3. The Main Result and Comparison
5. Discussion
- Information density is often low in image data, as missing patches from an image can often be mostly recovered by a neural network structure [11] or by a human brain (as you can often reconstruct the missing parts of an object while looking at it through a fence).
- Adversarial attacks usually introduce a minor perturbation to inputs, which is likely to be reduced or cancelled by (randomly) covering part of the image.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Report. Neural Network Market to Reach $38.71 Billion, Globally, by 2023, Says Allied Market Research. 2020. Available online: https://www.globenewswire.com/fr/news-release/2020/04/02/2010880/0/en/Neural-Network-Market-to-reach-38-71-billion-Globally-by-2023-Says-Allied-Market-Research.html (accessed on 1 December 2022).
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the ICLR, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. In Proceedings of the ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The Limitations of Deep Learning in Adversarial Settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbruecken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar] [CrossRef]
- Ma, X.; Li, B.; Wang, Y.; Erfani, M.S.; Wijewickrema, N.R.S.; Houle, E.M.; Schoenebeck, G.; Song, D.; Bailey, J. Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Cohen, G.; Sapiro, G.; Giryes, R. Detecting Adversarial Samples Using Influence Functions and Nearest Neighbors. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 15–19 June 2020; pp. 14441–14450. [Google Scholar] [CrossRef]
- Xu, W.; Evans, D.; Qi, Y. Feature Squeezing: Detecting Adversarial Examples in Deep Neural Networks. In Proceedings of the NDSS, San Diego, CA, USA, 18–21 February 2018. [Google Scholar]
- Meng, D.; Chen, H. MagNet: A Two-Pronged Defense against Adversarial Examples. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security Association for Computing Machinery (CCS ’17), New York, NY, USA, 30 October–3 November 2017; pp. 135–147. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Mustafa, A.; Khan, S.; Hayat, M.; Goecke, R.; Shen, J.; Shao, L. Adversarial defense by restricting the hidden space of deep neural networks. In Proceedings of the ICCV, Seoul, Korea, 27 October–2 November 2019; pp. 3385–3394. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 21–23 June 2022; pp. 15979–15988. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Wu, X.; Jha, S.; Swami, A. Distillation as a Defense to Adversarial Perturbations Against Deep Neural Networks. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 582–597. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial examples in the physical world. In Proceedings of the ICLR Workshop, Toulon, France, 24–26 April 2017. [Google Scholar]
- Liao, F.; Liang, M.; Dong, Y.; Pang, T.; Hu, X.; Zhu, J. Defense Against Adversarial Attacks Using High-Level Representation Guided Denoiser. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1778–1787. [Google Scholar] [CrossRef]
- Samangouei, P.; Kabkab, M.; Chellappa, R. Defense-GAN: Protecting classifiers against adversarial attacks using generative models. arXiv 2018, arXiv:1805.06605. [Google Scholar]
- Salman, H.; Sun, M.; Yang, G.; Kapoor, A.; Kolter, J.Z. Denoised Smoothing: A Provable Defense for Pretrained Classifiers. In Proceedings of the NeurIPS 2020, Virtual, 6–12 December 2020. [Google Scholar]
- Song, Y.; Kim, T.; Nowozin, S.; Ermon, S.; Kushman, N. PixelDefend: Leveraging Generative Models to Understand and Defend against Adversarial Examples. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lee, S.; Lee, H.; Yoon, S. Adversarial Vertex Mixup: Toward Better Adversarially Robust Generalization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 269–278. [Google Scholar] [CrossRef]
- Potdevin, Y.; Nowotka, D.; Ganesh, V. An Empirical Investigation of Randomized Defenses against Adversarial Attacks. arXiv 2019, arXiv:1909.05580v1. [Google Scholar]
- Gu, S.; Rigazio, L. Towards Deep Neural Network Architectures Robust to Adversarial Examples. In Proceedings of the ICLR Workshop, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Cisse, M.; Bojanowski, P.; Grave, E.; Dauphin, Y.; Usunier, N. Parseval Networks: Improving Robustness to Adversarial Examples. In Proceedings of the 34th International Conference on Machine Learning ICML’17, Sydney, Australia, 6–11 August 2017; pp. 854–863. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Sierra Nevada, Spain, 16–17 December 2011. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Rauber, J.; Brendel, W.; Bethge, M. Foolbox: A Python toolbox to benchmark the robustness of machine learning models. In Proceedings of the Reliable Machine Learning in the Wild Workshop, 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–29 May 2017; pp. 39–57. [Google Scholar] [CrossRef]
- Levine, A.; Feizi, S. Robustness certificates for sparse adversarial attacks by randomized ablation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 4585–4593. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Cheng, L.; Fang, P.; Liang, Y.; Zhang, L.; Shen, C.; Wang, H. TSGB: Target-Selective Gradient Backprop for Probing CNN Visual Saliency. IEEE Trans. Image Process. 2022, 31, 2529–2540. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar] [CrossRef]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 839–847. [Google Scholar] [CrossRef]
- Seshia, S.A.; Desai, A.; Dreossi, T.; Fremont, D.J.; Ghosh, S.; Kim, E.; Shivakumar, S.; Vazquez-Chanlatte, M.; Yue, X. Formal Specification for Deep Neural Networks. In Proceedings of the Automated Technology for Verification and Analysis; Lahiri, S.K., Wang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 20–34. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, Y. Convergence analysis of two-layer neural networks with relu activation. arXiv 2017, arXiv:1705.09886v2. [Google Scholar]
- Seshia, S.A.; Sadigh, D.; Sastry, S.S. Toward Verified Artificial Intelligence. Commun. ACM 2022, 65, 46–55. [Google Scholar] [CrossRef]


| Attack Method | 0 | ||||
|---|---|---|---|---|---|
| Benign | 84.18% | 85.31% | 84.59% | 82.65% | 76.14% |
| FGSM L1 = 15 | 63.53% | 70.17% | 78.37% | 82.63% | 85.30% |
| FGSM L1 = 20 | 63.01% | 64.82% | 73.70% | 79.25% | 82.14% |
| FGSM L2 = 0.3 | 67.36% | 75.95% | 82.46% | 84.62% | 87.55% |
| FGSM L2 = 0.4 | 66.23% | 70.18% | 78.33% | 81.89% | 84.66% |
| FGSM Linf = 0.01 | 48.88% | 68.87% | 76.07% | 81.05% | 83.74% |
| FGSM Linf = 0.02 | 40.76% | 53.77% | 61.30% | 68.77% | 70.61% |
| BIM L1 = 10 | 59.02% | 67.66% | 79.63% | 84.71% | 87.88% |
| BIM L1 = 15 | 58.23% | 51.27% | 68.89% | 80.91% | 84.91% |
| BIM L2 = 0.3 | 61.86% | 61.60% | 75.69% | 83.21% | 87.04% |
| BIM L2 = 0.4 | 61.57% | 49.33% | 68.02% | 80.88% | 84.25% |
| BIM Linf = 0.01 | 38.29% | 57.77% | 72.21% | 81.80% | 86.14% |
| BIM Linf = 0.015 | 37.15% | 39.75% | 58.60% | 77.06% | 82.61% |
| PGD L1 = 1 | 58.49% | 64.60% | 79.17% | 85.44% | 88.11% |
| PGD L1 = 20 | 57.69% | 54.85% | 73.67% | 83.48% | 86.89% |
| PGD L2 = 0.3 | 62.30% | 71.87% | 82.82% | 86.42% | 89.19% |
| PGD L2 = 0.4 | 61.63% | 62.71% | 77.28% | 84.45% | 87.83% |
| PGD Linf = 0.01 | 40.29% | 65.37% | 77.61% | 84.78% | 88.26% |
| PGD Linf = 0.015 | 37.16% | 49.63% | 67.64% | 81.45% | 85.63% |
| CW L2 = 1 | 63.11% | 95.46% | 95.87% | 91.28% | 93.24% |
| DeepFool L2 = 0.6 | 53.97% | 74.01% | 80.90% | 84.20% | 87.22% |
| DeepFool L2 = 0.8 | 52.61% | 68.15% | 76.07% | 81.19% | 83.86% |
| DeepFool Linf = 0.01 | 50.70% | 75.72% | 82.95% | 85.23% | 87.59% |
| DeepFool Linf = 0.015 | 44.32% | 67.31% | 75.12% | 80.44% | 83.81% |
| Masked | Classification Accuracy | |||||
|---|---|---|---|---|---|---|
| Training | Testing | Benign | BIM Linf = 0.01 | PGD Linf = 0.01 | CW L2 = 1.0 | DeepFool Linf = 0.01 |
| × | × | 84.18% | 38.29% | 40.29% | 63.11% | 50.70% |
| √ | × | 84.65% | 3.16% | 6.13% | 15.89% | 35.72% |
| × | √ | 49.39% | 67.98% | 69.37% | 70.06% | 67.98% |
| √ | √ | 82.65% | 81.80% | 84.78% | 91.28% | 85.23% |
| Training | 4 × 4 | 4 × 4 | 8 × 8 | 8 × 8 | 8 × 8 |
|---|---|---|---|---|---|
| Test | 2 × 2 | 4 × 4 | 2 × 2 | 4 × 4 | 8 × 8 |
| Benign | 73.23% | 76.92% | 63.11% | 82.65% | 82.89% |
| FGSM L1 = 15 | 86.63% | 83.84% | 85.34% | 82.63% | 75.68% |
| FGSM L1 = 20 | 83.20% | 79.39% | 82.74% | 79.25% | 71.72% |
| FGSM L2 = 0.3 | 89.54% | 87.13% | 86.17% | 84.62% | 79.84% |
| FGSM L2 = 0.4 | 86.63% | 83.41% | 85.34% | 81.89% | 75.11% |
| FGSM Linf = 0.01 | 86.10% | 82.11% | 84.42% | 81.05% | 73.63% |
| FGSM Linf = 0.02 | 73.64% | 67.07% | 73.93% | 68.77% | 59.87% |
| BIM L1 = 10 | 89.21% | 85.66% | 87.64% | 84.71% | 75.67% |
| BIM L1 = 15 | 84.62% | 79.36% | 85.61% | 80.91% | 65.50% |
| BIM L2 = 0.3 | 87.52% | 83.55% | 86.12% | 83.21% | 71.88% |
| BIM L2 = 0.4 | 83.64% | 78.06% | 85.50% | 80.88% | 65.82% |
| BIM Linf = 0.01 | 86.60% | 81.86% | 86.47% | 81.80% | 68.67% |
| BIM Linf = 0.015 | 81.26% | 72.97% | 83.62% | 77.06% | 56.05% |
| PGD L1 = 15 | 88.99% | 84.76% | 86.64% | 85.44% | 76.14% |
| PGD L1 = 20 | 85.78% | 80.08% | 86.23% | 83.48% | 71.13% |
| PGD L2 = 0.3 | 90.35% | 87.03% | 88.07% | 86.42% | 78.77% |
| PGD L2 = 0.4 | 88.01% | 83.48% | 87.20% | 84.45% | 74.79% |
| PGD Linf = 0.01 | 88.64% | 84.05% | 86.61% | 84.78% | 73.89% |
| PGD Linf = 0.015 | 84.57% | 77.20% | 84.46% | 81.45% | 65.54% |
| CW L2 = 1 | 94.78% | 95.25% | 89.53% | 91.28% | 93.94% |
| DeepFool L2 = 0.6 | 88.54% | 87.10% | 85.03% | 84.20% | 80.31% |
| DeepFool L2 = 0.8 | 85.73% | 82.75% | 82.65% | 81.19% | 75.53% |
| DeepFool Linf = 0.01 | 90.33% | 88.21% | 85.42% | 85.23% | 80.42% |
| DeepFool Linf = 0.015 | 86.03% | 82.66% | 82.16% | 80.44% | 74.92% |
| Attack Method | Attack | Defense | Improvement |
|---|---|---|---|
| Benign | 82.65% | ||
| FGSM L1 = 15 | 35.48% | 82.63% | 47.15% |
| FGSM L1 = 20 | 33.02% | 79.25% | 46.23% |
| FGSM L2 = 0.3 | 38.29% | 84.62% | 46.33% |
| FGSM L2 = 0.4 | 35.27% | 81.89% | 46.62% |
| FGSM Linf = 0.01 | 33.02% | 81.05% | 48.03% |
| FGSM Linf = 0.02 | 28.27% | 68.77% | 40.50% |
| BIM L1 = 10 | 10.23% | 84.71% | 74.48% |
| BIM L1 = 15 | 6.70% | 80.91% | 74.21% |
| BIM L2 = 0.3 | 9.43% | 83.21% | 73.78% |
| BIM L2 = 0.4 | 8.06% | 80.88% | 72.82% |
| BIM Linf = 0.01 | 3.16% | 81.80% | 78.64% |
| BIM Linf = 0.015 | 1.06% | 77.06% | 76.00% |
| PGD L1 = 15 | 8.75% | 85.44% | 76.69% |
| PGD L1 = 20 | 6.36% | 83.48% | 77.12% |
| PGD L2 = 0.3 | 12.47% | 86.42% | 73.95% |
| PGD L2 = 0.4 | 9.01% | 84.45% | 75.44% |
| PGD Linf = 0.01 | 6.13% | 84.78% | 78.65% |
| PGD Linf = 0.015 | 2.30% | 81.45% | 79.15% |
| CW L2 = 1 | 15.89% | 91.28% | 75.39% |
| DeepFool L2 = 0.6 | 34.64% | 84.20% | 49.56% |
| DeepFool L2 = 0.8 | 31.81% | 81.19% | 49.38% |
| DeepFool Linf = 0.01 | 35.72% | 85.23% | 49.51% |
| DeepFool Linf = 0.015 | 32.26% | 80.44% | 48.18% |
| LeNet + MNIST | ResNet18 + SVHN | |||||||
|---|---|---|---|---|---|---|---|---|
| Attack Method | Attack | Defense | Improvement | Attack | Defense | Improvement | ||
| Benign | - | 96.13% | - | 91.65% | ||||
| FGSM L1 | 10 | 44.12% | 68.94% | 24.82% | 15 | 50.47% | 76.84% | 26.37% |
| FGSM L1 | 20 | 28.35% | 49.50% | 21.15% | 20 | 45.85% | 70.25% | 24.40% |
| FGSM L2 | 0.8 | 34.85% | 58.60% | 23.75% | 0.4 | 53.17% | 80.40% | 27.23% |
| FGSM L2 | 1.0 | 30.28% | 52.82% | 22.54% | 0.6 | 46.77% | 71.48% | 24.71% |
| FGSM Linf | 0.03 | 36.26% | 61.82% | 25.56% | 0.01 | 57.12% | 85.40% | 28.28% |
| FGSM Linf | 0.04 | 28.58% | 50.31% | 21.73% | 0.02 | 46.06% | 68.95% | 22.89% |
| BIM L1 | 4 | 8.98% | 59.49% | 50.51% | 10 | 15.46% | 80.37% | 64.91% |
| BIM L1 | 6 | 2.26% | 44.17% | 41.91% | 12 | 11.54% | 75.85% | 64.31% |
| BIM L2 | 0.2 | 16.55% | 69.23% | 52.68% | 0.25 | 21.75% | 84.40% | 62.65% |
| BIM L2 | 0.3 | 3.79% | 49.04% | 45.25% | 0.3 | 16.59% | 81.37% | 64.78% |
| BIM Linf | 0.015 | 11.72% | 70.94% | 59.22% | 0.01 | 16.06% | 86.31% | 70.25% |
| BIM Linf | 0.02 | 3.62% | 56.33% | 52.71% | 0.02 | 2.58% | 71.00% | 68.42% |
| PGD L1 | 4 | 16.04% | 71.79% | 55.75% | 14 | 15.09% | 84.14% | 69.05% |
| PGD L1 | 6 | 3.37% | 54.75% | 51.38% | 16 | 12.11% | 82.35% | 70.24% |
| PGD L2 | 0.2 | 22.98% | 77.87% | 54.89% | 0.4 | 16.40% | 84.22% | 67.82% |
| PGD L2 | 0.4 | 1.26% | 48.85% | 47.59% | 0.5 | 12.17% | 81.37% | 69.20% |
| PGD Linf | 0.015 | 11.64% | 70.90% | 59.26% | 0.01 | 10.10% | 84.45% | 74.35% |
| PGD Linf | 0.02 | 3.27% | 56.38% | 53.11% | 0.02 | 4.69% | 80.51% | 75.82% |
| CW L2 | 1.5 | 0.20% | 93.39% | 93.19% | 1.8 | 21.70% | 96.05% | 74.35% |
| DeepFool L2 | 0.6 | 32.62% | 61.05% | 28.43% | 0.5 | 59.78% | 87.09% | 27.31% |
| DeepFool L2 | 0.8 | 26.49% | 51.39% | 24.90% | 0.7 | 53.87% | 82.22% | 28.35% |
| DeepFool Linf | 0.05 | 24.77% | 47.26% | 22.49% | 0.01 | 57.10% | 88.06% | 30.96% |
| DeepFool Linf | 0.07 | 22.50% | 39.76% | 17.26% | 0.02 | 46.39% | 72.98% | 26.59% |
| Attack Method | MagNet | Denoised Smoothing | Parseval Networks | PCL | MAD |
|---|---|---|---|---|---|
| Benign | 82.32% | 77.92% | 77.89% | 83.47% | 82.65% |
| FGSM L1 = 15 | 67.41% | 81.97% | 43.20% | 74.94% | 82.63% |
| FGSM L1 = 20 | 65.68% | 76.50% | 33.11% | 70.53% | 79.25% |
| FGSM L2 = 0.3 | 72.15% | 85.88% | 52.41% | 79.54% | 84.62% |
| FGSM L2 = 0.4 | 69.75% | 81.70% | 42.69% | 75.32% | 81.89% |
| FGSM Lin = 0.01 | 57.81% | 82.83% | 44.22% | 75.56% | 81.05% |
| FGSM Lin = 0.02 | 44.96% | 65.25% | 20.75% | 62.72% | 68.77% |
| BIM L1 = 10 | 66.56% | 80.11% | 45.23% | 64.03% | 84.71% |
| BIM L1 = 15 | 62.63% | 68.58% | 26.22% | 48.03% | 80.91% |
| BIM L2 = 0.3 | 67.63% | 77.36% | 38.57% | 61.26% | 83.21% |
| BIM L2 = 0.4 | 65.73% | 68.06% | 24.96% | 48.34% | 80.88% |
| BIM Linf = 0.01 | 51.34% | 75.51% | 29.54% | 59.83% | 81.80% |
| BIM Linf = 0.015 | 42.84% | 62.41% | 13.52% | 43.31% | 77.06% |
| PGD L1 = 15 | 67.08% | 79.83% | 37.84% | 66.63% | 85.44% |
| PGD L1 = 20 | 64.66% | 72.81% | 24.64% | 53.18% | 83.48% |
| PGD L2 = 0.3 | 71.98% | 84.65% | 48.20% | 76.08% | 86.42% |
| PGD L2 = 0.4 | 69.44% | 79.17% | 35.14% | 66.70% | 84.45% |
| PGD Linf = 0.01 | 56.92% | 81.17% | 36.89% | 72.22% | 84.78% |
| PGD Linf = 0.015 | 47.79% | 70.74% | 19.35% | 54.74% | 81.45% |
| CW L2 = 1 | 92.58% | 99.74% | 43.42% | 89.48% | 91.28% |
| DeepFool L2 = 0.6 | 63.84% | 65.04% | 34.10% | 49.95% | 84.20% |
| DeepFool L2 = 0.8 | 60.45% | 57.97% | 44.51% | 47.68% | 81.19% |
| DeepFool Linf = 0.01 | 62.79% | 81.43% | 30.49% | 58.80% | 85.23% |
| DeepFool Linf = 0.015 | 54.26% | 71.68% | 9.49% | 53.28% | 80.44% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhang, C.; Zhao, F.; Fang, L. A Mask-Based Adversarial Defense Scheme. Algorithms 2022, 15, 461. https://doi.org/10.3390/a15120461
Xu W, Zhang C, Zhao F, Fang L. A Mask-Based Adversarial Defense Scheme. Algorithms. 2022; 15(12):461. https://doi.org/10.3390/a15120461
Chicago/Turabian StyleXu, Weizhen, Chenyi Zhang, Fangzhen Zhao, and Liangda Fang. 2022. "A Mask-Based Adversarial Defense Scheme" Algorithms 15, no. 12: 461. https://doi.org/10.3390/a15120461
APA StyleXu, W., Zhang, C., Zhao, F., & Fang, L. (2022). A Mask-Based Adversarial Defense Scheme. Algorithms, 15(12), 461. https://doi.org/10.3390/a15120461








