Phase-Type Survival Trees to Model a Delayed Discharge and Its Effect in a Stroke Care Unit
Abstract
1. Introduction
2. Materials and Methods
2.1. Phase Type Survival Tree (PHTST)
2.2. PHTST Construction
2.3. Extended PHTST
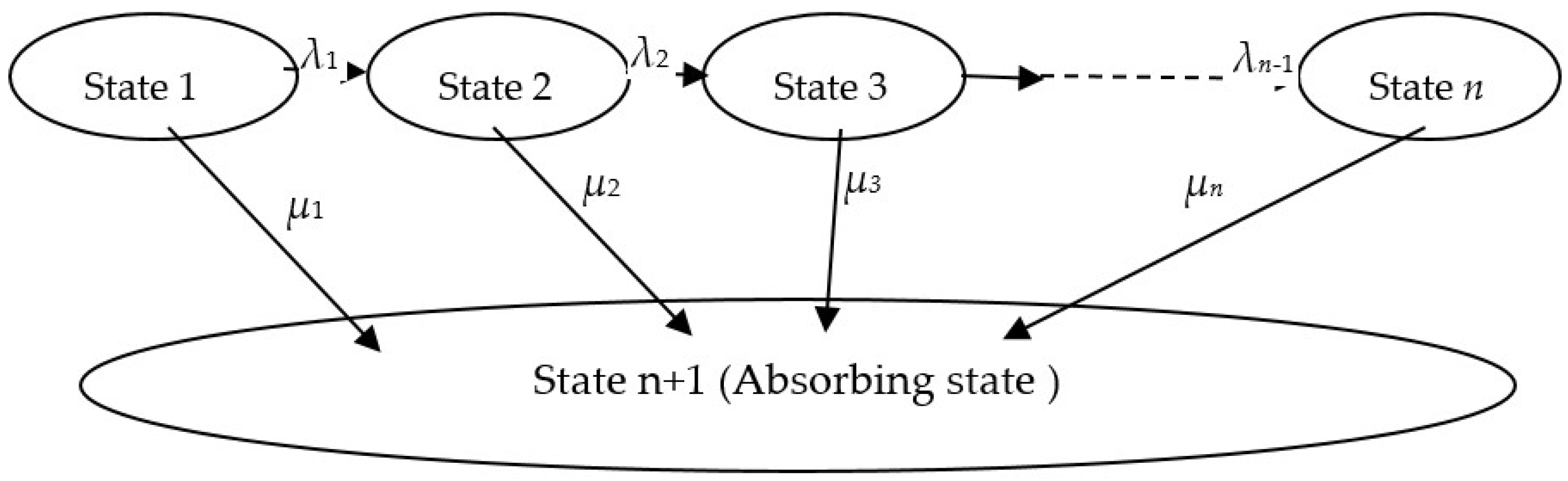
2.4. Modelling Blocking State
2.4.1. Single-Absorbing State

2.4.2. Multi-Absorbing State
3. Results
3.1. The Stroke Unit of the Belfast City Hospital
3.1.1. Discharge Delay Distribution without Clustering Based on Discharge Destinations
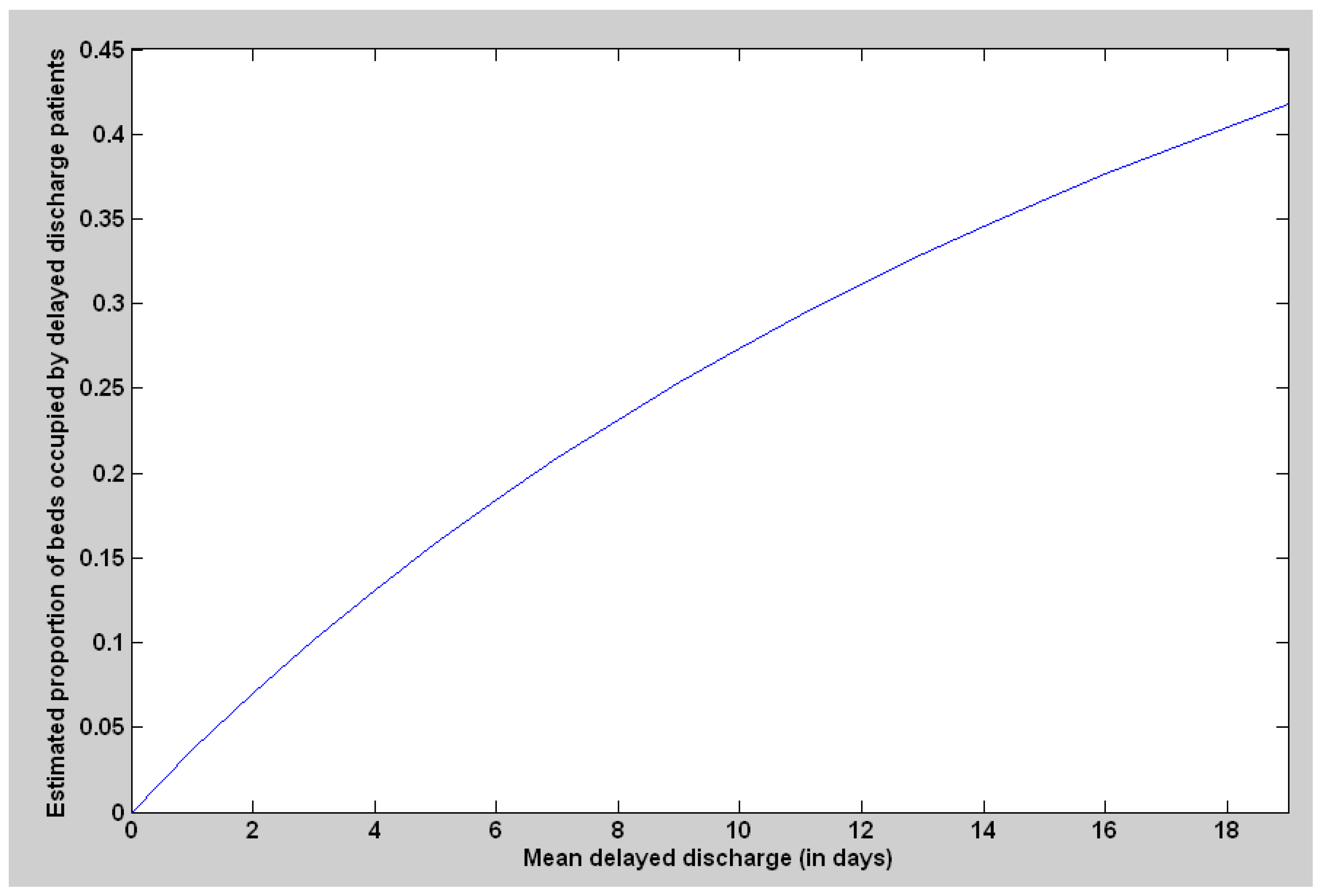
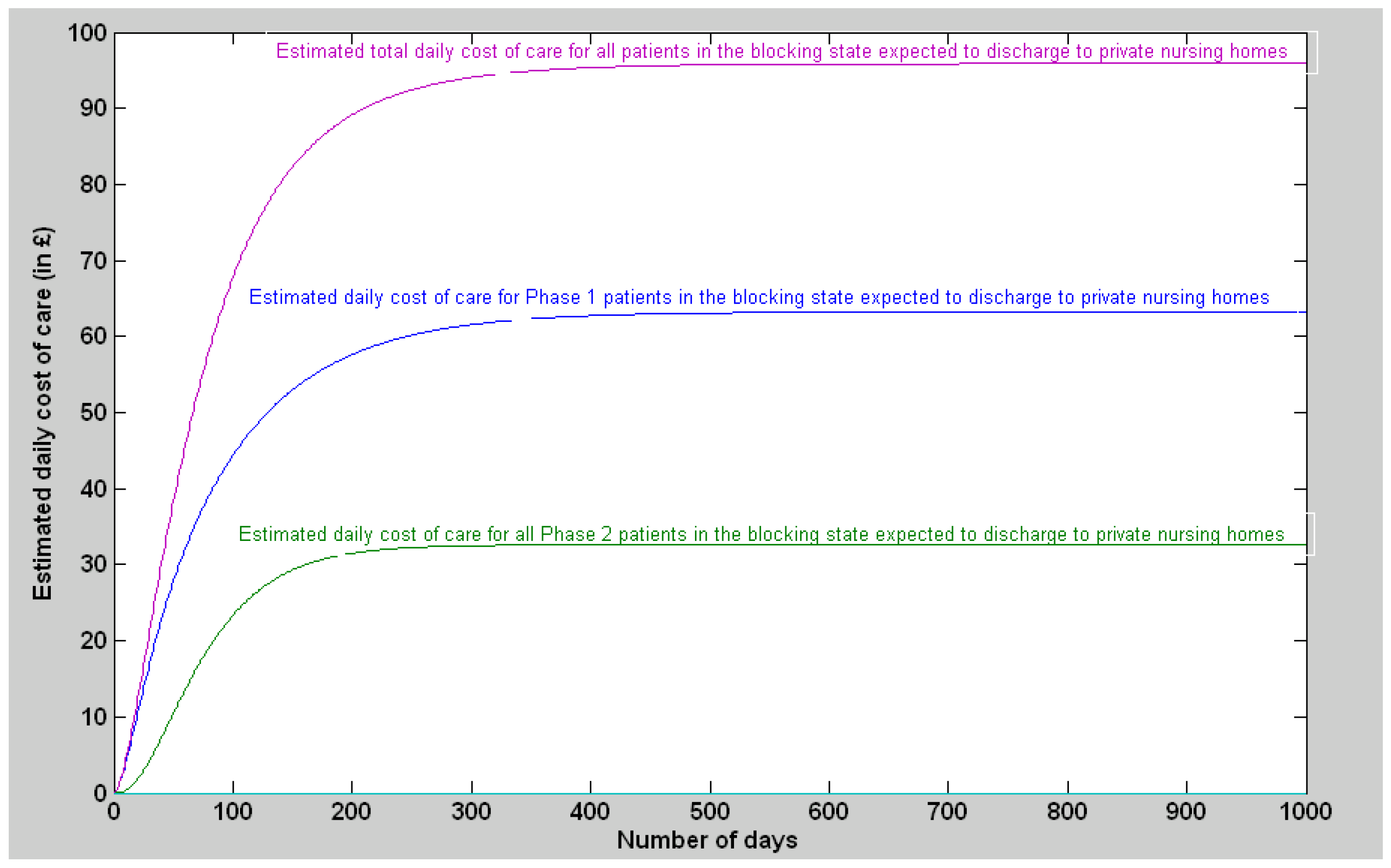
3.1.2. Discharge Delay for the Patients Expected to Be Discharged to Private Nursing Homes
3.1.3. Discharge Delay with the Patients Expected to Be Discharged to Other Destinations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, L.; Abello, A.; Thurecht, L. Length of Hospital Stay by Older Australians: Bed-Blocking or Not. National Centre for Social and Economic Modelling (NATSEM); University of Canberra: Canberra, Australia, 2011. [Google Scholar]
- Gaughan, J.; Gravelle, H.; Siciliani, L. Testing the Bed-Blocking Hypothesis: Does Nursing and Care Home Supply Reduce Delayed Hospital Discharges? Health Econ. 2015, 24, 32–44. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, J.D.; Price-Lloyd, N.; Smithies, M.; Williams, J. A queueing model of activities in an intensive care unit. IMA J. Manag. Math. 2006, 17, 277–288. [Google Scholar] [CrossRef]
- Griffiths, J.D.; Jones, M.; Read, M.S.; Williams, J.E. A simulation model of bed-occupancy in a critical care unit. J. Simul. 2010, 4, 52–59. [Google Scholar] [CrossRef]
- Hendy, P.; Patel, J.; Kordbacheh, T.; Laskar, N.; Harbord, M. In-depth analysis of delays to patient discharge: A metropolitan teaching hospital experience. Clin. Med. 2012, 12, 320–323. [Google Scholar] [CrossRef] [PubMed]
- Micallef, A.; Buttigieg, S.C.; Tomaselli, G.; Garg, L. Defining Delayed Discharges of Inpatients and Their Impact in Acute Hospital Care: A Scoping Review. Int. J. Health Policy Manag. 2020, 11, 103. [Google Scholar] [CrossRef] [PubMed]
- Price-Lloyd, N.; Griffiths, J.D.; Williams, J.E. Modelling a Critical Care Directorate. In Proceedings of the 31st Meeting of the EURO Working Group on OR Applied to Health Services (ORAHS, 2005), Southampton, UK, 24 July–5 August 2005; p. 8. [Google Scholar]
- Swanson, J. Bed Blocking and the City: An Analysis of the Factors Explaining Variation in the Number of Days Associated with Specific Measures Relevant to Patient Discharges One Year after Implementation of the Coordination Reform within the Municipality of Oslo. Master’s Thesis, University of Oslo, Oslo, Norway, 2013. [Google Scholar]
- Jasinarachchi, K.H.; Ibrahim, I.R.; Keegan, B.C.; Mathialagan, R.; McGourty, J.C.; Phillips, J.R.; Myint, P.K. Delayed transfer of care from NHS secondary care to primary care in England: Its determinants, effect on hospital bed days, prevalence of acute medical conditions and deaths during delay, in older adults aged 65 years and over. BMC Geriatr. 2009, 9, 4. [Google Scholar] [CrossRef] [PubMed]
- National Audit Office 2000. Inpatient Admissions and Bed Management in NHS Acute Hospitals; The Stationery Office: London, UK, 2000; pp. 51–52. Available online: http://nao.org.uk/publications/nao_reports/9900254es.pdf (accessed on 13 July 2022).
- Schluep, M.; Bogousslavsky, J.; Regli, F.; Tendon, M.; Prod’Hom, L.; Kleiber, C. Justification of Hospital Days and Epidemiology of Discharge Delays in a Department of Neurology. Neuroepidemiology 1994, 13, 40–49. [Google Scholar] [CrossRef]
- National Audit Office 2003. Ensuring the Effective Discharge of Older Patients from NHS Acute Hospitals, The Stationery Office, London 2003. Available online: http://www.publications.parliament.uk/pa/cm200203/cmselect/cmpubacc/459/459.pdf (accessed on 13 July 2022).
- Kydd, A. The patient experience of being a delayed discharge. J. Nurs. Manag. 2008, 16, 121–126. [Google Scholar] [CrossRef]
- Kuluski, K.; Cadel, L.; Marcinow, M.; Sandercock, J.; Guilcher, S.J. Expanding our understanding of factors impacting delayed hospital discharge: Insights from patients, caregivers, providers and organizational leaders in Ontario, Canada. Health Policy 2022, 126, 310–317. [Google Scholar] [CrossRef]
- Green, M.A.; Dorling, D.; Minton, J.; Pickett, K.E. Could the rise in mortality rates since 2015 be explained by changes in the number of delayed discharges of NHS patients? J. Epidemiol. Community Health 2017, 71, 1068–1071. [Google Scholar] [CrossRef]
- Baumann, M.; Evans, S.; Perkins, M.; Curtis, L.; Netten, A.; Fernandez, J.-L.; Huxley, P. Organisation and features of hospital, intermediate care and social services in English sites with low rates of delayed discharge. Health Soc. Care Community 2007, 15, 295–305. [Google Scholar] [CrossRef] [PubMed]
- Giraldo, D.M.; Navarro, A.; Sánchez-Quijano, A.; Villegas, A.; Asencio, R.; Lissen, E. Impact of delayed discharge for nonmedical reasons in a tertiary hospital internal medicine department. Rev. Clin. Esp. 2012, 212, 229–234. [Google Scholar]
- Lenzi, J.; Mongardi, M.; Rucci, P.; Di Ruscio, E.; Vizioli, M.; Randazzo, C.; Toschi, E.; Carradori, T.; Fantini, M.P. Sociodemographic, clinical and organisational factors associated with delayed hospital discharges: A cross-sectional study. BMC Health Serv. Res. 2014, 14, 128. [Google Scholar] [CrossRef] [PubMed]
- Tan, E.S.; Bonnett, T.J.; Abdelhafiz, A.H. Delayed discharges due to initiation of warfarin in atrial fibrillation: A prospective audit. Am. J. Geriatr. Pharmacother. 2007, 5, 232–235. [Google Scholar] [CrossRef] [PubMed]
- DeCoster, C.; Roos, N.P.; Carrière, K.C.; Peterson, S. Inappropriate hospital use by patients receiving care for medical conditions: Targeting utilization review. Can. Med. Assoc. J. 1997, 157, 889–896. [Google Scholar]
- Mohammed, A.; Thomas, B.M.; Hullin, M.G.; McCreath, S.W. Audit of orthopaedic bed utilisation. Health Bull. 2001, 59, 353–355. [Google Scholar]
- Vetter, N. Inappropriately delayed discharge from hospital; What do we know? Br. Med. J. 2003, 326, 927–928. [Google Scholar] [CrossRef]
- Worthington, A.D.; Oldham, J.B. Delayed discharge from rehabilitation after brain injury. Clin. Rehabil. 2006, 20, 79–82. [Google Scholar] [CrossRef]
- Van Straten, A.; van der Meulen, J.H.; van den Bos, G.A.; Limburg, M. Length of hospital stay and discharge delays in stroke patients. Stroke 1997, 28, 137–140. [Google Scholar] [CrossRef]
- Hermans, E.; Anten, H.W.; Diederiks, J.P.; Philipsen, H.; Beeren, H.W. Patient characteristics with predictive significance for ‘blocked bed’ problems in the neurological department of a general hospital. Ned. Tijdschr. Voor Geneeskd. 1995, 139, 890–894. [Google Scholar]
- Kendrick, S.; Conway, M. Increasing Emergency Hospital Admissions among Older People in Scotland; A Whole System Account, Whole System Working Paper 1; ISD: Edinburgh, UK, 2003. [Google Scholar]
- Lewis, H.; Purdie, G. The blocked bed; a prospective study. N. Z. Med. J. 1988, 14, 575–576. [Google Scholar]
- Audit Scotland. Moving on? An Overview of Delayed Discharges in Scotland, A Report Prepared on 23 June 23rd 2005 for the Auditor General/Accounts Commission. 2005. Available online: https://www.audit-scotland.gov.uk/docs/health/2005/nr_050623_delayed_discharges.pdf (accessed on 13 July 2022).
- Audit Scotland. Moving on? A Handbook on Modelling the Whole System for Delayed Discharge in Tayside. 2005. Available online: http://www.audit-scotland.gov.uk/docs/health/2005/nr_050623_delayed_discharges_hdbook.pdf (accessed on 13 July 2022).
- Ou, L.; Young, L.; Chen, J.; Santiano, N.; Baramy, L.-S.; Hillman, K. Discharge delay in acute care: Reasons and determinants of delay in general ward patients. Aust. Health Rev. 2009, 33, 513–521. [Google Scholar] [CrossRef] [PubMed]
- Victor, C.R.; Healy, J.; Thomas, A.; Seargeant, J. Older patients and delayed discharge from hospital. Health Soc. Care Community 2000, 8, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Glasby, J.; Littlechild, R.; Pryce, K. Show Me the Way to Go Home: A Narrative Review of the Literature on Delayed Hospital Discharges and Older People. Br. J. Soc. Work 2004, 34, 1189–1197. [Google Scholar] [CrossRef]
- Hubbard, G.; Huby, G.; Wyke, S.; Themessl-Huber, M. A Research Review on Tackling Delayed Discharge; Scottish Executive Social Research: Edinburgh, UK, 2004; ISBN 0-7559-3825-9. Available online: https://www.webarchive.org.uk/wayback/archive/20150221082009/http://www.gov.scot/Publications/2004/10/20042/44602 (accessed on 13 July 2022).
- Feigal, J.; Park, B.; Bramante, C.; Nordgaard, C.; Menk, J.; Song, J. Homelessness and discharge delays from an urban safety net hospital. Public Health 2014, 128, 1033–1035. [Google Scholar] [CrossRef]
- Mustafa, F.; Gilligan, P.; Obu, D.; O’Kelly, P.; O’Hea, E.; Lloyd, C.; Kelada, S.; Heffernan, A.; Houlihan, P. ‘Delayed discharges and boarders’: A 2-year study of the relationship between patients experiencing delayed discharges from an acute hospital and boarding of admitted patients in a crowded ED. Emerg. Med. J. 2016, 33, 636–640. [Google Scholar] [CrossRef]
- Lim, S.C.; Doshi, V.; Castasus, B.; Lim, J.K.H.; Mamun, K. Factors causing delay in discharge of elderly patients in an acute care hospital. Ann. Acad. Med. Singap. 2006, 35, 27–32. [Google Scholar]
- Landeiro, F.; Leal, J.; Gray, A.M. The impact of social isolation on delayed hospital discharges of older hip fracture patients and associated costs. Osteoporos. Int. 2015, 27, 737–745. [Google Scholar] [CrossRef]
- Bryan, K.; Gage, H.; Gilbert, K. Delayed transfers of older people from hospital: Causes and policy implications. Health Policy 2006, 76, 194–201. [Google Scholar] [CrossRef]
- Benson, R.T.; Drew, J.C.; Galland, R.B. A Waiting List to Go Home: An Analysis of Delayed Discharges from Surgical Beds. Ann. R. Coll. Surg. Engl. 2006, 88, 650–652. [Google Scholar] [CrossRef]
- Wong, H.; Wu, R.C.; Tomlinson, G.; Caesar, M.; Abrams, H.; Carter, M.; Morra, D. How much do operational processes affect hospital inpatient discharge rates? J. Public Health 2009, 31, 546–553. [Google Scholar] [CrossRef]
- El-Eid, G.R.; Kaddoum, R.; Tamim, H.; Hitti, E.A. Improving hospital discharge time: A successful implementation of six sigma methodology. Medicine 2015, 94, e633. [Google Scholar] [CrossRef]
- Majeed, M.U.; Williams, D.T.; Pollock, R.; Amir, F.; Liam, M.; Foong, K.S.; Whitaker, C.J. Delay in discharge and its impact on unnecessary hospital bed occupancy. BMC Health Serv. Res. 2012, 12, 410. [Google Scholar] [CrossRef] [PubMed]
- Holland, D.E.; Pacyna, J.E.; Gillard, K.L.; Carter, L.C. Tracking discharge delays: Critical first step toward mitigating process breakdowns and inefficiencies. J. Nurs. Care Qual. 2016, 31, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Swinkels, A.; Mitchell, T. Delayed transfer from hospital to community settings: The older person’s perspective. Health Soc. Care Community 2009, 17, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Holmås, T.H.; Islam, M.K.; Kjerstad, E. Between two beds: Inappropriately delayed discharges from hospitals. Int. J. Health Care Financ. Econ. 2013, 13, 201–217. [Google Scholar] [CrossRef]
- Devapriam, J.; Gangadharan, S.; Pither, J.; Critchfield, M. Delayed discharge from intellectual disability in-patient units. Psychiatr. Bull. 2014, 38, 211–215. [Google Scholar] [CrossRef]
- Falcone, D.; Bolda, E.; Leak, S.C. Waiting for placement: An exploratory analysis of determinants of delayed discharges of elderly hospital patients. Health Serv. Res. 1991, 26, 339–374. [Google Scholar]
- Venkataraman, R.; Panousis, K.; Deakin, A.H.; Sale, G.; Picard, F. Warfarin—An expensive cause of delay in discharge of elective arthroplasty patients. Eur. Orthop. Traumatol. 2014, 6, 77–82. [Google Scholar] [CrossRef]
- Grimmer, K.; Moss, J.; Falco, J. Experiences of elderly patients regarding independent community living after discharge from hospital: A longitudinal study. Int. J. Qual. Health Care 2004, 16, 465–472. [Google Scholar] [CrossRef][Green Version]
- Barton, M.; McClean, S.; Gillespie, J.; Garg, L.; Wilson, D.; Fullerton, K. Is it beneficial to increase the provision of thrombolysis?—A discrete-event simulation model. QJM Int. J. Med. 2012, 105, 665–673. [Google Scholar] [CrossRef] [PubMed]
- Garg, L.; McClean, S.; Barton, M.; Meenan, B.; Fullerton, K. An extended phase type survival tree for patient pathway prognostication. In Proceedings of the 2010 IEEE Workshop on Health Care Management (WHCM), Venice, Italy, 18–20 February 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Garg, L.; McClean, S.I.; Barton, M.; Meenan, B.J.; Fullerton, K. Intelligent Patient Management and Resource Planning for Complex, Heterogeneous, and Stochastic Healthcare Systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2012, 42, 1332–1345. [Google Scholar] [CrossRef]
- Garg, L.; McClean, S.I.; Barton, M.; Meenan, B.J.; Fullerton, K.; Kontonatsios, G.; Trovati, M.; Konkontzelos, I.; Xu, X.; Farid, M. Evaluating Different Selection Criteria for Phase Type Survival Tree Construction. Big Data Res. 2021, 25, 100250. [Google Scholar] [CrossRef]
- McClean, S.; Barton, M.; Garg, L.; Fullerton, K. A modeling framework that combines markov models and discrete-event simulation for stroke patient care. ACM Trans. Model. Comput. Simul. 2011, 21, 1–26. [Google Scholar] [CrossRef]
- McClean, S.; Garg, L.; Gillespie, J.; Fullerton, K. Costing Mixed Coxian Phase-type Systems in a given time interval. In Proceedings of the 26th IEEE International Symposium on Computer-Based Medical Systems, Porto, Portugal, 20–22 June 2013; pp. 369–372. [Google Scholar]
- McClean, S.; Gillespie, J.; Garg, L.; Barton, M.; Scotney, B.; Kullerton, K. Using phase-type models to cost stroke patient care across health, social and community services. Eur. J. Oper. Res. 2014, 236, 190–199. [Google Scholar] [CrossRef]
- Gillespie, J.; McClean, S.; Scotney, B.; Garg, L.; Barton, M.; Fullerton, K. Costing hospital resources for stroke patients using phase-type models. Health Care Manag. Sci. 2011, 14, 279–291. [Google Scholar] [CrossRef]
- Gillespie, J.; McClean, S.; Garg, L.; Barton, M.; Scotney, B.; Fullerton, K. A multi-phase DES modelling framework for patient-centred care. J. Oper. Res. Soc. 2016, 67, 1239–1249. [Google Scholar] [CrossRef]
- Barton, M.; McClean, S.I.; Garg, L.; Fullerton, K. Modelling Stroke Patient Pathways using Survival Analysis and Simulation Modelling. In Proceedings of the XIIIth International Conference “Applied Stochastic Models and Data Analysis” (ASMDA-2009), Vilnius, Lithuania, 30 June–3 July 2009; pp. 370–373. [Google Scholar]
- McClean, S.; Garg, L.; Barton, M.; Fullerton, K.; Millard, P. Using Markov Systems to Plan Stroke Services. In Intelligent Patient Management; Springer: Berlin/Heidelberg, Germany, 2009; pp. 241–256. [Google Scholar]
- Saka, O.; McGuire, A.; Wolfe, C. Cost of stroke in the United Kingdom. Age Ageing 2008, 38, 27–32. [Google Scholar] [CrossRef]
- Fackrell, M. Modelling healthcare systems with phase-type distributions. Health Care Manag. Sci. 2008, 12, 11–26. [Google Scholar] [CrossRef]
- Marshall, A.H.; McClean, S. Using Coxian Phase-Type Distributions to Identify Patient Characteristics for Duration of Stay in Hospital. Health Care Manag. Sci. 2004, 7, 285–289. [Google Scholar] [CrossRef]
- Garg, L.; McClean, S.; Meenan, B.J.; Millard, P. Phase-Type Survival Trees and Mixed Distribution Survival Trees for Clustering Patients’ Hospital Length of Stay. Informatica 2011, 22, 57–72. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwartz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- McQuarrie, A.D. A small-sample correction for the Schwarz SIC model selection criterion. Stat. Probab. Lett. 1999, 44, 79–86. [Google Scholar] [CrossRef]
- Wu, T.-J.; Sepulveda, A. The weighted average information criterion for order selection in time series and regression models. Stat. Probab. Lett. 1998, 39, 1–10. [Google Scholar] [CrossRef]
- Chen, P.; Wu, T.-J.; Yang, J. A comparative study of model selection criteria for the number of signals. IET Radar Sonar Navig. 2008, 2, 180–188. [Google Scholar] [CrossRef]
- Barton, M.; McClean, S.; Garg, L.; Fullerton, K. Modelling costs of bed occupancy and delayed discharge of post-stroke patients. In Proceedings of the 2010 IEEE Workshop on Health Care Management (WHCM), Venice, Italy, 18–20 February 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Garg, L.; Chukwu, E.; Nasser, N.; Chakraborty, C.; Garg, G. Anonymity preserving IoT-based COVID-19 and other infectious disease contact tracing model. IEEE Access 2020, 8, 159402–159414. [Google Scholar] [CrossRef]
- Chukwu, E.; Garg, L. A Systematic Review of Blockchain in Healthcare: Frameworks, Prototypes, and Implementations. IEEE Access 2020, 8, 21196–21214. [Google Scholar] [CrossRef]


















| Node | Covariate | Covariate Value | Number of Patients | Mean LOS | Standard Deviation (LOS) | Coefficient of Variation | WIC | Number of Phases | Total WIC | Gain in WIC |
|---|---|---|---|---|---|---|---|---|---|---|
| All | Complete dataset | Root node | 1985 | 29.01 | 52.84 | 1.82 | 16,847.73 | 3 | 16,847.73 | - |
| 1 (Root node) | Gender | Male | 933 | 26.59 | 44.06 | 1.66 | 7736.85 | 2 | 16,845.79 | 1.94 |
| Female | 1052 | 31.15 | 59.47 | 1.91 | 9108.94 | 3 | ||||
| Age | Young | 624 | 19.26 | 39.15 | 2.03 | 4650.09 | 2 | 16,729 | 118.73 | |
| Old | 1361 | 33.48 | 57.49 | 1.72 | 12,078.9 | 3 | ||||
| Diagnosis | Hemorrhagic | 154 | 33.6 | 56.45 | 1.68 | 1338.96 | 3 | 16,567.05 | 280.68 | |
| Cerebral | 655 | 36.66 | 47.68 | 1.3 | 5978.78 | 2 | ||||
| TIA | 425 | 9.31 | 19.95 | 2.14 | 2612.38 | 2 | ||||
| Other | 751 | 32.54 | 65.05 | 2 | 6636.92 | 2 | ||||
| 2 Hemorrhagic | Gender | Male | 80 | 28.2 | 52.1 | 1.85 | 660.85 | 4 | 1332.41 | 6.55 |
| Female | 74 | 39.45 | 60.25 | 1.53 | 671.56 | 2 | ||||
| Age | Young | 50 | 24.56 | 55.12 | 2.24 | 370.13 | 4 | 1324.75 | 14.21 | |
| Old | 104 | 37.95 | 56.56 | 1.49 | 954.63 | 2 | ||||
| 3 Cerebral | Gender | Male | 302 | 33.71 | 49.88 | 1.48 | 2694.19 | 2 | 5981.96 | −3.18 |
| Female | 353 | 39.19 | 45.55 | 1.16 | 3287.78 | 2 | ||||
| Age | Young | 194 | 24.07 | 42.45 | 1.76 | 1586.02 | 2 | 5949.18 | 29.61 | |
| Old | 461 | 41.96 | 48.79 | 1.16 | 4363.16 | 2 | ||||
| 4 TIA | Gender | Male | 207 | 8.7 | 22.68 | 2.61 | 1229.17 | 2 | 2619.64 | −7.26 |
| Female | 218 | 9.89 | 16.94 | 1.71 | 1390.47 | 2 | ||||
| Age | Young | 176 | 5.84 | 11.16 | 1.91 | 924.58 | 2 | 2593.06 | 19.32 | |
| Old | 249 | 11.77 | 24.02 | 2.04 | 1668.48 | 2 | ||||
| 5 Other strokes | Gender | Male | 344 | 30.74 | 43.41 | 1.41 | 3014.02 | 2 | 6645.27 | −8.35 |
| Female | 407 | 34.07 | 78.8 | 2.31 | 3631.25 | 2 | ||||
| Age | Young | 204 | 24.96 | 43.76 | 1.75 | 1662.38 | 2 | 6611.95 | 24.97 | |
| Old | 547 | 35.37 | 71.17 | 2.01 | 4949.57 | 2 | ||||
| 6 Hemorrhagic Young | Gender | Male | 29 | 30.52 | 69.11 | 2.26 | 226.49 | 2 | 375.19 | −5.07 |
| Female | 21 | 16.33 | 22.81 | 1.4 | 148.71 | 2 | ||||
| 7 Hemorrhagic Old | Gender | Male | 51 | 26.88 | 39.2 | 1.46 | 437.87 | 2 | 954.43 | 0.19 |
| Female | 53 | 48.6 | 67.58 | 1.39 | 516.56 | 2 | ||||
| 8 Cerebral Young | Gender | Male | 104 | 24.67 | 49.27 | 2 | 853.33 | 2 | 1591.24 | −5.22 |
| Female | 90 | 23.37 | 32.94 | 1.41 | 737.91 | 2 | ||||
| 9 Cerebral Old | Gender | Male | 198 | 38.45 | 49.67 | 1.29 | 1836.51 | 2 | 4369.07 | −5.92 |
| Female | 263 | 44.6 | 47.94 | 1.07 | 2532.56 | 2 | ||||
| 10 TIA Young | Gender | Male | 88 | 5.74 | 11.33 | 1.97 | 460.65 | 2 | 933.56 | −8.98 |
| Female | 88 | 5.93 | 11 | 1.85 | 472.91 | 2 | ||||
| 11 TIA Old | Gender | Male | 119 | 10.89 | 28.08 | 2.58 | 767.35 | 2 | 1674.19 | −5.71 |
| Female | 130 | 12.58 | 19.53 | 1.55 | 906.85 | 2 | ||||
| 12 Other strokes Young | Gender | Male | 119 | 30.11 | 52.77 | 1.75 | 1006.47 | 3 | 1665.64 | −3.26 |
| Female | 85 | 17.75 | 24.66 | 1.75 | 659.17 | 2 | ||||
| 13 Other strokes Old | Gender | Male | 225 | 31.08 | 37.52 | 1.21 | 2000.22 | 2 | 4955.54 | −5.97 |
| Female | 322 | 38.37 | 87.17 | 2.27 | 2955.32 | 2 |
| Node | Destination | Number of Patients | Mean LOS | Standard Deviation (LOS) | Coefficient of Variation | WIC | Number of Phases | Degrees of Freedom () | Total WIC | Gain in WIC |
|---|---|---|---|---|---|---|---|---|---|---|
| 6 Hemorrhagic Young | All | 50 | 24.56 | 55.12 | 2.24 | 370.13 | 4 | 7 | - | - |
| Death | 17 | 16.41 | 40.62 | 2.48 | 98.52 | 2 | 10 | 369.19 | 0.94 | |
| Other | 33 | 28.76 | 60.83 | 2.12 | 270.67 | 4 | ||||
| 14 Hemorrhagic Old Male | All | 51 | 26.88 | 39.2 | 1.46 | 437.87 | 2 | 3 | - | - |
| Death | 21 | 10.9 | 14.73 | 1.35 | 141.1 | 2 | 7 | 395.23 | 42.64 | |
| Other | 27 | 31.89 | 38.85 | 1.22 | 243.81 | 1 | ||||
| PNH | 3 | 93.67 | 67.48 | 0.72 | 10.32 | 2 | ||||
| 15 Hemorrhagic Female | All | 53 | 48.6 | 67.58 | 1.39 | 516.56 | 2 | 3 | - | - |
| Death | 27 | 24.15 | 35.47 | 1.47 | 223.82 | 2 | 7 | 490.63 | 25.93 | |
| Other | 24 | 74.17 | 85.36 | 1.15 | 257.48 | 1 | ||||
| PNH | 2 | 74.17 | 85.36 | 1.15 | 9.33 | 2 | ||||
| 8 Cerebral Young | All | 194 | 24.07 | 42.45 | 1.76 | 1586.02 | 2 | 3 | - | - |
| Death | 14 | 21.29 | 35.22 | 1.65 | 112.65 | 2 | 7 | 1585.46 | 0.56 | |
| Other | 174 | 22.28 | 40.5 | 1.82 | 1405.34 | 2 | ||||
| PNH | 6 | 82.33 | 63.22 | 0.77 | 67.48 | 1 | ||||
| 9 Cerebral Old | All | 461 | 41.96 | 48.79 | 1.16 | 4363.16 | 2 | 3 | - | - |
| Death | 112 | 35.66 | 46.4 | 1.3 | 1028.5 | 1 | 5 | 4339.19 | 23.97 | |
| Other | 296 | 36.94 | 43.09 | 1.17 | 2732.54 | 2 | ||||
| PNH | 53 | 83.34 | 62.02 | 0.74 | 578.15 | 1 | ||||
| 10 TIA Young | All | 176 | 5.84 | 11.16 | 1.91 | 924.58 | 2 | 3 | - | - |
| Death | 2 | 57.5 | 12.5 | 0.22 | 8.47 | 2 | 7 | 890.83 | 33.75 | |
| Other | 173 | 4.8 | 7.77 | 1.62 | 873.57 | 2 | ||||
| PNH | 1 | 81 | 0 | 0 | 8.79 | 1 | ||||
| 11 TIA Old | All | 249 | 11.77 | 24.02 | 2.04 | 1668.48 | 2 | 3 | - | - |
| Death | 11 | 33.27 | 30.31 | 0.91 | 101.53 | 1 | 5 | 1655.42 | 13.06 | |
| Other | 231 | 10.58 | 23.32 | 2.2 | 1497.54 | 2 | ||||
| PNH | 7 | 17.29 | 18.01 | 1.04 | 56.35 | 1 | ||||
| 12 Other strokes Young | All | 204 | 24.96 | 43.76 | 1.75 | 1662.38 | 2 | 3 | - | - |
| Death | 22 | 20.27 | 27.84 | 1.37 | 179.13 | 1 | 7 | 1638.66 | 23.72 | |
| Other | 179 | 25.13 | 45.48 | 1.81 | 1454.59 | 2 | ||||
| PNH | 3 | 49.33 | 19.48 | 0.39 | 4.94 | 2 | ||||
| 13 Other strokes Old | All | 547 | 35.37 | 71.17 | 2.01 | 4949.57 | 2 | 3 | - | - |
| Death | 142 | 41.82 | 123.73 | 2.96 | 1295.56 | 2 | 11 | 4895.2 | 54.37 | |
| Other | 358 | 28.27 | 33.35 | 1.18 | 3104.34 | 3 | ||||
| PNH | 47 | 70.02 | 50.18 | 0.72 | 495.31 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garg, L.; McClean, S.; Meenan, B.; Barton, M.; Fullerton, K.; Buttigieg, S.C.; Micallef, A. Phase-Type Survival Trees to Model a Delayed Discharge and Its Effect in a Stroke Care Unit. Algorithms 2022, 15, 414. https://doi.org/10.3390/a15110414
Garg L, McClean S, Meenan B, Barton M, Fullerton K, Buttigieg SC, Micallef A. Phase-Type Survival Trees to Model a Delayed Discharge and Its Effect in a Stroke Care Unit. Algorithms. 2022; 15(11):414. https://doi.org/10.3390/a15110414
Chicago/Turabian StyleGarg, Lalit, Sally McClean, Brian Meenan, Maria Barton, Ken Fullerton, Sandra C. Buttigieg, and Alexander Micallef. 2022. "Phase-Type Survival Trees to Model a Delayed Discharge and Its Effect in a Stroke Care Unit" Algorithms 15, no. 11: 414. https://doi.org/10.3390/a15110414
APA StyleGarg, L., McClean, S., Meenan, B., Barton, M., Fullerton, K., Buttigieg, S. C., & Micallef, A. (2022). Phase-Type Survival Trees to Model a Delayed Discharge and Its Effect in a Stroke Care Unit. Algorithms, 15(11), 414. https://doi.org/10.3390/a15110414








