Domination and Independent Domination in Extended Supergrid Graphs ^†

Abstract

Supergrid graphs are derived by computing stitch paths for computerized embroidery machines. In the past, we have studied the Hamiltonian-related properties of supergrid graphs and their subclasses of graphs. In this paper, we propose a generalized graph class for supergrid graphs called extended supergrid graphs. Extended supergrid graphs include grid graphs, supergrid graphs, diagonal supergrid graphs, and triangular supergrid graphs as subclasses of graphs. In this paper, we study the problems of domination and independent domination on extended supergrid graphs. A dominating set of a graph is the subset of vertices on it, such that every vertex of the graph is in this set or adjacent to at least a vertex of this set. If any two vertices in a dominating set are not adjacent, this is called an independent dominating set. Domination and independent domination problems find a dominating set and an independent dominating set with the least number of vertices on a graph, respectively. The domination and independent domination set problems on grid graphs are known to be NP-complete, meaning that these two problems on extended supergrid graphs are also NP-complete. However, the complexities of these two problems in other subclasses of graphs remain unknown. In this paper, we first prove that these two problems on diagonal supergrid graphs are NP-complete, then, by a simple extension, we prove that these two problems on supergrid graphs and triangular supergrid graphs are also NP-complete. In addition, these two problems on rectangular supergrid graphs are known to be linearly solvable; however, the complexities of these two problems on rectangular triangular-supergrid graphs remain unknown. This paper provides tight upper bounds on the sizes of the minimum dominating and independent dominating sets for rectangular triangular-supergrid graphs.

1. Introduction

For a graph G, we denote the vertex and edge sets of G as $V(G$) and $E\left(G\right)$, respectively. Let v be a vertex of $V\left(G\right)$, and let S be a subset of $V\left(G\right)$. We denote the subgraph induced by S as $G\left[S\right]$. The degree of vertex v in G is denoted by $de{g}_G\left(v\right)$, which represents the number of edges incident with v in G. The set of neighbors of a vertex v in G is denoted by $N_G\left(v\right)=\{u\in V\left(G\right)|(u,v)\in E\left(G\right)\}$ and $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$. The neighborhood set of vertex set S in G is defined as $N_G\left(S\right)={\cup }_{v\in S}{N}_G\left(v\right)-S$ and $N_G\left[S\right]=N_G\left(S\right)\cup S$. Let $D\subseteq V\left(G\right)$; a set D is said to dominate vertex v if $N_G\left[v\right]\cap D\ne \varnothing$. In addition, we can say that vertex v dominates its neighbors and itself. We say that D dominates S when D dominates every vertex of set S. If D dominates $V\left(G\right)$, set D is said to be a dominating set of G. The domination number of a graph G, expressed as $\gamma \left(G\right)$, is the minimum size of a dominating set of G. A minimum dominating set of graph G is a dominating set with size $\gamma \left(G\right)$. The domination problem is to find a minimum dominating set of a graph, and is a well-known NP-complete problem for general graphs [1]. However, the problem remains NP-complete when the input is restricted to certain special classes of graphs, including grid graphs [2], 4-regular planar graphs [1], etc.

In the literature, the problems of domination and its variants have been extensively studied. A variant of the domination problem is to find a minimum dominating set that satisfies some special conditions. For example, the connected domination problem is to compute a minimum dominating set such that the subgraph induced by it is connected, and the dominating cycle problem is to find a cycle with the least number of vertices to dominate the input graph. In the past, many scholars have proposed many applications for dominating sets and their variants. For instance, in distributed network applications the domination problem is to find the minimum number of control centers placed in the network to ensure that each node is close to at least one center. In a guard location system, the connected domination problem is to locate the fewest number of guards, allowing them to connect to each other in order to protect each other and monitor other locations. For related concepts and applications of these problems, we refer the reader to two survey books in [3,4]. In this paper, the domination problem, as well as one variant called the independent domination problem, are studied.

A set of vertices is called independent if any two vertices in it are not adjacent. An independent dominating set of a graph G is a dominating set I satisfying I as an independent set. The independent domination number of a graph G, expressed as ${\gamma }_{\mathrm{ind}}\left(G\right)$, is the minimum cardinality of an independent domination set in G. Because an independent dominating set of a graph G is a dominating set of G, $\gamma \left(G\right)⩽{\gamma }_{\mathrm{ind}}\left(G\right)$ for any graph G. That is, $\gamma \left(G\right)$ provides a trivial lower bound for ${\gamma }_{\mathrm{ind}}\left(G\right)$. The independent domination problem on graph G is to find an independent dominating set with size ${\gamma }_{\mathrm{ind}}\left(G\right)$. This problem is NP-complete for general graphs [1], and remains NP-complete for grid graphs [2], comparability graphs, bipartite graphs [5], sat-graphs [6], line graphs [7], chordal bipartite graphs [8], etc. However, when the input is in some special class of graphs, it allows polynomial-time algorithms, including permutation graphs, interval graphs [9], chordal graphs [10], circular-arc graphs [11], AT-free graphs [12], bounded clique-width graphs [13], etc. For more relevant works on independent domination, we refer the reader to a survey in [14], and more results in [15,16,17,18]. For other relevant works and comparisons, the reader is referred to [19,20,21].

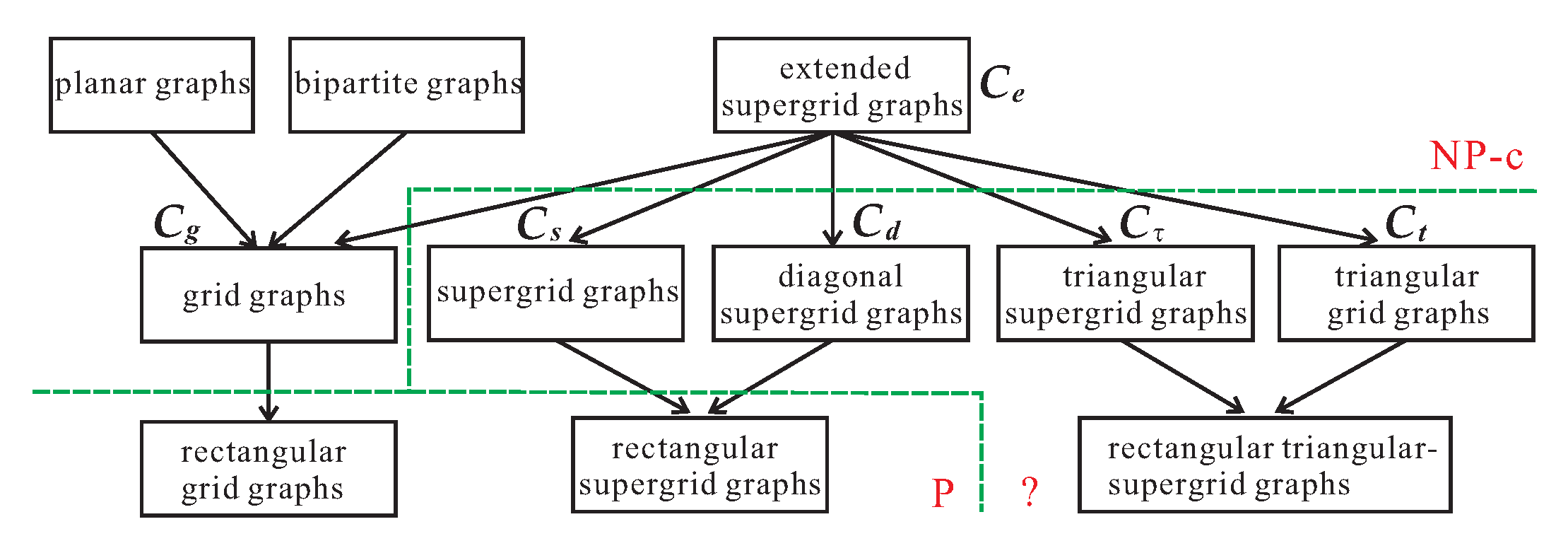
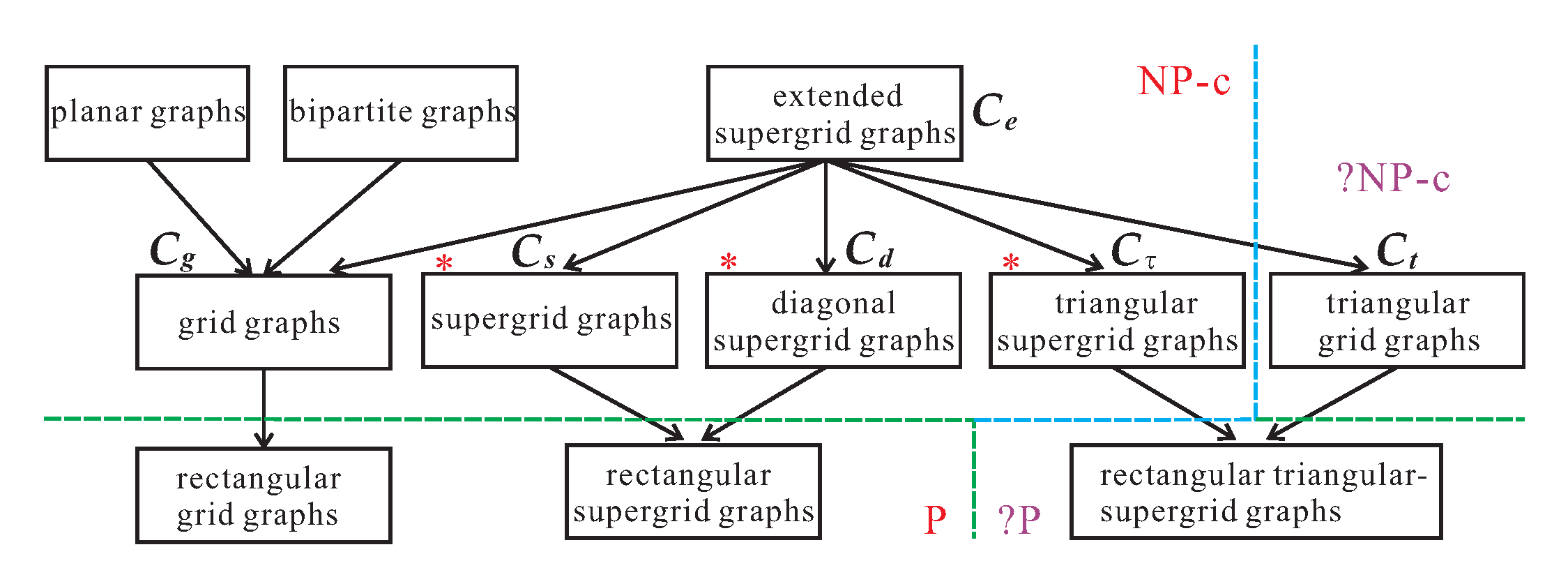
Supergrid graphs have been proposed for computing the stitch traces for computerized embroidery machines [22]. Unfortunately, the Hamiltonian cycle and path problems on supergrid graphs have been shown to be NP-complete in [22]. Thus, we studied the complexities of the Hamiltonian and longest paths for the special classes of supergrid graphs in [23,24,25,26,27]. In this paper, we expand supergrid graphs to a generalized graph class called extended supergrid graphs. In general, a supergrid graph is not a grid graph, and vice versa. Extended graphs contain supergrid, grid, diagonal supergrid, triangular supergrid graphs as graph subcalsses. Generally, rectangular grid graphs form a subclass of grid graphs, rectangular supergrid graphs form a subclass of supergrid and diagonal supergrid graphs, and rectangular triangular-supergrid graphs are a subclass of triangular supergrid graphs. However, the intersection of rectangular grid graphs, rectangular supergrid graphs, and rectangular triangular-supergrid graphs is empty, except for certain special paths. In this paper, we study the complexities of domination and independent domination problems for extended supergrid graphs and their subclasses. The domination problem on grid graphs is known to be NP-complete [2]. Thus, the studied problems are NP-complete as well for extended supergrid graphs. In [28], we provided a rough proof to claim that the domination and independent domination problems on supergrid graphs are NP-complete. In this paper, we present a full proof to show that the domination and independent domination problems on diagonal supergrid graphs are NP-complete. By a simple extension, we verify that these two problems for supergrid and triagular supergrid graphs are NP-complete as well. On the other hand, the domination and independent domination numbers of rectangular grid graphs have been computed in [18,29,30,31]. In [28], we solved the domination and independent domination problems on rectangular supergrid graphs in linear time. However, the complexities of the domination and independent domination problems on rectangular triangular-supergrid graphs remain unknown. In this paper, we provide a tight upper bound of the domination and independent domination numbers for rectangular triangular-supergrid graphs.

The remainder of this paper is organized as follows. Section 2 describes the symbols used in this paper, definitions, and several known related results. In Section 3, we first prove the domination and independent domination problems on diagonal supergrid graphs to be NP-complete in detail. We then extend this result into supergrid and triangular supergrid graphs. In Section 4, we provide a tight upper bound of the domination and independent domination numbers for rectangular triangular-supergrid graphs. Finally, concluding remarks are made in Section 5.

2. Preliminaries

In this section, we define the notation used in the paper and present results in the literature that are relevant to our work. For graph theory terms not defined here, the reader is referred to [32]. Let G be an undirected and simple graph with a vertex set $V\left(G\right)$ and an edge set $E\left(G\right)$. A (simple) path P in G, expressed as $v_1\to v_2\to \dots \to v_{\left|P\right|-1}\to v_{\left|P\right|}$, is a sequence $(v_1,v_2,\dots ,v_{\left|P\right|-1},v_{\left|P\right|})$ of distinct vertices such that $(v_i,v_{i+1})\in E\left(G\right)$ for $1⩽i<\left|P\right|$. We use “$v_i\in P$” to mean “$v_i$ is a vertex that appears in P” and the edge “$(v_i,v_{i+1})\in P$” to mean “P visits edge $(v_i,v_{i+1})$”. The path from vertex $v_1$ to vertex $v_k$ is represented as the $(v_1,v_k)$-path, and to avoid confusion we use $P_n$ to denote a path with n vertices. To simplify notation, we use % for modulo arithmetic throughout the rest of this paper. The following lemma shows the domination and independent domination numbers $\gamma \left(P_n\right)$ and ${\gamma }_{\mathrm{ind}}\left(P_n\right)$ of path $P_n$ provided in [30], and can be easily proven by induction on n.

Lemma 1.

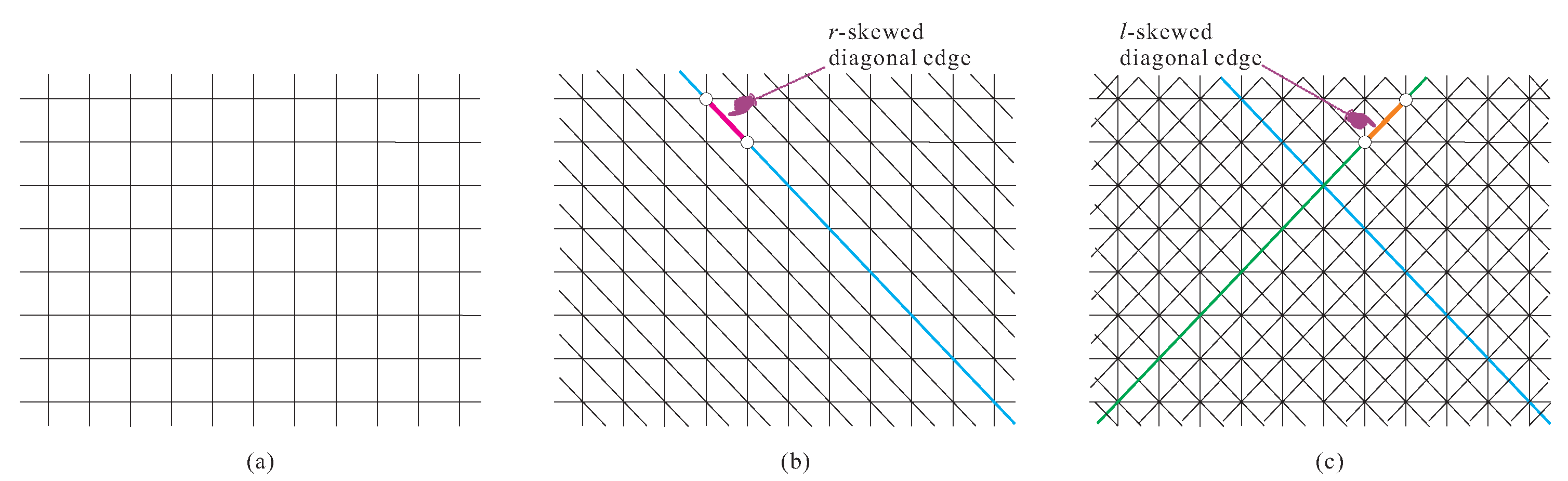
(see [30]). $\gamma \left(P_n\right)={\gamma }_{\mathrm{ind}}\left(P_n\right)=\lfloor \frac{n+2}{3}\rfloor =\lceil \frac{n}{3}\rceil$, where n denotes the number of vertices in path $P_n$.

Due to the above lemma, the following proposed graph classes do not contain paths as graph subclasses. We introduce extended supergrid graphs and its subclasses of graphs as follows. Let $S^{\infty }$ be an infinite graph such that its vertex set $V\left(S^{\infty }\right)$ contains all points of the Euclidean plane with integer coordinates and its edge set $E\left(S^{\infty }\right)=\left\{(u,v)\right|$$|u_x-v_x|⩽1$ and $|u_y-v_y|⩽1\}$, where ${\mu }_x$ and ${\mu }_y$ represent the x and y coordinates of vertex $\mu$, respectively, expressed as $\mu =({\mu }_x,{\mu }_y)$ for $\mu \in V\left(S^{\infty }\right)$. We call $S^{\infty }$ the two-dimensional integer supergrid. Suppose $(u,v)\in E\left(S^{\infty }\right)$. In the graph we represent, when $u_y<v_y$, this indicates that vertex u is above v, and when $u_x<v_x$, u is to the left of v. If $u_x=v_x$ (respectively, $u_y=v_y$), then $(u,v)$ is called a vertical (respectively, horizontal) edge; otherwise, it is called a diagonal edge. There are two types of diagonal edges $(u,v)$: if $v_x=u_x-1$ and $v_y=u_y+1$, then diagonal edge $(u,v)$ is called l-skewed; otherwise, it is called r-skewed. In our graph representation, when $(u,v)$ is a l-skewed diagonal edge and u is above v, u is located at the upper right of v in the plane; otherwise, u is located in the upper left of v in the plane. The two-dimensional integer grid $G^{\infty }$ is an infinite graph that satisfies $V\left(G^{\infty }\right)=V\left(S^{\infty }\right)$ and $E\left(G^{\infty }\right)=\left\{(u,v)\right|$$(u,v)$ is a horizontal or vertical edge}. In addition, the two-dimensional triangular integer grid $T^{\infty }$ is an infinite graph satisfying $V\left(T^{\infty }\right)=V\left(S^{\infty }\right)$ and $E\left(T^{\infty }\right)=\left\{(u,v)\right|$$(u,v)$ is a horizontal, vertical, or r-skewed diagonal edge}. 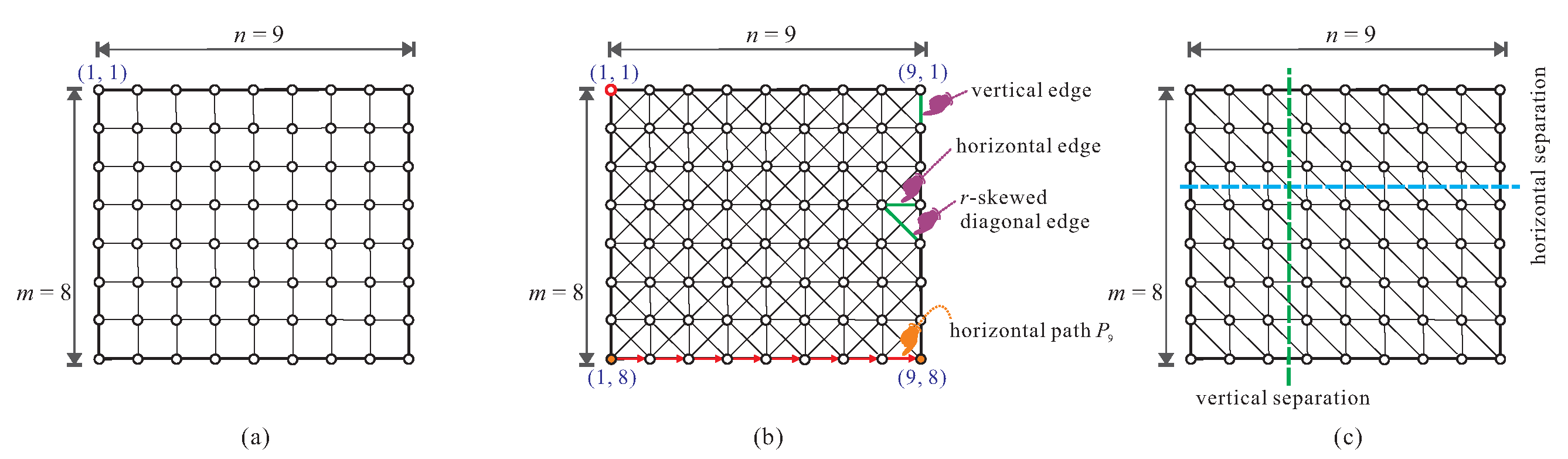For example, Figure 1a–c depicts partial fragments of the infinite graphs $G^{\infty }$, $T^{\infty }$ and $S^{\infty }$, respectively.

An extended supergrid graph is a finite connected subgraph of $S^{\infty }$, while a grid graph (respectively, triangular grid graph, supergrid graph) is a finite and vertex-induced subgraph of $G^{\infty }$ (respectively, $T^{\infty }$, $S^{\infty }$). Note that an extended supergrid graph is not necessarily a vertex-induced subgraph of $S^{\infty }$. Thus, extended supergrid graphs contain grid graphs, triangular grid graphs, and supergrid graphs as subclasses of graphs. A diagonal supergrid graph is an extended supergrid graph with an edge set that contains at least one l-skewed and one r-skewed diagonal edge, and a triangular supergrid graph is an extended supergrid graph such that its edge set contains at least one r-skewed diagonal edge and no l-skewed diagonal edges. In general, a diagonal supergrid graph is not necessarily a supergrid graph, and vice versa. The same applies to triangular supergrid graphs and triangular grid graphs. Let ${\mathcal{C}}_e$, ${\mathcal{C}}_g$, ${\mathcal{C}}_s$, ${\mathcal{C}}_d$, ${\mathcal{C}}_{\tau }$, and ${\mathcal{C}}_t$ be the graph classes of extended supergrid, grid, supergrid, diagonal supergrid, triangular supergrid, and triangular grid graphs, respectively. Then, ${\mathcal{C}}_g,{\mathcal{C}}_s,{\mathcal{C}}_d,{\mathcal{C}}_{\tau },{\mathcal{C}}_t\subset {\mathcal{C}}_e$, ${\mathcal{C}}_g\cap {\mathcal{C}}_s={\mathcal{C}}_g\cap {\mathcal{C}}_t={\mathcal{C}}_s\cap {\mathcal{C}}_t=\varnothing$, ${\mathcal{C}}_s\cap {\mathcal{C}}_d\ne \varnothing$, and ${\mathcal{C}}_{\tau }\cap {\mathcal{C}}_t\ne \varnothing$. Figure 2 shows the relationship among these graph classes and indicates the complexities of the studied problems for these graph classes. Obviously, all grid graphs are bipartite [33] and planar; however, (extended, diagonal, triangular) supergrid graphs and triangular grid graphs may not be bipartite. Let $G_g$, $G_s$, and $G_t$ be a grid, supergrid, and triangular grid graph, respectively. Let $\nu \in V\left(G_g\right)$, $\mu \in V\left(G_s\right)$, and $\omega \in V\left(G_t\right)$. Then, $N_{G_g}\left(\nu \right)\subseteq \{({\nu }_x,{\nu }_y+1),({\nu }_x,{\nu }_y-1),({\nu }_x+1,{\nu }_y),({\nu }_x-1,{\nu }_y)\}$, $N_{G_s}\left(\mu \right)\subseteq \{({\mu }_x,{\mu }_y+1),({\mu }_x,{\mu }_y-1),({\mu }_x+1,{\mu }_y),({\mu }_x-1,{\mu }_y),({\mu }_x-1,{\mu }_y-1),({\mu }_x-1,{\mu }_y+1),({\mu }_x+1,{\mu }_y-1),({\mu }_x+1,{\mu }_y+1)\}$, and $N_{G_t}\left(\omega \right)\subseteq \{({\omega }_x,{\omega }_y+1),({\omega }_x,{\omega }_y-1),({\omega }_x+1,{\omega }_y),({\omega }_x-1,{\omega }_y),({\omega }_x-1,{\omega }_y-1),({\omega }_x+1,{\omega }_y+1)\}$. That is, $de{g}_{G_g}\left(\nu \right)⩽4$, $de{g}_{G_s}\left(\mu \right)⩽8$, and $de{g}_{G_t}\left(\omega \right)⩽6$.

A rectangular grid graph, denoted $G_{m\times n}$, is the Cartesian product of paths $P_m$ and $P_n$; thus, $(u,v)\in E\left(G_{m\times n}\right)$ if and only if their distance is 1, that is, $|u_x-v_x|+|u_y-v_y|=1$, where $P_i$ is the simple path with i vertices. A rectangular supergrid (called King’s) graph, denoted $R_{m\times n}$, is the strong product of paths $P_m$ and $P_n$; thus, $(u,v)\in E\left(R_{m\times n}\right)$ if and only if their distance is less than or equal to $\sqrt{2}$, that is, $0⩽|u_x-v_x|⩽1$ and $0⩽|u_y-v_y|⩽1$. A rectangular triangular-supergrid graph, denoted $T_{m\times n}$, is obtained from $G_{m\times n}$ by adding edges $(u,v)$ for $u,v\in V\left(G_{m\times n}\right)$, $u_x=v_x-1$, and $u_y=v_y-1$, i.e., adding diagonal r-skewed edge to each square of $G_{m\times n}$. Then, for $v\in V\left(G_{m\times n}\right)$, $u\in V\left(R_{m\times n}\right)$ and $w\in V\left(T_{m\times n}\right)$, we have $de{g}_{G_{m\times n}}\left(v\right)⩽4$, $de{g}_{R_{m\times n}}\left(u\right)⩽8$, and $de{g}_{T_{m\times n}}\left(v\right)⩽6$. Furthermore, for $m,n⩾2$, $2⩽de{g}_{G_{m\times n}}\left(v\right)$, $3⩽de{g}_{R_{m\times n}}\left(u\right)$, and $2⩽de{g}_{T_{m\times n}}\left(w\right)$. Note that we use $(1,1)$ to denote the coordinates of the upper-left-most vertex of a (grid, supergrid, triangular supergrid) graph in the figures. For example, Figure 3a–c shows $G_{8\times 9}$, $R_{8\times 9}$ and $T_{8\times 9}$, respectively. Notice that $G_{m\times n}$, $R_{m\times n}$, and $T_{m\times n}$ are not paths; hence, $m,n⩾2$. Without loss of generality, we assume that $n⩾m⩾2$ for these rectangular graphs.

A path in an extended supergrid graph is called a horizontal (respectively, vertical) path if all of its edges are horizontal (respectively, vertical) edges. For instance, the arrow lines in Figure 3b depict a horizontal path $P_9$. In [28,34], the domination number $\gamma \left(R_{m\times n}\right)$ and the independent domination number ${\gamma }_{\mathrm{ind}}\left(R_{m\times n}\right)$ of $R_{m\times n}$ are computed as follows:

Lemma 2.

(see [28,34]). $\gamma \left(R_{m\times n}\right)={\gamma }_{\mathrm{ind}}\left(R_{m\times n}\right)=\lceil \frac{m}{3}\rceil \lceil \frac{n}{3}\rceil$.

The complexities of the domination and independent domination problems on rectangular triangular-supergrid graphs remain open. In this paper, we provide a tight upper bound of $\gamma \left(T_{m\times n}\right)$ and ${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$. To simplify notation, for a dominating set D of graph G and the subgraph H of G, we denote the restriction from D to H as $D_{|H}$. In our method, a partition may be made on a rectangular triangular-supergrid graph which is split into two disjoint parts, and is defined below.

Definition 1.

Let T be a rectangular triangular-supergrid graph. The separation operation on T is to divide T into two vertex-disjoint rectangular triangular-supergrid subgraphs $T_1$ and $T_2$, that is, $V\left(T\right)=V\left(T_1\right)\cup V\left(T_2\right)$ and $V\left(T_1\right)\cap V\left(T_2\right)=\varnothing$. If a separation consists of a set of horizontal edges, it is called vertical, and if it consists of a set of vertical edges, it is called horizontal. For example, the bold vertical (respectively, horizontal) dashed line in Figure 3c represents a vertical (respectively, horizontal) separation on $T_{8\times 9}$ divided into $T_{8\times 3}$ and $T_{8\times 6}$(respectively, $T_{3\times 9}$ and $T_{5\times 9}$).

3. NP-Completeness Results

The domination and independent domination problems on grid graphs have been shown to be NP-complete [2]; thus, they are NP-complete for extended supergrid graphs as well, as extended supergrid graphs contain grid graphs as a subclass of graphs (see Figure 2). However, their complexities for diagonal supergrid, triangular supergrid, and supergrid graphs remain unknown. In [28], we have provided a rough proof to claim that they are NP-complete for supergrid graphs. In this section, we present a complete proof to show that they are NP-complete for diagonal supergrid graphs. We then expand this to verify that they are NP-complete for supergrid and triangular supergrid graphs as well. To demonstrate this, we establish a polynomial-time reduction from the domination problem on grid graphs. In [2], Clark et al. provided the following theorem:

Theorem 1.

(see [2]). The domination problem on grid graphs is NP-complete.

We reduce the domination problem on grid graphs to the domination problem on diagonal supergrid graphs. Consider a grid graph $G_g$; a diagonal supergrid graph $G_d$ is constructed to satisfy that $G_g$ has a dominating set D of size $\left|D\right|⩽k$ if and only if $G_d$ contains a dominating set $D^{\prime }$ of size $|D^{\prime }|⩽k+2|E\left(G_g\right)|$. The steps for constructing the diagonal supergrid graph $G_d$ from the grid graph $G_g$ are as follows. First, the input grid graph $G_g$ is enlarged to transform each edge of $G_g$ into a vertical or horizontal path with seven edges, that is, each edge of $G_g$ is enlarged by a factor of seven. The enlarged grid graph is represented as $G_g^{\prime }$. For example, Figure 4b shows the grid graph $G_g^{\prime }$ enlarged from $G_g$ in Figure 4a. The second step is to replace each $(u,v)$-path of the graph $G_g^{\prime }$ with a special diagonal supergrid graph, where $u,v\in V\left(G_g\right)$. This special diagonal supergrid is a $(u,v)$-path with seven edges, and contains at least one l-skewed and one r-skewed edges; we call it snake $(u,v)$-path and denote it as $S(u,v)$. For a snake $(u,v)$-path $S(u,v)$, u and v are said to be the connectors of $S(u,v)$. Figure 4c shows a snake $(u,v)$-path. Then, the constructed graph is a diagonal supergrid graph $G_d$. For example, Figure 4d depicts a diagonal supergrid graph $G_d$ constructed from the grid graph $G_g$ in Figure 4a.

Next, we propose a method for placing snake paths on the enlarged grid graph $G_g^{\prime }$ such that any two snake paths are vertex-disjoint except for their connectors. Consider a square of a grid graph $G_g$ with vertices $(i,j)$, $(i,j+1)$, $(i+1,j)$, $(i+1,j+1)$. Then, these four vertices are the connectors of the corresponding snake paths. If $i,j$ are both odd or even, we place the four snake paths as shown in Figure 5a; otherwise, we place these snake paths as shown in Figure 5b. Then, in a corresponding square of an enlarged grid $G_g^{\prime }$, at most two snake paths are placed inside it and opposite each other. In addition, the two snake paths inside the corresponding square are separated by at least two integer points. Therefore, none of the vertices are repeated except for the connectors of the snake paths. Algorithm 1 illustrates the detailed steps above for placing snake paths. For example, Figure 6 describes the arrangement of snake paths in $G_d$ for $G_g=G_{16\times 16}$. Then, the following property holds immediately.

Lemma 3.

Algorithm 1 arranges the snake paths of $G_d$ such that these paths are vertex-disjoint except for their connectors.

The construction algorithm of diagonal supergrid graph $G_d$ is formally presented as Algorithm 1. Because a snake path is a diagonal supergrid graph and the input grid graph $G_g$ contains at least one edge, the constructed graph $G_d$ of Algorithm 1 is a diagonal supergrid graph. In addition, each edge of $G_g$ is enlarged a constant number of times, and each enlarged edge is replaced with one snake path, Algorithm 1 runs in $O\left(\right|V\left(G_g\right)|+|E\left(G_g\right)\left|\right)$-linear time. Thus, the following lemma holds true.   

Algorithm 1: The diagonal supergrid graph construction algorithm
	Input: A grid graph $G_g$. (see Figure 4a)
	Output: A diagonal supergrid graph $G_d$. (see Figure 4d)
	Method: // $\phantom{(}$an algorithm for constructing a diagonal supergrid graph from a grid graph$\phantom{(}$
1.	enlarge $G_g$ to a grid graph $G_g^{\prime }$, so that each edge of $G_g$ is transformed into a  vertical or horizontal path with 7 edges; (see Figure 4b)
2.	let $G_d=G_g^{\prime }$;
3.	foreach enlarged $(u,v)$-path $P(u,v)$ in $G_g^{\prime }$, where $u,v\in V\left(G_g\right)$ do$\phantom{(}$
4.			let $u=(u_x,u_y)$ and $v=(v_x,v_y)$ be the vertices in grid graph $G_g$ with $u_x⩽v_x$
			and $u_y⩽v_y;$
5.			let $S(u,v)$ be the snake $(u,v)$-path corresponding to $P(u,v);$
			// Note that if $v_x=u_x+1$, then $P(u,v)$ is a horizontal path; otherwise, $P(u,v)$ is a
			vertical path
6.			if$v_x=u_x+1$then
7.					if$u_y\%2=1$then
8.							if$u_x\%2=1$then
9.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is above $P(u,v);$
10.							else
11.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is below $P(u,v);$
12.					else
13.							if$u_x\%2=1$then
14.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is below $P(u,v);$
15.							else
16.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is above $P(u,v);$
17.			else
18.					if$u_x\%2=1$then
19.							if$u_y\%2=1$then
20.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is to the right of
									$P(u,v);$
21.							else
22.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is to the left of
									$P(u,v);$
23.					else
24.							if$u_y\%2=1$then
25.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is to the left of
									$P(u,v);$
26.							else
27.									replace $P(u,v)$ with $S(u,v)$ in $G_d$ so that $S(u,v)$ is to the right of
									$P(u,v);$
28.	output$G_d$.

Lemma 4.

Given a grid graph $G_g$, Algorithm 1 constructs a diagonal supergrid graph $G_d$ in $O\left(\right|V\left(G_g\right)|+|E\left(G_g\right)\left|\right)$-linear time.

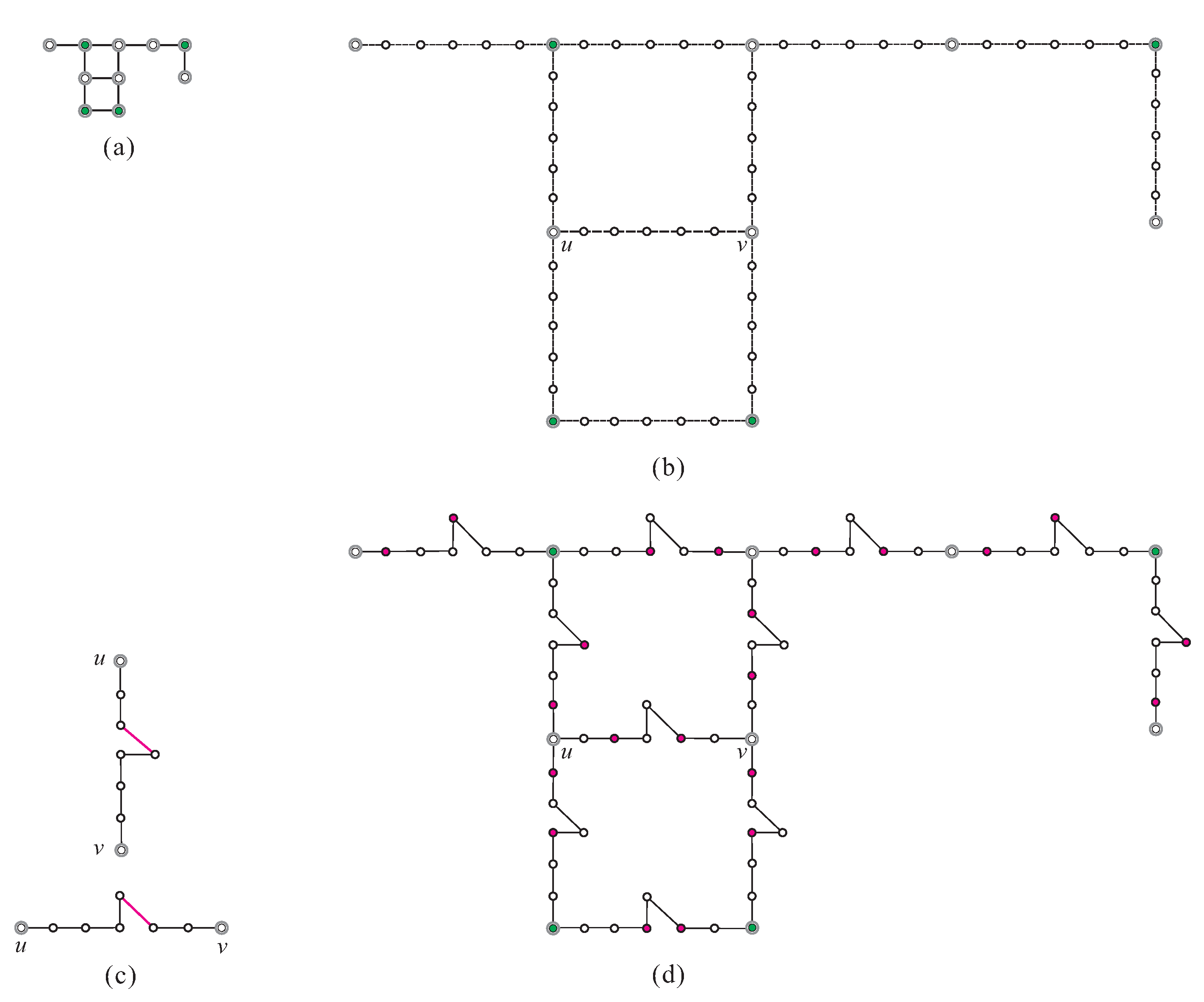
Next, we verify that grid graph $G_g$ has a dominating set D of size $\left|D\right|⩽k$ if and only if diagonal supergrid graph $G_d$ contains a dominating set $D^{\prime }$ of size $|D^{\prime }|⩽k+2|E\left(G_g\right)|$. Before providing the proof, we first observe several properties of the snake path. Note that the snake path is a simple path $P_8$ with eight vertices. Recall that for a dominating set D of graph G and the subgraph H of G, we denote the restriction from D to H as $D_{|H}$. Let $D^{\prime }$ be a dominating set of diagonal supergrid graph $G_d$, and let $S(u,v)$ be a snake path with connectors u and v in $G_d$. Let $u_d\in N_{G_d}\left(u\right)\cap D^{\prime }$ if $u\notin D^{\prime }$, and $v_d\in N_{G_d}\left(v\right)\cap D^{\prime }$ if $v\notin D^{\prime }$. Then, $u_d$ and $v_d$ dominate u and v, respectively, if $u,v\notin D^{\prime }$. According to whether u and v are in $D^{\prime }$, we consider the following situations.

Case 1: $u,v\in D^{\prime }$. Because $D^{\prime }$ is a dominating set of $G_d$, $G_d[S(u,v)-(N_{G_d}\left[u\right]\cup N_{G_d}\left[v\right])]$ is a path $P_4$ with four vertices. Per Lemma 1, $\gamma (S(u,v)-(N_{G_d}\left[u\right]\cup N_{G_d}\left[v\right]))=2$ (see Figure 7a). Therefore, $|D_{\left|S\right(u,v)-\{u,v\}}^{\prime }|⩾2$ and $\gamma (S(u,v)-(N_{G_d}\left[u\right]\cup N_{G_d}\left[v\right]))=2$.

Case 2: either $u\in D^{\prime }$ or $v\in D^{\prime }$. Without loss of generality, assume $u\in D^{\prime }$ and $v\notin D^{\prime }$. Consider that $S(u,v)$ does not contain $v_d$. Then, $G_d[S(u,v)-(N_{G_d}\left[u\right]\cup \left\{v\right\})]$ is a path $P_5$ with five vertices. Per Lemma 1, $\gamma (S(u,v)-(N_{G_d}\left[u\right]\cup \left\{v\right\}))=2.$ On the other hand, Consider that $S(u,v)$ contains $v_d$. Then, $G_d[S(u,v)-N_{G_d}\left[u\right]]$ is a path $P_6$ with six vertices. Per Lemma 1, $\gamma (S(u,v)-N_{G_d}\left[u\right])=2$ (see Figure 7b). In any case, $\gamma (S(u,v)-(N_{G_d}\left[u\right]\cup \left\{v\right\})=\gamma (S(u,v)-N_{G_d}\left[u\right]))=2$, $|D_{\left|S\right(u,v)}^{\prime }|⩾3$, and if $D^{\prime }-S(u,v)$ does not dominate v then there exists a vertex $v_d$ in $D^{\prime }\cap S(u,v)$ such that $v_d$ dominates v.

Case 3: $u,v\notin D^{\prime }$. Depending on the positions of $u_d$ and $v_d$, we have the following three subcases.

Case 3.1: $u_d,v_d\notin S(u,v)$. In this subcase, $\{u_d,v_d\}\cap S(u,v)=\varnothing$. Then, $S(u,v)-\{u,v\}$ is a path $P_6$ with six vertices. Per Lemma 1, $\gamma \left(S\right(u,v)-\{u,v\left\}\right)=2$ (see Figure 7c). Thus, $|D_{\left|S\right(u,v)}^{\prime }|⩾2$.

Case 3.2: either $u_d\notin S(u,v)$ or $v_d\notin S(u,v)$. Without loss of generality, assume that $u_d\in S(u,v)$ and $v_d\notin S(u,v)$. Then, $S(u,v)-(N_{G_d}\left(u_d\right)\cup \left\{v\right\})$ is a path $P_4$ with four vertices. Per Lemma 1, $\gamma (S(u,v)-(N_{G_d}\left(u_d\right)\cup \left\{v\right\}))=2$ (see Figure 7d). Thus, $|D_{|S(u,v)-(N_{G_d}\left(u_d\right)\cup \left\{v\right\})}^{\prime }|⩾2$ and $|D_{\left|S\right(u,v)}^{\prime }|⩾3$. Then, $\gamma \left(S\right(u,v)-\{u,v\left\}\right)=3$.

Case 3.3: $u_d,v_d\in S(u,v)$. In this subcase, it needs at least one other vertex of $S(u,v)$ to dominate $S(u,v)-(N_{G_d}\left(u_d\right)\cup N_{G_d}\left(v_d\right))$. Thus, $|D_{\left|S\right(u,v)}^{\prime }|⩾3$ and $\gamma \left(S\right(u,v\left)\right)=3$.

It follows from the above cases that we can conclude the following lemma.

Lemma 5.

Let $D^{\prime }$ be a dominating set of diagonal supergrid graph $G_d$ constructed by Algorithm 1, and let $S(u,v)$ be a snake path with connectors u and v in $G_d$. Then, the following statement holds:

(1) 

If $u,v\in D^{\prime }$, then $\gamma (S(u,v)-(N_{G_d}\left[u\right]\cup N_{G_d}\left[v\right]))=2$ and $|D_{\left|S\right(u,v)-\{u,v\}}^{\prime }|⩾2$ (see Figure 7a).

(2) 

If $u\in D^{\prime }$ and $v\notin D^{\prime }$, then $\gamma (S(u,v)-N_{G_d}\left[u\right])=\gamma (S(u,v)-(N_{G_d}\left[u\right]\cup \left\{v\right\}))=2$, $|D_{\left|S\right(u,v)}^{\prime }|⩾3$, and if $D^{\prime }-S(u,v)$ does not dominate v, then there exists a vertex $v_d$ in $D^{\prime }\cap S(u,v)$ such that $v_d$ dominates v (see Figure 7b).

(3) 

If $u,v\notin D^{\prime }$, then

if $(N_{G_d}\left(u\right)-S(u,v))\cap D^{\prime }\ne \varnothing$ and $(N_{G_d}\left(v\right)-S(u,v))\cap D^{\prime }\ne \varnothing$, then $\gamma \left(S\right(u,v)-\{u,v\left\}\right)=2$ and $|D_{\left|S\right(u,v)}^{\prime }|⩾2$ (see Figure 7c); otherwise, $\gamma \left(S\right(u,v)-\{u,v\left\}\right)=3$ and $|D_{\left|S\right(u,v)}^{\prime }|⩾3$ (see Figure 7d).

Figure 7. The minimum dominating set of $S(u,v)$ in $G_d$ for (a) $u,v\in D^{\prime }$, (b) $u\in D^{\prime }$ and $v\notin D^{\prime }$, (c) $u,v\notin D^{\prime }$ and $(N_{G_d}\left(u\right)-S(u,v))\cap D^{\prime }\ne \varnothing$ and $(N_{G_d}\left(v\right)-S(u,v))\cap D^{\prime }\ne \varnothing$, and (d) $u,v\notin D^{\prime }$ and, $(N_{G_d}\left(u\right)-S(u,v))\cap D^{\prime }=\varnothing$ or $(N_{G_d}\left(v\right)-S(u,v))\cap D^{\prime }=\varnothing$, where $D^{\prime }$ is a dominating set of $G_d$ and filled circles represent vertices in $D^{\prime }$.

Figure 7. The minimum dominating set of $S(u,v)$ in $G_d$ for (a) $u,v\in D^{\prime }$, (b) $u\in D^{\prime }$ and $v\notin D^{\prime }$, (c) $u,v\notin D^{\prime }$ and $(N_{G_d}\left(u\right)-S(u,v))\cap D^{\prime }\ne \varnothing$ and $(N_{G_d}\left(v\right)-S(u,v))\cap D^{\prime }\ne \varnothing$, and (d) $u,v\notin D^{\prime }$ and, $(N_{G_d}\left(u\right)-S(u,v))\cap D^{\prime }=\varnothing$ or $(N_{G_d}\left(v\right)-S(u,v))\cap D^{\prime }=\varnothing$, where $D^{\prime }$ is a dominating set of $G_d$ and filled circles represent vertices in $D^{\prime }$.

Based on the above lemma, we prove that grid graph $G_g$ contains a dominating set D with $\left|D\right|⩽k$ if and only if diagonal supergrid graph $G_d$ has a dominating set $D^{\prime }$ with $|D^{\prime }|⩽k+2|E\left(G_g\right)|$. We first prove that the only if part is as follows.

Lemma 6.

Suppose grid graph $G_g$ has a dominating set D with size $\left|D\right|⩽k$. Then, diagonal supergrid graph $G_d$ contains a dominating set $D^{\prime }$ with size $|D^{\prime }|⩽k+2|E\left(G_g\right)|$.

Proof. 

We construct a dominating set $D^{\prime }$ of $G_d$ from D such that the size of $D^{\prime }$ is no greater than $k+2\left|E\right(G_g\left)\right|$. Initially, let $D^{\prime }=D$. Let $(u,v)$ be an edge of the grid graph $G_g$, and let $S(u,v)=u\to w_1\to w_2\to w_3\to w_4\to w_5\to w_6\to v$ be the snake $(u,v)$-path in the diagonal supergrid graph $G_d$ constructed from $(u,v)$, as depicted in Figure 7a. Consider the following three cases.

Case 1: $u,v\in D$. In this case, $w_1$ and $w_6$ are dominated by u and v, respectively. Let $P^{\prime }=w_2\to w_3\to w_4\to w_5$. Per Lemma 1, $\gamma \left(P^{\prime }\right)=2$. Then, $\{w_3,w_5\}$ is a minimum dominating set of $P^{\prime }$. Let $D^{\prime }=D^{\prime }\cup \{w_3,w_5\}$. Then, $D^{\prime }$ dominates $V\left(S\right(u,v\left)\right)$ and $|D^{\prime }|=|D^{\prime }|+2$. Figure 7a shows such a dominating set of $S(u,v)$.

Case 2: either $u\in D$ or $v\in D$. Without loss of generality, assume that $u\in D$ and $v\notin D$. Then, $w_1$ is dominated by u. Consider that v is not dominated by $D^{\prime }$. Let $P^{\prime }=w_2\to w_3\to w_4\to w_5\to w_6\to v$. Per Lemma 1, $\gamma \left(P^{\prime }\right)=2$. Then, $\{w_3,w_6\}$ is a minimum dominating set of $P^{\prime }$. Let $D^{\prime }=D^{\prime }\cup \{w_3,w_6\}$. Then, $D^{\prime }$ dominates $V\left(S\right(u,v\left)\right)$ and $|D^{\prime }|=|D^{\prime }|+2$. Figure 7b depicts such a dominating set of $S(u,v)$. On the other hand, consider that v is dominated by $D^{\prime }$. Let $P^{\prime }=w_2\to w_3\to w_4\to w_5\to w_6$. Per Lemma 1, $\gamma \left(P^{\prime }\right)=2$. Then, $\{w_3,w_6\}$ is a minimum dominating set of $P^{\prime }$. Let $D^{\prime }=D^{\prime }\cup \{w_3,w_6\}$. Then, $D^{\prime }$ dominates $V\left(S\right(u,v\left)\right)$ and $|D^{\prime }|=|D^{\prime }|+2$.

Case 3: $u,v\notin D$. Because D is a dominating set of $G_g$, there exist two vertices $z_1\in N_{G_g}\left(u\right)$ and $z_2\in N_{G_g}\left(v\right)$ such that $z_1$ and $z_2$ dominate u and v, respectively. Let $S(z_1,u)$ and $S(z_2,v)$ be the snake paths of $G_d$ constructed from edges $(z_1,u)$ and $(z_2,v)$, respectively. In our construction algorithm of $D^{\prime }$, we compute the dominating sets of $S(z_1,u)$ and $S(z_2,v)$ before the dominating set of $S(u,v)$, where $z_1,z_2\in D$ and $u,v\notin D$. From Case 2, we can find one vertex of $S(z_1,u)\cap N_{G_d}\left(u\right)$ (respectively, $S(z_2,v)\cap N_{G_d}\left(v\right)$) to dominate u (respectively, v) before computing the dominating set of $S(u,v)$ (see Figure 7b). By Lemma 1, there exists a set $\{w_2,w_5\}$ of $S(u,v)-\{u,v\}$ such that it dominates $V\left(S\right(u,v\left)\right)-\{u,v\}$; see Figure 7c. Let $D^{\prime }=D^{\prime }\cup \{w_2,w_5\}$. Then, $D^{\prime }$ dominates $V\left(S\right(u,v\left)\right)$ and $|D^{\prime }|=|D^{\prime }|+2$.

Based on the above cases, we construct a dominating set $D^{\prime }$ of $G_d$ by the following steps. Initially, let $D^{\prime }=D$ and let $(u,v)\in E\left(G_g\right)$. For each $u,v\in D$, we construct a dominating set of $S(u,v)$ via Case 1. We then construct a dominating set of $S(u,v)$ by Case 2 for each $u\in D$ and $v\notin D$. Finally, for each $u,v\notin D$, a dominating set of $S(u,v)$ is constructed via Case 3. From the above cases, $|D^{\prime }|=|D^{\prime }|+2$ after processing each snake path of $G_d$. Thus, we construct a dominating set $D^{\prime }$ of $G_d$ with size $|D^{\prime }|=|D|+2|E\left(G_g\right)|⩽k+2|E\left(G_g\right)|$ after computing dominating sets of all snake paths in $G_d$. For example, Figure 4a shows the dominating set D of $G_g$ with $\left|D\right|=4$, and the constructed dominating set $D^{\prime }$ of $G_d$ from D is shown in Figure 4d, where $|D^{\prime }|=|D|+2|E\left(G_g\right)|=4+2·11=26$. This completes the proof of the lemma. □

Next, we prove that the if part is in Lemma 7. Recall that for a dominating set D of graph G and the subgraph H of G, the restriction of D to H is represented as $D_{|H}$.

Lemma 7.

Suppose diagonal supergrid graph $G_d$ has a dominating set $D^{\prime }$ with $|D^{\prime }|⩽k+2|E\left(G_g\right)|$. Then, grid graph $G_g$ contains a dominating set D with size $\left|D\right|⩽k$.

Proof. 

We show that there exists a dominating set D of $G_g$ with size k or less. To prove this lemma, we first construct a dominating set $\widehat{D}$ of $G_d$ obtained from $D^{\prime }$ such that $|\widehat{D}|⩽|D^{\prime }|$ and remove all vertices not in $G_g$ from $\widehat{D}$, resulting in a dominating set D of $G_g$. Initially, let $\widehat{D}=D^{\prime }$. Consider a snake path $S(u,v)=u\to w_1\to w_2\to w_3\to w_4\to w_5\to w_6\to v$ of $G_d$ constructed from edge $(u,v)$ of $G_g$. Let $u_d$ (respectively, $v_d$) be in $D^{\prime }$ such that it dominates u (respectively, v) if $u\notin D^{\prime }$ (respectively, $v\notin D^{\prime }$). Depending on whether $u,v\in D^{\prime }$, we have the following three cases:

Case 1: $u,v\in D^{\prime }$. Let $P^{\prime }=w_2\to w_3\to w_4\to w_5$. By Lemma 1, $\gamma \left(P^{\prime }\right)=2$. Let $W=\{w_3,w_5\}$ be a minimum dominating set of $S(u,v)-(N_{G_d}\left[u\right]\cup N_{G_d}\left[v\right])$. If $|{\widehat{D}}_{\left|S\right(u,v)}|>4$, then let $\widehat{D}=\widehat{D}-{\widehat{D}}_{\left|S\right(u,v)}\cup W\cup \{u,v\}$, that is, $|{\widehat{D}}_{\left|S\right(u,v)}|=4$, after processing $S(u,v)$ for $u,v\in D^{\prime }$.

Case 2: either $u\in D^{\prime }$ or $v\in D^{\prime }$. Without loss of generality, assume that $u\in D^{\prime }$ and $v\notin D^{\prime }$. Then, $w_1$ is dominated by u. Let $P^{\prime }=w_2\to w_3\to w_4\to w_5\to w_6\to v$. By Statement (2) of Lemma 5, at least two vertices of $P^{\prime }$ are in $D^{\prime }$. Let $W=\{w_3,w_6\}$ be a minimum dominating set of $S(u,v)-N_{G_d}\left[u\right]$; see Figure 7b. If $|{\widehat{D}}_{\left|S\right(u,v)}|>3$ or $w_6\notin \widehat{D}$, then let $\widehat{D}=\widehat{D}-{\widehat{D}}_{\left|S\right(u,v)}\cup W\cup \left\{u\right\}$, that is, $|{\widehat{D}}_{\left|S\right(u,v)}|=3$ in this case. In addition, $\widehat{D}$ dominates v after processing $S(u,v)$ for $u\in D^{\prime }$ and $v\notin D^{\prime }$.

Case 3: $u,v\notin D^{\prime }$. First, consider that $de{g}_{G_g}\left(u\right)=1$ and $de{g}_{G_g}\left(v\right)=1$. Then, $E\left(G_g\right)=\left\{(u,v)\right\}$ and $G_d$ only contains a snake path $S(u,v)$. By Lemma 1, $|D^{\prime }|⩾3$. Let $\widehat{D}=\{u,w_3,w_6\}$. Then, $\widehat{D}$ is a dominating set of $G_d$ with size 3. Let $D=\widehat{D}-\{w_3,w_6\}$; hence, D is a dominating set of $G_g$ with size 1. Then, $3⩽|D^{\prime }|⩽k+2·1$, and hence $\left|D\right|=1⩽k$. Thus, the lemma holds when $u,v\notin D^{\prime }$ and $de{g}_{G_g}\left(u\right)=de{g}_{G_g}\left(v\right)=1$. In the following, suppose that $de{g}_{G_g}\left(u\right)\ne 1$ or $de{g}_{G_g}\left(v\right)\ne 1$. Then, there exists at least one vertex $z_1$ of $G_g$ such that $z_1\in N_{G_g}\left(u\right)$ or $z_1\in N_{G_g}\left(v\right)$. Without loss of generality, assume that $(z_1,u)\in E\left(G_g\right)$. We pick $z_1$ to satisfy the requirement that if $z_1\notin D^{\prime }$, then $N_{G_g}\left(u\right)\cap D^{\prime }=\varnothing$. Let $S(z_1,u)=z_1\to x_1\to x_2\to x_3\to x_4\to x_5\to x_6\to u$ be the snake path of $G_d$ constructed from edge $(z_1,u)$ of $G_g$, as shown in Figure 8a. Depending on whether $z_1\in D^{\prime }$, there are two subcases.

Case 3.1: $z_1\notin D^{\prime }$. In this subcase, $N_{G_g}\left(u\right)\cap D^{\prime }=\varnothing$. Suppose that $u_d\in S(u,v)$. By Statement (3) of Lemma 5, $|D_{\left|S\right(u,v)}^{\prime }|⩾3$. Let $\widehat{D}=\widehat{D}-D_{\left|S\right(u,v)}^{\prime }\cup \{u,w_3,w_6\}$. Then, the size of $\widehat{D}$ does not increase and $u\in \widehat{D}$. On the other hand, suppose that $u_d\in S(z_1,u)$. By Statement (3) of Lemma 5, $|D_{\left|S\right(z_1,u)}^{\prime }|⩾3$. Let $\widehat{D}=\widehat{D}-D_{\left|S\right(z_1,u)}^{\prime }\cup \{u,x_1,x_4\}$. Then, the size of $\widehat{D}$ does not increase and $u\in \widehat{D}$. In any case, we can set $u\in \widehat{D}$ and $|\widehat{D}|$ does not increase. Then, it is the same as Case 2. Figure 8a depicts such a case.

Case 3.2: $z_1\in D^{\prime }$. In this subcase, $\gamma \left(S(z_1,u)\right)=3$ and $\{z_1,x_3,x_6\}$ is a minimum dominating set of $S(z_1,u)$; see Figure 8b,c. If $|D_{\left|S\right(z_1,u)}^{\prime }|>3$ or $x_6\notin D^{\prime }$, let $\widehat{D}=\widehat{D}-D_{\left|S\right(z_1,u)}^{\prime }\cup \{z_1,x_3,x_6\}$. Depending on whether $de{g}_{G_g}\left(v\right)=1$, we consider the following subcases.

Case 3.2.1: $de{g}_{G_g}\left(v\right)\ne 1$. In this subcase, there exists a vertex $z_2$ of $N_{G_g}\left(v\right)$. We pick such a vertex $z_2$, which is the same as that of $z_1$. Let $S(z_2,v)=z_2\to y_1\to y_2\to y_3\to y_4\to y_5\to y_6\to v$ be the snake path of $G_d$ constructed from edge $(z_2,v)$ of $G_g$, as shown in Figure 8b. If $z_2\notin D^{\prime }$, then it is the same as Case 3.1. Consider that $z_2\in D^{\prime }$. Then, $\{z_2,y_3,y_6\}$ is a minimum dominating set of $S(z_2,v)$ and v is dominated by $y_6$. If $|D_{\left|S\right(z_2,v)}^{\prime }|>3$ or $y_6\notin D^{\prime }$, then let $\widehat{D}=\widehat{D}-D_{\left|S\right(z_2,v)}^{\prime }\cup \{z_2,y_3,y_6\}$. In addition, u and v are dominated by $\widehat{D}$ after processing $S(z_1,u)$ and $S(z_2,v)$. By Statement (3) of Lemma 5, $\gamma \left(S\right(u,v)-\{u,v\left\}\right)=2$. Let $\{w_2,w_5\}$ be a minimum dominating set of $S(u,v)-\{u,v\}$. If $|D_{\left|S\right(u,v)}^{\prime }|>2$, then let $\widehat{D}=\widehat{D}-D_{\left|S\right(u,v)}^{\prime }\cup \{w_2,w_5\}$. Figure 8b depicts a such construction of $\widehat{D}$.

Case 3.2.2: $de{g}_{G_g}\left(v\right)=1$. In this subcase, $w_6$ dominates v; see Figure 8c. By Statement (3) of Lemma 5, $|D_{\left|S\right(u,v)}^{\prime }|⩾3$. We then set u to be in $\widehat{D}$ and re-compute the minimum dominating set of $S(u,v)$, that is, $\widehat{D}=\widehat{D}-D_{\left|S\right(u,v)}^{\prime }\cup \{u,w_3,w_6\}$. Then, $|\widehat{D}|$ does not increase and $u\in \widehat{D}$. Figure 8c shows a such minimum dominating set of $S(z_1,u)\cup S(u,v)$ in this subcase.

Figure 8. The dominating set of snake path $S(u,v)$ in $G_d$ where $u,v\notin D^{\prime }$, where (a) $z_1\notin D^{\prime }$, (b) $z_1\in D^{\prime }$ and $de{g}_{G_g}\left(v\right)\ne 1$, and (c) $z_1\in D^{\prime }$ and $de{g}_{G_g}\left(v\right)=1$. Note that $D^{\prime }$ is a dominating set of $G_d$; the filled circles represent vertices of $D^{\prime }$.

Figure 8. The dominating set of snake path $S(u,v)$ in $G_d$ where $u,v\notin D^{\prime }$, where (a) $z_1\notin D^{\prime }$, (b) $z_1\in D^{\prime }$ and $de{g}_{G_g}\left(v\right)\ne 1$, and (c) $z_1\in D^{\prime }$ and $de{g}_{G_g}\left(v\right)=1$. Note that $D^{\prime }$ is a dominating set of $G_d$; the filled circles represent vertices of $D^{\prime }$.

From the above cases, we can construct a dominating set $\widehat{D}$ of $G_d$ from $D^{\prime }$ such that $|\widehat{D}|⩽|D^{\prime }|$, as follows. First, for each $u,v\notin D^{\prime }$ we construct dominating sets of $S(u,v)$ via Case 3. Then, for each $u\in D^{\prime }$ and $v\notin D^{\prime }$ we construct dominating sets of $S(u,v)$ via Case 2. Finally, we construct dominating sets of $S(u,v)$ via Case 1 for $u,v\in D^{\prime }$. For example, given a dominating set $D^{\prime }$ of $G_d$ with size 22 in Figure 9a, the constructed dominating set $\widehat{D}$ of $G_d$ with size 22 from $D^{\prime }$ is depicted in Figure 9b. Then, $\widehat{D}$ satisfies the following properties:

(p1)

$|\widehat{D}|⩽|D^{\prime }|$,

(p2)

for each snake $(u,v)$-path $S(u,v)$, $|\widehat{D}\cap (S(u,v)-\{u,v\})|=2$, and

(p3)

for each snake $(u,v)$-path $S(u,v)$ with $u,v\notin \widehat{D}$, there exist $z_1\in N_{G_g}\left(u\right)$ and $z_2\in N_{G_g}\left(v\right)$ such that $z_1,z_2\in \widehat{D}$ while $de{g}_{G_g}\left(u\right)\ne 1$ and $de{g}_{G_g}\left(v\right)\ne 1$.

Figure 9. (a) The dominating set $D^{\prime }$ of $G_d$ with size 22, and (b) a dominating set $\widehat{D}$ of $G_d$ with size 22 ($⩽|D^{\prime }|$) obtained from $D^{\prime }$. Solid lines indicate the edges of $G_d$, double circles represent the vertices of $G_g$, and filled circles indicate the vertices in a dominating set of $G_d$.

Figure 9. (a) The dominating set $D^{\prime }$ of $G_d$ with size 22, and (b) a dominating set $\widehat{D}$ of $G_d$ with size 22 ($⩽|D^{\prime }|$) obtained from $D^{\prime }$. Solid lines indicate the edges of $G_d$, double circles represent the vertices of $G_g$, and filled circles indicate the vertices in a dominating set of $G_d$.

Then, a dominating set D of $G_g$ is obtained from $\widehat{D}$ according to the following steps:

(s1)

initially, let $D=\widehat{D}$;

(s2)

remove from D all vertices of D that are not in $D_g$;

(s3)

the result set D is a dominating set of $G_g$.

Because for each snake path $S(u,v)$, $\widehat{D}\cap S(u,v)$ contains exactly two vertices that are not in $G_g$, we obtain $\left|D\right|=|\widehat{D}|-2|E\left(G_g\right)|$. Then, $\left|D\right|=|\widehat{D}|-2|E\left(G_g\right)|⩽|D^{\prime }|-2|E\left(G_g\right)|⩽(k+2|E\left(G_g\right)\left|\right)-2|E\left(G_g\right)|=k$. Therefore, we construct a dominating set D of $G_g$ of size $\left|D\right|⩽k$. □

It immediately follows from Lemmas 6 and 7 that the following lemma is summarized:

Lemma 8.

Let $G_g$ be a grid graph, and let $G_d$ be a diagonal supergrid graph constructed from $G_g$ by Algorithm 1. Then, $G_g$ has a dominating set D with size $\left|D\right|⩽k$ if and only if $G_d$ contains a dominating set $D^{\prime }$ with size $|D^{\prime }|⩽k+2|E\left(G_g\right)|$.

Obviously, the domination problem on a diagonal supergrid graph is in NP. By Theorem 1 and Lemmas 4 and 8 we derive the following theorem:

Theorem 2.

The domination problem for diagonal supergrid graphs is NP-complete.

The dominating sets of diagonal supergrid graphs constructed in Lemmas 6 and 7 can be easily modified to be independent dominating sets. Therefore, the independent domination problem on diagonal supergrid graphs is NP-complete as well, and the following corollary holds true.

Corollary 1.

The independent domination problem for diagonal supergrid graphs is NP-complete.

Through the construction of diagonal supergrid graph $G_d$, we can see that $G_d$ is a supergrid graph which is a vertex-induced subgraph of the infinite two-dimensional supergrid $S^{\infty }$. Therefore, the following theorem holds immediately.

Theorem 3.

The domination and independent domination problems for supergrid graphs are NP-complete.

The NP-complete results above can be easily extended to triangular supergrid graphs. Recall that a triangular supergrid graph is an extended supergrid graph of which the edge set contains at least one r-skewed diagonal edge and does not contain any l-skewed diagonal edges. To verify that the domination problem on a triangular supergrid graph is NP-complete, we modify Algorithm 1 as follows:

Step 1:

enlarge the input grid graph $G_g$ to another grid graph $G_g^{\prime }$ such that each edge of $G_g$ is transformed into a horizontal or vertical path with six edges (see Figure 10b);

Step 2:

for each horizontal (respectively, vertical) $(u,v)$-path in $G_g^{\prime }$ where $u,v\in V\left(G_g\right)$, replace it by a horizontal (respectively, vertical) triangle path $T(u,v)$ connecting u and v (see Figure 10c);

Step 3:

the constructed graph is a triangular supergrid graph $G_{\tau }$ (see Figure 10d), and outputs $G_{\tau }$.

Figure 10. (a) A grid graph $G_g$, (b) grid graph $G_g^{\prime }$ by magnifying each edge of $G_g$ by a factor of six, (c) (horizontal or vertical) triangle $(u,v)$-path $T(u,v)$, and (d) a triangular supergrid graph $G_{\tau }$ constructed from $G_g^{\prime }$ by replacing each of its enlarged paths with the triangle path in (c).

Figure 10. (a) A grid graph $G_g$, (b) grid graph $G_g^{\prime }$ by magnifying each edge of $G_g$ by a factor of six, (c) (horizontal or vertical) triangle $(u,v)$-path $T(u,v)$, and (d) a triangular supergrid graph $G_{\tau }$ constructed from $G_g^{\prime }$ by replacing each of its enlarged paths with the triangle path in (c).

We can see that each triangle path is a path with eight vertices. Thus, Lemma 5 holds for $G_{\tau }$. By Lemma 8, $G_g$ has a dominating set D of size $\left|D\right|⩽k$ if and only if $G_{\tau }$ contains a dominating set $D^{\prime }$ of size $|D^{\prime }|⩽k+2|E\left(G_g\right)|$. Therefore, the following theorem holds immediately.

Theorem 4.

The domination and independent domination problems on triangular supergrid graphs are NP-complete.

4. The Domination and Independent Domination Numbers of Rectangular Triangular-Supergrid Graphs

In this section, we first compute $\gamma \left(T_{m\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$ for a rectangular triangular-supergrid graph $T_{m\times n}$ with $n⩾m$ and $3⩾m⩾2$. We then provide an upper bound of $\gamma \left(T_{m\times n}\right)$ and ${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$ for $n⩾m⩾4$. First, we consider $n⩾m$ and $m=2$, as follows.

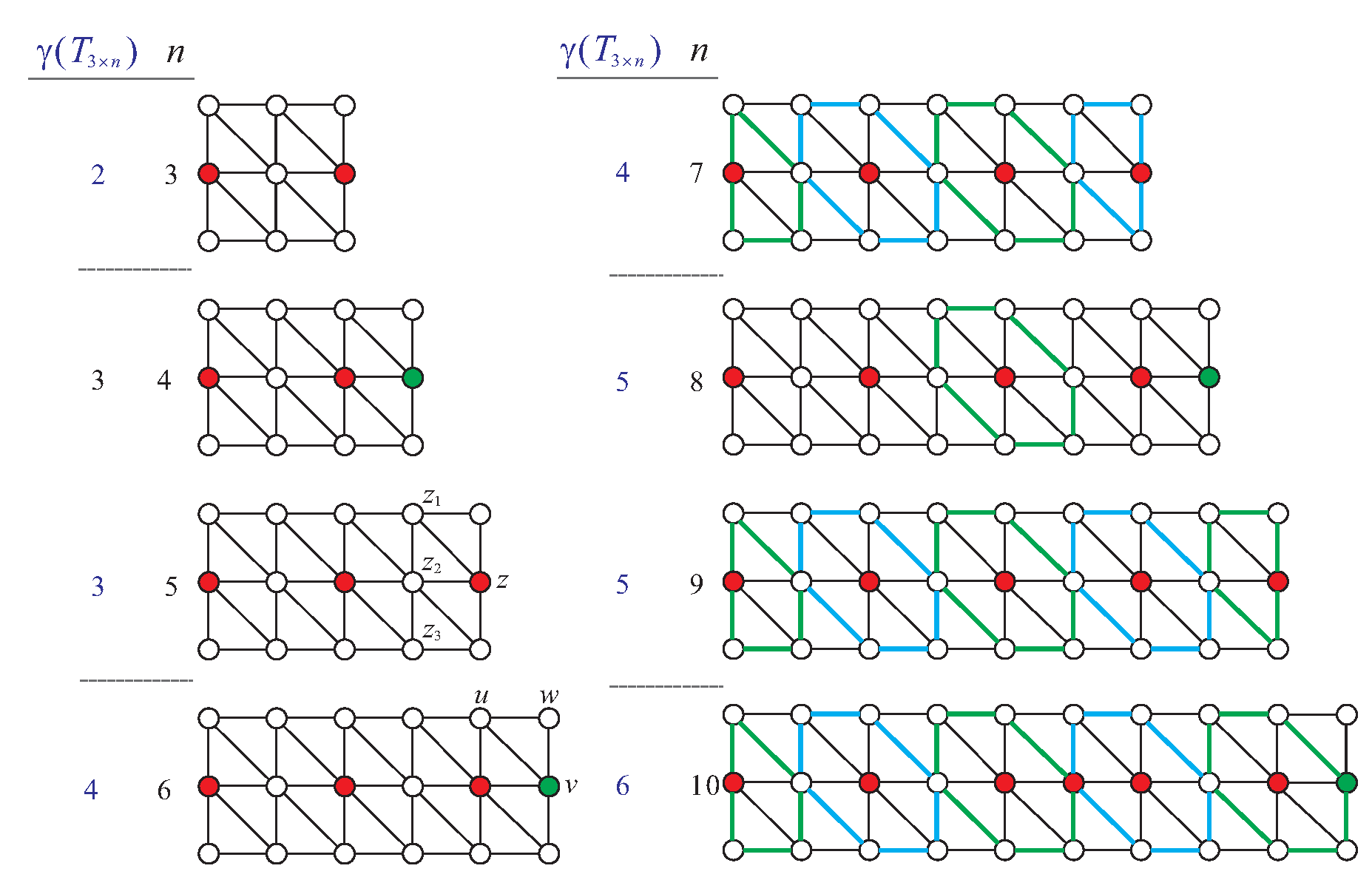
Lemma 9.

$\gamma \left(T_{2\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{2\times n}\right)=\lceil \frac{2n}{5}\rceil$.

Proof. 

Through the structure of $T_{2\times n}$, a vertex of $T_{2\times n}$ dominates at most five vertices, including its four neighbors and itself. Thus, $\gamma \left(T_{2\times n}\right)⩾\lceil \frac{2n}{5}\rceil$. We compute a dominating set of $T_{2\times n}$ with size $\lceil \frac{2n}{5}\rceil$, as follows. First, we make $\lfloor \frac{n}{5}\rfloor$ or $\lfloor \frac{n}{5}\rfloor -1$ vertical separations on $T_{2\times n}$ to obtain $\lceil \frac{n}{5}\rceil$ subgraphs ${\mathtt{T}}_1$, ${\mathtt{T}}_2$, …, ${\mathtt{T}}_{\lfloor \frac{n}{5}\rfloor }$, ${\mathtt{T}}^{*}$ of $T_{2\times n}$ such that ${\mathtt{T}}_i$, $1⩽i⩽\lfloor \frac{n}{5}\rfloor$ is a rectangular triangular-supergrid graph $T_{2\times 5}$ and ${\mathtt{T}}^{*}$ is a $T_{2\times j}$, $1⩽j⩽4$, if $n\%5\ne 0$. Note that ${\mathtt{T}}^{*}=\varnothing$ when $n\%5=0$. Let ${\mu }_i=(2,2)$ and ${\nu }_i=(4,1)$ be two vertices of ${\mathtt{T}}_i$ for $1⩽i⩽\lfloor \frac{n}{5}\rfloor$, and let $D^{\prime }={\cup }_{1⩽i⩽\lfloor \frac{n}{5}\rfloor }\{{\mu }_i,{\nu }_i\}$. Then, $D^{\prime }$ is a dominating set of $T_{2\times n}-{\mathtt{T}}^{*}$. Consider that ${\mathtt{T}}^{*}$ does exist, i.e., $n\%5\ne 0$. Then, ${\mathtt{T}}^{*}=T_{2\times j}$ for $1⩽j⩽4$. We then compute one or two vertices $\mu$ and $\nu$ of ${\mathtt{T}}^{*}$ as follows: if $j=1$, let $\mu =(1,2)$; otherwise, if $j=2$, let $\mu =(2,2)$. Furthermore, if $j=3$, let $\mu =(2,2)$ and $\nu =(3,1)$; otherwise, if $j=4$, let $\mu =(2,2)$ and $\nu =(4,2)$. Then, $\{\mu ,\nu \}$ dominates ${\mathtt{T}}^{*}$. Let $D=D^{\prime }\cup \{\mu ,\nu \}$. Then, $\left|D\right|=\lceil \frac{2n}{5}\rceil$ and D dominates $T_{2\times n}$. Thus, $\gamma \left(T_{2\times n}\right)=\lceil \frac{2n}{5}\rceil$. By the above construction, we can see that D is an independent dominating set of $T_{2\times n}$; hence, ${\gamma }_{\mathrm{ind}}\left(T_{2\times n}\right)=\lceil \frac{2n}{5}\rceil$. For instance, Figure 11 depicts our constructed (independent) dominating set of $T_{2\times n}$ for $2⩽n⩽10$. □

Next, we compute $\gamma \left(T_{3\times n}\right)$ and ${\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)$ as the following lemma.

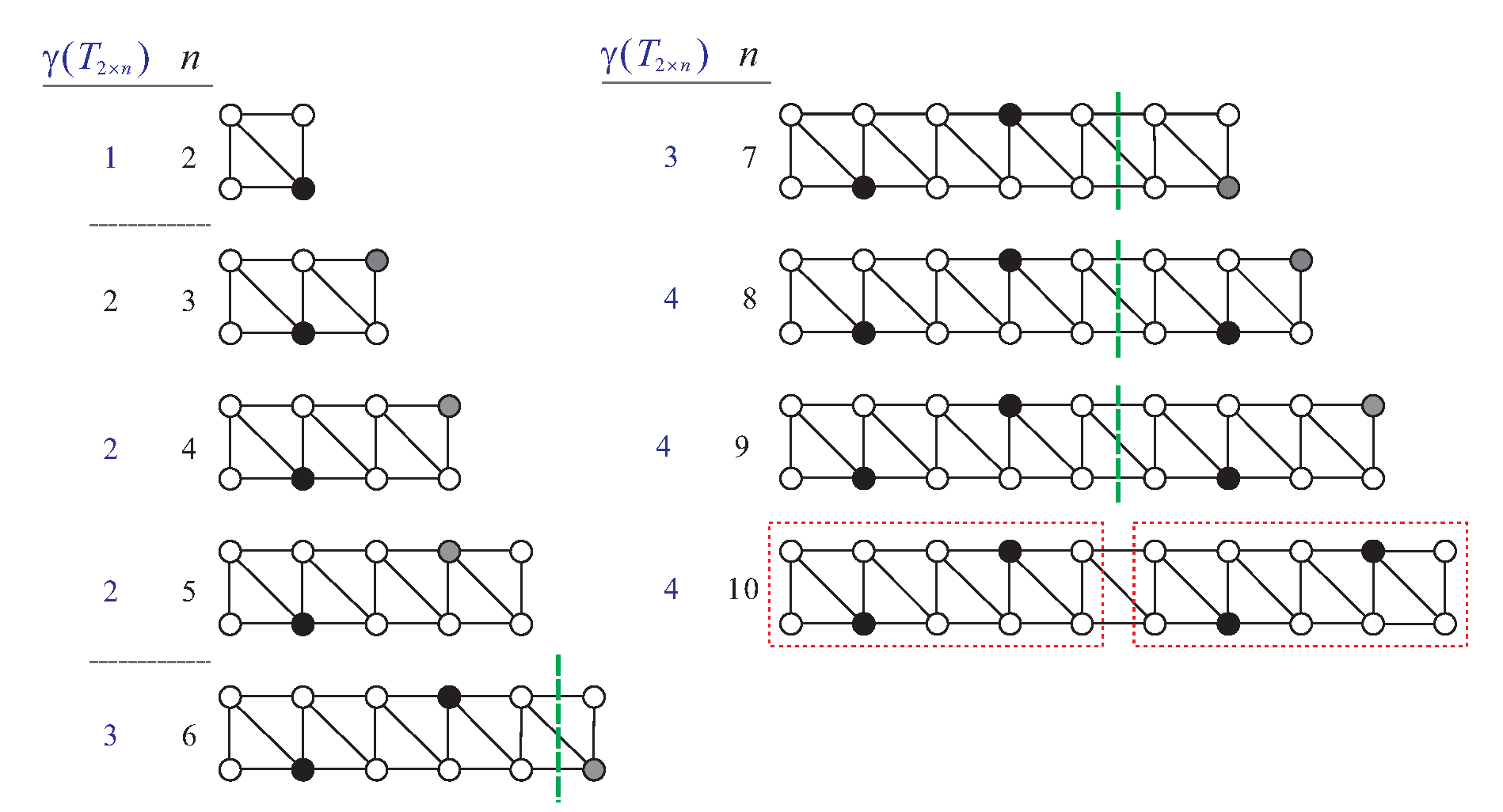
Lemma 10.

$\gamma \left(T_{3\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)=\lfloor \frac{n}{2}\rfloor +1$.

Proof. 

We first claim the following:

(C1)

There exists a minimum dominating set $D_n$ of $T_{3\times n}$ with size $\lfloor \frac{n}{2}\rfloor +1$ such that $D_n=\left\{(1+2i,2)\right|0⩽i⩽\lfloor \frac{n}{2}\rfloor \}$ if $n\%2=1$; otherwise, $D_n=\left\{(1+2i,2)\right|0⩽i⩽\lfloor \frac{n}{2}\rfloor -1\}\cup \left\{(n,2)\right\}$.

(C2)

For any minimum dominating set ${\widehat{D}}_n$ of $T_{3\times n}$, $\widehat{D}$ does not contain vertex $(n,3)$, and if $n\%2=1$, then $\widehat{D}$ contains vertex $(n,2)$ and does not contain vertex $(n,1)$.

We prove the above claims by induction on n, where $n⩾3$. Initially, let $n=3$, 4, or 5. By inspecting $T_{3\times 3}$, $T_{3\times 4}$, and $T_{3\times 5}$, it is easy to verify that the above claims hold true; see Figure 12. Assume that the claims hold when $n=k$ and $k⩾5$. Then, there exists no minimum dominating set of $T_{3\times k}$ containing vertex $(k,3)$, and there exists a minimum dominating set $D_k$ of $T_{3\times k}$ with size $\lfloor \frac{k}{2}\rfloor +1$ such that $D_k=\left\{(1+2i,2)\right|0⩽i⩽\lfloor \frac{k}{2}\rfloor \}$ if $k\%2=1$; otherwise, $D_k=\left\{(1+2i,2)\right|0⩽i⩽\lfloor \frac{k}{2}\rfloor -1\}\cup \left\{(k,2)\right\}$. In addition, if $k\%2=1$, then any minimum dominating set ${\widehat{D}}_k$ of $T_{3\times k}$ satisfies the requirement that ${\widehat{D}}_k$ contains vertex $(k,2)$ and does not contain vertices $(k,1)$ and $(k,3)$. Now, suppose that $n=k+1$. There are two possible cases.

Case 1: $k\%2=1$. Let $k=2t+1$, $t⩾1$. By induction hypothesis, any minimum dominating set ${\widehat{D}}_k$ of $T_{3\times k}$ does not contain vertex $(k,1)$; hence, ${\widehat{D}}_k$ does not dominate vertex $(k+1,1)$. Thus, $\gamma \left(T_{3\times (k+1)}\right)>\gamma (T_{3\times k)}$. Let $D_{k+1}=D_k\cup \left\{(k+1,2)\right\}$. Then, $|D_{k+1}|=|D_k|+1=t+2$; hence, $D_{k+1}$ is a minimum dominating set of $T_{3\times (k+1)}$. Therefore, Claim (C1) holds true in this case. Next, we verify Claim (C2). Let $u=(k,1)$, $v=(k+1,2)$, and let $w=(k+1,1)$. Assume by contradiction that $\tilde{D}$ is a minimum domination set of $T_{3\times (k+1)}$ satisfying the requirement that $\tilde{D}$ contain vertex $(k+1,3)$. To dominate w, one of $u,v,w$ must be in $\tilde{D}$. Consider that $u\in \tilde{D}$. Then, $|{\tilde{D}}_{|T_{3\times k}}|>\gamma \left(T_{3\times k}\right)$ by induction hypothesis. Then, $\tilde{D}={\tilde{D}}_{|T_{3\times k}}\cup \left\{(k+1,3)\right\}$; hence, $|\tilde{D}|>\gamma \left(T_{3\times k}\right)+1$. Thus, $|\tilde{D}|⩾\gamma \left(T_{3\times k}\right)+2$. This contradicts our above construction $D_{k+1}$ of $T_{3\times (k+1)}$ with size $|D_{k+1}|=\gamma \left(T_{3\times k}\right)+1=t+2$. In addition, consider that w or v is in $\tilde{D}$. Then, ${\tilde{D}}_{|T_{3\times (k-1)}}\cup \{v,(k+1,3)\}\subseteq \tilde{D}$; hence, $|\tilde{D}|⩾|{\tilde{D}}_{|T_{3\times (k-1)}}|+2$. By induction hypothesis, $|{\tilde{D}}_{|T_{3\times (k-1)}}|⩾|D_{k-1}|=\lfloor \frac{k-1}{2}\rfloor +1=\lfloor \frac{2t}{2}\rfloor +1=t+1$. Then, $|\tilde{D}|⩾|\tilde{D}|T_{3\times (k-1)}|+2⩾t+3$. Thus, $|\tilde{D}|>|D_{k+1}|$, where $|D_{k+1}|=t+2$ and $D_{k+1}$ is a dominating set of $T_{3\times (k+1)}$; hence, a contradiction occurs. By contradiction, there exists no minimum domination set of $T_{3\times (k+1)}$ containing vertex $(k+1,3)$. Thus, Claim (C2) holds true when $n=k+1$.

Case 2: $k\%2=0$. In this case, let $D_{k+1}=D_k-\left\{(k,1)\right\}\cup \left\{(k+1,2)\right\}$. Then, $|D_{k+1}|=|D_k|=\lfloor \frac{k}{2}\rfloor +1$. Because $T_{3\times k}$ is a subgraph of $T_{3\times (k+1)}$, $\gamma \left(T_{3\times k}\right)⩽\gamma \left(T_{3\times (k+1)}\right)$, it is true that $D_{k+1}$ is a minimum dominating set of $T_{3\times (k+1)}$. Thus, Claim (C1) holds true in this case. Next, we verify Claim (C2) in this case. By similar arguments to those proving Case 1, we can verify that there exists no minimum domination set of $T_{3\times (k+1)}$ containing vertices $(k+1,1)$ and $(k+1,3)$. Let $z=(k+1,2)$, $z_1=(k,1)$, $z_2=(k,2)$, $z_3=(k,3)$, and let $Z=\{z_1,z_2,z_3\}$, as shown in Figure 12. Assume by contradiction that there exists a minimum domination set $\tilde{D}$ of $T_{3\times (k+1)}$ such that $z\notin \tilde{D}$. To dominate $(k+1,1)$ and $(k+1,3)$, at least two vertices of Z are necessary. If $z_3\in \tilde{D}$, then $\tilde{D}$ is not a minimum dominating set of $T_{3\times k}$; by induction hypothesis, a contradiction occurs. Thus, $z_1,z_2\in \tilde{D}$. Let ${\tilde{D}}^{\prime }=\tilde{D}-\left\{(k,1)\right\}$. Then, ${\tilde{D}}^{\prime }$ remains a dominating set of $T_{3\times k}$, as $N_{T_{3\times k}}\left[z_1\right]\subset N_{T_{3\times k}}\left(z_2\right)$; that is, $\tilde{D}$ is not a minimum dominating set of $T_{3\times k}$. Thus, $|\tilde{D}|>\gamma \left(T_{3\times k}\right)$. This contradicts the requirement that $D_{k+1}$ constructed above be a dominating set of $T_{3\times (k+1)}$ with size $\gamma \left(T_{3\times k}\right)$. Thus, any minimum domination set of $T_{3\times (k+1)}$ contains vertex $z=(k+1,2)$. It follows from the above arguments that Claim (C2) holds true when $n=k+1$.

By the above cases, Claims (C1) and (C2) hold true when $n=k+1$. By induction, these claims hold true for $n⩾3$. Thus, $\gamma \left(T_{3\times n}\right)=\lfloor \frac{n}{2}\rfloor +1$. Figure 12 shows the minimum dominating set $D_n$ of $T_{3\times n}$ for $3⩽n⩽10$.

Because each independent dominating set of a graph is a dominating set for that graph, $\gamma \left(T_{3\times n}\right)⩽{\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)$. For the case of $n\%2=1$, $D_n$ in Claim (C1) is an independent set as well; hence, it is a minimum independent dominating set of $T_{3\times n}$. Consider $n\%2=0$. Let $D_n^{\prime }=D_n-\left\{(n,2)\right\}\cup \left\{(n,1)\right\}$. Then, $|D_n^{\prime }|=|D_n|$ and $D_n^{\prime }$ is an independent set. Thus, $D_n^{\prime }$ is a minimum independent dominating set of $T_{3\times n}$. In any case, we construct a minimum independent dominating set of $T_{3\times n}$ with size $\gamma \left(T_{3\times n}\right)$. Thus, $\gamma \left(T_{3\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)=\lfloor \frac{n}{2}\rfloor +1$. □

Figure 12. $\gamma \left(T_{3\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)=\lfloor \frac{n}{2}\rfloor +1$ for $3⩽n⩽10$; filled circles indicate the vertices in the minimum (independent) dominating set of $T_{3\times n}$.

Figure 12. $\gamma \left(T_{3\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)=\lfloor \frac{n}{2}\rfloor +1$ for $3⩽n⩽10$; filled circles indicate the vertices in the minimum (independent) dominating set of $T_{3\times n}$.

Next, we consider $n⩾m⩾4$ for a rectangular triangular-supergrid graph $T_{m\times n}$.

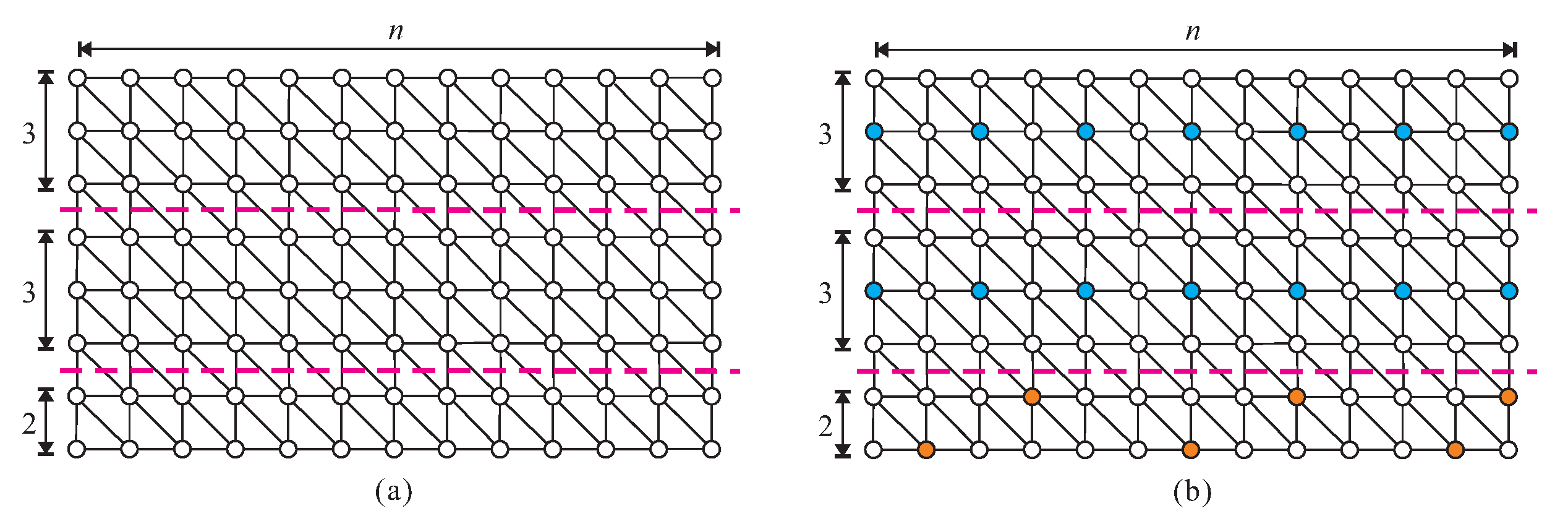
Lemma 11.

Let $T_{m\times n}$ be a rectangular triangular-supergrid graph with $n⩾m⩾4$. Then, $\gamma \left(T_{m\times n}\right)⩽\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$ and ${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)⩽\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$.

Proof. 

Based on Lemmas 1, 9 and 10, we compute an (independent) dominating set of $T_{m\times n}$ as follows. First, we make $\lfloor \frac{m}{3}\rfloor -1$ or $\lfloor \frac{m}{3}\rfloor$ horizontal separations on $T_{m\times n}$ to obtain $\lfloor \frac{m}{3}\rfloor$ disjoint subgraphs $T_{3\times n}$ and one $T_{(m-3·\lfloor \frac{m}{3}\rfloor )\times n}$ if $m\%3\ne 0$, as shown in Figure 13a. Let ${\mathtt{T}}_1$, ${\mathtt{T}}_2$, ⋯, ${\mathtt{T}}_{\lceil \frac{m}{3}\rceil }$ be partitioned subgraphs such that ${\mathtt{T}}_i$ is located above ${\mathtt{T}}_{i+1}$ for $1⩽i⩽\lceil \frac{m}{3}\rceil -1$. By Lemma 10, we can obtain a minimum (independent) dominating set $D_i$ of ${\mathtt{T}}_i$ with size $\lfloor \frac{n}{2}\rfloor +1$ for $1⩽i⩽\lceil \frac{m}{3}\rceil -1$. Depending on the number of $m\%3$, we consider the following cases:

Case 1: $m\%3=0$. In this case, let $D_{\lceil \frac{m}{3}\rceil }$ be the minimum (independent) dominating set of ${\mathtt{T}}_{\lceil \frac{m}{3}\rceil }$ constructed from the proof of Lemma 10, and let $D={\cup }_{1⩽i⩽\lceil \frac{m}{3}\rceil }{D}_i$. Then, $\left|D\right|=\lceil \frac{m}{3}\rceil (\lfloor \frac{n}{2}\rfloor +1)$.

Case 2: $m\%3=1$. In this case, let $D_{\lceil \frac{m}{3}\rceil }$ be the minimum (independent) dominating set of ${\mathtt{T}}_{\lceil \frac{m}{3}\rceil }$ constructed from Lemma 1. Then, $|D_{\lceil \frac{m}{3}\rceil }|=\lceil \frac{n}{3}\rceil$. Let $D={\cup }_{1⩽i⩽\lceil \frac{m}{3}\rceil -1}{D}_i\cup D_{\lceil \frac{m}{3}\rceil }$. Then, $\left|D\right|=(\lceil \frac{m}{3}\rceil -1)(\lfloor \frac{n}{2}\rfloor +1)+\lceil \frac{n}{3}\rceil ⩽\lceil \frac{m}{3}\rceil (\lfloor \frac{n}{2}\rfloor +1)$.

Case 3: $m\%3=2$. In this case, let $D_{\lceil \frac{m}{3}\rceil }$ be the minimum (independent) dominating set of ${\mathtt{T}}_{\lceil \frac{m}{3}\rceil }$ constructed from the proof of Lemma 9. Then, $|D_{\lceil \frac{m}{3}\rceil }|=\lceil \frac{2n}{5}\rceil$. Let $D={\cup }_{1⩽i⩽\lceil \frac{m}{3}\rceil -1}{D}_i\cup D_{\lceil \frac{m}{3}\rceil }$. Then, $\left|D\right|=(\lceil \frac{m}{3}\rceil -1)(\lfloor \frac{n}{2}\rfloor +1)+\lceil \frac{2n}{5}\rceil ⩽\lceil \frac{m}{3}\rceil (\lfloor \frac{n}{2}\rfloor +1)$.

In any case, we construct a (independent) dominating set D of $T_{m\times n}$ with size $\lceil \frac{m}{3}\rceil (\lfloor \frac{n}{2}\rfloor +1)=\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$ or less. For example, Figure 13b shows the constructed (independent) dominating set D of $T_{8\times 13}$ with size $2\times 7+6=(\lceil \frac{8}{3}\rceil -1)\times \lceil \frac{13+1}{2}\rceil +\lceil \frac{2\times 13}{5}\rceil ⩽\lceil \frac{8}{3}\rceil \lceil \frac{13+1}{2}\rceil$. That is, we obtain an upper bound $\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$ of $\gamma \left(T_{m\times n}\right)$ (${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$), and hence the lemma holds true. □

Figure 13. (a) Partitioning of $T_{m\times n}$ into $\lceil \frac{m}{3}\rceil$ disjoint subgraphs, and (b) an (independent) dominating set of $T_{m\times n}$. Solid dashed lines indicate separations and filled circles indicate vertices in the (independent) dominating set.

Figure 13. (a) Partitioning of $T_{m\times n}$ into $\lceil \frac{m}{3}\rceil$ disjoint subgraphs, and (b) an (independent) dominating set of $T_{m\times n}$. Solid dashed lines indicate separations and filled circles indicate vertices in the (independent) dominating set.

By the above lemma, we can see that each vertex in the constructed (independent) dominating set of $T_{m\times n}$ almost dominates six vertices. By the structure of $T_{m\times n}$, each vertex dominates at most seven vertices, including its six neighbors and itself. However, there exists no dominating set of $T_{m\times n}$ in which its each vertex dominates seven vertices. Thus, $\lceil \frac{mn}{7}\rceil <\gamma \left(T_{m\times n}\right)⩽{\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$. Because an independent dominating set of a graph is a dominating set of the graph, $\gamma \left(T_{m\times n}\right)$ provides a trivial lower bound of ${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$. Then, $\lceil \frac{mn}{7}\rceil <\gamma \left(T_{m\times n}\right)⩽{\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)⩽\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$ for $n⩾m⩾4$. Thus, we obtain a tight upper bound of $\gamma \left(T_{m\times n}\right)$ and ${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$. Using Lemmas 9–11, we can conclude the following theorem.

Theorem 5.

Let $T_{m\times n}$ be a rectangular triangular-supergrid graph with $n⩾m⩾2$. Then, $\lceil \frac{mn}{7}\rceil <\gamma \left(T_{m\times n}\right)⩽{\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$ if $n⩾m⩾4$, and

$$\gamma \left(T_{m\times n}\right)\left({\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)\right)\left\{\begin{array}{cc}=\lceil \frac{2n}{5}\rceil \hfill & ,if m=2;\hfill \\ =\lceil \frac{n+1}{2}\rceil \hfill & ,if m=3;\hfill \\ ⩽\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil \hfill & ,otherwise.\hfill \end{array}\right.$$

Proof. 

By Lemma 9, $\gamma \left(T_{2\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{2\times n}\right)=\lceil \frac{2n}{5}\rceil$. By Lemma 10, $\gamma \left(T_{3\times n}\right)={\gamma }_{\mathrm{ind}}\left(T_{3\times n}\right)=\lceil \frac{n+1}{2}\rceil$. Lemma 11 provides that $\gamma \left(T_{m\times n}\right)⩽\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$ and ${\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)⩽\lceil \frac{m}{3}\rceil \lceil \frac{n+1}{2}\rceil$ for $n⩾m⩾4$. In addition, $\lceil \frac{mn}{7}\rceil <\gamma \left(T_{m\times n}\right)⩽{\gamma }_{\mathrm{ind}}\left(T_{m\times n}\right)$ if $n⩾m⩾4$. Thus, the theorem holds true. □

5. Concluding Remarks

Here, we first introduce the class of extended supergrid graphs containing grid, triangular grid, supergrid, diagonal supergrid, and triangular supergrid graphs as subclasses. Domination and independent domination problems for grid graphs are known to be NP-complete, and they are NP-complete for extended supergrid graphs as well. However, the complexities of other subclasses of extended supergrid graphs remain unknown. In this paper, we first prove that the domination and independent domination problems on diagonal supergrid graphs are NP-complete. As this result can be immediately applie dto supergrid and triangular supergrid graphs, both problems are NP-complete for them as well. The studied problems on rectangular supergrid graphs and rectangular grid graphs have been solved in linear time. However, their complexities remain unknown for rectangular triangular-supergrid graphs. In this paper, we provide a tight upper bound of the domination and independent domination numbers for rectangular triangular-supergrid graphs. It might be interesting to obtain a lower bound of the domination and independent domination numbers for rectangular triangular-supergrid graphs, which we leave as an open question for future interested readers. Furthermore, the complexities of the domination and independent domination problems for triangular grid graphs remain unknown. We speculate that they are NP-complete. However, we are unable to verify this, and would like to publish it as an open problem for interested readers. Finally, we conclude the status of the complexities of the domination and independent domination problems for extended supergrid graphs in Figure 14.