Testing Some Different Implementations of Heat Convection and Radiation in the Leapfrog-Hopscotch Algorithm
Abstract
1. Introduction
2. The Examined Numerical Methods
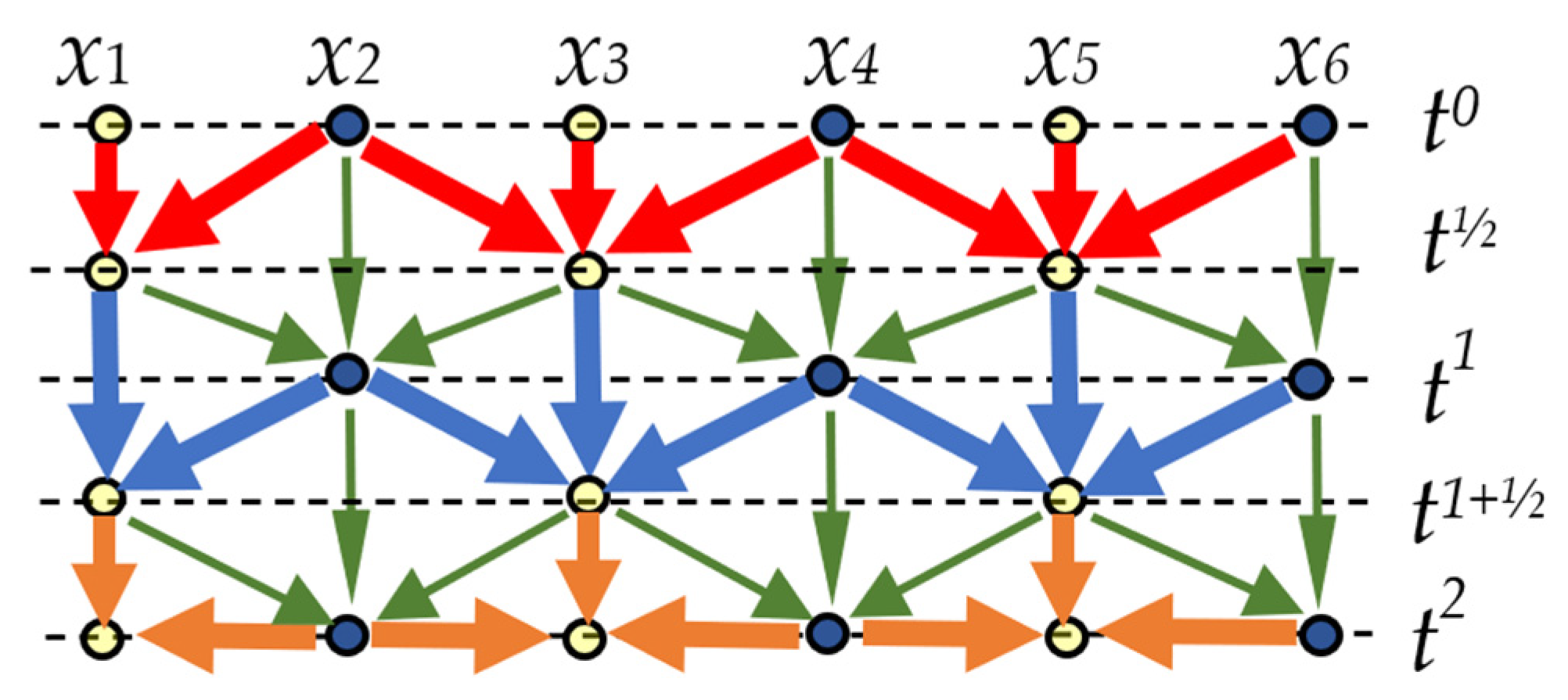
2.1. The Leapfrog-Hopscotch Method for the Heat Conduction Equation
2.2. Implementations of the Convection Term
2.3. Implementations of the Radiation Term
2.4. Methods Used for Comparison Purposes
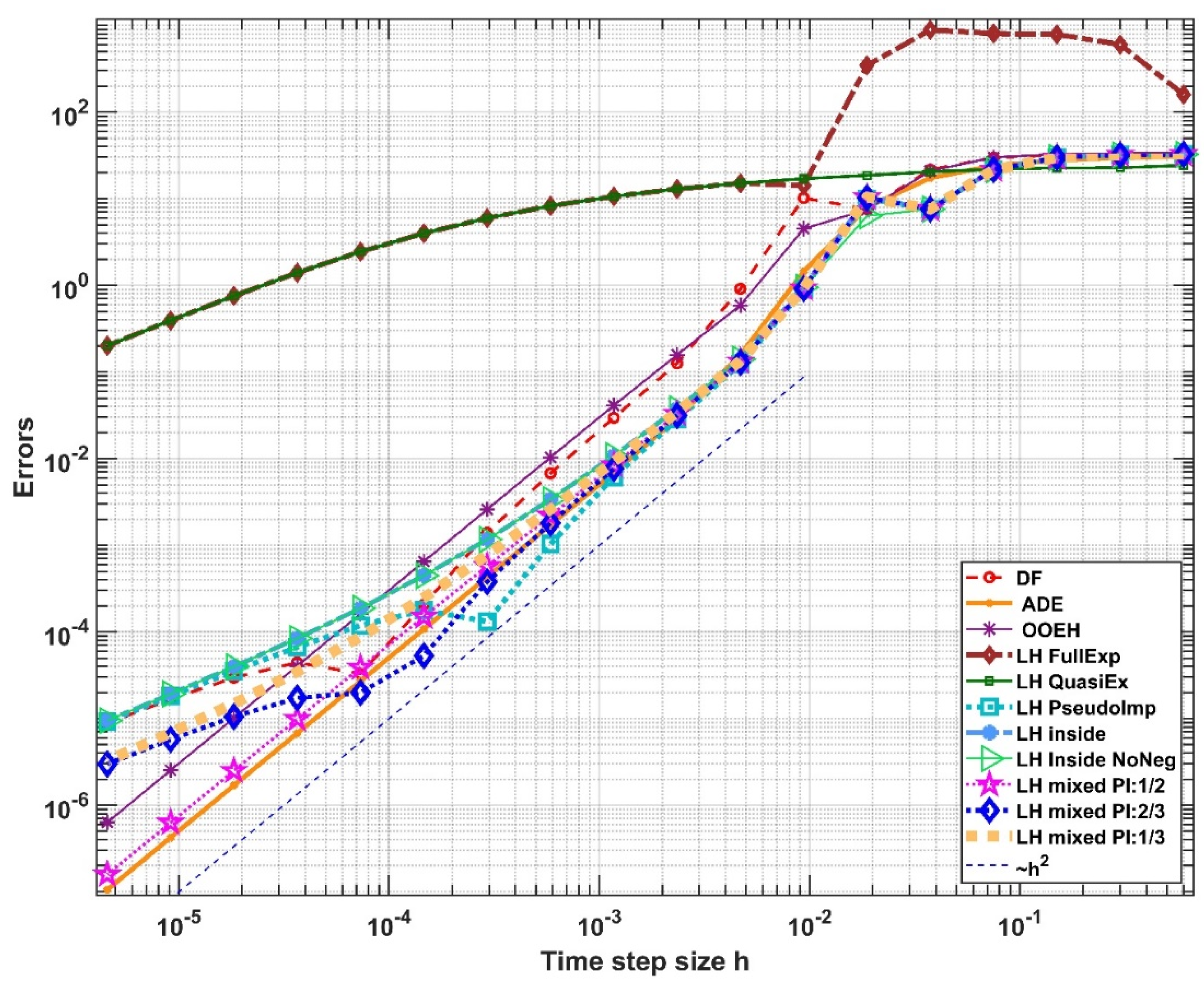
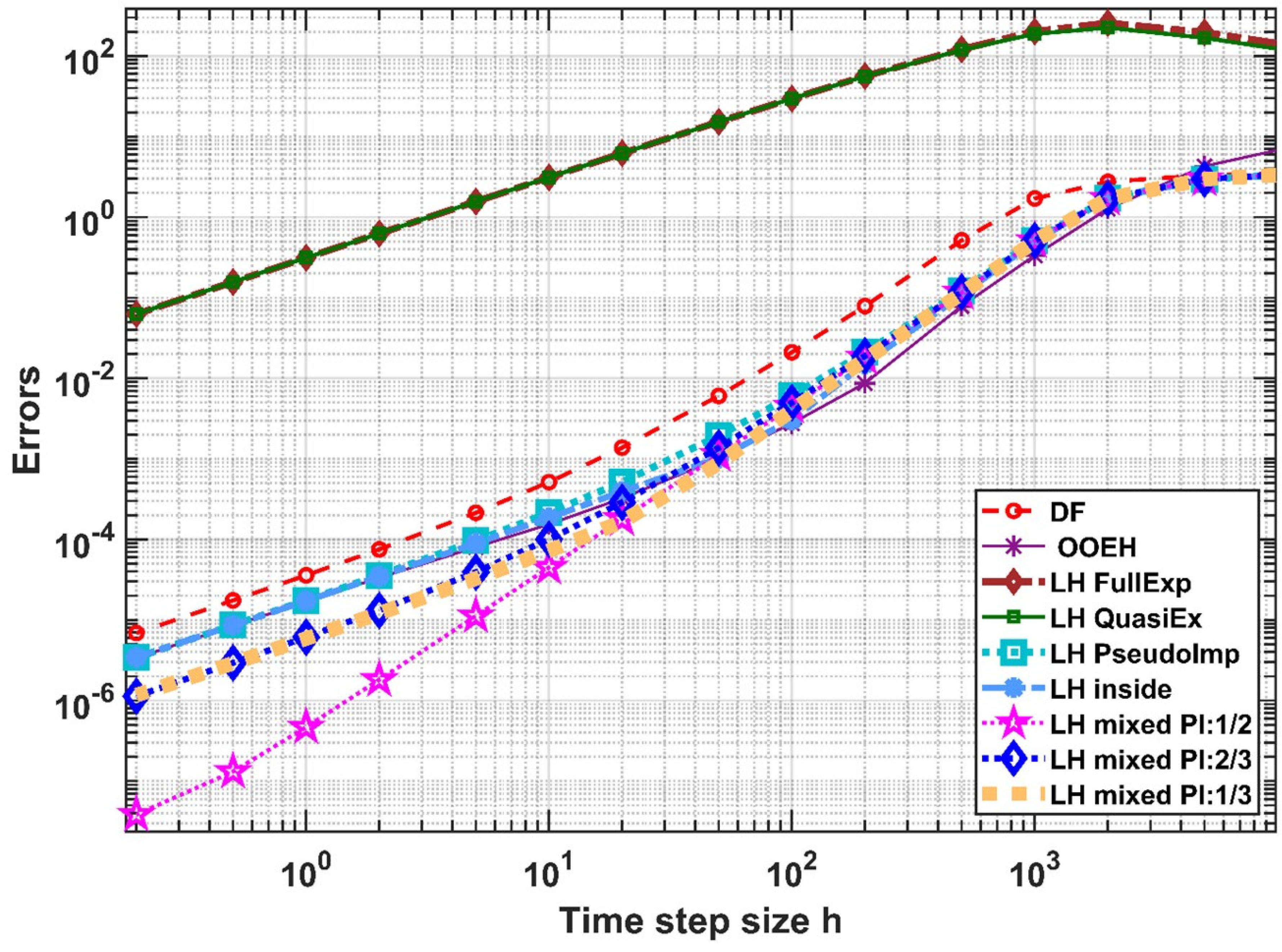
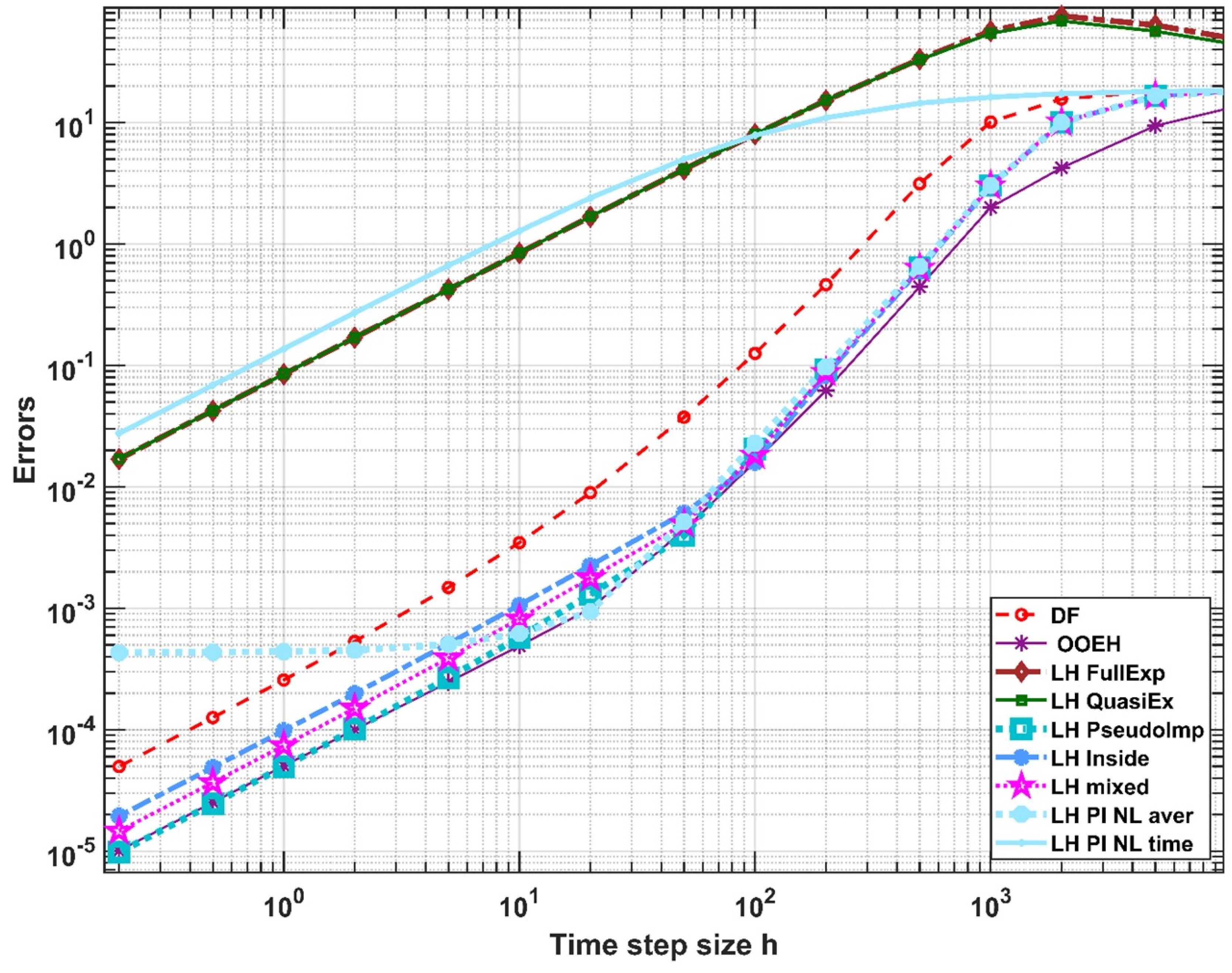
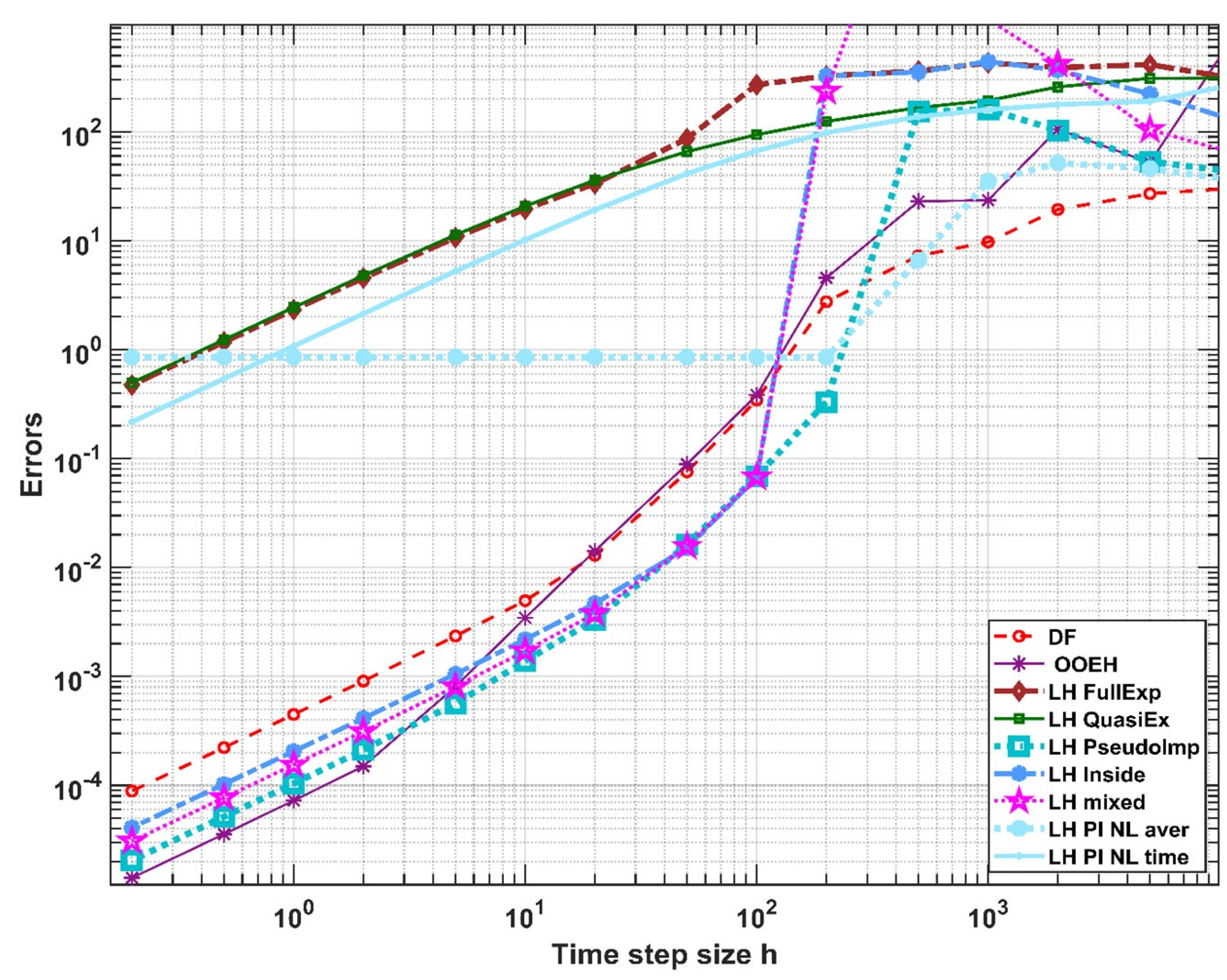
3. Numerical Experiments for the Convection Term
4. Analytical Results for the Conduction–Convection Case
4.1. Consistency
4.2. Stability
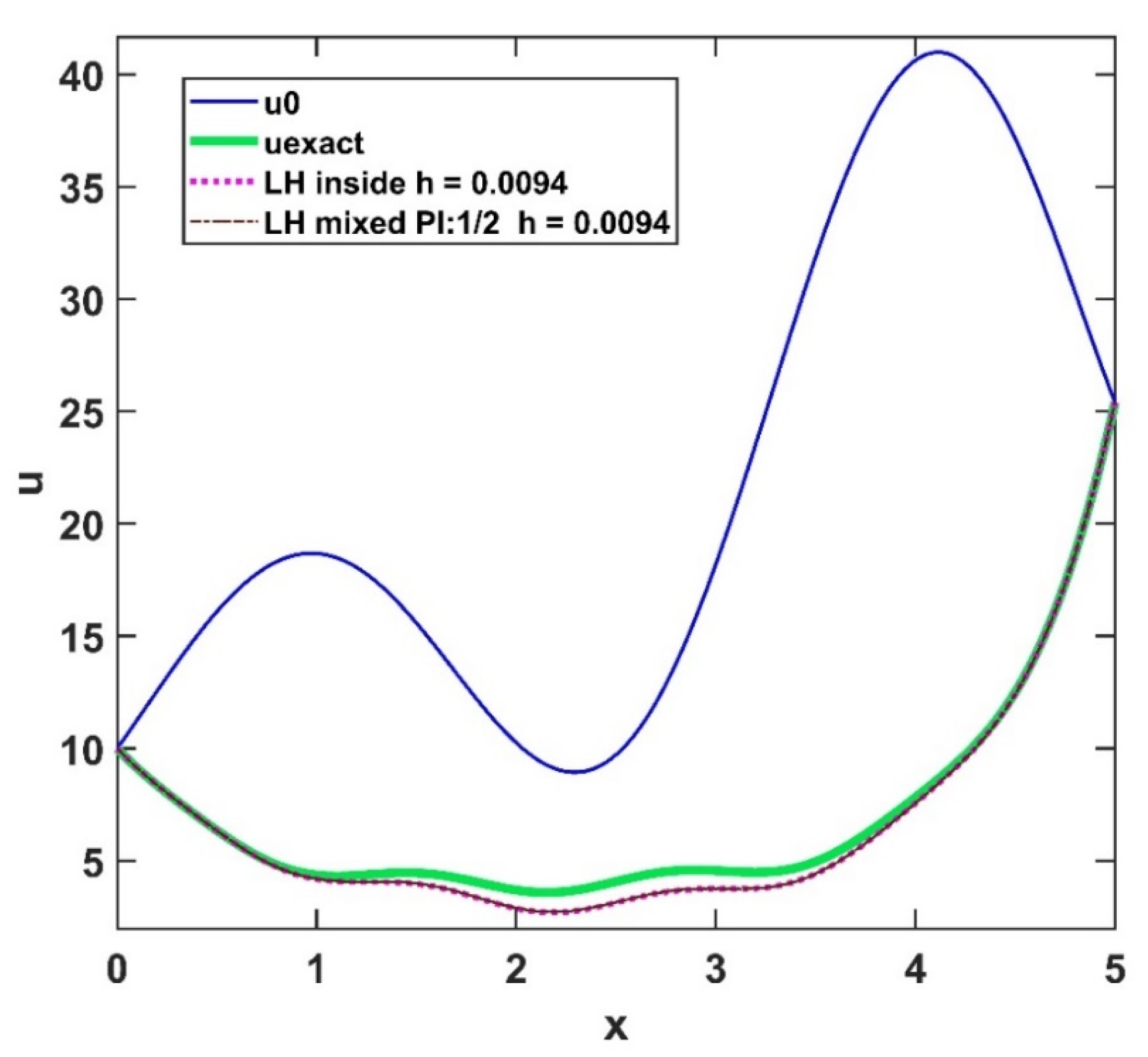
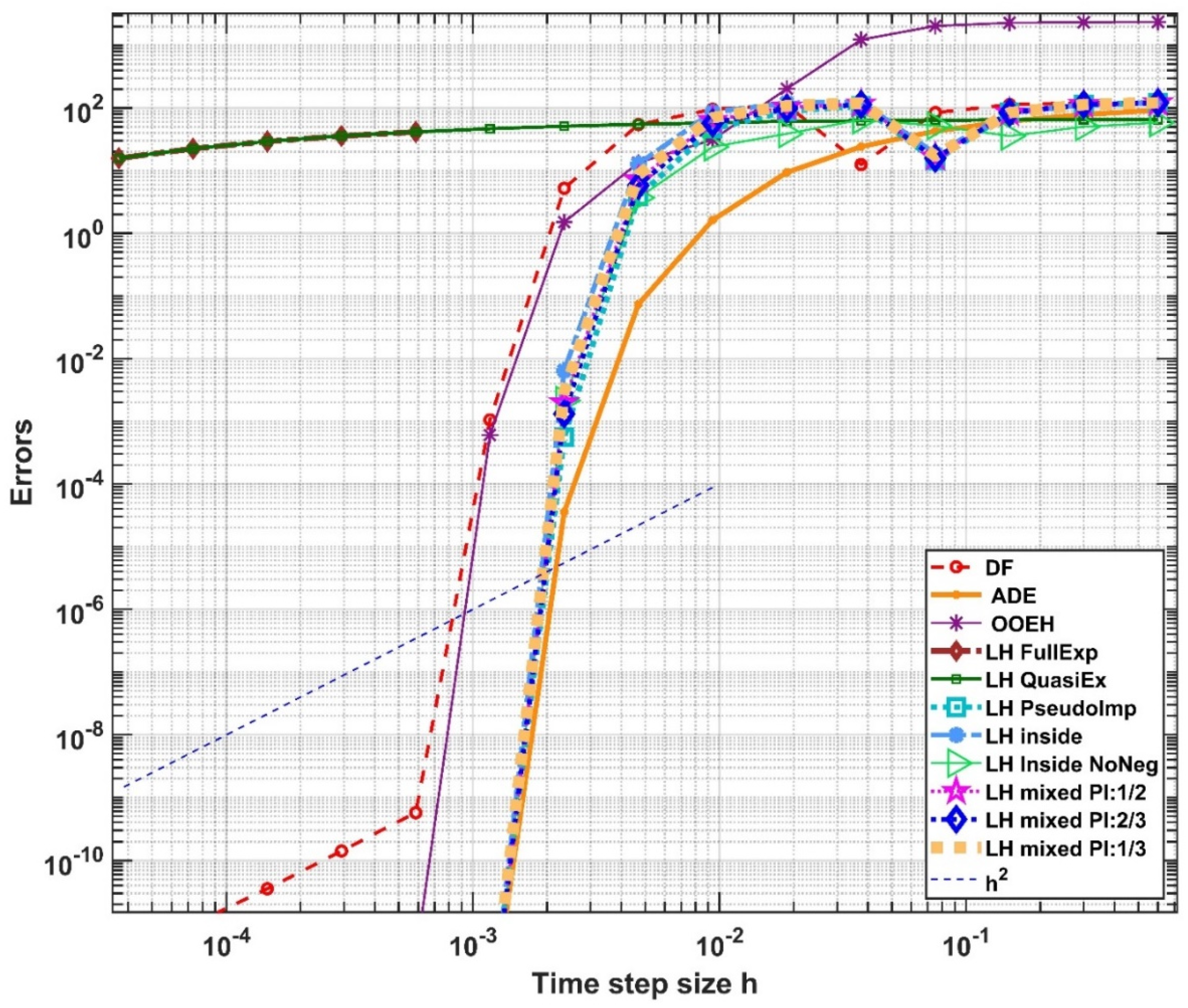
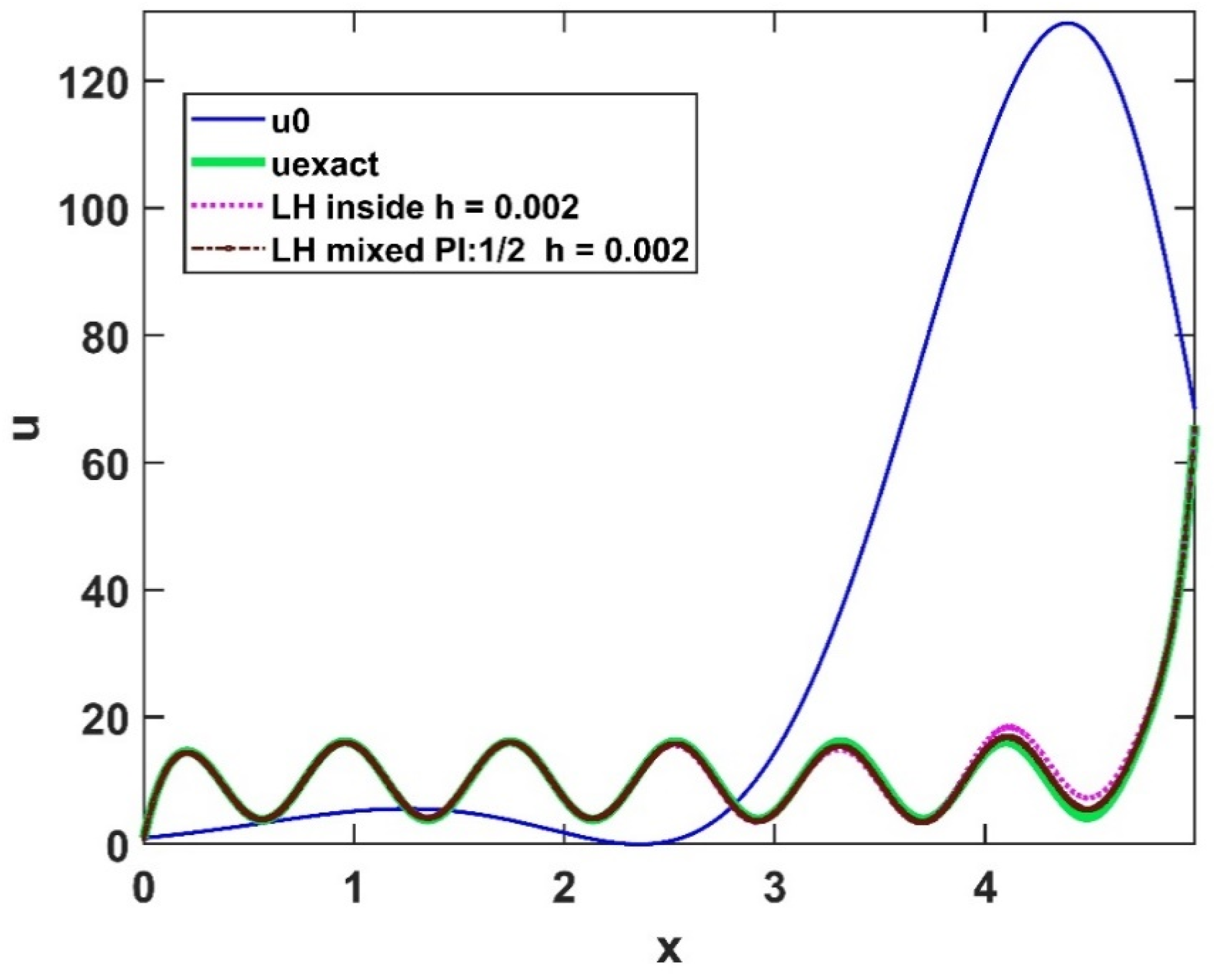
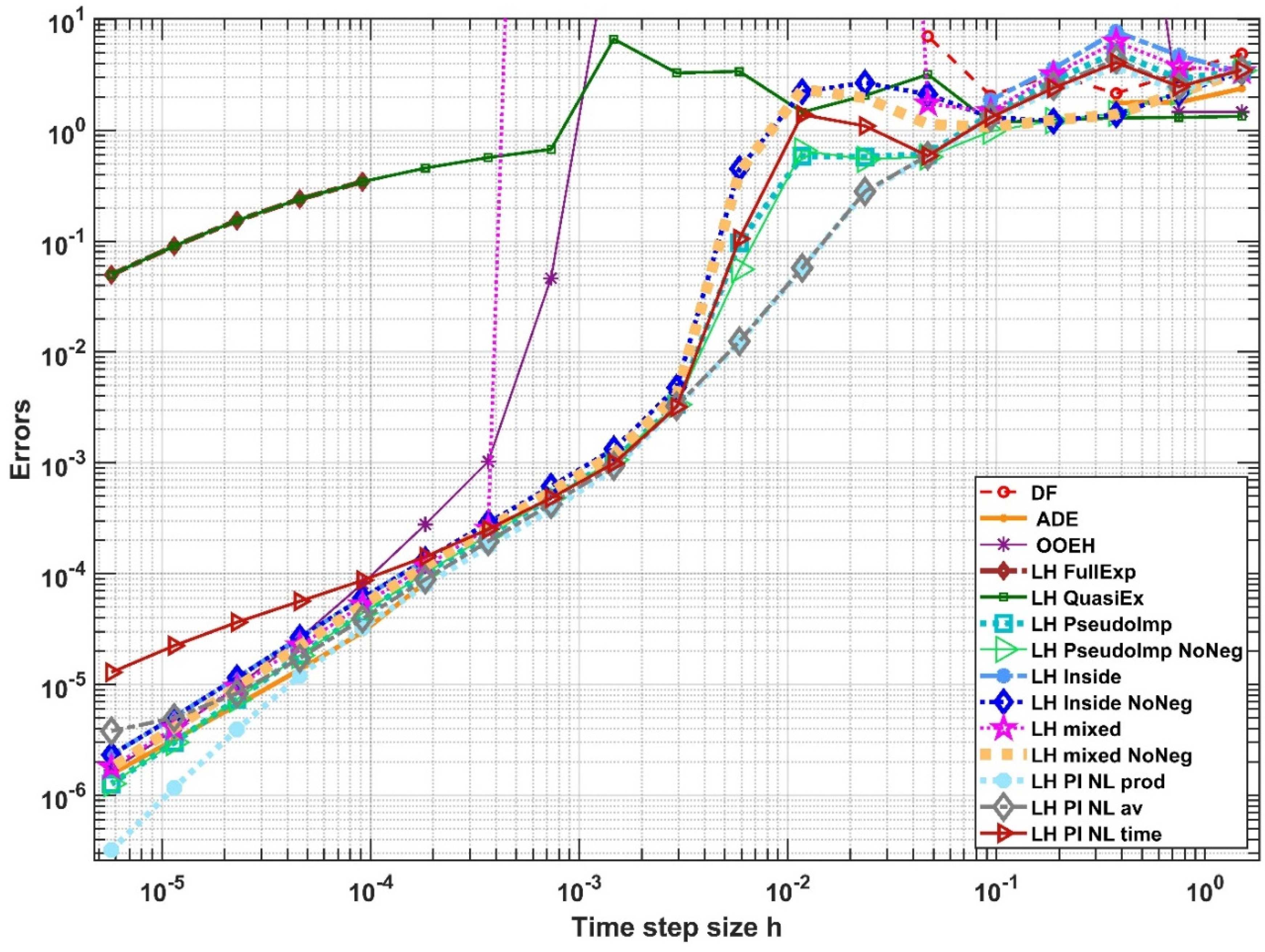
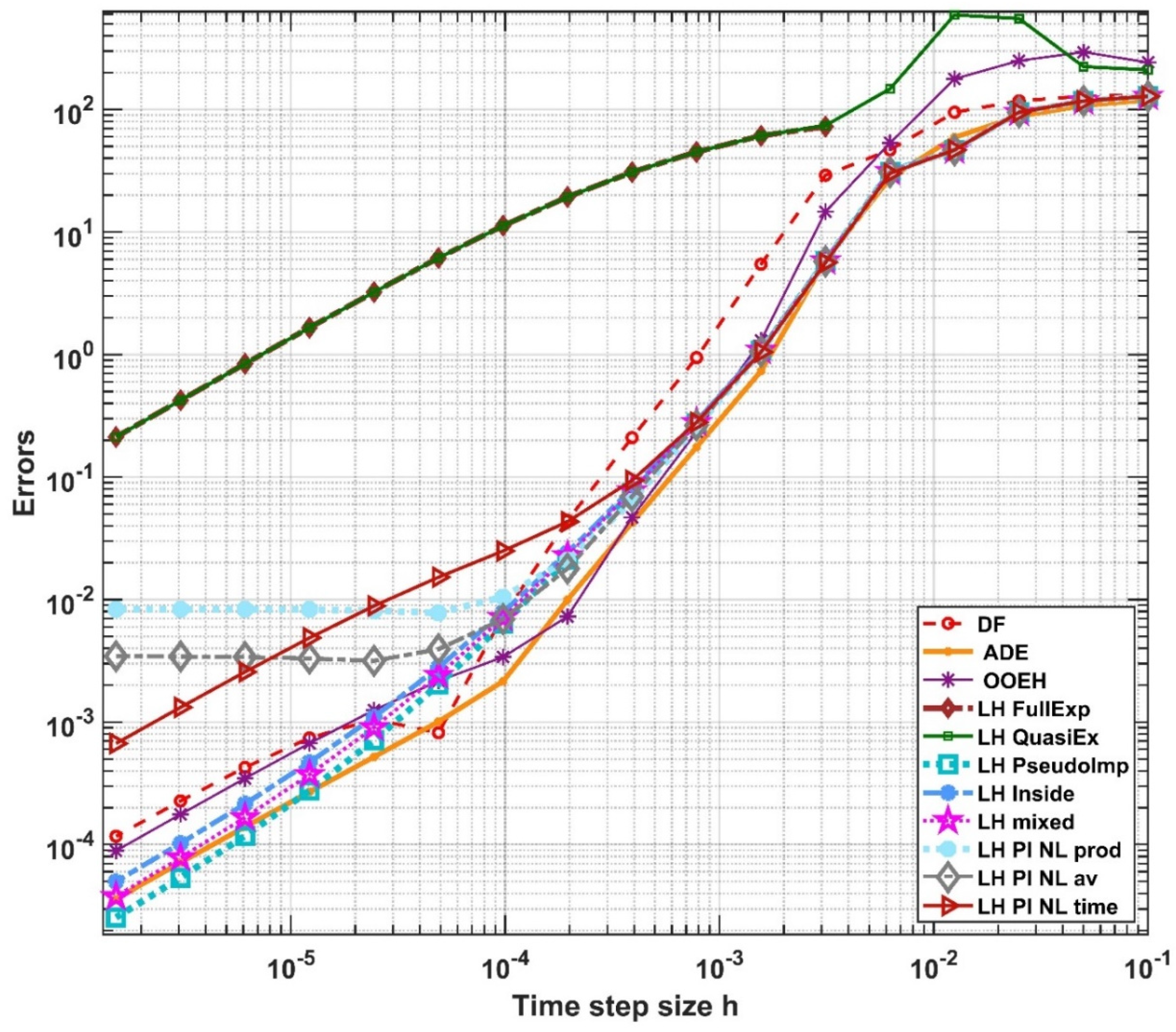
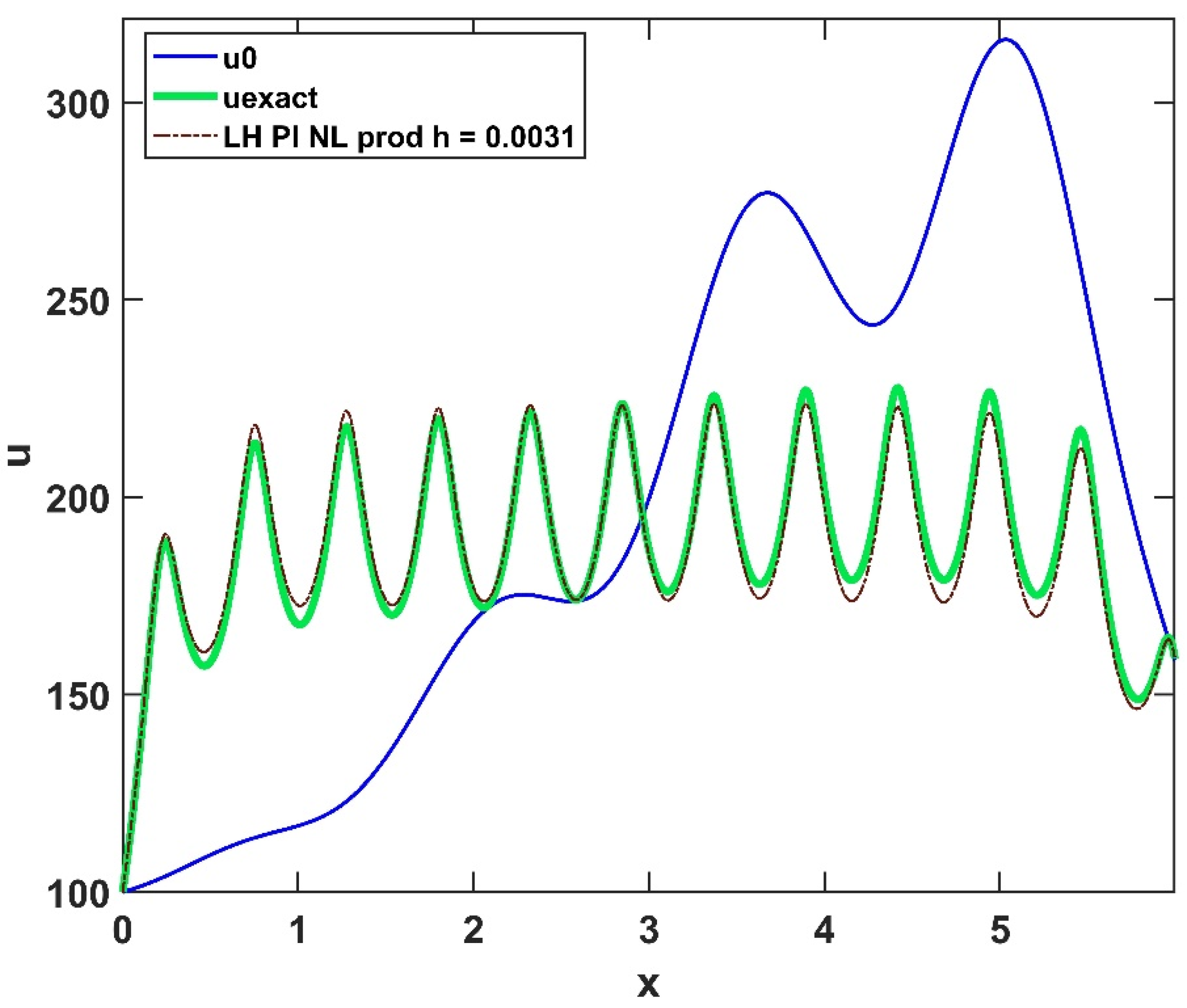
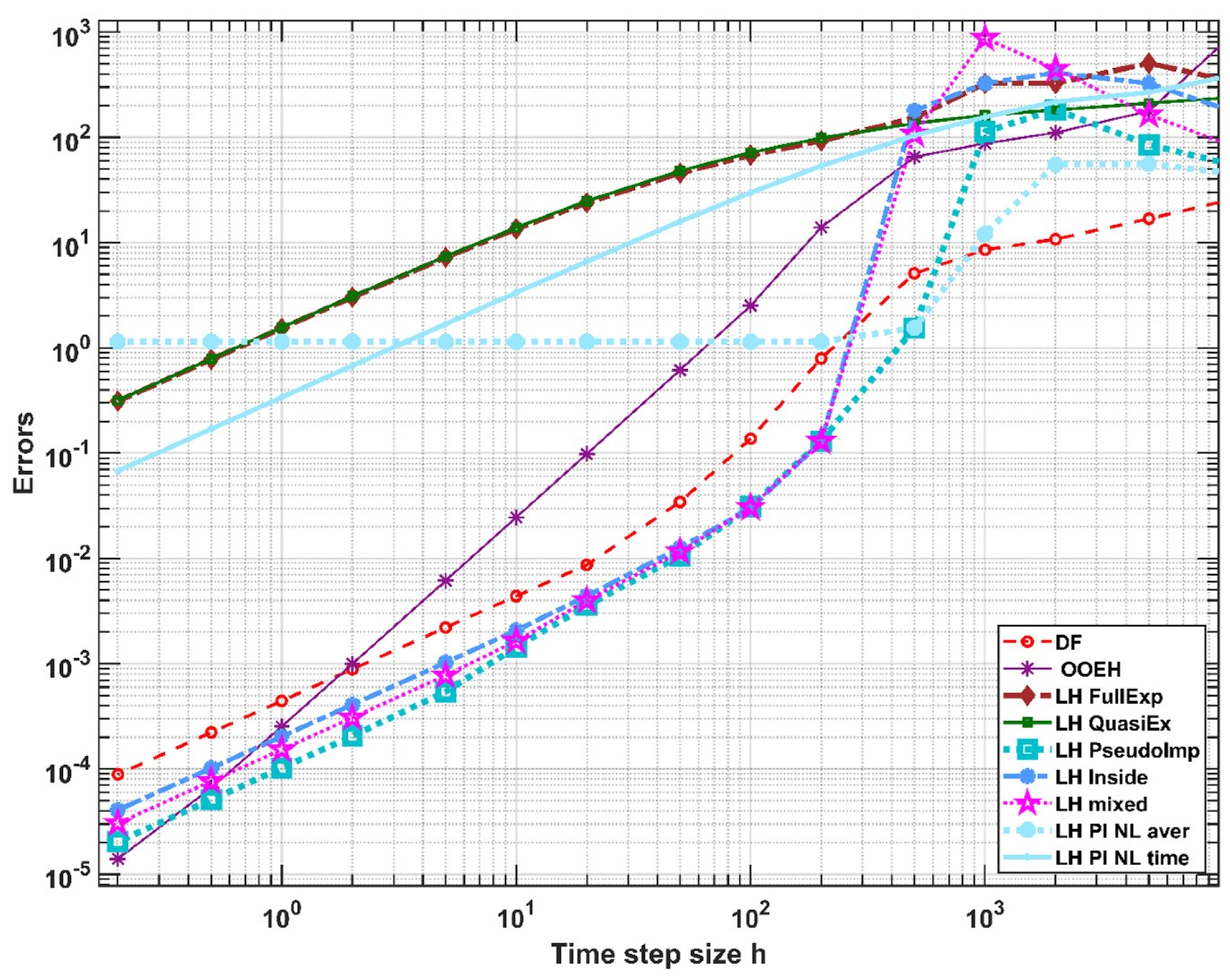
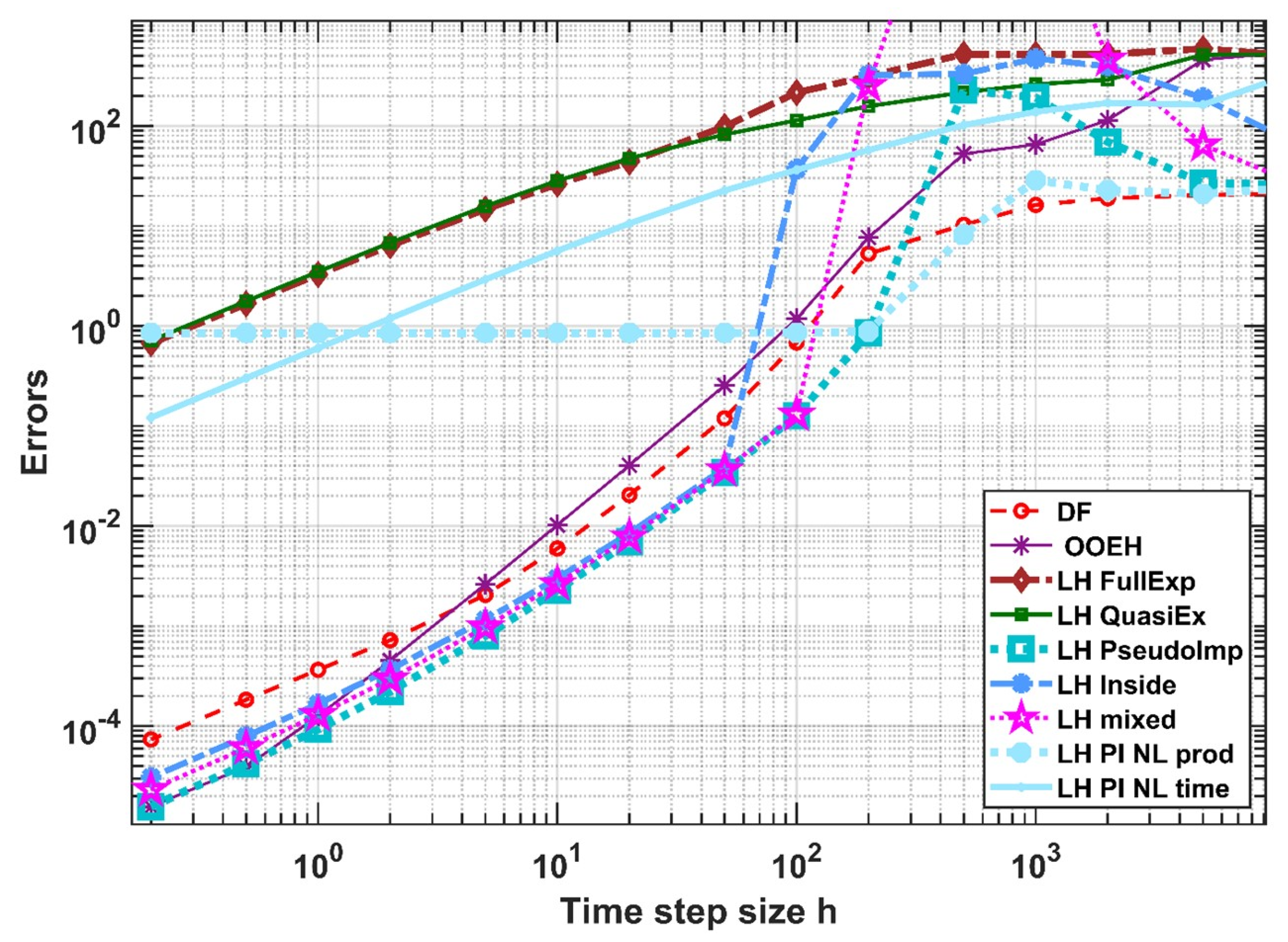
5. Numerical Experiments for the Radiation Term in 1D
5.1. Verification with an Analytical Reference Solution
5.2. Results in Case of a Numerical Reference Solution
6. Simulation of a Realistic Wall
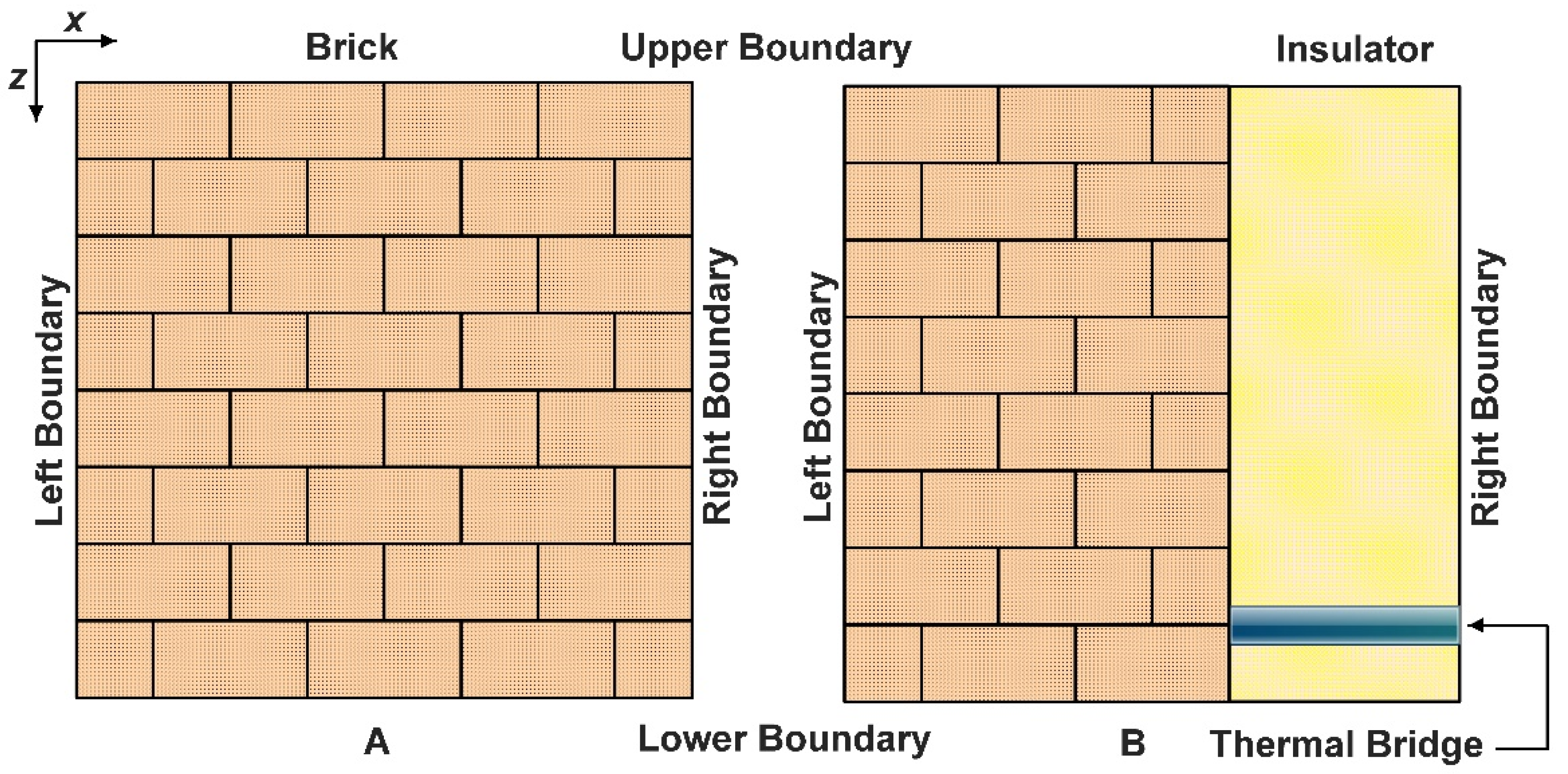
6.1. The Structure and the Materials of the Wall
- (A)
- A wall’s surface is examined, which is entirely built of brick.
- (B)
- Cross section of a wall with two layers composed of brick and rigid polyurethane foam insulator with a steel beam thermal bridge.
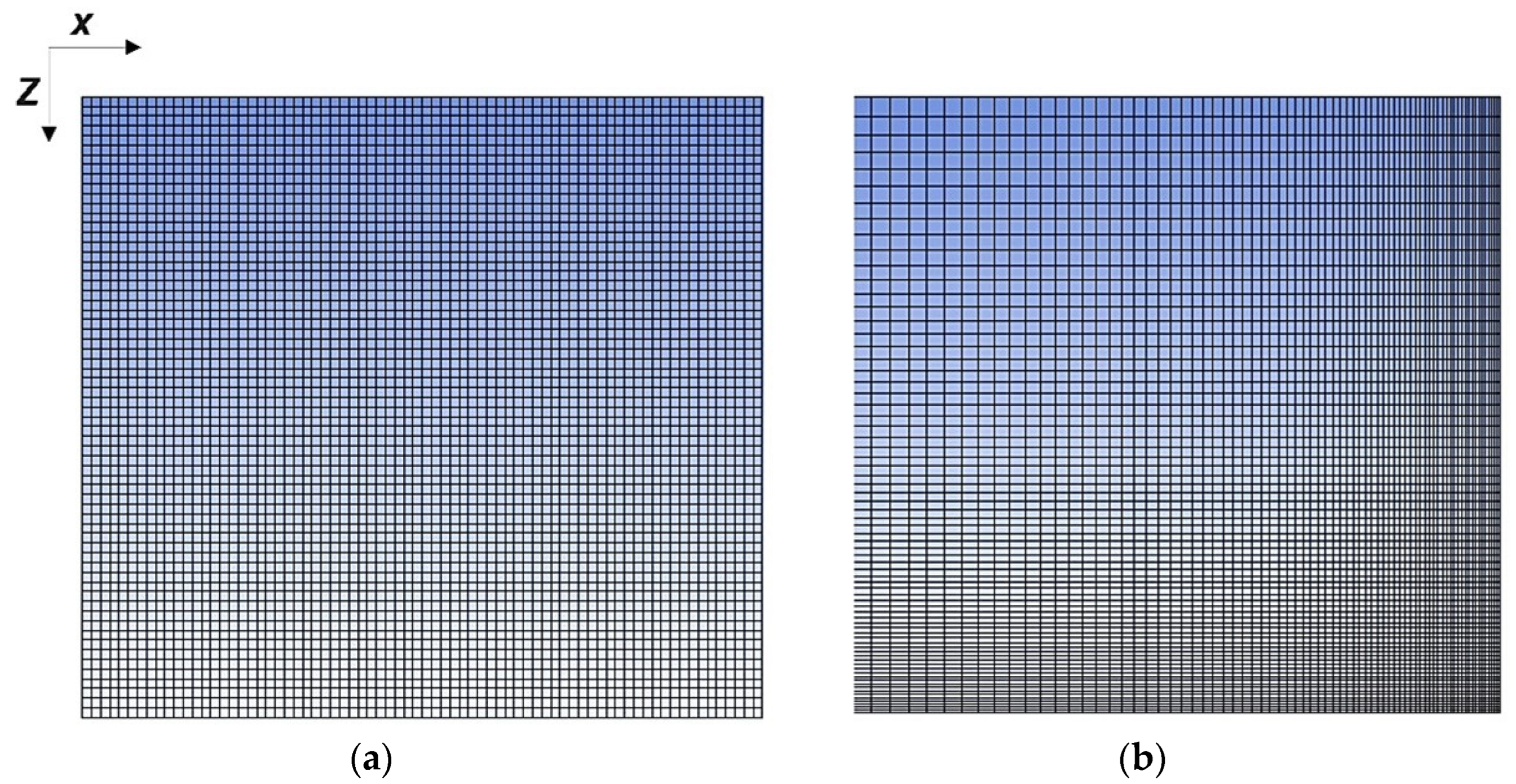
6.2. Mesh Construction
6.3. The Initial and the Boundary Conditions
- -
- the first portion of N (sunny side):
- -
- the second portion of N (shaded side):
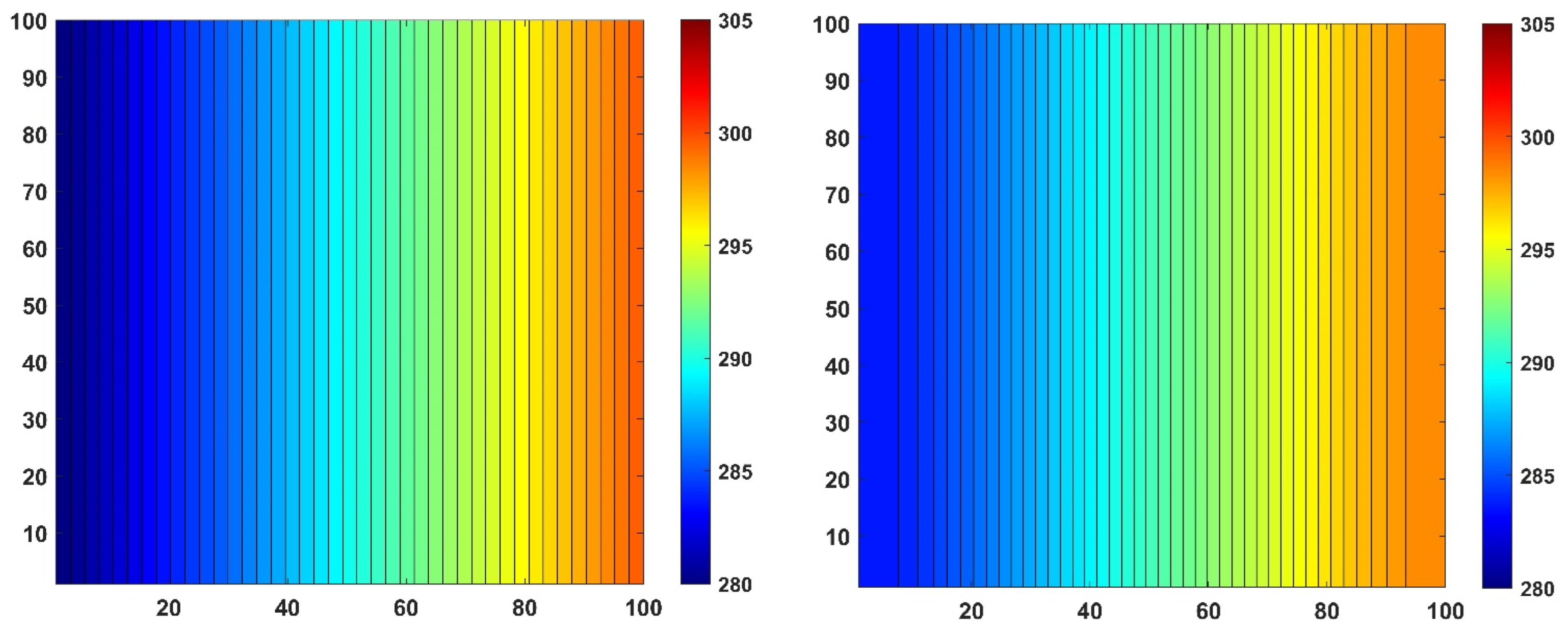
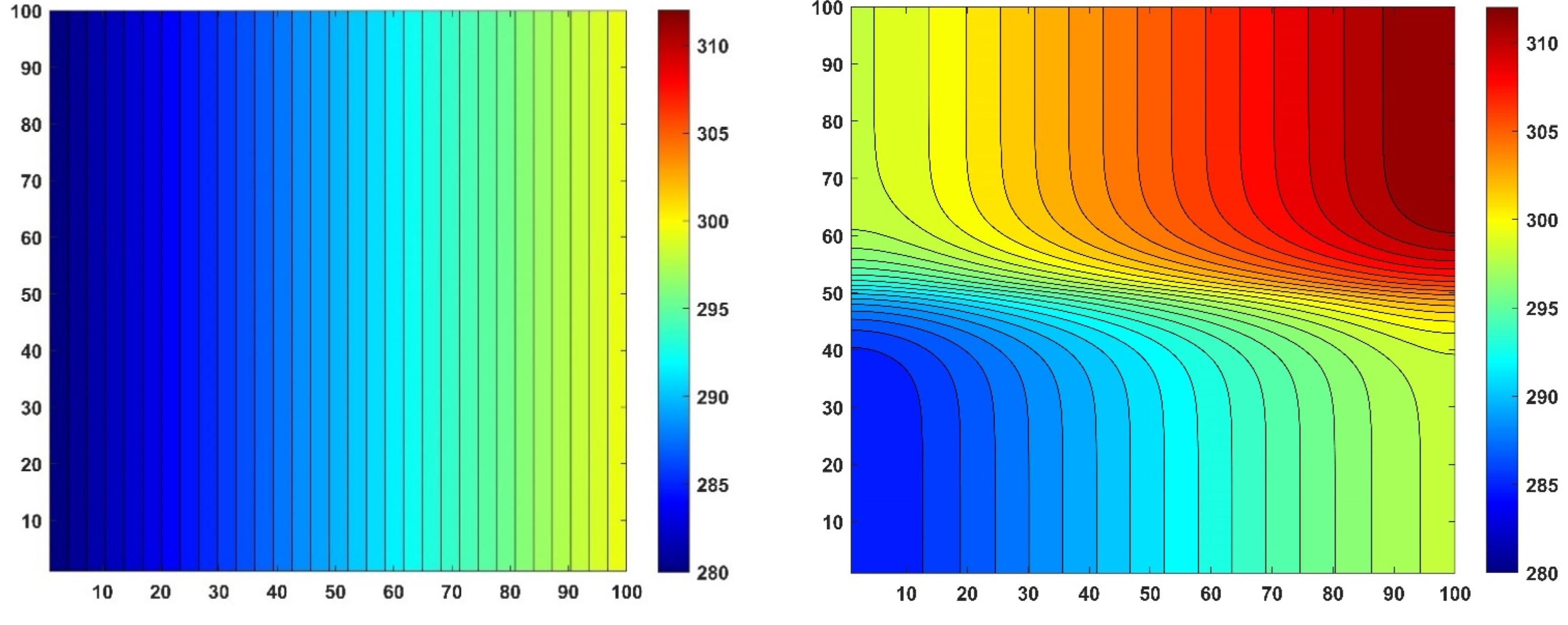
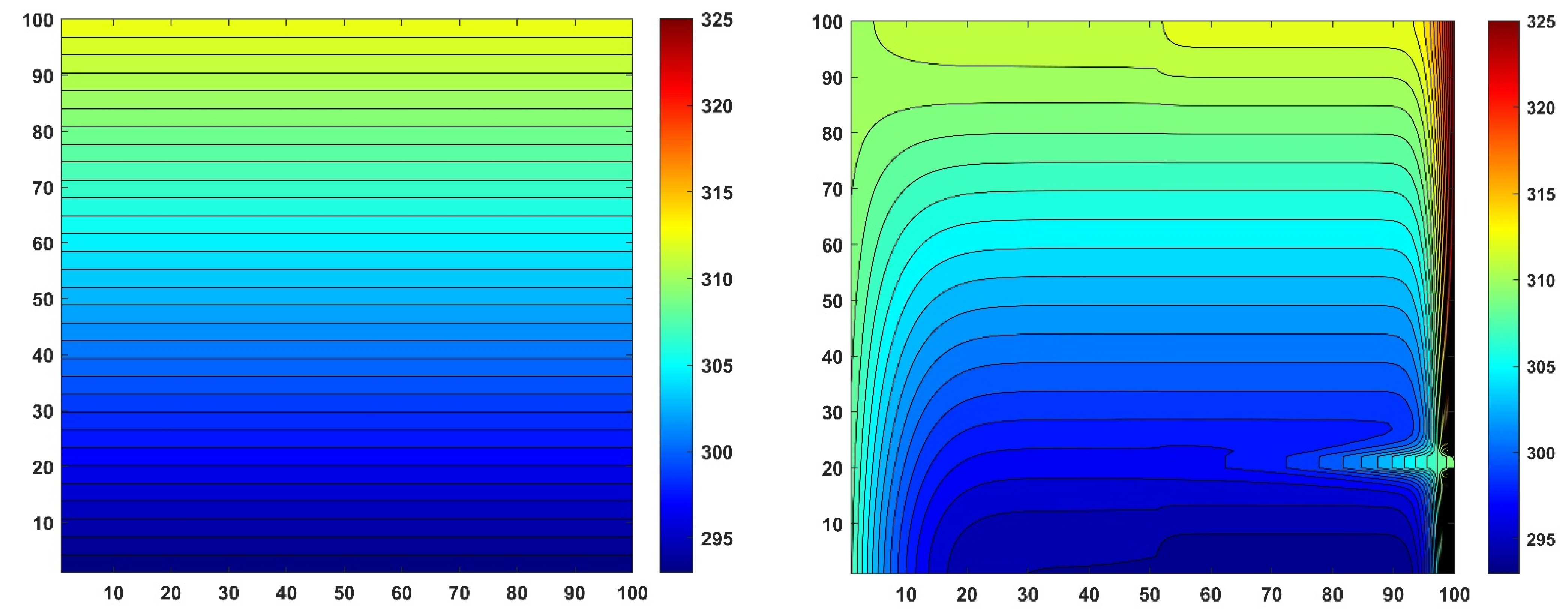
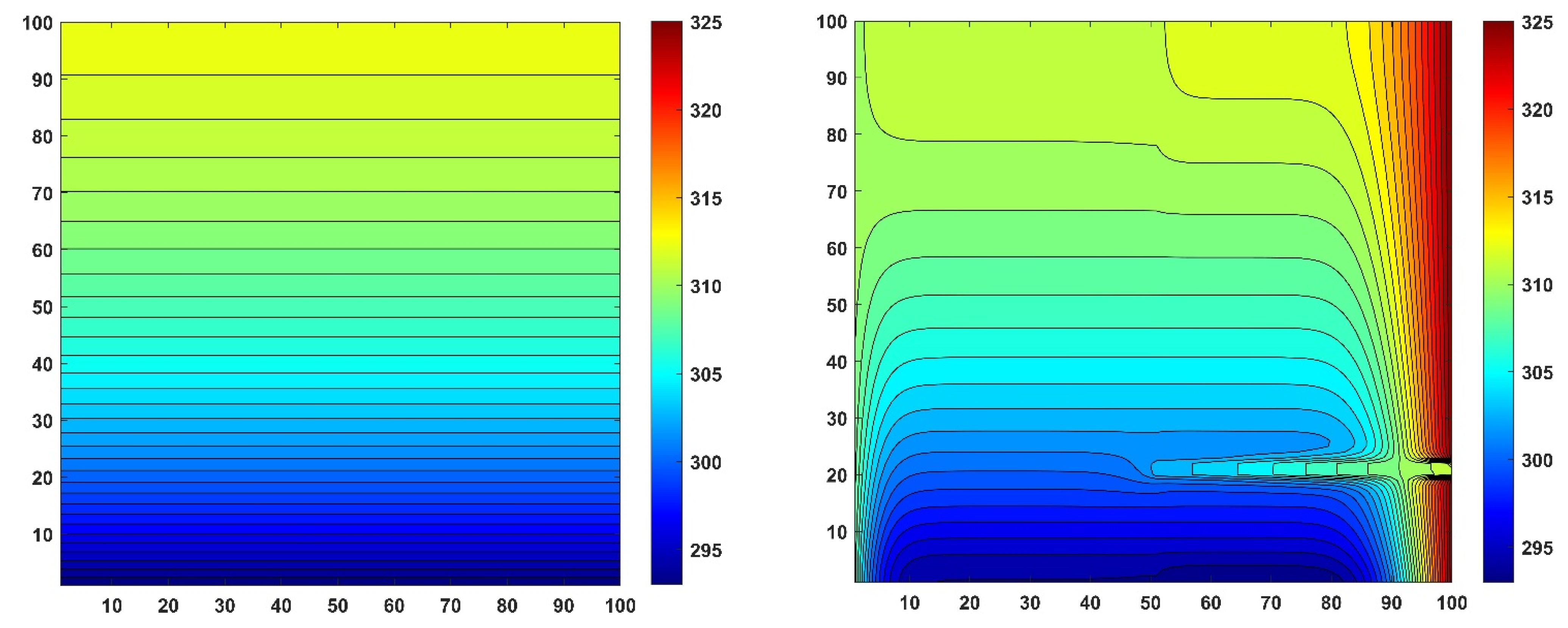
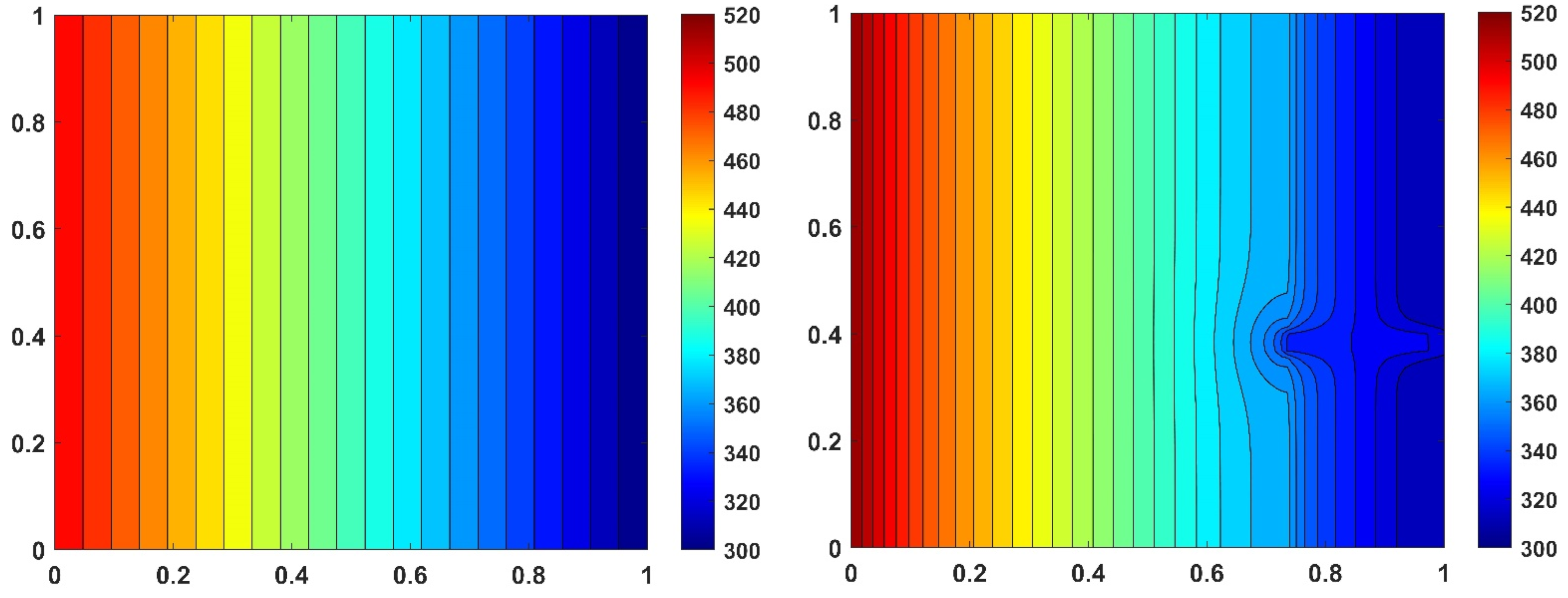
6.4. Results for the Surface of the Wall
6.5. Results for the Cross Section of the Insulated Wall with Thermal Bridging
7. Discussion and Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Greek Symbols | ||
| c | Specific heat (kJ/kg.K) | α | Thermal diffusivity (m2/s) |
| h | Time step size (sec) | Δ | Difference |
| hc | Heat transfer coefficient (W/m2.K) | ρ | Mass density (kg/m3) |
| K | Convection coefficient (1/sec) | σ | Coefficient of the radiation term (sec−1 K−3) |
| k | Thermal conductivity (W/m.K) | realistic values of non-black body (W/m2.K4) | |
| Q | Heat transfer rate (W) | Subscripts | |
| heat generation (W/m2) | a | Ambient air | |
| q | Heat source rate(1/K) | sunny | Sunny surface |
| t | time (sec) | shadow | Shadow surface |
| u | Temperature (Kº) | ||
References
- Ochoa, G.V.; Sanchez, W.E.; Truyoll, S.D.L.H. Experimental and theoretical study on free and force convection heat transfer. Contemp. Eng. Sci. 2017, 10, 1143–1152. [Google Scholar] [CrossRef]
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2009; ISBN 0073529362. [Google Scholar]
- Savović, S.M.; Djordjevich, A. Numerical solution of diffusion equation describing the flow of radon through concrete. Appl. Radiat. Isot. 2008, 66, 552–555. Available online: https://www.sciencedirect.com/science/article/pii/S0969804307002874 (accessed on 1 October 2022). [CrossRef] [PubMed]
- Suárez-Carreño, F.; Rosales-Romero, L. Convergency and stability of explicit and implicit schemes in the simulation of the heat equation. Appl. Sci. 2021, 11, 4468. [Google Scholar] [CrossRef]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. Borehole Heat Exchangers in aquifers: Simulation of the grout material impact. Rend. Online Soc. Geol. Ital. 2016, 41, 268–271. [Google Scholar] [CrossRef]
- Hundsdorfer, W.; Verwer, J. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations; Springer: Berlin/Heidelberg, Germany, 2003; Volume 33, ISBN 978-3-642-05707-6. [Google Scholar]
- Ndou, N.; Dlamini, P.; Jacobs, B.A. Enhanced Unconditionally Positive Finite Difference Method for Advection–Diffusion–Reaction Equations. Mathematics 2022, 10, 2639. [Google Scholar] [CrossRef]
- Amoah-mensah, J.; Boateng, F.O.; Bonsu, K. Numerical solution to parabolic PDE using implicit finite difference approach. Math. Theory Model. 2016, 6, 74–84. [Google Scholar]
- Mbroh, N.A.; Munyakazi, J.B. A robust numerical scheme for singularly perturbed parabolic reaction-diffusion problems via the method of lines. Int. J. Comput. Math. 2021, 99, 1139–1158. [Google Scholar] [CrossRef]
- Aminikhah, H.; Alavi, J. An efficient B-spline difference method for solving system of nonlinear parabolic PDEs. SeMA J. 2018, 75, 335–348. [Google Scholar] [CrossRef]
- Ali, I.; Haq, S.; Nisar, K.S.; Arifeen, S.U. Numerical study of 1D and 2D advection-diffusion-reaction equations using Lucas and Fibonacci polynomials. Arab. J. Math. 2021, 10, 513–526. [Google Scholar] [CrossRef]
- Singh, M.K.; Rajput, S.; Singh, R.K. Study of 2D contaminant transport with depth varying input source in a groundwater reservoir. Water Sci. Technol. Water Supply 2021, 21, 1464–1480. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, H.; Xing, Y. New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems. Mathematics 2022, 10, 2375. [Google Scholar] [CrossRef]
- Essongue, S.; Ledoux, Y.; Ballu, A. Speeding up mesoscale thermal simulations of powder bed additive manufacturing thanks to the forward Euler time-integration scheme: A critical assessment. Finite Elem. Anal. Des. 2022, 211, 103825. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0168874X22000981 (accessed on 28 August 2022). [CrossRef]
- Iserles, A. A First Course in the Numerical Analysis of Differential Equations; Cambridge University Press: Cambridge, UK, 2009; ISBN 9788490225370. [Google Scholar]
- Saghyan, A.; Lewis, D.P.; Hrabe, J.; Hrabetova, S. Extracellular diffusion in laminar brain structures exemplified by hippocampus. J. Neurosci. Methods 2012, 205, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Appadu, A.R. Performance of UPFD scheme under some different regimes of advection, diffusion and reaction. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 1412–1429. [Google Scholar] [CrossRef]
- Sanjaya, F.; Mungkasi, S. A simple but accurate explicit finite difference method for the advection-diffusion equation. J. Phys. Conf. Ser. 2017, 909, 1–5. [Google Scholar] [CrossRef]
- Pourghanbar, S.; Manafian, J.; Ranjbar, M.; Aliyeva, A.; Gasimov, Y.S. An efficient alternating direction explicit method for solving a nonlinear partial differential equation. Math. Probl. Eng. 2020, 2020, 9647416. [Google Scholar] [CrossRef]
- Al-Bayati, A.; Manaa, S.; Al-Rozbayani, A. Comparison of Finite Difference Solution Methods for Reaction Diffusion System in Two Dimensions. AL-Rafidain J. Comput. Sci. Math. 2011, 8, 21–36. [Google Scholar] [CrossRef][Green Version]
- Nwaigwe, C. An Unconditionally Stable Scheme for Two-Dimensional Convection-Diffusion-Reaction Equations; State University: Port Harcourt, Nigeria, 2022. [Google Scholar]
- Savović, S.; Drljača, B.; Djordjevich, A. A comparative study of two different finite difference methods for solving advection–diffusion reaction equation for modeling exponential traveling wave in heat and mass transfer processes. Ric. Mat. 2021, 71, 245–252. [Google Scholar] [CrossRef]
- Liu, H.; Leung, S. An Alternating Direction Explicit Method for Time Evolution Equations with Applications to Fractional Differential Equations. Methods Appl. Anal. 2020, 26, 249–268. Available online: http://arxiv.org/abs/2002.08461 (accessed on 20 August 2022). [CrossRef]
- Bouwer, A. The Du Fort and Frankel Finite Difference Scheme Applied to and Adapted for a Class of Finance Problems. Master’s Thesis, University of Pretoria, Pretoria, South Africa, 2008. [Google Scholar]
- Saleh, M.; Nagy, Á.; Kovács, E. Part 1: Construction and investigation of new numerical algorithms for the heat equation. Multidiszcip. Tudományok 2020, 10, 323–338. [Google Scholar] [CrossRef]
- Kovács, E.; Nagy, Á.; Saleh, M. A New Stable, Explicit, Third-Order Method for Diffusion-Type Problems. Adv. Theory Simul. 2022, 5, 2100600. Available online: https://onlinelibrary.wiley.com/doi/10.1002/adts.202100600 (accessed on 1 October 2022). [CrossRef]
- Nagy, Á.; Omle, I.; Kareem, H.; Kovács, E.; Barna, I.F.; Bognar, G. Stable, Explicit, Leapfrog-Hopscotch Algorithms for the Diffusion Equation. Computation 2021, 9, 92. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Kovács, E.; Majár, J.; Nagy, Á.; Askar, A.H. Explicit stable finite difference methods for diffusion-reaction type equations. Mathematics 2021, 9, 3308. [Google Scholar] [CrossRef]
- Kovács, E. A class of new stable, explicit methods to solve the non-stationary heat equation. Numer. Methods Partial Differ. Equ. 2020, 37, 2469–2489. [Google Scholar] [CrossRef]
- Saleh, M.; Kovács, E.; Barna, I.F.; Mátyás, L. New Analytical Results and Comparison of 14 Numerical Schemes for the Diffusion Equation with Space-Dependent Diffusion Coefficient. Mathematics 2022, 10, 2813. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Kovács, E.; Bolló, B. Comparison of Old and New Stable Explicit Methods for Heat Conduction, Convection, and Radiation in an Insulated Wall with Thermal Bridging. Buildings 2022, 12, 1365. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific Publishing: Singapore, 1993; ISBN 978-981-02-1458-6. [Google Scholar]
- Agbavon, K.M.; Appadu, A.R. Construction and analysis of some nonstandard finite difference methods for the FitzHugh–Nagumo equation. Numer. Methods Partial Differ. Equ. 2020, 36, 1145–1169. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows, Volume 1: Fundamentals of Numerical Discretization; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Barakat, H.Z.; Clark, J.A. On the solution of the diffusion equations by numerical methods. J. Heat Transf. 1966, 88, 421–427. [Google Scholar] [CrossRef]
- Gourlay, A.R.; McGuire, G.R. General Hopscotch Algorithm for the Numerical Solution of Partial Differential Equations. IMA J. Appl. Math. 1971, 7, 216–227. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Omle, I.; Kovács, E. A Comparative Study of Explicit and Stable Time Integration Schemes for Heat Conduction in an Insulated Wall. Buildings 2022, 12, 824. [Google Scholar] [CrossRef]
- Fayazbakhsh, M.A.; Bagheri, F.; Bahrami, M. A resistance-capacitance model for real-time calculation of cooling load in HVAC-R systems. J. Therm. Sci. Eng. Appl. 2015, 7, 41008. [Google Scholar] [CrossRef]
- Angelotti, A.; Alberti, L.; La Licata, I.; Antelmi, M. Borehole heat exchangers: Heat transfer simulation in the presence of a groundwater flow. J. Phys. Conf. Ser. 2014, 501, 12033. [Google Scholar] [CrossRef]
| Equation Number or Point | |||
|---|---|---|---|
| LH FullExp | Fully explicit | convection, Section 2.2 | (8) |
| radiation, Section 2.3 | (16) | ||
| LH QuasiEx | Quasi-exact | convection, Section 2.2 | (11) |
| radiation, Section 2.3 | (18) | ||
| LH PseudoImp | Pseudo-implicit, PI | convection, Section 2.2 | (13) |
| radiation, Section 2.3 | (20) | ||
| LH Inside | Inside (the numerator) | convection, Section 2.2 | (14) |
| radiation, Section 2.3 | (21) | ||
| LH Inside Noneg | Inside with the non-negative trick | convection, Section 2.2 | (14) + (24) |
| radiation, Section 2.3 | (21) + (24) | ||
| LH Mixed | Mixture of the pseudo-implicit and inside with the weight of the PI | convection, Section 2.2 | (15) |
| radiation, Section 2.3 | (22) | ||
| LH PI NL prod | Pseudo-implicit, nonlocal with product | radiation, Section 2.3, 1D | point 6 |
| LH PI NL av | Pseudo-implicit, nonlocal with space-average | radiation, Section 2.3, 1D | point 7 |
| radiation, Section 2.3, 2D | (39) | ||
| LH PI NL time | Pseudo-implicit, nonlocal with time-average | radiation, Section 2.3 | point 8 |
| Brick | 1900 | 840 | 0.73 |
| Rigid Polyurethane Foam | 320 | 1400 | 0.023 |
| Steel Beam | 7800 | 840 | 16.2 |
| All elements | 4 | 4 | 300 | 800 |
| Right Elements | 2 | 5 | 500 |
| Left Elements | 4 | 4 | 500 |
| Right Elements | 2 | 5 | 500 |
| Left Elements | 25 | 4 | 3500 |
| CFL Limit | Stiffness Ratio | ||
|---|---|---|---|
| Surface | |||
| cross section with thermal bridge | equidistant | ||
| non-equidistant | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askar, A.H.; Omle, I.; Kovács, E.; Majár, J. Testing Some Different Implementations of Heat Convection and Radiation in the Leapfrog-Hopscotch Algorithm. Algorithms 2022, 15, 400. https://doi.org/10.3390/a15110400
Askar AH, Omle I, Kovács E, Majár J. Testing Some Different Implementations of Heat Convection and Radiation in the Leapfrog-Hopscotch Algorithm. Algorithms. 2022; 15(11):400. https://doi.org/10.3390/a15110400
Chicago/Turabian StyleAskar, Ali Habeeb, Issa Omle, Endre Kovács, and János Majár. 2022. "Testing Some Different Implementations of Heat Convection and Radiation in the Leapfrog-Hopscotch Algorithm" Algorithms 15, no. 11: 400. https://doi.org/10.3390/a15110400
APA StyleAskar, A. H., Omle, I., Kovács, E., & Majár, J. (2022). Testing Some Different Implementations of Heat Convection and Radiation in the Leapfrog-Hopscotch Algorithm. Algorithms, 15(11), 400. https://doi.org/10.3390/a15110400








