Blocking Cyclic Job-Shop Scheduling Problems
Abstract
1. Introduction
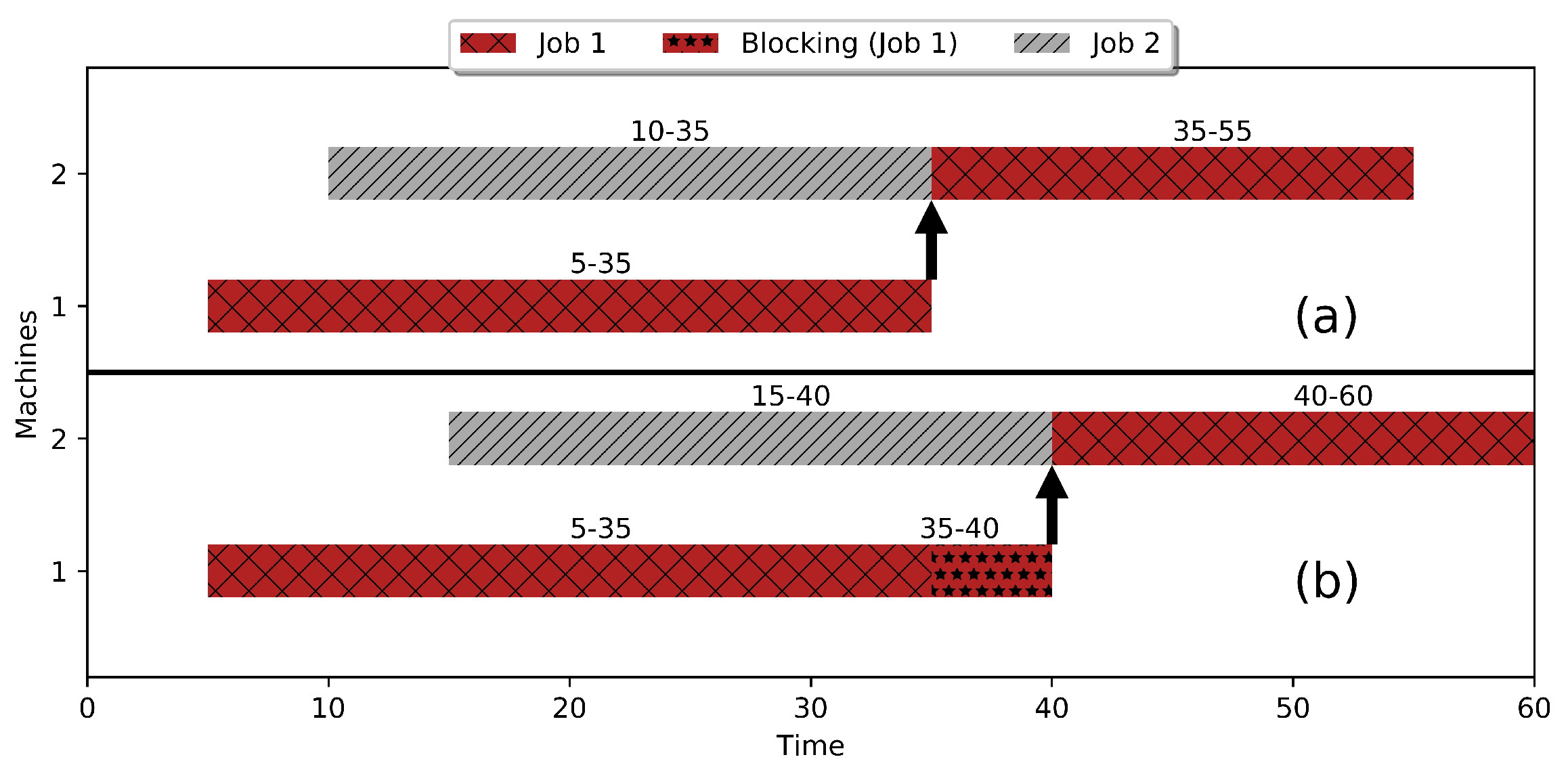
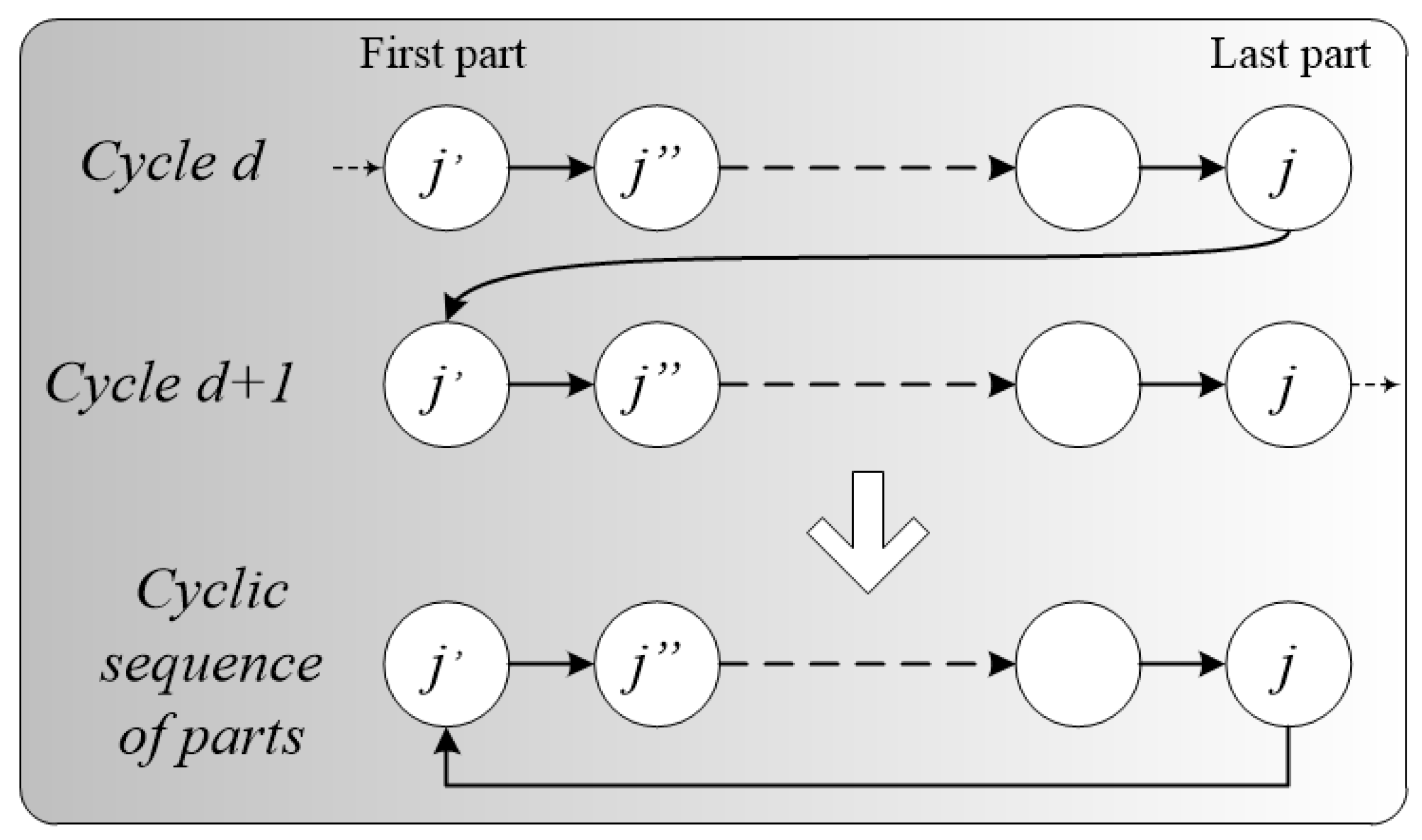
2. Blocking Cyclic Job Shop Scheduling
- Each machine has a set of operations to execute and can execute only one operation at a time.
- The operations of a job are linked by precedence constraints.
- Each job has its own unique path through the machines, independently of the other jobs.
- Each operation is assigned to one particular dedicated machine and executed with no interruption and without pre-emption for a fixed processing time.
- There are no buffers between machines, so jobs continue to occupy a machine after the end of an operation until the next machine is available.
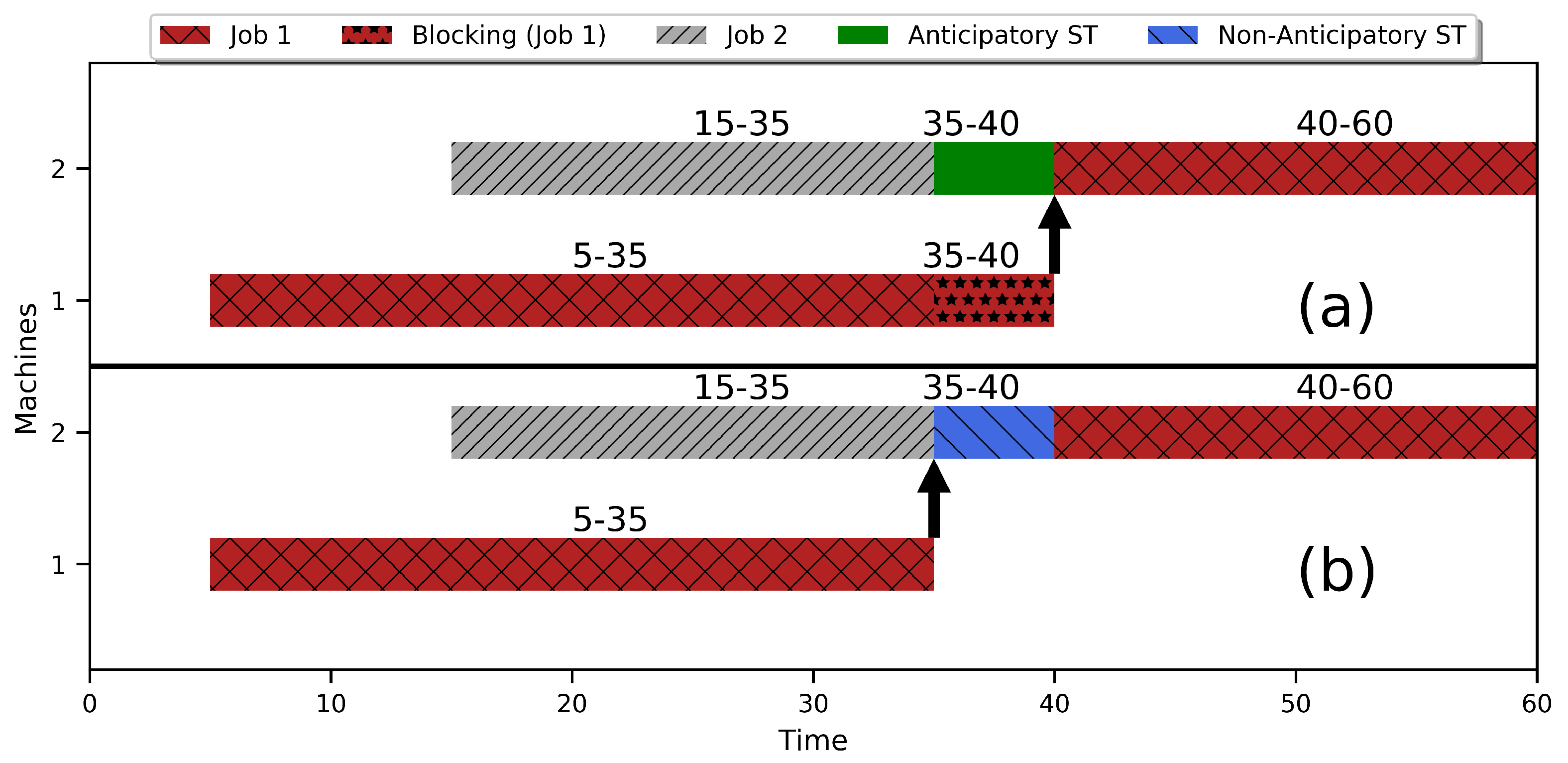
2.1. Sequence-Dependent Setup Times
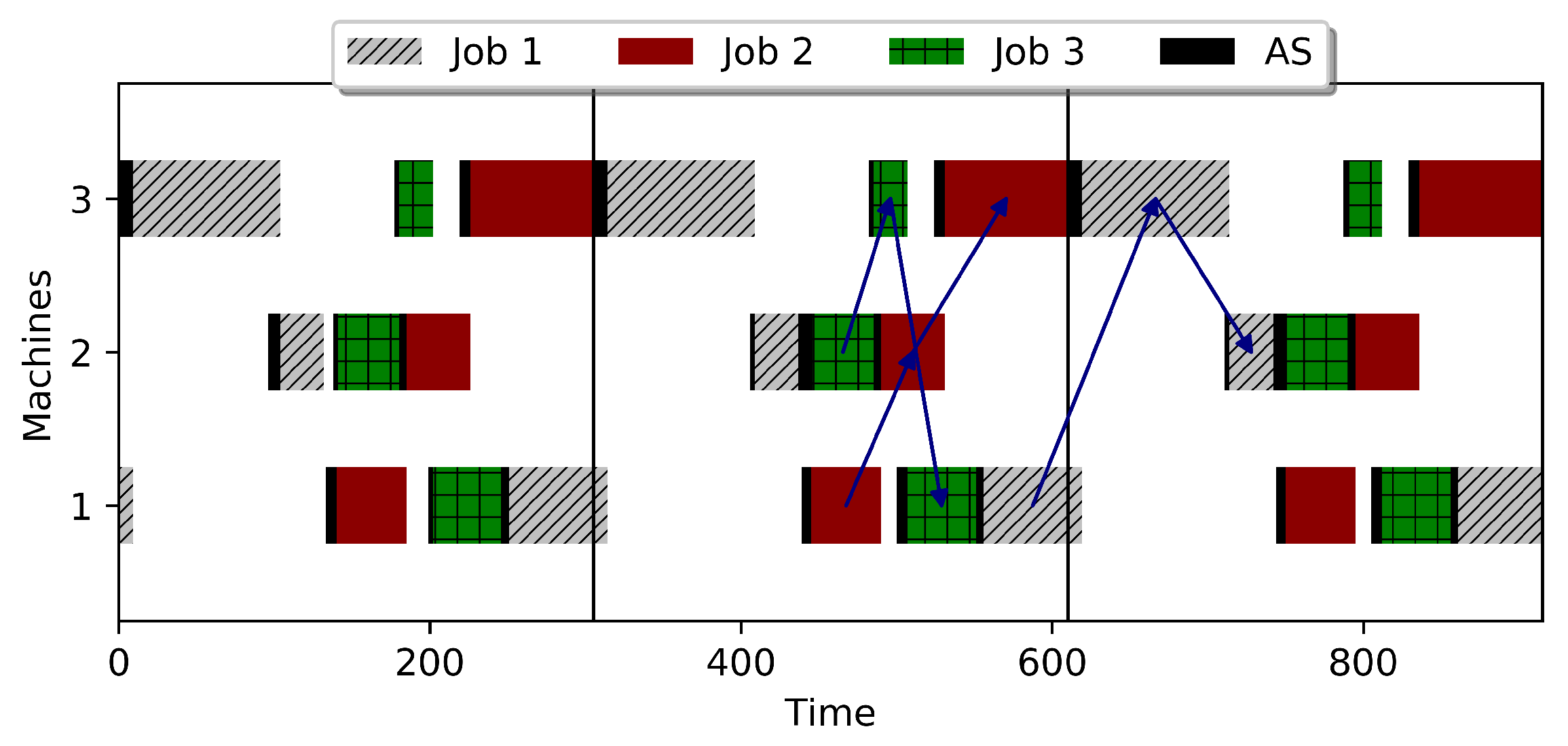
2.2. The Cyclic JSSP—An Example
3. Mathematical Formulation of a Basic Model
| 1 if job j immediately precedes job on machine m; 0 otherwise; | |
| 1 if machine m is occupied by job j at the beginning of a cycle; 0 otherwise; | |
| 1 if job j is the first job to depart from machine m after the beginning of the cycle; | |
| The departure time of job j from its operation; | |
| T | The cycle time; |
| An integer variable used to eliminate jobs’ sequence subtours on each machine m; | |
| W | A sufficiently large value, typically known as “Big M” in integer programming. |
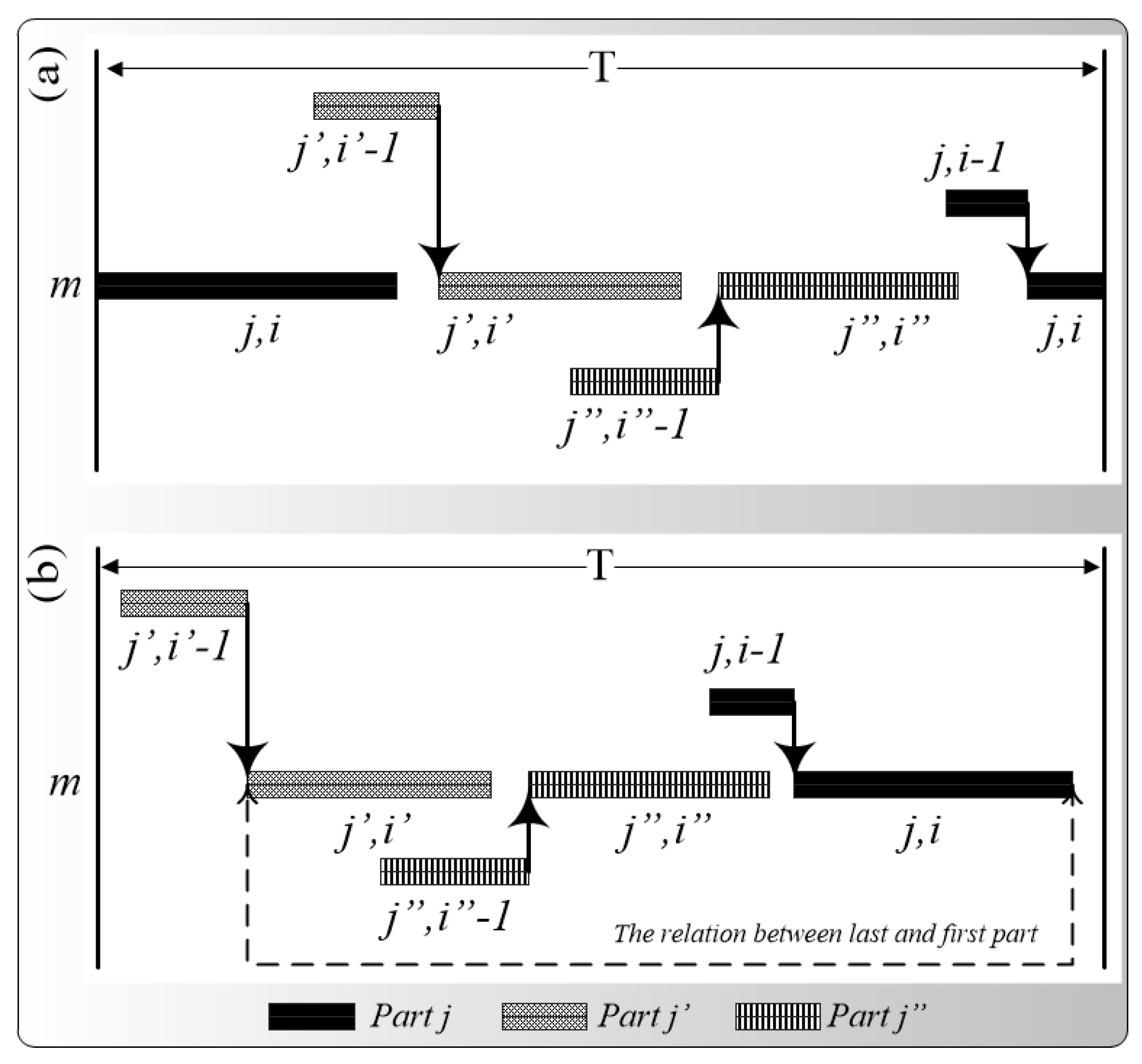
3.1. Occupied Machines Constraints
3.2. Processing Constraints of Each Part
3.3. Parts’ Sequence Determination on Machines
3.4. Operational Constraints of Each Machine
3.5. Proposed Mathematical Programming Model
4. Blocking CJSS Problem with Sequence-Dependent Setup Times
4.1. Blocking CJSS with Anticipatory Sequence-Dependent Setups (AS)
4.2. Blocking CJSS Problem with Nonanticipatory Sequence-Dependent Setups (NS)
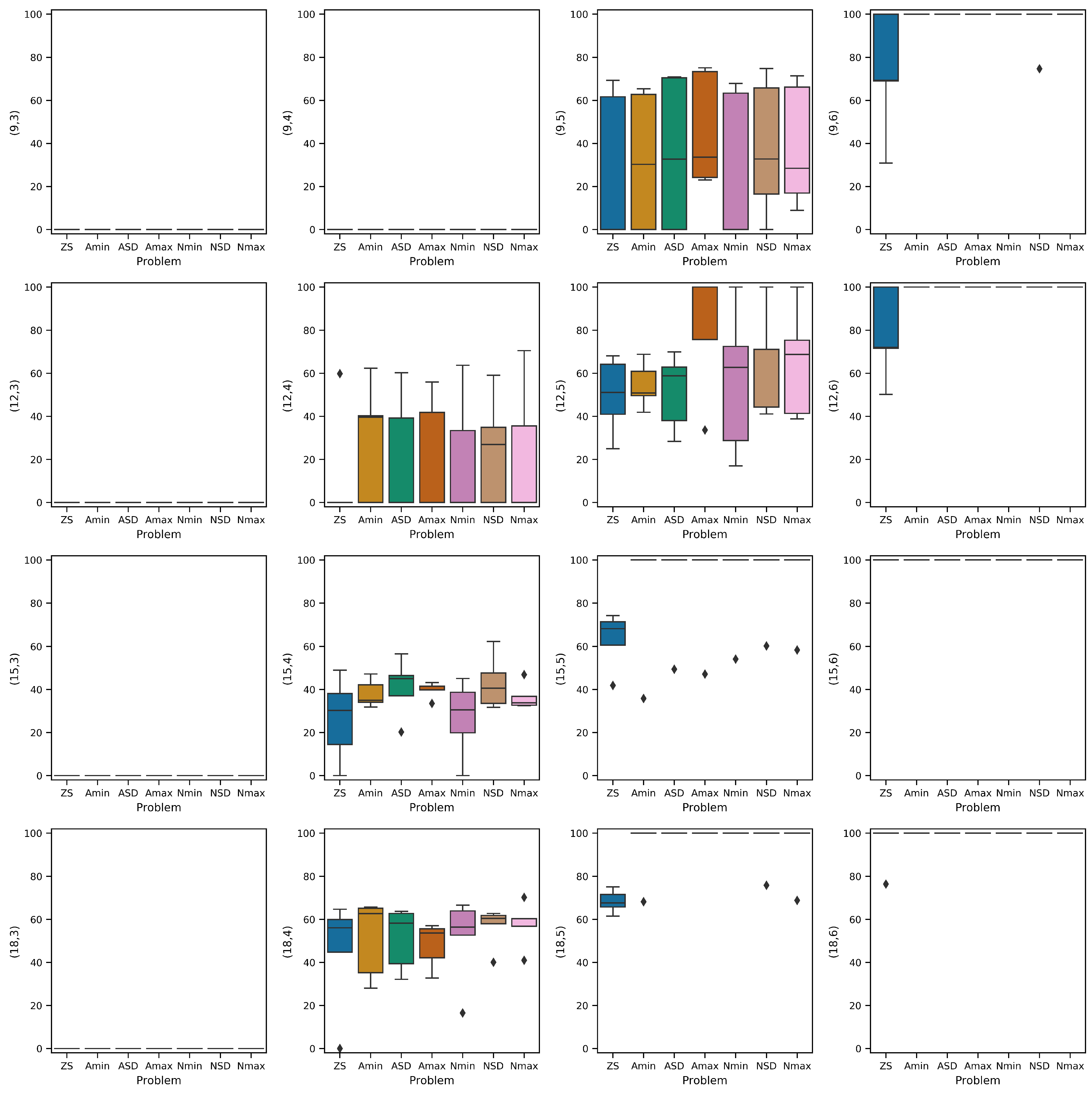
5. Experimental Settings and Results
6. Conclusions
- Previous studies on modelling the cyclic job-shop scheduling problem were based on performing operations in iterative cycles, whereas the proposed model in this research scheduled all the operations within a single cycle.
- Due to the scheduling within a single cycle, the proposed model could be simply extended to different resource constrained variants.
- Two kinds of sequence-dependent setups were considered based on anticipatory and nonanticipatory concepts.
- The nonanticipatory setups did not affect the blocking condition as the related job did not have to wait for the previous machine because of the related setup.
- The anticipatory setups directly affected the blocking conditions, as any part might need to wait on the previous machine until the related setup was completed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Generating Problem Instances
- The operation times of jobs on the machines are generated from the uniform distribution .
- The sequence-dependent setup times are generated from the uniform distribution .
- The standard maximum and minimum setup times are equal to the maximum and minimum of sequence-dependent setup times, respectively.
| Algorithm A1 Generate Problems. |
|
References
- Brucker, P.; Kampmeyer, T. Tabu search algorithms for cyclic machine scheduling problems. J. Sched. 2005, 8, 303–322. [Google Scholar] [CrossRef]
- Hanen, C. Study of a NP-hard cyclic scheduling problem: The recurrent job-shop. Eur. J. Oper. Res. 1994, 72, 82–101. [Google Scholar] [CrossRef]
- Brucker, P. Multiprocessor tasks. In Scheduling Algorithms; Springer: Berlin/Heidelberg, Germany, 2001; pp. 313–341. [Google Scholar]
- Wójcik, R.; Pempera, J. Designing cyclic schedules for streaming repetitive job-shop manufacturing systems with blocking and no-wait constraints. IFAC-PapersOnLine 2019, 52, 73–78. [Google Scholar] [CrossRef]
- Levner, E.; Kats, V.; De Pablo, D.A.L.; Cheng, T.E. Complexity of cyclic scheduling problems: A state-of-the-art survey. Comput. Ind. Eng. 2010, 59, 352–361. [Google Scholar]
- Šůcha, P.; Hanzálek, Z. A cyclic scheduling problem with an undetermined number of parallel identical processors. Comput. Optim. Appl. 2011, 48, 71–90. [Google Scholar] [CrossRef]
- Brauner, N.; Finke, G.; Kubiak, W. Complexity of one-cycle robotic flow-shops. J. Sched. 2003, 6, 355–372. [Google Scholar] [CrossRef]
- Lee, T.E.; Seo, J. Stochastic cyclic flow lines: Non-blocking, Markovian models. J. Oper. Res. Soc. 1998, 49, 537–548. [Google Scholar] [CrossRef]
- Xing, L.N.; Chen, Y.W.; Yang, K.W. Multi-population interactive coevolutionary algorithm for flexible job shop scheduling problems. Comput. Optim. Appl. 2011, 48, 139–155. [Google Scholar] [CrossRef]
- Grabowski, J.; Pempera, J. Sequencing of jobs in some production system. Eur. J. Oper. Res. 2000, 125, 535–550. [Google Scholar] [CrossRef]
- Ronconi, D.P. A note on constructive heuristics for the flowshop problem with blocking. Int. J. Prod. Econ. 2004, 87, 39–48. [Google Scholar] [CrossRef]
- Gong, H.; Tang, L.; Duin, C. A two-stage flow shop scheduling problem on a batching machine and a discrete machine with blocking and shared setup times. Comput. Oper. Res. 2010, 37, 960–969. [Google Scholar] [CrossRef]
- Martinez, S.; Dauzère-Pérès, S.; Gueret, C.; Mati, Y.; Sauer, N. Complexity of flowshop scheduling problems with a new blocking constraint. Eur. J. Oper. Res. 2006, 169, 855–864. [Google Scholar] [CrossRef]
- Lange, J.; Werner, F. Approaches to modeling train scheduling problems as job-shop problems with blocking constraints. J. Sched. 2018, 21, 191–207. [Google Scholar] [CrossRef]
- Kats, V.; Levner, E. Cyclic scheduling in a robotic production line. J. Sched. 2002, 5, 23–41. [Google Scholar] [CrossRef]
- Dawande, M.W.; Geismar, H.N.; Sethi, S.P.; Sriskandarajah, C. Throughput Optimization in Robotic Cells; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 101. [Google Scholar]
- Ayala, M.; Benabid, A.; Artigues, C.; Hanen, C. The resource-constrained modulo scheduling problem: An experimental study. Comput. Optim. Appl. 2013, 54, 645–673. [Google Scholar] [CrossRef][Green Version]
- Pempera, J.; Smutnicki, C. Open shop cyclic scheduling. Eur. J. Oper. Res. 2018, 269, 773–781. [Google Scholar] [CrossRef]
- Wang, J.; Pan, C.; Hu, H.; Li, L.; Zhou, Y. A cyclic scheduling approach to single-arm cluster tools with multiple wafer types and residency time constraints. IEEE Trans. Autom. Sci. Eng. 2018, 16, 1373–1386. [Google Scholar] [CrossRef]
- Elmi, A.; Nazari, A.; Thiruvady, D.; Durmusoglu, A. Cyclic Flow Shop Robotic Cell Scheduling Problem With Multiple Part Types. IEEE Trans. Eng. Manag. 2020. [Google Scholar] [CrossRef]
- Bożejko, W.; Uchroński, M.; Wodecki, M. Block approach to the cyclic flow shop scheduling. Comput. Ind. Eng. 2015, 81, 158–166. [Google Scholar] [CrossRef]
- Brucker, P.; Kampmeyer, T. Cyclic job shop scheduling problems with blocking. Ann. Oper. Res. 2008, 159, 161–181. [Google Scholar] [CrossRef]
- Song, J.S.; Lee, T.E. Petri net modeling and scheduling for cyclic job shops with blocking. Comput. Ind. Eng. 1998, 34, 281–295. [Google Scholar] [CrossRef]
- Cavory, G.; Dupas, R.; Goncalves, G. A genetic approach to solving the problem of cyclic job shop scheduling with linear constraints. Eur. J. Oper. Res. 2005, 161, 73–85. [Google Scholar] [CrossRef]
- Kechadi, M.T.; Low, K.S.; Goncalves, G. Recurrent neural network approach for cyclic job shop scheduling problem. J. Manuf. Syst. 2013, 32, 689–699. [Google Scholar] [CrossRef]
- Kampmeyer, T. Cyclic Scheduling Problems. Ph.D. Thesis, Universität Osnabrück, Osnabrück, Germany, 2006. [Google Scholar]
- Brucker, P.; Kampmeyer, T. A general model for cyclic machine scheduling problems. Discret. Appl. Math. 2008, 156, 2561–2572. [Google Scholar] [CrossRef]
- Brucker, P.; Burke, E.K.; Groenemeyer, S. A mixed integer programming model for the cyclic job-shop problem with transportation. Discret. Appl. Math. 2012, 160, 1924–1935. [Google Scholar] [CrossRef]
- Brucker, P.; Burke, E.K.; Groenemeyer, S. A branch and bound algorithm for the cyclic job-shop problem with transportation. Comput. Oper. Res. 2012, 39, 3200–3214. [Google Scholar] [CrossRef]
- Quinton, F.; Hamaz, I.; Houssin, L. A mixed integer linear programming modelling for the flexible cyclic jobshop problem. Ann. Oper. Res. 2020, 285, 335–352. [Google Scholar] [CrossRef]
- Gultekin, H.; Dalgıç, Ö.O.; Akturk, M.S. Pure cycles in two-machine dual-gripper robotic cells. Robot. Comput.-Integr. Manuf. 2017, 48, 121–131. [Google Scholar] [CrossRef][Green Version]
- Ghadiri Nejad, M.; Shavarani, S.M.; Güden, H.; Barenji, R.V. Process sequencing for a pick-and-place robot in a real-life flexible robotic cell. Int. J. Adv. Manuf. Technol. 2019, 103, 3613–3627. [Google Scholar] [CrossRef]
- Foumani, M.; Razeghi, A.; Smith-Miles, K. Stochastic optimization of two-machine flow shop robotic cells with controllable inspection times: From theory toward practice. Robot. Comput.-Integr. Manuf. 2020, 61, 101822. [Google Scholar] [CrossRef]
- Panwalkar, S.; Dudek, R.; Smith, M. Sequencing research and the industrial scheduling problem. In Proceedings of the Symposium on the Theory of Scheduling and Its Applications; Springer: Berlin/Heidelberg, Germany, 1973; pp. 29–38. [Google Scholar]
- Defersha, F.M.; Chen, M. A parallel genetic algorithm for a flexible job-shop scheduling problem with sequence dependent setups. Int. J. Adv. Manuf. Technol. 2010, 49, 263–279. [Google Scholar] [CrossRef]
- Framinan, J.M.; Leisten, R.; García, R.R. Manufacturing scheduling systems. In An integrated view on Models, Methods and Tools; Springer: Berlin/Heidelberg, Germany, 2014; pp. 51–63. [Google Scholar]
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer programming formulation of traveling salesman problems. J. ACM (JACM) 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]

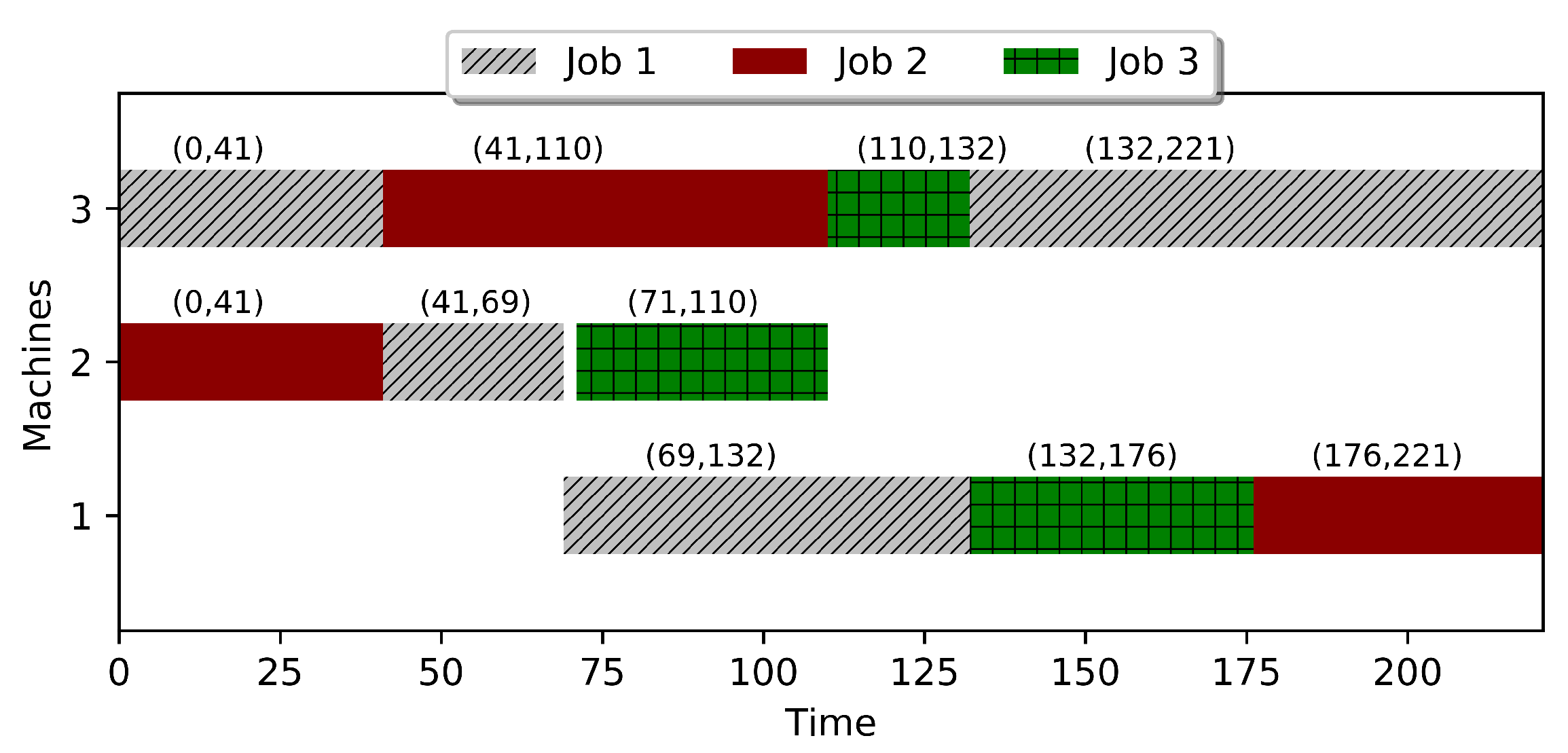
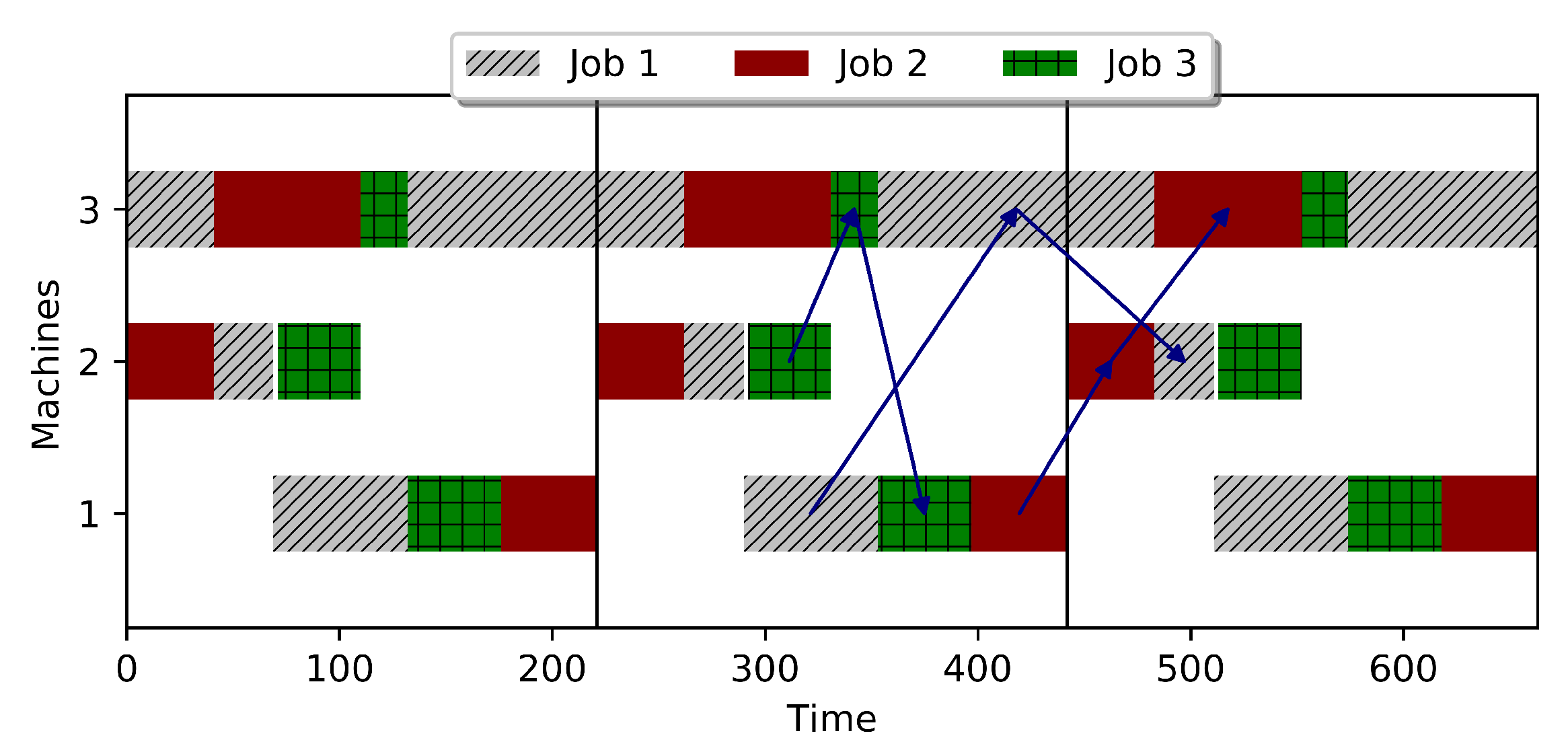



| Jobs | Machines | Processing Times | ||||
|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 2 | 63 | 95 | 28 |
| 2 | 1 | 2 | 3 | 45 | 41 | 69 |
| 3 | 2 | 3 | 1 | 39 | 22 | 44 |
| Machines | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||||
| Jobs | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 1 | 1 | 6 | 5 | 7 | 7 | 9 | 7 | 4 | 3 |
| 2 | 4 | 7 | 7 | 3 | 8 | 3 | 8 | 1 | 6 |
| 3 | 5 | 9 | 4 | 5 | 5 | 3 | 1 | 7 | 6 |
| K | J | #Cons | #Var | Cyclic JSS: Zero Setups | Anticipatory Setups | Nonanticipatory Setups | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BF | LB | Gap | Time | BF | LB | Gap | Time | BF | LB | Gap | Time | ||||
| 9 | 3 | 733 | 190 | 257 | 257 | 0 | 7.35 | 390 | 390 | 0 | 18.6 | 337 | 337 | 0 | 17.3 |
| 4 | 1313 | 289 | 270 | 270 | 0 | 5.09 | 441 | 441 | 0 | 6.92 | 335 | 335 | 0 | 7.77 | |
| 5 | 2157 | 406 | 535 | 164 | 69.27 | 3600 | 701 | 207 | 70.42 | 3600 | 660 | 166 | 74.80 | 3600 | |
| 6 | 3319 | 541 | 566 | 391 | 30.92 | 3600 | - | 444 | - | 3600 | - | 437 | - | 3600 | |
| 12 | 3 | 988 | 253 | 258 | 258 | 0 | 14.94 | 373 | 373 | 0 | 14.53 | 354 | 354 | 0 | 22.83 |
| 4 | 1769 | 385 | 335 | 335 | 0 | 308.59 | 468 | 468 | 0 | 684.56 | 431 | 431 | 0 | 386.49 | |
| 5 | 2904 | 541 | 529 | 189 | 64.21 | 3600 | 695 | 258 | 62.88 | 3600 | 741 | 214 | 71.08 | 3600 | |
| 6 | 4465 | 721 | - | 190 | - | 3600 | - | 223 | - | 3600 | - | 206 | - | 3600 | |
| 15 | 3 | 1243 | 316 | 313 | 313 | 0 | 11.07 | 449 | 449 | 0 | 9.15 | 411 | 411 | 0 | 18.75 |
| 4 | 2225 | 481 | 344 | 213 | 38.08 | 3600 | 457 | 251 | 44.99 | 3600 | 462 | 242 | 47.62 | 3600 | |
| 5 | 3651 | 676 | 568 | 330 | 41.90 | 3600 | 761 | 385 | 49.41 | 3600 | - | 285 | - | 3600 | |
| 6 | 5611 | 901 | - | 171 | - | 3600 | - | 200 | - | 3600 | - | 195 | - | 3600 | |
| 18 | 3 | 1498 | 379 | 275 | 275 | 0 | 17.42 | 365 | 365 | 0 | 26.56 | 360 | 360 | 0 | 26.95 |
| 4 | 2681 | 577 | 364 | 201 | 44.78 | 3600 | 519 | 315 | 39.36 | 3600 | 484 | 180 | 62.76 | 3600 | |
| 5 | 4398 | 811 | 600 | 171 | 71.55 | 3600 | - | 210 | - | 3600 | 721 | 175 | 75.79 | 3600 | |
| 6 | 6757 | 1081 | - | 184 | - | 3600 | - | 198 | - | 3600 | - | 193 | - | 3600 | |
| Rep | K | J | Best Found | Lower Bound | Gap | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ZS | Anticipatory | Nonanticipatory | ZS | Anticipatory | Nonanticipatory | ZS | Anticipatory | Nonanticipatory | |||||||||||||||
| Min | SD | Max | Min | SD | Max | Min | SD | Max | Min | SD | Max | Min | SD | Max | Min | SD | Max | ||||||
| 1 | 9 | 3 | 257 | 314 | 390 | 464 | 262 | 337 | 417 | 257 | 314 | 390 | 464 | 262 | 337 | 417 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 270 | 365 | 441 | 526 | 275 | 335 | 447 | 270 | 365 | 441 | 526 | 275 | 335 | 447 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 535 | 524 | 701 | 954 | 546 | 660 | 813 | 164 | 195 | 207 | 238 | 175 | 166 | 232 | 69.27 | 62.73 | 70.42 | 75.09 | 67.89 | 74.80 | 71.43 | ||
| 6 | 566 | - | - | - | - | - | - | 391 | 397 | 444 | 583 | 397 | 437 | 583 | 30.92 | - | - | - | - | - | - | ||
| 12 | 3 | 258 | 316 | 373 | 446 | 264 | 354 | 433 | 258 | 316 | 373 | 446 | 264 | 354 | 433 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 335 | 393 | 468 | 559 | 340 | 431 | 523 | 335 | 393 | 468 | 559 | 340 | 431 | 523 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 529 | 527 | 695 | - | 508 | 741 | 990 | 189 | 206 | 258 | 166 | 189 | 214 | 244 | 64.21 | 60.92 | 62.88 | - | 62.73 | 71.08 | 75.34 | ||
| 6 | - | - | - | - | - | - | - | 190 | 205 | 223 | 211 | 182 | 206 | 245 | - | - | - | - | - | - | - | ||
| 15 | 3 | 313 | 385 | 449 | 458 | 319 | 411 | 462 | 313 | 385 | 449 | 458 | 319 | 411 | 462 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 344 | 375 | 457 | 584 | 354 | 462 | 540 | 213 | 217 | 251 | 341 | 217 | 242 | 341 | 38.08 | 42.13 | 44.99 | 41.61 | 38.70 | 47.62 | 36.85 | ||
| 5 | 568 | 522 | 761 | - | 648 | - | - | 330 | 335 | 385 | 490 | 297 | 285 | 375 | 41.90 | 35.82 | 49.41 | - | 54.13 | - | - | ||
| 6 | - | - | - | - | - | - | - | 171 | 194 | 200 | 206 | 182 | 195 | 233 | - | - | - | - | - | - | - | ||
| 18 | 3 | 275 | 296 | 365 | 447 | 279 | 360 | 423 | 275 | 296 | 365 | 447 | 279 | 360 | 423 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 364 | 407 | 519 | 663 | 399 | 484 | 654 | 201 | 264 | 315 | 384 | 189 | 180 | 283 | 44.78 | 35.25 | 39.36 | 42.13 | 52.63 | 62.76 | 56.73 | ||
| 5 | 600 | - | - | - | - | 721 | 871 | 171 | 165 | 210 | 207 | 155 | 175 | 272 | 71.55 | - | - | - | - | 75.79 | 68.80 | ||
| 6 | - | - | - | - | - | - | - | 184 | 195 | 198 | 267 | 177 | 193 | 177 | - | - | - | - | - | - | - | ||
| 2 | 9 | 3 | 258 | 260 | 344 | 428 | 262 | 329 | 406 | 258 | 260 | 344 | 428 | 262 | 329 | 406 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 334 | 366 | 455 | 543 | 339 | 430 | 501 | 334 | 366 | 455 | 543 | 339 | 430 | 501 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 412 | 421 | 552 | 743 | 419 | 553 | 653 | 412 | 421 | 552 | 563 | 419 | 553 | 594 | 0 | 0 | 0 | 24.23 | 0 | 0 | 8.96 | ||
| 6 | 586 | - | - | - | - | - | - | 180 | 191 | 166 | 161 | 168 | 174 | 226 | 69.26 | - | - | - | - | - | - | ||
| 12 | 3 | 289 | 291 | 358 | 386 | 293 | 339 | 423 | 289 | 291 | 358 | 386 | 293 | 339 | 423 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 325 | 368 | 442 | 542 | 332 | 428 | 500 | 325 | 368 | 442 | 542 | 332 | 428 | 500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 500 | 613 | 553 | - | 421 | 662 | 776 | 295 | 301 | 396 | 459 | 300 | 369 | 455 | 41 | 50.85 | 28.39 | - | 28.74 | 44.26 | 41.37 | ||
| 6 | 776 | - | - | - | - | - | - | 387 | 432 | 475 | 618 | 335 | 393 | 490 | 50.13 | - | - | - | - | - | - | ||
| 15 | 3 | 292 | 372 | 392 | 462 | 297 | 383 | 452 | 292 | 372 | 392 | 462 | 297 | 383 | 452 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 367 | 411 | 539 | 671 | 373 | 571 | 599 | 314 | 280 | 339 | 404 | 373 | 339 | 404 | 14.44 | 31.87 | 37.11 | 39.79 | 0 | 40.63 | 32.55 | ||
| 5 | 614 | - | - | - | - | - | - | 175 | 184 | 227 | 249 | 160 | 189 | 422 | 71.49 | - | - | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 231 | 329 | 426 | 571 | 174 | 197 | 232 | - | - | - | - | - | - | - | ||
| 18 | 3 | 244 | 312 | 354 | 417 | 249 | 330 | 404 | 244 | 312 | 354 | 417 | 249 | 330 | 404 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 340 | 421 | 507 | 635 | 363 | 559 | 600 | 340 | 303 | 344 | 427 | 303 | 335 | 354 | 0 | 28.03 | 32.15 | 32.76 | 16.53 | 40.07 | 41 | ||
| 5 | 573 | - | - | - | - | - | - | 221 | 201 | 209 | 326 | 170 | 365 | 301 | 61.43 | - | - | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 199 | 211 | 212 | 266 | 189 | 202 | 242 | - | - | - | - | - | - | - | ||
| 3 | 9 | 3 | 207 | 302 | 345 | 398 | 213 | 297 | 361 | 207 | 302 | 345 | 398 | 213 | 297 | 361 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 376 | 394 | 475 | 569 | 382 | 470 | 554 | 376 | 394 | 475 | 569 | 382 | 470 | 554 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 433 | 552 | 718 | 863 | 439 | 554 | 679 | 166 | 191 | 209 | 230 | 161 | 190 | 230 | 61.66 | 65.35 | 70.87 | 73.36 | 63.33 | 65.78 | 66.15 | ||
| 6 | - | - | - | - | - | - | - | 349 | 364 | 401 | 550 | 353 | 401 | 550 | - | - | - | - | - | - | - | ||
| 12 | 3 | 265 | 269 | 338 | 415 | 269 | 324 | 402 | 265 | 269 | 338 | 415 | 269 | 324 | 402 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 362 | 460 | 524 | 583 | 368 | 487 | 566 | 362 | 275 | 524 | 583 | 368 | 356 | 566 | 0 | 40.22 | 0 | 0 | 0 | 26.90 | 0 | ||
| 5 | 555 | 615 | 699 | 930 | 629 | 669 | 908 | 177 | 192 | 210 | 227 | 173 | 193 | 284 | 68.06 | 68.81 | 69.97 | 75.64 | 72.47 | 71.18 | 68.72 | ||
| 6 | 714 | - | - | - | - | - | - | 203 | 203 | 216 | 340 | 194 | 240 | 297 | 71.56 | - | - | - | - | - | - | ||
| 15 | 3 | 229 | 239 | 300 | 390 | 235 | 295 | 363 | 229 | 239 | 300 | 390 | 235 | 295 | 363 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 410 | 451 | 580 | 638 | 384 | 556 | 631 | 209 | 238 | 252 | 362 | 211 | 210 | 335 | 48.96 | 47.23 | 56.55 | 43.26 | 45.12 | 62.30 | 46.91 | ||
| 5 | 729 | - | - | - | - | - | - | 187 | 196 | 193 | 201 | 174 | 191 | 170 | 74.31 | - | - | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 179 | 195 | 207 | 202 | 168 | 184 | 215 | - | - | - | - | - | - | - | ||
| 18 | 3 | 286 | 323 | 402 | 459 | 290 | 355 | 429 | 286 | 323 | 402 | 459 | 290 | 355 | 429 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 382 | 439 | 519 | 674 | 420 | 516 | 688 | 153 | 153 | 217 | 299 | 152 | 217 | 205 | 59.94 | 65.11 | 58.19 | 55.64 | 63.93 | 57.95 | 70.19 | ||
| 5 | 630 | - | - | - | - | - | - | 204 | 354 | 393 | 509 | 176 | 303 | 383 | 67.62 | - | - | - | - | - | - | ||
| 6 | 792 | - | - | - | - | - | - | 187 | 186 | 178 | 186 | 169 | 184 | 213 | 76.39 | - | - | - | - | - | - | ||
| 4 | 9 | 3 | 268 | 333 | 384 | 463 | 273 | 341 | 422 | 268 | 333 | 384 | 463 | 273 | 341 | 422 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 270 | 377 | 431 | 538 | 274 | 363 | 455 | 270 | 377 | 431 | 538 | 274 | 363 | 455 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 447 | 465 | 594 | 747 | 455 | 590 | 690 | 447 | 465 | 594 | 575 | 455 | 493 | 573 | 0 | 0 | 0 | 23.03 | 0 | 16.44 | 16.96 | ||
| 6 | 633 | - | - | - | - | - | - | 196 | 184 | 199 | 216 | 179 | 197 | 233 | 69.03 | - | - | - | - | - | - | ||
| 12 | 3 | 250 | 253 | 313 | 392 | 253 | 307 | 373 | 250 | 253 | 313 | 392 | 253 | 307 | 373 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 358 | 440 | 495 | 644 | 390 | 481 | 599 | 144 | 166 | 197 | 284 | 141 | 197 | 177 | 59.78 | 62.37 | 60.20 | 55.90 | 63.72 | 59.04 | 70.48 | ||
| 5 | 494 | 588 | 677 | - | - | - | - | 242 | 296 | 279 | 469 | 173 | 209 | 469 | 51.05 | 49.63 | 58.79 | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 400 | 406 | 440 | 592 | 406 | 440 | 592 | - | - | - | - | - | - | - | ||
| 15 | 3 | 244 | 307 | 350 | 426 | 249 | 327 | 392 | 244 | 307 | 350 | 426 | 249 | 327 | 392 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 304 | 363 | 512 | 598 | 309 | 411 | 529 | 304 | 236 | 274 | 350 | 248 | 273 | 350 | 0 | 34.99 | 46.48 | 41.47 | 19.87 | 33.58 | 33.84 | ||
| 5 | 620 | - | - | 922 | - | 787 | 991 | 244 | 332 | 367 | 487 | 179 | 313 | 413 | 60.59 | - | - | 47.18 | - | 60.23 | 58.32 | ||
| 6 | - | - | - | - | - | - | - | 205 | 210 | 221 | 263 | 185 | 201 | 245 | - | - | - | - | - | - | - | ||
| 18 | 3 | 263 | 265 | 345 | 411 | 268 | 329 | 405 | 263 | 265 | 345 | 411 | 268 | 329 | 405 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 382 | 450 | 518 | 687 | 390 | 484 | 680 | 168 | 168 | 193 | 295 | 170 | 185 | 294 | 56.08 | 62.67 | 62.74 | 57.06 | 56.41 | 61.80 | 56.76 | ||
| 5 | 673 | 632 | - | - | - | - | - | 168 | 201 | 233 | 263 | 163 | 177 | 195 | 75.07 | 68.18 | - | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 247 | 226 | 339 | 417 | 196 | 203 | 333 | - | - | - | - | - | - | - | ||
| 5 | 9 | 3 | 267 | 389 | 433 | 451 | 271 | 344 | 411 | 267 | 389 | 433 | 451 | 271 | 344 | 411 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 342 | 350 | 451 | 548 | 348 | 434 | 517 | 342 | 350 | 451 | 548 | 348 | 434 | 517 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 5 | 449 | 515 | 631 | 768 | 457 | 595 | 713 | 449 | 359 | 425 | 510 | 457 | 400 | 510 | 0 | 30.29 | 32.65 | 33.59 | 0 | 32.77 | 28.47 | ||
| 6 | - | - | - | - | - | 761 | - | 185 | 205 | 216 | 227 | 185 | 193 | 222 | - | - | - | - | - | 74.64 | - | ||
| 12 | 3 | 292 | 408 | 438 | 479 | 298 | 375 | 455 | 292 | 408 | 438 | 479 | 298 | 375 | 455 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 371 | 432 | 518 | 645 | 377 | 481 | 582 | 371 | 261 | 315 | 375 | 251 | 313 | 375 | 0 | 39.58 | 39.19 | 41.86 | 33.42 | 34.93 | 35.57 | ||
| 5 | 525 | 687 | 752 | 835 | 481 | 791 | 906 | 394 | 399 | 466 | 554 | 399 | 466 | 554 | 24.95 | 41.92 | 38.03 | 33.65 | 17.05 | 41.09 | 38.85 | ||
| 6 | 609 | - | - | - | - | - | - | 171 | 194 | 201 | 222 | 163 | 180 | 220 | 71.98 | - | - | - | - | - | - | ||
| 15 | 3 | 313 | 369 | 419 | 480 | 317 | 381 | 459 | 313 | 369 | 419 | 480 | 317 | 381 | 459 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 386 | 414 | 469 | 597 | 393 | 485 | 590 | 269 | 273 | 374 | 397 | 273 | 331 | 397 | 30.31 | 34.06 | 20.26 | 33.50 | 30.53 | 31.75 | 32.71 | ||
| 5 | 586 | - | - | - | - | - | - | 186 | 208 | 173 | 337 | 174 | 191 | 237 | 68.26 | - | - | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 186 | 196 | 201 | 203 | 177 | 184 | 245 | - | - | - | - | - | - | - | ||
| 18 | 3 | 282 | 306 | 382 | 441 | 286 | 358 | 439 | 282 | 306 | 382 | 441 | 286 | 358 | 439 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 446 | 486 | 565 | 684 | 460 | 518 | 729 | 158 | 167 | 205 | 317 | 154 | 205 | 289 | 64.67 | 65.71 | 63.72 | 53.66 | 66.60 | 60.46 | 60.36 | ||
| 5 | 562 | - | - | - | - | - | - | 192 | 188 | 230 | 264 | 177 | 205 | 261 | 65.76 | - | - | - | - | - | - | ||
| 6 | - | - | - | - | - | - | - | 203 | 208 | 224 | 283 | 187 | 211 | 252 | - | - | - | - | - | - | - | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmi, A.; Thiruvady, D.R.; Ernst, A.T. Blocking Cyclic Job-Shop Scheduling Problems. Algorithms 2022, 15, 375. https://doi.org/10.3390/a15100375
Elmi A, Thiruvady DR, Ernst AT. Blocking Cyclic Job-Shop Scheduling Problems. Algorithms. 2022; 15(10):375. https://doi.org/10.3390/a15100375
Chicago/Turabian StyleElmi, Atabak, Dhananjay R. Thiruvady, and Andreas T. Ernst. 2022. "Blocking Cyclic Job-Shop Scheduling Problems" Algorithms 15, no. 10: 375. https://doi.org/10.3390/a15100375
APA StyleElmi, A., Thiruvady, D. R., & Ernst, A. T. (2022). Blocking Cyclic Job-Shop Scheduling Problems. Algorithms, 15(10), 375. https://doi.org/10.3390/a15100375







