1. Introduction
In today′s world, economies and commodity markets swing rapidly; personal, organizational, and business networks are becoming more interconnected, instrumented, and intelligent [
1]. One of the important aspects of the business world is supply chain management. It works towards satisfying customers′ requirements through the efficient use of resources resulting in reducing cost and increasing profit margin for companies [
2]. With a highly competitive global market, supply chains have to be more responsive to customers′ needs. Supply chain represents all stages of a process; usually, researchers focus on materials that are manufactured to become an end product; however, the supply chain covers a wider range that extends beyond physical assets. For instance, looking at the banking sector, their main supply chain is of financial data that needs to be processed using available resources which are software and hardware processors.
One of the main instruments used in business networks for the management of the financial data supply chain is data batch processing (DBP). It plays a critical role in daily operations carried out in most organizations in different business fields. Data batch processing can be defined as the execution of data files as input batches using the available resources and gather the resulted files as output batches while satisfying files priorities, predecessors constraints, and time constraints [
3,
4]. The execution is carried out on the mainframe computer that runs at a scheduled time or on an as-needed basis without user interaction and minimal or no interaction with a computer operator [
3,
4]. The main feature of data batch processing is its ability to handle an enormous amount of data files which makes it attractive and essential to many organizations that are constantly dealing with heavy business activities [
5]. It contributes to the major part of the workload on mainframe computers that will often run a large number of business workflows with complex interrelations, requiring careful scheduling and prioritizing to ensure that all batch jobs run in the correct order and meet strict deadlines [
3,
4,
6].
Our research considers the case of processing end-of-day (EOD) operations which include highly important and frequently used activities and services such as: preparing customers’ bank statements; credit card processing bills; fraud detection data; merging the day′s transactions into master files; sorting data files for optimal processing; providing daily, weekly, monthly, and annual reports; invoices and bank statements; performing periodic payroll calculations; and applying interest to financial accounts [
4]. Banks seek to elevate their level of customer service by optimizing their data supply chain scheduling. This supply chain consists of the bank, a service provider that arranges the processing of data, and processors providing company that rents and leases processors and software to service providers. Also, in our research, data supply chains adopt the technique of lot streaming which is a technique that splits a given data job, each consisting of similar files, into tasks to allow overlapping of successive operations in processing systems thereby reducing the processing makespan.
The proposed work addresses the financial data supply chain scheduling problem from an operational perspective by considering the scheduling at an individual job level. The problem can be viewed as a single-stage supply chain scheduling problem where jobs are arranged to be processed by mainframe processors that can be modeled as a series of flow shop machines. Processors are leased and rented from manufacturing and supplying company as needed by a third-party company that performs the data scheduling. Data arrives raw and unprocessed from banks to a service provider which needs to manage scheduling them for processing as per the available resources (software and hardware) in the most efficient way. After processing, jobs must be returned back to banks where they will be charged for the provided service.
In order to address financial data supply chain, this research covers all aspects of data batch processing, being that it is the tool that manages banks′ financial data supply chain scheduling. The scheduling aspects of DBP are job priorities, precedence relationships, constraints in addition to cost. It is important to understand that cost consideration in data batch processing is vital due to the extremely high cost of the resources involved. However, previous research has overlooked the cost despite its importance, and the focus was on the effectiveness of the scheduling component of the process. The high cost of software and hardware resources used in the batch process and the patent rights of companies that own the platform made it not only beneficial, but also essential for DBP users to reduce the cost associated with it. Therefore, this research intends to bridge such a gap and provides a comprehensive study that covers the important aspects of data batch processing. Thus, the main contributions of this work can be summarized as follows:
Consider all types of costs related to the batch process which are the servers and software basic leasing cost, rental cost for additional resources needed in case of overload and extra work, penalty cost of failing to execute the batch process as per the Service Level Agreement (SLA), and the opportunity cost representing the cost of idling a resource for any period of time due to inefficient task allocation.
Develop an iterative dynamic scheduling algorithm (DCSDBP) to optimize the data batch processing considering the different costs, availability of resources, and customer service level agreement (SLA) along with the rest of the batch process factors such as the clients′ priorities, tasks predecessors and time.
Utilize the created optimization model to address the problem of controlling the availability of resources such as processors and software required to process input batches and balance the usage of current owned resources and the need to rent additional ones while maintaining the lowest possible cost for the whole data batch processing.
The rest of the paper is organized as follows:
Section 2, the background related to this work is presented. The data batch algorithm is presented in
Section 3. The illustrative example and sensitivity analysis are presented in
Section 4 and
Section 5 respectively. Finally, the conclusions are presented in
Section 6.
2. Literature Review
Supply chain management has another perspective when associated with the financial sector. An alternative concept appears that relates to information or data and supply chain known as Financial Information Supply Chain Management. The researchers in [
7] emphasized the need to improve financial operating processes in order to optimize financial data supply chain management by reducing processing time, improving efficiency, and decreasing associated costs of equipment and computers.
Other studies reached an aligned outcome such as the case study by [
8] to design, develop, and implement an inter-organizational system by the Reserve Bank of Australia (central bank) and other authorities to remodel data reporting by financial institutions in Australia. The research concluded that the complexity of data consumption patterns led to an increased interdependence within the financial information supply chain which requires developing data exchanges and commodity-like IT infrastructures.
Also, a study by [
9] stated that multiple governments have implemented Integrated Financial Management Information Systems to improve effectiveness and streamline business processes. Authors determine the need for automated financial operations to improve data supply chain efficiency.
The authors of [
7] believe that in order to improve financial performance, we need to utilize a tool from lean manufacturing. They state that although financial operations are not the same as manufacturing operations, they share more similarities than might be acknowledged. These similarities entitle the financial data supply chain to adopt batch processing and scheduling from lean manufacturing.
Batch processing is widely used because of its ability to meet business-critical functions. It is mainly applied when dealing with large, repeated jobs that can be carried out at a prescribed time. The batch process is complex posing a challenge to efficiently allocate the needed resources. In this section, related literature to approaches used in data batching is presented. Also, related work of using data batching in other fields is presented as well.
The scheduling problem was studied by many researchers since it is a critical issue in batch process operation and performance improvement. Page et al. [
10] considered eight common heuristics along with the genetic algorithm (GA) evolutionary strategy to dynamically schedule tasks to processors in a heterogeneous distributed system; they found that using multiple heuristics to generate schedules provides more efficient schedules than using each heuristic on its own. Méndez et al. [
11] classified and presented the different state-of-the-art optimization methods associated with the batch scheduling problem. Osman et al. [
12] proposed a model for data batch scheduling; they presented a dynamic, iterative framework to assign the required tasks to available resources taking into consideration the predecessors, constraints, and priority of each job. Al Sadawi et al. [
13] studied the data batch problem with the goal of minimizing costs and satisfying customer service level agreement. Lim and Chao [
14] used fuzzy inference systems to model the preferences of users and decide on the priority of each schedule with the goal of providing users with more efficient throughput. Xhafa and Abraham [
15] developed heuristic and metaheuristic methods to deal with scheduling in grid technologies which are considered more complicated than scheduling in classical parallel and distributed systems. Aida [
16] evaluated multiple job scheduling algorithms performance to investigate the effect of job size characteristics on job scheduling in a parallel computer system. Stoica et al. [
17] described a schedule based on the microeconomic paradigm for online scheduling of a set of parallel jobs in a multiprocessor system. The user was granted control over the performances of his jobs by providing him with a saving account containing an amount of money used to run the jobs. Stoica [
18] considered the problem of scheduling an online set of jobs on a parallel computer with identical processors by using simulation to compare three microeconomic policies with three variable partitioning policies. Islam et al. [
19] demonstrated higher revenue and better performance by using their proposed new scheduling heuristic called Normalized Urgency to prioritize jobs based on their urgency and their processing times.
A study by Damodaran and Vélez-Gallego [
20] developed a simulated annealing algorithm to evaluate the performance of batch systems in terms of total completion time with the goal of minimizing the processing time, and Mehta et al. [
21] proposed a parallel query scheduling algorithm by dividing the workload into batches and exploiting common operations within queries in a batch, resulting in significant savings compared to single query scheduling techniques. Grigoriev et al. [
22] developed a two-phased LP rounding technique that was used to assign resources to jobs and jobs to machines where a maximum number of units of a resource may be used to speed up the jobs, and the available amount of units of that resource must not be exceeded at any time. Also, Bouganim et al. [
23] studied execution plans performance of data integration systems where they proposed an execution strategy to reduce the query response time by concurrently executing several query fragments to overlap data delivery delays with the processing of these query fragments. Ngubiri and van Vliet [
24] proposed a new approach for parallel job schedulers fairness evaluation where jobs are not expected to have the same performance in a fair set up when they do not have the same resource requirements and arrive when the queue and system have different states. Arpaci-Dusseau and Culler [
25] used a proportional-share scheduler as a building-block and showed that extensions to the above scheduler for improving response time can still fairly allocate resources to a mix of sequential, interactive, and parallel jobs in a distributed environment.
From an economic point of view, Ferguson et al. [
26] adopted the human economic model and implemented it on resource allocation in a computer network system which resulted in limiting the complexity of resource sharing algorithms by decentralizing the control of resources. Additionally, Kuwabara et al. [
27] presented a market-based approach, where resources are allocated to activities through buying and selling of resources between agents and resource allocation in a multi-agent system. Chun and Culler [
28] presented a performance analysis of market-based batch schedulers for clusters of workstations using user-centric performance metrics as the basis for system evaluation. Also, Sairamesh et al. [
29] proposed a new methodology based on economic models to provide Quality of Service (QoS) guarantees to competing traffic classes in packet networks. Yeo et al. [
30] outlined a taxonomy that describes how market-based resource management systems can support utility-driven cluster computing; the taxonomy is used to survey existing market-based resource management systems to better understand how they can be utilized.
Islam et al. [
31] designed a framework that provides an admission control mechanism that only accepts jobs whose requested deadlines can be met and, once accepted, guarantees these deadlines. However, the framework is completely blind to the revenue these jobs can fetch for the supercomputer center. They analyzed the impact of job opportunity cost on the overall revenue of the supercomputer center and attempted to minimize it through predictive techniques. Mutz and Wolski [
32] presented a novel implementation of the Generalized Vickrey Auction that uses dynamic programming to schedule jobs and computes payments in pseudo-polynomial time. Mutz et al. [
33] proposed and evaluated the application of the Expected Externality Mechanism as an approach to solving the problem of efficiently and fairly allocating resources in a number of different computational settings based on economic principles. Tests indicated that the mechanism meets its theoretical predictions in practice and can be implemented in a computationally tractable manner.
Lavanya et al. [
34] proposed two task scheduling algorithms for heterogeneous systems. Their offline and online scheduling algorithms aimed at reducing the overall makespan of task allocation in cloud computing environments. The algorithms’ simulation proved that they outperformed standard algorithms in terms of makespan and cloud utilization. Minimizing makespan was the objective of the research conducted by Muter [
35] which tackled single and parallel batch processing machine scheduling. The author presented a reformulation for parallel batch processing machines and proposed an exact algorithm to solve this problem. Also, Jia et al. [
36] developed a mathematical model and a fuzzy ant colony optimization (FACO) algorithm to schedule parallel non-identical size jobs with fuzzy processing times. The batch processing utilized machines with different capacities and aimed at minimizing the makespan. Additionally, Li [
37] proposed two fast algorithms and a polynomial time approximation scheme (PTAS) to tackle the problem of scheduling n jobs on m parallel batching machines with inclusive processing set restrictions and non-identical capacities. The research aimed at finding a non-preemptive schedule to minimize makespan.
Another study by Josephson and Ramesh [
38] aimed at creating a task scheduling process by examining the various real times scheduling algorithm. The study presented a new algorithm for task scheduling in a multiprocessor environment. The authors used TORSCHE toolbox for developing real-time scheduling in addition to utilizing features of particle swarm optimization. The proposed algorithm succeeded in executing a maximum number of the process in a minimum time. Also, Ying et al. [
39] investigated the Distributed No-idle Permutation Flowshop Scheduling Problem (DNIPFSP) with the objective of minimizing the makespan. The authors proposed an Iterated Reference Greedy (IRG) algorithm that was compared with a state-of-the-art iterated greedy (IG) algorithm, as well as the Mixed Integer Linear Programming (MILP) model on two benchmark problems showing promising results.
An energy-efficient flexible job shop scheduling problem (EFJSP) with transportation was the core of research by Li and Lei [
40]. The authors developed an imperialist competitive algorithm with feedback to minimize makespan, total tardiness, and total energy consumption. The conducted experiments provided promising computational results, which proved the effectiveness of the proposed algorithm. Furthermore, a study addressing distributed unrelated parallel machines scheduling problem aiming at minimizing makespan in the heterogeneous production network was proposed by Lei et al. [
41]. A novel imperialist competitive algorithm with memory was developed by authors and experiments were conducted to test the performance of where the computational results proved the effectiveness of the algorithm. A study aimed at optimizing the trade-off between the total cost of tardiness and batch delivery was conducted by Rahman et al. [
42]. To achieve this goal, the authors proposed three new metaheuristic algorithms which are the Differential Evolution with different mutation strategy variation, a Moth Flame Optimization, and Lévy-Flight Moth Flame Optimization algorithm. The algorithms were validated through an industrial case study.
Luo [
43] tackled the dynamic flexible job shop scheduling problem under new job insertions. The goal of the research was to minimize the total tardiness; therefore, the authors proposed a deep Q-network (DQN). The developed DQN was trained using deep Q-learning and numerical experiments confirmed the superiority and generality of DQN. Also, Yun et al. [
44] suggested a genetic algorithm based energy-efficient design-time task scheduling algorithm for an asymmetric multiprocessor system. The proposed algorithm adaptively applies different generation strategies to solution candidates based on their completion time and energy consumption. Experiments proved that it minimized energy consumption compared to existing methods. Finally, Saraswati et al. [
45] aimed at minimizing the total tardiness in batch completion time using the metaheuristic approach of simulated annealing. The programming was done using Python programming. The research case study scheduled batches to parallel independent machines where the results of data processing demonstrated reduced total tardiness.
As concluded from the above survey, none of the articles found in the literature covered all aspects of data batch processing and scheduling. While some researchers concentrated on fulfilling the time constraint, others aimed at scheduling the maximum number of tasks effectively; however, none of the studies found in the literature considered cost during the scheduling process of data batches. This work tackles the significantly effective and widely used data batching process covering all its aspects. It will focus on scheduling a set of required jobs to be processed in a batch using the available resources (i.e., processors) as per the predecessors, job priorities and constraints stated in the SLA while batch job′s predecessors and priorities are specified by the client depending on the type of tasks handled. This work represents a major contribution to the literature since it comprises all aspects of the DBP including cost.
3. Data Batch Algorithm
This research tackles the financial data supply chain management for the banking and financial sector which mainly revolves around processing financial-related data using available resources. Those resources are usually software and hardware processors. A major tool used in the management of the financial data supply chain is data batch processing (DBP). Our study covers all aspects of data batch processing—such as job priorities, precedence task relation, and time constraints—in addition to different types of cost. It is vital to emphasize the importance of the cost aspect in data batch processing since the utilized resources′ costs are very high. Yet, previous research work has neglected considering DBP cost despite its significance. Therefore, this research is extremely important since it includes different types of DBP costs in addition to all other aspects in a scheduling algorithm.
The DBP which the financial sector relies heavily on has been bounded by the IT systems that drive banking businesses making them in severe need of rapid, efficient and effective processes to be able to focus on their clients holistically. They use DBP widely in their daily operations like processing end-of-day (EOD) jobs which include highly important and frequently used activities and services such as: preparing employees′ payroll, interest rate calculations, and customer′s bank statements, credit card processing bills, fraud detection data, and many others [
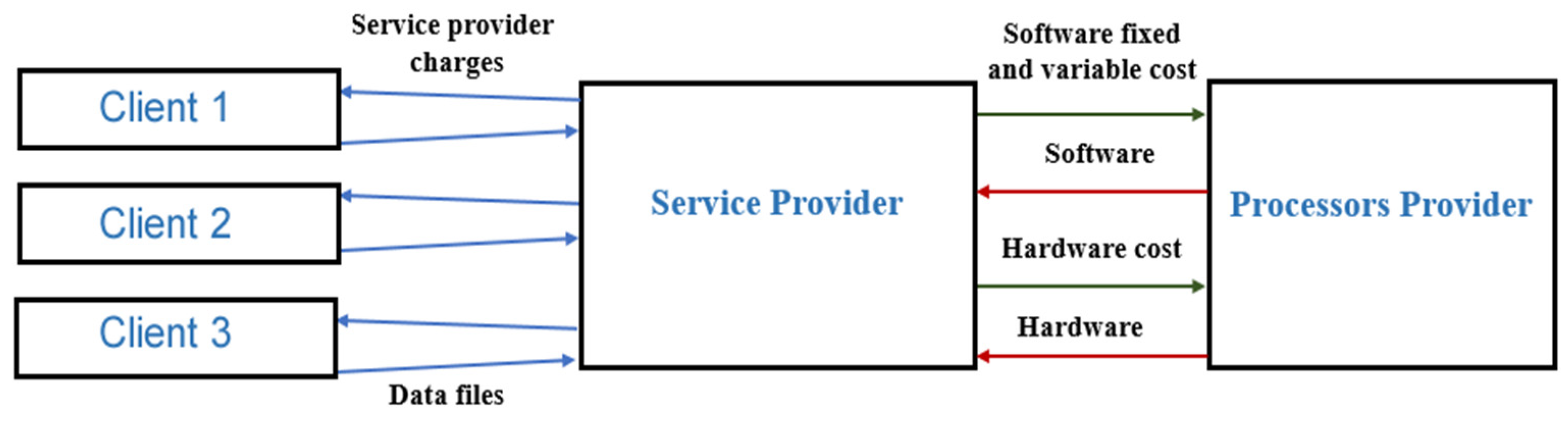
4]. Banks usually outsource DBP to a third-party company (service provider) that takes charge of arranging and processing the data and aggregating the output as shown in
Figure 1. The service provider company leases processors and software from a provider to perform the batch process for the bank based on a Service Level Agreement (SLA). The service provider usually operates after closing hours so there will be no more data entries or online intervention.
DBP begins with scheduling data, gathered in batches by type, to the available processor. The data files are scheduled while taking into consideration job priorities, predecessors and other constraints meaning that jobs will not be processed simultaneously but rather as per their schedule. The objective is to execute the tasks using the available resources to improve utilization, reduce cost and increase their profit while meeting the SLA. Each job consists of one or more executable data files. It is considered the surface layer of batch systems. A job consists of multiple tasks; therefore, the network of tasks is a detailed network view of jobs. In other words, a job is defined as a collection of tasks that are used to perform a computation. The developed dynamic scheduling algorithm considers cost types associated with the data batch scheduling which are: servers and software leasing cost, rental cost for additional resources needed in case of overload and extra work, penalty cost of failing to execute the batch process as per the (SLA), and the opportunity cost representing the cost of idling a resource for any period of time due to inefficient task allocation.
The data batching dynamic algorithm will be presented next. The algorithm will efficiently decide on resources allocation for the service provider to minimize the total operational cost. The service provider will batch process data for its clients one at a time according to a specific service agreement with that client.
3.1. Dynamic Cost Scheduling Algorithm for Data Batch Processing (DCSDBP)
Usually, given the current business practice dealing with such techniques, certain market-based rules govern the implementation of these scheduling processes. Therefore, the following assumptions underpinning the proposed algorithm are applied:
The service-providing company lease a fixed number of data processors.
Reserving processors is not allowed at the beginning or during the batch process scheduling. A processor is immediately acquired once a decision is made to rent it.
The characteristics of data files that will be processed as batches such as size and priorities are specified at the beginning of the scheduling process.
Hardware and software costs are incurred for processing data.
The hardware cost is a fixed amount.
Software cost will have fixed and variable cost amounts; the variable cost is charged based on usage per unit time.
Additional processors can be rented anytime during the execution; however, costs will be higher, 1.25 times, than the currently leased processors′ hardware and software fixed cost. Also, a software variable cost is charged per unit time of usage. These assumptions are derived from practices in the field.
Additional processors are rented only if there is a chance of not meeting the SLA.
When an additional processor is acquired, it will be accounted for from the time it is acquired until the end of the batch window.
Whenever an additional processor is rented at any time unit T, the endorsed fixed hardware and software costs will be calculated from the time of renting until the end of the batch process.
Each leased or additionally rented processor executes a single task at a time.
Different tasks can be processed in parallel. Parallel processing can occur only if there is no restriction due to priorities and predecessors relations provided in advance.
A single data file containing multiple tasks can be multi-processed on multiple processors at the same time if it is allowed by the tasks predefined predecessors relations and the hardware and software resources are available.
The iteration clock time unit is estimated by the time it takes to process the smallest size unit of the data file.
The total DBP time is a multiple of the iteration unit time. Files are allocated to processors until a predetermined SLA time is reached. A penalty cost is imposed on each delay unit of time if the SLA is exceeded. The total penalty cost is calculated by multiplying the time delay by the penalty cost per unit time.
At the beginning of each time unit T, files are allocated and resources are captured. However, at the end of the time period T, all resources are freed and ready for the next time period T.
3.1.1. Indices
| i,j | Data file. |
| k | Leased processor |
| r | Rented processor. |
| T | Clock discrete time |
3.1.2. Problem Parameters
| I | Set of data files. |
| Subset of the data files that are available for processing at any time T. |
| Required processing time for data file i. |
| SLA | Batch process time as agreed on in the SLA. |
| K | Set of all leased processors. |
| R | Set of rented processors. |
| Number of rented extra processors that can be acquired at any discrete time T. |
| Binary parameter equal to 1 if data file j immediately precedes data file i, and 0 otherwise (parameters of precedence/dependency matrix). |
| Data file weight based on precedence/dependency matrix. |
| Data file scheduling priority provided by the client. |
| Precedence/dependency matrix at each period T. |
| BW | Available batch process window. |
| Csf | Leased processor software fixed leasing cost. |
| Csv | Variable leasing cost per unit time of a processor software. |
| Ch | Leased processor hardware cost. |
| Cesf | Fixed rental cost per unit time of additional processor software. |
| Cesv | Variable rental cost per unit time of additional processor software. |
| Ceh | Rental cost per unit time of additional processor hardware. |
| Cp | Penalty cost per unit time for failing to execute the batch process as per the SLA. |
| ei | Number of times file i can be multi processed. |
| TCp | Delay time total penalty cost. |
| TH | Total cost of renting one additional processor at any time unit T. |
| Available files total multiprocessing ei at any time T. |
| Clock discrete time at which extra processor r is rented. |
| END | End of batch process. |
| TBC | Total batch process cost. |
3.1.3. Problem Variables
| Pk | Binary variable equal to1 if processor k is available and 0 otherwise. |
| Wr | Binary variable equal to1 if processor r is available and 0 otherwise. |
| Binary variable equal to 1 if data file i is available for processing at discrete time T, and 0 otherwise. |
| Number of times data file i has been processed. It is incremented by one every time data file i being processed. |
| Binary variable equal to 1 if T > SLA, and 0 otherwise. |
| UT | |
| Early start of file i. |
| Late start of file i. |
| Slack (the difference between early start and late start) of file i. |
| > 0, and 0 otherwise. |
3.1.4. Problem Decision Variables
| Binary variable equal to 1 if data file i allocated to processor k, and 0 otherwise. |
| Binary variable equal to 1 if data file i is allocated to extra processor r, and 0 otherwise. |
The DCSDBP algorithm is illustrated in
Figure 2 and the step-by-step description of the algorithm is as follows.
This step involves preparing the initial data which consists of the subset of data files that are ready for processing and the availability of leased and rented. We also set:
The extra processors′ utilization parameter to zero indicating that no extra processor is used at the beginning of the allocation process.
The data files processing parameters to zero meaning that files are not being processed yet. In addition to that, the time loop is initialized where time is set to zero. At the end of the step, we initialize all data needed to start the iterative algorithm.
Equation (2) indicates that leased processors are ready since the binary variable Pk is set to 1.
Equation (3) indicates that rented processors are ready since the binary variable Wr is set to 1.
Equation (4) indicates that the number of rented extra processors acquired at this time period VT is zero.
Equation (5) indicates that a data file i have never been processed since is set to zero.
Equation (6) indicates the beginning of the time loop of the algorithm where the time T is set to zero.
We assign parameters and weights to the subset of data files available for processing based on their precedence obtained from the dependency matrix.
is the weight for each data file. It is calculated using the precedence/dependency matrix by finding the number of files that depend on file i.
This step will indicate the set of data files available for processing which will serve as input for step 3 to start the scheduling of available files on the available processors.
In this step, the algorithm allocates files to processors. The model presented in this step will allocate files with the objective function (11) of minimizing data file allocation cost while taking into consideration priority, weight and criticality of each file included in each subset at any time T.
The first term considers the basic processors leasing cost, weight and priority βi at any time unit T. The second term considers the opportunity cost of not utilizing the leased processors at any time unit T. The third term handles the cost of renting additional processors, weight and priority βi at any time unit T. The fourth term considers the opportunity cost of not utilizing the additionally rented processors at any time T. the last term is concerned with the penalty cost of exceeding the SLA. The used in terms 1 and 3 ensures that files with higher priority and weight are scheduled first. BW is the available time during which processing can take place. It is used in Equation (11) to find what the fixed cost of resources per unit time is.
The constraint in Equation (12) is concerned with leased and additionally rented processors allocation and their availability to ensure that the total file allocation does not exceed either file multiprocessing
ei or file required remaining processing
ni or the total number of available basic and extra processors (
K,V) for any file
i at a certain time
T.
The constraint in Equation (13) ensures that the number of times a file is processed is less or equal to the needed processing time.
The constraint in Equation (14) ensures that exactly one data file is allocated to a single leased processor.
The constraint in Equation (15) ensures that exactly one data file is allocated to a single additionally rented processor.
The constraint in Equation (16) declares that the decision variable
Xik is binary, meaning that file
i either be assigned to a leased processor or not.
The constraint in Equation (17) declares that the decision variable Yir is binary, meaning that a file i either be assigned to an additionally rented processor or not.
At this stage, we check if an additional processor should be rented at this time unit to avoid delay and penalty cost. This step involves calculating the critical path duration for the rest of the unprocessed activities in the data files network at each time unit and compare it to the remaining time until the end of the batch process time that is agreed on in the SLA. A trade-off between the cost of renting an additional processor and the penalty cost is made, and according to that, it will be decided whether to rent a new processor or incur a penalty cost. Renting a new processor is subject to the condition that the total number of data files available for processing is higher than the total number of rented basic and extra processors.
In the above equations the slack for each file i is calculated and the critical path for the network UT is found for the files with slack equal to zero ( = 0).
Checking critical path duration against SLA
The above equations calculate the penalty cost TCp for all cases of critical path duration against SLA.
Cost of renting extra processor in case there is a delay
The above equations calculate the extra processor renting cost TH in case of a delay.
Amount of processing to completion Decision on renting extra processor
In the above equations, the number of rented extra processor increased by one if the penalty cost TCp is greater than the extra processor renting cost TH.
In this step, we are calculating the maximum completion time using CPM without considering splitting because the decision to multi-process a job is not taken yet. A job multi-processing means it can be split if needed to minimize the completion time of the batch process. CPM is not the only tool in this study to make the decision. Looking at Equations (29) and (31), the decision to rent an additional processor is based on another criterion. D was introduced which, as per Equation (29), ensures that no extra processor shall be rented unless there is an available task ready to be allocated to it. This ensures that no additional processor will be rented unless it will be used.
Each data file processing parameter is incremented by the number of times it was processed. When a file is fully processed, then it is removed from the subset for the following time unit and the rest of the process.
This step will update the file availability to determine if any file needs further processing or all files are completed.
When all files are processed, then the algorithm shall stop, else the model will go to step 7.
Then
Stop.
Increment iteration clock by one time unit until the DCSDBP algorithm allocates all files.
Go to Step 2
Steps 2 through 7 of the DCSDBP will be repeated until all tasks are allocated to available resources and there are no more jobs waiting in the queue.
The Total batch process cost is updated as follows:
The total cost and the completion time will be calculated at the end of the DCSDBP algorithm. The total batch process cost (C) = leased processors fixed hardware cost + leased processors fixed software cost+ leased processors variable software cost + leased processors opportunity cost + rented processors variable software cost + rented processors fixed software cost + rented processors hardware cost + rented processors opportunity cost + penalty cost.
4. Illustrative Example
In this section, we present a numerical example to illustrate the proposed DCSDBP algorithm. Consider a network of 15 data files with the precedence relations as shown in
Figure 3.
The precedence relationships are fixed relationships provided by the client that the service provider must use in processing the files; therefore, there cannot be any deadlocks relation.
Table 1 presents the different parameters’ values; these values are either given directly such as file′s multiprocessing
ei, processing time
ni and priority
βi, or derived from the files precedence relation such as file′s weight
αi^T and precedence parameter
Lij^T. The following data were also used: there are two available leased processors; maximum number of available processors than can be rented is 5,
SLA = 18 time units; batch window BW = 22 time unit; leased processor fixed software cost
Csf =
$10; leased processor hardware cost
Ch =
$100; leased processor variable software cost per time unit
Csv =
$2; rented processor fixed software cost
Cesf =
$12.5; rented processor Hardware Cost
Ceh =
$125; rented processor variable software cost per time unit
Cesv =
$2.5; penalty cost per time unit in case of exceeding the
SLA is
Cp =
$200.
The algorithm was programmed using LINGO 15.0 x64. The Lingo output shows that the files were processed in 20 time units, while 4 extra processors were rented, and the batch process exceeded the SLA by 2 time units, which indicates that penalty cost was imposed. Once the batch process started, the program sets all initialization conditions, which means that ready files subset is empty. At the beginning of each time unit T, the precedence parameters for all files are checked to determine which files are ready to be processed. All files having precedence parameter = 1 are considered ready and inserted to the ready files subset . It is worth mentioning that files 0 and 16 are start and end files with processing time ni = 0 which means they won′t be allocated to any processor. The reason of their existence is to start and end the network for critical path calculation purposes.
The algorithm started at T = 0 with files 1, 2, 3, 4, 6, 9, and 10 ready for processing; therefore, they were inserted into the ready files subset . At T = 0 files 4 and 6 were processed by leased processor 2 and 1 respectively because these files have the highest calculated weight and predetermined priority while the rest of ready files were shifted for the next time unit. At T = 1, the values of precedence parameter are updated for all files, so the ones that have not been processed or not finished processing still have the value of 1 and are consequently still included in the ready files subset while file 6 which has a processing time of 1 has the value of 0 and no longer exist in the subset since it is considered ready. Also, an additional processor was rented and utilized at that time unit because the criteria of renting a new processor was satisfied. It was found that the critical path of the remaining network activities exceeds the SLA, so the program needs to take an action to try to avoid the delay. The decision of renting a new processor is made since the cost of renting a new processor TH was found to be less than the penalty cost TCp at that time unit and also since there are ready files for the next time unit that exceeds the total number of available processor. During T = 1 file 4 was processed by leased processors 1 and 2, as well as by the additionally rented processor 1.
At T = 2 another additional processor was rented based on the above-explained mechanism. File 4 continued to be processed by leased processors 1 and rented processors 1 and 2 since it has a multiprocessing of = 3. Also, file 2 was processed by leased processor 2. At T = 3 an additional third processor was rented and file 1 was processed by leased processors 1 and 2 and rented processor 3 due to its multiprocessing criteria. File 4 was processed by rented processors 1 and 2 and by that it is considered ready. At T = 4 the forth additional processor was rented and used to process file 1 along with rented processors 1 and 3 while rented processor 2 and leased processor 1 were used to process file 3. File 5 was processed by leased processor 2. T = 5 had the same files allocations as T = 4. It is noted that the program did not rent any more extra processor starting from T = 5 onwards which means it utilized 4 out of the 5 processors available for renting and that is based on the renting mechanism. The same steps were executed on all files until the end of processing at T = 19 when all files were processed.
The batch process cost calculation was based on using Equation (46) by using the input values listed earlier in this section and the allocation results from Lingo output;
Table 2 demonstrates the detailed costs. Also,
Table 2 clarifies the cost of allocating files to leased processor and that includes hardware and software fixed costs as well as software variable cost. Similarly, rented processors allocation cost which includes hardware and software fixed costs as well as software variable cost is shown. Then the opportunity costs associated with each processor type is calculated. Penalty cost is determined at the end of the batch process and total cost is found by summing all costs for each time unit. In
Table 2, column (1) represents the time unit
T, column (2) shows the total number of existing leased processors K, column (3) identifies how many leased processors are actually being acquired at each time unit
T, column (4) calculates the leased processors variable cost
Csv while the fixed software
Csf and hardware
Ch costs are calculated at the end because they are not related to time. Leased processors opportunity cost is determined in column (5) as per Equation (27). For rented processors, column (6) shows the number of additionally rented processors
at that time unit
T, column (7) represents the number of rented processors actually being acquired at each time unit
T. In column (8), and based on model assumption 14 which states that rented processors are paid for from the time unit
T they are rented onwards, rented processors total allocation cost is calculated using all types of costs (extra fixed hardware cost
Ceh, extra fixed software cost
Cesf and extra variable software cost
Cesv). It is worth mentioning that in case of an additional processor being rented but not utilized due to unavailability of ready files, the total allocation cost will equal fixed hardware cost
Ceh plus fixed software cost
Cesf while the variable software cost
Cesv will not exist since the processor is not being utilized. Rented processors opportunity cost is found in column (9) using fixed hardware cost
Ceh plus fixed software cost
Cesf. Finally, column (10) sums all the above costs for each time unit
T.
At the end of
Table 2 leased fixed costs are added, they represent fixed hardware cost
Ch plus fixed software cost
Csf for each leased processor k. Also as mentioned above penalty cost is calculated based on number time units the processing is delayed beyond the
SLA. Since leased processors fixed hardware cost
Ch and fixed software cost
Csf are calculated per unit time by dividing them by
BW, remaining opportunity cost for basic processor exists in case the batch process time
END is less than batch window
BW. It represents the opportunity cost of the leased processors for the time units between the end of batch process
END and
BW.
From
Table 2, we can see that from
T = 0 until
T = 17, the basic allocation cost was showing the utilization of both leased processors, which explains the zero value for opportunity cost of leased processors during the same period. However, at
T = 18 and 19 one leased processor was utilized and that ended up in variable allocation cost for one processor and opportunity cost for the other. It can be also noticed that from
T = 0 up to
T = 10, every rented processor was utilized which ended in zero opportunity cost. After
T = 10 some rented processors were not utilized due to unavailability of ready files such as at
T = 11 where 3 out of 4 rented processors were utilized. Also at
T = 12, 13, 16, 17, 18, and 19 none of the rented processors were utilized due to the unavailability of ready files.
The above illustrative example shows the effectiveness of the developed algorithm in allocating files to processors. The algorithm managed to allocate highly prioritized and weighted files before the ones with lower priority and weight. Also, the algorithm will advise renting the necessary number of extra processors to accomplish the batch process goal while trying to minimizing cost. In the illustrated example, the program rented 4 extra processors to achieve minimum real batch process time, which is 20 time units. Although that exceeds the SLA specified time of 18 time units, it is the minimum possible execution time for this network due to network logic and predecessors′ relations.
The illustrative example shows that the batch processing is performed using a set of assumptions and constraints under which the problem makes the best decision at that time unit. Decisions are made dynamically based on the current status and previous decisions. This decision process ascertains that the best decision is taken at each iteration. We do not define the global network (of all feasible assignments of jobs to servers) to perform a direct optimization on it, we rather generate the subnetwork of feasible assignments at each iteration (Step 3 of the algorithm). This sequence of optimum decision-making ensures that the solution at the end is global. Not being optimal would mean that a better solution exists at some stage in the optimization process, which would contradict stage 3 as built.