Abstract
In hybrid mixed-flow workshop scheduling, there are problems such as mass production, mass manufacturing, mass assembly and mass synthesis of products. In order to solve these problems, combined with the Spark platform, a hybrid particle swarm algorithm that will be parallelized is proposed. Compared with the existing intelligent algorithms, the parallel hybrid particle swarm algorithm is more conducive to the realization of the global optimal solution. In the loader manufacturing workshop, the optimization goal is to minimize the maximum completion time and a parallelized hybrid particle swarm algorithm is used. The results show that in the case of relatively large batches, the parallel hybrid particle swarm algorithm can effectively obtain the scheduling plan and avoid falling into the local optimal solution. Compared with algorithm serialization, algorithm parallelization improves algorithm efficiency by 2–4 times. The larger the batches, the more obvious the algorithm parallelization improves computational efficiency.
1. Introduction
The traditional shop scheduling model takes single shop scheduling as the goal, but, in actual discrete manufacturing [1], the job shop and the flow shop are closely connected. The production process includes parts processing, component assembly and product assembly. In this production environment, optimizing one of the workshops leads to a mismatch between the progress of parts processing and subsequent component-assembly and final assembly workshops, resulting in a large amount of inventory and prolonging the product cycle, affecting the production process. Therefore, in the face of the problem of hybrid mixed-flow workshop scheduling, it is necessary to establish integrated scheduling of multiple workshops from the perspective of overall optimization.
The current solutions to the hybrid workshop scheduling problem include accurate calculations for low-complexity and small-scale problems [2,3,4] and heuristic algorithms. Due to accurate calculation, the calculation time increases exponentially with the complexity of the workshop scheduling problem and the application value is limited. For heuristic algorithms, it performs well on today’s workshop scheduling problems, so heuristic algorithms are widely used today. Smutnicki [5] proposed an approximation algorithm based on tabu search, with the goal of minimizing processing time and studying a mixed flow shop with a limited intermediate buffer area. Wang et al. [6] proposed a multi-objective genetic algorithm to study the integrated scheduling problem of flow shop with buffer. Seidgar et al. [7] considered the coordination trade-off model of maximum process time and average completion time and used intelligent algorithms to solve and study the optimization of two-stage flow-shop scheduling with assembly tasks. Na et al. [8] proposed an evolutionary algorithm using three-segment coding to study the production planning and scheduling of mixed-flow products in flexible workshops with processing tasks and assembly tasks. Zhang et al. [9] used an optimized genetic algorithm to solve the problems of minimum total completion time and long equipment idle time for single-piece and small-batch hybrid workshop scheduling. Teymourian [10] faced the problem of assembly job mixed-flow shop scheduling, to the artificial immune algorithm they added the ant colony algorithm to change the antibody to avoid falling into the local minimum and obtain a better scheduling plan. Lou et al. [11] proposed an immune cloning algorithm to solve the problem when studying the optimization problem of hybrid workshop scheduling and achieved an effective solution. Hu et al. [12] proposed a genetic algorithm for multi population parallel and population screening and updating in a phased convergence manner to study the hybrid mixed-flow workshop scheduling problem. Li et al. [13] investigated hybrid mixed-flow workshop scheduling by proposing a hybrid genetic algorithm with the goal of minimizing cache area inventory. Lu et al. [14] proposed the game particle swarm optimization algorithm to study the hybrid mixed-flow workshop scheduling with the goal of parts shop uniformity and minimum inventory. Wang [15] proposed an immune genetic algorithm to study hybrid mixed-flow workshop scheduling with the objective of minimizing the maximum completion time. Tang et al. [16] proposed an improved immune genetic algorithm that introduced a multi-agent negotiation mechanism and simulated annealing algorithm to study the mixed scheduling problem of job shop and flow shop.
Intelligent algorithms are widely used in solving actual complex engineering problems. Nejah et al. [17] introduced the advantages and disadvantages of different intelligent algorithms in 3D indoor deployment problems and evaluated the performance of different intelligent algorithms on 3D indoor deployment problems. Mnasri et al. [18] introduced the application and analysis of existing hybrid intelligent algorithms on the deployment of sensor nodes in wireless sensor networks. The particle swarm optimization algorithm (PSO) stands out among many intelligent algorithms for its advantages, such as high solution accuracy and fast convergence speed. Zhao et al. [19] proposed an improved particle swarm algorithm with decreasing disturbance index on the multi-objective job shop scheduling problem. Mansour et al. [20] faced the problem of shop scheduling with congestion constraints and proposed a combination of a local search algorithm based on probabilistic perturbation and a particle swarm algorithm. Experiments show that the improved algorithm can quickly obtain the best solution; Jamrus et al. [21] proposed a hybrid genetic particle swarm optimization algorithm for flexible job shop scheduling. Experiments show that the proposed algorithm has high solution quality and good practicability. The particle swarm optimization algorithm has a wide range of applications in solving practical problems. Therefore, this paper also uses an improved particle swarm algorithm to solve the problem.
Spark [22,23] is a memory-based distributed computing framework. Comparing the Spark and Hadoop platforms, Hadoop is suitable for offline batch processing of files, but is not suitable for iterative operations. When Spark deals with iterative problems, it does not need to store the results of the iterations to disk, which makes up for the inefficiency of Hadoop Mapreduce that reads operations from the disk every time it deals with iterative problems. When programming Spark in parallel, the input data are decomposed into multiple batch processing fragments, the data are converted into RDD (resilient distributed datasets) and the data are encapsulated in RDD. Through the parallel operation of RDD, the parallel operation of data processing is realized [24]. The basic idea of realizing the parallel particle swarm algorithm is to convert the particle swarm to RDD and initialize it to multiple small populations of the same size. After parallel processing of these small populations, a feasible solution is finally obtained [25,26]. According to the idea of parallelization, a parallel hybrid particle swarm optimization algorithm is proposed for the mixed-flow hybrid workshop scheduling problem.
The existing intelligent algorithm adopts three-stage coding [13,15] to solve the hybrid mixed-flow workshop scheduling problem, which is only applicable to the case of a small batch. Nowadays, the scale and complexity of workshop scheduling are constantly increasing. In the case of relatively large batches, it is easy to fall into the problem of local optimization using its existing three-stage coding intelligent algorithm. Therefore, in the case of a large batch, three-stage coding is not used in the problem of hybrid mixed-flow workshop scheduling. Each workshop is coded independently for independent scheduling. The independent scheduling optimization of the workshop leads to a too long running time of the algorithm. Therefore, the algorithm is improved by combining Spark to realize the parallelization of the algorithm and reduce the running time of the algorithm. In this paper, a hybrid mixed-flow workshop scheduling model is established. In the case of a large batch, a hybrid particle swarm optimization parallelization algorithm based on Spark is proposed to avoid the algorithm falling into local optimization and the workshop scheduling scheme can be obtained effectively and quickly. It has important theoretical significance and application value to solve the problem of hybrid mixed-flow workshop scheduling.
2. Problem Description and Modeling
The hybrid mixed-flow workshop is composed of three parts: the first part is the parts-processing workshop, which is produced in batches; the second part is the flow shop of the component-assembly workshop, which is assembled in units; the third part is the flow shop for the final assembly of the product, which is assembled in units, as shown in Figure 1 below.
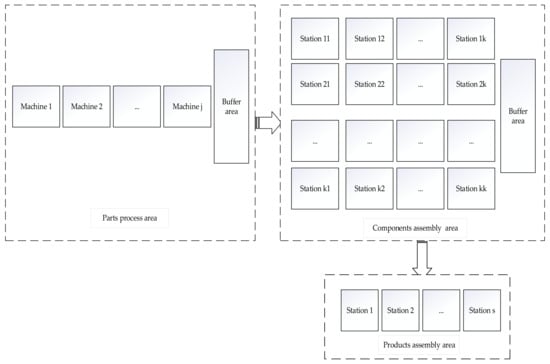
Figure 1.
Hybrid mixed-flow workshop.
The parts-processing workshop consists of j machines, processing i parts; the component-assembly workshop is composed of k assembly stations, producing x components; the product-assembly workshop consists of s assembly stations to produce y products. For the convenience of research, the following assumptions are given [13]:
- (1)
- At the beginning, all equipment and assembly stations are ready to perform production tasks at any time.
- (2)
- Different types of parts can be produced in the workshop and the sequence, processing machine and time in the production process of the parts are known.
- (3)
- The assembly time of different types of parts and products at the stations on the assembly line is known.
- (4)
- The process time of the same type of products, components and parts on the machine and the workstation is the same.
- (5)
- In the job shop, only the processes of the same part have process constraints and there are no process constraints between different parts.
- (6)
- The process time of the process includes the preparation time and transportation time of the process.
- (7)
- The parts-process workshop processes a batch of parts for the components-assembly workshop and the product-assembly workshop; or the parts-assembly workshop processes certain parts for the assembly station of the product-assembly workshop. Moreover, if the assembly station does not need more, then these parts or components are temporarily stored in the buffer zone. Ignore the delivery time.
The objective function is to minimize the maximum completion time and the model is as follows:
In Equation (1), represents the maximum completion time when all parts i are processed on j machines in the parts-processing workshop; represents the maximum completion time of all components in the assembly shop x in k stations; represents the maximum completion time for all products y in the product-assembly workshop to complete assembly at s workstations.
In the actual production process, the parts-processing workshop must meet the process constraints and equipment constraints. Parts are processed in corresponding machines and processes in accordance with process constraints and equipment constraints. In the assembly process, the component-assembly workshop and the product-assembly workshop, in accordance with the process and station constraints, operate at the corresponding assembly position and complete the pre-process before proceeding to the next process operation. The completion time of the workpiece at the station on the assembly line should meet the sum of the completion time of the previous product at this station and the maximum completion time of the workpiece at the previous station and the processing time at the current station. The constraints are as follows.
Parts-processing workshop:
Component-assembly workshop and product-assembly workshop:
In Equations (2) and (3), the value of is 1 and 0; 0 means that the device is placed in front of to process and 1 means other. The value of also has two values of 0 and 1; 0 means that the workpiece is placed in front of the workpiece and is processed by the equipment and 1 means others. is the time when the part is completed on the machine ; is the time required to process the part on the machine . In Equations (4)–(6), the values of are 0 and 1; 1 means that the workstation h is placed in front of k to assemble the workpiece x, 0 means other. The values of are 0 and 1; 1 means that the workpiece x is placed before g and works on workstation k and 0 means others.
At present, the intelligent algorithm deals with the hybrid mixed-flow workshop scheduling model. The algorithm uses three-level coding [15] for unified scheduling and solving. However, as the batches of parts and assembly components and products become larger and larger, this kind of coding can easily fall into a local optimal situation. Therefore, in order to solve this problem, each workshop is independently coded. Independently optimize scheduling for each workshop. This process increases the complexity of the algorithm and increases the running time. Therefore, the proposed algorithm is parallelized to reduce the running time of the algorithm and improve the efficiency of the algorithm.
3. Parallelized Hybrid Particle Swarm Algorithm Based on Spark
3.1. Parallel Hybrid Particle Swarm Algorithm
The particle swarm algorithm is a simulation of bird predation. In the process of solving, the solution of each particle corresponds to the position of the particle. The particle swarm algorithm has two attributes, speed and position. Speed represents the speed of movement and position represents the direction of movement.
The shop scheduling problem is a discrete optimization problem, the solution space is in different continuous domains. Because the traditional particle swarm algorithm particles fall into update stagnation and fall into the local optimal situation, combine the genetic algorithm and particle swarm algorithm to solve the shortcomings of traditional particle swarm algorithm and construct a parallelized hybrid particle swarm algorithm. The algorithm flow is as shown in Figure 2.
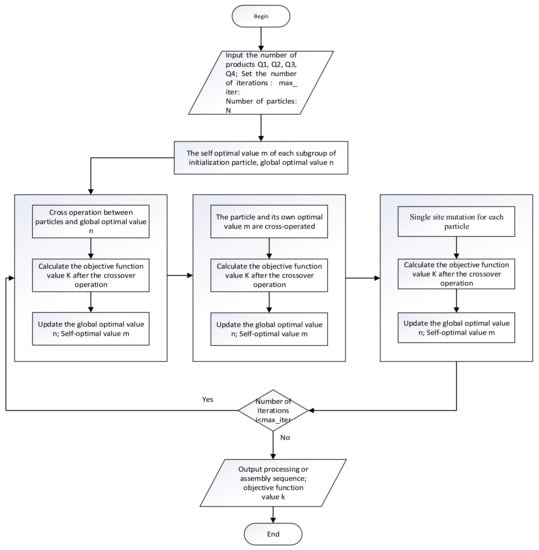
Figure 2.
The main process of parallelized hybrid particle swarm optimization.
The pseudo code of the Algorithm 1 is as follows.
| Algorithm 1. Hybrid Particle Swarm Algorithm | |
| 1 | *Initialization*/ |
| 2 | Generate N random workpiece sequences in each workshop according to the number of input products; solve the objective function value k after the crossover operation, according to Equations (2)–(6); max_iter is the maximum number of iterations; i corresponds to each particle population; ii corresponds to the number of iterations. |
| 3 | Set initial values for: max_ iter, N; i, ii |
| 4 | Initialize and solve the particle swarm’s own optimal m and global optimal value n according to the default order of the workpiece; |
| 5 | for ii in rang(max_iter): |
| /*The particles and the global optimal particles are cross-operated*/ | |
| 6 | for i in rang(N): |
| 7 | Cross operation between each particle and the global optimal particle; |
| 8 | Update N; |
| 9 | Solve the objective function after crossover: k = fitness(N); |
| 10 | Output the optimal new_n value of the most global particle swarm; its own optimal value new_m |
| /*Update m, n*/ | |
| 11 | If new_n < n then n = new_n; If new_m < m then m = new_m; |
| 13 | end for |
| /*The particle and its own optimal history particle perform cross operation*/ | |
| 14 | for i in rang(N): |
| 15 | Each particle crosses with its own optimal history particle |
| 16 | Update N; |
| 17 | Solve the objective function after crossover: k = fitness(N); |
| 18 | Output the optimal new_n value of the most global particle swarm; its own optimal value new_m |
| /*Update m, n*/ | |
| 19 | If new_n < n then n = new_n; If new_m < m then m = new_m; |
| 20 | end for |
| /*Single-site mutation for each particle swarm */ | |
| 21 | for i in rang(N): |
| 22 | Random single-site mutations for each particle swarm; |
| 23 | Update N; |
| 24 | Calculate the objective function value after mutation: k = fitness(N); |
| 25 | Output the optimal new_n value of the most global particle swarm; its own optimal value new_m |
| /*Update m, n*/ | |
| 26 | If new_n < n then n = new_n; If new_m < m then m = new_m; |
| 27 | end for |
| 28 | end for |
| 29 | /*Output*/ |
| 30 | Output the global optimal k and corresponding N workpiece production sequencing |
3.2. Detailed Design of the Algorithm
3.2.1. Coding Scheme Design
The research problem is mixed mixed-flow workshop scheduling, in which there are job workshops and flow workshops and the coding methods in genetic coding are compared. The three workshops are designed with a unified coding. After the coding design is completed, the workshops are independently optimized and dispatched. First, determine the minimum production ratio of the number of products produced according to actual needs. According to the minimum production ratio, determine the minimum production ratio for the product-assembly workshop, component-assembly workshop and parts-processing workshop, then perform independent coding. In the workshop, letters and numbers are used to represent products, components and parts. The same letters represent the same products, components and parts. If we need to put into production, the P, Q and R products are 2, 1 and 2; the number of required components X and Y is 2 and 3; the parts required for parts processing A, B and C are 2, 1 and 2. Then, the coding method in the product-assembly workshop can be (P1, P2, Q1, R1, R2); the coding of the component-assembly workshop is (X1, X2, Y1, Y2, Y3); the coding of the part processing workshop is (A1, A2, A3, B1, C1, C2, C3).
3.2.2. Crossover and Mutation
Enter the number of artifacts to generate N (total number of particles) random artifact sequences. After crossover and mutation with the global optimal value and its own optimal value, respectively, filter and update the one that can produce a better target value particle. In this step, the crossover and mutation operations can be regarded as random walk operations on the permutation group of the workpieces arranged in order. The mutation is a single-step walk of exchange and the crossover can be a walk formed by a combination of multiple basic exchanges. This step is similar to the speed update in the classic PSO. Whether to perform a walk is only True or False in this algorithm. This step simulates the weighting factor [27] in the classic PSO. Crossing with the local (self) and global optimal values, respectively, simulates the two velocity terms in the classic PSO. Both the mutation and crossover operations have a certain degree of randomness, which ensures that a single particle can jump out of the local optimal solution possibility.
3.2.3. Parallelization of Hybrid Particle Swarm Algorithm
Pyspark is a tool of Spark and a library of sparkAPI written in python provided by Spark. Parallelization is achieved through Pyspark. First, the PSO coding is converted into a parallel RDD, then the process of solving the objective function is applied to all the particles through the Map operation provided by Spark. The time for each particle to be transformed into the objective function is summarized to obtain the optimal result.
4. Instance Verification
4.1. Examples of Mixed Mixed-Flow Workshop Scheduling
Now, we take the loader manufacturing workshop as an example [15] to verify the model and algorithm. The production system is composed of the parts-processing workshop, component-assembly workshop and product-assembly workshop. The four products produced are Q1, Q2, Q3, and Q4. The corresponding parts and component demand matrix of the products are shown in Table 1, below.

Table 1.
Product demand matrix.
The parts-processing workshop mainly produces eight kinds of self-made parts. The set of parts is {A, B, C, D, E, F, G, H} and the set of machines in the workshop is {M1, M2, ⋯, M10}. The parts in batches are processed on the machine. The processing time and process sequence are shown in Table 2 below and the time unit is s.

Table 2.
Parts-processing time and process sequence.
The component-assembly workshop is mainly responsible for the assembly of components X and Y. The assembly time and steps are shown in Table 3 below and the unit is s.

Table 3.
Component-assembly process and time.
The final assembly line of the product has 33 assembly stations and the corresponding assembly time and procedures for products Q1, Q2, Q3 and Q4 are shown in Table 4 below and the unit is s.

Table 4.
Product final assembly process and time.
During the planning period, the tasks for the production of products Q1, Q2, Q3 and Q4 are divided into 320 units, 160 units, 320 units and 320 units. The minimum production ratio is 2:1:2:2. According to the known conditions, it can be known that the required parts X and Y are divided into 480 and 640 and the minimum production ratio is 3:4. The required parts A–H are 480, 640, 480, 640, 480, 640, 480 and 640, respectively, and the minimum production ratio is 3:4:3:4:3:4:3:4. Calculate according to the parallelized particle swarm algorithm, set the size of the population to 20 and the number of iterations to 300.
It runs in a 64-bit stand-alone Windows 10 operating system, 32 G running memory, 10 cores and 20 threads. In Spark’s Local mode, parallel computing of algorithms is realized. In the case of local[N] mode, the optimal plans for the assembly scheduling of parts, components and products are obtained, respectively, {E1, G1, F1, D1, G2, D2, F2, B1, F3, C1, F4, A1, H1, A2, E2, C2, B2, A3, D3, H2, H3, G3, B3, D4, H4, B4, C3, E3}; {X1, X2, Y1, Y2, Y3, Y4, X3}; {Q3, Q1, Q1, Q3, Q2, Q4, Q4}; the total completion time is 15,508 s. Using the immune genetic algorithm IA [15], the total completion time is 15,679 s. Using the PSO algorithm, the total completion time is 15,660 s. Figure 3 shows the evolution curve of this algorithm.
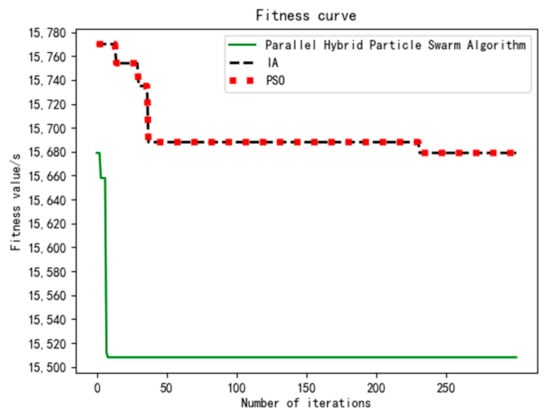
Figure 3.
Algorithm evolution curve.
In this paper, the parallel hybrid particle swarm optimization (PHPSO), IA and PSO algorithms are set to the same number of iterations of 50. Cbest is the optimal value of the operation, Aver is the average value of the operation and the relative deviation of the value dev [28]. Among them, dev1 is the comparison between PHPSO and IA and dev2 is the comparison between PHPSO and PSO. If dev is positive, the solution obtained by the compared algorithm is better. If dev is negative, the solution obtained by PHPSO is better. Table 5 shows algorithm comparison.

Table 5.
Algorithm comparison.
It can be seen from Table 5, that PHPSO finds the optimal value within 50 iterations of running time and the IA and PSO algorithms cannot find the optimal solution, indicating that the PHPSO algorithm has a good ability to find the optimal solution. The average value obtained by PHPSO in 50 iterations is smaller, indicating that the algorithm has a strong global search ability, avoiding the limitation of the algorithm that is easy to fall into the local optimum and the algorithm has strong convergence.
The parallel hybrid particle swarm optimization algorithm is compared with immune genetic algorithm IA and PSO. A stand for IA or PSO algorithms. The comparison results of the largest completion time of parts-, components- and product-assembly workshops are shown in Table 6. The deviation obtained by the hybrid particle swarm algorithm solution and the IA solution is

Table 6.
Comparison of results.
From Table 6, we can see that the PHPSO algorithm used in this article has a better solution than the GA algorithm and the PSO algorithm in the parts workshop and product-assembly workshop. Through the analysis of the results, the parallelized hybrid particle swarm optimization algorithm can achieve overall optimization.
4.2. Computing Performance
To test the parallelization performance of the hybrid particle swarm algorithm, set the population to 20 and the number of iterations to 40. Compare the running time of algorithm serialization and algorithm parallelization. The tested data are as follows: when the number of products is 7, the ratio of products is [2:1:2:2]; when the number of products is 10, the ratio of products is [2:3:2:3]; when the number of products is 14, the ratio of products is [3:4:5:2]. Compared with the running time of algorithm parallelization and algorithm serialization, the computing speed is greatly improved by 2–4 times. As the number of products input increases, the speed increases more obviously, reflecting the advantage of the Spark platform in processing a large amount of data. The running time of the algorithm is shown in Figure 4 below.
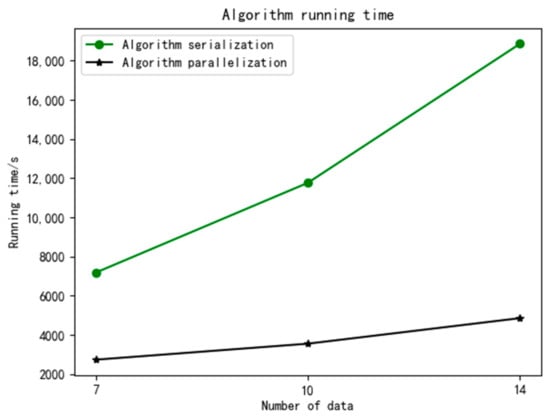
Figure 4.
Algorithm running time.
4.3. Results Discussion
In the case of a large batch in the hybrid mixed-flow workshop scheduling problem, the algorithm in this paper can effectively solve the job shop scheduling problem and avoid the algorithm falling into local optimization. Combined with the Spark platform, the parallel design of the algorithm is realized. Compared with the serial operation of the algorithm, the parallel design of the algorithm improves the efficiency of the algorithm. When the bulk becomes larger, the demand data are also more complex and the enhancement of the efficiency of the algorithm is also more obvious, in line with the advantages of the Spark platform for big data processing. This paper also has limitations. Because this paper is a single objective optimization, there are many influencing factors in the actual job shop scheduling, such as inventory cost, so the next research should apply the proposed algorithm to the job shop scheduling of multi-objective optimization.
5. Conclusions
In this paper, a parallel hybrid particle swarm optimization algorithm is proposed for hybrid mixed-flow workshop scheduling problem. The Spark platform is combined with intelligent algorithms to solve the problem of workshop scheduling in high-volume situations. This can provide some reference for solving large-scale data processing in workshop scheduling.
In the future, it is necessary to apply the parallel hybrid particle swarm algorithm to the multi-objective shop scheduling problem. Consider combining the intelligent algorithm for solving multi-objectives with the algorithm in this paper to improve it, so that it can be applied to the problem of multi-objective workshop scheduling.
Author Contributions
Conceptualization, T.Z.; methodology, T.Z.; software, Y.C.; validation, T.Z.; formal analysis, T.Z.; investigation, Y.C.; data curation, J.W.; writing—original draft preparation, T.Z.; writing—review and editing, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lefkowitz, I.; Schoeffler, J.D. Multilevel control structures for three discrete manufacturing processes. IFAC Proc. Vol. 1972, 5, 96–103. [Google Scholar] [CrossRef]
- Djellab, H.; Djellab, K. Preemptive hybrid flowshop scheduling problem of interval orders. Eur. J. Oper. Res. 2002, 137, 37–49. [Google Scholar] [CrossRef]
- Bolat, A.; Al-Harkan, I.; Al-Harbi, B. Flow-shop scheduling for three serial stations with the last two duplicate. Comput. Oper. Res. 2005, 32, 647–667. [Google Scholar] [CrossRef]
- Guirchoun, S.; Martineau, P.; Billaut, J.C. Total completion time minimization in a computer system with a server and two parallel processors. Comput. Oper. Res. 2005, 32, 599–611. [Google Scholar] [CrossRef]
- Smutnicki, C. A two-machine permutation flow shop scheduling problem with buffers. Oper.-Res.-Spektrum 1998, 20, 229–235. [Google Scholar] [CrossRef]
- Wang, B.; Rao, Y.; Shao, X.; Xu, C. A MOGA-based Algorithm for Sequencing a Mixed-model Fabrication/Assembly System. Zhongguo Jixie Gongcheng/China Mech. Eng. 2009, 20, 1434–1438. [Google Scholar] [CrossRef]
- Seidgar, H.; Kiani, M.; Abedi, M.; Fazlollahtabar, H. An efficient imperialist competitive algorithm for scheduling in the two-stage assembly flow shop problem. Int. J. Prod. Res. 2014, 52, 1240–1256. [Google Scholar] [CrossRef]
- Na, H.; Park, J. Multi-level job scheduling in a flexible job shop environment. Int. J. Prod. Res. 2014, 52, 3877–3887. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Software, S.O. Single piece and small batch mixed-shop scheduling algorithm. China Sci. Pap. 2015, 10, 962–966. [Google Scholar]
- Komaki, G.M.; Teymourian, E.; Kayvanfar, V. Minimising makespan in the two-stage assembly hybrid flow shop scheduling problem using artificial immune systems. Int. J. Prod. Res. 2016, 54, 963–983. [Google Scholar] [CrossRef]
- Lou, G.; Cai, Z. Improved hybrid immune clonal selection genetic algorithm and its application in hybrid shop scheduling. Clust. Comput. 2018, 22, 3419–3429. [Google Scholar] [CrossRef]
- Hu, H.; Lu, J.; Li, Y. Study of mixed-model hybrid shop fuzzy scheduling problem based on multi-populations parallel genetic algorithm. J. Zhejiang Univ. Technol. 2012, 40, 554–558. [Google Scholar] [CrossRef]
- Li, X.; Lu, J.; Chai, G.; Tang, H.; Jiang, L. Hybrid Genetic Algorithm for Mixed-model Hybrid-shop Scheduling Problem. Zhongguo Jixie Gongcheng/China Mech. Eng. 2012, 23, 935–940. [Google Scholar] [CrossRef]
- Lu, J.; Hu, H.; Dong, Q. Game theory and particle swarm optimization for mixed-model hybrid-shop scheduling problem. J. Zhejiang Univ. Technol. 2015, 43, 398–404. [Google Scholar]
- Wang, M. Research on Multi-level Hybrid Workshop Integrated Scheduling Based on Immune Genetic Algorithm. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2020. [Google Scholar]
- Tang, H.; Ding, B.; Li, X.; Lu, J. Improved immune genetic algorithm for mixed-model scheduling problem. China Mech. Eng. 2014, 25, 1189. [Google Scholar] [CrossRef]
- Nasri, N.; Mnasri, S.; Val, T. 3D node deployment strategies prediction in wireless sensors network. Int. J. Electron. 2020, 107, 808–838. [Google Scholar] [CrossRef]
- Mnasri, S.; Nasri, N.; Val, T. The Deployment in the Wireless Sensor Networks: Methodologies, Recent Works and Applications. In Proceedings of the International Conference on Performance Evaluation and Modeling in Wired and Wireless Networks (PEMWN 2014), Sousse, Tunisia, 4–7 November 2014. [Google Scholar]
- Zhao, F.; Tang, J.; Wang, J.; Jonrinaldi, N.A. An improved particle swarm optimization with decline disturbance index (DDPSO) for multi-objective job-shop scheduling problem. Comput. Oper. Res. 2014, 45, 38–50. [Google Scholar] [CrossRef]
- Mansour, E.; Bassem, J.; Patrick, S. Combinatorial particle swarm optimization for solving blocking flowshop scheduling problem. J. Comput. Des. Eng. 2016, 3, 295–311. [Google Scholar] [CrossRef]
- Jamrus, T.; Chien, C.F.; Gen, M.; Sethanan, K. Hybrid particle swarm optimization combined with genetic operators for flexible job-shop scheduling under uncertain processing time for semiconductor manufacturing. IEEE Trans. Semicond. Manuf. 2017, 31, 32–41. [Google Scholar] [CrossRef]
- Zaharia, M.; Chowdhury, M.; Franklin, M.J.; Shenker, S.; Stoica, I. Spark: Cluster computing with working sets. HotCloud 2010, 10, 95. [Google Scholar]
- Dongfei, S.O.N.G.; Hua, X.U. Research and Parallelization of DBSCAN Algorithm. Comput. Eng. Appl. 2018, 54, 52–56. [Google Scholar]
- Qiu, R. The Parallel Design and Application of the CURE Algorithm Based on Spark Platform. Master’s Thesis, South China University of Technology, Guangzhou, China, 2014. [Google Scholar]
- Li, F. Parallel Programming of Particle Swarm Optimization Algorithm Based on Spark and Its Application in Reservoir Scheduling. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2017. [Google Scholar]
- Peng, A.; Peng, Y.; Zhou, H. Multi-core parallel computation for deriving joint operating rule curves in multi-reservoir system under the condition of inter-basin water transfer. J. Hydraul. Eng. China 2014, 45, 1284–1292. [Google Scholar] [CrossRef]
- Shi, Y. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Gu, X.; Huang, M.; Liang, X. An improved genetic algorithm with adaptive variable neighborhood search for FJSP. Algorithms 2019, 12, 243. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).