1. Introduction
Stochastic Gradient Descent [
1] (SGD) is the dominant method for solving optimization problems. SGD iteratively updates the model parameters by moving them in the direction of the negative gradient calculated on a mini-batch scaled by the step length, typically referred to as the learning rate. It is necessary to decay this learning rate as the algorithm proceeds to ensure convergence. Manually adjusting the learning rate decay in SGD is not easy. To address this problem, several methods have been proposed that automatically reduce the learning rate. The basic intuition behind these approaches is to adaptively tune the learning rate based on only recent gradients, therefore limiting the reliance on the update to only a few past gradients. ADAptive Moment estimation [
2] (ADAM) is one of several methods based on this update mechanism [
3]. On the other hand, adaptive optimization methods such as ADAM, even though they have been proposed to achieve a rapid training process, are observed to generalize poorly with respect to SGD or even fail to converge due to unstable and extreme learning rates [
4]. To try to overcome the problems of both of these types of optimizers and at the same time try to exploit their advantages, we propose an optimizer that combines them in a new meta-optimizer.
As depicted in
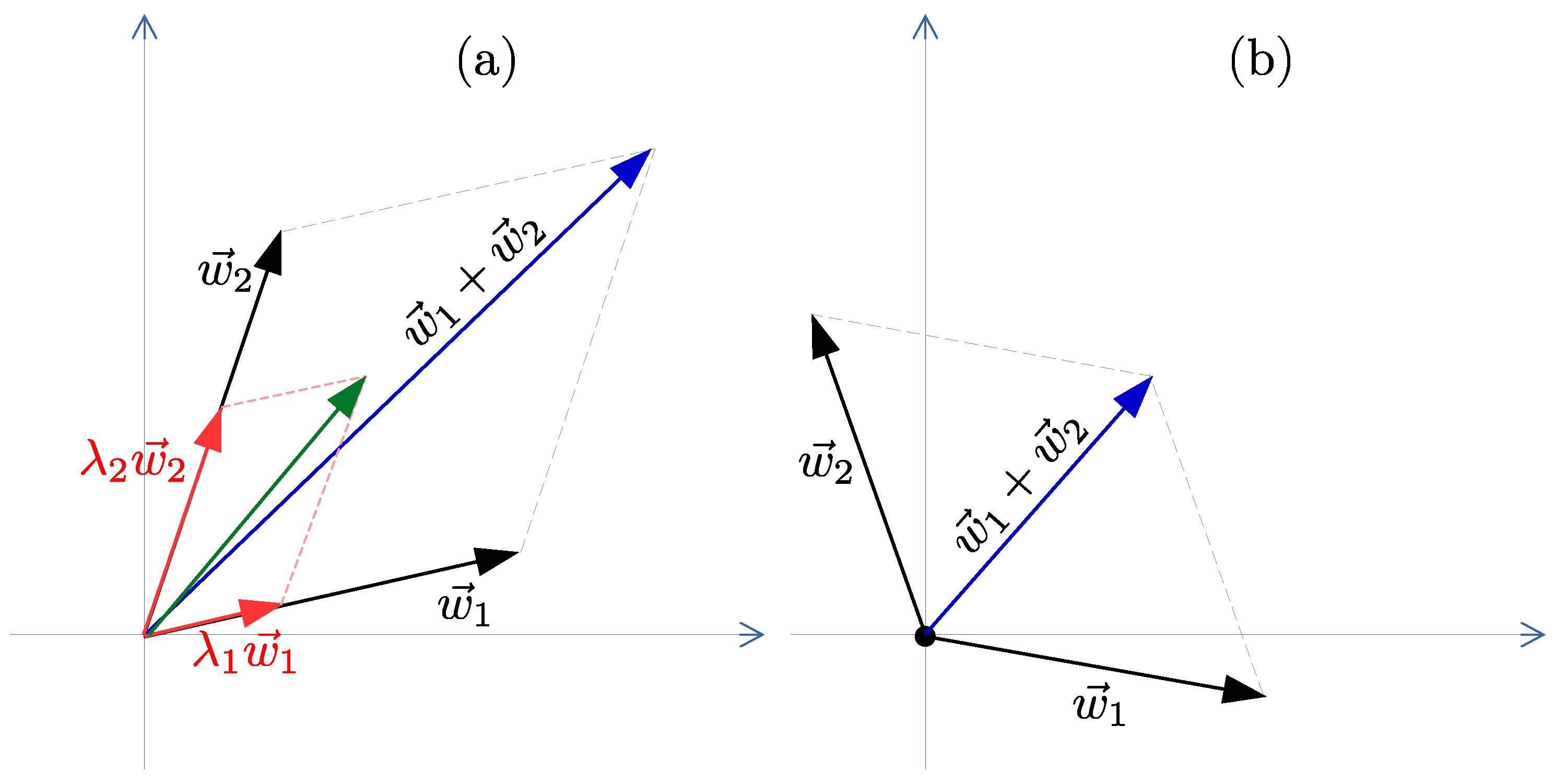
Figure 1, the basic idea of the ATMO optimizer proposed here is to combine two different known optimizers and automatically go quickly towards the direction of both on the surface of the loss function when the two optimizers agree (see geometric example in
Figure 2a). When the two optimizers used in the combination do not agree, our solution always goes towards the predominant direction between the two but slowing down the speed (see example of
Figure 2b).
In the literature, there are many papers that compare neural models trained with the use of different optimizers [
5,
6,
7,
8] or that propose modifications for existing optimizers [
4,
9,
10], always aimed at improving the results on a subset of problems. Each paper demonstrates that an optimizer is better than the others, but as the problem changes, this type of result is no longer valid and we have to start from scratch. Our method can be combined with other methods like Genetically Trained DNN [
11], which combines learning using gradient descent with genetic algorithms. The genetic part, after a selected number of epochs, selects a new population through three states called selection, crossover, and manipulation. In general, a Genetically Trained DNN is very different from our proposal, which combines two gradient descent methods together. However, the genetic method can also be used with ATMO.
In our paper, we propose combining two different optimizers like SGD and ADAM to overcome the performances of the single optimizers in very different problems.
Below are the main contributions of this paper:
We show experimentally that the combination of two different optimizers in a new meta-optimizer leads to a better generalization capacity in different contexts.
We describe ATMO using Adam and SGD but show experimentally that other types of optimizers can be profitably combined.
We release the source code and setups of the experiments [
12].
2. Related Work
In the literature, there are not many papers that try to combine different optimizers together. In this section, we report some of the more recent papers that in some ways use different optimizers in the same learning process.
In [
13], the authors investigate a hybrid strategy, called
SWATS (SWitching from Adam To Sgd), which starts training with an adaptive optimization method and switches to SGD when appropriate. This idea starts from the observation that despite superior training results, adaptive optimization methods such as ADAM generalize poorly compared to SGD because they tend to work well in the early part of the training but are overtaken by SGD in the later stages of training. In concrete terms, SWATS is a simple strategy that goes from Adam to SGD when an activation condition is met. The experimental results obtained in this paper are not so different from ADAM or SGD when used individually, so the authors concluded that using SGD with perfect parameters is the best idea. In our proposal, we want to combine two well-known optimizers to create a new one that simultaneously uses two different optimizers from the beginning to the end of the training process.
ESGD is a population-based Evolutionary Stochastic Gradient Descent framework for optimizing deep neural networks [
14]. In this approach, individuals in the population optimized with various SGD-based optimizers using distinct hyper-parameters are considered competing species in the context of coevolution. The authors experimented with optimizer pools consisting of SGD and ADAM variants, where it is often observed that ADAM tends to be aggressive early on but stabilizes quickly, while SGD starts slowly but can reach a better local minimum. ESGD can automatically choose the appropriate optimizers and their hyper-parameters based on the fitness value during the evolution process so that the merits of SGD and ADAM can be combined to seek a better local optimal solution to the problem of interest. In the method we propose, we do not need another approach, such as the evolutionary one, to decide which optimizer to use and with which hyper-parameters, but it is the same approach that decides the contribution of SGD and that of ADAM at each step.
In this paper, we also compare our ATMO optimizer with
ADAMW [
15,
16] (ADAM with decoupled Weight decay regularization), which is a version of ADAM in which weight decay is decoupled from
regularization. This optimizer offers good generalization performance, especially for text analysis, and since we also perform some experimental tests on text classification, then we also compare our optimizer with ADAMW. In fact, ADAMW is often used with BERT [
17] applied to well-known datasets for text classification.
Padam [
18] (Partially ADAM) is one of the recent Adam derivates that achieves very interesing results. It bridges the generalization gap for adaptive gradient methods by introduceing a partial adaptive parameter to control the level of adaptiveness of the optimization procedure. We principally use ATMO with a combination of ADAM and SGD, but we test the generalization of this method also by combining Padam and SGD [
12] to compare with many other optimizers (Table 1).
3. Preliminaries
Training neural networks is equivalent to solving the following optimization problem:
where
is a loss function and
w are the weights.
The iterations of an
SGD [
1] optimizer can be described as:
where
denotes the weights
w at the
k-th iteration,
denotes the learning rate, and
denotes the stochastic gradient calculated at
. To propose a stochastic gradient that is calculated as generically as possible, we introduce the
weight decay [
19] strategy, often used in many SGD implementations. The weight decay can be seen as a modification of the
gradient, and in particular, we describe it as follows:
where
is a small scalar called weight decay. We can observe that if the weight decay
is equal to zero; then
. Based on the above, we can generalize Equation (
2) to the following one that includes weight decay:
The SGD algorithm described up to here is usually used in combination with
momentum, and in this case, we refer to it as
SGD(M) [
20] (Stochastic Gradient Descend with Momentum). SGD(M) almost always works better and faster than SGD because the momentum helps accelerate the gradient vectors in the right direction, thus leading to faster convergence. The iterations of SGD(M) can be described as follows:
where
is the momentum parameter and for
,
is initialized to 0. The simpler methods of momentum have an associated
damping coefficient [
21], which controls the rate at which the momentum vector decays. The dampening coefficient changes the momentum as follows:
where
is the dampening value, so the final SGD with momentum and dampening coefficients can be seen as follows:
Nesterov momentum [
22] is an extension of the moment method that approximates the future position of the parameters that takes into account the movement. The SGD with nesterov transforms again the
of Equation (
5); more precisely:
The complete SGD algorithm, used in this paper, is shown in Algorithm 1.
| Algorithm 1 Stochastic Gradient Descent (SGD). |
Input: the weights , learing rate , weight decay , momentum , dampening d, boolean
function(, , , d, )
if then
if then
else
end if
if then
end if
end if
return
end function
for batches do
end for |
ADAM [
2] (ADAptive Moment estimation) optimization algorithm is an extension to SGD that has recently seen broader adoption for deep learning applications in computer vision and natural language processing. ADAM’s equation for updating the weights of a neural network by iterating over the training data can be represented as follows:
where
and
are estimates of the first moment (the mean) and the second moment (the non-centered variance) of the gradients respectively; hence the name of the method.
,
and
are three new introduced hyper-parameters of the algorithm.
AMSGrad [
23] is a stochastic optimization method that seeks to fix a convergence issue with Adam based optimizers. AMSGrad uses the maximum of past squared gradients
rather than the exponential average to update the parameters:
The complete ADAM algorithm used in this paper is shown in Algorithm 2.
| Algorithm 2 ADAptive Moment estimation (ADAM). |
Input: the weights , learing rate , weight decay , , , , boolean
function (,, , , , , )
if then
else
end if
return
end function
for batches do
end for |
4. Proposed Approach
In this section, we develop the proposed new optimization method called ATMO. Our goal is to propose a strategy that automatically combines the advantages of an adaptive method like ADAM with the advantages of SGD throughout the entire learning process. This strategy can by applied to every combination of optimizer, but we focused on ADAM and SGD combination. This combination of optimizers is summed, as shown in
Figure 2, where
and
represent the displacements on the ADAM and SGD on the surface of the loss function, while
represents the displacement obtained thanks to our optimizer. Below, we explain each line of the ATMO algorithm represented in Algorithm 3.
The ATMO optimizer has only two hyper-parameters which are and , used to balance the contribution of ADAM and SGD, respectively. It also uses all the hyper-parameters inherited from SGD and ADAM. In this paper, we assume the use of the most common implementation of gradient descent used in the field of deep learning, namely mini-batch gradient descent, which divides the training dataset into small batches that are used to calculate the model error and update the model coefficients . For each mini-batch, we calculate the contribution derived from the two components ADAM and SGD and then update all the coefficients as described in the three following subsections.
4.1. ADAM Component
The complete ADAM algorithm is defined in Algorithm 2. In order to use ADAM in our optimizer, we have extracted the
function, which calculates and returns the increments
for the coefficients
, as defined in Equation (
16).
Note that if the components of the two vectors and are not all equal, then the direction has changed with respect to the natural gradient.
The same
function also returns the new learning rate
defined in Equation (
17), useful when a variable learning rate is used. In this last case, ATMO uses
to calculate a new learning rate at each step.
Now, having
and
, we can directly modify the weights
exactly as done in the ADAM optimizer and described in Equation (
18).
4.2. SGD Component
As for the ADAM component, the SGD component, defined in Algorithm 1, has also been divided into two parts: the
function, which returns the increment to be given to the weight
, and the formula to update the weights as defined in Equation (
10). The
value returned by the
function is exactly the value defined in Equation (
9), which we use directly for our ATMO optimizer.
4.3. The ATMO Optimizer
The proposed approach can be summarized as follows:
where
is a scalar for the SGD component and
is another scalar for the ADAM component used for balancing the two contributions of the two optimizers.
is the learning rate of the proposed ATMO optimizer, while
is the learning rate of ADAM defined in Equation (
17).
and
are the two increments define in Equations (
16) and (
9), respectively.
Equation (
18) can be expanded in the following Equation (
19) to make explicit what elements are involved in the weights update step used by our ATMO optimizer.
where
and
are two parameters of the ADAM optimizer,
is defined in Equation (
12), and
is defined in Equation (
11).
The ATMO algorithm can be easily implemented by the following pseudo code defined in Algorithm 3 and by calling the two functions
defined in Algorithm 2 and
defined in Algorithm 1. We can also show that convergence is guaranteed for the ATMO optimizer if we assume that convergence has been guaranteed for the two optimizers SGD and ADAM.
| Algorithm 3 ATMO on mixing ADAM and SGD. |
Input: the weights , , , learing rate , weight decay , other SGD and ADAM
parameters …
for batches do
end for |
Theorem 1. (ATMO Cauchy necessary convergence condition). If ADAM and SGD are two optimizers whose convergence is guaranteed, then the Cauchy necessary convergence condition is also true for ATMO.
Proof. Under the conditions in which the convergence of ADAM and SGD is guaranteed [
23,
24], we can say that
and
converge at
∞. That implies the following:
We can observe that
, so we can obtain the following:
The thesis is that
respects the Cauchy necessary convergence condition, so:
and for Equation (
21), this last equality is trivially true:
□
Theorem 2. (ATMO convergence) If for it is valid that and where and are two finite real values, then .
Proof. We can write ATMO series as:
This can be rewritten for
as:
□
This last theorem does not exclude the possibility that ATMO converges even if ADAM or SGD or both do not converge, for example, due to some unsuitable parameters. In this paper, this aspect is not proven.
4.4. Geometric Explanation
We can see optimizers as two explorers
and
who want to explore an environment (the surface of a loss function). If the two explorers agree to go in a similar direction, then they quickly go in that direction (
). Otherwise, if they disagree and each prefers a different direction than the other, then they proceed more cautiously and slower (
). As we can see in
Figure 2a, if the directions of the displacement of
and
are similar then the amplitude of the resulting new displacement
is increased, however, as shown in
Figure 2b, if the directions of the two displacements
and
are not similar, then the amplitude of the new displacement
us decreased.
In our approach, the sum
is weighted (see red vectors in
Figure 2a), so one of the two optimizers SGD or ADAM can become more relevant than the other in the choice of direction for ATMO; hence, the direction resultant may tend towards one of the two. In ATMO, we set the weight of the two contributions so as to have a sum
in order to maintain a learning rate of the same order of magnitude.
Another important component that greatly affects the ATMO shift module at each training step is its learning rate, defined in Equation (
18), which combines
and
. The shifts are scaled using the learning rate, so there is a situation where ATMO gets more thrust than the ADAM and SGD starting shifts. In particular, we can imagine that the displacement vector of ADAM has a greater magnitude than SGD and the learning rate of SGD is greater than that of ADAM. In this case, the ATMO shift has a greater vector magnitude than SGD and a higher ADAM learning rate, which can cause a large increase in the ATMO shift towards the search of a minimum.
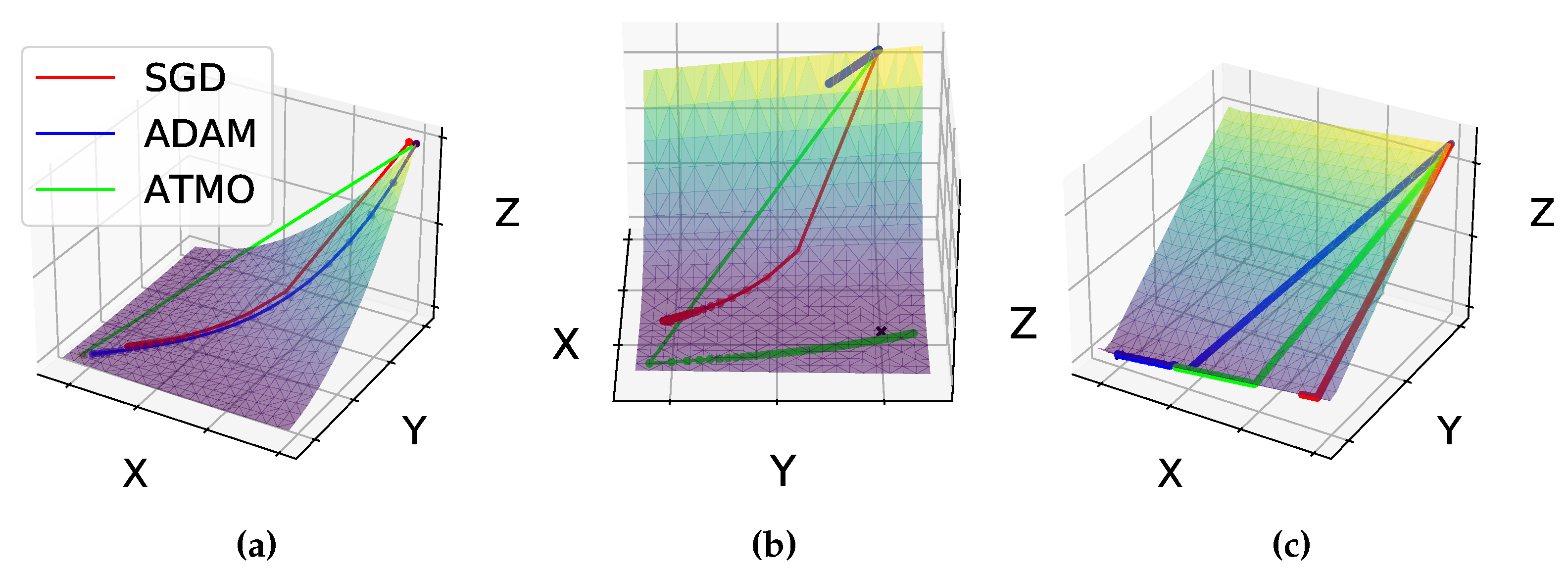
4.5. Toy Examples
To better understand our proposal, we built a toy example where we highlight the main behaviour of ATMO. The toy examples, even if they are not a true example of a deep learning model, can be easily visualized because the exploration surface can be plotted in three dimensions.
More precisely, we consider the following example:
We set
,
,
,
, dampening
,
and
. As we can see in
Figure 3a, our ATMO optimizer goes faster towards the minimum value after only two epochs, and SGD is fast at the first epoch; however, it decreases its speed soon after and comes close to the minimum after 100 epochs, and ADAM instead reaches its minimum after 25 epochs. Our approach can be fast when it gets a large
from SGD and a large
from ADAM.
Another toy example can be done with the benchmark Rosenbrook [
25] function:
We set
and
, weight
and weight
,
,
, and default parameter for ADAM and SGD. The ATMO optimizer sets
. The comparative result for the minimization of this function is shown in
Figure 3b. In this experiment, we can see how, by combining the two optimizers ADAM and SGD, we can obtain a better result than the single optimizers. For this function, going from the starting point towards the direction of the maximum slope means moving away from the minimum, and therefore it takes many training epochs to approach the minimum.
Let us use a final toy example to highlight the behavior of the ATMO optimizer. In this case we look for the minimum of the function
. We set the weights
and
,
,
and use all the default parameters for ADAM and SGD. ATMO assigns the same value
for the two lambdas hyper-parameters. In
Figure 3b, we can see how not all the paths between the paths of ADAM and SGD are the best choice. Since ATMO, as shown in
Figure 2, goes towards an average direction with respect to that of ADAM and SGD, then in this case ADAM arrives first at the minimum point.
4.6. Dynamic
To avoid selecting the best two lambdas of Equation (
18) for each experiment, we introduce an approach that automatically changes the two lambdas during training. Motivated by experiments showing how selecting the correct lambdas can greatly affect the results, we studied a solution to avoid having to find the best two hyper-parameters for each experiment. In fact, experiments show that ADAM is usually better than SGD at the beginning of training while SGD performs better in the final phase [
14] (see also the example in
Figure 4). Following the idea of SWAT [
13] to hard-switch from an optimizer to another, we introduce an approach that linearly changes the two lambdas from
,
to
,
, in order to exploit the peculiarities of ADAM and SGD. This approach changes the two hyper-parameters at each epoch, and in particular we have
with
, where
P is the maximum number of epochs and
is the current epoch.
5. Datasets
In this section, we briefly describe the datasets used in the experimental phase.
The
Cifar10 [
26] dataset consists of 60,000 images divided into 10 classes (6000 per class) with a training set size and test set size of 50,000 and 10,000, respectively. Each input sample is a low-resolution color image of size
. The 10 classes are airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks.
The
Cifar100 [
26] dataset consist of 60,000 images divided into 100 classes (600 per classes) with a training set size and test set size of 50,000 and 10,000, respectively. Each input sample is a
colour image with a low resolution.
The
Corpus of Linguistic Acceptability (CoLA) [
27] is another dataset that contains 9594 sentences belonging to training and validation sets and excludes 1063 sentences belonging to a set of tests kept out. In our experiment, we only used the training and test sets.
The
AG’s news corpus [
28,
29] is the last dataset used in our experiments. It is a dataset that contains news articles from the web subdivided into four classes. It has 30,000 training samples and 1900 test samples.
6. Experiments
The optimizer ATMO proposed is a generic solution not oriented exclusively to image analysis, so we conducted experiments on both image classification and text document classification. By doing so, we are able to give a clear indication of the behavior of the proposed optimizer in different contexts, also bearing in mind that many problems, such as audio recognition, can be traced back to image analysis. In all the experiments, unless differently specified, , , , , dampening , and a batch size near to the maximum our hardware can support. The hyper-parameters are set to obtain good results without trying to maximize accurac; this is because if the loss function is the same, all well-set optimizers find the same minimum in the long run.
In
Table 1, we apply Dynamic ATMO method by combining Padam [
18] with SGD to compare it with other recently proposed solutions, and it shows that many other optimizers can be combined with our proposed method. In this experiment,
for Padam changes from 1 to 0 in the first 100 epochs. We trained ATMO for 200 epochs in total with
, which is multiplied by 0.1 at epoch 100 and 150 and
,
. The partial adaptive parameter for Padam was set to
.
6.1. Experiments with Images
In this first group of experiments, we used two well-known image datasets for: (1) conducting an analysis of the two main parameters of ATMO,
and
; (2) comparing the performance of ATMO with respect to the two starting optimizers SGD and ADAM; (3) analyzing the behavior of ATMO with different neural models. The datasets used in this first group of experiments are Cifar10 and Cifar100, and and the results are summarized in
Table 2 and
Table 3. The neural models we compared are Resnet18 and Resnet34 [
30,
31]. For each model, we used, respectively, 1024 and 512 as batch size. We analyzed different values of
and
and also Dynamic ATMO.
For both Cifar10 and Cifar100 experiments, we used the following parameters: 350 epoch, Momentum 0.95, weight decay 0.0005 and learning rate 0.001, with Cosine Annealing for learning rate reduction. We performed simple data augmentation with random horizontal flip and random crops. Dynamic ATMO linearly changes the optimizer lambda from , and , .
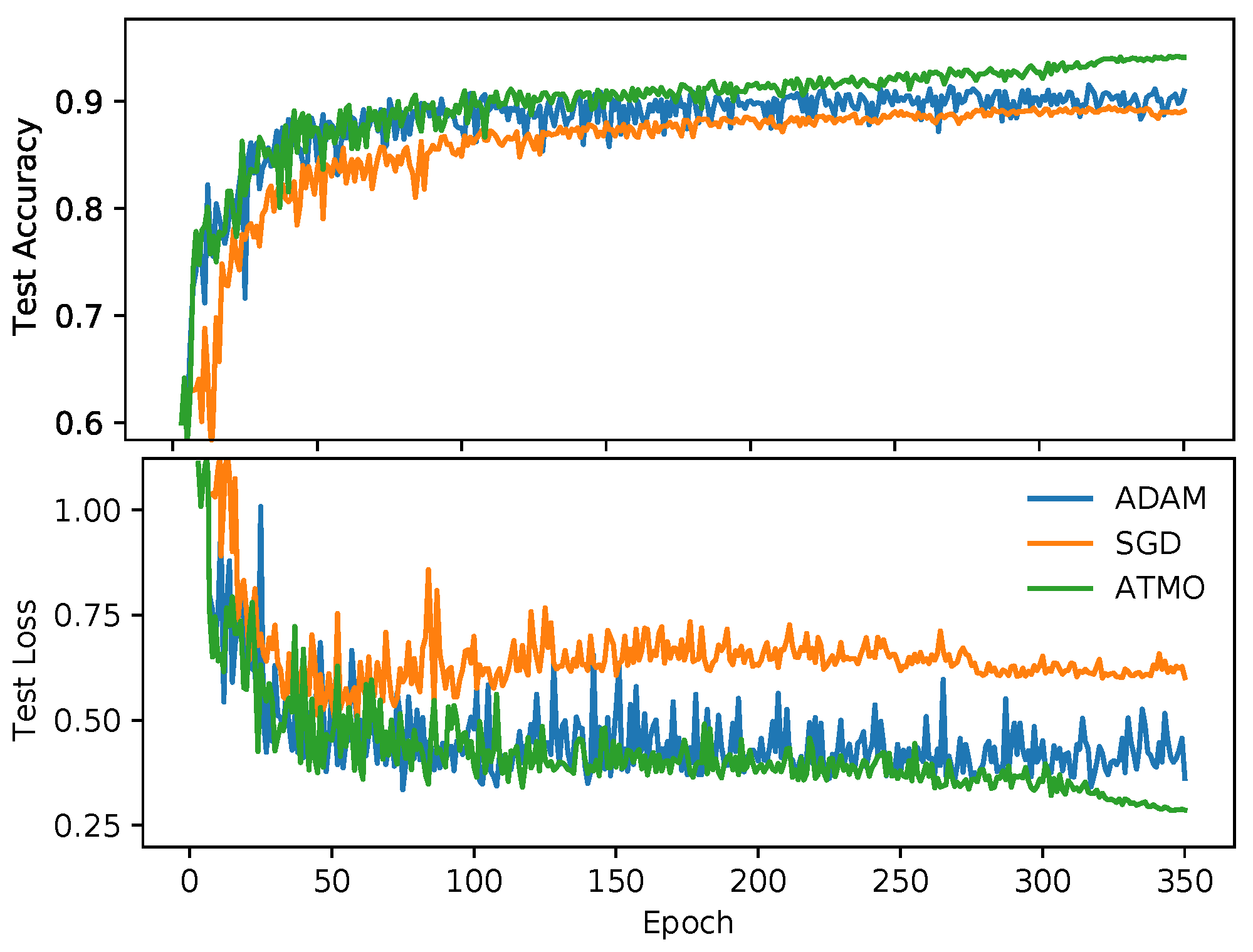
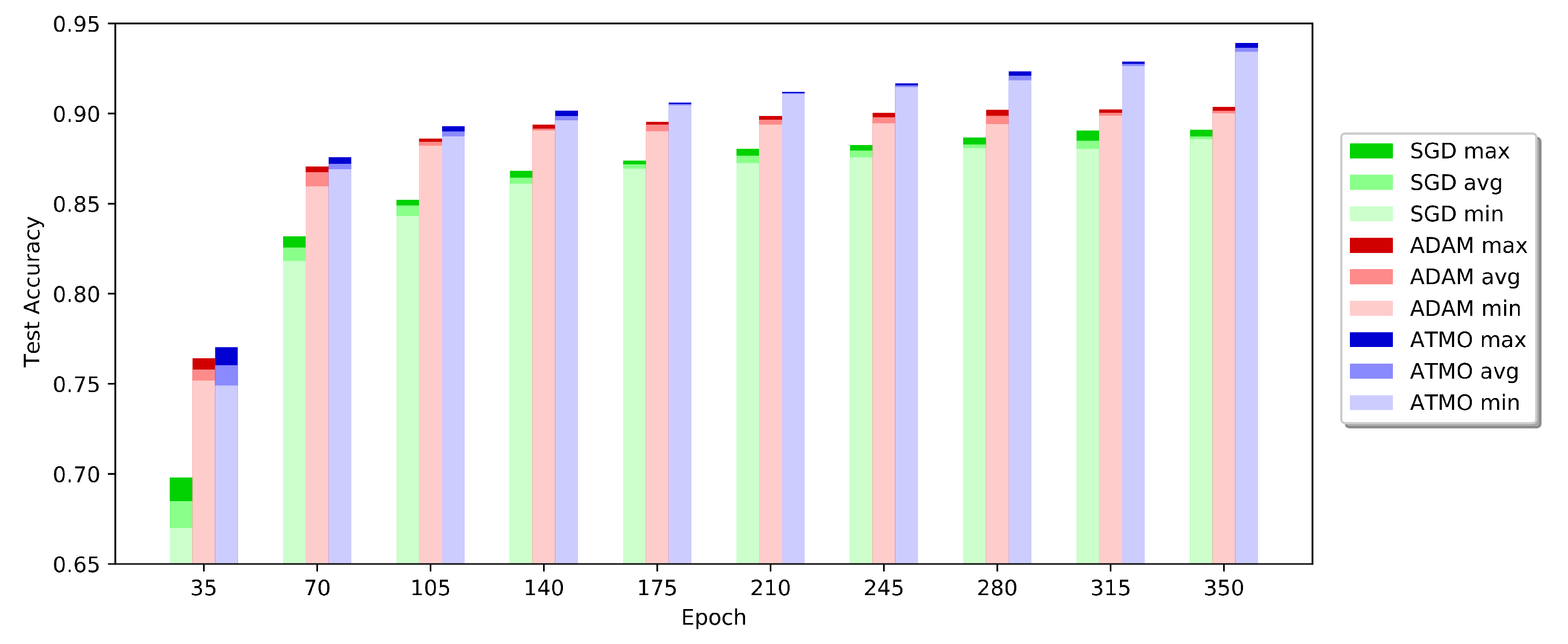
To better understand what happens during the training phase, in
Figure 4, we represent the accuracy of the test and the corresponding loss values of the experiments that produced the best results with Resnet18 on Cifar10. We can see also the effectivenes of Dynamic ATMO without epoch noise in
Figure 5. As we can see in the first part of training, ADAM has a good growth, so Dynamic ATMO inherits this trend. As we can see, Dynamic ATMO overcomse others optimizers because it has the convergence speed of ADAM in the early stages of the learning process, while in the late stage, it benefits more and more from SGD. Therefore, in general, we can say that the ATMO optimizer leads to better generalization than the other optimizers used. In addition, looking at the results obtained with the Resnet34, we can say that all configuration of ATMO exceeds the average and the maximum accuracies of SGD and ADAM.
In conclusion, as we have seen from the results shown in
Table 2 and
Table 3, the proposed method leads to a better generalization than the other optimizers used in each experiment. We get better results both by setting
and
well, and also even when we do not use the best set of parameters.
6.2. Experiments with Text Documents
In this last group of experiments, we used the two datasets of text documents: CoLA and AG’s News. As a neural model, we used a model based on BERT [
17], which is one of the best techniques for working with text documents. To run fewer epochs, we used a pre-trained version [
32] of BERT. In these experiments, we also introduced the comparison with the AdamW optimizer, which is usually the optimizer used in BERT-based models.
For the CoLA dataset, we set
, momentum
, and batch size equal to 100. We ran the experiments five times for 50 epochs. For the AG’s News dataset, we set the same parameters used for CoLA, but we only ran it for 10 epochs because it achieved good results in the firsts epochs and also because the dataset was very large and therefore took more time. In these experiments with text analysis, we did not use the Dynamic ATMO approach because we used a very small number of epochs. We can see all the results in
Table 4. Even for text analysis problems, we can confirm the results of the experiments done on images: although AdamW sometimes has better performances than ADAM, ATMO performs better.
6.3. Time Analysis
We also provide a study about the average computational time of ATMO compared with other optimizers. We computed the mean computational time for one epoch in seconds. The experiments were conducted on different datasets as well as different neural models. We conducted all the experiments on a Nvidia 1080 with 8 GB of RAM.
We report the results in
Table 5. Considering each row of the table, we can conclude that the computation time is almost the same for all optimizers, and the differences depend on the operating system overhead. We can therefore conclude that our approach does not add computation time overhead.
7. Conclusions
In this paper, we introduced ATMO (AdapTive Meta Optimizer), which is a new combined optimization method that combines the capability of two different optimizers into one. We demonstrated through experiments that our ATMO meta-optimizer can outperform the performance of individual optimizers introducing a negligible time complexity. To balance the contribution of the optimizers used within ATMO, we introduced two new hyperparameters , and showed experimentally that, using ADAM and SGD, the combination of these two hyperparameters can be set automatically without having to manually configure them. In the present work, we also tried to combine different optimizers such as Padam and SGD, obtaining also in this case the best accuracy compared to the accuracies present in the literature.
Author Contributions
Conceptualization, N.L. and R.L.G.; methodology, N.L., I.G. and R.L.G.; software, N.L.; validation, N.L., I.G. and R.L.G.; formal analysis, N.L., I.G. and R.L.G.; resources, N.L. and R.L.G.; writing—original draft preparation, N.L. and I.G.; writing—review and editing, N.L. and I.G.; visualization, N.L. and R.L.G.; supervision, N.L. and I.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zaheer, M.; Reddi, S.; Sachan, D.; Kale, S.; Kumar, S. Adaptive methods for nonconvex optimization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; pp. 9793–9803. [Google Scholar]
- Luo, L.; Xiong, Y.; Liu, Y.; Sun, X. Adaptive Gradient Methods with Dynamic Bound of Learning Rate. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bera, S.; Shrivastava, V.K. Analysis of various optimizers on deep convolutional neural network model in the application of hyperspectral remote sensing image classification. Int. J. Remote Sens. 2020, 41, 2664–2683. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. Adadelta: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Kobayashi, T. SCW-SGD: Stochastically Confidence-Weighted SGD. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 1746–1750. [Google Scholar]
- Zhang, Z. Improved adam optimizer for deep neural networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar]
- Pawełczyk, K.; Kawulok, M.; Nalepa, J. Genetically-trained deep neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 63–64. [Google Scholar]
- Landro Nicola, G.I.; Riccardo, L.G. Mixing ADAM and SGD: A Combined Optimization Method with Pytorch. 2020. Available online: https://gitlab.com/nicolalandro/multi_optimizer (accessed on 18 June 2021).
- Keskar, N.S.; Socher, R. Improving generalization performance by switching from adam to sgd. arXiv 2017, arXiv:1712.07628. [Google Scholar]
- Cui, X.; Zhang, W.; Tüske, Z.; Picheny, M. Evolutionary stochastic gradient descent for optimization of deep neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; pp. 6048–6058. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Loshchilov, I.; Hutter, F. Fixing Weight Decay Regularization in Adam. 2018. Available online: https://openreview.net/forum?id=rk6qdGgCZ (accessed on 18 June 2020).
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Chen, J.; Zhou, D.; Tang, Y.; Yang, Z.; Gu, Q. Closing the generalization gap of adaptive gradient methods in training deep neural networks. arXiv 2018, arXiv:1806.06763. [Google Scholar]
- Krogh, A.; Hertz, J.A. A simple weight decay can improve generalization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1992; pp. 950–957. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Damaskinos, G.; Mhamdi, E.M.E.; Guerraoui, R.; Patra, R.; Taziki, M. Asynchronous Byzantine machine learning (the case of SGD). arXiv 2018, arXiv:1802.07928. [Google Scholar]
- Liu, C.; Belkin, M. Accelerating SGD with momentum for over-parameterized learning. arXiv 2018, arXiv:1810.13395. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. arXiv 2019, arXiv:1904.09237. [Google Scholar]
- Lee, J.D.; Simchowitz, M.; Jordan, M.I.; Recht, B. Gradient descent only converges to minimizers. In Proceedings of the Conference on Learning Theory, New York, NY, USA, 23–26 June 2016; pp. 1246–1257. [Google Scholar]
- Rosenbrock, H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Citeseer: University Park, PA, USA, 2009. [Google Scholar]
- Warstadt, A.; Singh, A.; Bowman, S.R. Neural Network Acceptability Judgments. arXiv 2018, arXiv:1805.12471. [Google Scholar] [CrossRef]
- Gulli, A. AG’s Corpus of News Articles. 2005. Available online: http://groups.di.unipi.it/~gulli/\AG_corpus_of_news_articles.html (accessed on 15 October 2020).
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 649–657. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Targ, S.; Almeida, D.; Lyman, K. Resnet in resnet: Generalizing residual architectures. arXiv 2016, arXiv:1603.08029. [Google Scholar]
- Huggingface.co. Bert Base Uncased Pre-Trained Model. Available online: https://huggingface.co/bert-base-uncased (accessed on 15 October 2020).
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).