1. Introduction
Testing statistical hypotheses is a main branch of inferential statistics (see [
1]). A statistical hypothesis is an assertion about a parameter of the probability distribution of a random variable.
After the introduction of the notion of fuzzy sets by Zadeh [
2], many approaches have been proposed for fuzzy hypothesis testing, using fuzzy set theory (see [
3]).
The problem of testing hypotheses with fuzzy data was analyzed for the first time in [
4] and in the sequel in [
5,
6], where the author extended both Neyman–Pearson and Bayes theories to this framework (in [
5]) and worked on the same problem in the context of fuzzy decision problems (in [
6]).
Fuzzy hypothesis testing with crisp data is presented in [
7] in the sense of Neyman–Pearson, using the extension principle and
-cuts, where fuzzy critical regions are introduced, leading to a fuzzy conclusion, as well as in [
8,
9], where the author provides new definitions for the probability of type I and type II errors and presented the best test for the one-parameter exponential family. The problem of testing fuzzy hypotheses when the observations are crisp is also studied in [
10], where the authors give new definitions for the probability of type I and type II errors and prove a version of the Neyman–Pearson Lemma. They also study the problem of testing hypotheses from a Bayesian point of view for which the observations are ordinary and the hypotheses are fuzzy (see [
11]).
In [
12], testing hypotheses about the mean of a fuzzy random variable is introduced. This approach is applicable to practical situations where either the observed data or the hypotheses are fuzzy (formalized in linguistic terms). These fuzzy tests result in a fuzzy decision for the acceptance or rejection of the null hypotheses with a degree of confidence between 0 and 1. They are generalizations of the classical tests, so that they are reduced to the classical tests if both the data and the parameters are crisp. Fuzzy hypothesis tests are also developed in [
13,
14,
15] for cases in which the available data are fuzzy and in [
16], where the authors propose fuzzy hypothesis testing for a proportion with crisp data as the exact generalized one-tailed hypergeometric test with fuzzy hypotheses. Fuzzy hypothesis testing in the framework of the randomized and non-randomized hypergeometric test for a proportion is presented in [
17].
In [
18], the fuzzy
p-value concept is used for testing hypotheses with fuzzy data and in [
19] it is generalized on the basis of Zadeh’s probability measure of fuzzy events [
2] for testing fuzzy hypotheses with crisp data. In [
20], a fuzzy
p-value is obtained, using fuzzy test statistics constructed by fuzzy estimators for cases in which both the data and the hypotheses are crisp.
Two different ways of making inference from set-valued data are presented in [
21]. A detailed review on possibilistic interpretations of statistical tests (where hypotheses and/or data are fuzzy) and statistical decisions is presented in [
22,
23] and a comprehensive review with regard to statistical properties of different approaches for calculating fuzzy
p-values, in [
24].
In [
25], the authors demonstrate how to accomplish a fuzzy test with fuzzy data and fuzzy formulated hypotheses and discuss the defuzzification of fuzzy test decisions by means of the signed distance method. In [
26], the author reviews and compares the R packages “FPV” and “Fuzzy.p.value” for hypothesis testing in fuzzy environments by using the fuzzy
p-value for decision making.
In [
27], the authors systematically review the literature, identifying papers proposing advances in fuzzy hypothesis testing and its applications. Then, they look at each contained paper through the lens of the key research questions.
In [
28,
29], fuzzy hypotheses testing is developed for cases in which both the data and the hypotheses are crisp. This approach uses fuzzy critical values and fuzzy test statistics constructed by fuzzy estimators produced by a set of confidence intervals. So, the null hypothesis
is rejected or not at a certain significance level, comparing a fuzzy statistic
constructed by a proper fuzzy estimator with fuzzy critical values
, created using probabilistic concepts. In [
30], this approach is generalized using fuzzy statistics produced by non asymptotic fuzzy estimators (see [
31]) and a degree of rejection or acceptance of the null hypothesis.
As it is proved in [
32], the possibility distribution (see [
2]) induced by confidence intervals around the mode is identical to the one obtained by the maximal specificity probability–possibility transformation. Based on this principle, we develop in this paper possibilistic fuzzy statistical tests of crisp hypotheses, which lead to a possibility of rejection or acceptance of the null hypothesis for cases in which both the hypothesis and the data are crisp, whereas the other fuzzy tests (for example, those of [
12]) give crisp results when applied in such cases.
This paper is organized as follows. The next section is concerned with classical hypotheses testing. In
Section 3, we present the concept of fuzzy estimators and, also, find out that in the examples of [
29,
33,
34,
35], the unbiased fuzzy estimator of the variance
introduced in [
29] is not implemented as described there and propose its correct implementation. In
Section 4, we develop possibilistic hypothesis tests for cases in which both the data and the hypotheses are crisp. In
Section 5,
Section 6 and
Section 7, we present fuzzy hypothesis tests about the mean and the variance, and compare their results as well as the results of the respective tests developed in [
29,
30] with those of crisp statistics (Examples 2 and 3).
2. Classical Hypothesis Testing
In classical crisp statistics, the problem of testing a hypothesis for a parameter
of the distribution of a random variable
X is deciding whether to reject or accept the null hypothesis
at a significance level
against the alternative hypothesis
from a random sample of observations of
X, using a test statistic
U, which is evaluated for the sample observations, resulting in a value
u. The space of possible values of
U is decomposed into a rejection region and its complement, the acceptance region [
1]. Depending on the alternative hypothesis
, the rejection region has one of the following forms:
(a)
, if the alternative hypothesis is
(one sided test from the right), where the following is true:
(b)
, if the alternative hypothesis is
(one sided test from the left), where the following is true:
(c)
, if the alternative hypothesis is
(two sided test), where the following is true:
and
are the critical values of the test, which are determined by the distribution of
U. So,
is rejected if the value
u of the test statistic
U is in the rejection region and not rejected if
u is in the acceptance region.
If the value
u of the test statistic of a hypothesis test is close to its critical value, then the crisp test is unstable since a very small change in the sample may lead from rejection to no rejection of
or vice-versa, as shown in Example 1. Using a degree of rejection or acceptance of
(see [
30]) the above problem is eliminated.
3. Fuzzy Estimation
The estimation of a parameter of the probability density function (or probability function of a discrete random variable) of a distribution is one of the main purposes of inferential statistics.
Let
X be a random variable with probability density function (or probability function for a discrete random variable)
, where
is nan unknown parameter, which has to be estimated from a random sample of observations
of
X. For the estimation of
, a statistic
U is used (estimator of
), which is a function of
. For a specific sample where
are the observed values of
, a point estimator
for
is obtained, which is not of high interest since the probability of this being the required value of
is zero. A way to estimate
in the crisp statistics is to find a
confidence interval for
in which the value of
can be found with probability
. We use
here since
, usually employed for confidence intervals, is reserved for
-cuts of fuzzy numbers. Usually,
or
or
or
or
for
,
,
,
or
confidence intervals. Starting arbitrarily with
(we could begin with
or
, etc.) and using
as the
confidence interval, we have the following confidence intervals:
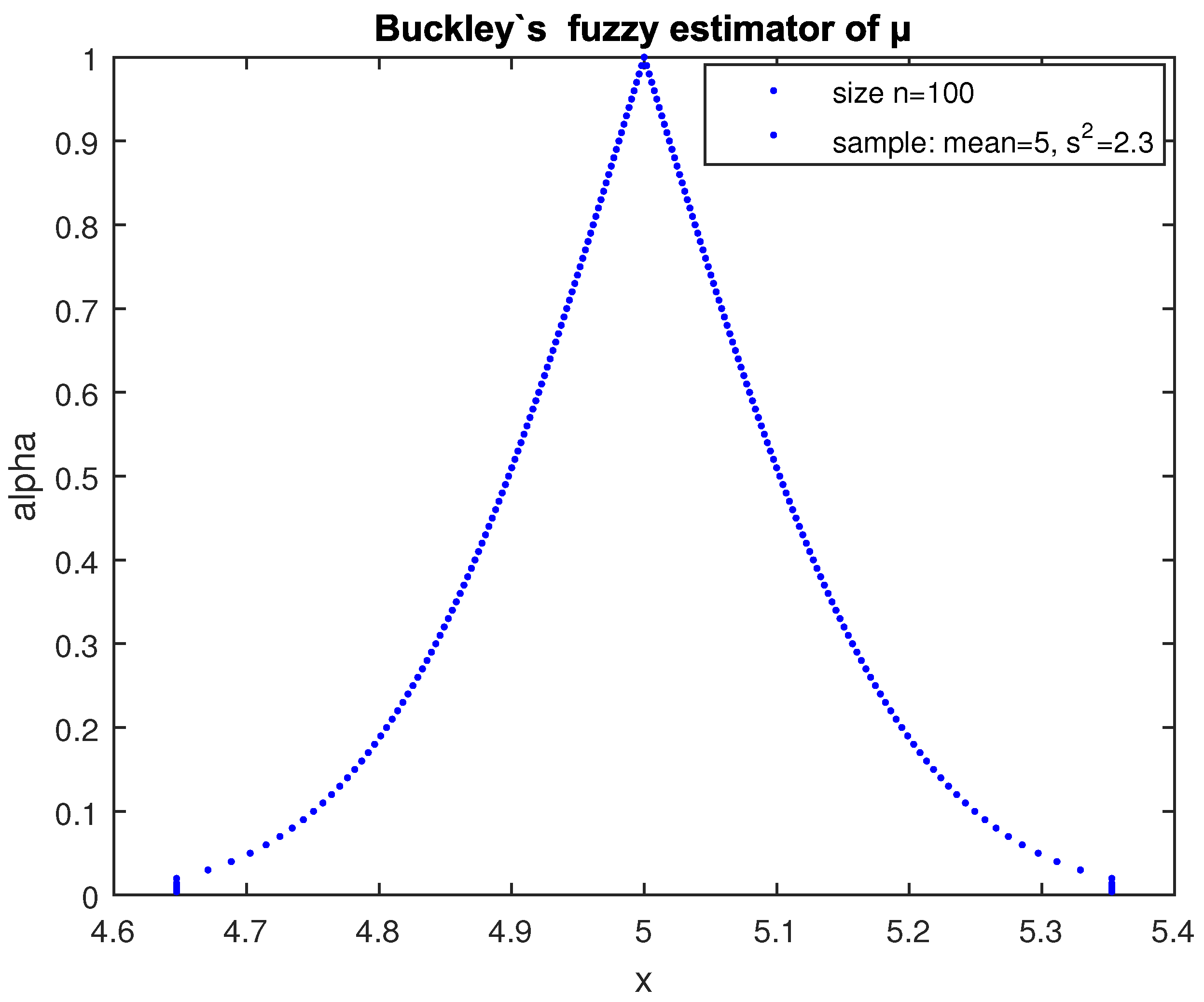
Among other methods, a fuzzy estimation method is proposed in [
29], according to which by placing all the above confidence intervals one on the top of the other, a triangular shaped fuzzy number
is constructed, the
cuts of which are the confidence intervals:
To finish the “bottom” of
in order to make it a complete fuzzy number, one needs to drop its graph straight down to complete its
cuts (see
Figure 1). So, a fuzzy estimator
of
is produced from a given sample, the possibility distribution of which are the confidence intervals of
The fuzzy estimator produced in this way contains much more information than just a single interval estimate.
For the construction of test statistics used in fuzzy hypothesis testing about an unknown parameter
, we use the fuzzy estimator
, the
-cuts of the possibility distribution of which are the confidence intervals of
since, as proved in [
32], this possibility distribution is identical to the one obtained by the maximal specificity probability–possibility transformation. In order to easily handle the possibility representation, especially for further computations, the possibility distribution is restricted to the interval that corresponds to the largest
confidence interval for the considered probability distribution (see [
32]).
3.1. Estimation of the Mean of a Normal Variable with Known Variance
If the random variable
X follows normal distribution with known variance
, then the
confidence interval of the mean
of
X derived from a random sample of observations of
X of size
n and sample mean
is [
1].
where
and
, the inverse distribution function of the standard normal distribution. So according to (6), the
-cuts of the possibility distribution of the fuzzy estimator
of mean are as follows (see [
29,
30]):
where
Implementing (7), we get the fuzzy estimator
of
Figure 2.
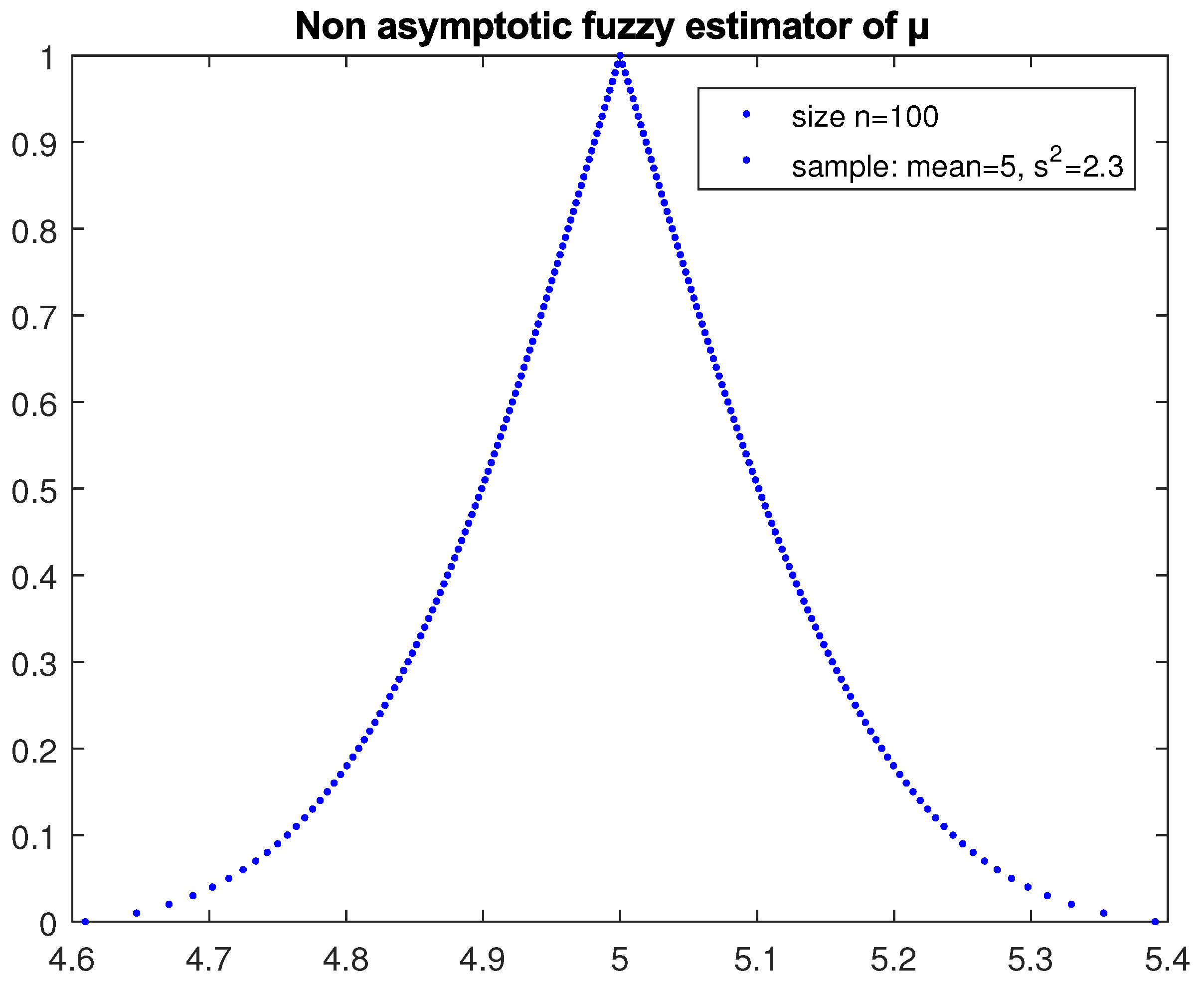
3.2. Estimation of the Mean of a Random Variable from a Large Sample (with Unknown Variance)
If the random variable
X follows any distribution, then, according to the central limit theorem (see [
1]), the
confidence interval of the mean
of
X derived from a random sample of observations of
X of large size
n (
) with sample mean and variance
and
is given by (6), substituting
with
s. So according to (5), the
-cuts of the possibility distribution of the fuzzy estimator
of the mean are as follows:
where
is given by (8).
3.3. Estimation of the Variance of a Normal Variable
If the random variable
X follows normal distribution, then the
confidence interval of the variance
of
X derived from a random sample of observations of
X of size
n and sample variance
is as follows [
1]:
where (
the inverse distribution function of the
distribution)
So according to (5), the
-cuts of the possibility distribution of the fuzzy estimator of the variance
are as follows:
Therefore, the
-cuts of the fuzzy estimator of the standard deviation
of
X are as follows:
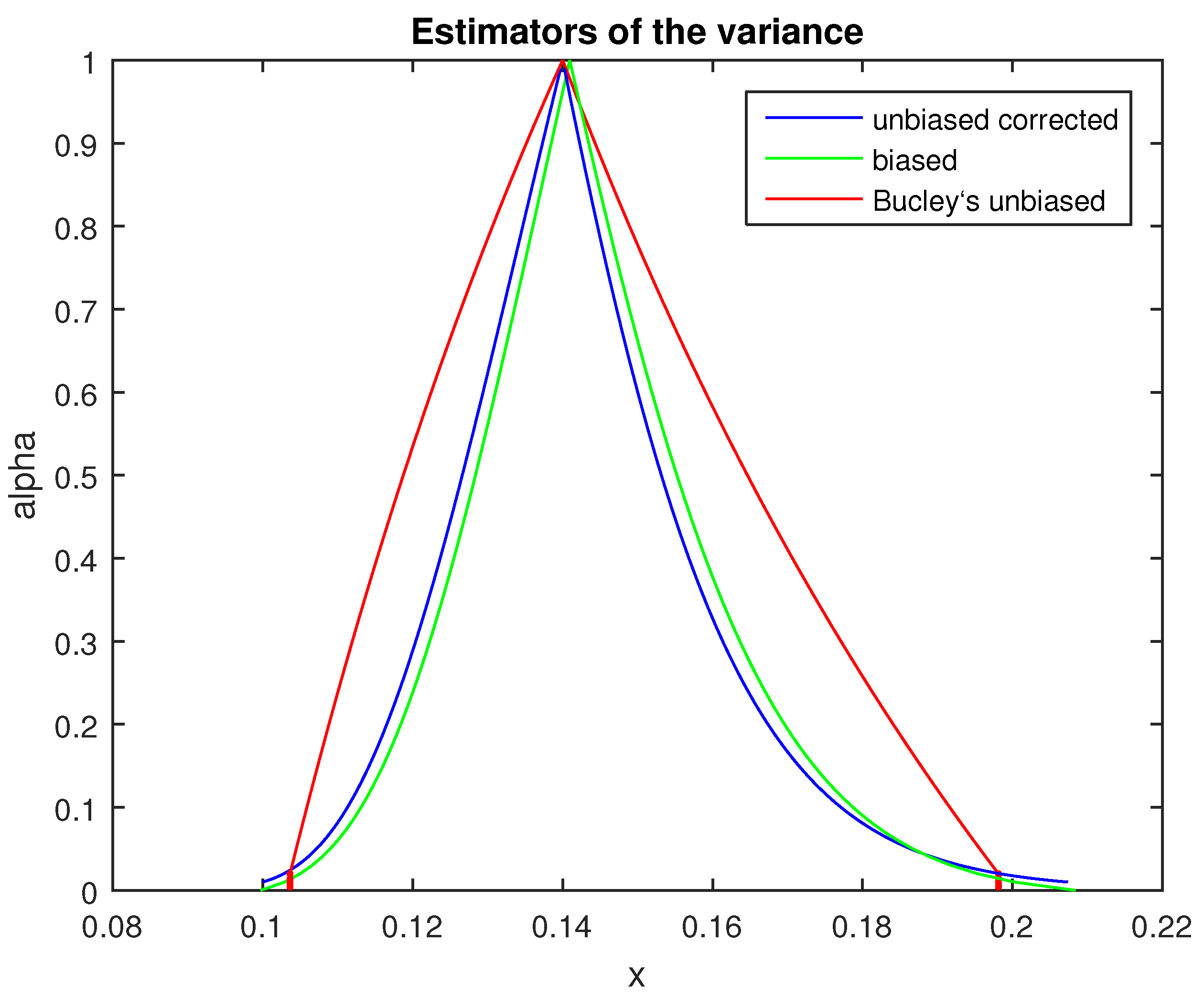
It can be shown that the above fuzzy estimator is biased because its core is not at . A fuzzy estimator of a parameter is defined as biased if its core is not at the crisp point estimator of the parameter.
In [
29], an unbiased fuzzy estimator
of the variance
of a normal random variable is obtained from a sample of size
n and variance
by putting one above the other for the following confidence intervals:
where
and (
the inverse distribution function of the
distribution)
For a value of
, the corresponding value of
is as follows [
29]:
where
the probability density function of the
distribution. The range of this one to one and onto function is
. So, the
cuts of the correct unbiased fuzzy estimator
are as follows:
where the function
and its inverse
(it gives
as a function of
) are implemented numerically.
In the implementation of
of [
29], the
-cuts defined by (14) (instead of its
-cuts of (18)) are used for the construction of
and the statistics generated by it.
As illustrated in
Figure 3, the shape of the correct implementation (18) of
is significantly different than the shape of its implementation used in [
29] and quite similar to the shape of the biased estimator
.
4. Possibilistic Statistical Tests of Crisp Hypotheses
We denote by 1 the rejection and by 0 the acceptance of a hypothesis
for a parameter
of the distribution of a random variable
X from a sample of
n observations
of
X. Hence, a possibilistic test of a crisp hypothesis
with alternative
is a decision rule, defined as two functions:
, which gives the degree in which the observed value
u of the test statistic
U belongs to the rejection region (see
Section 1) (the possibility of the proposition “
u is in the rejection region”), and
, which gives the degree in which the observed value
u of the test statistic
U belongs to the acceptance region (see
Section 1) (the possibility of the proposition “
u is in the acceptance region”).
Using the fuzzy estimator
of
(see
Section 2) and interval arithmetics, we derive the
-cuts of the possibility distribution
of the respective fuzzy test statistic
. So, the possibilities of rejection or acceptance of
are as follows:
(a) For
one sided test from the right (alternative hypothesis
), the possibility of rejection of
is equal to the Necessity of Strict Dominance index (see [
23,
36]).
which represents the necessity that the fuzzy set
strictly dominates the fuzzy set of the right critical value
, the membership function of which is as follows:
where
is the critical value of the one sided from the right, defined in (1). So if the core of
is at the right of
, (19) gives the following:
where
is the left part of the possibility distribution
and
is the ordinate of the point of intersection of
with the vertical at
.
The possibility of acceptance of
is as follows:
which represents the necessity that the fuzzy set
strictly dominates the fuzzy set of
. So if the core of
is at the left of
, (22) gives the following:
where
is the right part of the possibility distribution
and
is the ordinate of the point of intersection of
with the vertical at
.
(b) For
, the one sided test from the left (alternative hypothesis
), the possibility of rejection of
is equal to the Necessity of Strict Dominance index of
to
, where the membership function of the critical value
is as follows (
the critical value of the one sided from the left defined in (2)):
So if the core of
is at the left of
, (25) gives the following:
where
is the ordinate of the point of intersection of the right part
of the possibility distribution of
with the vertical at
.
The possibility of acceptance of
is as follows:
So if the core of
is at the right of
, (27) gives the following:
where
is the ordinate of the point of intersection of the left part
of the possibility distribution of
with the vertical at
.
(c) For the
two-sided test (alternative hypothesis
), the possibility of rejection of
is equal to the following:
where (
and
are the critical values of the two-sided defined in (3)).
So if the core of
is at the right of
, (33) gives the following:
where
and if it is at the left of
, it gives the following:
where
.
The possibility of acceptance of
is as follows:
So if the core of
is between
and
, (34) gives the following:
where
and
(the ordinates of the point of intersection of the right part
of the possibility distribution of
with the vertical at
and of its left part
with the vertical at
).
If the possibility of the rejection or acceptance of is very low (for example lower than ), then we cannot make a decision on rejecting or accepting .
5. Tests on the Mean of a Normal Distribution with Known Variance or of Any Distribution from a Large Sample
We test at the significance level the null hypothesis for the mean of a random variable X, which follows the normal distribution with known variance , using a random sample of observations of X of size n.
In the crisp case, we test
, using the statistic (see [
1]).
where
is the statistic of the sample mean. It is known that under the null hypothesis (
)
Z follows the standard normal distribution
, so
is rejected from a given sample:
(a) For the
one sided test from the right, if
(b) For the one sided test from the left, if ,
(c) For the
two sided test, if
or
, where
the value of the statistic (35) for the given sample,
and
the inverse distribution function of the standard normal distribution. Meanwhile,
is not rejected if
.
In the fuzzy case, the test of
is based on the fuzzy statistic
which is generated by substituting
in (35) with the fuzzy estimator
of the mean value for the given sample, the
cuts of the membership function of which are given by (7).
From (38), (7) and interval arithmetics follow that the
cuts of the possibility distribution of the fuzzy statistic
are as follows:
Hence, the
cuts of the possibility distribution of
for the given sample are as follows:
where
the crisp value of the statistic
Z for this sample, which is given by (36).
The membership functions of the critical values
and
of the one-sided tests are as follows:
and for the two-sided test,
Having the cuts of the possibility distribution of the fuzzy statistic of (39) and the critical values and , we can evaluate the possibility of the rejection or acceptance of from (21), (23), (26), (28) for and (40) for one sided tests or from (31), (32), (34) and (41) for the two-sided test.
If the sample is large and
X follows any distribution, then in the crisp case, we test
using the statistic
where
is the statistic of the sample mean and
s, the sample standard deviation [
1]. It is known that under the null hypothesis (
),
Z follows the standard normal distribution
according to the central limit theorem [
1], so
is rejected or not by one sided tests, using (21), (23), (26), (28) for
given in (39) for the following sample value:
of the statistic
Z or (31), (32), (34) for the two-sided test.
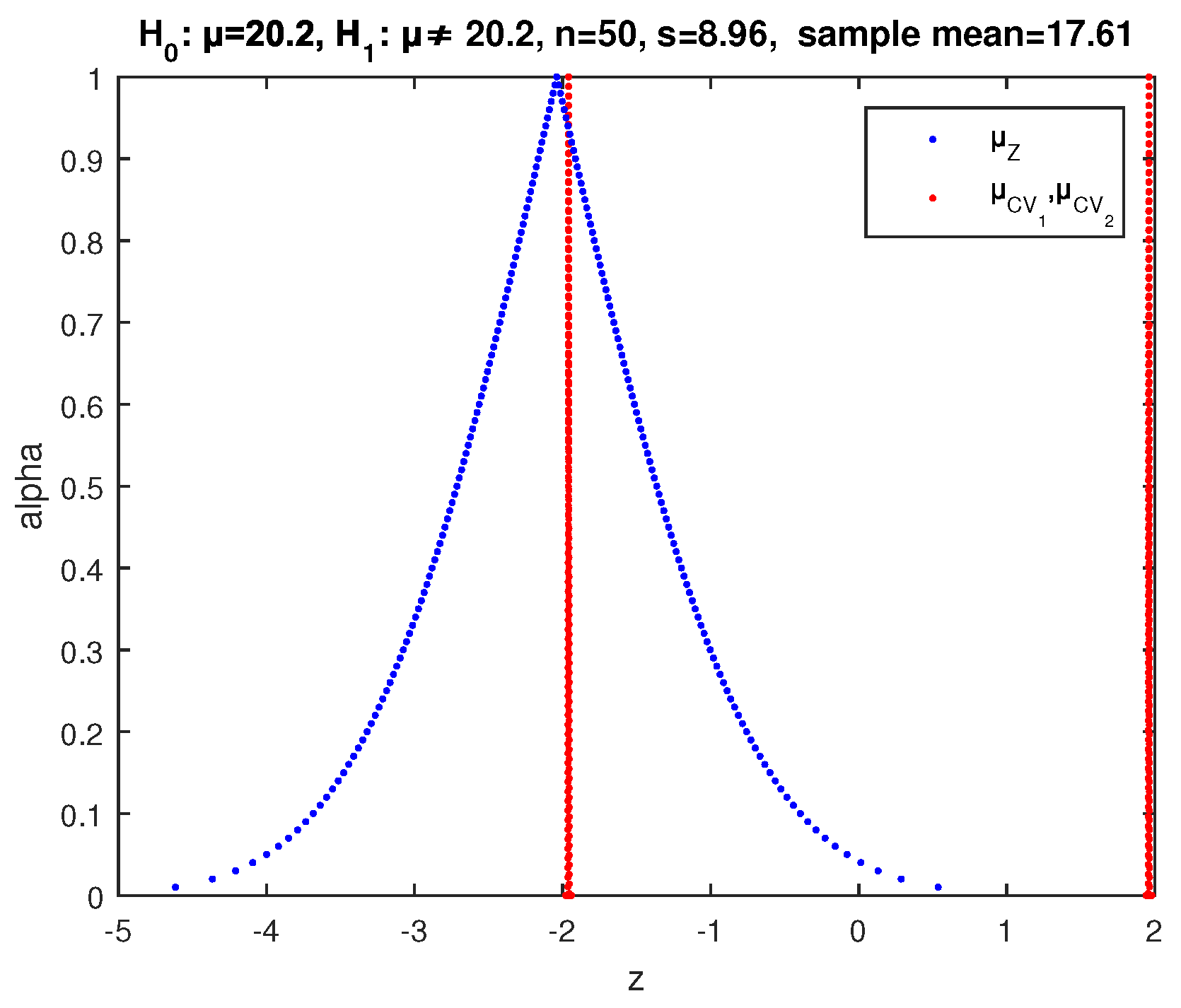
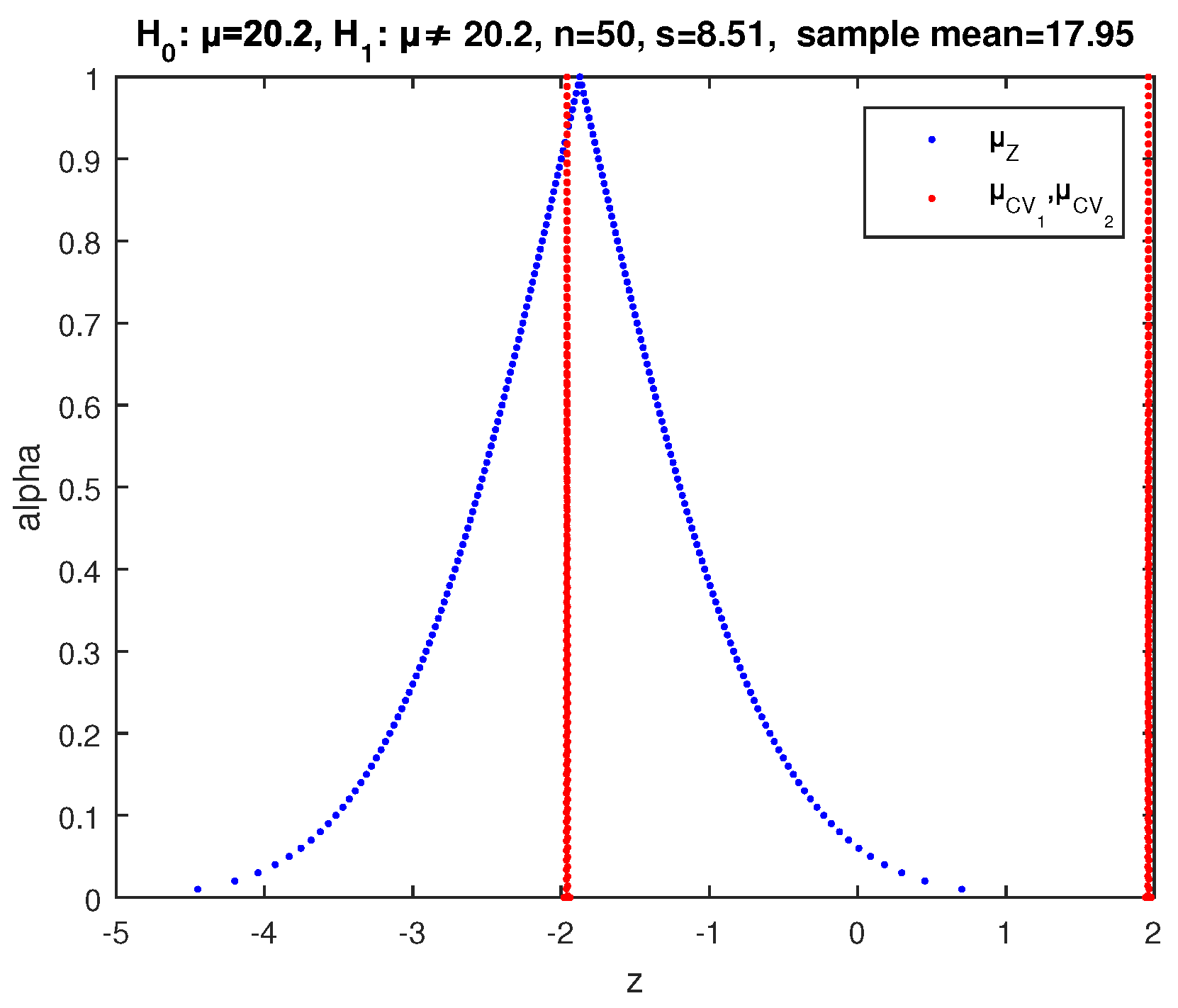
Example 1. We test the null hypothesis at significance level with alternative (two-sided test) for the mean value μ of the temperature X, using the two large random samples of 50 observations each of the Appendix A (monthly values for selected Greek weather stations) [37]. The mean and the standard deviation of the first sample are
and
, so in the crisp test, we evaluate the value of the statistic
Z for the first sample from (42):
is rejected by this crisp test.
For the second sample the mean and variance are
and
, so the value of the statistic
Z in this case is the following:
Therefore, since the following is true:
is not rejected by the crisp test.
Applying the above described two-sided fuzzy test of
, implementing the possibility distribution (39) of
for the value
of (42) and the critical values (41) for the first sample, we get the results of
Figure 4, where the point of intersection of
and
has
. So according to (32), the possibility of rejection of
is
. Hence, we cannot make a decision on whether to reject or not
from this sample.
Implementing (39) and (41) for the second sample, we take
Figure 5, where the point of intersection of
and
has
, so according to (34), the possibility of acceptance of
is
. Therefore, we cannot make a decision on whether to reject or not
from this sample.
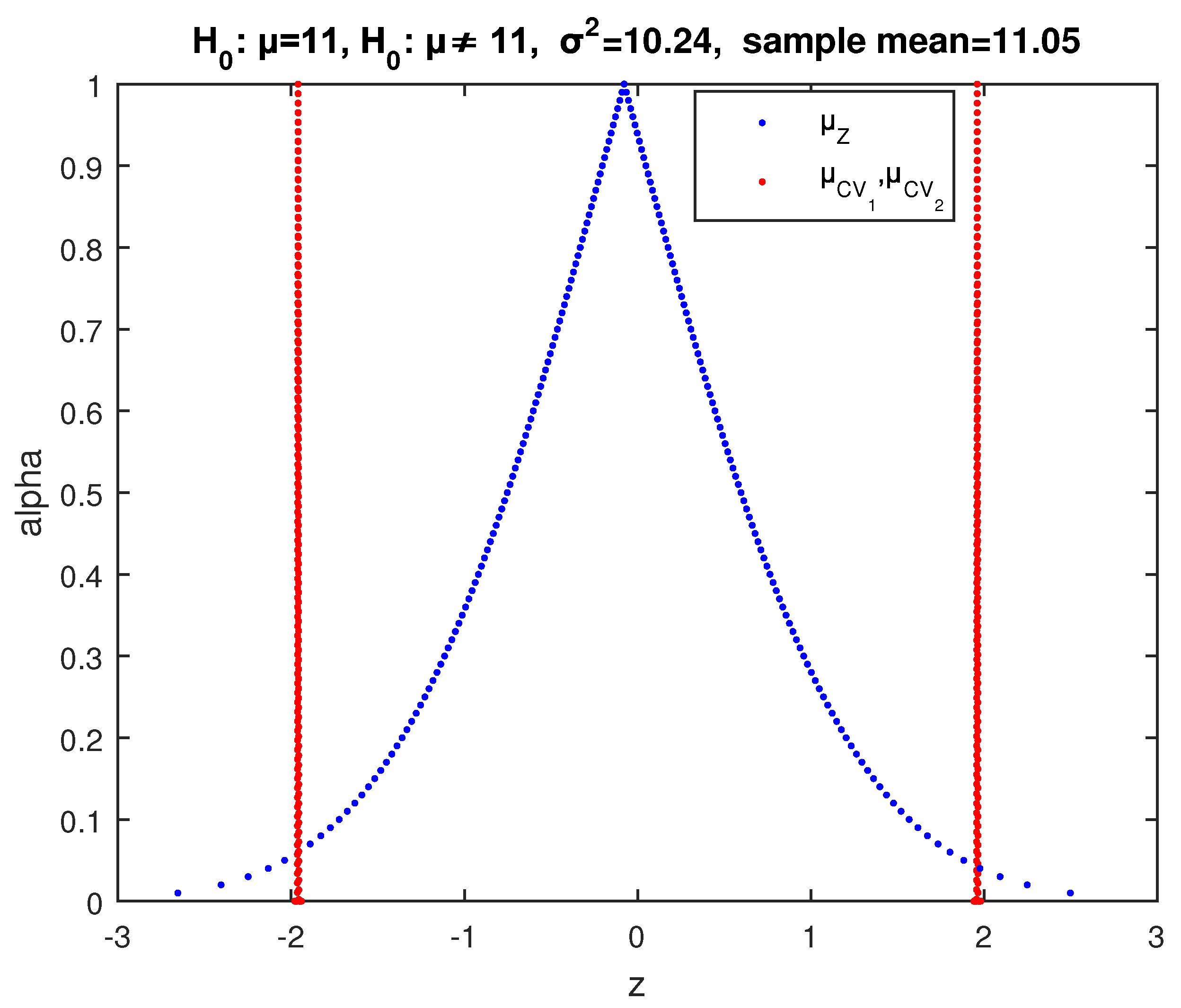
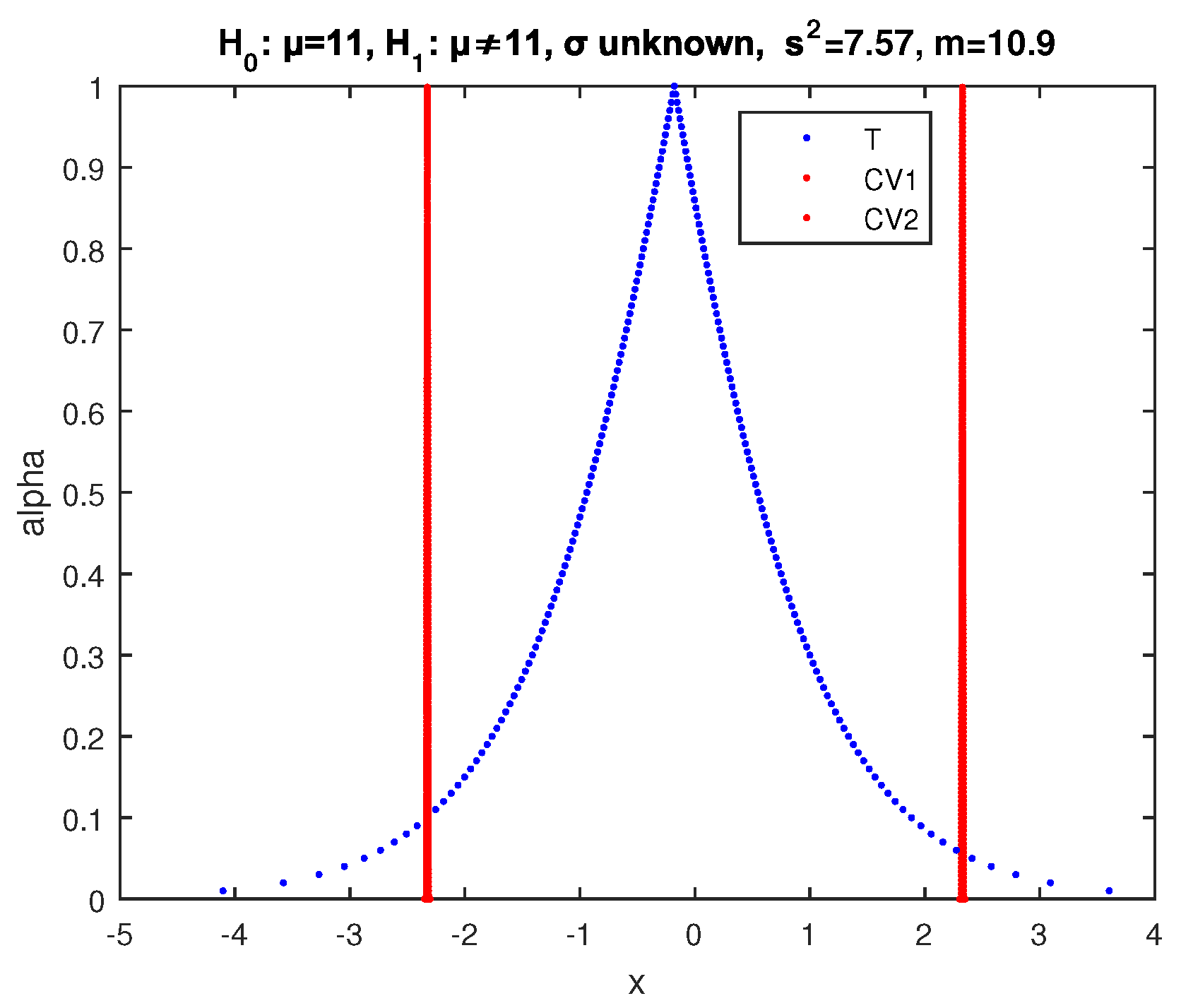
Example 2. We test at significance level the null hypothesis with alternative (two-sided test) for the mean μ of a random variable X, which follows normal distribution with variance , using a sample of observations with sample mean .
The value of the test statistic (35) is found by (36) to be as follows:
so the crisp
p-value of the test is as follows:
Therefore, in this case, the crisp test gives acceptance of with a very high p-value (near to the maximum value, 1).
We apply the above two-sided fuzzy test of
implementing (39) and (41). So, we obtain the results of
Figure 6, where the core of
is between the cores of
and the point of intersection of
, and
has
and of
and
has
. Hence, according to (34), the possibility of acceptance of
is as follows:
so
is accepted by this test with possibility
.
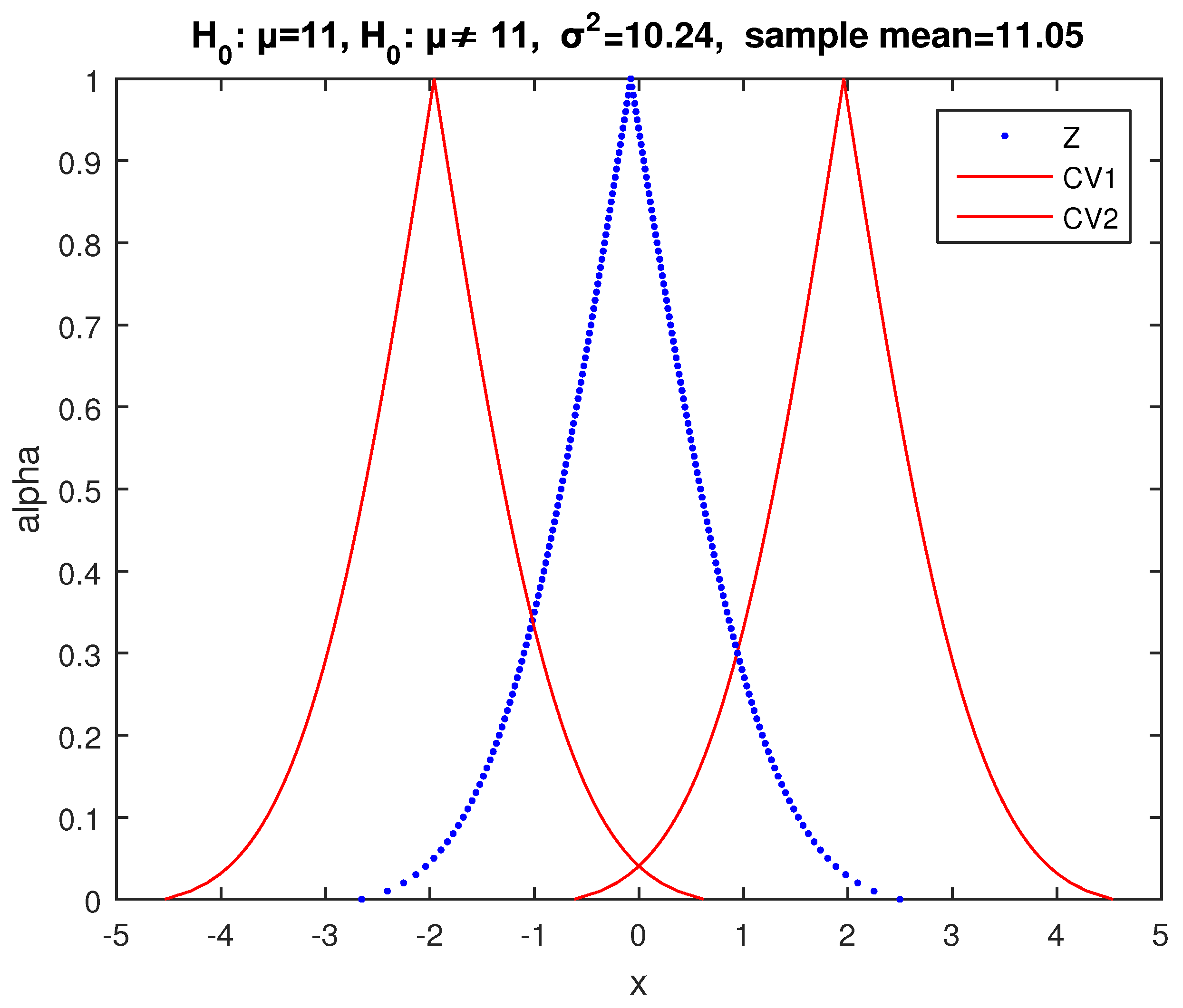
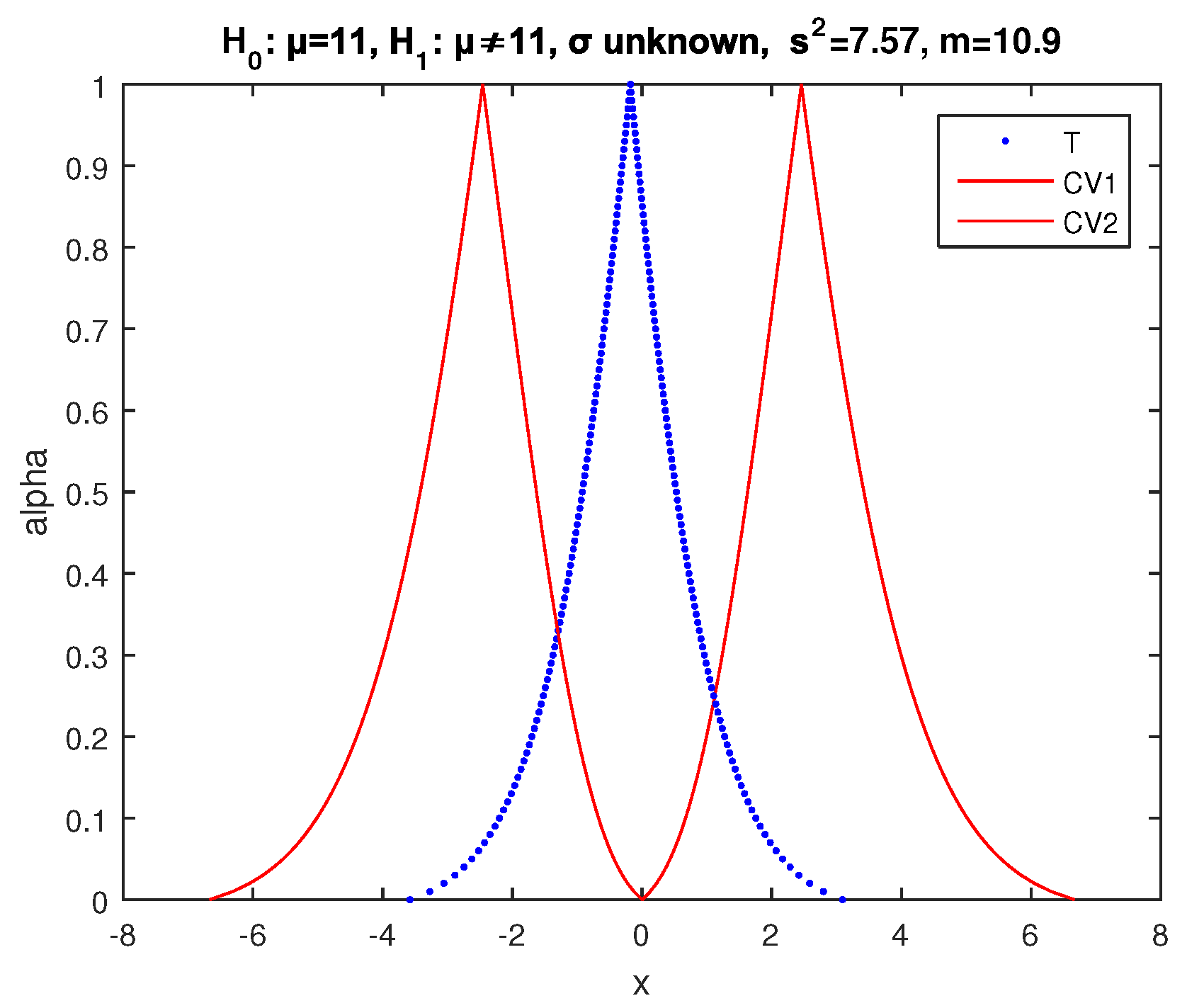
Applying the respective test of [
29,
30], we get the results of
Figure 7, where we see that the possibility of acceptance of
is much lower than 1:
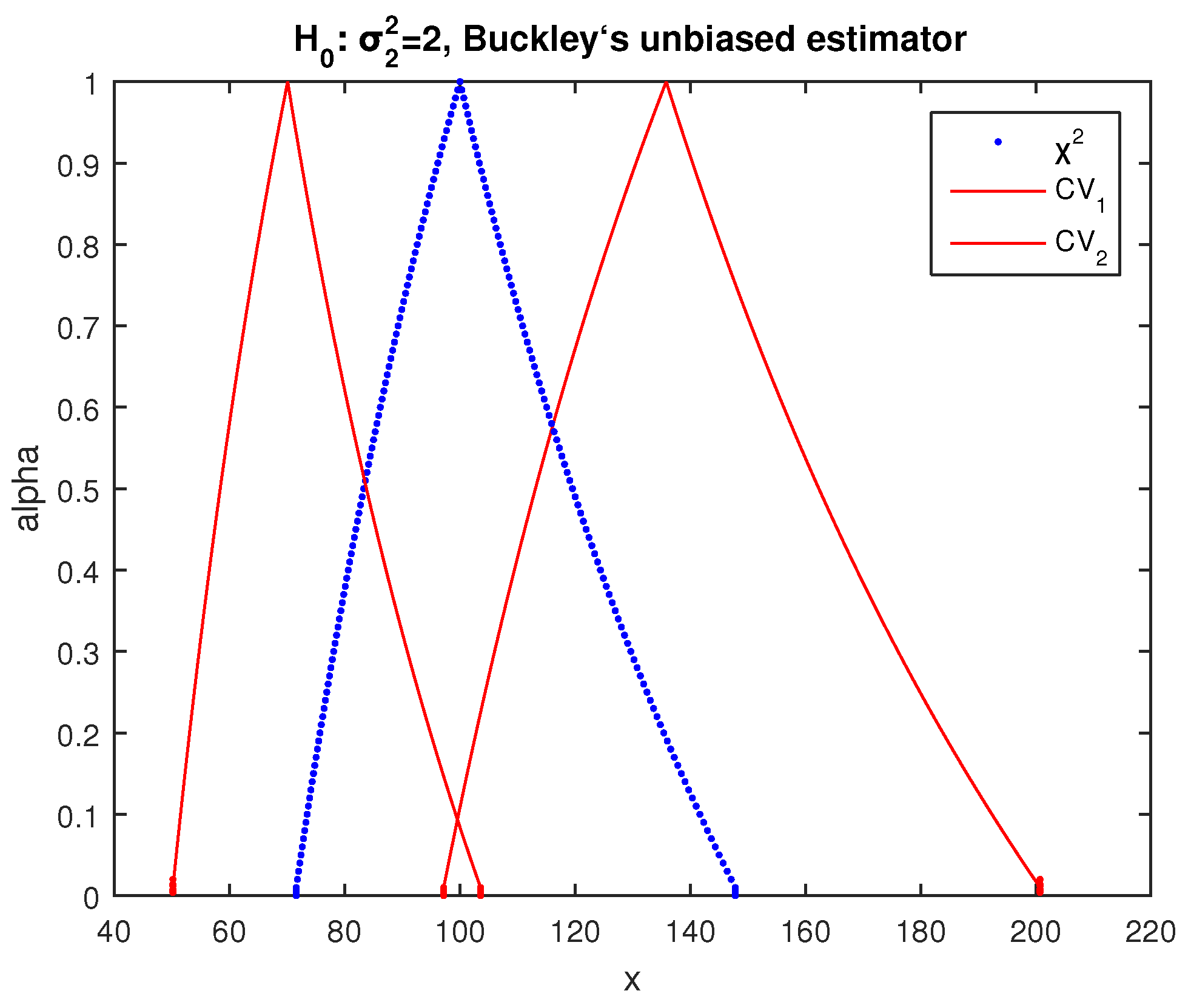
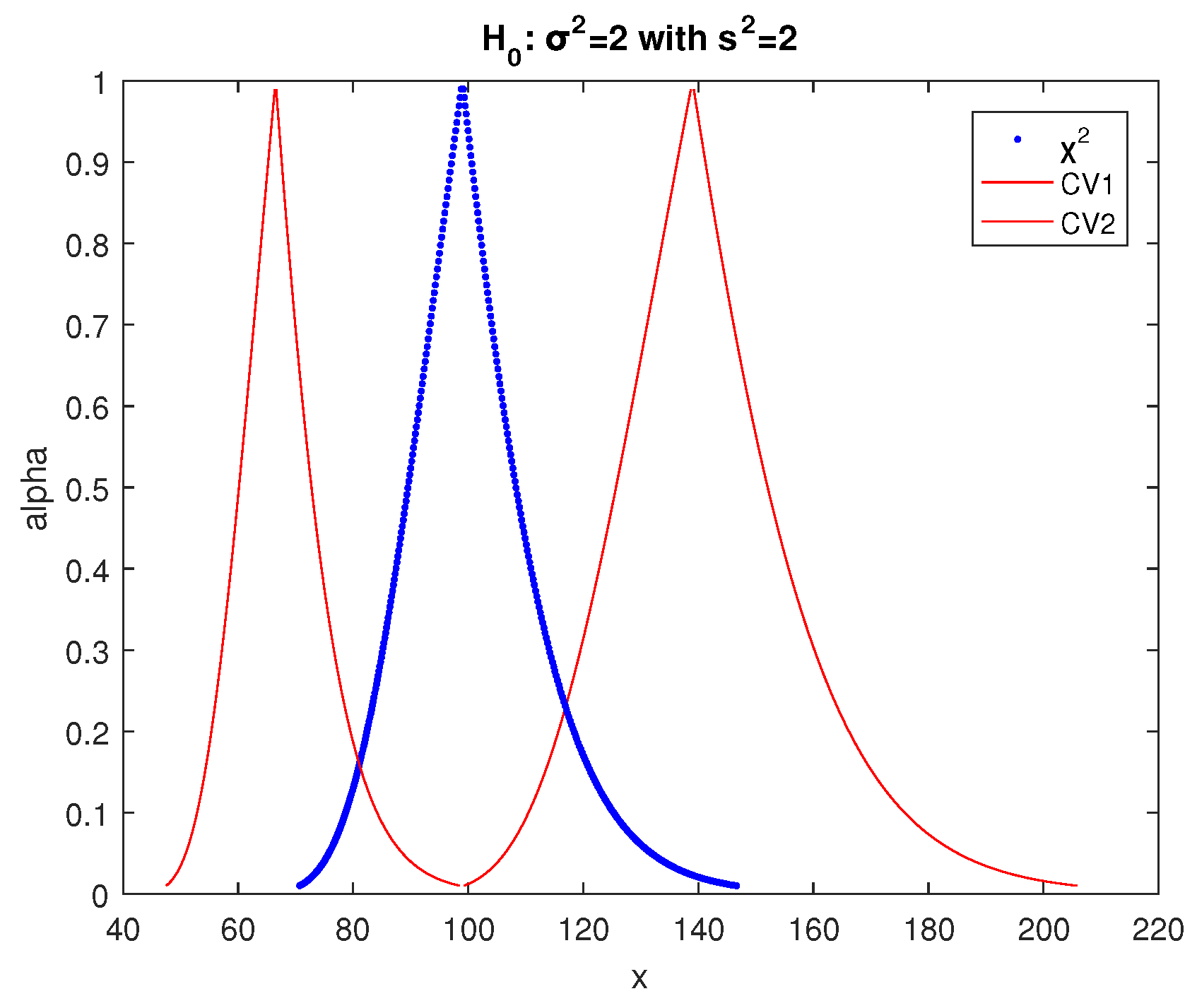
6. Hypotheses Tests for the Variance of a Normal Distribution
We test at significance level the null hypothesis for the variance of a normal random variable X, using a random sample of observations of X of size n and variance .
In the crisp case, we test
, using the test statistic
where
is the sample variance, which follows
distribution with
degrees of freedom under the null hypothesis [
1].
is rejected from a given random sample (omitting in
the implied
degrees of freedom):
(a) For
one-sided test from the left (alternative
), if
and
is the inverse distribution function of the
distribution.
(b) For
one-sided test from the right (alternative
), if
(c) For
two-sided test (alternative
), if
where
and
the crisp value of the statistic (43). Otherwise,
is not rejected.
In the fuzzy case for the test of
, we use the fuzzy statistic
generated by substituting
in (43) with a fuzzy estimator
of the following variance:
Using the
cuts of the unbiased fuzzy estimator given in (14) and interval arithmetics, we obtain from (48) the
cuts of the possibility distribution of the following test statistic:
As illustrated in
Figure 8 and
Figure 9, the shape of this test statistic is significantly different than the shape of the respective test statistic produced by the implementation of
used in [
29], which is as expected since the shape of the two implementations (14) and (18) of
are different.
The membership functions of the critical values
and
of one-sided tests are as follows:
and for the two-sided test
where
the inverse distribution function of the
distribution with
degrees of freedom.
Having the cuts of the possibility distribution of the fuzzy statistic and the critical values and , we can evaluate the possibility of rejection or acceptance of from (21), (23), (26), (28) for and (50) for one sided tests or from (31), (32), (34) and (51) for two sided test.
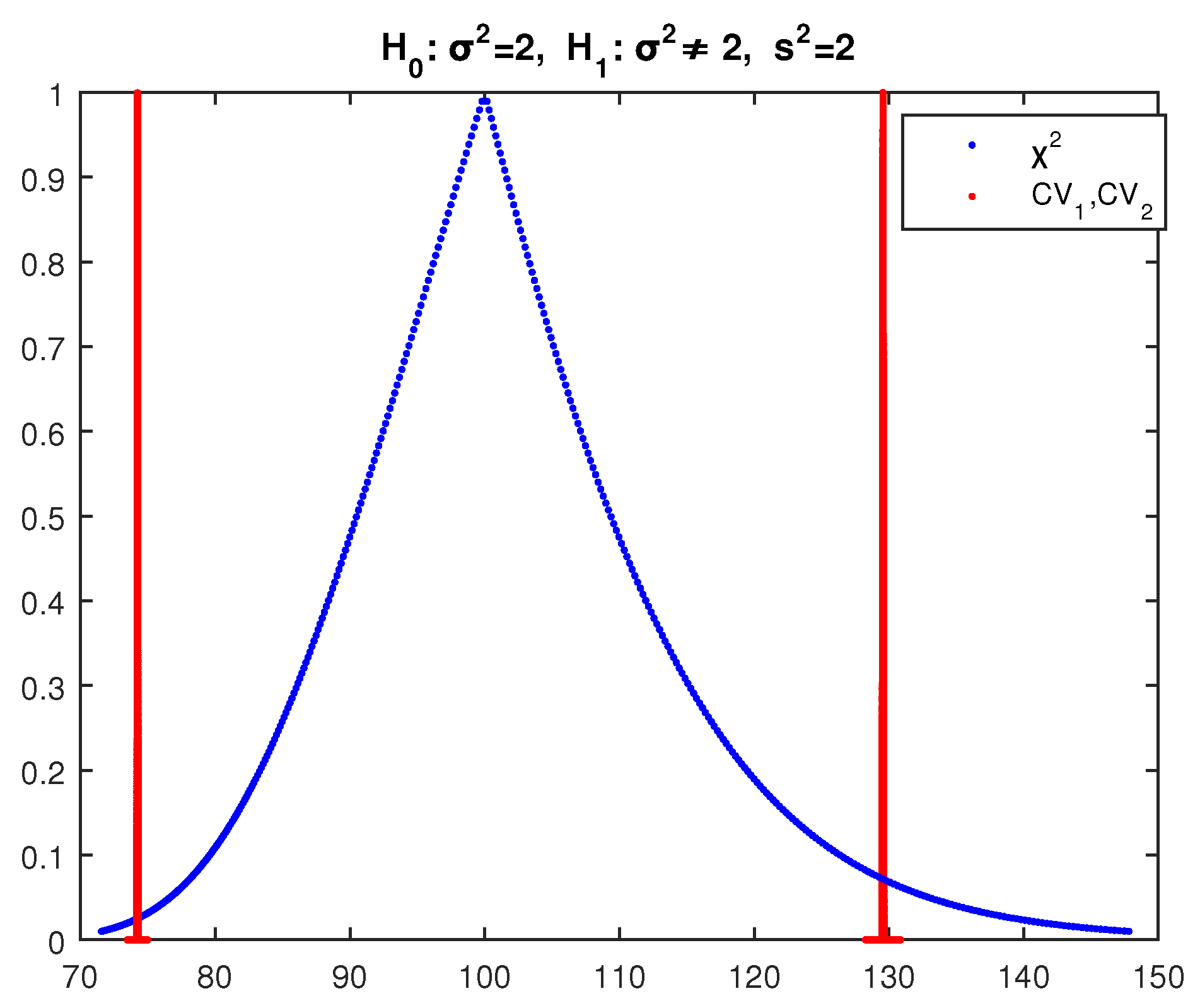
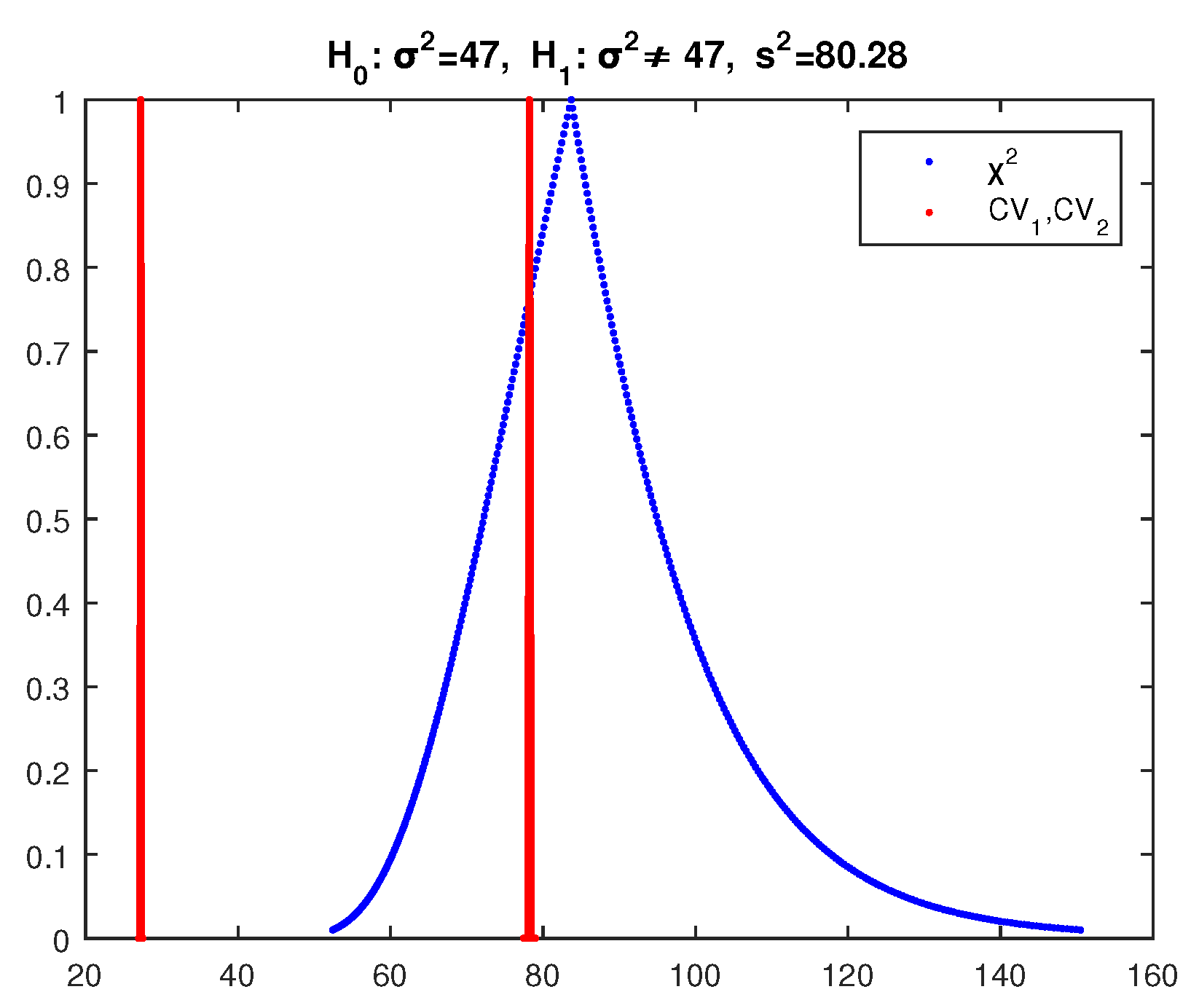
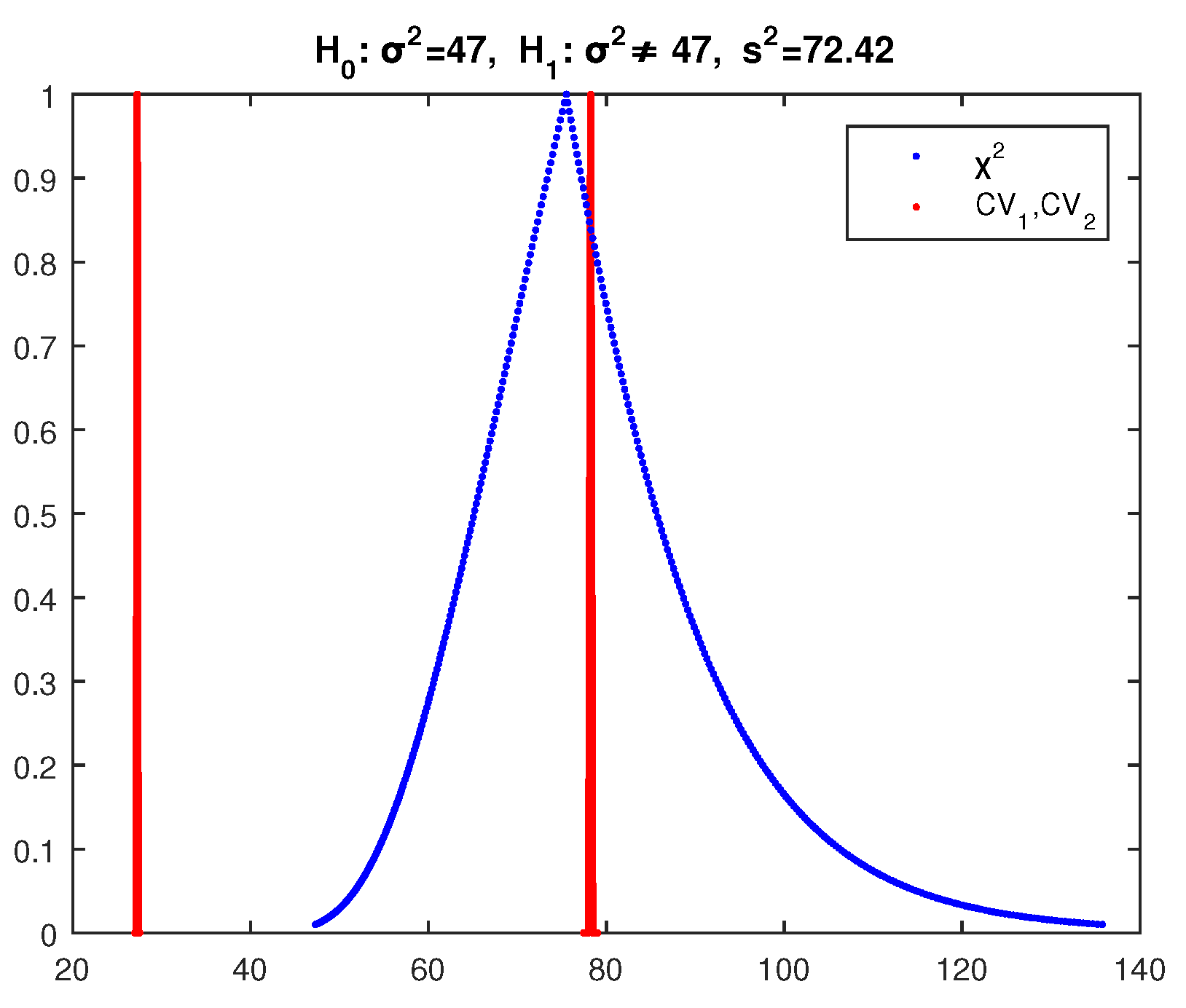
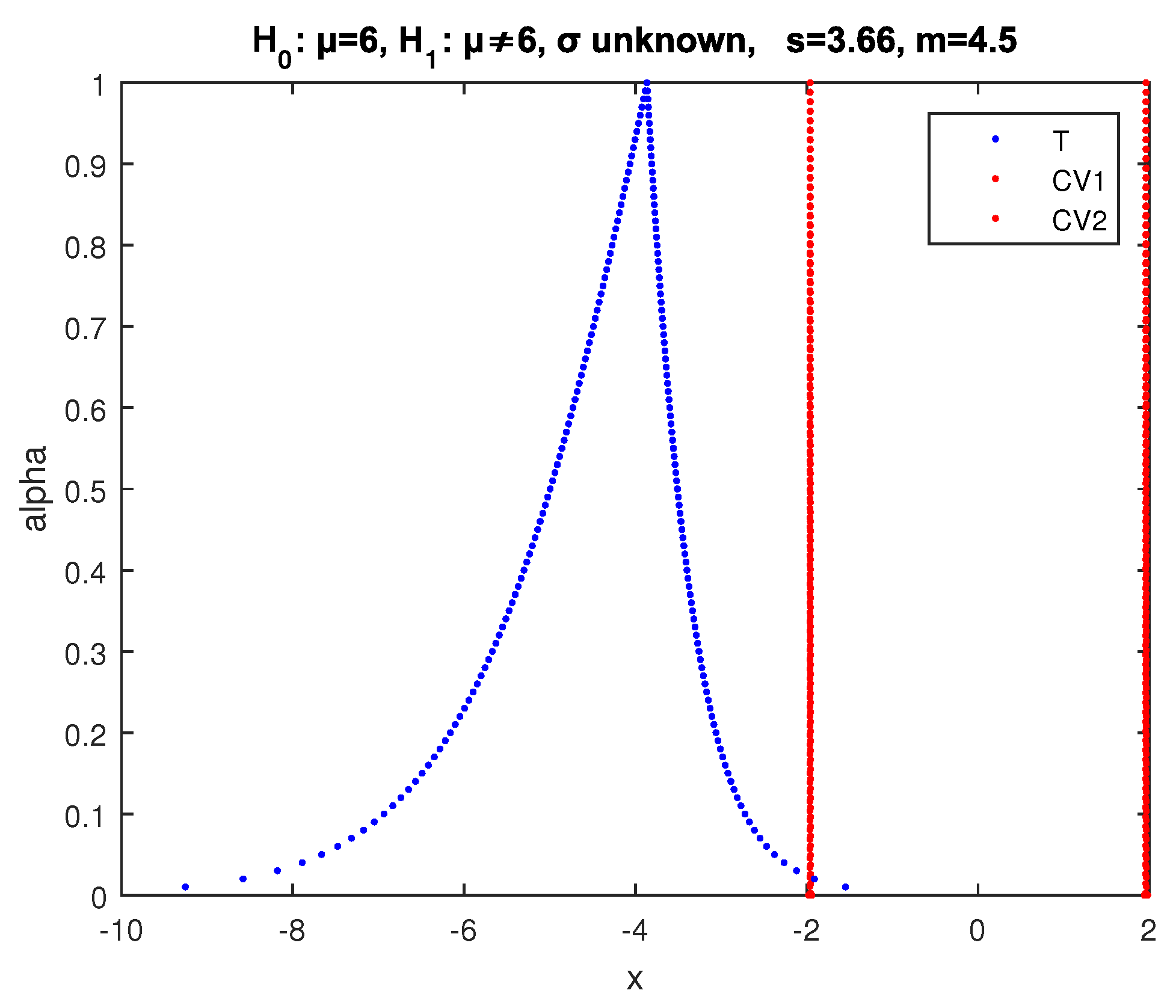
Example 3. We test at significance level the null hypothesis with alternative for the variance of a normal random variable, using a random sample of 101 observations with sample variance .
The crisp test in this case gives acceptance of with the largest possible difference between the test statistic and the critical values since the p-value is 1 (the test statistic is exactly in the middle of the no-rejection region), so it is the best case for the acceptance of .
Applying the above fuzzy test, we get the results of
Figure 8, where the core of
is between the cores of
and
and the point of intersection of
, and
has
and of
and
,
, so according to (34) the possibility of acceptance of
is as follows:
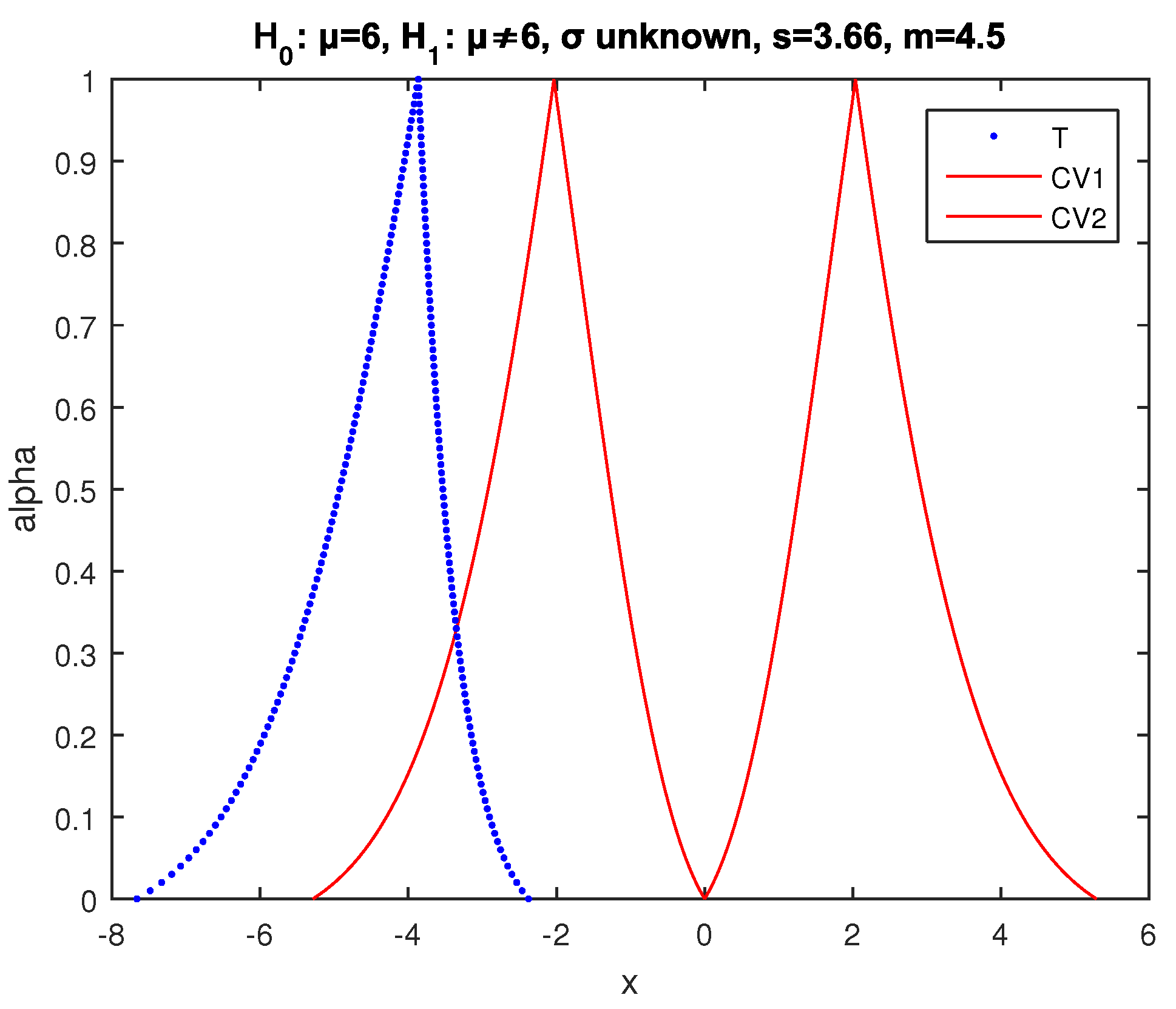
The respective fuzzy test of
of [
29] gives the results of
Figure 9, where the possibility of acceptance of
is as follows:
and the test of
of [
30] gives the results of
Figure 10, where the possibility of acceptance of
is as follows:
The results of the fuzzy hypothesis tests proposed in this paper are in much better agreement with the results of the respective crisp tests than the results of the respective tests of [
29]. This happens because of the following:
- (1)
The former are based on the correct implementation of , according to the theory, whereas the latter contain the error of using -cuts instead of -cuts.
- (2)
The tests of [
29] use fuzzy critical values, which are created using probabilistic concepts.
The above are illustrated by the characteristic case of the hypothesis test of Example 3 in which the crisp value of the test statistic is exactly in the middle of the acceptance region (
p-value
), which is the best case of acceptance. As shown in this example, the test, which uses the implementation of
of [
29], gives a significantly lower possibility of acceptance of
(
) than the test which uses our implementation of (
). So, the latter is in much better agreement with the crisp statistical tests than the former.
The possibilistic tests developed in this paper are in better agreement with the results of the respective crisp tests than the results of the tests of [
30], which also use the same fuzzy critical values as [
29]. This is illustrated in Examples 2 and 3 in which the crisp value of the test statistic is exactly in the middle of the acceptance region. As shown in these examples, the tests of [
30] give a significantly lower degree of acceptance of
(
for Example 2 and
for Example 3) than the respective tests of this paper (
for both examples). So, the latter are in better agreement with the crisp statistical test than the former. This happens in all relevant examples (statistic in the middle of the acceptance region).
Example 4. We test the null hypothesis at significance level with alternative (two-sided test) for the variance of the temperature X, using the two large random samples of 50 observations each of the Appendix A (monthly values for selected Greek weather stations) [37]. The crisp value of the test statistic (43) for the first sample is found by (47) to be as follows (the sample variance is
):
The critical values of this crisp test are (
, the inverse distribution function of the
distribution).
So since , is rejected by the crisp test for this sample.
For the second sample (variance
), the value of the test statistic (43) is found by (47) to be as follows:
So since is not rejected by the crisp test for this sample.
Applying the above fuzzy test for the first sample, we get the results of
Figure 11, where the core of
is at the right of the core of
and their point of intersection has
. So according to (31), the possibility of rejection of
is as follows:
For the second sample, we get the results of
Figure 12, where the core of
is between the cores of
and
and the point of intersection of
and
has
and of
and
,
. So according to (34), the possibility of acceptance of
is as follows:
Therefore, we cannot make a decision on accepting from this test.
7. Hypothesis Tests for the Mean of a Normal Random Variable with Unknown Variance
We test at significance level the null hypothesis for the mean value of a random variable X, which follows normal distribution with unknown variance, using a random sample of observations of X of size n with sample mean and variance and .
In this case, the test statistic is
where
and
S are the statistics of the sample mean and the standard deviation.
It is known [
1] that under the null hypothesis (
),
T follows
t distribution with
degrees of freedom. So in the crisp case,
is rejected from a given random sample:
(a) For the
one sided test from the right (alternative
), if
, where
the value of the statistic (52),
the critical value of the test and
is the inverse distribution function of the
t distribution with
degrees of freedom.
(b) For the one sided test from the left (alternative ), if .
(c) For the two-sided test ( alternative ), if or while, if , then is not rejected.
In the fuzzy case for the test of
we use the following fuzzy statistic:
which is generated by substituting
and
S in (52) with the fuzzy estimators
and
of the mean and standard deviation. The
cuts of
are given by (13) and (as described in [
29,
30]) the
cuts of the possibility distribution of
are as follows:
From (53), (55), (56), (13) and fuzzy number arithmetics follows that the
cuts of the possibility distribution of the fuzzy statistic
are as follows:
where
.
The membership functions of the critical values
and
of the one-sided tests are as follows:
and for the two-sided test,
where
is the inverse distribution function of the
t distribution with
degrees of freedom.
Having the cuts (57) of the possibility distribution of the fuzzy statistic T and the critical values and , we can evaluate the possibility of rejection or acceptance of from (21), (23), (26), (28) for and (58) for one-sided tests or from (31), (32), (34) and (59) for the two-sided test.
Example 5. We test the null hypothesis at significance level with alternative (two sided test) for the mean μ of a normal random variable X, using a sample of observations with sample mean and variance and .
In the crisp case, the value of the statistic (52) is evaluated by (53)
so the
value is
, which is much higher than the significance level
. Hence,
is accepted by the crisp test with high
p-value (the test statistic is almost at the center of the acceptance region).
We apply the above two-sided fuzzy test of
, implementing (57) and (59). So, we obtain the results of
Figure 13, where the core of
is between the cores of
and
and the points of intersection of
and
and of
and
have
and
. Hence, according to (34), the possibility of acceptance of
is
so
is accepted by this test with possibility
.
Applying the respective test of [
29,
30], we get the results of
Figure 14, where we see that the possibility of acceptance of
is as follows:
Example 6. We test the null hypothesis at significance level with alternative (two sided test) for the mean μ of a normal random variable X, using a sample of observations with sample mean and variance and .
In the crisp case, the value of the statistic (52) is evaluated by (53)
so the
value is
, which is almost zero. Hence,
is rejected by the crisp test.
We apply the above test implementing (57) and (59). So, we take the results of
Figure 15, where the core of
is at the left of the core of
and the point of intersection of
and
has
. Hence, according to (32), the possibility of rejection of
is
.
Applying the respective test of [
30], we get the results of
Figure 16, where we see that the possibility of acceptance of
is as follows:
A similar result with even lower possibility of acceptance is obtained by the respective test of [
29].