1. Introduction
The financial market’s continuous development causes complex links among many types of financial institutions, including governments, investment banks, firms, and so on. These institutions connect with each other through asset holdings, ownerships, and some other obligatory relationships to create complex financial networks [
1]. Once a complex financial network is formed, the collapse of some institution nodes spreads through the network, which also puts neighboring institutions at risk and causes more institutions to fall into crisis, thus gradually promoting the spread of financial risk. Through the amplification of the financial network, the collapse of some institutions will easily trigger the cascading effect of a series of failures in the network and then evolve into systemic financial risk. Hart and Zingales (2009) defined systemic risk as the occurrence of extreme events such as institutional failure in the financial system, which is transmitted from one institution to multiple institutions and eventually produces a negative external spillover risk to the real economy [
2]. For example, the global financial crisis in 2008 was triggered by the liquidity crisis, which was caused by the default of the US sub-prime mortgage contract. The risk first spread to the entire mortgage market then gradually spread to other financial markets, finally forming a global financial crisis [
3]. This financial crisis highlighted the complex interconnections between financial institutions, which may provide the channel for risk contagion, thereby promoting the occurrence of systemic risk.
The emergence of systemic financial risk has a serious negative impact on the stable growth of the whole economy. For example, the global financial crisis triggered by the U.S. sub-prime mortgage crisis in 2008 has caused serious economic losses to countries all over the world. This event fully reveals the possible impact and damage systemic financial risk can have on the financial system. When a financial network produces systemic risk, a large number of financial institutions close down; the functioning of the financial system is damaged; and this can even lead to a sharp, short, super cyclical retrogression of the economy. Some economists at the Bank for International Settlements conducted a study on the macro economy in the mid-1970s and concluded that the imbalance of the macro economy will lead to a significant increase in the vulnerability of the financial system. Therefore, research on the systemic risk of financial networks is still an important issue that needs to be explored. The effective control of financial systemic risk is of great significance in the development of the real economy and the quality of national life.
In recent years, researchers have made some advancements in the study of financial systemic risk based on complex network theory. For example, Douglas W. Diamond et al. (1983), based on the network of asset value flow, concluded that increasing market diversity and increasing the interconnection of financial institutions can effectively reduce the diversification risk [
4]; Simone Lenz et al. (2012) found that, as the average degreeof the network increases, the systemic risk of banking financial network will show a trend of first increasing and then decreasing—namely, an “inverted U-shaped” functional relationship [
5]. Matteo Chinazzi et al. (2013) studied the contribution of systemic risk mainly from the perspectives of network relevance, the heterogeneity of banking institutions, the uncertainty of the financial market, and other factors. The authors found that the association between bank assets and liabilities is an important factor in the formation of systemic risk, and that network relevance as a communication channel can expand the scale of risk [
6]. Raffestin (2014) pointed out that portfolio diversification makes individual investors safer but also establishes a link between them through jointly held assets, which creates an “endogenous covariance” between the assets and investors and improves systemic risk by rapidly spreading the impact in the whole system [
7]. Based on the endogenous network model, Qianting Ma et al. (2018) found that the network structure is closely related to the systemic risk of banks. That is, with the expansion of the network node size, the number of bankrupt banks significantly increases and the systemic risk also significantly increases [
8]. Yang et al. (2019) used the data of U.S. commercial banks from 2000 to 2013 and found that bank diversification is related to the increase in systemic risk through empirical analysis. Moreover, the impact of diversification on systemic risk is more significant in large and medium-sized banks [
9]. These studies show that there is a close relationship between the systemic risk of a financial network and the network structure.
This paper aims to study bank correlation networks. In fact, the correlation network has been widely used in related research in the financial field. For example, Mantegna [
10] first used the stock correlation network to analyze the return correlation of S & P 500 stocks and found a hierarchical clustering structure among stocks. Subsequently, many other researchers analyzed the relationship between the stock market and the topological structure of the network by establishing the stock correlation network [
11,
12,
13]. In the stock correlation network, the nodes of the network represent stocks and the connecting edges between nodes represent the price fluctuation association among stocks. Referring to the idea of establishing a stock correlation network, this paper will establish a bank correlation network according to the correlation of many banks’ investment portfolios with different types of asset. In a bank correlation network, a network node represents a bank, while the correlation coefficient of the asset portfolio between any two bank nodes is taken as the weight of the connecting edge between the two nodes. It is believed that overlapping portfolios—i.e., the holding of common assets between banks—is a major factor in risk contagion. If banks have many common investment portfolios, risks will be spread among them through asset price fluctuations. At present, many researchers have studied the risk contagion caused by overlapping portfolios and the systemic risk of the financial system, including May and Arinaminpathy [
14], Beale et al. [
15], Glasserman and Young [
16], and Caccioli et al. [
17]. Therefore, motivated by these works, we will establish a bank-related network, based on the ratio of investment portfolios between banks, and discuss some potential relationships between network structure and systemic risk.
At present, there are still some difficulties in the research of the systemic risk of real financial networks, mainly due to the large scale of real financial networks in which the number of nodes is often in the tens of thousands and the connection of edges is also very complex. The efficiency of studying systemic risk by examining the network average degree, clustering coefficient, asset diversity, leverage, and other general topological characteristics of the whole financial system is often unsatisfactory. Therefore, it is necessary for us to find a method to simplify the financial network model which can divide the network into many sub-networks with different structures and study the differences in risks between different sub-networks. One of the most commonly used methods is community structure division [
18]: according to the degree of connection between network nodes, a complex network can be divided into several small communities, with tight connections within the community and sparse connections between the communities. As a topological property of local aggregation, the term community has different practical significance in real networks. At present, the community division method has been widely used in many fields, such as in social networks, biological networks, information networks, and so on [
19,
20,
21,
22]. Johnson et al. (2016) constructed a network based on the information of Russian social networking sites and mined 196 organizations supporting ISIS through community division, which provided very important guidance for the collection of anti-terrorism intelligence [
22]. At present, there have been few studies exploring the differences in network structure between different communities of a financial network or the correlation between the structure and the systemic risk. This paper will use the community division method to deal with large-scale networks of bank correlation and filter the divided communities into sub-networks. Then, the different characteristics between community sub-networks will be analyzed and the potential law of systemic risk from the level of community structure will be further explored. In particular, we will focus on the relationship between the systemic risk of community sub-networks and community structural variables, such as community size.
In this paper, we establish a bank correlation network of each state based on the U.S. Commercial Bank Balance Sheet Data (CBBSD) from Wharton Research Data Services. Then, the bank correlation network of each state is divided into a number of community sub-networks using community division methods. By analyzing the differences in the distribution of node importance between different communities, combined with the fact that the ranking results of node importance in a sub-network and the original network are highly consistent, we test the effectiveness of the community division. Besides, the robustness of the community division results is further tested by extracting a portion of statistically significant edges from the bank correlation network.
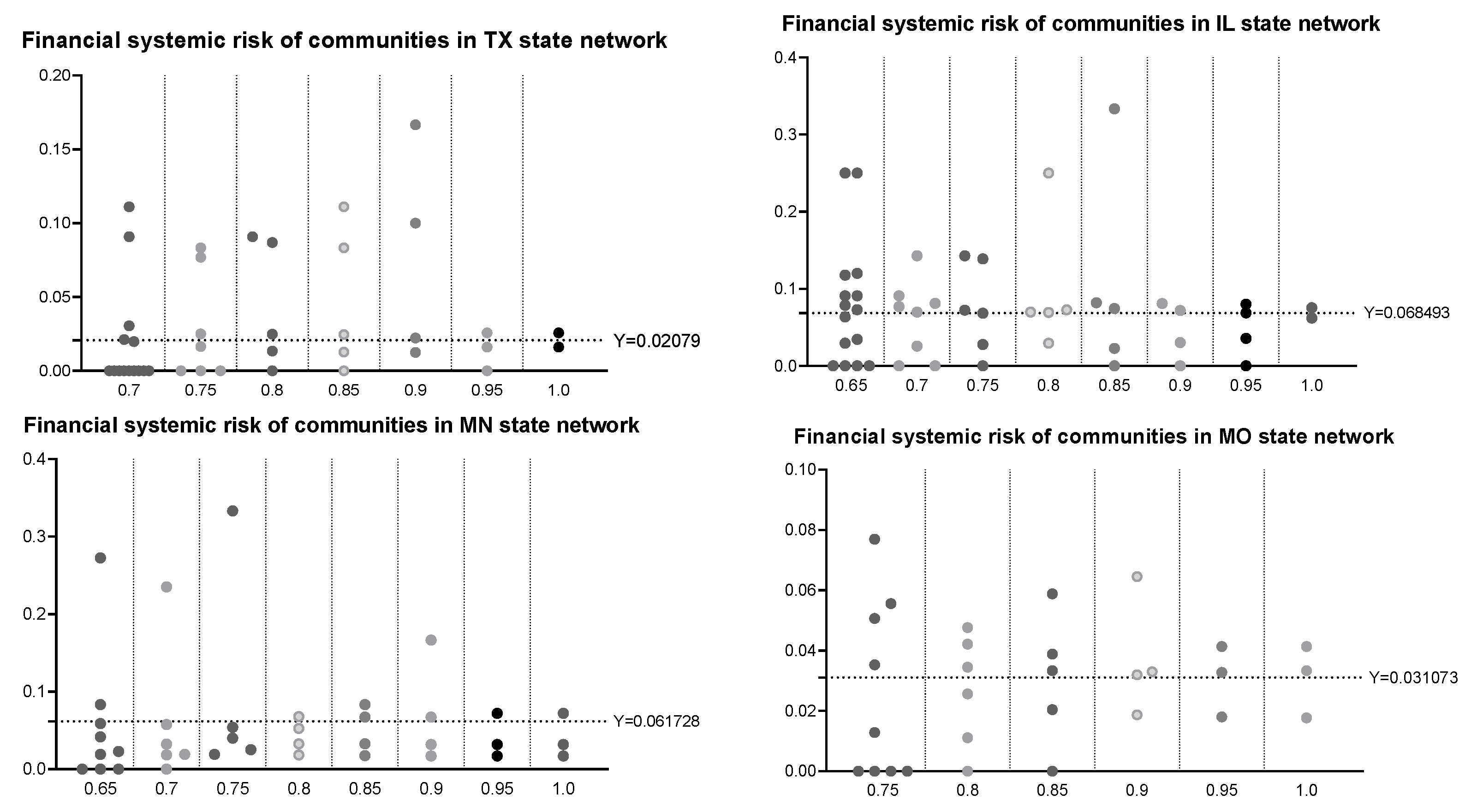
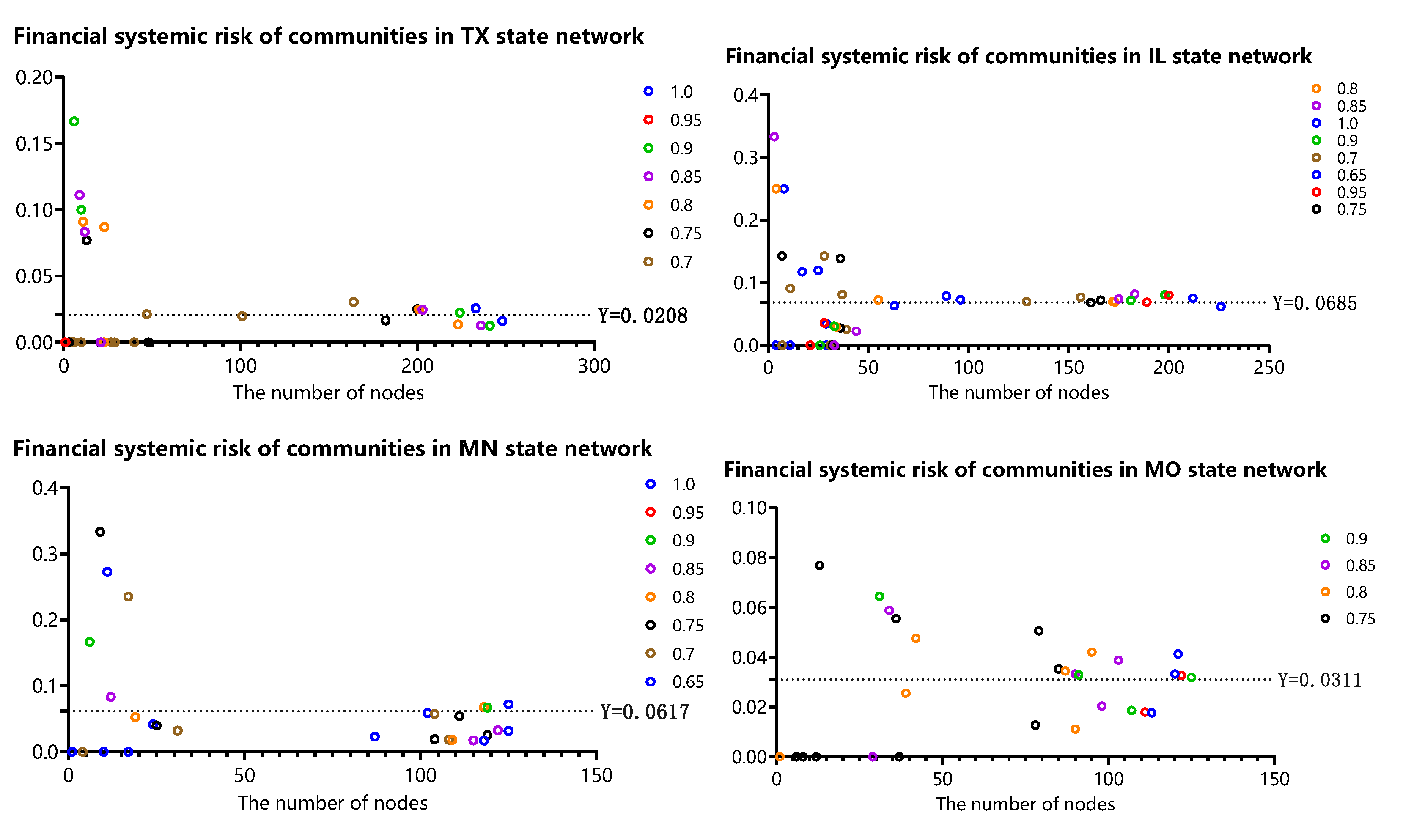
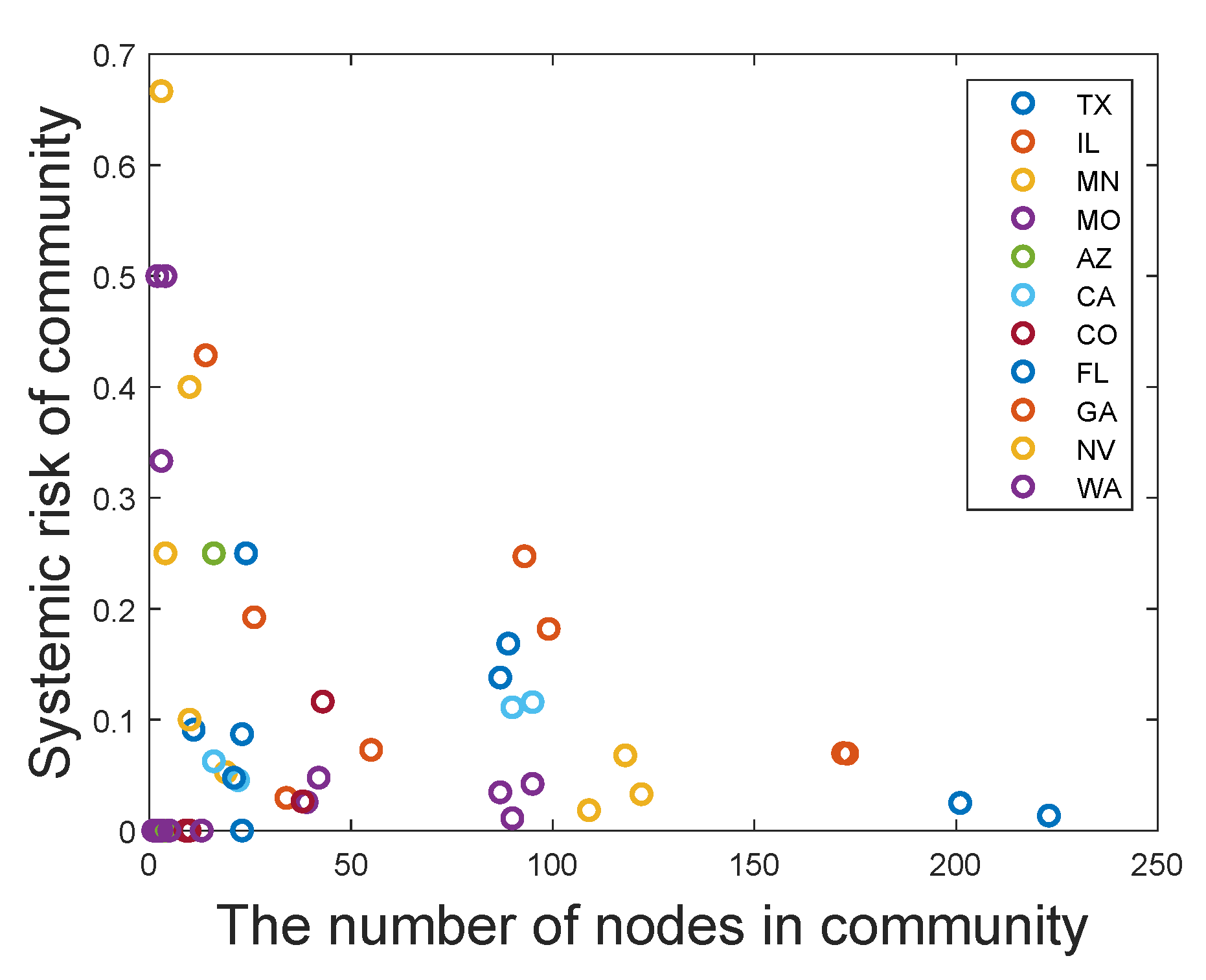
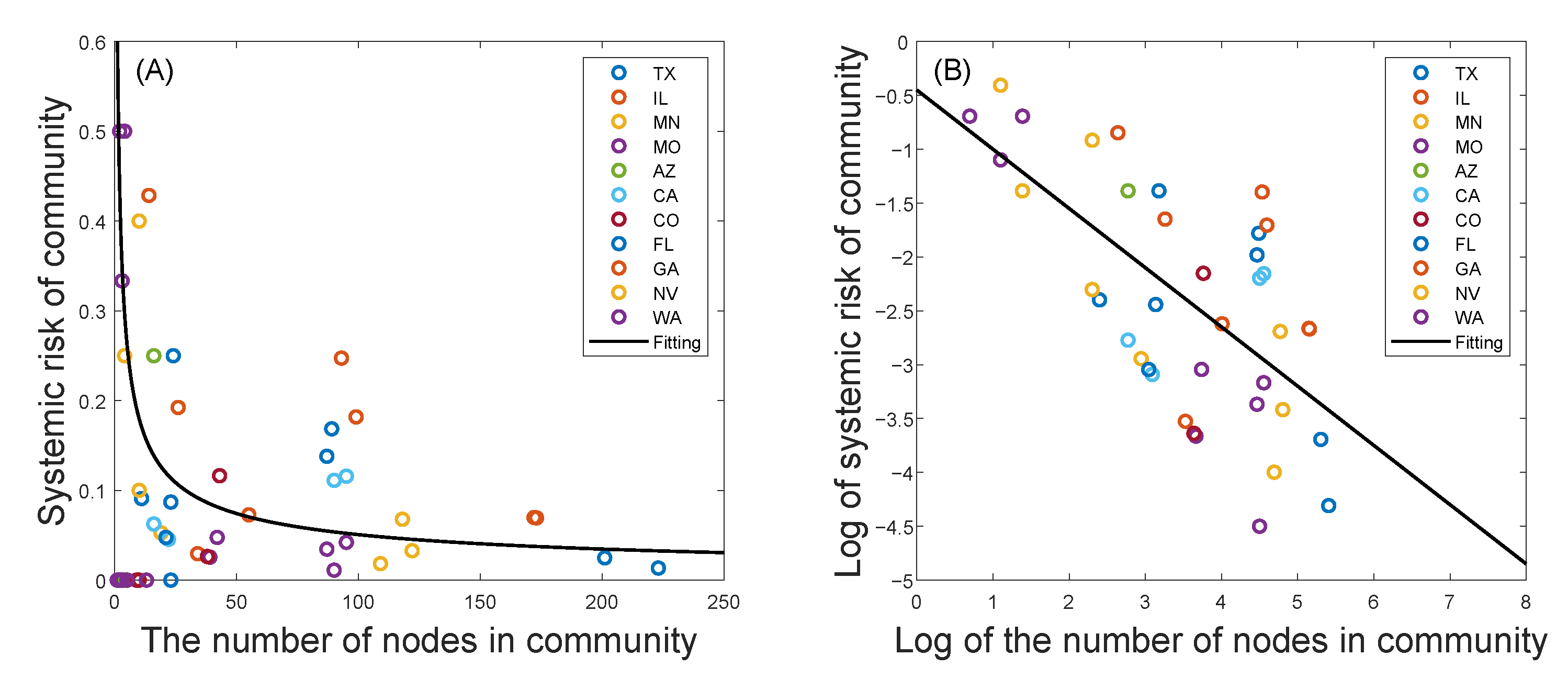
Then, based on the U.S. commercial bank failure data provided by the Federal Deposit Insurance Corporation, we study the systemic risk of each state network. Applying the proportion of bank failures in a network to measure its systemic risk, we analyze the differences in systemic risk between different communities for higher-risk states and find that there are significant differences in systemic risk among communities of different sizes: (1) The systemic risk of a relatively small-scale community will appear to have obvious volatility in that the systemic risk may be quite large or quite small. Namely, for a small-scale community, the range of possible systemic risk is very wide. Meanwhile, there is an extremely high probability that the systemic risk of a small-scale community will be quite large. However, the systemic risk of a larger-scale community is relatively stable and low. (2) If only communities with failed banks are considered, the regression analysis further shows that the influence of the size of the community on systemic risk roughly conforms with the law of power law distribution. Such a relationship between the scale of the community and systemic risk reveals that, in addition to studying financial risk from the perspective of the entire financial network system, we should also consider analyzing financial risk from the community structure level, which will have an important guiding role in the supervision of the financial system.
2. The Network Model and Analytical Methods
2.1. A Bank–Asset Bilateral Network Model
A complex network can be regarded as a set of non-empty finite point
V and a binary relation
E, where
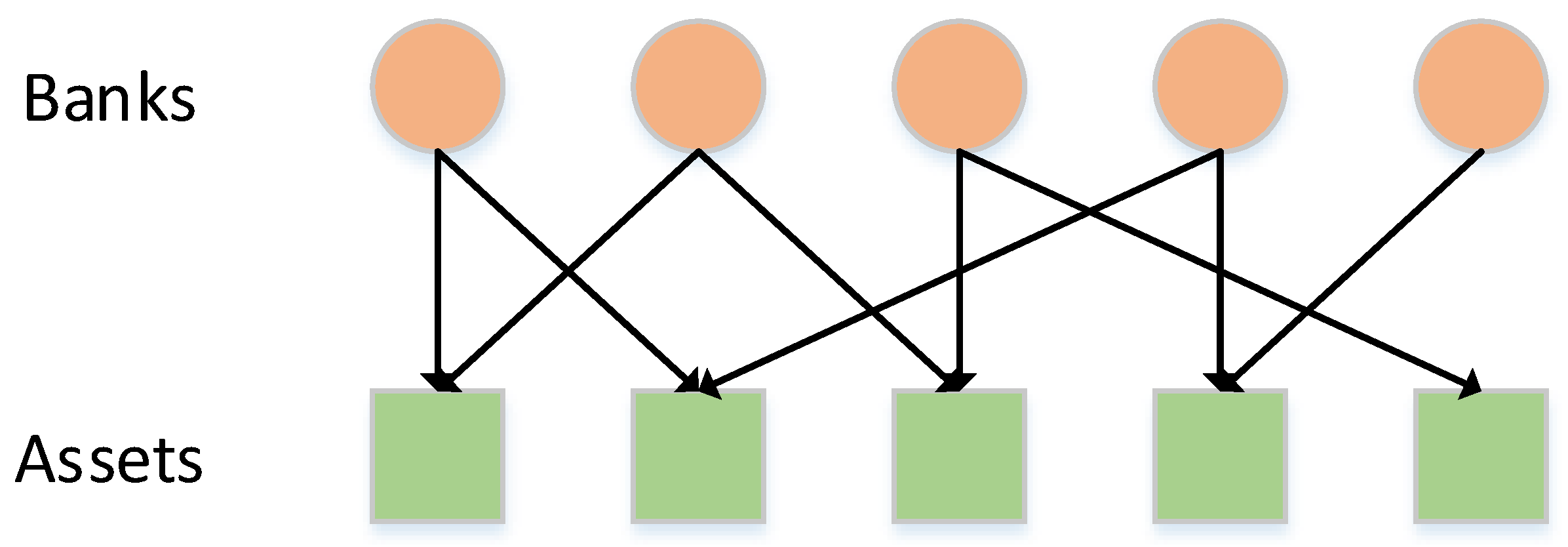
E refers to the edge set formed by the specific relationship between nodes. For a bank–asset bipartite network model, commercial banks and assets are regarded as 2 groups of nodes with different properties. The directional connection represents the relationship between banks holding assets. As shown in
Figure 1, if commercial bank
i holds asset
j, a link from bank
i to asset
j is generated.
When establishing complex networks of real systems, we take the proportion of asset investment as the weight of the edges. First, we establish a matrix , in which the element represents the value of the asset j held by bank i. Then, we divide each by the sum of the elements in the i-th row in matrix A and derive a quantity . represents the percentage of the total value of each asset held by the bank i. After that, we establish an investment matrix E, whose -th entry equals and where the sum of the elements in each row of E is equal to 1. The element is used to represent the weight of the edge between bank node i and asset node j. According to matrix E, the bank–asset bipartite network model can be constructed. For the bipartite network, the edges are directional and only exist between bank nodes and asset nodes. Since the two group nodes can be effectively connected, the relationship between the banks and the assets in the financial system can be displayed more truly and intuitively.
2.2. A Bank Correlation Network Model
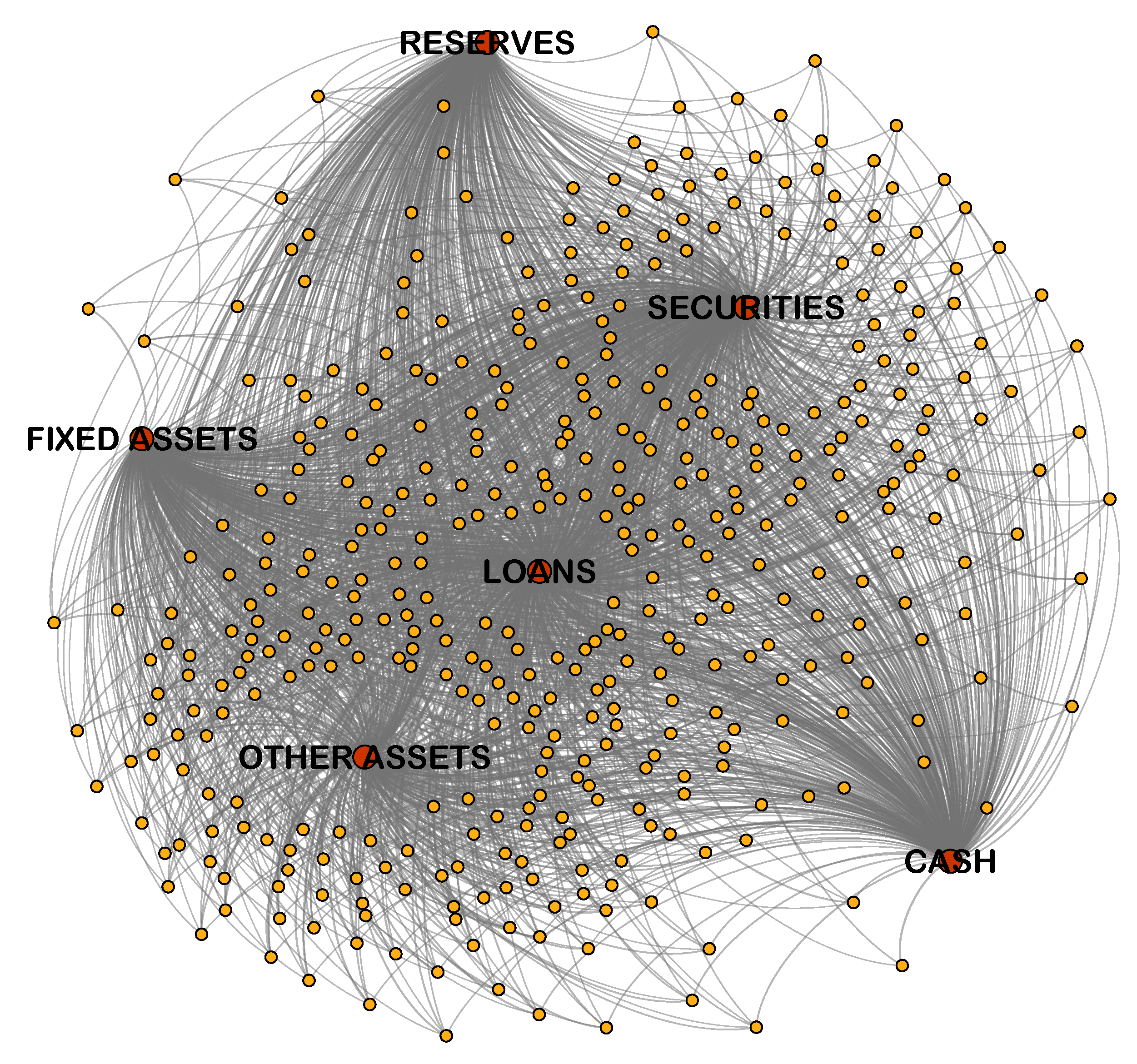
Based on a bank–asset bipartite network, we construct connected edges among banks based on the correlation of all banks’ investment portfolios and establish a connected network model among banks [
23]. For any 2 bank nodes
i and
j, we calculate the correlation coefficient
of their investment portfolio vector and obtain the correlation coefficient matrix:
where
. The value of
is close to 1, indicating a strong positive correlation between two bank nodes’ investment portfolios; conversely, a value close to −1 indicates a strong negative correlation. In order to avoid the negative weight of the connected edges in the network, we refer to the work of Mantegna (1999) [
10] and convert the correlation coefficient
to the distance value
, whose calculation formula is as follows:
where
. At this point, the relationship between
and
is monotonically decreasing. In order to ensure that the correlation coefficient and the weight of the edge change in the same direction, we introduce another formula as follows:
According to this formula, we obtain the final weight matrix . By combining this with the set of nodes, the bank correlation network can be constructed. The correlation network is a weighted and undirected network. Furthermore, since there is a correlation-based connection between any two banks, the network is a complete network model.
2.3. Community Division and Louvain Algorithm
Newman et al. (2003) defined a quantity called modularity to measure the quality of community structure [
24]. Modularity refers to the ratio of edges in the community to all edges in the network minus the expected value of such a ratio when the degree of all nodes in the network remains the same but the connections are uniformly randomly generated. The formula of modularity is as follows:
where
m represents the sum of the weights of all edges in the network,
represents the sum of the weights of all edges of node
i,
represents the weight of the edges between node
i and node
j, and
and
represent the community including node
i and
j. The function
indicates whether node
i and node
j are in the same community. If they are in the same community,
; otherwise, it is
. The module
Q can reflect the closeness of the nodes within the community, and its value range is [0, 1]. The larger the value of
Q is, the closer the community is.
Based on the concept of modularity, Vincent et al. (2008) proposed a fast community division algorithm, the Louvain algorithm [
25], which can accelerate the running time and rapid convergence of a community merger. The idea of the algorithm is: first, each node is regarded as an independent community. At this time, the number of communities is the same as the number of nodes. Then, we allocate node
i to the communities where its neighbor nodes are located in turn and calculate the modular change
after the allocation. The neighbor node with the largest value of
is recorded as
k. If the largest value of
is greater than 0, then we allocate node
i to the community where that neighbor node is located; otherwise, it remains unchanged. We repeat this process until the community structure to which all nodes belong is no longer changed, then the first iteration ends. In the process, the formula for calculating
when moving an isolated node
i to a community
C is as follows:
where
is the sum of the weights of the edges inside the community
C,
is the sum of the weights of the edges incident to nodes in
C,
is the sum of the weights of the edges incident to node
i,
represents the sum of the weights of the edges from
i to the nodes in community
C, and
m represents the sum of the weights of all the edges in the network.
At the end of the first-stage iteration, the local modularity will reach its maximum value. Then, the second stage is opened, and all the nodes in the same community are regarded as a new node. This new node will have a closed loop pointing to itself, whose weight is sum of the weights of the edges in the community. The weight of the edges between any two new nodes is the sum of the weights of all the edges between the two communities. Then, we repeat the process of the first-stage iteration until the modularity of the entire network is no longer changed and the community structure is divided.
In addition, Renaud Lambiote (2003) introduced a parameter called “Resolution” to flexibly control the number and size of community division [
26]. The resolution parameter can enlarge and reduce the number and scale of the community so as to realize the community division under different resolution levels and help to find the appropriate resolution level. When the resolution parameter approaches 1, the division is rough, the community scale is large, and the number of communities is small. When the resolution parameter approaches 0, the division is refined, the community scale is small, and the number of communities is large.
2.4. Nodes Importance and PageRank Algorithm
A node’s importance reflects the importance of the node in the network. There are many methods to measure the importance of nodes, such as node centrality, K-shell decomposition, the PageRank algorithm, and the LeaderRank algorithm [
27]. We will apply the PageRank algorithm [
28] developed by Lawrence Page to rank the importance of nodes, which has both speed and accuracy. The PageRank algorithm was originally developed to rank web pages by importance, and its basic assumption is that: (1) if a web page can be linked by many other web pages, the importance of the web page is higher; (2) if a highly important page links to another page, the importance of the page being linked to will also increase. The PageRank algorithm initially assigns the same importance score to each page, then designs an iterative algorithm based on these two assumptions to calculate the updated importance score of each page until the score is stable. The PageRank algorithm can be applied to any entity set that has the characteristic of mutual reference, and it is also suitable for ranking the importance of the nodes in a complex network. The PageRank value (PR) of node
i can be expressed as follows:
where
is the PageRank value of the node
i to be evaluated,
is the damping factor, and
can be understood as the probability of a random jump to other nodes. Generally,
,
represents the collection of all nodes pointing to node
i, and
represents the sum of the weights of node
j pointing to other nodes. The
value is closely related to the in-degree of the node, and when the in-degree of a node is large, the
value of that node tends to be larger.
Some studies show that, in a real network, the degree of most nodes is often very low and a few nodes will have a higher degree (these are called the central nodes). Only these central nodes can have a strong impact on other nodes. For many nodes, their connection path to the central nodes may be quite long, so the influence of the central nodes on them may be slow. To find out which other nodes will affect these nodes faster and more directly, the communities in which these nodes are located should also be explored, and their status in the community and their connections with other nodes should be judged. Therefore, the risk of a node is also most likely to be related to the community in which it is affected, which gives us a certain theoretical basis for studying the financial systemic risk from the perspective of community.
Since there are many methods of community division and the result of the division is not unique, it is necessary for us to use certain methods to test the reliability of the obtained community division result. In our previous paper [
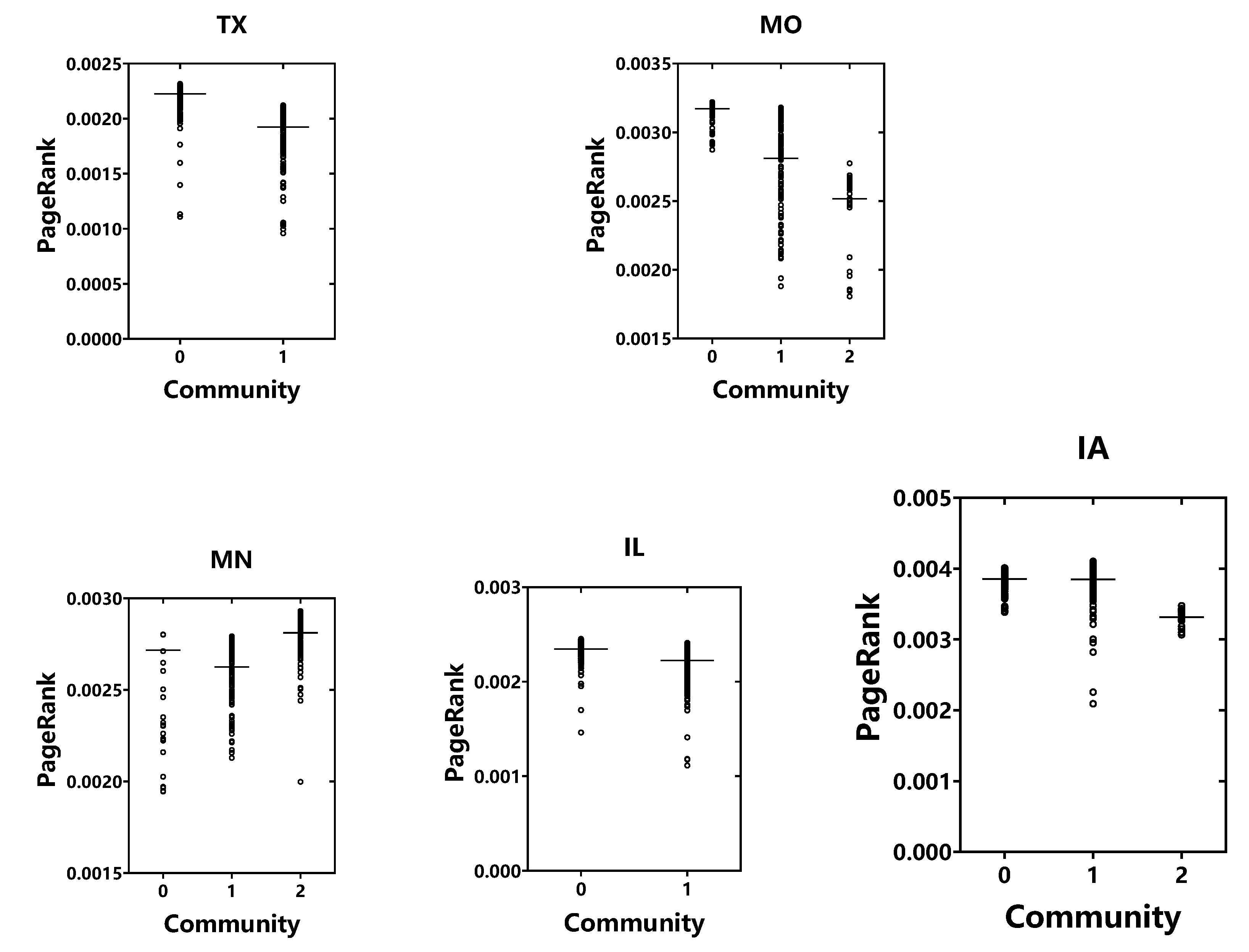
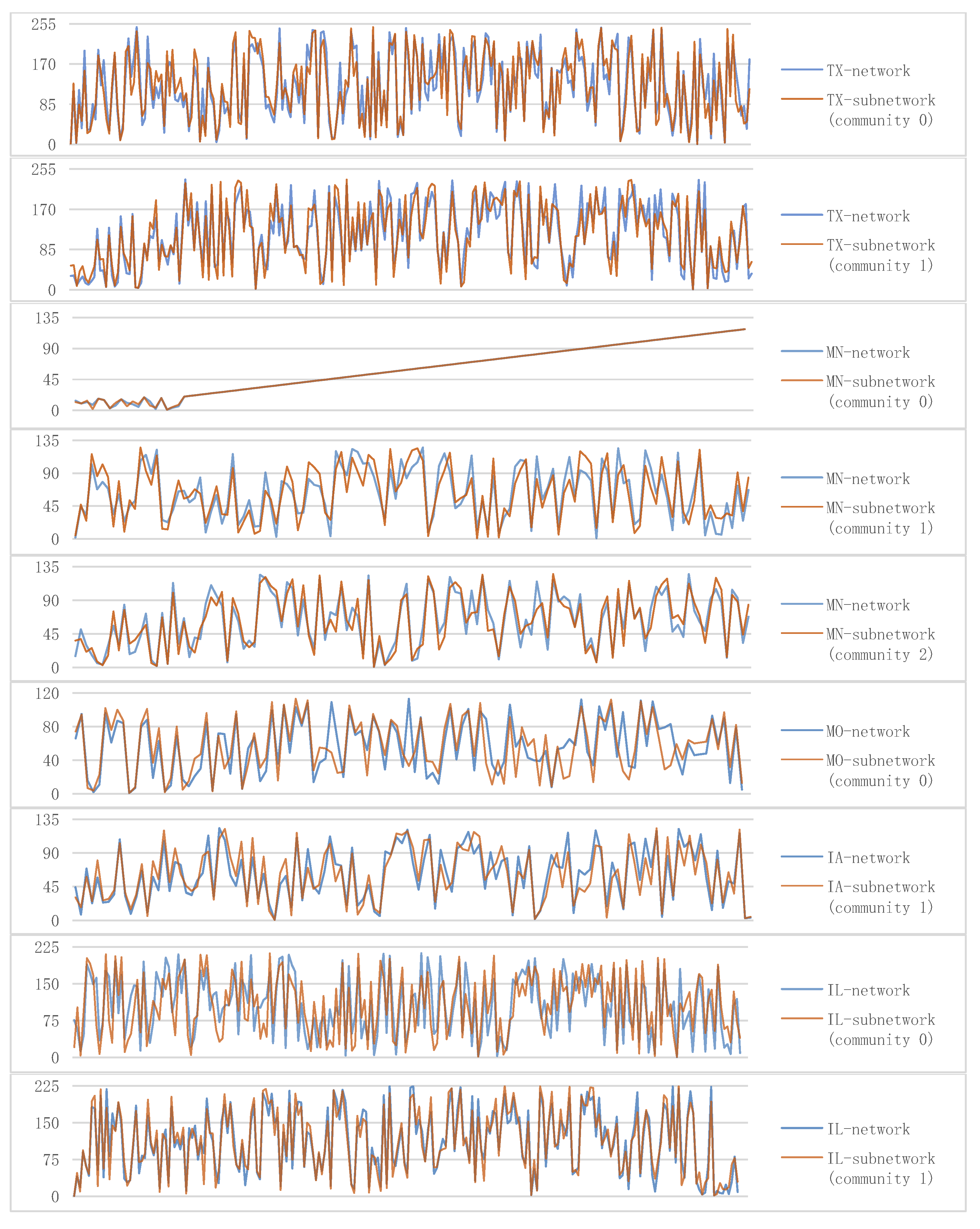
29], we used the Lovain algorithm to divide the communities of several types of networks with typical structures and analyzed the importance of nodes in the community sub-network. The results obtained show that there are obvious differences in the importance of nodes between different communities, and the importance ranking of all nodes in a community sub-network is highly consistent with their importance ranking in the original network, which fully demonstrates the significant effect of the community division. Based on this, we will first test the effectiveness of community structure division on bank correlation networks through the analysis of nodes importance, further analyze the differences in systemic risk between different community networks, and then explore the general law of financial systemic risk and community structure.
5. Conclusions
This paper studies the systemic risks of real financial networks based on the division of community structure. In a large-scale real financial network, the use of the community division method to analyze and monitor a community sub-network can effectively simplify the network model and allow for the exploration of the potential laws of the network, which plays an important role in the study of financial network systemic risk.
Firstly, based on the investment portfolio data of all commercial banks in the United States in 2008, the correlation between banks is calculated, a correlation network model of commercial banks in each state is constructed, and the community structure of each correlation network is divided. The distribution of node importance among different communities is obviously different. Moreover, for a community sub-network, the importance ranking of all nodes in a community sub-network is highly consistent with their ranking in the original network, which verifies the effectiveness of community division for the bank correlation network established in this paper. In addition, the robustness of the community division results is tested by extracting a portion of statistically significant edges from the bank correlation network.
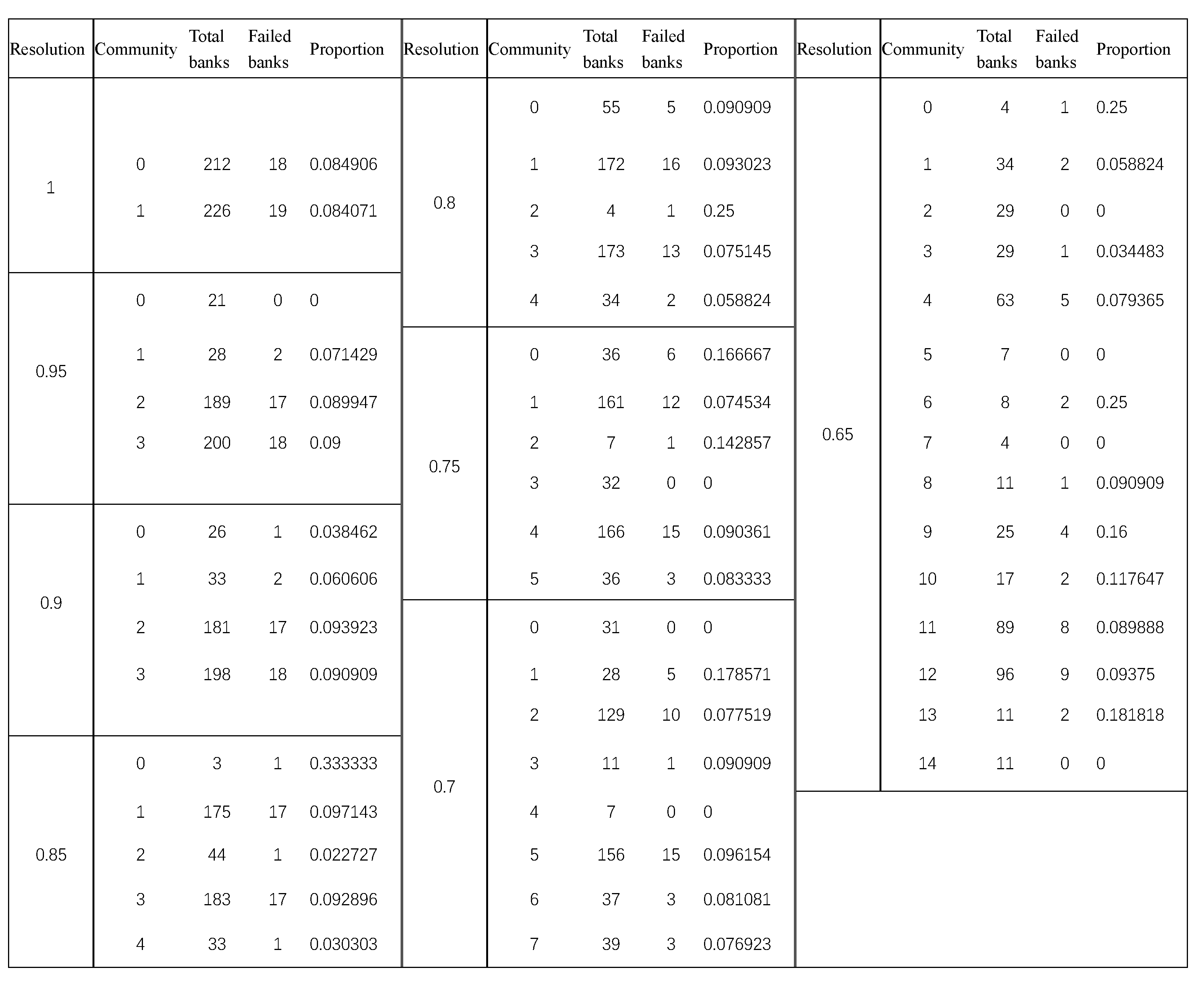
Then, we use the proportion of bank failures from 2008 to 2013 to measure the systemic risk and found that, for small communities, the financial systemic risk will appear to have obvious volatility. Specifically, systemic risk may be quite large or quite small, and the range of possible systemic risk is very wide. Meanwhile, there is an extremely high probability that the systemic risk of a small-scale community will be quite large. With the number of nodes in the community increasing, the systemic risk will tend towards a stable and low level. However, if only communities with failed bank are considered, the systemic risk will gradually decrease with the increase in community size, which almost conforms to the law of power law distribution. Therefore, the application of community structure division can help to identify communities with high financial systemic risk, thereby reducing the scope of network supervision from a whole network to a community sub-network, which plays a guiding role in maintaining the stability of the financial system and controlling the risk of the financial system.
In the future, it will be valuable to obtain, if possible, more actual data on bank liabilities or interbank interconnections to carry out more in-depth research and analysis. Besides this, we will further investigate the order of bank failures, analyze the type of communities in which they are located, and try to obtain the latest data to analyze the dynamic behavior of the network and assess the change in systemic risk over time. In addition, differences in actual conditions such as industry and national conditions will lead to the existence of many types of networks with different topology characteristics. In the follow-up study, the applicability of our research method in more different types of networks will be further discussed.