Abstract
We present linear-time algorithms computing the reversed Lempel–Ziv factorization [Kolpakov and Kucherov, TCS’09] within the space bounds of two different suffix tree representations. We can adapt these algorithms to compute the longest previous non-overlapping reverse factor table [Crochemore et al., JDA’12] within the same space but pay a multiplicative logarithmic time penalty.
1. Introduction
The non-overlapping reversed Lempel–Ziv (LZ) factorization was introduced by Kolpakov and Kucherov [1] as a helpful tool for detecting gapped palindromes, i.e., substrings of a given text T of the form for two strings S and G, where denotes the reverse of S. This factorization is defined as follows: Given a factorization for a string T, it is the non-overlapping reversed LZ factorization of T if each factor , for , is either the leftmost occurrence of a character or the longest prefix of whose reverse has an occurrence in . It is a greedy parsing in the sense that it always selects the longest possible such prefix as the candidate for the factor . The factorization can be written like a macro scheme [2], i.e., by a list storing either plain characters or pairs of referred positions and lengths, where a referred position is a previous text position from where the characters of the respective factor can be borrowed. Among all variants of such a left-to-right parsing using the reversed as a reference to the formerly parsed part of the text, the greedy parsing achieves optimality with respect to the number of factors [3] ([Theorem 3.1]) since the reversed occurrence of can be the prefix of any suffix in , and thus fulfills the suffix-closed property [3] ([Definition 2.2]).
Kolpakov and Kucherov [1] also gave an algorithm computing the reversed LZ factorization in time using bits of space, by applying Weiner’s suffix tree construction algorithm [4] on the reversed text . Later, Sugimoto et al. [5] presented an online factorization algorithm running in time using bits of space. We can also compute the reversed LZ factorization with the longest previous non-overlapping reverse factor table storing the longest previous non-overlapping reverse factor for each text position. There are algorithms [6,7,8,9,10] computing in linear time for strings whose characters are drawn from alphabets with constant sizes; their used data structures include the suffix automaton [11], the suffix tree of , the position heap [12], and the suffix heap [13]. Finally, Crochemore et al. [14] presented a linear-time algorithm working with integer alphabets by leveraging the suffix array [15]. To find the longest gapped palindromes of the form with the length of G restricted in a given interval , Dumitran et al. [16] ([Theorem 1]) restricted the distance of the previous reverse occurrence relative to the starting position of the respective factor within in their modified definition of , and achieved the same time and space bounds of [14]. However, all mentioned linear-time approaches use either pointer-based data structures of bits, or multiple integer arrays of length n to compute or the reversed LZ factorization.
1.1. Our Contribution
The aim of this paper is to compute the reversed LZ factorization in less space while retaining the linear time bound. For that, we follow the idea of Crochemore et al. [14] ([Section 4]) who built text indexing data structures on to compute for an artificial character #. However, they need random access to the suffix array, which makes it hard to achieve linear time for working space bounds within bits. We can omit the need for random access to the suffix array by a different approach based on suffix tree traversals. As a precursor of this line of research we can include the work of Gusfield [17] ([APL16]) and Nakashima et al. [18]. The former studies the non-overlapping Lempel–Ziv–Storer–Szymanski (LZSS) factorization [2,19] while the latter the Lempel–Ziv-78 factorization [20]. Although their used techniques are similar to ours, they still need bits of space. To actually improve the space bounds, we follow two approaches: On the one hand, we use the leaf-to-root traversals proposed by Fischer et al. [21] ([Section 3]) for the overlapping LZSS factorization [2] during which they mark visited nodes acting as signposts for candidates for previous occurrences of the factors. On the other hand, we use the root-to-leaf traversals proposed in [22] for the leaves corresponding to the text positions of T to find the lowest marked nodes whose paths to the root constitute the lengths of the non-overlapping LZSS factors. Although we mimic two approaches for computing factorizations different to the reversed LZ factorization, we can show that these traversals on the suffix tree of help us to detect the factors of the reversed LZ factorization. Our result is as follows:
Theorem 1.
Given a text T of length whose characters are drawn from an integer alphabet with size , we can compute its reversed LZ factorization
- in time using bits (excluding the read-only text T), or
- in time using bits,
for a selectable parameter .
On the downside, we have to admit that the results are not based on new tools, but rather a combination of already existing data structures with different algorithmic ideas. On the upside, Theorem 1 presents the first linear-time algorithm computing the reversed LZ factorization using a number of bits linear to the input text T, which is bits for . Interestingly, this has not yet been achieved for the seemingly easier non-overlapping LZSS factorization, for which we have time within the same space bound [22] ([Theorem 1]). We can also adapt the algorithm of Theorem 1 to compute , but losing the linear time for the -bits solution:
Theorem 2.
Given a text T of length whose characters are drawn from an integer alphabet with size , we can compute a -bits representation of its longest previous non-overlapping reverse factor table
- in time using bits (excluding the read-only text T), or
- in time using bits,
for a selectable parameter . We can augment our representation with an -bits data structure to provide constant-time random access to entries.
We obtain the -bits representation of with the same compression technique used for the permuted longest common prefix array [23] ([Theorem 1]), see [24] ([Definition 4]) for several other examples.
1.2. Related Work
To put the above theorems into the context of space-efficient factorization algorithms that can also compute factor tables like , we briefly list some approaches for different variants of the LZ factorization and of . We give Table 1 as an overview. We are aware of approaches to compute the overlapping and non-overlapping LZSS factorization, as well as the longest previous factor (LPF) table [25,26] and the longest previous non-overlapping table [14]. We can observe in Table 1 that only the overlapping LZSS factorization does not come with a multiplicative time penalty when working within bits. Note that the time and space bounds have an additional multiplicative penalty (unlike described in the references therein) because the currently best construction algorithms of the compressed suffix tree (described later in Section 2) works in time and needs bits of space [27] ([Section 6.1]).

Table 1.
Complexity bounds of related approaches described in Section 1.2 for a selectable parameter .
Regarding space-efficient algorithms computing the LZSS factorization, we are aware of the linear-time algorithm of Goto and Bannai [28] using bits of working space. For bits of space, Kärkkäinen et al. [29] can compute the factorization in time, which got improved to by Kosolobov [30]. Finally, the algorithm of Belazzougui and Puglisi [31] uses bits of working space and time.
Another line of research is the online computation of . Here, Okanohara and Sadakane [32] gave a solution that works in bits of space and needs time. This time bound got recently improved to by Prezza and Rosone [33].
1.3. Structure of This Article
This article is structured as follows: In Section 2, we start with the introduction of the suffix tree representations we build on the string , and introduce the reversed LZ factorization in Section 3. We present in Section 3.2 our solution for the claim of Theorem 1 without the referred positions, which we compute subsequently in Section 3.3. Finally, we introduce in Section 4, and give two solutions for Theorem 2. One is a derivation of our reversed-LZ factorization algorithm of Section 3.2.2 (cf. Section 4.1), the other is a translation of [14] ([Algorithm 2]) to suffix trees (cf. Section 4.2).
2. Preliminaries
With lg we denote the logarithm to base two. Our computational model is the word RAM model with machine word size for a given input size n. Accessing a word costs time.
Let T be a text of length whose characters are drawn from an integer alphabet with . Given with , then X, Y and Z are called a prefix, substring and suffix of T, respectively. We call the i-th suffix of T, and denote a substring with . For , and denote the empty set and the empty string, respectively. The reverse of T is the concatenation . We further write .
Given a character , and an integer j, the rank query counts the occurrences of c in , and the select query gives the position of the j-th c in T, if it exists. We stipulate that . If the alphabet is binary, i.e., when T is a bit vector, there are data structures [35,36] that use extra bits of space, and can compute and in constant time, respectively. There are representations [37] with the same constant-time bounds that can be constructed in time linear in . We say that a bit vector has a rank-support and a select-support if it is endowed by data structures providing constant time access to and , respectively.
From now on, we assume that there exist two special characters # and $ that do not appear in T, with for every character . Under this assumption, none of the suffixes of and has another suffix as a prefix. Let . R has length .
The suffix tree of R is the tree obtained by compacting the suffix trie, which is the trie of all suffixes of R. has leaves and at most internal nodes. The string stored in a suffix tree edge e is called the label of e. The children of a node v are sorted lexicographically with respect to the labels of the edges connecting the children with v. We identify each node of the suffix tree by its pre-order number. We do so implicitly such that we can say, for instance, that a node v is marked in a bit vector , i.e., , but actually have , where i is the pre-order number of v. The string label of a node v is defined as the concatenation of all edge labels on the path from the root to v; v’s string depth, denoted by , is the length of v’s string label. The operation returns the node with string label or the root node, given that the string label of v is S with or a single character, respectively. is undefined for the root node.
The leaf corresponding to the i-th suffix is labeled with the suffix number . We write for the suffix number of a leaf . The leaf-rank is the preorder rank () of a leaf among the set of all leaves. For instance, the leftmost leaf in has leaf-rank 1, while the rightmost leaf has leaf-rank . To avoid confusing the leaf-rank with the suffix number of a leaf, let us bear in mind that the leaf-ranks correspond to the lexicographical order of the suffixes (represented by the leaves) in R, while the suffix numbers induce a ranking based on the text order of R’s suffixes. In this context, the function returns the leaf whose suffix number is . The reverse function of on leaves is that returns the leaf whose suffix number is , or if (We do not need to compute for a leaf with , but want to compute for the border case .).
In this article, we focus on the following two representations: the compressed suffix tree (CST) [23,38] and the succinct suffix tree (SST) [21] ([Section 2.2.3]). Both can be computed in time, where the former is due to a construction algorithm given by Belazzougui et al. [27] ([Section 6.1]), and the latter due to [21] ([Theorem 2.8]), see Table 2. These two representations provide some of the above described operations in the time bounds listed in Table 3. Each representation additionally stores the pointer _ to the leaf with suffix number 1, and supports the following operations in constant time, independent of :

Table 2.
Construction time and needed space in bits for the succinct suffix tree (SST) and compressed suffix tree (CST) representations, cf. [21] ([Section 2.2]).

Table 3.
Time bounds for certain operations needed by our LZ factorization algorithms. Although not explicitly mentioned in [21], the time for is obtained with the Burrows–Wheeler transform [39] stored in the CST [38] ([A.1]) by constant-time partial rank queries, see [27] ([Section 3.4]) or [38] ([A.4]).
- returns the leaf-rank of the leaf ;
- returns the depth of the node v, which is the number of nodes on the path between v and the root (exclusive) such that root has depth zero;
- returns the level-ancestor of the on depth d; and
- returns the lowest common ancestor (LCA) of u and v.
As previously stated, we implicitly represent nodes by their pre-order numbers such that the above operations actually take pre-order numbers as arguments.
3. Reversed LZ Factorization
A factorization of T of size z partitions T into z substrings . Each such substring is called a factor. A factorization is called reversed LZ factorization if each factor is either the leftmost occurrence of a character or the longest prefix of that occurs at least once in , for . A similar but much well-studied factorization is the non-overlapping LZSS factorization, where each factor is either the leftmost occurrence of a character or the longest prefix of that occurs at least once in , for . See Figure 1 for an example and a comparison of both factorizations. In what follows, let z denote the number of reversed-LZ factors of T.
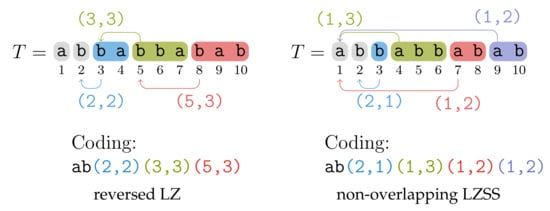
Figure 1.
The reversed LZ and the non-overlapping LZSS factorization of the string . A factor F is visualized by a rounded rectangle. Its coding consists of a mere character if it has no reference; otherwise, its coding consists of its referred position p and its length ℓ such that for the reversed LZ factorization, and for the non-overlapping LZSS factorization.
3.1. Coding
We classify factors into fresh and referencing factors: We say that a factor is fresh if it is the leftmost occurrence of a character. We call all other factors referencing. A referencing factor has a reference pointing to the ending position of its longest previous non-overlapping reverse occurrence; as a tie break, we always select the leftmost such ending position. We call this ending position the referred position of . More precisely, the referred position of a factor is the smallest text position j with and . If we represent each referencing factor as a pair consisting of its referred position and its length, we obtain the coding shown in Figure 1. Although our tie breaking rule selecting the leftmost position among all candidates for the referred position seems up to now arbitrary, it technically simplifies the algorithm in that we only have to index the very first occurrence.
3.2. Factorization Algorithm
In the following, we describe our factorization algorithm working with . This algorithm performs traversals on paths connecting leaves with the root, during which it marks certain nodes. One kind of these marked nodes are phrase leaves: A phrase leaf is a leaf whose suffix number is the starting position of a factor. We say that a phrase leaf corresponds to a factor F if the suffix number of ℓ is the starting position of F. We call all other leaves non-phrase leaves. Another kind are witnesses, a notion borrowed from [21] ([Section 3]): Witnesses are nodes that create a connection between referencing factors and their referred positions. We formally define them as follows: given is the phrase leaf corresponding to a referencing factor F, the witness w of F is the LCA of and a leaf with suffix number (with ) such that is the longest substring in that is a prefix of . The smallest such j is the referred position of , which is needed for the coding in Section 3.1. See Figure 2 for a sketch of the setting. In what follows, we show that the witness of a referencing factor F is the node whose string label is F. Generally speaking, for each substring S of T, there is always a node whose string label has S as a prefix, but there maybe no node whose string label is precisely S. This is in particular the case for the non-overlapping LZSS factorization [22] ([Section 3.1]). Here, we can make use of the fact that the suffix number for a referred position j is always larger than the length of T, which we want to factorize:
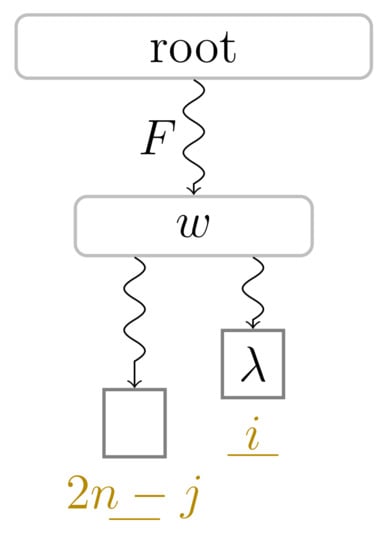
Figure 2.
Witness node w of a referencing factor F starting at text position i. Given j is the referred position of F, the witness w of F is the node in the suffix tree having (a) F as a prefix of its string label and (b) the leaves with suffix numbers and i in its subtree. lemWitness shows that w is uniquely defined to be the node whose string label is F.
Lemma 1.
The witness of each referencing factor exists and is well-defined.
Proof.
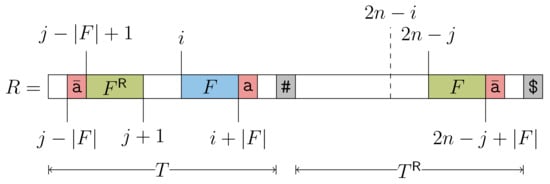
To show that each referencing factor is indeed the string label of an node, we review the definition of right-maximal repeats: A right-maximal repeat is a substring of R having at least two occurrences and with . A right-maximal repeat is the string label of an node since this node has at least two children; those two children are connected by edges whose labels start with and , respectively. It is therefore sufficient to show that each factor F is a right-maximal repeat. Given j is the referred position of , . If , then , and thus F is a right-maximal repeat. For the other case that , assume that F is not a right-maximal repeat. Then . However, this means that F is not the longest reversed factor being a prefix of , a contradiction. We visualized the situation in Figure 3. □

Figure 3.
A reversed-LZ factor F starting at position i in R with a referred position . If with , then we could extend F by one character, contradicting its definition to be the longest prefix of whose reverse occurs in . Hence, and F is a right-maximal repeat.
Consequently, the referred position of a factor is the smallest text position j in T with and one of the two equivalent conditions hold:
- ; or
- and have the longest common prefix of length ℓ.
3.2.1. Overview
We explain our factorization algorithm in terms of a cooperative game with two players (We use this notation only for didactic purposes; the terminology must not be confused with game theory. Here, the notion of player is basically a subroutine of the algorithm having private and shared variables.), whose pseudo code we sketched in Algorithm 1. Player 1 and Player 2 are allowed to access the leaves with suffix numbers in the ranges and , respectively. Player 1 (resp. Player 2) starts at the leaf with the smallest (resp. largest) suffix number, and is allowed to access the leaf with the subsequently next (resp. previous) suffix number via (resp. ). Hence, Player 1 simulates a linear forward scan in the text T, while Player 2 simulates a linear backward scan in . Both players take turns at accessing leaves at the same pace. To be more precise, in the i-th turn, Player 1 processes the leaf with suffix number i, whereas Player 2 processes the leaf with suffix number . In one turn, a player accesses a leaf and maybe performs a traversal on the path connecting the root with . For such a traversal, we use level ancestor queries to traverse each node on the path in constant time. Whenever Player 2 accesses the leaf with suffix number n (shared among both players), the game ends; at that time both players access the same leaf (cf. Line 6 in Algorithm 1). In the following, we call this game a pass (with the meaning that we pass all relevant text positions). Depending on the allowed working space, our algorithm consists of one or two passes (cf. Section 3.3). The goal of Player 2 is to keep track of all nodes she visits. Player 2 does this by maintaining a bit vector of length such that stores whether a node v has already been visited by Player 2, where we represent a node v by its pre-order number when using it as an index of a bit vector. To keep things simple, we initially mark the root node in at the start of each pass. By doing so, after the i-th turn of Player 2 we can read any substring of by a top-down traversal from the suffix tree root, only visiting nodes marked in . This is because of the invariant that the set of nodes marked in is upper-closed, i.e., if a node v is marked in , then all its ancestors are marked in as well.
The goal of Player 1 is to find the phrase leaves and the witnesses. For that, she maintains two bit vectors and of length n and , respectively, whose entries are marked similarly to by using the suffix numbers () of the leaves accessed by Player 1 and preorder numbers of the internal nodes. We initially mark _ in since text position 1 is always the starting position of the fresh factor . By doing so, after the i-th turn of Player 1 we know the ending positions of those factors contained in , which are marked in . To sum up, after the i-th turn of both players we know the computed factors starting at text positions up to i thanks to Player 1, and can find the factor lengths thanks to Player 2, which we explain in detail in Section 3.2.2. There, we will show that the actions of Player 2 allow Player 1 to determine the starting position of the next factor. For that, she computes the string depth of the lowest ancestor marked in of the previously visited phrase leaf. See Appendix A.
As a side note: since we are only interested in the factorization of (omitting the appended # at position n), we do not need Player 1 to declare the leaf with suffix number n a phrase leaf. We also terminate the algorithm when both players meet at position n without checking whether we have found a new factor starting at position n.
| Algorithm 1: Algorithm of Section 3.2.2 computing the non-overlapping reversed LZ factorization. The function is described in Section 3.3. |
 |
3.2.2. One-Pass Algorithm in Detail
In detail, a pass works as follows: at the start, Player 1 and Player 2 select and , i.e., the leaves with suffix numbers 1 and , respectively. Now the players take action in alternating turns, starting with Player 1. Nevertheless, we first explain the actions of Player 2, since Player 2 acts independently of Player 1, while Player 1’s actions depend on Player 2.
Suppose that Player 2 is at a leaf (cf. Line 20 of Algorithm 1). Player 2 traverses the path from to the root upwards and marks all visited nodes in until arriving at a node v already marked in (such a node exists since we mark the root in at the beginning of a pass.). When reaching the marked node v, we end the turn of Player 2, and move Player 2 to at Line 23 (and terminate the whole pass in Line 6 when this leaf has suffix number n). The foreach loop (Line 20) of the algorithm can be more verbosely expressed with a loop iterating over all depth offsets d in increasing order while computing until either reaching the root or a node marked in . Subsequently, the turn of Player 1 starts (cf. Line 7). We depict the state after the first turn of Player 2 in Figure 4.
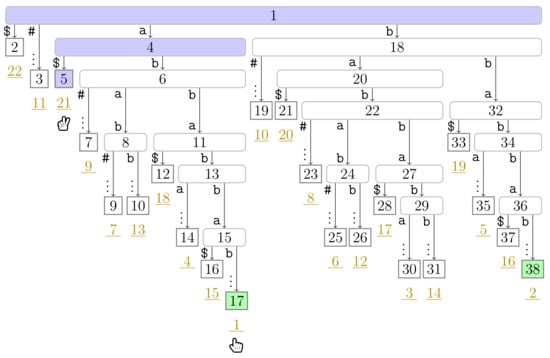
Figure 4.
Suffix tree of used in Section 3.2, where is our running example. The nodes are labeled by their preorder numbers. The suffix number of each leaf is the underlined number drawn in dark yellow below . We trimmed the label of each edge to a leaf having more than two characters and display only the first character and the vertical dots ‘⋮’ as a sign of omission. The tree shows the state of Algorithm 1 after the first turn of both players. The nodes visited by Player 2 are colored in blue ( ), the phrase leaves are colored in green (
), the phrase leaves are colored in green ( ). Player 1 and 2 are represented by the hands
). Player 1 and 2 are represented by the hands  and
and  , respectively, pointing to the respective leaves they visited during the first turn.
, respectively, pointing to the respective leaves they visited during the first turn.
 ), the phrase leaves are colored in green (
), the phrase leaves are colored in green ( ). Player 1 and 2 are represented by the hands
). Player 1 and 2 are represented by the hands  and
and  , respectively, pointing to the respective leaves they visited during the first turn.
, respectively, pointing to the respective leaves they visited during the first turn.
If Player 1 is at a non-phrase leaf , we skip the turn of Player 1, move Player 1 to at Line 19, and let Player 2 take action. Now suppose that Player 1 is at a phrase leaf corresponding to a factor F. Then we traverse the path from the root to downwards to find the lowest ancestor w of marked in . If w is the root node, then F is a fresh factor (cf. Line 11), and we know that the next factor starts immediately after F (cf. Line 13). Consequently, the leaf is a phrase leaf. Otherwise, w is the witness of , and (cf. Line 14). Hence, is the suffix number of the phrase leaf that Player 1 will subsequently access. We therefore mark w and in and in , respectively (cf. Lines 16 and 18). We depict the fifth turn of our running example in Figure 5, during which Player 1 marks a witness node. Finally, we end the turn of Player 1, move Player 1 to at Line 19, and let Player 2 take action.
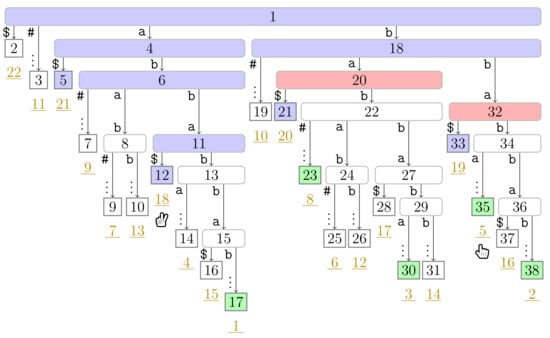
Figure 5.
Continuation of Figure 4 with the state at the fifth turn of Player 1. Additionally to the coloring used in Figure 4, witnesses are colored in red ( ). In this figure, Player 1 just finished her turn on making the node with preorder number 32 the witness w of the leaf with suffix number 5. With w we know that the factor starting at text position 5 has the length and that the next phrase leaf has suffix number 8. For visualization purposes, we left the hand (
). In this figure, Player 1 just finished her turn on making the node with preorder number 32 the witness w of the leaf with suffix number 5. With w we know that the factor starting at text position 5 has the length and that the next phrase leaf has suffix number 8. For visualization purposes, we left the hand ( ) of Player 2 below the leaf of her last turn.
) of Player 2 below the leaf of her last turn.
 ). In this figure, Player 1 just finished her turn on making the node with preorder number 32 the witness w of the leaf with suffix number 5. With w we know that the factor starting at text position 5 has the length and that the next phrase leaf has suffix number 8. For visualization purposes, we left the hand (
). In this figure, Player 1 just finished her turn on making the node with preorder number 32 the witness w of the leaf with suffix number 5. With w we know that the factor starting at text position 5 has the length and that the next phrase leaf has suffix number 8. For visualization purposes, we left the hand ( ) of Player 2 below the leaf of her last turn.
) of Player 2 below the leaf of her last turn.
Correctness. When Player 1 accesses the leaf with suffix number i, Player 2 has processed all leaves with suffix numbers . Due to the leaf-to-root traversals of Player 2, each node marked in has a leaf with a suffix number in in its subtree. In particular, a node w is marked in if and only if the string label of w is a substring of . Because , the longest prefix of having a reversed occurrence in is therefore one of the string labels of the nodes marked in . In particular, we search the longest string label among those nodes, which we obtain with the lowest ancestor of marked in .
3.2.3. Time Complexity
First, let us agree on that we never compute the suffix number of a leaf since this is a costly operation for CST (cf. Table 3). Although we need the suffix numbers at multiple occasions, we can infer them if each player maintains a counter for the suffix number of the currently visited leaf. A counter is initialized with 1 (resp. ) and becomes incremented (resp. decremented) by one when moving to the succeeding (resp. preceding) leaf in suffix number order. This works since both players traverse the leaves linearly in the order of the suffix numbers (either in ascending or descending order).
Player 2 visits n leaves, and visits only unvisited nodes during a leaf-to-root traversal. Hence, Player 2’s actions take overall time.
Player 1 also visits n leaves. Since Player 1 has no business with the non-phrase leaves, we only need to analyze the time spent by Player 1 for a phrase leaf corresponding to a factor F: If F is fresh, then the root-to-leaf traversal ends prematurely at the root, and hence we can determine in constant time whether F is fresh or not. If F is referencing, we descend from the root to the lowest ancestor w marked in , and compute to determine the suffix number of the next phrase leaf (cf. Line 15 of Algorithm 1). Since , we visit at most nodes before reaching w. Computing takes time for the SST, and time for the CST. This seems costly, but we compute for each factor only once. Since the sum of all factor lengths is n, we spend time or time for computing all factor lengths when using the SST or the CST, respectively. We finally obtain the time bounds stated in Theorem 1 for computing the factorization.
3.3. Determining the Referred Position
Up to now, we can determine the reversed-LZ factors with marking the starting position of each factor with a one. Yet, we have not the referred positions necessary for the coding of the factors (cf. Section 3.1). To obtain them, we have two options: The first option is easier but comes with the requirement for a support data structure on for the operation
- returning the maximum among all suffix numbers of the leaves in the subtree rooted in v.
We can build such a support data structure in time (resp. time) using bits to support in time (resp. time) for the SST (resp. CST); see [22] ([Section 3.3]). Being able to query , we can directly compute the referred position of a factor F when discovering its witness w during a turn of Player 1 by . gives us the suffix number of a leaf that has already been accessed by Player 2 since Player 2 accesses the leaves in descending order with respect to the suffix numbers, and w must have already been accessed by Player 2 during a leaf-to-root traversal (otherwise w would not have been marked in ). Since , the referred position of F is . Consequently, we can compute the coding of the factors during a single pass (cf. Line 17 of Algorithm 1), and are done when the pass finishes.
The second option does not need to compute and retains the linear time bound when using CST. Here, the idea is to run an additional pass, whose pseudo code is given in Algorithm 2. For this additional pass, we do the following preparations: Let be the number of witnesses, which is at most z since there can be multiple factors having the same witness. We keep and marking the phrase leaves and the witnesses, respectively. However, we clear such that Player 2 has again the job to log her visited nodes in . We augment with a rank-support such that we can enumerate the witnesses with ranks from 1 to at most , which we call the witness rank. We additionally create an array W of bits. We want to store the referred position for each witness w such that we can read the respective referred position from W when Player 1 accesses w. We assign the task for maintaining W to Player 2. Player 2 can handle this task by taking additional action when visiting a witness (i.e., a node marked in ) during a leaf-to-root traversal: When visiting a witness node w with witness rank i from a leaf , we write if w is not yet marked in (cf. Line 15 in Algorithm 2). Like before, Player 2 terminates her turn whenever she visits an already visited node. The actions of Player 1 differ in that she no longer needs to compute and : When Player 1 visits a phrase leaf , she locates the lowest ancestor w of marked in , which has to be marked in , too (as a side note: storing the depth of the witness of each phrase leaf in a list, sorted by the suffix numbers of these leaves, helps us to directly jump to the respective witness in constant time. We can encode this list as a bit vector of length by storing each depth in unary coding (cf. [22] ([Section 3.4])). Nevertheless, we can afford the root-to-witness traversals of Player 1 since we visit at most nodes in total.). With the rank-support on , we can compute w’s witness rank i, and obtain the referred position of with (cf. Line 10 of Algorithm 2). We show the final state after the first pass in Figure 6, together with W computed in the second pass.
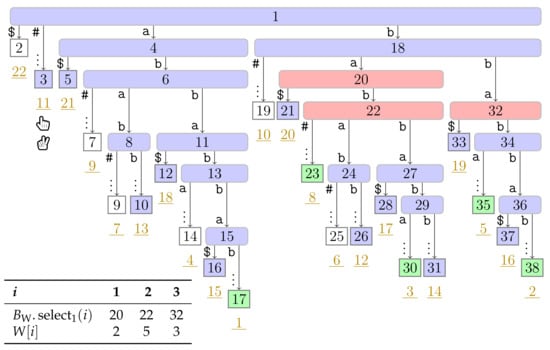
Figure 6.
State of our running example at termination of Algorithm 1. We have computed the bit vector of length storing a one at the entries , and 8, i.e., the suffix numbers of the phrase leaves, which are marked in green ( ), and the bit vector of length 38 (the maximum preorder number of an node) storing a one at the entries , and 32, i.e., the preorder numbers of the witnesses, which are colored red (
), and the bit vector of length 38 (the maximum preorder number of an node) storing a one at the entries , and 32, i.e., the preorder numbers of the witnesses, which are colored red ( ). During the second pass described in Section 3.3, we compute W storing the referred positions in the order of the witness ranks (left table).
). During the second pass described in Section 3.3, we compute W storing the referred positions in the order of the witness ranks (left table).
 ), and the bit vector of length 38 (the maximum preorder number of an node) storing a one at the entries , and 32, i.e., the preorder numbers of the witnesses, which are colored red (
), and the bit vector of length 38 (the maximum preorder number of an node) storing a one at the entries , and 32, i.e., the preorder numbers of the witnesses, which are colored red ( ). During the second pass described in Section 3.3, we compute W storing the referred positions in the order of the witness ranks (left table).
). During the second pass described in Section 3.3, we compute W storing the referred positions in the order of the witness ranks (left table).
Overall, the time complexity is time when working with either the SST or the CST. We use additional bits of space for the rank-support of , but costly bits for the array W. However, we can bound by since is the number of distinct reversed LZ factors, and by an enumeration argument [40] ([Thm. 2]), a text of length n can be partitioned into at most distinct factors. Hence, we can store W in bits of space. With that, we finally obtain the working space bound of bits for the CST solution as claimed in Theorem 1.
| Algorithm 2: Determining the referred positions in a second pass described in Section 3.3. |
 |
4. Computing
The longest previous non-overlapping reverse factor table is an array such that is the length of the longest prefix of occurring as a substring of . (Appending # at the end is not needed, but simplifies the analysis for having precisely n characters.) Having , we can iteratively compute the reversed LZ factorization because with for .
The counterpart of for the non-overlapping LZSS factorization is the longest previous non-overlapping factor table , which is defined similarly, but stores the maximal length of the longest common prefix (LCP) of with all substrings for . See Table 4 for a comparison. Analogously to [34] ([Corollary 5]) or [24] ([Definition 4]) for the longest previous factor table [22,26] ([Lemma 1]) for , holds the following property:

Lemma 2
([14] (Lemma 2)). for .
Hence, we can encode in bits by writing the differences in unary, obtaining a bit sequence of (a) n ones for the n entries and (b) many zeros. We can decode this bit sequence by reading the differences linearly because we know that .
4.1. Adaptation of the Single-Pass Algorithm
Having an -bits representation of gives us hope to find an algorithm computing in a total workspace space of bits. Indeed, we can adapt our algorithm devised for the reversed LZ factorization to compute . For that, we just have to promote all leaves to phrase leaves such that the condition in Line 7 of Algorithm 1 is always true. Consequently, Player 1 performs a root-to-leaf traversal for finding the lowest node marked in of each leaf. By doing so, the time complexity becomes , however, since we visit at most many nodes during the root-to-leaf traversals (there are strings like for which this sum becomes ).
To lower this time bound, we follow the same strategy as in [22] ([Section 3.5]) or [34] ([Lemma 6]) using and Lemma 2: After Player 1 has computed for w being the lowest ancestor marked in of the leaf with suffix number , we cache for the next turn of Player 1 such that Player 1 can start the root-to-leaf traversal to the leaf with suffix number i directly from and thus skips the nodes from the root to . This works because is the ancestor of with , and must have been marked in since . See Figure 7 for a visualization. By skipping the nodes from the root to , we visit only many nodes during the i-th turn of Player 1. A telescoping sum together with Lemma 2 shows that Player 1 visits nodes in total.
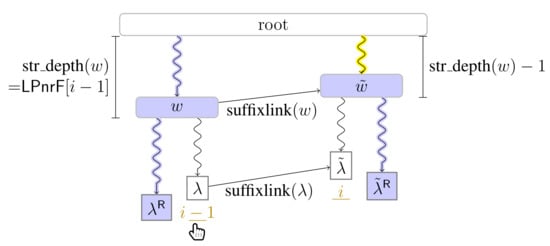
Figure 7.
Setting of Section 4.1. Nodes marked in are colored in blue ( ). Curly arcs symbolize paths that can visit multiple nodes (which are not visualized). When visiting the lowest ancestor of marked in for computing , Player 1 determines such that she can skip the nodes on the path from the root to the leaf for computing (these nodes are symbolized by the curly arc highlighted in yellow (
). Curly arcs symbolize paths that can visit multiple nodes (which are not visualized). When visiting the lowest ancestor of marked in for computing , Player 1 determines such that she can skip the nodes on the path from the root to the leaf for computing (these nodes are symbolized by the curly arc highlighted in yellow ( ) on the right). There are leaves and with suffix numbers of at least and , respectively, since otherwise w would not have been marked in by Player 2.
) on the right). There are leaves and with suffix numbers of at least and , respectively, since otherwise w would not have been marked in by Player 2.
 ). Curly arcs symbolize paths that can visit multiple nodes (which are not visualized). When visiting the lowest ancestor of marked in for computing , Player 1 determines such that she can skip the nodes on the path from the root to the leaf for computing (these nodes are symbolized by the curly arc highlighted in yellow (
). Curly arcs symbolize paths that can visit multiple nodes (which are not visualized). When visiting the lowest ancestor of marked in for computing , Player 1 determines such that she can skip the nodes on the path from the root to the leaf for computing (these nodes are symbolized by the curly arc highlighted in yellow ( ) on the right). There are leaves and with suffix numbers of at least and , respectively, since otherwise w would not have been marked in by Player 2.
) on the right). There are leaves and with suffix numbers of at least and , respectively, since otherwise w would not have been marked in by Player 2.
The final bottleneck for CST are the n evaluations of to compute the actual values of (cf. Line 15 of Algorithm 1). Here, we use a support data structure on CST for [34] ([Lemma 6]), which can be constructed in time, uses bits of space, and answers in time. This finally gives Theorem 2.
4.2. Algorithm of Crochemore et al.
We can also run the algorithm of Crochemore et al. [14] ([Algorithm 2]) with our suffix tree representations to obtain the same space and time bounds as stated in Theorem 2. For that, let us explain this algorithm in suffix tree terminology: For each leaf with suffix number i, the idea for computing is to scan the leaves for the leaf with being the referred position, and hence the string depth of is . To compute , we approach from the left and from the right to find (resp. ) having the deepest LCA with among all leaves to the left (resp. right) side of whose suffix numbers are greater than . Then either or is . Let and . Then , and the referred position is either or , depending on whose respective LCA has the deeper string depth. Note that the referred positions in this algorithm are not necessarily always the leftmost possible ones.
Correctness. Let j be the referred position of the leaf with suffix number i such that and have the LCP F of length . Due to Lemma 1, there is a suffix tree node w whose string label is F. Consequently, and the leaf with suffix number are in the subtree rooted at w. Now suppose that we have computed and according to the above described algorithm. On the one hand, let us first assume that (the case is treated symmetrically). By definition of , there is a descendant of w with the string depth , and has both and in its subtree. However, this means that and have a common prefix longer than , a contradiction to storing the length of the longest such LCP. On the other hand, let us assume that . Then w is a descendant of the node being the LCA of and . Without loss of generality, let us stipulate that the leaf with suffix number is to the right of (the other case to the left of works with by symmetry). Then is to the left of , i.e., is between and . Since , this contradicts the selection of to be the closest leaf on the right hand side of with a suffix number larger than .
Finding the Starting Points. Finally, to find the starting points of and being initially the leaves with the maximal suffix number to the left and to the right of , respectively, we use a data structure for answering.
- returning the leaf with the maximum suffix number among all leaves whose leaf-ranks are in .
We can modify the data structure computing in Section 3.3 to return the leaf-rank instead of the suffix number (the used data structure for first computes the leaf-rank and then the respective suffix number). Finally, we need to take the border case into account that is the leftmost leaf or the rightmost leaf in the suffix tree, in which case we only need to approach from the right side or from the left side, respectively.
The algorithm explained up to now already computes correctly, but visits leaves per entry, or leaves in total. To improve this bound to leaves, we apply two tricks. To ease the explanation of these tricks, let us focus on the right-hand side of ; the left-hand side is treated symmetrically.
Overview for Algorithmic Improvements. Given we want to compute , we start with a pointer to a leaf to the right of with suffix number larger than , and approach with from the right until there is no leaf closer to on its right side with a suffix number larger than . Then is , and we can compute being the string depth of the LCA of and . If we scan linearly the suffix tree leaves to reach with the pointer , this gives us leaves to process. Now the first trick lets us reduce the number of these leaves up to many for computing . The broad idea is that with the operation we can find a leaf closer to whose LCA is at least one string depth deeper than the LCA with the previously processed leaf. In total, the first trick helps us to compute by processing at most many leaves. In the second trick, we show that we can reuse the already computed neighboring leaves and by following their suffix links such we process at most many leaves (instead of ) for computing . Finally, by a telescoping sum, we obtain a linear number of leaves to process.
First Trick. The first trick is to jump over leaves whose respective suffixes all share the same longest common prefix with . We start with being the leaf on the right-hand side of with the largest suffix number. As long as , we search the leftmost leaf between and (to be more precise: ) with . Having , we consider:
- If (meaning is to the right of and there is no leaf between and ), we terminate.
- Otherwise, we set to the leaf with the largest suffix number among the leaves with leaf-ranks in the range . If , we set and recurse. Otherwise we terminate.
On termination, because there is no leaf on the right of closer to than with and . Hence, is the referred position, and we continue with the computation of . See Figure 8 for a visualization.
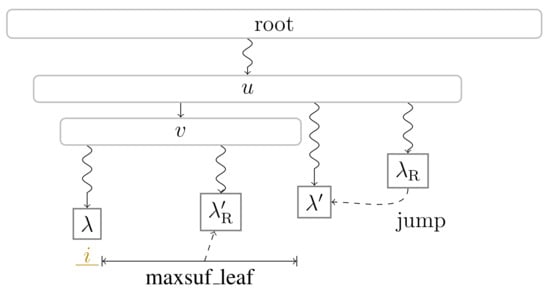
Figure 8.
Computing with [14] ([Algorithm 2]) as explained in Section 4.2. Starting at the leaf , we jump to the leftmost leaf with . Then, we use the operation returning the leaf-rank of the leaf having the largest suffix number among the query interval . If , we recurse by setting . The LCA of and is at least as deep as the child v of u on the path towards (the figure shows the case that ), and hence is at least if we recurse.
Broadly speaking, the idea is that the closer gets to , the deeper the string depth of becomes. However, we have to stop when there is no closer leaf with a suffix number larger than . So we first scan until reaching a having the same lowest common ancestor with , and then search within the interval of leaves between and for the remaining leaf with the largest suffix number. We search for because we can jump from to with a range minimum query on the LCP array returning the index of the leftmost minimum in a given range. We can answer this query with an -bits data structure in or time for the SST or the CST, respectively, and build it in time or time (cf. [22] ([Section 3.3]) and [41] ([Lemma 3]) for details). However, with this algorithm, we may visit as many leaves as since each jump from to via brings us at least one value closer to . To lower this bound to leaf-visits, we again make use of Lemma 2 (cf. Section 4.1), but exchange with (or respectively ) in the statement of the lemma.
Second Trick. Assume that we have computed with . We subsequently set , but also . Now has suffix number i. If , then the string depth of the is , and is lexicographically larger than ; hence is to the right of with (generally speaking, given two leaves and whose LCA is not the root, then if and only if .). Otherwise (), we reset . By doing so, we assure that is always a leaf to the right of with (if such a leaf exists), and that we have already skipped string depths for the search of with . Since , the telescoping sum shows that we visit leaves in total.
In total, we obtain an algorithm that visits leaves, and spends or time per leaf when using the SST or the CST, respectively. We need bits of working space on top of since we only need the values , , , and to compute . We note that Crochemore et al. [14] do not need the suffix tree topology, since they only access the suffix array, its inverse, and the LCP array, which we translated to leaves and the string depths of their LCAs.
5. Open Problems
There are some problems left open, which we would like to address in what follows:
5.1. Overlapping Reversed LZ Factorization
Crochemore et al. [14] ([Section 5]) gave a variation of that supports overlaps, and called the resulting array the longest previous reverse factor table , where is the maximum length ℓ such that for a . The respective factorization, called the overlapping reversed LZ factorization, was proposed by Sugimoto et al. [5] ([Definition 4]): A factorization is called the overlapping reversed LZ factorization of T if each factor is either the leftmost occurrence of a character or the longest prefix of that has at least one reversed occurrence in starting before , for . We can compute the overlapping reversed LZ factorization with analogously to computing the (non-overlapping) reversed LZ factorization with . As an example, the overlapping reversed LZ factorization of is . Table 4 gives an example for .
Since by definition, the overlapping factorization seems more likely to have fewer factors. Unfortunately, this factorization cannot be expressed in a compact coding like Section 3.1 that stores enough information to restore the original text. To see this, take a palindrome P, and compute the overlapping reversed LZ factorization of . The factorization creates the two factors a and . The second factor is since . However, a coding of the second factor needs to store additional information about P to support restoring the characters of this factor. It seems that we need to store the entire left arm of P, including the middle character for odd palindromes.
Besides searching for an efficient coding for the overlapping reversed LZ factorization, we would like to improve the working space bounds needed for its computation. All algorithms we are aware of [5,14] embrace Manacher’s algorithm [42,43] to find the maximal palindromes of each text position. To run in linear time, Manacher stores the arm lengths of these palindromes in a plain array of bits. Unfortunately, we are unaware of any time/space trade-offs regarding this array.
5.2. Computing in Linear Time with Compressed Space
Having a -bit representation for four different kinds of longest previous factor tables (we can exchange with in the proof of Lemma 2), we wonder whether it is possible to compute any of these variants in linear time with bits of space. If we want to compute or within a working space of bits, it seems hard to achieve linear running time. That is because we need access to the string depth of the suffix tree node w for each entry (resp. ), where w is the lowest node having the leaf with suffix number i and a leaf with a suffix number less than i (resp. greater than for ) in its subtree, cf. [34] ([Lemma 6]) for and the actions of Player 1 in Section 4.1 for . While we need to compute for determining the starting position of the subsequent factor (i.e., suffix number of the next phrase leaf, cf. Line 16) for the reversed LZ factorization, the algorithms for computing (cf. [34] ([Lemma 6]) or [44] ([Section 3.4.4])) and work independently of the computed factor lengths and therefore can store a batch of -queries. Our question would be whether there is a such that we can accesses suffix array positions with a -bits suffix array representation in time. (We can afford storing integers of bits in bits.) Grossi and Vitter [45] ([Theorem 3]) have a partial answer for sequential accesses to suffix array regions with large LCP values. Belazzougui and Cunial [24] ([Theorem 1]) experienced the same problem for computing matching statistics, but could evade the evaluation of with backward search steps on the reversed Burrows–Wheeler transform. Unfortunately, we do not see how to apply their solution here since the referred positions of and have to belong to specific text ranges (which is not the case for matching statistics).
5.3. Applications in Compressors
Although it seems appealing to use the reversed LZ factorization for compression, we have to note that the bounds for the number of factors z are not promising:
Lemma 3.
The size of the reversed LZ factorization can be as small as and as large as n.
Proof.
The lower bound is obtained for with since for with being a (not necessarily proper) prefix of . For the upper bound, we consider the ternary string whose factorization consists only of factors of length one since has no substring of T of length 2 (namely, ab, bc, or ca) as a substring (cf. [46] ([Theorem 5])). □
Even for binary alphabets, there are strings for which :
Lemma 4
([46] (Theorem 9)). There exists an infinite text T whose characters are drawn from the binary alphabet such that, for every substring S of T with , is not a substring of T.
Funding
This work is funded by the JSPS KAKENHI Grant Numbers JP18F18120 and JP21K17701.
Data Availability Statement
Not applicable.
Acknowledgments
We thank a CPM’2021 reviewer for pointing out that it suffices to store W in bits of space in Section 3.3, and that the currently best construction algorithm of the compressed suffix tree indeed needs time instead of just time.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Flip Book
In this appendix, we provide a detailed execution of the algorithm sketched in Figure 4, Figure 5 and Figure 6 by showing the state per turn and per player in Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9,
Figure A10, Figure A11, Figure A12, Figure A13, Figure A14, Figure A15, Figure A16, Figure A17,
Figure A18, Figure A19, Figure A20 and Figure A21. In our running example, each player has 10 turns.
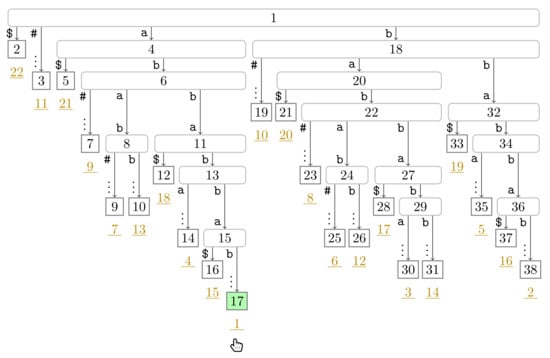
Figure A1.
Flip Book: Initial State.
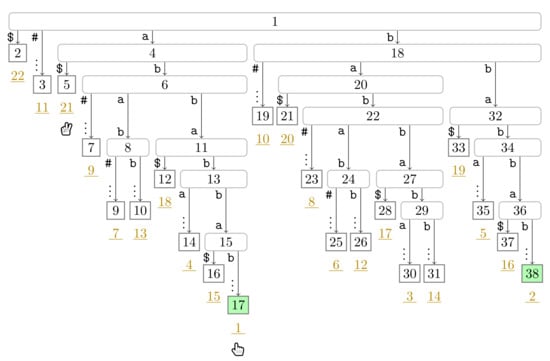
Figure A2.
Flip Book: End of Turn 1 of Player 1.
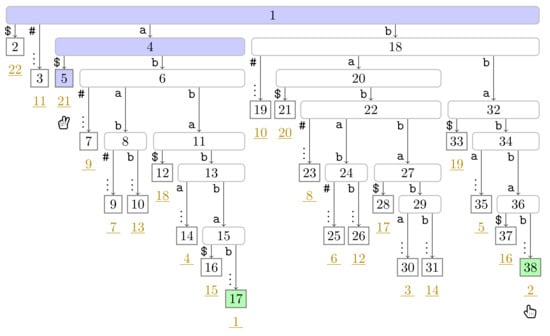
Figure A3.
Flip Book: End of Turn 1 of Player 2.
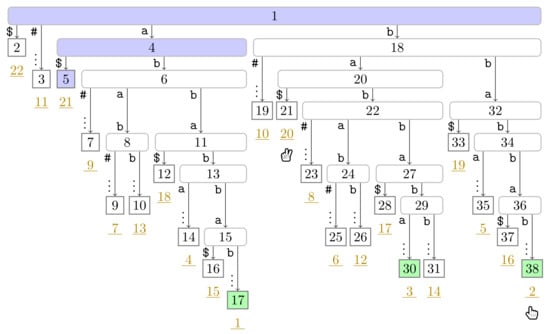
Figure A4.
Flip Book: End of Turn 2 of Player 1.
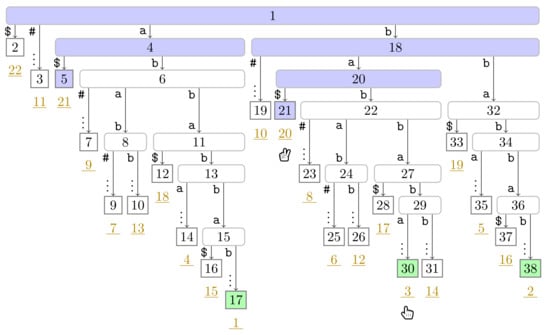
Figure A5.
Flip Book: End of Turn 2 of Player 2.
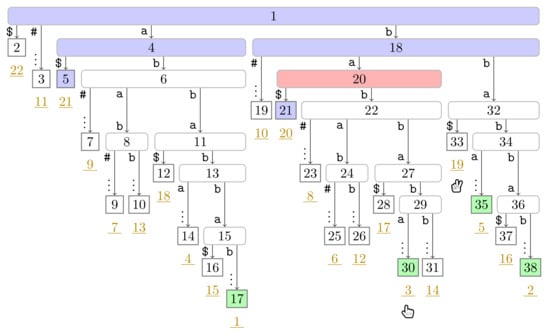
Figure A6.
Flip Book: End of Turn 3 of Player 1.
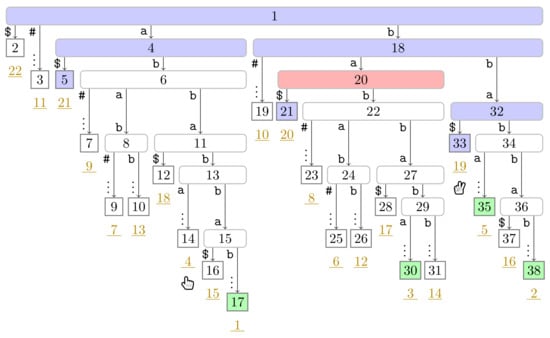
Figure A7.
Flip Book: End of Turn 3 of Player 2.
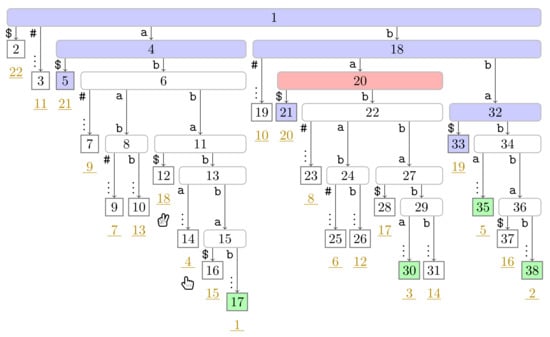
Figure A8.
Flip Book: End of Turn 4 of Player 1.
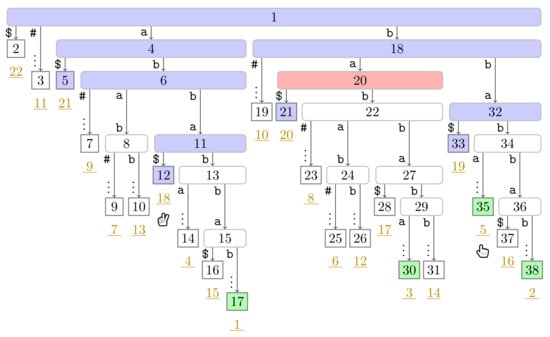
Figure A9.
Flip Book: End of Turn 4 of Player 2.
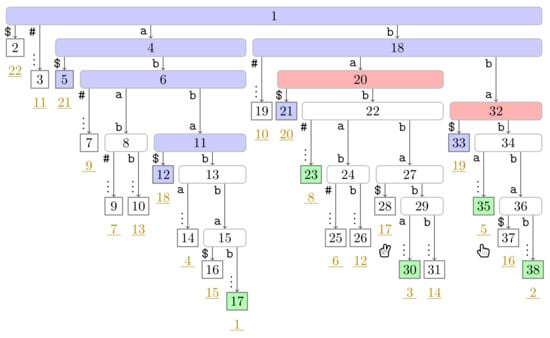
Figure A10.
Flip Book: End of Turn 5 of Player 1.
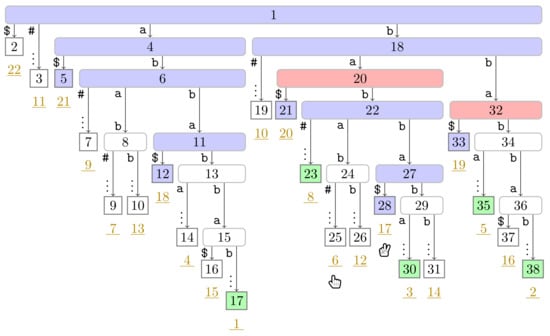
Figure A11.
Flip Book: End of Turn 5 of Player 2.
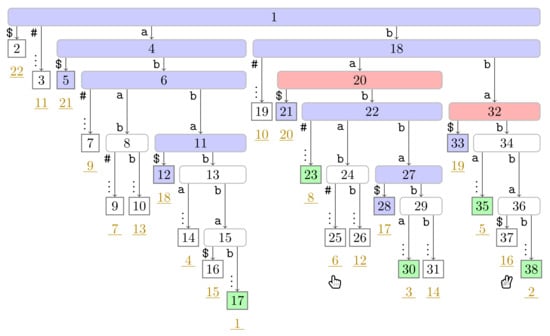
Figure A12.
Flip Book: End of Turn 6 of Player 1.
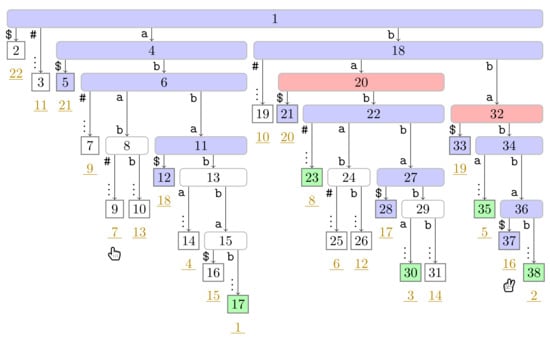
Figure A13.
Flip Book: End of Turn 6 of Player 2.
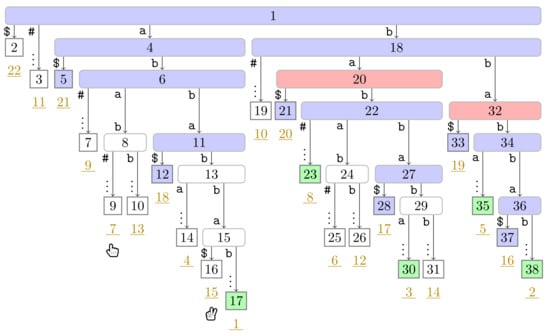
Figure A14.
Flip Book: End of Turn 7 of Player 1.
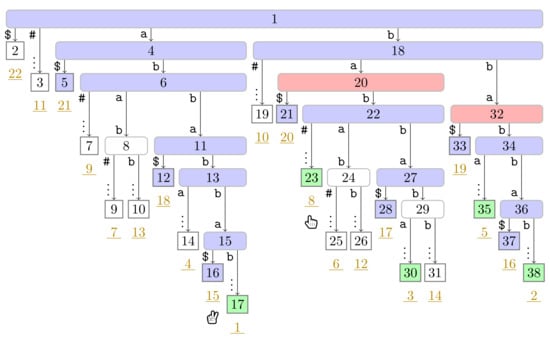
Figure A15.
Flip Book: End of Turn 7 of Player 2.
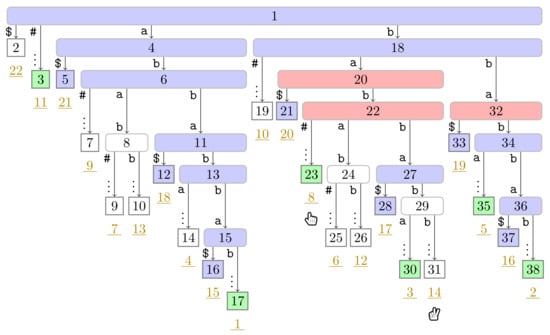
Figure A16.
Flip Book: End of Turn 8 of Player 1.
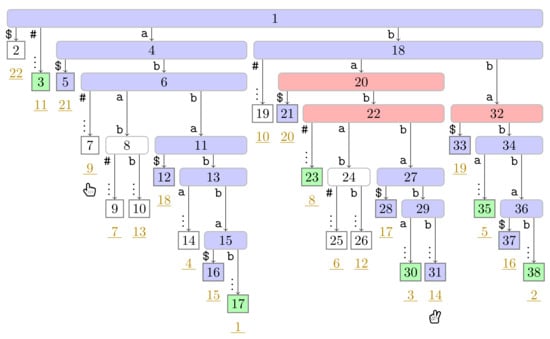
Figure A17.
Flip Book: End of Turn 8 of Player 2.
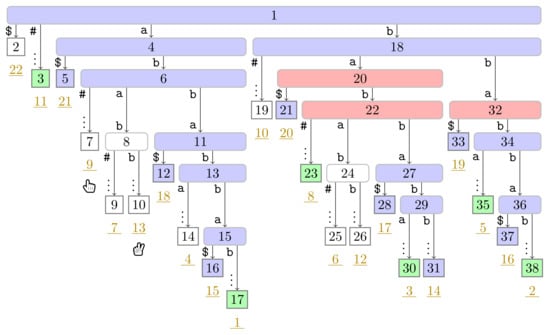
Figure A18.
Flip Book: End of Turn 9 of Player 1.
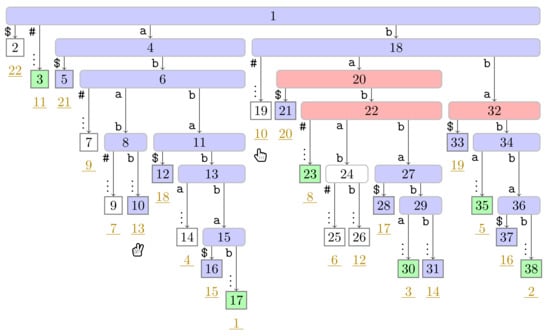
Figure A19.
Flip Book: End of Turn 9 of Player 2.
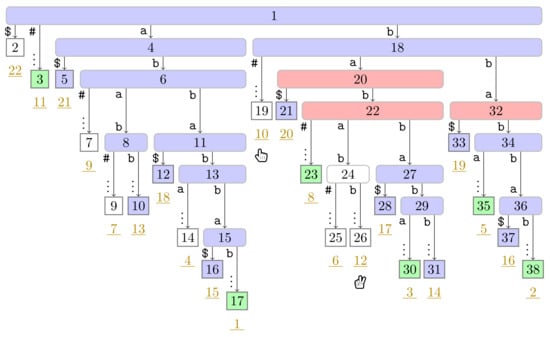
Figure A20.
Flip Book: End of Turn 10 of Player 1.
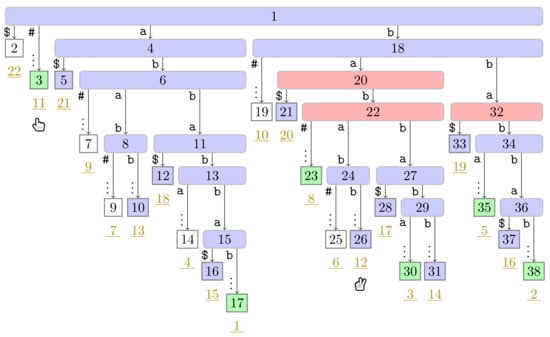
Figure A21.
Flip Book: End of Turn 10 of Player 2.
References
- Kolpakov, R.; Kucherov, G. Searching for gapped palindromes. Theor. Comput. Sci. 2009, 410, 5365–5373. [Google Scholar] [CrossRef][Green Version]
- Storer, J.A.; Szymanski, T.G. Data compression via textural substitution. J. ACM 1982, 29, 928–951. [Google Scholar] [CrossRef]
- Crochemore, M.; Langiu, A.; Mignosi, F. Note on the greedy parsing optimality for dictionary-based text compression. Theor. Comput. Sci. 2014, 525, 55–59. [Google Scholar] [CrossRef]
- Weiner, P. Linear Pattern Matching Algorithms. In Proceedings of the 14th Annual Symposium on Switching and Automata Theory (swat 1973) SWAT, Iowa City, IA, USA, 15–17 October 1973; pp. 1–11. [Google Scholar]
- Sugimoto, S.; Tomohiro, I.; Inenaga, S.; Bannai, H.; Takeda, M. Computing Reversed Lempel–Ziv Factorization Online. Available online: http://stringology.org/papers/PSC2013.pdf#page=115 (accessed on 15 April 2021).
- Chairungsee, S.; Crochemore, M. Efficient Computing of Longest Previous Reverse Factors. In Proceedings of the Computer Science and Information Technologies, Yerevan, Armenia, 28 September–2 October 2009; pp. 27–30. [Google Scholar]
- Badkobeh, G.; Chairungsee, S.; Crochemore, M. Hunting Redundancies in Strings. In International Conference on Developments in Language Theory; LNCS; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6795, pp. 1–14. [Google Scholar]
- Chairungsee, S. Searching for Gapped Palindrome. Available online: https://www.sciencedirect.com/science/article/pii/S0304397509006409 (accessed on 15 April 2021).
- Charoenrak, S.; Chairungsee, S. Palindrome Detection Using On-Line Position. In Proceedings of the 2017 International Conference on Information Technology, Singapore, 27–29 December 2017; pp. 62–65. [Google Scholar]
- Charoenrak, S.; Chairungsee, S. Algorithm for Palindrome Detection by Suffix Heap. In Proceedings of the 2019 7th International Conference on Information Technology: IoT and Smart City, Shanghai China, 20–23 December 2019; pp. 85–88. [Google Scholar]
- Blumer, A.; Blumer, J.; Ehrenfeucht, A.; Haussler, D.; McConnell, R.M. Building the Minimal DFA for the Set of all Subwords of a Word On-line in Linear Time. In International Colloquium on Automata, Languages, and Programming; LNCS; Springer: Berlin/Heidelberg, Germany, 1984; Volume 172, pp. 109–118. [Google Scholar]
- Ehrenfeucht, A.; McConnell, R.M.; Osheim, N.; Woo, S. Position heaps: A simple and dynamic text indexing data structure. J. Discret. Algorithms 2011, 9, 100–121. [Google Scholar] [CrossRef]
- Gagie, T.; Hon, W.; Ku, T. New Algorithms for Position Heaps. In Annual Symposium on Combinatorial Pattern Matching; LNCS; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7922, pp. 95–106. [Google Scholar]
- Crochemore, M.; Iliopoulos, C.S.; Kubica, M.; Rytter, W.; Walen, T. Efficient algorithms for three variants of the LPF table. J. Discret. Algorithms 2012, 11, 51–61. [Google Scholar] [CrossRef]
- Manber, U.; Myers, E.W. Suffix Arrays: A New Method for On-Line String Searches. SIAM J. Comput. 1993, 22, 935–948. [Google Scholar] [CrossRef]
- Dumitran, M.; Gawrychowski, P.; Manea, F. Longest Gapped Repeats and Palindromes. Discret. Math. Theor. Comput. Sci. 2017, 19, 205–217. [Google Scholar]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Nakashima, Y.; Tomohiro, I.; Inenaga, S.; Bannai, H.; Takeda, M. Constructing LZ78 tries and position heaps in linear time for large alphabets. Inf. Process. Lett. 2015, 115, 655–659. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar] [CrossRef]
- Fischer, J.; Tomohiro, I; Köppl, D.; Sadakane, K. Lempel–Ziv Factorization Powered by Space Efficient Suffix Trees. Algorithmica 2018, 80, 2048–2081. [Google Scholar] [CrossRef]
- Köppl, D. Non-Overlapping LZ77 Factorization and LZ78 Substring Compression Queries with Suffix Trees. Algorithms 2021, 14, 44. [Google Scholar] [CrossRef]
- Sadakane, K. Compressed Suffix Trees with Full Functionality. Theory Comput. Syst. 2007, 41, 589–607. [Google Scholar] [CrossRef]
- Belazzougui, D.; Cunial, F. Indexed Matching Statistics and Shortest Unique Substrings. In International Symposium on String Processing and Information Retrieval; LNCS; Springer: Cham, Switzerland, 2014; Volume 8799, pp. 179–190. [Google Scholar]
- Franek, F.; Holub, J.; Smyth, W.F.; Xiao, X. Computing Quasi Suffix Arrays. J. Autom. Lang. Comb. 2003, 8, 593–606. [Google Scholar]
- Crochemore, M.; Ilie, L. Computing Longest Previous Factor in linear time and applications. Inf. Process. Lett. 2008, 106, 75–80. [Google Scholar] [CrossRef]
- Belazzougui, D.; Cunial, F.; Kärkkäinen, J.; Mäkinen, V. Linear-time String Indexing and Analysis in Small Space. ACM Trans. Algorithms 2020, 16, 17:1–17:54. [Google Scholar] [CrossRef]
- Goto, K.; Bannai, H. Space Efficient Linear Time Lempel–Ziv Factorization for Small Alphabets. In Proceedings of the 2014 Data Compression Conference, Snowbird, UT, USA, 26–28 March 2014; pp. 163–172. [Google Scholar]
- Kärkkäinen, J.; Kempa, D.; Puglisi, S.J. Lightweight Lempel–Ziv Parsing. In International Symposium on Experimental Algorithms; LNCS; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7933, pp. 139–150. [Google Scholar]
- Kosolobov, D. Faster Lightweight Lempel–Ziv Parsing. In International Symposium on Mathematical Foundations of Computer Science; LNCS; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9235, pp. 432–444. [Google Scholar]
- Belazzougui, D.; Puglisi, S.J. Range Predecessor and Lempel–Ziv Parsing. In Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, Arlington, VA, USA, 10–12 January 2016; pp. 2053–2071. [Google Scholar]
- Okanohara, D.; Sadakane, K. An Online Algorithm for Finding the Longest Previous Factors. In European Symposium on Algorithms; LNCS; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5193, pp. 696–707. [Google Scholar]
- Prezza, N.; Rosone, G. Faster Online Computation of the Succinct Longest Previous Factor Array. In Conference on Computability in Europe; LNCS; Springer: Cham, Switzerland, 2020; Volume 12098, pp. 339–352. [Google Scholar]
- Bannai, H.; Inenaga, S.; Köppl, D. Computing All Distinct Squares in Linear Time for Integer Alphabets. In Proceedings of the 28th Annual Symposium on Combinatorial Pattern Matching (CPM 2017), Warsaw, Poland, 4–6July 2017; Volume 78, LIPIcs. pp. 22:1–22:18. Available online: https://link.springer.com/chapter/10.1007/978-3-662-48057-1_16 (accessed on 16 April 2021).
- Jacobson, G. Space-efficient Static Trees and Graphs. In Proceedings of the 30th Annual Symposium on Foundations of Computer Science Research, Triangle Park, NC, USA, 30 October–1 November 1989; pp. 549–554. [Google Scholar]
- Clark, D.R. Compact Pat Trees. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1996. [Google Scholar]
- Baumann, T.; Hagerup, T. Rank-Select Indices Without Tears. In Proceedings of the Algorithms and Data Structures—16th International Symposium, WADS 2019, Edmonton, AB, Canada, 5–7 August 2019; LNCS. Volume 11646, pp. 85–98. [Google Scholar]
- Munro, J.I.; Navarro, G.; Nekrich, Y. Space-Efficient Construction of Compressed Indexes in Deterministic Linear Time. In Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, Barcelona, Spain, 16–19 January 2017; pp. 408–424. [Google Scholar]
- Burrows, M.; Wheeler, D.J. A Block Sorting Lossless Data Compression Algorithm; Technical Report 124; Digital Equipment Corporation: Palo Alto, CA, USA, 1994. [Google Scholar]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Fischer, J.; Mäkinen, V.; Navarro, G. Faster entropy-bounded compressed suffix trees. Theor. Comput. Sci. 2009, 410, 5354–5364. [Google Scholar] [CrossRef]
- Manacher, G.K. A New Linear-Time “On-Line” Algorithm for Finding the Smallest Initial Palindrome of a String. J. ACM 1975, 22, 346–351. [Google Scholar] [CrossRef]
- Apostolico, A.; Breslauer, D.; Galil, Z. Parallel Detection of all Palindromes in a String. Theor. Comput. Sci. 1995, 141, 163–173. [Google Scholar] [CrossRef][Green Version]
- Köppl, D. Exploring Regular Structures in Strings. Ph.D. Thesis, TU Dortmund, Dortmund, Germany, 2018. [Google Scholar]
- Grossi, R.; Vitter, J.S. Compressed Suffix Arrays and Suffix Trees with Applications to Text Indexing and String Matching. SIAM J. Comput. 2005, 35, 378–407. [Google Scholar] [CrossRef]
- Fleischer, L.; Shallit, J.O. Words Avoiding Reversed Factors, Revisited. arXiv 2019, arXiv:1911.11704. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).