Subpath Queries on Compressed Graphs: A Survey
Abstract
1. Introduction
Terminology
2. The Labeled Path Case: Indexing Compressed Text
2.1. The Entropy Model: Compressed Suffix Arrays
- supports accessing any in constant time [17], and
- can be stored in bits of space, where is the zero-order empirical entropy of and denotes the number of occurrences of in .
2.2. The Repetitive Model
3. Indexing Labeled Graphs and Regular Languages
- Count: given a pattern (a string) , return the number of nodes reached by a path labeled with .
- Locate: given a pattern , return a representation of all nodes reached by a path labeled with .
3.1. Graph Compression
3.2. Conditional Lower Bounds
3.3. Hypertext Indexing
3.4. Prefix Sorting: Model and Terminology
- there is only one node, deemed the source state (or start state), without incoming edges, and
- any state is reachable from the source state.
- we will be able to search strings forward (that is, left-to-right). In particular, this will enable testing membership of words in the language recognized by an indexed NFA in a natural on-line (character-by-character) fashion ( traditionally, BWT-based text indexes are based on suffix sorting and support backward search of patterns in the text).
- We will be able to transfer powerful language-theoretic results to the field of compressed indexing. For example, a co-lexicographic variant of the Myhill-Nerode theorem [66] will allow us to minimize the number of states of indexable DFAs.
3.5. Indexing Labeled Trees
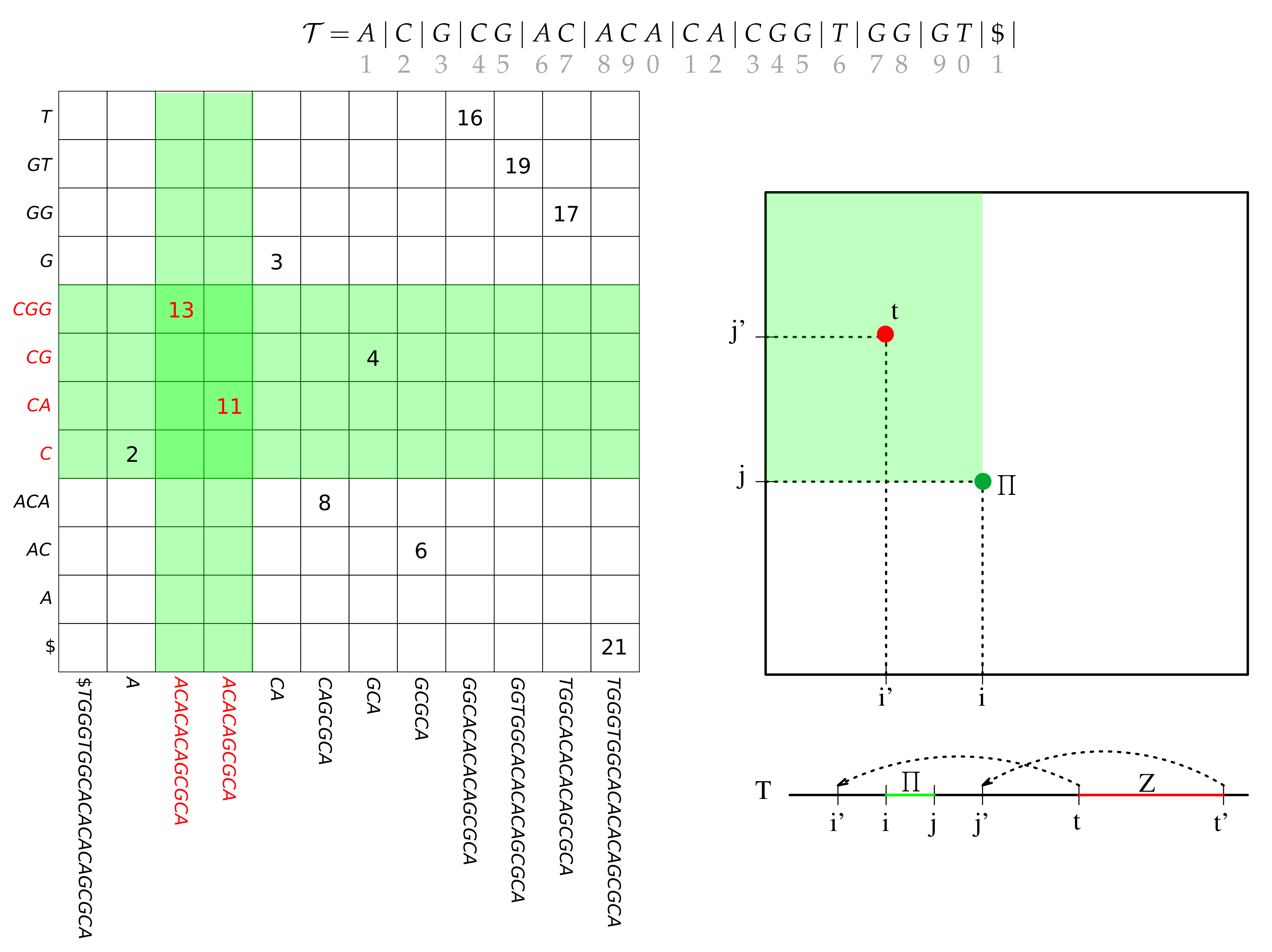
3.5.1. The Prefix Array of a Labeled Tree
3.5.2. The XBW Transform
3.5.3. Inverting the XBWT
3.5.4. Subpath Queries
3.5.5. Compression
3.6. Further Generalizations
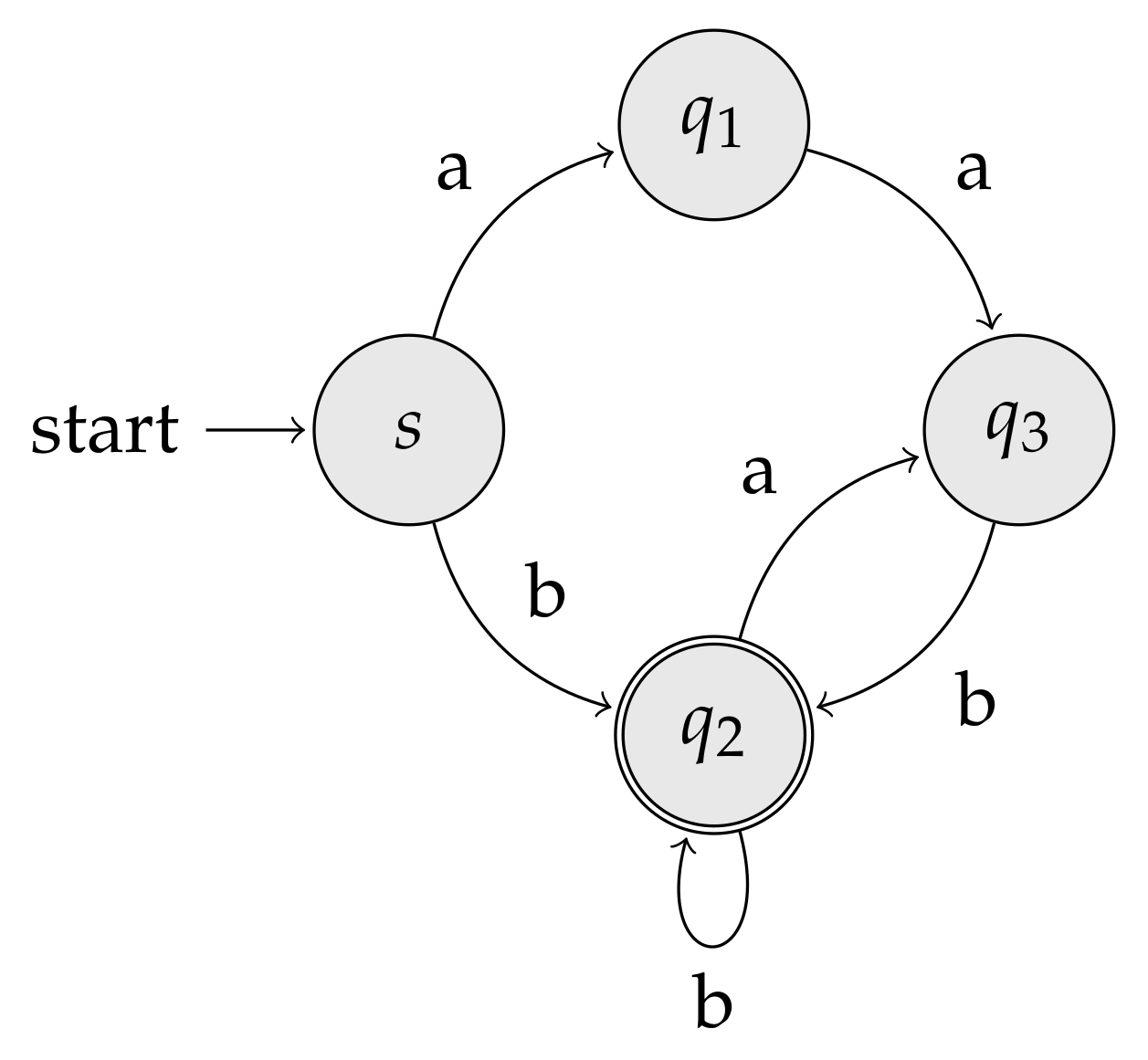
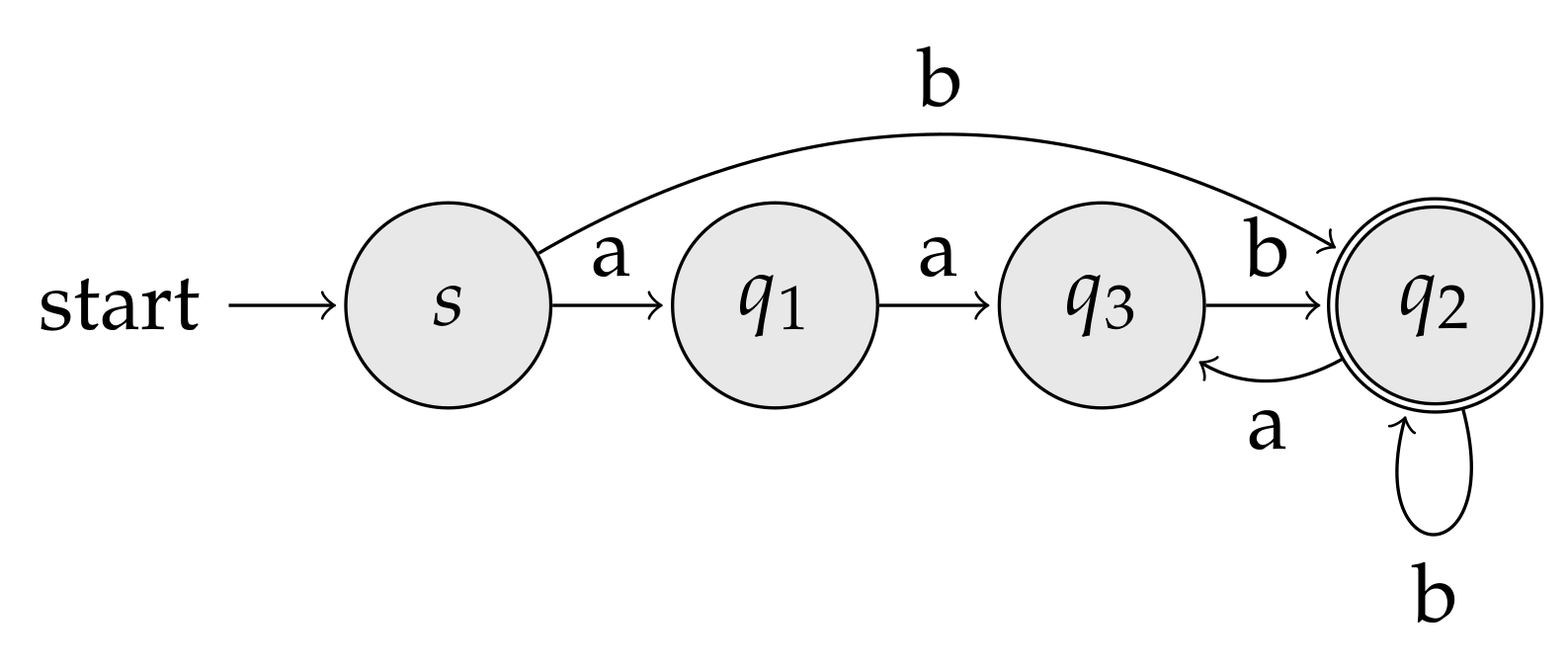
3.7. Wheeler Graphs
- (i)
- all states with in-degree zero come first in the ordering,
- (ii)
- if , then , and
- (iii)
- if and , then .
3.7.1. Subpath Queries
3.7.2. Compression
3.7.3. Sorting and Recognizing Wheeler Graphs
3.7.4. Wheeler Languages
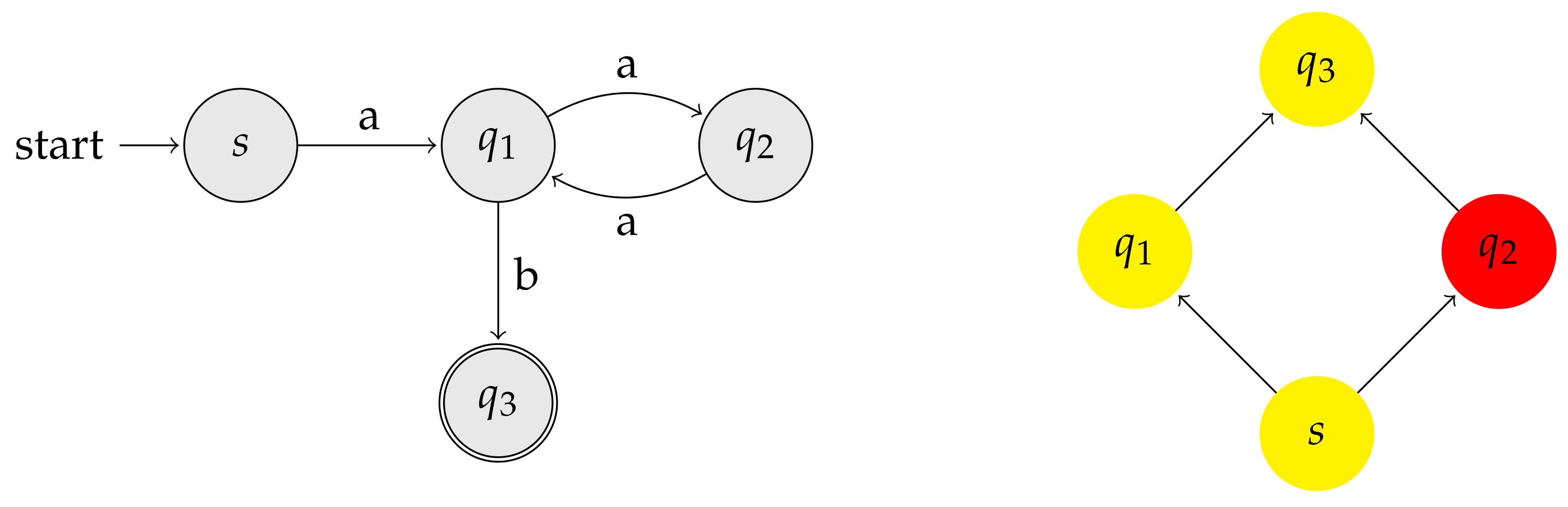
3.8. p-Sortable Automata
- (i)
- all states with in-degree zero come first in the ordering,
- (ii)
- if , then , and
- (iii)
- if and , then .
3.8.1. Subpath Queries
3.8.2. Compression
4. Conclusions and Future Challenges
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BWT | Burrows-Wheeler Transform |
| DFA | Deterministic Finite Automaton |
| GCSA | Generalized Compressed Suffix Array |
| NFA | Nondeterministic Finite Automaton |
| PA | Prefix array |
| SA | Suffix Array |
| XBWT | eXtended Burrows-Wheeler Transform |
| Text (string to be indexed) | |
| Pattern to be aligned on the labeled graph | |
| Alphabet | |
| Size of the alphabet: | |
| e | Number of edges in a labeled graph |
| m | Pattern length: |
| n | Length of a text or number of nodes in a labeled graph |
| p | Number of chains in a chain decomposition of the automaton’s partial order (Section 3.8) |
References
- Karp, R.M.; Rabin, M.O. Efficient randomized pattern-matching algorithms. IBM J. Res. Dev. 1987, 31, 249–260. [Google Scholar] [CrossRef]
- Galil, Z. On improving the worst case running time of the Boyer-Moore string matching algorithm. Commun. ACM 1979, 22, 505–508. [Google Scholar] [CrossRef]
- Apostolico, A.; Giancarlo, R. The Boyer-Moore-Galil string searching strategies revisited. SIAM J. Comput. 1986, 15, 98–105. [Google Scholar] [CrossRef]
- Knuth, D.E.; Morris, J.H., Jr.; Pratt, V.R. Fast Pattern Matching in Strings. SIAM J. Comput. 1977, 6, 323–350. [Google Scholar] [CrossRef]
- Navarro, G. Compact Data Structures—A Practical Approach; Cambridge University Press: Cambridge, UK, 2016; p. 536. ISBN 978-1-107-15238-0. [Google Scholar]
- Mäkinen, V.; Belazzougui, D.; Cunial, F.; Tomescu, A.I. Genome-Scale Algorithm Design; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Navarro, G.; Mäkinen, V. Compressed Full-Text Indexes. ACM Comput. Surv. 2007, 39, 2. [Google Scholar] [CrossRef]
- Navarro, G. Indexing Highly Repetitive String Collections, Part I: Repetitiveness Measures. Available online: https://arxiv.org/abs/2004.02781 (accessed on 10 November 2020).
- Navarro, G. Indexing Highly Repetitive String Collections, Part II: Compressed Indexes. Available online: https://link.springer.com/chapter/10.1007/978-3-642-35926-2_29 (accessed on 10 November 2020).
- The Computational Pan-Genomics Consortium. Computational pan-genomics: Status, promises and challenges. Briefings Bioinform. 2016, 19, 118–135. [Google Scholar] [CrossRef]
- Manber, U.; Myers, G. Suffix arrays: A new method for on-line string searches. In Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 22–24 January 1990; pp. 319–327. [Google Scholar]
- Baeza-Yates, R.A.; Gonnet, G.H. A New Approach to Text Searching. In Proceedings of the 12th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR’89), Cambridge, MA, USA, 25–28 June 1989; ACM: New York, NY, USA, 1989; pp. 168–175. [Google Scholar] [CrossRef]
- Gonnet, G.H.; Baeza-Yates, R.A.; Snider, T. New Indices for Text: Pat Trees and Pat Arrays. Inf. Retr. Data Struct. Algorithms 1992, 66, 82. [Google Scholar]
- Weiner, P. Linear pattern matching algorithms. In Proceedings of the 14th Annual Symposium on Switching and Automata Theory (swat 1973), Iowa City, IA, USA, 15–17 October 1973; pp. 1–11. [Google Scholar]
- Kärkkäinen, J.; Ukkonen, E. Lempel-Ziv parsing and sublinear-size index structures for string matching. In Proceedings of the 3rd South American Workshop on String Processing (WSP’96), Recife, Brazil, 8–9 August 1996. [Google Scholar]
- Ferragina, P.; Manzini, G. Opportunistic data structures with applications. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 390–398. [Google Scholar]
- Grossi, R.; Vitter, J.S. Compressed Suffix Arrays and Suffix Trees with Applications to Text Indexing and String Matching (Extended Abstract). In Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing (STOC’00), Portland, OR, USA, 21–23 May 2000; Association for Computing Machinery: New York, NY, USA, 2000; pp. 397–406. [Google Scholar] [CrossRef]
- Elias, P. Efficient Storage and Retrieval by Content and Address of Static Files. J. ACM 1974, 21, 246–260. [Google Scholar] [CrossRef]
- Fano, R.M. On the Number of Bits Required to Implement an Associative Memory; Project MAC; Massachusetts Institute of Technology: Cambridge, MA, USA, 1971. [Google Scholar]
- Burrows, M.; Wheeler, D.J. A Block-Sorting Lossless Data Compression Algorithm. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.3.8069 (accessed on 10 November 2020).
- Langmead, B.; Trapnell, C.; Pop, M.; Salzberg, S.L. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009, 10, R25. [Google Scholar] [CrossRef]
- Li, H.; Durbin, R. Fast and accurate short read alignment with Burrows—Wheeler transform. Bioinformatics 2009, 25, 1754–1760. [Google Scholar] [CrossRef]
- Kreft, S.; Navarro, G. On Compressing and Indexing Repetitive Sequences. Theor. Comput. Sci. 2013, 483, 115–133. [Google Scholar] [CrossRef]
- Gagie, T.; Navarro, G.; Prezza, N. Fully Functional Suffix Trees and Optimal Text Searching in BWT-Runs Bounded Space. J. ACM 2020, 67. [Google Scholar] [CrossRef]
- Mäkinen, V.; Navarro, G. Succinct suffix arrays based on run-length encoding. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching, Jeju Island, Korea, 19–22 June 2005. [Google Scholar]
- Sirén, J.; Välimäki, N.; Mäkinen, V.; Navarro, G. Run-Length Compressed Indexes Are Superior for Highly Repetitive Sequence Collections. In Proceedings of the 15th International Symposium on String Processing and Information Retrieval (SPIRE), Melbourne, Australia, 10–12 November 2008; pp. 164–175. [Google Scholar]
- Claude, F.; Navarro, G. Improved Grammar-Based Compressed Indexes. In Proceedings of the 19th International Symposium on String Processing and Information Retrieval (SPIRE), Cartagena de Indias, Colombia, 21–25 October 2012; pp. 180–192. [Google Scholar]
- Navarro, G.; Prezza, N. Universal compressed text indexing. Theor. Comput. Sci. 2019, 762, 41–50. [Google Scholar] [CrossRef]
- Kempa, D.; Prezza, N. At the Roots of Dictionary Compression: String Attractors. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2018), Los Angeles, CA, USA, 25–29 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 827–840. [Google Scholar] [CrossRef]
- Kociumaka, T.; Navarro, G.; Prezza, N. Towards a Definitive Measure of Repetitiveness. In Proceedings of the 14th Latin American Symposium on Theoretical Informatics (LATIN), Sao Paulo, Brazil, 25–19 May 2020. to appear. [Google Scholar]
- Gagie, T.; Navarro, G.; Prezza, N. On the approximation ratio of Lempel-Ziv parsing. In Proceedings of the Latin American Symposium on Theoretical Informatics, Buenos Aires, Argentina, 14–19 April 2018. [Google Scholar]
- Christiansen, A.R.; Ettienne, M.B.; Kociumaka, T.; Navarro, G.; Prezza, N. Optimal-Time Dictionary-Compressed Indexes. ACM Trans. Algorithms 2020, 31, 1–39. [Google Scholar] [CrossRef]
- Maneth, S.; Peternek, F. A Survey on Methods and Systems for Graph Compression. arXiv 2015, arXiv:1504.00616. [Google Scholar]
- Besta, M.; Hoefler, T. Survey and Taxonomy of Lossless Graph Compression and Space-Efficient Graph Representations. arXiv 2019, arXiv:1806.01799. [Google Scholar]
- Ferragina, P.; Luccio, F.; Manzini, G.; Muthukrishnan, S. Compressing and Indexing Labeled Trees, with Applications. J. ACM 2009, 57, 1–33. [Google Scholar] [CrossRef]
- Ferres, L.; Fuentes-Sepúlveda, J.; Gagie, T.; He, M.; Navarro, G. Fast and Compact Planar Embeddings. Comput. Geom. Theory Appl. 2020, 89, 101630. [Google Scholar] [CrossRef]
- Chakraborty, S.; Grossi, R.; Sadakane, K.; Rao Satti, S. Succinct Representation for (Non) Deterministic Finite Automata. arXiv 2019, arXiv:1907.09271. [Google Scholar]
- Brisaboa, N.; Ladra, S.; Navarro, G. Compact Representation of Web Graphs with Extended Functionality. Inf. Syst. 2014, 39, 152–174. [Google Scholar] [CrossRef]
- Jansson, J.; Sadakane, K.; Sung, W.K. Ultra-succinct representation of ordered trees with applications. J. Comput. Syst. Sci. 2012, 78, 619–631. [Google Scholar] [CrossRef]
- Hucke, D.; Lohrey, M.; Benkner, L.S. Entropy Bounds for Grammar-Based Tree Compressors. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1687–1691. [Google Scholar]
- Gańczorz, M. Using Statistical Encoding to Achieve Tree Succinctness Never Seen Before. In Proceedings of the 37th International Symposium on Theoretical Aspects of Computer Science (STACS 2020), Montpellier, France, 10–13 March 2020. [Google Scholar]
- Hucke, D.; Lohrey, M.; Benkner, L.S. A Comparison of Empirical Tree Entropies. In String Processing and Information Retrieval; Boucher, C., Thankachan, S.V., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 232–246. [Google Scholar]
- Engelfriet, J. Context-Free Graph Grammars. In Handbook of Formal Languages: Volume 3 Beyond Words; Rozenberg, G., Salomaa, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 125–213. [Google Scholar] [CrossRef]
- Maneth, S.; Peternek, F. Grammar-based graph compression. Inf. Syst. 2018, 76, 19–45. [Google Scholar] [CrossRef]
- Maneth, S.; Peternek, F. Constant delay traversal of grammar-compressed graphs with bounded rank. Inf. Comput. 2020, 273, 104520. [Google Scholar] [CrossRef]
- Gawrychowski, P.; Jez, A. LZ77 factorisation of trees. In Proceedings of the 36th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2016), Madras, India, 15–17 December 2016. [Google Scholar]
- Bille, P.; Gørtz, I.L.; Landau, G.M.; Weimann, O. Tree Compression with Top Trees. In Automata, Languages, and Programming; Fomin, F.V., Freivalds, R., Kwiatkowska, M., Peleg, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–171. [Google Scholar]
- Alanko, J.; Gagie, T.; Navarro, G.; Seelbach Benkner, L. Tunneling on Wheeler Graphs. In Proceedings of the 2019 Data Compression Conference (DCC), Snowbird, UT, USA, 26–29 March 2019; pp. 122–131. [Google Scholar] [CrossRef]
- Prezza, N. On Locating Paths in Compressed Tries. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms (SODA’21), Alexandria, VA, USA, 10–13 January 2021; ACM, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2021. [Google Scholar]
- Gagie, T.; Manzini, G.; Sirén, J. Wheeler graphs: A framework for BWT-based data structures. Theor. Comput. Sci. 2017, 698, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Backurs, A.; Indyk, P. Which regular expression patterns are hard to match? In Proceedings of the 2016 IEEE 57th Annual Symposium on Foundations of Computer Science (FOCS), New Brunswick, NJ, USA, 9–11 October 2016; pp. 457–466. [Google Scholar]
- Equi, M.; Mäkinen, V.; Tomescu, A.I. Conditional Indexing Lower Bounds Through Self-Reducibility. arXiv 2020, arXiv:2002.00629. [Google Scholar]
- Equi, M.; Mäkinen, V.; Tomescu, A.I. Graphs cannot be indexed in polynomial time for sub-quadratic time string matching, unless SETH fails. arXiv 2020, arXiv:2002.00629. [Google Scholar]
- Equi, M.; Grossi, R.; Mäkinen, V.; Tomescu, A.I. On the Complexity of String Matching for Graphs. In Proceedings of the 46th International Colloquium on Automata, Languages and Programming (ICALP 2019), Patras, Greece, 9–12 July 2019. [Google Scholar] [CrossRef]
- Impagliazzo, R.; Paturi, R. On the Complexity of K-SAT. J. Comput. Syst. Sci. 2001, 62, 367–375. [Google Scholar] [CrossRef]
- Potechin, A.; Shallit, J. Lengths of words accepted by nondeterministic finite automata. Inf. Process. Lett. 2020, 162, 105993. [Google Scholar] [CrossRef]
- Williams, R. A New Algorithm for Optimal 2-Constraint Satisfaction and Its Implications. Theor. Comput. Sci. 2005, 348, 357–365. [Google Scholar] [CrossRef]
- Gibney, D.; Hoppenworth, G.; Thankachan, S.V. Simple Reductions from Formula-SAT to Pattern Matching on Labeled Graphs and Subtree Isomorphism. arXiv 2020, arXiv:2008.11786. [Google Scholar]
- Abboud, A.; Bringmann, K. Tighter Connections Between Formula-SAT and Shaving Logs. In Proceedings of the 45th International Colloquium on Automata, Languages, and Programming (ICALP 2018), Prague, Czech Republic, 9–13 July 2018; Chatzigiannakis, I., Kaklamanis, C., Marx, D., Sannella, D., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2018; Volume 107, pp. 8:1–8:18. [Google Scholar] [CrossRef]
- Amir, A.; Lewenstein, M.; Lewenstein, N. Pattern matching in hypertext. J. Algorithms 2000, 35, 82–99. [Google Scholar] [CrossRef]
- Ferragina, P.; Mishra, B. Algorithms in Stringomics (I): Pattern-Matching against “Stringomes”. BioRxiv 2014, 001669. [Google Scholar] [CrossRef]
- Thachuk, C. Indexing hypertext. J. Discret. Algorithms 2013, 18, 113–122. [Google Scholar] [CrossRef]
- Manber, U.; Wu, S. Approximate String Matching with Arbitrary Costs for Text and Hypertext. Available online: https://www.worldscientific.com/doi/abs/10.1142/9789812797919_0002 (accessed on 10 November 2020).
- Navarro, G. Improved approximate pattern matching on hypertext. In LATIN’98: Theoretical Informatics; Lucchesi, C.L., Moura, A.V., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 352–357. [Google Scholar]
- Alanko, J.; D’Agostino, G.; Policriti, A.; Prezza, N. Regular Languages meet Prefix Sorting. In Proceedings of the 2020 ACM-SIAM Symposium on Discrete Algorithms, Salt Lake City, UT, USA, 5–8 January 2020; pp. 911–930. [Google Scholar] [CrossRef]
- Nerode, A. Linear automaton transformations. Proc. Am. Math. Soc. 1958, 9, 541–544. [Google Scholar] [CrossRef]
- Kosaraju, S.R. Efficient Tree Pattern Matching. In Proceedings of the 30th Annual Symposium on Foundations of Computer Science (SFCS’89), Triangle Park, NC, USA, 30 October–1 November 1989; pp. 178–183. [Google Scholar]
- Ferragina, P.; Luccio, F.; Manzini, G.; Muthukrishnan, S. Structuring labeled trees for optimal succinctness, and beyond. In Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2005), Pittsburgh, PA, USA, 23–25 October 2005; pp. 184–196. [Google Scholar] [CrossRef]
- Belazzougui, D.; Navarro, G. Optimal Lower and Upper Bounds for Representing Sequences. ACM Trans. Algorithms 2015, 11, 31. [Google Scholar] [CrossRef]
- Arroyuelo, D.; Navarro, G.; Sadakane, K. Stronger Lempel-Ziv Based Compressed Text Indexing. Algorithmica 2012, 62, 54–101. [Google Scholar] [CrossRef]
- Raman, R.; Raman, V.; Rao, S.S. Succinct Indexable Dictionaries with Applications to Encoding K-Ary Trees and Multisets. In Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’02), San Francisco, CA, USA, 6–8 January 2002. [Google Scholar]
- Mantaci, S.; Restivo, A.; Rosone, G.; Sciortino, M. An Extension of the Burrows Wheeler Transform and Applications to Sequence Comparison and Data Compression. In Combinatorial Pattern Matching; Apostolico, A., Crochemore, M., Park, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 178–189. [Google Scholar]
- Mantaci, S.; Restivo, A.; Rosone, G.; Sciortino, M. An extension of the Burrows—Wheeler transform. Theor. Comput. Sci. 2007, 387, 298–312. [Google Scholar] [CrossRef]
- Mantaci, S.; Restivo, A.; Sciortino, M. An extension of the Burrows Wheeler transform to k words. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 29–31 March 2005; p. 469. [Google Scholar]
- Bowe, A.; Onodera, T.; Sadakane, K.; Shibuya, T. Succinct de Bruijn Graphs. In Algorithms in Bioinformatics; Raphael, B., Tang, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 225–235. [Google Scholar]
- Sirén, J.; Välimäki, N.; Mäkinen, V. Indexing Graphs for Path Queries with Applications in Genome Research. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 375–388. [Google Scholar] [CrossRef]
- Sirén, J. Indexing variation graphs. In Proceedings of the Ninteenth Workshop on Algorithm Engineering and Experiments (ALENEX), Barcelona, Spain, 16–17 January 2017; pp. 13–27. [Google Scholar]
- Mäkinen, V.; Cazaux, B.; Equi, M.; Norri, T.; Tomescu, A.I. Linear Time Construction of Indexable Founder Block Graphs. arXiv 2020, arXiv:2005.09342. [Google Scholar]
- Na, J.C.; Kim, H.; Min, S.; Park, H.; Lecroq, T.; Léonard, M.; Mouchard, L.; Park, K. FM-index of alignment with gaps. Theor. Comput. Sci. 2018, 710, 148–157. [Google Scholar] [CrossRef]
- Na, J.C.; Kim, H.; Park, H.; Lecroq, T.; Léonard, M.; Mouchard, L.; Park, K. FM-index of alignment: A compressed index for similar strings. Theor. Comput. Sci. 2016, 638, 159–170. [Google Scholar] [CrossRef]
- Durbin, R. Efficient haplotype matching and storage using the positional Burrows—Wheeler transform (PBWT). Bioinformatics 2014, 30, 1266–1272. [Google Scholar] [CrossRef] [PubMed]
- Claude, F.; Navarro, G.; Ordónez, A. The wavelet matrix: An efficient wavelet tree for large alphabets. Inf. Syst. 2015, 47, 15–32. [Google Scholar] [CrossRef]
- Grossi, R.; Gupta, A.; Vitter, J.S. High-Order Entropy-Compressed Text Indexes. In Proceedings of the Fourteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’03), Baltimore, MD, USA, 12–14 January 2003. [Google Scholar]
- Baier, U. On Undetected Redundancy in the Burrows-Wheeler Transform. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching (CPM 2018), Qingdao, China, 2–4 July 2018; Navarro, G., Sankoff, D., Zhu, B., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2018; Volume 105, pp. 3:1–3:15. [Google Scholar] [CrossRef]
- Bentley, J.W.; Gibney, D.; Thankachan, S.V. On the Complexity of BWT-Runs Minimization via Alphabet Reordering. In Proceedings of the 28th Annual European Symposium on Algorithms (ESA 2020), Pisa, Italy, 7–9 September 2020; Grandoni, F., Herman, G., Sanders, P., Eds.; Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2020; Volume 173, pp. 15:1–15:13. [Google Scholar] [CrossRef]
- Gibney, D.; Thankachan, S.V. On the Hardness and Inapproximability of Recognizing Wheeler Graphs. In Proceedings of the 27th Annual European Symposium on Algorithms (ESA 2019), Munich/Garching, Germany, 9–11 September 2019; Bender, M.A., Svensson, O., Herman, G., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2019; Volume 144, pp. 51:1–51:16. [Google Scholar] [CrossRef]
- Gibney, D. Wheeler Graph Recognition on 3-NFAs and 4-NFAs. In Proceedings of the Open Problem Session, International Workshop on Combinatorial Algorithms, Pisa, France, 23–25 July 2020. [Google Scholar]
- Alanko, J.; D’Agostino, G.; Policriti, A.; Prezza, N. Wheeler languages. arXiv 2020, arXiv:2002.10303. [Google Scholar]
- Cotumaccio, N.; Prezza, N. On Indexing and Compressing Finite Automata. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms (SODA’21); ACM, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2021; to appear. [Google Scholar]
- Rabin, M.O.; Scott, D. Finite Automata and Their Decision Problems. IBM J. Res. Dev. 1959, 3, 114–125. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prezza, N. Subpath Queries on Compressed Graphs: A Survey. Algorithms 2021, 14, 14. https://doi.org/10.3390/a14010014
Prezza N. Subpath Queries on Compressed Graphs: A Survey. Algorithms. 2021; 14(1):14. https://doi.org/10.3390/a14010014
Chicago/Turabian StylePrezza, Nicola. 2021. "Subpath Queries on Compressed Graphs: A Survey" Algorithms 14, no. 1: 14. https://doi.org/10.3390/a14010014
APA StylePrezza, N. (2021). Subpath Queries on Compressed Graphs: A Survey. Algorithms, 14(1), 14. https://doi.org/10.3390/a14010014




