An Exploratory Landscape Analysis-Based Benchmark Suite
Abstract
1. Introduction
2. Background
2.1. Benchmark Functions
- Separable functions
- Functions with low or moderate conditioning
- Functions with high conditioning and unimodal
- Multi-modal functions with an adequate global structure
- Multi-modal functions with a weak global structure
2.2. Landscape Analysis
- Multi-modality, which refers to the number of local optima in the fitness landscape.
- Global structure, which refers to the underlying structure of a fitness landscape when removing local optima.
- Separability, which describes if an objective function can be decomposed into subproblems in which all the variables in each subproblem are independent of the variables in the other subproblems.
- Variable scaling, which describes the effect that scale has on the behavior of algorithms in different dimensions.
- Search space homogeneity, which describes the phase transitions between different areas of the fitness landscape, i.e., how the properties of the fitness landscape vary in different areas of the search space.
- Basin size homogeneity, which describes the differences in the sizes of the basins of attractions.
- Global to local optima contrast, which describes the difference in fitness values between local and global optima.
- Plateaus, which refers to areas of a fitness landscape in which the fitness values do not fluctuate significantly.
- Dispersion (disp): Defined by Lunacek and Whitley [24], these measures describe the global structure of the objective function.
- Information content (ic): Defined by Muñoz et al. [25], these measures calculate the differences between points in the sampled fitness values to determine the ruggedness of the fitness landscape.
- Level-set (ela_level): Defined by Mersmann et al. [17], these measures split the initial sample into two groups, and then the performance of multiple classification algorithms is measured.
- Meta-model (ela_meta): Defined by Mersmann et al. [17], these measures determine how well the sampled fitness values fit linear and quadratic models.
- Nearest better clustering (nbc): Defined by Kerschke et al. [26], these measures calculate various statistics based on the comparison of the distances between the sample points’ nearest neighbor and their nearest neighbor that has a better fitness value.
- Principal component analysis measures (pca): Defined by Kerschke and Trautmann [23], these measures perform principal component analysis on the sampled values in both the decision variable and fitness spaces.
- y-distribution features (ela_distr): Defined by Mersmann et al. [17], these measures describe the distribution of the fitness values obtained by the sampling algorithm.
2.3. Coverage of the Problem Space
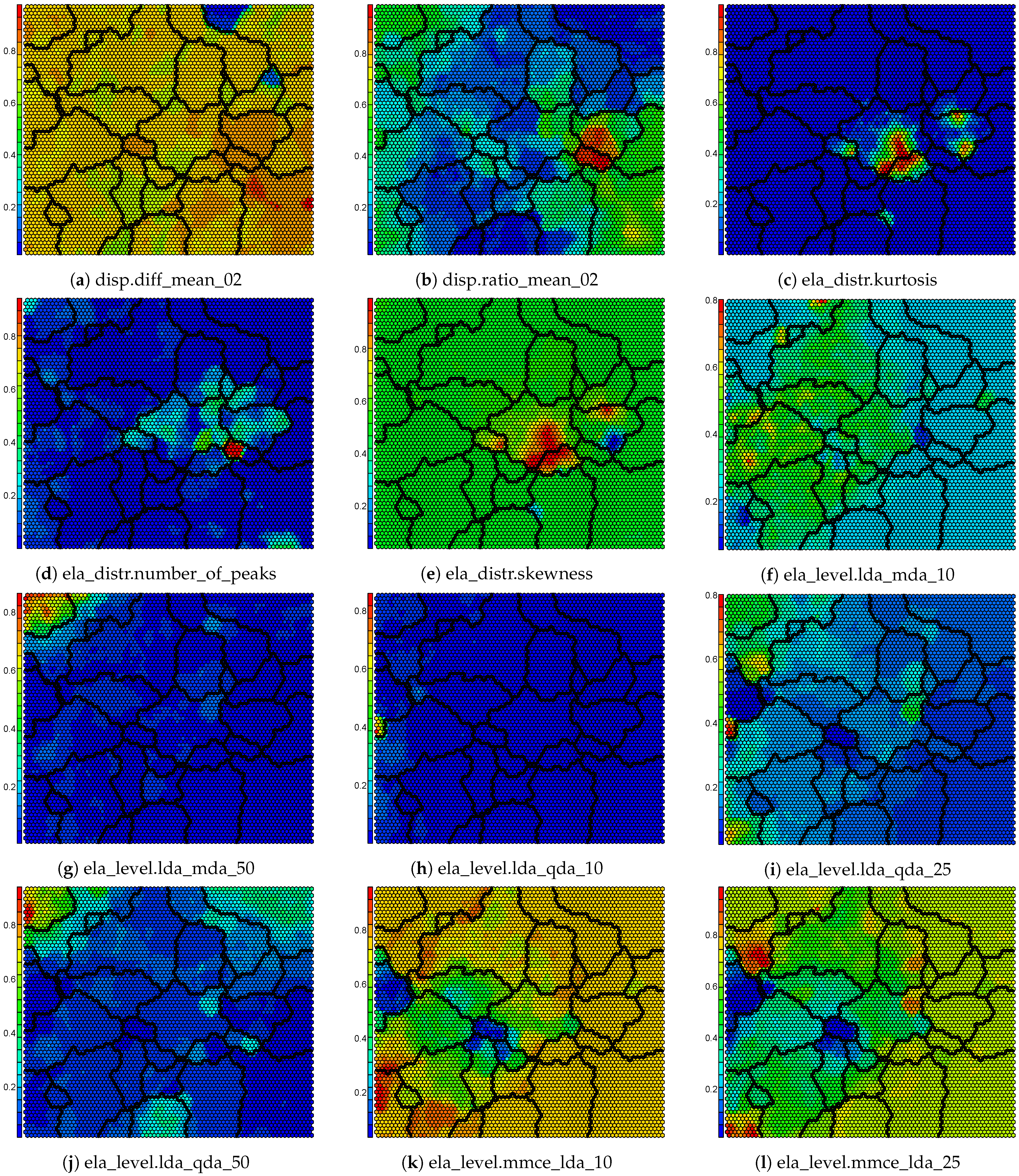
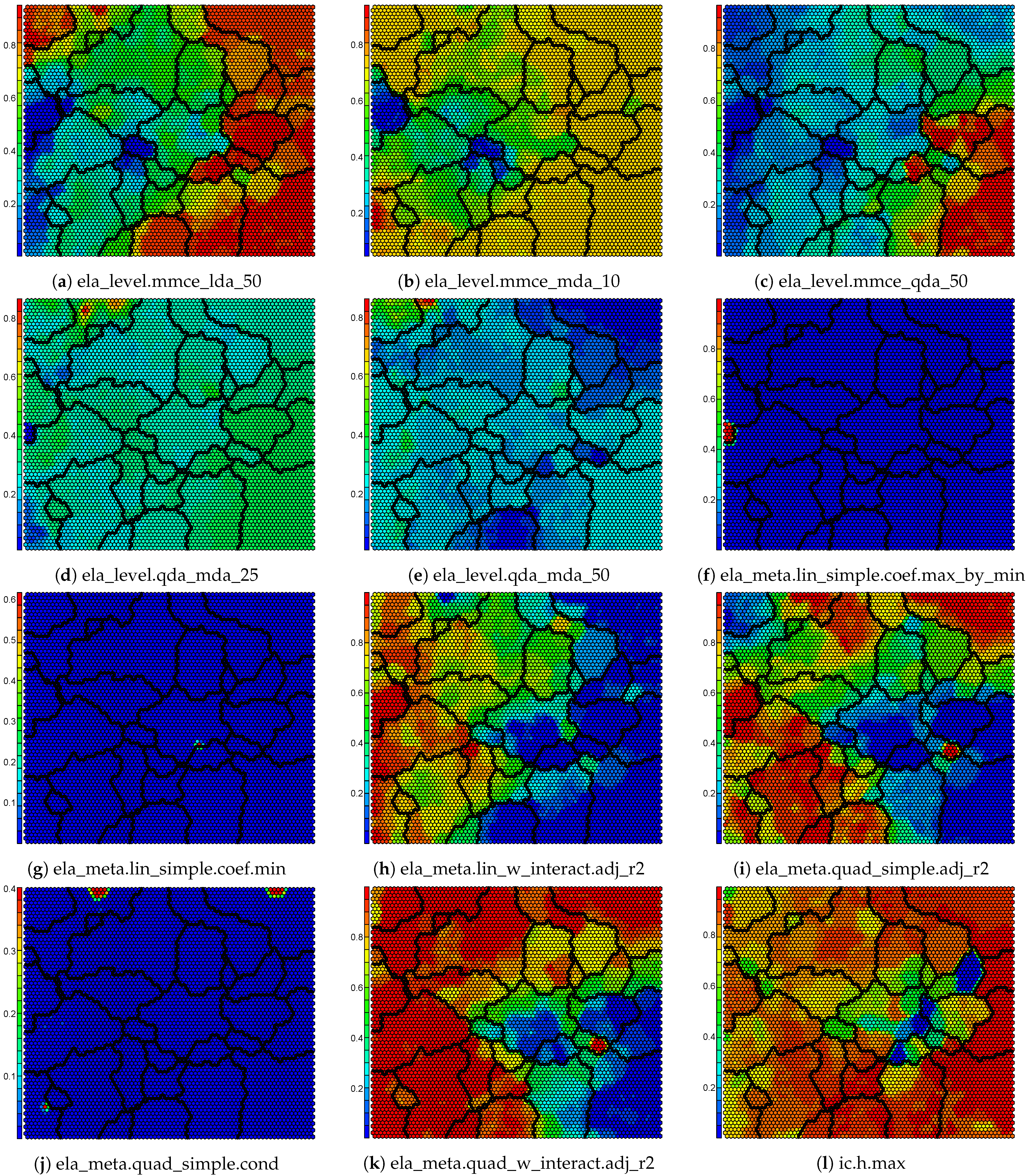
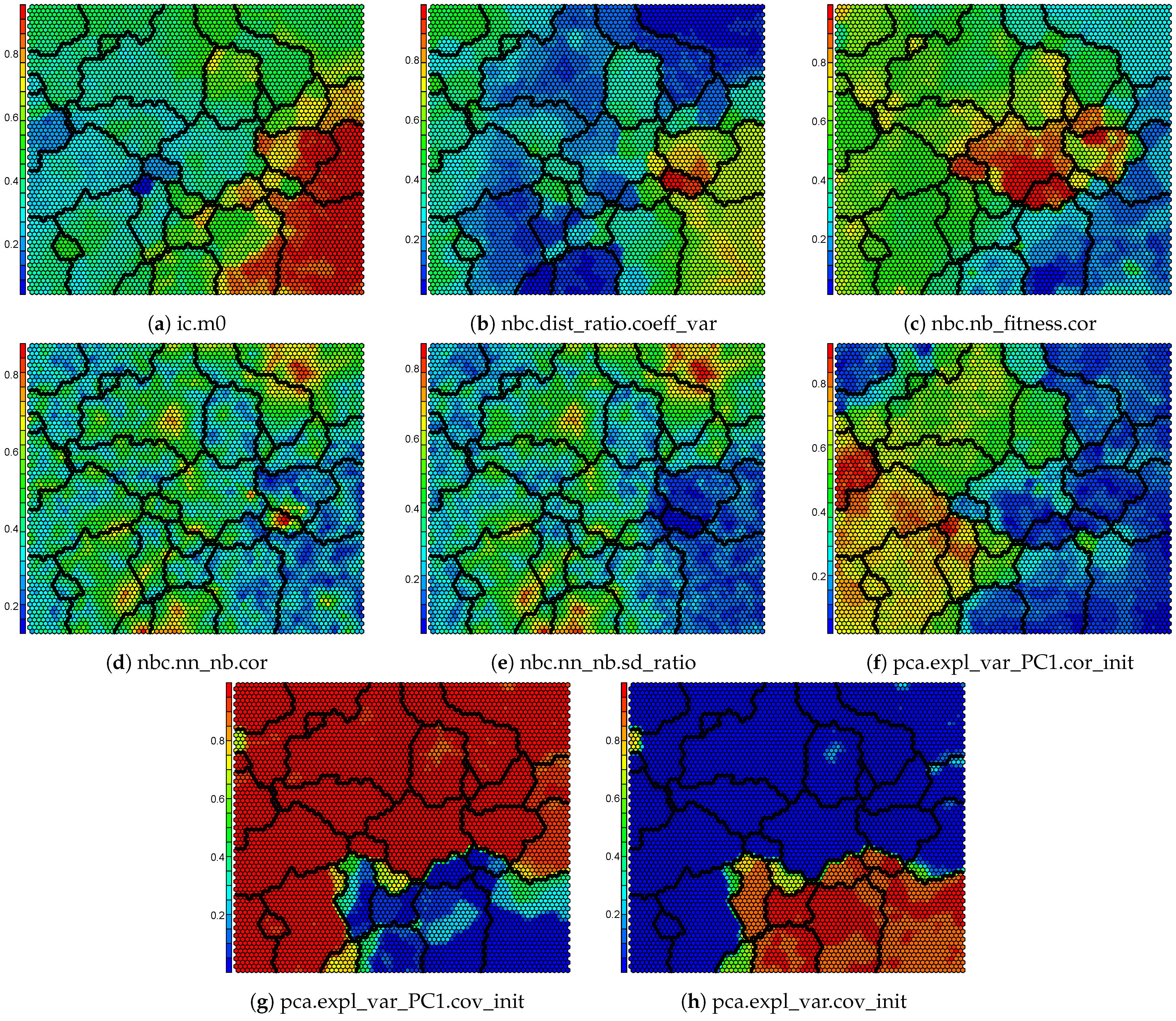
2.4. Self-Organizing Feature Map
3. Robustness of Exploratory Landscape Analysis Measures
3.1. Determining Robustness
- Choose the sample sizes to be investigated.
- For each sample size , calculate the measure for r independent runs.
- Perform the Levene trend test on the above samples, for each pair of sample sizes, and . In this case, there groups. Obtain the test statistic and p-value.
- For each pair of sample sizes, if the resulting p-value is less than or equal to the predefined significance level, , then the null hypothesis is rejected. This implies that it is likely that there is a monotonic decrease in the variance between the sample sizes. If the p-value is greater than , then the null hypothesis cannot be rejected. It is then said that there is strong evidence that the variance between tequivalencyhe different sample sizes is equal.
- Zero occurrences: This implies that there is no evidence that the variance is lower for any sample size. The smallest sample size is chosen as the point of robustness since there is no decrease in variance from increasing sample size.
- One occurrence: The first sample size after the occurrence is chosen to be the point of robustness.
- Two or more consecutive occurrences: The first sample size after the chain of consecutive occurrences is chosen as the point of robustness.
- Two or more non-consecutive occurrences: The first sample size after the first chain of consecutive occurrences is chosen as the point of robustness.
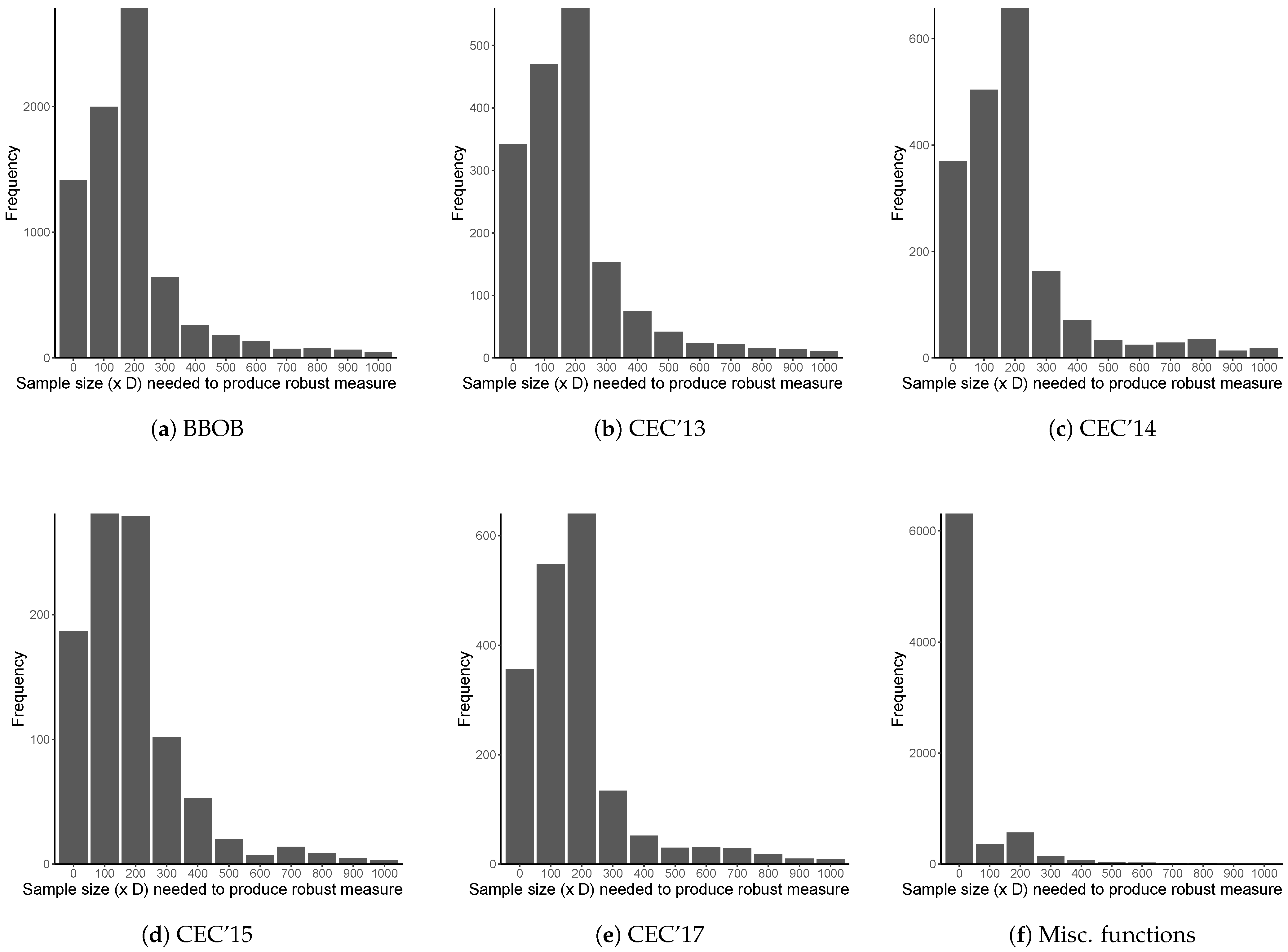
3.2. Empirical Procedure
- the BBOB benchmark suite, which contains 24 benchmark functions. This study focuses on only the first five instances of these functions, for a total of 120 benchmark functions;
- the CEC 2013 benchmark suite, which contains 28 benchmark functions [2];
- the CEC 2014 benchmark suite, which contains 30 benchmark functions [3];
- the CEC 2015 benchmark suite, which contains 15 benchmark functions [4];
- the CEC 2017 benchmark suite, which contains 29 benchmark functions [5]; and
- 118 miscellaneous benchmark functions obtained from various sources listed in Section 2.
3.3. Results and Discussion
4. Benchmark Suite Proposal
4.1. Preprocessing
- Determine the sample size used to sample ELA measures. This was determined in the previous section as .
- Identify ELA measures that do not provide useful information, in other words, measures that are not expressive [27].
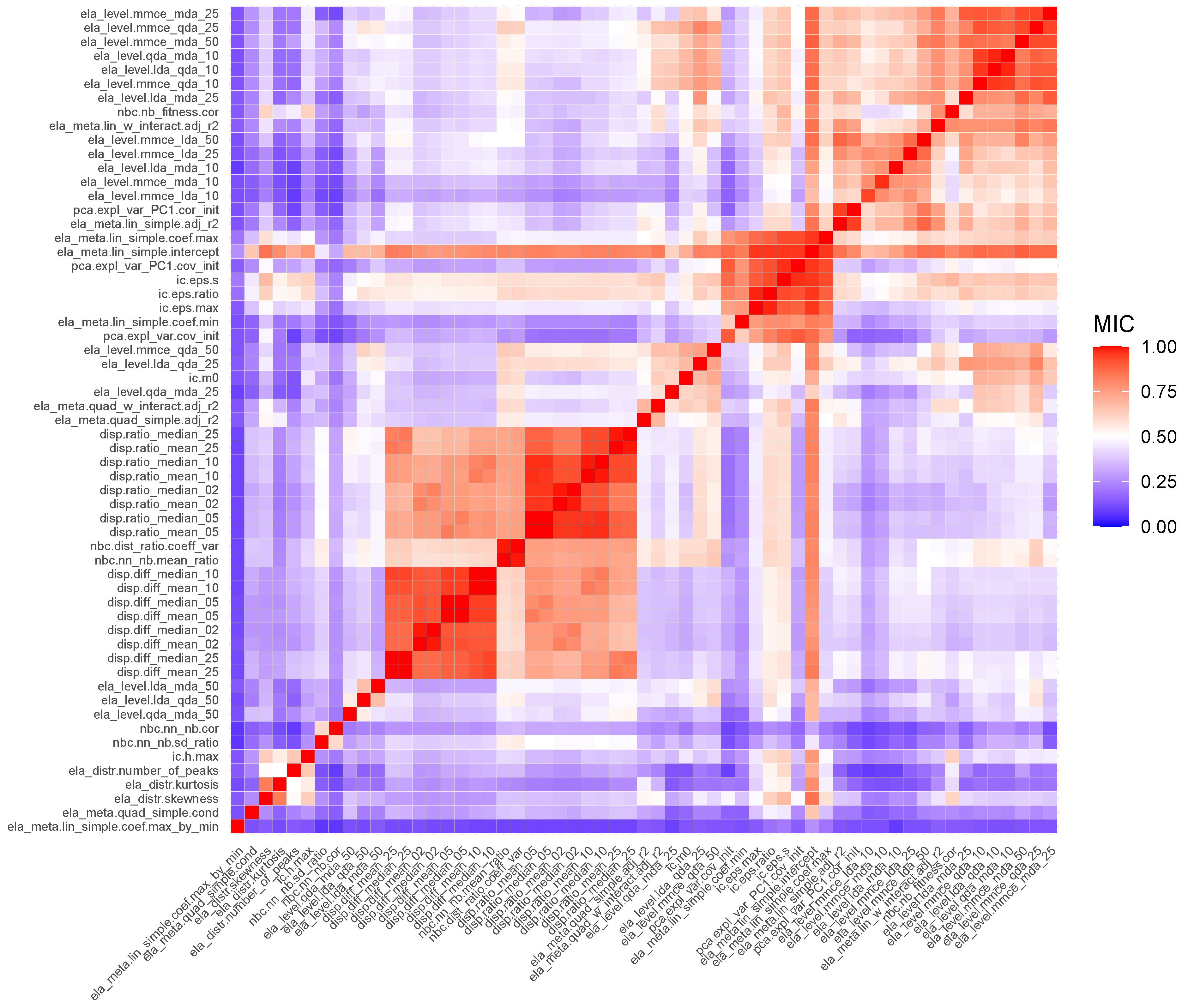
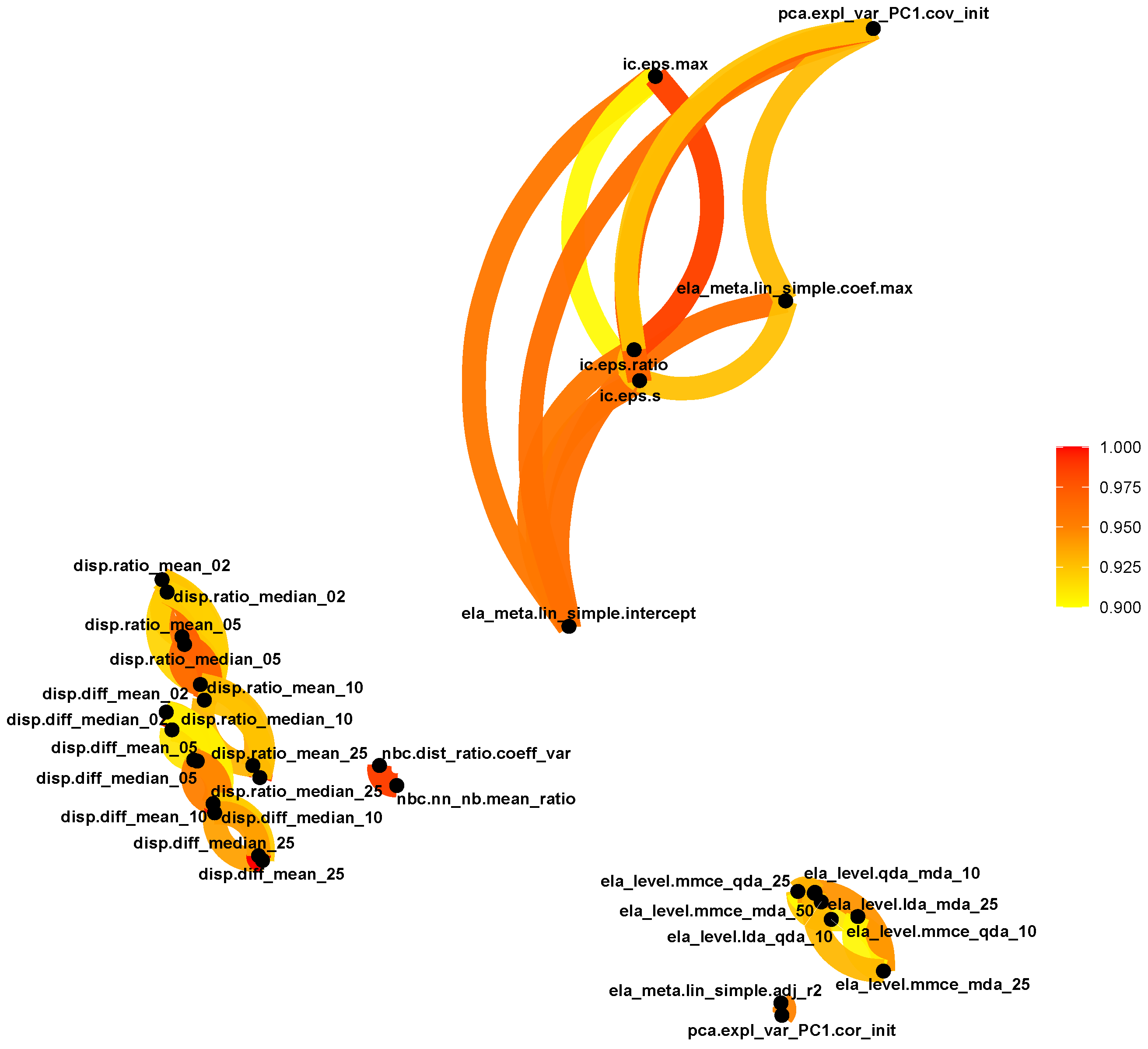
- Identify ELA measures that are highly correlated to prevent multicollinearity.
- It produces values in between 0 and 1, with 0 indicating that there is no association between the two variables, and 1 indicating that the variables have a perfect noiseless relationship. This allows for easy interpretation of the MIC score.
- It captures a wide range of relationships, both functional and non-functional.
- It is symmetric, which implies that .
|
|
4.2. Self-Organizing Feature Map
4.3. Selecting a Benchmark Suite
- Functions from the miscellaneous group are preferable, as they do not require additional information such as rotation matrices and shift vectors, which is the case with the CEC and BBOB benchmark suites.
- Functions from the BBOB benchmark suite are preferred over functions from CEC benchmark suites, as there is a large amount of information, such as algorithm performance, for the BBOB benchmark suite.
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FLA | fitness landscape analysis |
| ELA | exploratory landscape analysis |
| LA | landscape analysis |
| SOM | Self-organizing feature map |
| GECCO | Genetic and Evolutionary Computation Conference |
| CEC | IEEE Congress on Evolutionary Computation |
| MIC | Maximal information coefficient |
Appendix A. Associations between ELA Measures
Appendix B. Component Maps for the Self-Organizing Map
References
- Rice, J.R. The Algorithm Selection Problem. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 1976; Volume 15, pp. 65–118. [Google Scholar] [CrossRef]
- Liang, J.; Qu, B.; Suganthan, P.; Hernández-Díaz, A. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization. 2013. Available online: https://al-roomi.org/multimedia/CEC_Database/CEC2013/RealParameterOptimization/CEC2013_RealParameterOptimization_TechnicalReport.pdf (accessed on 20 February 2021).
- Liang, J.; Qu, B.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization. 2013. Available online: https://bee22.com/resources/Liang%20CEC2014.pdf (accessed on 20 February 2021).
- Liang, J.; Qu, B.; Suganthan, P.; Chen, Q. Problem Definitions and Evaluation Criteria for the Cec 2015 Competition on Learning-Based Real-Parameter Single Objective Optimization. 2014. Available online: https://al-roomi.org/multimedia/CEC_Database/CEC2015/RealParameterOptimization/LearningBasedOptimization/CEC2015_LearningBasedOptimization_TechnicalReport.pdf (accessed on 20 February 2021).
- Wu, G.; Mallipeddi, R.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition and Special Session on Constrained Single Objective Real-Parameter Optimization. 2016. Available online: https://www.researchgate.net/profile/Guohua-Wu-5/publication/317228117_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2017_Competition_and_Special_Session_on_Constrained_Single_Objective_Real-Parameter_Optimization/links/5982cdbaa6fdcc8b56f59104/Problem-Definitions-and-Evaluation-Criteria-for-the-CEC-2017-Competition-and-Special-Session-on-Constrained-Single-Objective-Real-Parameter-Optimization.pdf (accessed on 20 February 2021).
- Hansen, N.; Finck, S.; Ros, R.; Auger, A. Real-Parameter Black-Box Optimization Benchmarking 2009: Noiseless Functions Definitions; Research Report RR-6829; INRIA: Le Chesnay-Rocquencourt, France, 2009; Available online: https://hal.inria.fr/inria-00362633v2 (accessed on 26 February 2021).
- Jamil, M.; Yang, X. A Literature Survey of Benchmark Functions For Global Optimization Problems. arXiv 2013, arXiv:1308.4008. [Google Scholar]
- Adorio, E.P.; Diliman, U. Mvf-Multivariate Test Functions Library in C for Unconstrained Global Optimization; GeoCities: Quezon City, Philippines, 2005; pp. 100–104. [Google Scholar]
- Al-Roomi, A.R. Unconstrained Single-Objective Benchmark Functions Repository; 2015; Available online: https://www.al-roomi.org/component/content/article?id=175:generalized-rosenbrock-s-valley-banana-or-2nd-de-jong-s-function (accessed on 26 February 2021).
- Hedar, A.R. Test Functions for Unconstrained Global Optimization; System Optimization Laboratory, Kyoto University: Kyoto, Japan, 25 May 2013; Available online: http://www-optima.amp.i.kyotou.ac.jp/member/student/hedar/Hedar_files/TestGO.htm (accessed on 26 February 2021).
- Garden, R.W.; Engelbrecht, A.P. Analysis and classification of optimisation benchmark functions and benchmark suites. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1641–1649. [Google Scholar]
- Muñoz, M.A.; Smith-Miles, K. Generating New Space-Filling Test Instances for Continuous Black-Box Optimization. Evol. Comput. 2020, 28, 379–404. [Google Scholar] [CrossRef]
- Škvorc, U.; Eftimov, T.; Korošec, P. Understanding the problem space in single-objective numerical optimization using exploratory landscape analysis. Appl. Soft Comput. 2020, 90, 106138. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Halgamuge, S.K. Similarity of Continuous Optimization Problems from the Algorithm Performance Perspective. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2949–2957. [Google Scholar]
- Christie, L.A.; Brownlee, A.E.I.; Woodward, J.R. Investigating Benchmark Correlations When Comparing Algorithms with Parameter Tuning. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, GECCO’18, Kyoto, Japan, 15–19 July 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 209–210. [Google Scholar] [CrossRef]
- Malan, K.M.; Engelbrecht, A.P. A survey of techniques for characterising fitness landscapes and some possible ways forward. Inf. Sci. 2013, 241, 148–163. [Google Scholar] [CrossRef]
- Mersmann, O.; Bischl, B.; Trautmann, H.; Preuss, M.; Weihs, C.; Rudolph, G. Exploratory landscape analysis. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; pp. 829–836. [Google Scholar]
- Lang, R.; Engelbrecht, A. On the Robustness of Random Walks for Fitness Landscape Analysis. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 1898–1906. [Google Scholar]
- Kerschke, P.; Preuss, M.; Wessing, S.; Trautmann, H. Low-Budget Exploratory Landscape Analysis on Multiple Peaks Models. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, GECCO’16, Denver, CO, USA, 20–24 July 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 229–236. [Google Scholar] [CrossRef]
- Bossek, J. smoof: Single- and Multi-Objective Optimization Test Functions. R J. 2017, 9, 103. [Google Scholar] [CrossRef]
- CIlib Benchmarks. Available online: https://github.com/ciren/benchmarks (accessed on 26 February 2021).
- Mersmann, O.; Preuss, M.; Trautmann, H. Benchmarking evolutionary algorithms: Towards exploratory landscape analysis. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Krakov, Poland, 11–15 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 73–82. [Google Scholar]
- Kerschke, P.; Trautmann, H. Comprehensive Feature-Based Landscape Analysis of Continuous and Constrained Optimization Problems Using the R-package flacco. In Applications in Statistical Computing—From Music Data Analysis to Industrial Quality Improvement; Studies in Classification, Data Analysis, and Knowledge Organization; Bauer, N., Ickstadt, K., Lübke, K., Szepannek, G., Trautmann, H., Vichi, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 93–123. [Google Scholar] [CrossRef]
- Lunacek, M.; Whitley, D. The dispersion metric and the CMA evolution strategy. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 477–484. [Google Scholar]
- Muñoz, M.A.; Kirley, M.; Halgamuge, S.K. Exploratory landscape analysis of continuous space optimization problems using information content. IEEE Trans. Evol. Comput. 2014, 19, 74–87. [Google Scholar] [CrossRef]
- Kerschke, P.; Preuss, M.; Wessing, S.; Trautmann, H. Detecting funnel structures by means of exploratory landscape analysis. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 265–272. [Google Scholar]
- Renau, Q.; Dréo, J.; Doerr, C.; Doerr, B. Expressiveness and robustness of landscape features. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 2048–2051. [Google Scholar]
- Renau, Q.; Doerr, C.; Dreo, J.; Doerr, B. Exploratory landscape analysis is strongly sensitive to the sampling strategy. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Leiden, The Netherlands, 5–9 September 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 139–153. [Google Scholar]
- Bartz-Beielstein, T.; Doerr, C.; Bossek, J.; Chandrasekaran, S.; Eftimov, T.; Fischbach, A.; Kerschke, P.; Lopez-Ibanez, M.; Malan, K.M.; Moore, J.H.; et al. Benchmarking in Optimization: Best Practice and Open Issues. arXiv 2020, arXiv:2007.03488. [Google Scholar]
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef]
- Iivarinen, J.; Kohonen, T.; Kangas, J.; Kaski, S. Visualizing the clusters on the self-organizing map. In Proceedings of the Conference on Artificial Intelligence Research in Finland, Turku, Finland, 29–31 August 1994; pp. 122–126. [Google Scholar]
- Muñoz Acosta, M.A.; Kirley, M.; Smith-Miles, K. Analyzing randomness effects on the reliability of Landscape Analysis. Nat. Comput. 2020. [Google Scholar] [CrossRef]
- Levene, H. Contributions to probability and statistics. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling; Stanford University Press: Redwood City, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Brown, M.B.; Forsythe, A.B. Robust tests for the equality of variances. J. Am. Stat. Assoc. 1974, 69, 364–367. [Google Scholar] [CrossRef]
- Neuhäuser, M.; Hothorn, L.A. Parametric location-scale and scale trend tests based on Levene’s transformation. Comput. Stat. Data Anal. 2000, 33, 189–200. [Google Scholar] [CrossRef]
- Hui, W.; Gel, Y.; Gastwirth, J. lawstat: An R Package for Law, Public Policy and Biostatistics. J. Stat. Softw. Artic. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Lim, T.S.; Loh, W.Y. A comparison of tests of equality of variances. Comput. Stat. Data Anal. 1996, 22, 287–301. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Albanese, D.; Filosi, M.; Visintainer, R.; Riccadonna, S.; Jurman, G.; Furlanello, C. Minerva and minepy: A C engine for the MINE suite and its R, Python and MATLAB wrappers. Bioinformatics 2013, 29, 407–408. [Google Scholar] [CrossRef]
- Wehrens, R.; Buydens, L.M.C. Self- and Super-Organizing Maps in R: The kohonen Package. J. Stat. Softw. 2007, 21, 1–19. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement Ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Lang, R.D. Ela_benchmark. 2021. Available online: https://zenodo.org/record/4539080#.YDnclNwRVPY (accessed on 6 February 2021).
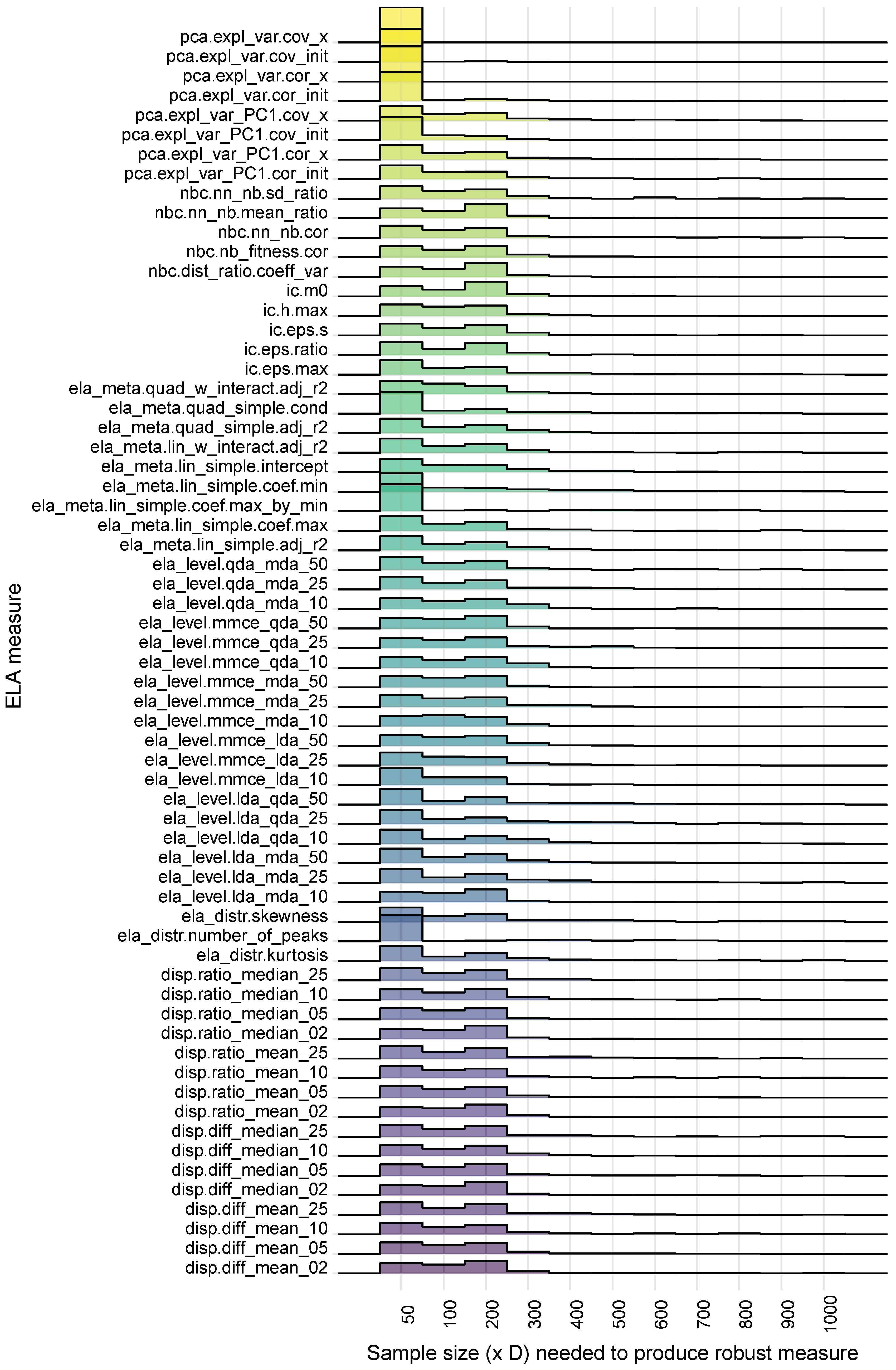
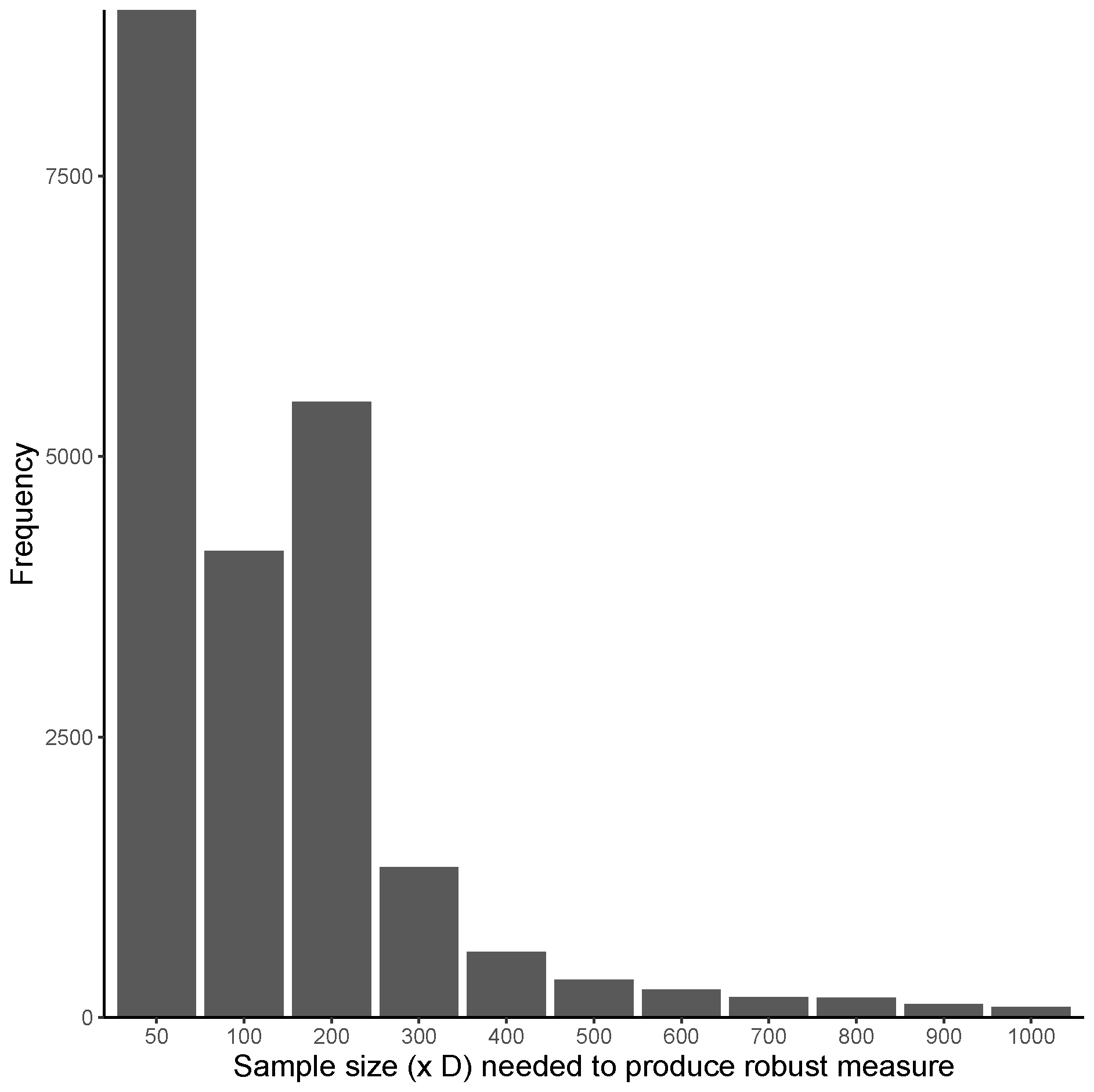


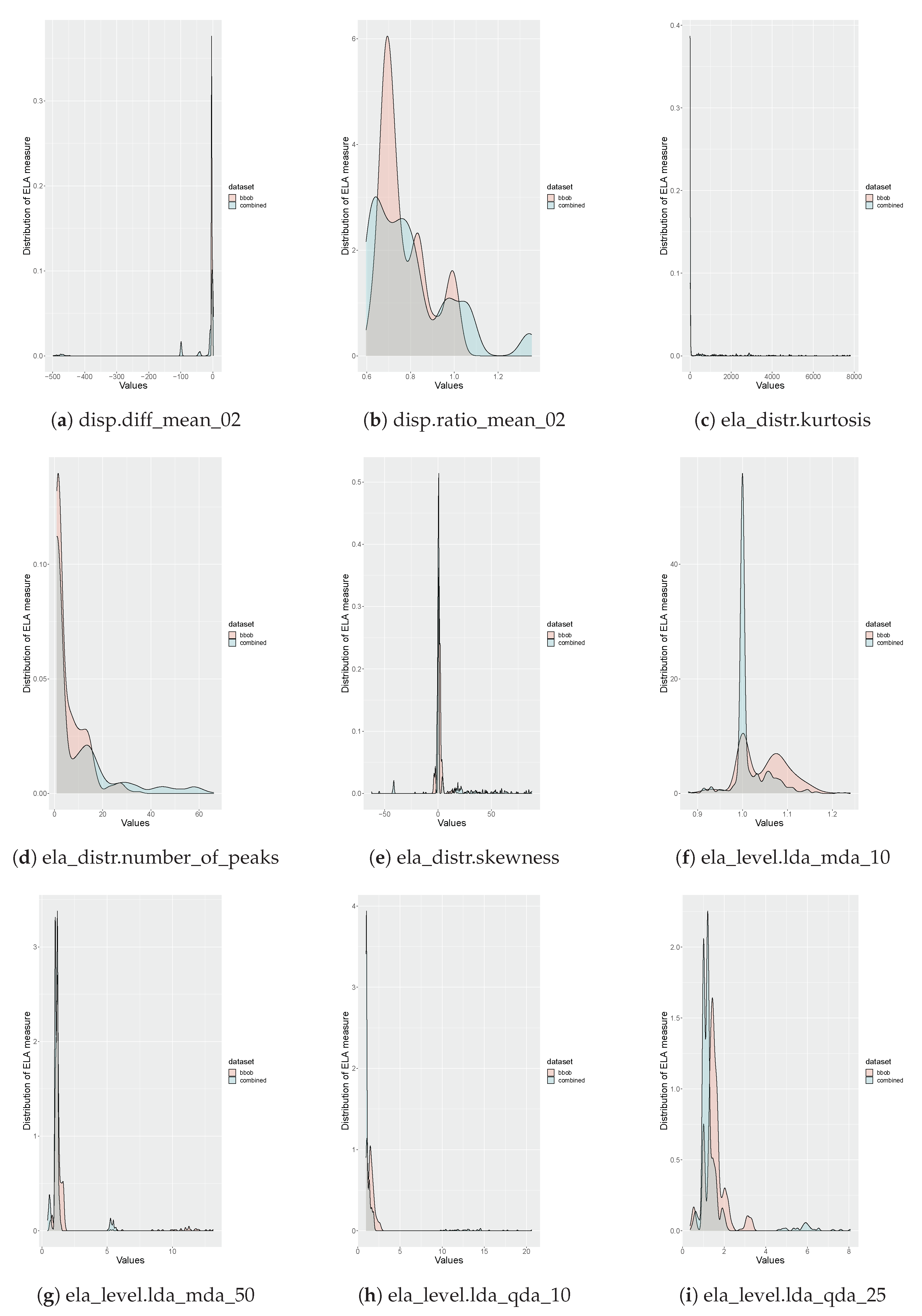
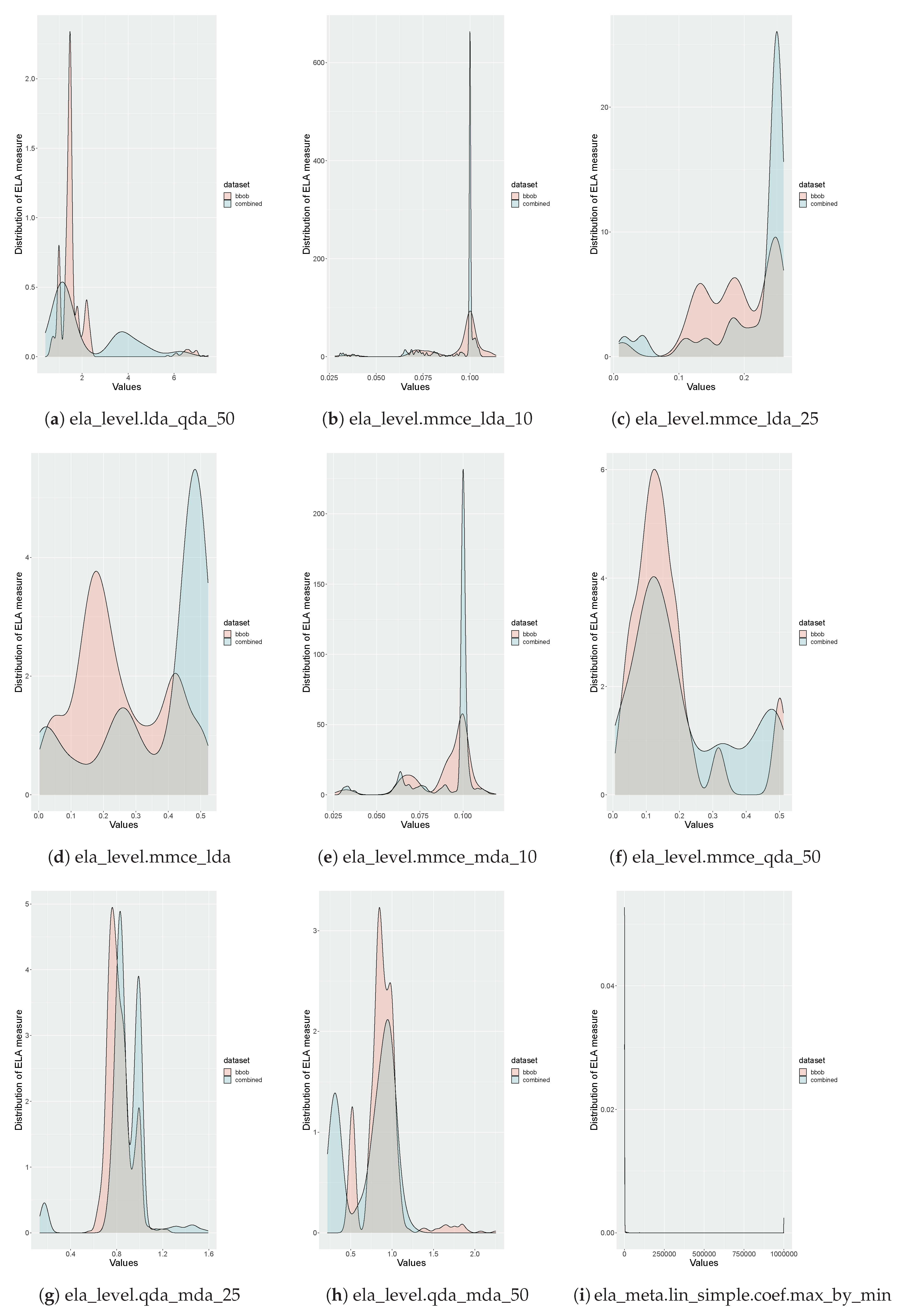
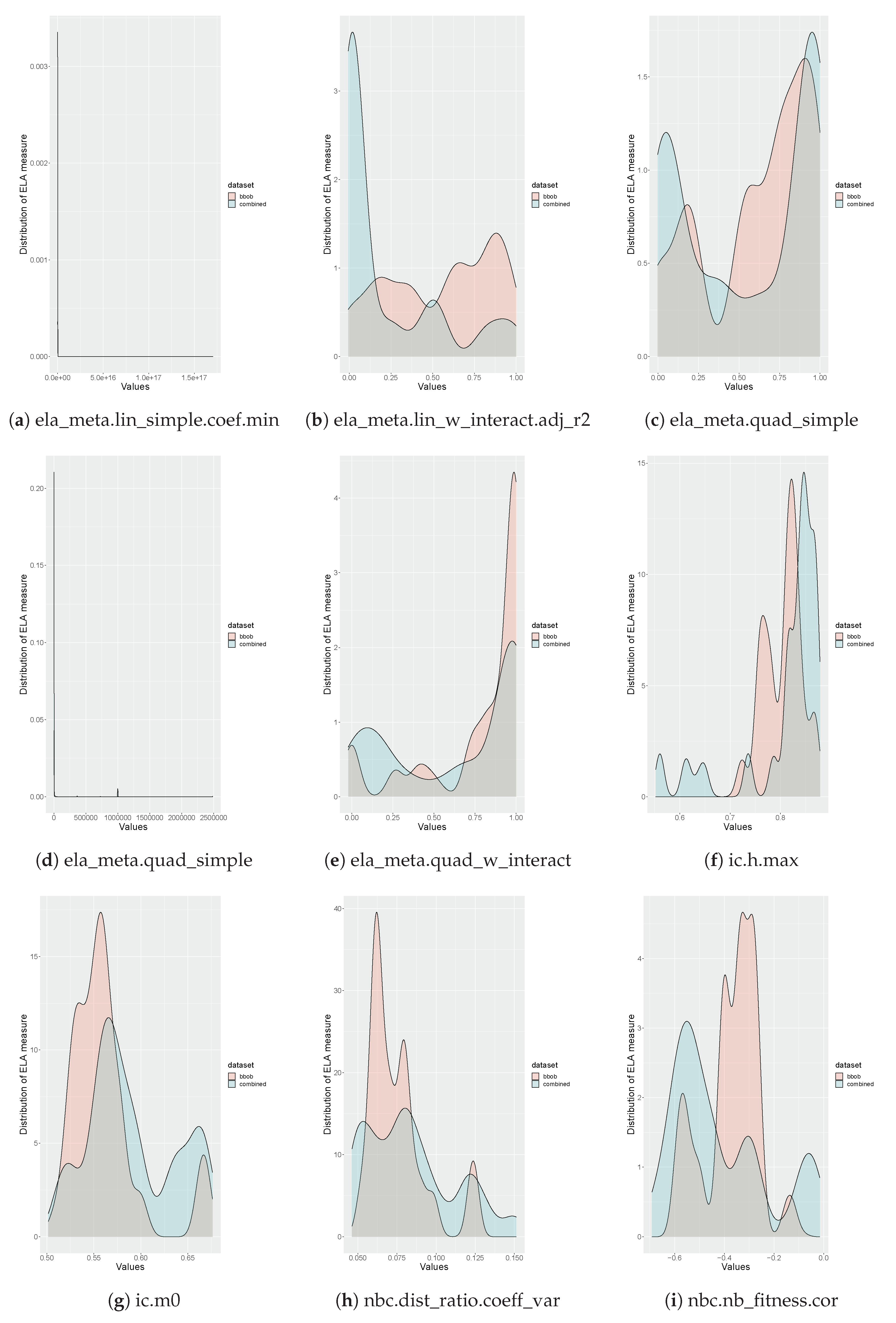
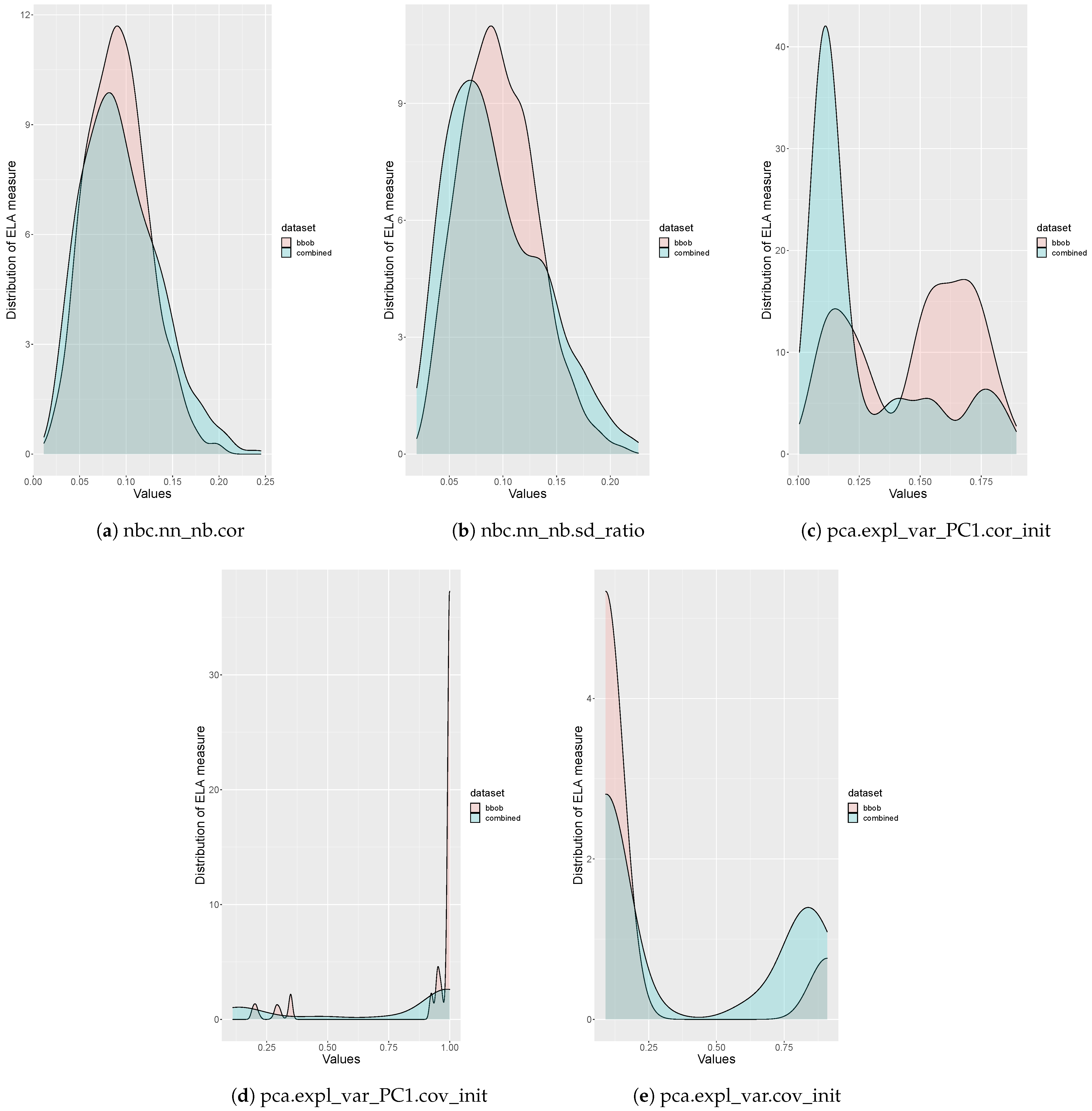
| ELA Measure | 10% | 25% | 50% | 75% | 90% | 95% | 99% | 100% |
|---|---|---|---|---|---|---|---|---|
| disp.diff_mean_02 | 50 | 50 | 100 | 200 | 300 | 300 | 700 | 1000 |
| disp.diff_mean_05 | 50 | 50 | 100 | 200 | 300 | 400 | 800 | 1000 |
| disp.diff_mean_10 | 50 | 50 | 100 | 200 | 400 | 700 | 1000 | 1000 |
| disp.diff_mean_25 | 50 | 50 | 100 | 200 | 300 | 500 | 700 | 1000 |
| disp.diff_median_02 | 50 | 50 | 100 | 200 | 200 | 300 | 500 | 600 |
| disp.diff_median_05 | 50 | 50 | 100 | 200 | 200 | 400 | 800 | 1000 |
| disp.diff_median_10 | 50 | 50 | 100 | 200 | 300 | 600 | 900 | 1000 |
| disp.diff_median_25 | 50 | 50 | 100 | 200 | 300 | 400 | 900 | 1000 |
| disp.ratio_mean_02 | 50 | 50 | 100 | 200 | 300 | 300 | 700 | 1000 |
| disp.ratio_mean_05 | 50 | 50 | 100 | 200 | 300 | 400 | 700 | 1000 |
| disp.ratio_mean_10 | 50 | 50 | 100 | 200 | 400 | 700 | 1000 | 1000 |
| disp.ratio_mean_25 | 50 | 50 | 100 | 200 | 400 | 400 | 600 | 900 |
| disp.ratio_median_02 | 50 | 50 | 100 | 200 | 200 | 300 | 500 | 900 |
| disp.ratio_median_05 | 50 | 50 | 100 | 200 | 200 | 400 | 800 | 1000 |
| disp.ratio_median_10 | 50 | 50 | 100 | 200 | 300 | 500 | 900 | 1000 |
| disp.ratio_median_25 | 50 | 50 | 100 | 200 | 300 | 400 | 900 | 1000 |
| ela_distr.kurtosis | 50 | 50 | 100 | 200 | 500 | 700 | 1000 | 1000 |
| ela_distr.number_of_peaks | 50 | 50 | 50 | 50 | 500 | 700 | 900 | 1000 |
| ela_distr.skewness | 50 | 50 | 100 | 200 | 500 | 800 | 1000 | 1000 |
| ela_level.lda_mda_10 | 50 | 50 | 100 | 200 | 200 | 300 | 400 | 700 |
| ela_level.lda_mda_25 | 50 | 50 | 100 | 200 | 400 | 600 | 1000 | 1000 |
| ela_level.lda_mda_50 | 50 | 50 | 100 | 200 | 300 | 500 | 700 | 1000 |
| ela_level.lda_qda_10 | 50 | 50 | 100 | 200 | 400 | 600 | 800 | 1000 |
| ela_level.lda_qda_25 | 50 | 50 | 100 | 300 | 500 | 700 | 900 | 1000 |
| ela_level.lda_qda_50 | 50 | 50 | 100 | 200 | 500 | 700 | 900 | 1000 |
| ela_level.mmce_lda_10 | 50 | 50 | 100 | 200 | 200 | 400 | 700 | 1000 |
| ela_level.mmce_lda_25 | 50 | 50 | 100 | 200 | 300 | 400 | 800 | 800 |
| ela_level.mmce_lda_50 | 50 | 50 | 100 | 200 | 300 | 400 | 700 | 900 |
| ela_level.mmce_mda_10 | 50 | 50 | 100 | 200 | 300 | 300 | 600 | 1000 |
| ela_level.mmce_mda_25 | 50 | 50 | 100 | 200 | 300 | 400 | 900 | 1000 |
| ela_level.mmce_mda_50 | 50 | 50 | 100 | 200 | 200 | 300 | 600 | 800 |
| ela_level.mmce_qda_10 | 50 | 50 | 100 | 200 | 300 | 300 | 700 | 1000 |
| ela_level.mmce_qda_25 | 50 | 50 | 100 | 200 | 400 | 500 | 800 | 1000 |
| ela_level.mmce_qda_50 | 50 | 50 | 100 | 200 | 200 | 300 | 400 | 600 |
| ela_level.qda_mda_10 | 50 | 50 | 100 | 200 | 300 | 400 | 700 | 900 |
| ela_level.qda_mda_25 | 50 | 50 | 100 | 200 | 400 | 500 | 900 | 1000 |
| ela_level.qda_mda_50 | 50 | 50 | 100 | 200 | 400 | 700 | 900 | 1000 |
| ela_meta.lin_simple.adj_r2 | 50 | 50 | 100 | 200 | 300 | 500 | 900 | 1000 |
| ela_meta.lin_simple.coef.max | 50 | 50 | 100 | 200 | 300 | 400 | 900 | 1000 |
| ela_meta.lin_simple.coef.max_by_min | 50 | 50 | 50 | 50 | 600 | 700 | 900 | 1000 |
| ela_meta.lin_simple.coef.min | 50 | 50 | 50 | 300 | 600 | 700 | 1000 | 1000 |
| ela_meta.lin_simple.intercept | 50 | 50 | 100 | 200 | 400 | 500 | 800 | 900 |
| ela_meta.lin_w_interact.adj_r2 | 50 | 50 | 100 | 200 | 300 | 500 | 900 | 900 |
| ela_meta.quad_simple.adj_r2 | 50 | 50 | 100 | 200 | 300 | 500 | 900 | 1000 |
| ela_meta.quad_simple.cond | 50 | 50 | 50 | 200 | 400 | 600 | 800 | 900 |
| ela_meta.quad_w_interact.adj_r2 | 50 | 50 | 100 | 200 | 300 | 300 | 400 | 800 |
| ic.eps.max | 50 | 50 | 100 | 200 | 400 | 700 | 900 | 1000 |
| ic.eps.ratio | 50 | 50 | 100 | 200 | 300 | 300 | 700 | 1000 |
| ic.eps.s | 50 | 50 | 100 | 200 | 300 | 500 | 900 | 1000 |
| ic.h.max | 50 | 50 | 100 | 200 | 300 | 400 | 700 | 900 |
| ic.m0 | 50 | 50 | 200 | 200 | 200 | 300 | 500 | 600 |
| nbc.dist_ratio.coeff_var | 50 | 50 | 100 | 200 | 200 | 300 | 500 | 800 |
| nbc.nb_fitness.cor | 50 | 50 | 100 | 200 | 300 | 400 | 600 | 1000 |
| nbc.nn_nb.cor | 50 | 50 | 100 | 200 | 400 | 600 | 1000 | 1000 |
| nbc.nn_nb.mean_ratio | 50 | 50 | 200 | 200 | 200 | 300 | 600 | 800 |
| nbc.nn_nb.sd_ratio | 50 | 50 | 100 | 200 | 300 | 600 | 800 | 1000 |
| pca.expl_var_PC1.cor_init | 50 | 50 | 100 | 200 | 400 | 700 | 900 | 1000 |
| pca.expl_var_PC1.cor_x | 50 | 50 | 100 | 200 | 400 | 600 | 800 | 900 |
| pca.expl_var_PC1.cov_init | 50 | 50 | 50 | 100 | 200 | 400 | 900 | 1000 |
| pca.expl_var_PC1.cov_x | 50 | 50 | 100 | 200 | 400 | 600 | 800 | 900 |
| pca.expl_var.cor_init | 50 | 50 | 50 | 50 | 200 | 300 | 900 | 1000 |
| pca.expl_var.cor_x | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| pca.expl_var.cov_init | 50 | 50 | 50 | 50 | 50 | 100 | 300 | 900 |
| pca.expl_var.cov_x | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| Number of Clusters | Davies–Bouldin Score |
|---|---|
| 20 | 1.3568 |
| 21 | 1.3758 |
| 22 | 1.3566 |
| 23 | 1.3481 |
| 24 | 1.3228 |
| 25 | 1.3593 |
| 26 | 1.3350 |
| 27 | 1.3412 |
| 28 | 1.3726 |
| 29 | 1.3594 |
| 30 | 1.3498 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, R.D.; Engelbrecht, A.P. An Exploratory Landscape Analysis-Based Benchmark Suite. Algorithms 2021, 14, 78. https://doi.org/10.3390/a14030078
Lang RD, Engelbrecht AP. An Exploratory Landscape Analysis-Based Benchmark Suite. Algorithms. 2021; 14(3):78. https://doi.org/10.3390/a14030078
Chicago/Turabian StyleLang, Ryan Dieter, and Andries Petrus Engelbrecht. 2021. "An Exploratory Landscape Analysis-Based Benchmark Suite" Algorithms 14, no. 3: 78. https://doi.org/10.3390/a14030078
APA StyleLang, R. D., & Engelbrecht, A. P. (2021). An Exploratory Landscape Analysis-Based Benchmark Suite. Algorithms, 14(3), 78. https://doi.org/10.3390/a14030078







