Abstract
When several Nash equilibria exist in the game, decision-makers need to refine their choices based on some refinement concepts. To this aim, the notion of a -proper equilibria set for polymatrix games is used to develop 0–1 mixed linear programs and compute -proper Nash equilibria. A Branch-and-Bound exact arithmetics algorithm is proposed. Experimental results are provided on polymatrix games randomly generated with different sizes and densities.
1. Introduction
For quite a long time, Nash equilibrium solutions have been depicted as the most desirable outcome for games [1]. Avis and Fukuda [2], Audet et al. [3], and Audet, Belhaiza, and Hansen [4] proposed algorithmic approaches to enumerate the extreme Nash equilibria of two-player games. Daskalakis et al. [5] and Hazan and Krauthgamer [6] focused on the complexity of Nash equilibrium computation for two-player games. Etessami and Yannakis [7] focused on the complexity of approximated Nash equilibria computation for three and more player finite games.
Yanovskaya [8] used the Complementary Pivoting Method to compute Nash equilibria for polymatrix games. Howson [9], Eaves [10], and Howson and Rosenthal [11] used a similar approach. In particular, Quintas [12] demonstrated that a Nash equilibria set is a union of a finite number of convex polytopes for polymatrix games. Miller and Zucker [13] reduced the polymatrix game equilibrium computation problem to a copositive-plus linear complementarity problem (LCP) that requires a single-time application of Lemke’s algorithm [14]. On the same line, Wilson [15] adapted the Lemke and Howson algorithm [16] originally designed for two-player games to n-player games. Govindan and Wilson [17] developed polymatrix game sequences to approximate n-player games Nash equilibrium solutions. The enumeration of all polymatrix game extreme Nash equilibria was addressed in [4]. Strekalovskii and Ekhbat [18] reduced the search for Nash equilibria to a simple optimization problem. They also brought a simple proof on the existence of a Nash equilibrium for polymatrix games.
Meanwhile, an important concern emerged as decision-makers facing multiple Nash equilibria needed to refine their choices using more strict criteria. Although many refinement concepts were introduced, results on polymatrix games are quite limited. Papadimitriou and Roughgarden [19] demonstrated that the computation of a polymatrix game correlated equilibrium may be achieved in polynomial time. Belhaiza [20] demonstrated that perfect equilibria sets for polymatrix games are also unions of finite numbers of convex polytopes, possibly disjoint.
The proper refinement of the Nash equilibrium concept was introduced by Myerson [21] with the idea that reasonable players should try much harder to avoid the most costly mistakes than they should try to avoid the less costly ones. In fact, the proper refinement defines more stability conditions related to small rationality imperfections also called “trembling-hand perfection”. Myerson [21] demonstrated that there is always at least one proper equilibrium for any game in strategic form. For bimatrix games, Belhaiza et al. [22] introduced the concept of a set of -proper equilibria. They used sequences of quadratic programs to validate or reject the properness of a given Nash equilibrium point.
This paper brings theoretical and computational results on proper Nash equilibria for polymatrix games. To the best of our knowledge, no such results were published before. The sections of this paper are ordered as follows. Section 2 gives a formal description of polymatrix games. Section 3 recalls the definition of -proper equilibria and proposes a novel formulation of the -properness conditions. Section 4 proposes mixed 0–1 quadratic and linear formulations to detect -proper and non-proper Nash equilibria, and shows on a three-player polymatrix game how -proper sequences of equilibria can be analytically generated. Section 5 presents a Branch-and-Bound algorithm for polymatrix games -proper equilibria computation. The algorithm is based on a mixed 0–1 linear program combining Nash equilibrium primal and dual conditions and the -properness conditions. Finally, computational results on polymatrix games randomly generated are presented in Section 6.
2. Polymatrix Games
A polymatrix is a strategic interaction of players in a non-cooperative and normal setting, where the payoff of each player is the total sum of a series of partial payoffs. Particularly, when , such interaction defines a bimatrix game. With as the set of all players, every player formulates his choice over a set of strategies , where is finite and all element strategies are pure. A given player i’s partial payoff matrix with respect to a player j’s strategic decisions is a matrix denoted by . A partial payoff is rewarded to player i, if player i selects his strategy and player j selects his strategy . We define the matrix of player i’s payoffs with respect to all players. The overall payoff for player i with respect to any choice in pure strategies of the n players, is
Hence, a given player i’s payoff with respect to player j’s decisions is not related to the remaining players’ choices. Every player i sets a mixed strategy vector over his set of pure strategies and seeks to maximize his total game payoff. The vector is such that , where for every , represents the probability that player i selects his strategy . A given player i’s mixed strategies vector belongs to the set where is a one-row matrix with all entries set to 1. The game total payoff for player i is
Polymatrix games are used in some applications where the players’ payoff matrices are additive. For instance, Belhaiza et al. [23] used a polymatrix game to model a manager–controller–board of directors’ conflict. As for other strategic form games, a polymatrix game has indeed at least one Nash equilibrium as shown in [1]. We can define a Nash equilibrium as a n-tuple of mixed strategies such that for any other n-tuple the following condition is satisfied
Differently stated, a Nash equilibrium is a situation where a given player i’s payoff with respect to all remaining players is maximized, and similarly for all other players in N. A polymatrix game set of Nash equilibria is the union of a finite number of polytopes, also referred to as maximal Nash subsets. The set of extreme Nash equilibria is defined as the set of all different vertices of all the maximal Nash subsets. Any extreme Nash equilibrium is an extreme point of at least one of the maximal Nash subsets. Hence, a subset is considered as a Nash subset, if and only if for every pair of elements , such that and , we have and , for all . Hence, and are interchangeable. A given Nash subset T is considered as maximal if it is shown that it is not properly contained in any another Nash subset [24].
3. Set of -Proper Equilibria
The proper refinement originates from the assumption that reasonable players should try much harder to avoid more costly mistakes than they should try to avoid less costly ones. While it is well known that any proper equilibrium is always perfect, a perfect Nash equilibrium may be non-proper. Given a finite game in strategic form, Myerson [21] defines a proper equilibrium as the limit of an infinite sequence of -proper equilibria, when converges to zero. We here apply Myerson’s definition of the -proper equilibrium to polymatrix games. Let us first note and as the and rows of the payoff matrix of player i, respectively.
Definition 1.
A polymatrix game profile is ϵ-proper, for , if for all :
For a given and , we now introduce the following set such that:
In the above, is a binary variable, and the parameter is set to a sufficiently large value. The following Proposition 1 gives a novel formulation of the -properness conditions and shows that each element of is an -proper equilibrium.
Proposition 1.
If , for and , then X is an ϵ-proper equilibrium.
Proof.
Assume that , for and . Let k and q be indices in , such that . The inequalities ensure that the binary combination and is impossible. Moreover,
- -
- if and , then ;
- -
- if , then implies that and , thus .
It follows that conditions (1) are satisfied. Finally, with , for all , conditions (2) are satisfied. □
Proposition 2 states that every -proper equilibrium belongs to , for every sufficiently small value of .
Proposition 2.
If is an ϵ-proper equilibrium for a given , there exists a real number , such that , for .
Proof.
If a profile is an -proper equilibrium for some , for all , conditions (1) can be reformulated using the binary variables , for all :
Finally, conditions (2) ensure the existence of a , such that , for all and for all . Then, for every such that :
Thus, for any , such that . □
The set can now be called a set of -proper equilibria. Myerson [21] also showed that for every finite game in strategic form the set of proper equilibria is non-empty. Hence, such a sequence of -proper equilibria exists for every polymatrix game. Finding such sequences is not an easy task. While we proposed a 0–1 mixed quadratic programming approach to generate such sequences for bimatrix games [22], we now extend our approach to polymatrix games.
4. Computation of Proper Equilibria
Trying analytically to obtain such sequences of -proper equilibria would be unsuccessful if the equilibrium is non-proper. Therefore, one should try to detect equilibrium profiles that could help generate such sequences, and eliminate equilibrium profiles offering no possibility. To do so, we propose 0–1 mixed quadratic formulations that help detect the existence of -proper equilibria. To overcome the numerical noise that may appear while performing quadratic optimization with infinitesimal , we propose a 0–1 mixed linear formulation and implement it using exact arithmetics. We also show how the analytical computation of -proper equilibria could be performed, provided that -proper equilibria close to a Nash equilibrium are detected.
4.1. Mixed 0–1 Quadratic Formulations
We now propose a sequence of parametrized 0–1 mixed quadratic programs with optimal solutions defining a sequence of -proper equilibria while converges to 0.
Proposition 3.
A Nash equilibrium is proper if and only if the following 0–1 mixed quadratic program is feasible for all , and if .
Proof.
Assume that is the optimal solution of for a known Nash equilibrium . Proposition 1 asserts that is an -proper equilibrium. In addition, the convergence conditions are here reformulated through the minimization of such that to make sure that the -proper equilibrium converges towards .
Hence, if the 0–1 mixed quadratic program is feasible for all and converging to 0, we may conclude from proposition (2) that there always exists an -proper equilibrium .
In addition, if the Nash equilibrium is proper, the optimal objective value converges necessarily towards 0, when converges to 0, to force the solution to converge towards simultaneously. We can also add that in this case.
Otherwise, if does not converge towards 0, when converges to 0, such -proper sequence does not even exist, when converges to 0. In this case, it is obvious that the given Nash equilibrium cannot be proper. □
In conclusion, if converges to 0, while converges to 0, it is possible to obtain a sequence -proper converging to , when converges to 0. Therefore, we have to compute the values of for some small values of .
Corollary 1.
If is the optimal solution to the 0–1 mixed quadratic program (), for some , then is an -proper equilibrium, and if , then .
Proof.
If , then the 0–1 mixed quadratic program (), for , is a relaxation of the same 0–1 mixed quadratic program (), but for . The main difference between the two programs lies in fact in the conditions of and :
Thus, and . □
Hence, there exists only two probable outcomes when computing for tiny values of . The first possible outcome corresponds to the case where is found to be bounded from below by a strictly positive value . The second possible outcome corresponds to the case where converges to zero.
Case 1: When is found to be bounded from below by an strictly positive indicates that there are no -proper equilibria close to , for values less than . Therefore, would not be proper.
Now, let us assume that converges to some value , when converges to 0 as in (). We then define a 0–1 mixed quadratic program under the same conditions of , but with and seeking to maximize . When the optimal objective value of this program is found to be equal to , we can obviously conclude that it is not possible to obtain a sequence of -proper equilibria converging to the Nash equilibrium . Hence, the Nash equilibrium is not proper.
Proposition 4.
Consider the following 0–1 mixed quadratic program:
If the optimal objective value of is zero for a given , the Nash equilibrium is not proper.
Proof.
If the optimal objective value of () is equal to 0, it is not possible to obtain a sequence -proper converging to . Therefore, the Nash equilibrium is not proper. □
At this stage, a numerical noise may appear with infinitesimal values of . It is risky to rely just on the nonlinear optimization results to detect -properness of a Nash equilibrium. The following mixed 0–1 linear formulations are proposed to overcome this problem.
4.2. Mixed 0–1 Linear Formulation
It is possible to resolve all numerical issues due to the non-linear formulation if is set to a fixed value. The following Corollary 2 can be formulated. It establishes a 0–1 mixed linear formulation from Proposition 4.
Corollary 2.
For a given , consider the following 0–1 mixed linear program
If the optimal objective value of is equal to 0, or is unfeasible, the Nash equilibrium is not proper.
The proof of this corollary is trivial (see Proof of Proposition 3). Hence, we can rely on the 0–1 mixed linear optimization results to certify that an equilibrium is non-proper. Computationally, this can be done using exact arithmetics. Exact arithmetics perform operations on real numbers defined as rationals instead of floats or doubles. A rational number consists of two very large integers, namely a numerator and a denominator. Overloading the elementary operators to handle algebraic operations on these rationals is fundamental. A Greatest Common denominator function is useful to reduce the size of the stored Big Integers. Exact arithmetics was successfully used by Audet et al. [25] and Avis et al. [26] in the context of two-person games equilibrium enumeration and refinement. The automatic detection of non-proper Nash equilibria can then safely be carried out for polymatrix games.
Case 2: converges to zero If converges towards zero, we can conclude on the existence of at least one sequence of -proper equilibria necessarily close to the given Nash equilibrium we are testing for properness. Computationally speaking, unless exact arithmetics is used here, this may not be enough to conclude on the properness of the given Nash equilibrium. Therefore, it is imperative to use exact arithmetics to get consistent results.
As an extension of Corollary 2, the following Corollary 3 can be formulated, when is set to a fixed value.
Corollary 3.
For some , consider the mixed 0–1 linear program of corollary 2:
If the optimal objective value of converges to 0 and remains strictly positive, when ϵ converges to 0, then is a proper equilibrium.
Proof.
Let be the optimal solution to (4), for some given equilibrium profile .
If is strictly positive, Proposition (1) ensures that is an -proper equilibrium.
Hence, if the optimal objective value converges to 0 and remains strictly positive when converges to 0, remains an -proper equilibrium and converges to the equilibrium . Therefore, is a proper equilibrium. □
Since it is based on a linear formulation, this corollary resolves all numerical issues due to the nonlinear formulation of Proposition 3. First, we illustrate our results with a polymatrix game where one of the extreme Nash equilibria is not perfect. With the following example, we show how the Corollary 3 can be applied.
Example Consider the three players polymatrix game , where the following matrices , and detail the payoffs of players I, II, and III.
Using exact arithmetic, the E-MIP algorithm [4,25] enumerated three different extreme Nash equilibria for this game, as detailed in Table 1.

Table 1.
Extreme Nash equilibria.
The optimization results in Table 2 (as shown in [20], a triplet of linear programs was used to conclude on the perfectness of the extreme Nash equilibria) and Table 3 point towards the existence of -proper equilibria sequences close to extreme Nash equilibria 1 and 3.

Table 2.
Optimization results.

Table 3.
Optimization results for equilibrium 3.
The optimization results in Table 3 show how the value of decreases while converges to 0 and the quest of -proper equilibria close to extreme Nash equilibrium 3 is successful.
The following figure (Figure 1) illustrates how the value of converges to 0, when converges to 0, for the extreme Nash equilibrium 3.
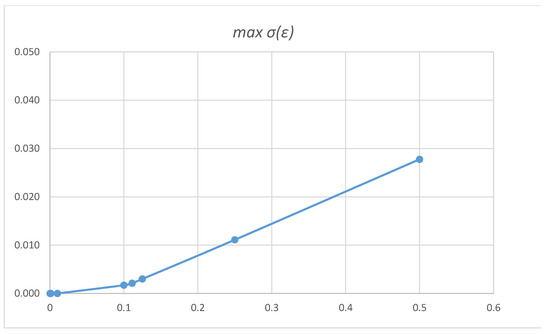
Figure 1.
Eq3; Plot of .
4.3. Analytical Computation
We now use the optimization results in Table 2 and Table 3 to analytically generate sequences of -proper equilibria from extreme Nash equilibrium 3. In the extreme Nash equilibrium 3 strategy profile, player I randomizes on and . A sequence of -proper equilibria should then take into account that player II is indifferent between his first and third strategies. One should think that if player I is not indifferent between his first and third strategies, he would have to assign to the less interesting strategy a probability less than times the probability of the other strategy.
Therefore,
Thus, we have
One should also note that this is satisfied by equilibrium 3. Hence, player II would have to assign a probability larger than to his third strategy.
Simultaneously, a sequence of -proper equilibria should take into account that player II is indifferent between his first and third strategies. Therefore,
Thus, we have
This condition is satisfied by equilibrium 3. Taking into account that and would receive very small but strictly positive probabilities, player I would have to assign a probability less than to his first strategy, and player III would have to assign a probability less than to his second strategy.
Finally, a sequence of -proper equilibria would take into account that player III is indifferent between his first and second strategies. Therefore,
Thus, we have
This condition is also satisfied by equilibrium 3. Player II would have to assign a probability less than to his first strategy.
We here detail some of the steps to generate a sequence of -proper equilibria converging to the extreme Nash equilibrium 3.
We first set , , , and , where .
With conditions (3), we obtain and .
Since needs to be less than , we have
For simplification purposes, we consider that player I would be indifferent between his second and fourth strategies, which yields . This assumption does not eliminate the possibility for player I to have a marked preference for one of these two strategies.
We then set and substitute condition (5) in (4).
We obtain
Since , because player I prefers his first strategy to his second, we obtain a lower bound on :
Then, by (5) we have and , where
It has now been made clear that we obtained a sequence of -proper equilibria converging to the extreme Nash equilibrium 3 when converges to 0.
5. Branch-and-Bound Algorithm for -Proper Equilibrium Computation
We now propose a Branch-and-Bound algorithm for - proper equilibrium computation. The algorithm is based on a 0–1 mixed linear program which provides at optimality an -proper equilibrium to a polymatrix game. The 0–1 mixed linear program combines Nash equilibrium primal and dual conditions detailed in [4] and the -properness conditions. Note that here is set to a fixed rational value which is strictly positive, but very close to
5.1. The 0–1 Mixed Linear Master Program
The following 0–1 mixed linear program combines the Nash equilibrium primal and dual conditions, for polymatrix games, and the -properness conditions aforementioned. The optimization of using exact arithmetics, provides at optimality a Nash equilibrium and an -proper equilibrium X, when is set to a fixed value.
Proposition 5.
Given a polymatrix game, for some consider the 0–1 mixed linear program :
This 0–1 mixed linear program is always feasible for any and its optimal objective value is always strictly positive.
The mixed strategies vector is a Nash equilibrium of the given polymatrix game and the completely mixed strategies vector is an ϵ-proper equilibrium.
Proof.
Constraints (9)–(12) assert that is a Nash equilibrium of the given polymatrix game (see [4]). Constraints (13) and (14) assert that is an -proper equilibrium as shown earlier. For any given polymatrix game, the set of Nash equilibria and the set of proper equilibria are non-empty. Therefore, for any there exists a pair of vectors and X such that is a Nash equilibrium, and X is an -proper equilibrium. Hence, the optimal objective value is always strictly positive. □
The mixed 0–1 linear program serves as the master program in the proposed -proper Branch-and-Bound algorithm.
5.2. The -Proper Branch-and-Bound Algorithm
Let P be defined as a master linear program obtained after relaxation of the 0–1 conditions in . The proposed -proper Branch-and-Bound algorithm follows a principal branching tree scheme and many secondary branching trees. At every vertex on the principal tree, a binary branching is performed on one of the 0–1 variables. At every vertex of the principal tree, the algorithm solves a master linear program P with at most two constraints fixing one or more binary variables and cutting one or more binary variables combinations. Each time a Nash equilibrium is obtained, the objective function value is compared to a recorded maximum . In the case where the optimal objective is equal to zero or lower than , the given principal tree vertex and its sons cannot provide any -proper equilibrium with a larger than . The current stored serves as a bound to shorten the algorithm’s execution.
At every vertex of a secondary tree node, a linear sub-program Q is solved. This linear sub-program Q results from the master linear program P, with one combination of binary variables fixing constraints and at most two constraints fixing one or more continuous x variables. If a Nash equilibrium is obtained, the objective function value is compared to a recorded maximum . Again, in the case where the optimal objective is equal to zero or lower than , the given secondary tree vertex and its sons cannot provide any -proper equilibrium with a larger than .
The -proper Branch-and-Bound algorithm is formally stated as follows.
Step 1: Initialization.
Define:
- -
- P; Master linear program defined by the relaxation of the 0–1 conditions in
- -
- Sub-program defined by a secondary linear program where the U and V variables in P are fixed.
- -
- , X; ’s real decision variables.
- -
- ; ’s binary decision variables.
- -
- ; List of Nash equilibria visited.
- -
- ; List of -proper Nash equilibria obtained.
- -
- ; Depth level reached in the principal tree.
- -
- ; Principal tree root node.
- -
- C; Current node.
- -
- , ; Real decision variables on the strategy of player i
- -
- ; Binary decision variables on the strategy of player i
- -
- ; Binary decision variables on the and strategies of player i
- -
- ; Best value of found.
Set C = CR, and Go to step 2.
Step 2: Solving master program.
If , solve current node’s program P.
- -
- If the program P is infeasible or the optimal objective is equal to 0; STOP.
- -
- Else;
- -
- If , Go to step 3.
- -
- Else, Let be the solution obtained;
- -
- If the optimal objective of P is less than , STOP.
- -
- Else, if the optimal objective of P is ≥,
Update, AddX to E and to and Go to step 4.
Step 3: Principal Branching.
Select a binary variable or over which no principal branching was performed.
Let
If set and
- -
- Set or selected to 1 in P and Go to step 2.
- -
- Set or selected to 0 in P and Go to step 2.
Step 4: Secondary Branching.
Set binary variable vectors V and U at their values in
For every : Set and Go to step 5.
Step 5: Solving subprogram.
Solve to optimality.
- -
- If the program Q is infeasible or the optimal objective is equal to 0; STOP.
- -
- Else, if the optimal objective of is less than , STOP.
- -
- If the optimal objective of is , Update = , Add to E and X to . Go to step 4.
The sets E and are non-empty and contain respectively all Nash equilibria and all -proper equilibria encountered. The maximum value of is The last element entering corresponds to
Theorem 1.
The ϵ-proper Branch-and-Bound algorithm generates at least one ϵ-proper equilibrium for any polymatrix game.
Proof.
The algorithm searches for all possible ways to satisfy the Nash equilibrium, complementary slackness, and properness conditions through the principal branching tree and the secondary trees. If is the unique -proper equilibrium, there exists at least one path in the algorithm’s generated branching tree leading to it. □
The complexity of the -proper Branch-and-Bound algorithm is certainly non-polynomial. It increases exponentially when the size of the polymatrix game increases.
6. Experimental Results
Table 4 presents the computational results obtained on randomly generated sets of three-player polymatrix games with different sizes and density. The size of the polymatrix games generated goes from to The density of the polymatrix games generated goes from % to 100 %. The entries of the polymatrix games generated are integers. The optimization of the master and secondary linear programs P and Q uses a C++ implementation of the Simplex algorithm in exact arithmetics.

Table 4.
-proper experimental results.
In Table 4, column (Size) lists the different numbers of strategies for each player before elimination of strategies strongly dominated. The column (d) lists the different densities of the partial payoff matrices generated. The column () lists the values of the parameter used. The column () indicates the average number of -proper equilibria encountered over 10 polymatrix games randomly generated. Finally, the value (Time) indicates the average time in seconds required to find an -proper equilibrium with a maximum value of . Finally, the experimental results are obtained under MS Windows on workstations equipped with 3.3 GHz Intel Core i5 vPro processors and 3.2 GB RAM.
In particular, one can observe that reducing the partial payoff matrices density increases the computing time required to find an -proper equilibrium as it also increases the total number of -proper equilibria detected for the polymatrix game.
7. Conclusions
In this paper we have shown how to compute -proper Nash equilibria for polymatrix games. The notion of a set of -proper equilibria for polymatrix games was used to develop a class of 0–1 mixed linear programs to detect proper and non-proper Nash equilibria. Consequently, a 0–1 mixed linear program was proposed to compute an -proper Nash equilibrium for a polymatrix game. We have finally presented our experimental results on randomly generated polymatrix games. A future extension of this work should naturally tackle proper equilibrium computation for more general forms of n-player games.
Funding
This work was partly funded by King Fahd University of Petroleum and Minerals research grant POC19103 and the Interdisciplinary Research Center on Smart Mobility and Logistics research grant INML2107. This support is gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
References
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Avis, D.; Fukuda, K. A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Discret. Comput. Geom. 1992, 8, 295–313. [Google Scholar] [CrossRef]
- Audet, C.; Hansen, P.; Jaumard, B.; Savard, G. Enumeration of all extreme equilibrium strategies of bimatrix games. Siam J. Sci. Comput. 2001, 23, 323–338. [Google Scholar] [CrossRef]
- Audet, C.; Belhaiza, S.; Hansen, P. Enumeration of all Extreme Equilibria in Game Theory: Bimatrix and Polymatrix Games. J. Optim. Theory Appl. 2006, 129, 349–372. [Google Scholar] [CrossRef]
- Daskalakis, C.; Goldberg, P.; Papadimitriou, C. The complexity of computing a Nash equilibrium. Siam J. Comput. 2009, 39, 195–259. [Google Scholar] [CrossRef]
- Hazan, E.; Krauthgamer, R. How hard is it to approximate the best Nash equilibrium? Siam J. Comput. 2011, 40, 79–91. [Google Scholar] [CrossRef]
- Etessami, K.; Yannakakis, M. On the complexity of Nash equilibria and other fixed points. Siam J. Comput. 2010, 39, 2531–2597. [Google Scholar] [CrossRef]
- Yanovskaya, E.B. Equilibrium points in polymatrix games. Latv. Math. Collect. 1968, 8, 381–384. [Google Scholar]
- Howson, J.T. Equilibria of polymatrix games. Manag. Sci. 1972, 18, 312–318. [Google Scholar] [CrossRef]
- Eaves, C.B. Polymatrix games with joint constraints. Siam J. Appl. Math. 1973, 24, 418–423. [Google Scholar] [CrossRef]
- Howson, J.T.; Rosenthal, R.W. Bayesian equilibria of finite two-person games with incomplete information. Manag. Sci. 1974, 21, 313–315. [Google Scholar] [CrossRef]
- Quintas, L. A Note on Polymatrix Games. Int. J. Game Theory 1989, 18, 261–272. [Google Scholar] [CrossRef]
- Miller, D.A.; Zucker, S.W. Copositive-plus Lemke Algorithm Solves Polymatrix Games. Oper. Res. Lett. 1991, 10, 285–290. [Google Scholar] [CrossRef]
- Lemke, C.E. Bimatrix equilibrium points and mathematical programming. Manag. Sci. 1965, 11, 681–689. [Google Scholar] [CrossRef]
- Wilson, R. Computing Equilibria of N-Person Games. Siam J. Appl. Math. 1971, 21, 80–87. [Google Scholar] [CrossRef]
- Lemke, C.E.; Howson, J.T. Equilibrium points of bimatrix games. Siam J. Appl. Math. 1964, 12, 413–423. [Google Scholar] [CrossRef]
- Govindan, S.; Wilson, R. Computing Nash equilibria by iterated polymatrix approximation. J. Econ. Dyn. Control 2004, 28, 1229–1241. [Google Scholar] [CrossRef]
- Strekalovskii, A.S.; Enkhbat, R. Polymatrix games and Optimization Problems. Autom. Remote Control 2014, 75, 632–645. [Google Scholar] [CrossRef]
- Papadimitriou, C.H.; Roughgarden, T. Computing Correlated Equilibria in Multi-Player Games. J. ACM 2008, 55, 1–29. [Google Scholar] [CrossRef]
- Belhaiza, S. Computing Perfect Nash Equilibria for Polymatrix Games. Game Theory 2014, 2014, 937070. [Google Scholar] [CrossRef]
- Myerson, R.B. Refinements of the Nash equilibrium concept. Int. J. Game Theory 1978, 7, 73–80. [Google Scholar] [CrossRef]
- Belhaiza, S.; Audet, C.; Hansen, P. On Proper Refinement of Bimatrix Games Nash Equilibria. Automatica 2012, 48, 297–303. [Google Scholar] [CrossRef]
- Belhaiza, S.; Charrad, S.; M’Hallah, R. On the Performance of Managers and Controllers: A Polymatrix Game Approach for the Manager-Controller-Board of Directors’ Conflict. J. Optim. Theory Appl. 2018, 177, 584–602. [Google Scholar] [CrossRef]
- Borm, P.E.M.; Jansen, M.J.M.; Potters, J.A.M.; Tijs, S.H. On the structure of the set of perfect equilibria in bimatrix games. O-R Spektrum 1993, 15, 17–20. [Google Scholar] [CrossRef][Green Version]
- Audet, C.; Belhaiza, S.; Hansen, P. A new sequence form approach for the enumeration and refinement of all extreme Nash equilibria for extensive form games. Int. Game Theory Rev. 2009, 11, 437–451. [Google Scholar] [CrossRef]
- Avis, D.; Rosenberg, G.D.; Savani, R.; von Stengel, B. Enumeration of Nash equilibria for two-player games. Econ. Theory 2009, 42, 9–37. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).