Short Communication: Optimally Solving the Unit-Demand Envy-Free Pricing Problem with Metric Substitutability in Cubic Time

Abstract

In general, the unit-demand envy-free pricing problem has proven to be APX-hard, but some special cases can be optimally solved in polynomial time. When substitution costs that form a metric space are included, the problem can be solved in $O(n^4)$ time, and when the number of consumers is equal to the number of items—all with a single copy so that each consumer buys an item—a $O(n^3)$ time method is presented to solve it. This work shows that the first case has similarities with the second, and, by exploiting the structural properties of the costs set, it presents a $O(n^2)$ time algorithm for solving it when a competitive equilibrium is considered or a $O(n^3)$ time algorithm for more general scenarios. The methods are based on a dynamic programming strategy, which simplifies the calculations of the shortest paths in a network; this simplification is usually adopted in the second case. The theoretical results obtained provide efficiency in the search for optimal solutions to specific revenue management problems.

1. Introduction

Suppose that a seller has n different items, each one with $c_j$ copies, and there are m consumers, each interested in buying a single copy of an item. The seller knows the valuation $v_{ij}$, the largest amount that consumer i is willing to pay for a copy of item j. If consumer i buys a copy of item j, their utility is $v_{ij}-p_j$, which is the difference between the valuation and the purchase price. The seller needs to decide which item j (a copy of it) will be sold (or not) to consumer i, i.e., to set an allocation of items, and what the price of each item will be so that consumers who buy a copy of the same item pay the same price for it, and the copy of item j sold to consumer i is the one that maximizes their (non-negative) utility, thus satisfying the envy-freeness (the concept of envy-freeness used in this work is different from that introduced by Foley [1], in which all buyers prefer their allocations to the allocations obtained by other agents, which some recent authors, such as Bilò et al. [2], Brânzei et al. [3], and Monaco et al. [4] call pair envy-freeness) property. The goal is to maximize the revenue from the sale of copies of items, i.e., the sum of prices of all copies sold.

The problem above is the unit-demand envy-free pricing problem (UDEFP), and was presented by Guruswami et al. [5], after which several variants and special cases were studied. These authors have shown that the general problem is APX-hard, even if each item exists in unlimited supply and each consumer has equal valuations (of either 1 or 2) for all of the items in which they have any interest. In addition, they provided a $O(logn)$-approximation algorithm based on a maximum-weight-matching strategy.

Chen et al. [6] considered the following case of the UDEFP: The seller has a single item with unlimited supply, and n consumers are in different locations. Each consumer i assigns a valuation $v_i$ to the item if the purchase is made in their own location and a substitution cost ${\delta }_{ij}$ that is subtracted from $v_i$ if the purchase is made in location j. In addition, the cost set ${\left\{{\delta }_{ij}\right\}}_{1\le i,j\le n}$ has a metric space structure (that is, the function $\delta :{\{1,\dots ,n\}}^2⟶\mathbb{R}$ satisfies, for any $1\le i,j,k\le n$, 1) ${\delta }_{ij}=0⟺i=j$ (identity of indiscernibles), ${\delta }_{ij}={\delta }_{ji}$ (symmetry), and ${\delta }_{ij}\le {\delta }_{ik}+{\delta }_{kj}$ (triangle inequality)), which they called metric substitutability. Thus, if consumer i buys the item at location j, their utility is $v_i-(p_j+{\delta }_{ij})$. In this scenario, they showed that the problem can be solved optimally in polynomial time by proving that every consumer receives an item in their own location; then, a perfect graph with $O(n^2)$ vertices is constructed, and in this graph is found a maximum-weighted independent set whose weight corresponds to the optimal revenue. Therefore, by using the ellipsoid method [7], this strategy takes $O(n^4)$ time to find a maximum-weighted independent set and, thus, an optimal envy-free pricing.

Another special case of the UDEFP that can be solved optimally in polynomial time was studied by Arbib et al. [8]. They considered that the items have a single copy and the number of consumers is equal to the number of items, i.e., $m=n$, which they called envy-free perfect matching (EFPM), so that each consumer buys an item. A maximum-weight perfect matching in the bipartite graph of consumers and items was used to find the allocation, and then a network consisting of $n+1$ nodes and $n^2$ arcs was constructed, whose shortest paths from nodes $1\le j\le n$ to an auxiliary node 0 coincided with the envy-free prices of the corresponding items. Therefore, by using a Fibonacci heap [9] to find a maximum-weight perfect matching and the Bellman–Ford algorithm [10] to find the shortest paths, this strategy took $O(n^3)$ time to find an optimal envy-free pricing.

This work aims to reduce the time complexity in the search for an optimal envy-free pricing in the UDEFP in the metric substitutability case. The main hypothesis that led the authors to pursue this goal is that the validity of the triangular inequality on the substitution costs provides a means of simplifying the search for the shortest paths in the constructed network in order to model the problem, thus providing the development of a combinatorial algorithm that runs in cubic time for this special case. Therefore, by proving that UDEFP with metric substitutability is, in some sense, a particular case of EFPM, we show that it is possible to reduce the time complexity involved in finding optimal solutions for that case.

2. Materials and Methods

2.1. Literature Review

To create an intuition aimed at increasing the performance in the search for optimal solutions for the UDEFP with metric substitutability, the strategies used in the heuristics, approximation algorithms, and exact methods proposed in the works about the UDEFP that were found were analyzed. Table 1 shows a summary of the results in particular cases of the UDEFP, in addition to those already mentioned in the introduction.

Table 1. Algorithmic results for the UDEFP.

Problem Properties	Result	Author, Year
The number of items n is constant	$(1+ϵ)$-approximation algorithm	Hartline and Koltun, 2005 [11]
The consumers’ valuations satisfy the Monge property	$O(m{n}^2)$ exact algorithm	Günlük, 2008 [12]
Consumers grouped into segments	Heuristic algorithms	Shioda et al., 2011 [13]
Every buyer evaluates at most two items with a positive valuation	$O(m^2{n}^2)$ exact algorithm	Chen and Deng, 2014 [14]
Consumers grouped into segments	Heuristic algorithms	Mykelbust et al., 2016 [15]
$m>>n$; the valuations of every buyer type come from the same support	1.88-approximation algorithm	Anshelevich et al., 2017 [16]

2.2. The Algorithms’ Design Scheme

To design our algorithms, first, we transform an instance of the UDEFP with metric substitutability into an instance of the EFPM. The properties of the main diagonal of the valuation matrix in this new approach are used to define an allocation. A network whose arc lengths are based on specific relations of the entries of the valuation matrix is constructed and, since the shortest paths to a single target node correspond to the envy-free prices that maximize the revenue, we use the triangle inequality to simplify the calculations of these shortest paths with a dynamic programming strategy instead of resorting to the use of the Bellman–Ford algorithm.

3. Results

3.1. Clearing Prices

First, let us consider that all consumers buy the item. In this way, the allocation and pricing are determined so that there is a market-clearing competitive equilibrium, and the solutions are Pareto Efficient [17].

3.1.1. Reduction of the Udefp with Metric Substitutability into the Efpm

An instance of the UDEFP with metric substitutability consists of: n, the number of consumers; $v_i$, the valuation of consumer i if the item is purchased in their own location; ${\delta }_{ij}$, the substitution cost that is subtracted from $v_i$ if the purchase is made in location j, such that the cost set ${\left\{{\delta }_{ij}\right\}}_{1\le i,j\le n}$ has a metric space structure. These instances can be modeled as vertex- and edge-weighted undirected graphs, as shown in Figure 1.

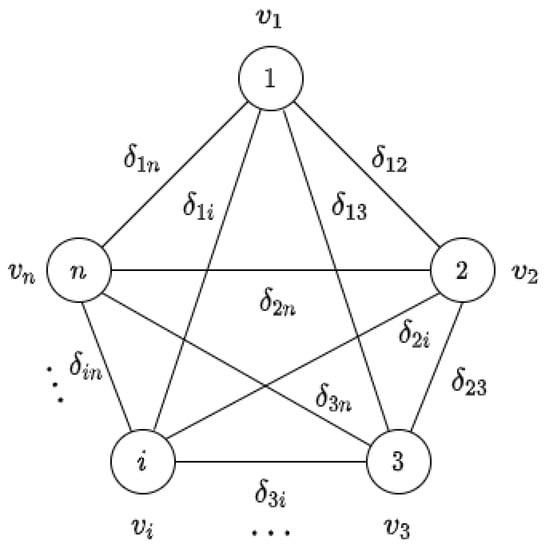
Figure 1. An instance of the UDEFP with metric substitutability.

For the EFPM, an instance consists of n, the number of consumers and items, and $V=(v_{ij})$, the valuation matrix. These instances can be modeled as bipartite edge-weighted graphs $G=G(I\cup J,E)$, where I represents the consumer set, J represents the item set, and the weight of the edge connecting vertex i to vertex j represents the valuation assigned by consumer i for item j, as shown in Figure 2.

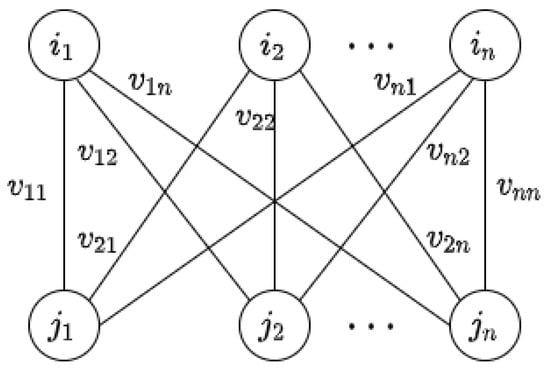
Figure 2. An instance of the EFPM.

Thus, setting $v_{ij}=v_i-{\delta }_{ij}$ for all $1\le i,j\le n$, it is easy to see that, from the abstract point of view, the UDEFP with metric substitutability is a particular case of the EFPM. With this approach, the rows of V represent the consumers, and the columns represent the locations.

3.1.2. Allocation

From the First Welfare Theorem [17], we know that an optimal allocation for the EFPM maximizes the social welfare, i.e., the sum of valuations of the buyers for their allocations. In terms of mathematical linear programming, this allocation is a solution for the model:

$$\begin{array}{cccc}\hfill {\displaystyle max\sum _{i=1}^n\sum _{j=1}^n{x}_{ij}{v}_{ij}}& & & \\ \hfill {\displaystyle \mathrm{s}.\mathrm{t}.\sum _{j=1}^n{x}_{ij}}& =\hfill & 1,\hfill & \forall 1\le i\le n\\ \hfill {\displaystyle \sum _{i=1}^n{x}_{ij}}& =\hfill & 1,\hfill & \forall 1\le j\le n\\ \hfill x_{ij}& \in \hfill & \{0,1\},\hfill & \forall 1\le i,j\le n.\end{array}$$

This linear program also models the maximum-weight perfect matching in the bipartite graph shown in Figure 2. Since $v_{ii}=v_i>v_i-{\delta }_{ij}=v_{ij}$ for all $1\le i,j\le n$ with $i\ne j$, we have that the n-by-n identity matrix is the one that maximizes $tr({\Pi }^{T}V)$, i.e., the sum of the elements on the main diagonal of ${\Pi }^{T}V$, where $\Pi$ is an n-by-n permutation matrix. Thus, the solution of the model above is $x_{ij}=1$ if $i=j$ or $x_{ij}=0$ otherwise, where $x_{ij}$ are the binary variables.

These considerations about the optimal allocation allow us to state the following proposition.

Proposition 1.

Every consumer buys the item in their own location.

3.1.3. Pricing

Once an allocation is found, let us consider the following network: The set of nodes consists of nodes $0,1,\dots ,n$; there is an arc from each node $1\le i\le n$ to node 0 with weight $v_{ii}=v_i$; there is an arc from node i to node j for all $1\le i,j\le n$ such that $i\ne j$ with weight $v_{ii}-v_{ij}={\delta }_{ij}$. Thus, the shortest paths from nodes $1\le i\le n$ to node 0 correspond to the envy-free prices $p_1,\dots ,p_n$ [8]. The network is shown in Figure 3.

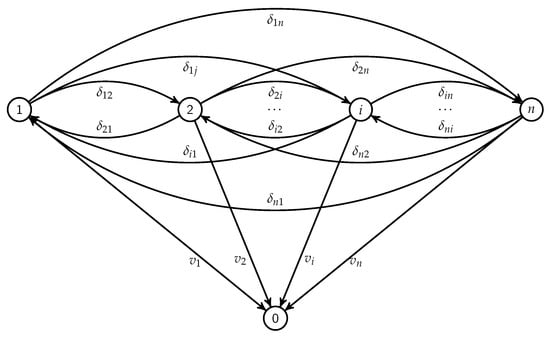
Figure 3. The network constructed to find the envy-free prices.

Instead of using the Bellman–Ford algorithm to find the shortest paths to node 0, we will explore the metric structure of the cost set to simplify the calculations, but, before that, we will see that it is possible to find a particular price without having to calculate the corresponding shortest path.

Lemma 1.

If $v_1\le v_2\le \dots \le v_n$, then $p_1=v_1$.

Proof. 

In fact, if $p_1>v_1$, the envy-freeness condition of non-negative maximum utility is violated. If $p_1<v_1$, the other prices would be forced down until the other buyers’ utilities were at least $v_{i1}-p_1$ for all $2\le i\le n$, and then the prices would not maximize the revenue, from which the results follow. □

We are now able to iteratively find the remaining prices from this first discovery.

Lemma 2.

If $v_1\le v_2\le \dots \le v_n$, then $p_i={min}_{1\le j<i}\{v_i,v_j+{\delta }_{ij}\}$ for all $2\le i\le n$.

Proof. 

From the metric structure of the cost set, we have ${\delta }_{ij}\le {\delta }_{ik}+{\delta }_{kj}$ for all $1\le i,j,k\le n$. Thus, the shortest path from node i to node 0 consists of either the arc connecting node i to node 0 with weight $v_i$ or the arcs connecting node i to some node j and node j to node 0 with weights ${\delta }_{ij}$ and $v_j$, respectively. Since $v_i\le v_k$ for all $i\le k$, we have $v_i\le v_k+{\delta }_{ik}$ for all $i\le k$, and then ${min}_{1\le j<i}\{v_i,v_j+{\delta }_{ij}\}\le v_k+{\delta }_{ik}$ for all $2\le i\le n$ with $i\le k$, from which the results follow. □

3.1.4. The Algorithm

The considerations made above allow us to present an algorithm for finding an optimal solution for the UDEFP with metric substitutability and clearing prices. The procedure is described in the following Algorithm 1.

Algorithm 1 Find an optimal clearing envy-free pricing.

1: Perform a permutation $\pi$ such that $v_{{\pi }^{-1}(1)}\le v_{{\pi }^{-1}(2)}\le \dots \le v_{{\pi }^{-1}(n)}$  2: $p_{{\pi }^{-1}(1)}\leftarrow v_{{\pi }^{-1}(1)}$  3: $p_{{\pi }^{-1}(i)}\leftarrow {min}_{1\le j<i}\{v_{{\pi }^{-1}(i)},v_{{\pi }^{-1}(j)}+{\delta }_{{\pi }^{-1}(i){\pi }^{-1}(j)}\}$ for all $2\le i\le n$

This algorithm allows us to state the following theorem:

Theorem 1.

The UDEFP with metric substitutability and clearing prices can be solved optimally in $O(n^2)$ time.

Proof. 

Lemma 1 ensures that Line 2 returns an optimal price for consumer ${\pi }^{-1}(1)$, and Lemma 2 ensures that Line 3 returns optimal prices for the others. The permutation in Line 1 can be performed in $O(n^2)$ with any classical sorting algorithm, and Line 3 performs $n-1$ times $O(n)$ operations. Therefore, the overall time complexity of the algorithm is $O(n^2)$. □

3.2. General Scenario

In some cases, it may happen that not selling the item in some locations may increase revenue. As an example, let us consider two consumers with $v_1=10,v_2=4$, and ${\delta }_{12}={\delta }_{21}=1$. Thus, $\mathbf{p}$ = (5, 4) is the optimal clearing envy-free pricing with revenue 9, but ${\mathbf{p}}^{\prime }$ = (10, 10) is an envy-free pricing with revenue 10, where consumer 2 does not buy the item.

It is clear that Proposition 1 also holds in the general scenario (since higher valuations produce higher prices), with the following modification:

Proposition 2.

Every buyer makes the purchase in their own location.

Instead of using brute force to check all of sub-allocation combinations of the allocation defined in Section 3.1.2, it is easy to see that we just need to look at allocations to higher-valued consumers. Thus, if $v_1\ge v_2\ge \dots \ge v_n$, we can compute the prices and revenue of the leading principal submatrices of the valuation matrix V, and then we choose the allocation and prices with the highest revenue. The procedure is described in the following Algorithm 2.

Algorithm 2 Find an optimal envy-free pricing.

1: Perform a permutation $\sigma$ such that $v_{{\sigma }^{-1}(1)}\ge v_{{\sigma }^{-1}(2)}\ge \dots \ge v_{{\sigma }^{-1}(n)}$  2: Use Algorithm 1 to compute the prices in the k-by-k matrix of consumers ${\sigma }^{-1}(1),\dots ,{\sigma }^{-1}(k)$ for all $1\le k\le n$. If $k<n$, $p_i\leftarrow v_{{\sigma }^{-1}(1)}$ for all $k<i\le n$  3: Choose the allocation and prices that generate the maximum revenue

This second algorithm allows us to state the following theorem.

Theorem 2.

The UDEFP with metric substitutability can be solved optimally in $O(n^3)$ time.

Proof. 

It is easy to see that the highest computational cost is in Line 2. This line performs n times $O(n^2)$ operations with Theorem 1, from which the result follows. □

4. Discussion and Conclusions

Our results about the properties of optimal allocations and envy-free prices are in agreement with those presented by Chen et al. [6]: Each consumer who buys the item makes the purchase in their own location, and the price paid by a consumer is either the valuation in their own location or the price paid by another consumer plus its substitution cost for the location of that consumer, i.e., for each buyer $1\le i\le n$, we have $p_i=v_i$ or $p_i=p_j+{\delta }_{ij}$ for some $j\ne i$ (more specifically, $j<i$), with $p_j=v_j$.

In order to justify this last statement, let us suppose that there is an i such that $p_i=v_j+{\delta }_{ij}$ for some $j<i$ with $v_j\ne p_j$. This implies that $p_j<v_j$, and then $p_j=v_k+{\delta }_{jk}$ for some $k<j$. Since ${\delta }_{ik}\le {\delta }_{ij}+{\delta }_{jk}$, we would have $v_k+{\delta }_{ik}\le v_k+{\delta }_{ij}+{\delta }_{jk}=p_j+{\delta }_{ij}<v_j+{\delta }_{ij}$, and then $p_i\ne {min}_{1\le j^{\prime }<i}\{v_i,v_{j^{\prime }}+{\delta }_{i{j}^{\prime }}\}$, which is a contradiction.

Our approach to the UDEFP with metric substitutability in terms of EFPM allowed, in addition to the presentation of alternative theoretical proofs, the reduction of the time complexity in the search for optimal solutions to the problem. Furthermore, we note that the symmetry property of the cost set was not required in order to find an optimal envy-free pricing. Thus, we can assume that ${\delta }_{ij}$ does not necessarily have to be equal to ${\delta }_{ji}$ (but positive) when $i\ne j$, which adds more subjectivity to the modeling of the problem, making it more realistic. In this way, the instances of the UDEFP with metric substitutability become networks with weights on nodes and arcs (see Figure 4).

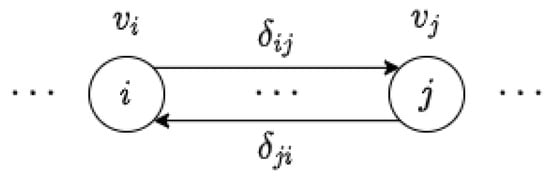
Figure 4. An instance of the UDEFP with metric substitutability and non-symmetric costs.

An interesting question that can be studied in future work is the verification of whether, by strengthening the triangular inequality and transforming the cost set into an ultrametric space, the UDEFP with (ultra)metric substitutability can be optimally solved in a time less than $O(n^2)$ in the competitive equilibrium scenario or less than $O(n^3)$ in general.