Abstract
Due to its ability to significantly improve the wireless communication efficiency, the intelligent reflective surface (IRS) has aroused widespread research interest. However, it is a challenge to obtain perfect channel state information (CSI) for IRS-related channels due to the lack of the ability to send, receive, and process signals at IRS. Since most of the existing channel estimation methods are developed to obtain cascaded base station (BS)-IRS-user devices (UDs) channel, this paper studies the problem of computation and communication resource allocation of the IRS-assisted federated learning (FL) system based on the imperfect CSI. Specifically, we take the statistical CSI error model into consideration and formulate the training time minimization problem subject to the rate outage probability constraints. In order to solve this issue, the semi-definite relaxation (SDR) and the constrained concave convex procedure (CCCP) are invoked to transform it into a convex problem. Subsequently, a low-complexity algorithm is proposed to minimize the delay of the FL system. Numerical results show that the proposed algorithm effectively reduces the training time of the FL system base on imperfect CSI.
1. Introduction
In recent years, with the advancement of 5G technology, the internet of things (IoT) has seen rapid development. In the world of “internet of everything”, many sensors are deployed in the environment to collect information in real time and generate a large amount of data. The traditional machine learning (ML) framework stores data on a central node, and its all functions are implemented on this node. However, such a centralized learning framework has high latency and poses a great challenge to privacy protection. Fortunately, due to the significant increase in data processing capabilities of mobile devices, the concept of edge learning has been introduced to solve these problems, which processes data at the edge rather than at the cloud center. Federated learning (FL) is one of the most promising edge learning frameworks, where user devices (UDs) only send local models calculated by local resource to the base station (BS) without sharing local data [1,2].
In FL, the time and energy consumed in model training are the important aspects of its performance, which depends on firmly the allocated computation resources for local model training and communication resources for model transmission between BS and UDs [3]. In addition, due to the limited computing power and energy reserve of UDs, the problem of joint computation and communication resource allocation is crucial for the deployment of FL in wireless networks. The authors proposed a resource management algorithm for the multi-access edge computing enabled FL system in [4,5]. In [6,7], the resource scheduling problem was studied under imperfect channel state information (CSI).
Due to the development of the metamaterial technology, an emerging paradigm called intelligent reflector surfaces (IRS) was introduced into the field of wireless communications. IRS can significantly improve the wireless communication efficiency by adjusting the phase shift of the incident signal using passive reflective elements, which are low-cost and low energy [8,9]. Thus, this attracts people to study the beneficial effects of IRS in FL [10,11,12]. However, these studies are based on the assumption that perfect CSI can be obtained. Unfortunately, due to the lack of the ability to receive, send and process signals for IRS, it is a challenge to estimate IRS-related channels, including the UDs-IRS channel and the IRS-BS channel, which thus have attracted widespread research attention. At present, channel estimation of IRS-related channels can be divided into two methods. One is to directly estimate IRS-related channels [13,14]. In [13], some active channel components can be equipped on the IRS to enable it to receive, send and process signals. The authors proposed a channel estimation protocol to estimate the channel by adjusting the reflective elements ON/OFF in [14]. However, these methods will bring additional cost, such as hardware cost and power consumption cost, which will cause an unaffordable burden on the IRS. The other is to estimate the cascade UD-IRS-BS channel. The advantage of this method is that the cascaded channel can be estimated without additional hardware and power cost. Therefore, there are a lot of works dedicated to IRS cascaded channel estimation [15,16,17,18]. In [15,16], the transmission protocol was proposed to estimate the cascaded channel. The author studied the robust transmission design base on imperfect CSI in [17,18].
Against the above background, this paper studies the computation and communication resource allocation problem in IRS-assisted FL systems based on imperfect CSI. Specifically, we aim to design the resource allocation algorithm to minimize the delay of FL. The main contributions of this paper can be summarized as follows:
- In this paper, we study the FL system assisted by IRS under the imperfect CSI, and outage probability is introduced to characterize the impact of imperfect CSI. We aim to minimize the delay of FL by jointly designing the computation and communication resource allocation;
- Due to the non-convex form of the objective function, the coupling effect of multiple variables and the binary constraint brought by the user selection vector, the optimization problem is difficult to solve. By introducing additional variables and invoking the semi-definite relaxation (SDR) and the constrained concave convex procedure (CCCP) techniques, we convert it into a convex optimization problem. Then, a low-complexity algorithm is proposed to optimize the computation and communication resources allocation;
- The simulation results demonstrate that the effectiveness of proposed algorithm in reducing the training time of the FL system base on imperfect CSI.
The rest of this paper is organized as follows. The system model and channel model are described in Section 2. In Section 3, we formulate the latency minimization problem. The iterative algorithm to find the local optimal solution of the latency minimization problem is given in Section 4. In Section 5, we discuss the simulation results. Finally, our conclusions are drawn in Section 6.
: In the paper, scalars, vectors and matrices are denote by lowercase letters, lowercase bold letters and uppercase bold letters, respectively. denotes the space of complex matrix. j denotes the imaginary unit. denotes the identity matrix with appropriate dimensions. and represent the Hermitian transpose and the trace, respectively. denotes the cumulative distribution function (CDF) of the variable X. Finally, denotes the circularly symmetric complex Gaussian (CSCG) associated with zero-mean and variance . The other parameters used in the paper are listed in Table 1. The acronyms used in the paper are listed in Table 2.

Table 1.
Key symbols.

Table 2.
Acronyms.
2. System Model and Channel Model
In this section, we introduce the IRS-assisted FL system model, its CSI error model and outage probability as follows.
2.1. System Model
An FL system with IRS is considered as shown in Figure 1, where an IRS, composed of N reflective elements, deployed in the system to assist the communication between a single-antenna BS and K single-antenna UDs. UDs and reflective elements are indexed by and . In the FL system, after receiving the global model from the BS, UDs train it to obtain the local models using the local dataset. Then, the local models are sent to BS to be aggregated into a new global model. This process is repeated until the accuracy of the learning model is reached. Specifically, the process can be divided into three steps, which are “local model computation”, “local model transmission”, and “global model aggregation and broadcast” [19,20]. The details are as follows:
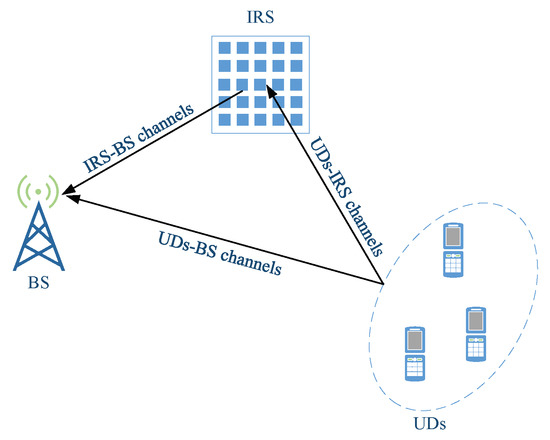
Figure 1.
An FL system model with IRS.
2.1.1. Local Model Computation
At this step, UDs use local sample subsets to update the global model, which is received from BS. Assuming that local sample subsets are enough in each UD, from which are taken out for local training. Let denotes the number of CPU cycles required to train one sample data, and denotes CPU frequency. The time and energy consumed on local training of the k-th UD can be expressed as:
where L is the number of local iteration, and denotes the effective capacitance coefficient of the k-th UD’s computing chipset [21].
2.1.2. Local Model Transmission
After finishing local model computation, the local models are sent to BS via multiple channel access, such as the frequency division multiple access (FDMA) or the time division multiple access (TDMA) [19]. In this paper, we adopt FDMA for communication between BS and UDs. The total band width is equally divided into K sub-channels, each of which has a bandwidth b. Let denotes the k-th UD’s transmit power, and the transmission rate of the k-th UD can be written as
where is the composite channels spanning from the k-th UD to BS. The channel from the k-th UD to IRS and from IRS to BS are, respectively, modeled by and , and the direct channel from the k-th UD to BS is modeled by . denotes the noise power spectral density. The phase shift effect of IRS is defined as a diagonal matrix, that is , where for . Accordingly, the delay and energy consumed in this step can be written as
where d denotes the size of local model.
2.1.3. Global Model Aggregation and Broadcast
At this step, BS receives the local models from all UDs and aggregate them to obtain the global model. Then, the global model is broadcast to each UD for the next iteration. Due to the powerful computing capability and transmission power of the BS, the delay in this step is neglected compared with other steps. Furthermore, because of the stable energy supply in BS, the energy consumed is also ignored [20].
2.2. Imperfect Channel Model
In the IRS-assisted FL system, there are two kinds of channels, that are direct UDs-BS channel and cascaded UDs-IRS-BS channel. For cascaded channel, it is a challenge to directly obtain the IRS-related channels due to the passive features of the IRS. Thus, we focus on channel error models in the cascaded UDs-IRS-BS channel.
The composite channel from the k-th UD to BS can be rewritten as
where , , . Assuming that both direct UDs-BS channels and cascaded UDs-IRS-BS channels are imperfect, which can be represented as
where and stand for the direct UDs-BS estimated channel and cascaded UDs-IRS-BS estimated channel, respectively. and are estimated error followed the CSCG distribution, i.e., and , where and , respectively, represent variance of the direct channel estimation and cascaded channels estimation. Thus, the composite channel from k-th UD to BS can be further rewritten as
where and . Due to the lack of correlation of estimation errors for the different channel, we have
2.3. Outage Probability
Outage probability is an important performance measurement, typically used to characterize the events that the instantaneous data rate is less than the target rate under imperfect CSI [22]. Defining the transmission target rate of the k-th UD as , and the outage probability can be written as
where and . It is obvious that is a random variable that obeys non-central chi-squared distribution with degrees of freedom 2, and its non-central parameter is , i.e., . Due to that the generalized Marcum Q-function is the complementary cumulative distribution function (CCDF) or reliability function of the normalized non-central chi-squared distribution with degrees of freedom, the outage probability can be rewritten as [23]
where , denotes modified Bessel function of order n. In order to obtain the closed expression of the outage probability, we approximate the non-central chi-square distribution with the central chi-square distribution, which can written as [22]
where when n is a positive integer. Thus, the closed expression of the outage probability can be approximately written as
3. Problem Formulation
Due to differences in the calculation and communication capabilities of UDs, we aim for minimizing FL delay under imperfect CSI by jointly optimizing the user selection vector , UDs’ CPU frequency , transmit power , the IRS phase shifts vector , interrupt transmission rate . Assuming that each UD uploads its local model after finishing local model computation. Moreover, the BS starts aggregation until receiving the local model from all UDs. The total delay of FL under one communication round can be expressed as . Thus, the delay minimization problem is formulated as
where Equation (16) denotes the energy constraint and is the maximum energy consumption of the k-th UD in FL; Equation (17) is the constraint of outage probability and is limit of the outage probability; Equation (18) represents the range of the phase shift; Equations (19) and (20) denote the range of CPU frequency and transmit power, where and , respectively, represent the upper and lower bounds of range, and is the maximum transmit power; Finally, Equations (21) and (22) denote the constraints of user selection vector, where represents the total number of UDs participating in this model training. , where indicates that k-th UD participate in this model training, and , otherwise.
4. Resource Allocation Design for Delay Minimization
Problem is non-convex due to the binary constraints, the coupling effect between variables and the min-max form of the objective function. Additionally, it is a mixed integer non-linear programming (MINLP) which is NP-hard. Thus, it is a challenge to find its solution. In order to solve the optimization problem, a low-complexity iterative algorithm is proposed.
In the problem , the objective function, Equations (16)–(18) and (22) are non-convex. Next, we solve them in turn. First, for the Equation (22), it is a binary constraint, which can be equivalent to
Note that optimization variable is a continuous value between 0 and 1. However, Equation (24) is a non-convex. In order to deal with the Equation (24), we reformulate problem as
where is usually a constant and represents a penalty factor for penalizing the objective function that any is not equal to 0 or 1 [24]. In order to solve the min–max form of the objective function, the variable T is introduced. Therefore, the problem can be reformulated as
Note that although we introduce the variable T to solve the min–max form of the objective function, it also brings a new non-convex Equation (27). Due to non-convex Equations (16)–(18) and (27), the problem is still difficult to solve.
For Equation (16), its non-convexity comes from the form of the second term. By replacing the variable with a new variable , the Equation (16) can be rewritten as
Note that the problem is a non-convex quadratically constrained quadratic program (QCQP). By introducing variables and , the problem can be rewritten as
where , , , and Rank() represents the rank of matrix . Due to non-convex Equations (27), (32) and (34), problem still cannot be solved directly. For the Equation (34), SDR can be invoked to relax it. Furthermore, by introducing the variable , the Equation (32) can be rewritten as
It is obvious that the Equation (32) is converted into Equation (35) by introducing variables, which is convex. However, it also brings a non-convex Equation (36). Next, the CCCP is invoked to solve this issue, which main idea is that when the original problem is difficult to optimize, the algorithm does not directly seek its local optimal solution, but looks for its approximation problem to solve iteratively [25].
For a given point at the n-th iteration, the function has a lower bound, that is
where . Thus, Equation (36) can be rewritten as
Note that is convex, while , and are non-convex. For a given point at the n-th iteration, both and have an upper bound, which are given as
As such, Equation (27) can be approximated by
Now, Equation (45) is also convex. For a given point at the -th iteration, the problem can be reformulated as
It is clear that the problem is a convex semi-definite program (SDP). Finally, we solve it directly by using standard optimization packages, such as CVX [26]. However, note that is a relaxed problem, which usually cannot lead to a rank-one solution. Thus, Gaussian randomization is invoked to construct a rank-one solution [27]. For the optimal obtained by solving problem , it is close to 0 or 1 due to the punishment item. Rounding operation is run to obtain 0 or 1. The algorithm to find a feasible solution for problem is summarized in Algorithm 1.
| Algorithm 1: Local optimal iterative algorithm. |
1. Initialization Initialize the a feasible initial point . Initialize the maximum number of iterations and penalty factor Initialize iteration index and accuracy index . 2. Joint optimization of , , , , and repeat • Calculate by • Calculate by solving problem for a given point • Calculate accuracy • untilor 3. Output optimal , , , and find from by SVD and Gaussian randomization. = , = , = , = |
Based on the Algorithm 1 description, the complexity analysis of the proposed algorithm is performed. The problem is a SDR problem, which can be solved by using the interior point method. Therefore, we analyzed the complexity of the proposed algorithm based on this method. At each iteration, the worst case complexity of solving problem is on the order of , and the complexity of finding variable is negligible. Therefore, the overall complexity of the Algorithm 1 can be evaluated by , where represents the required iterations number to achieve the target accuracy [28,29].
5. Numerical Results
In this section, we evaluate the performance of proposed scheme in the IRS-assisted FL systems. In the simulation scenario, the BS and IRS are located at (300 m, 0 m) and (30 m, 30 m), respectively. In total, 20 UDs are randomly distributed in a circular area centered at (0 m, 0 m) with radius of 20 m. For channel models, both the large-scale fading and small-scale fading are considered. The large-scale fading model is expressed as , where and x are the path loss exponent and the link distance in meters, respectively. denotes the path loss at the reference distance of 1 m, which is set as −30 dB. The pass loth exponent of the direct UDs-BS channel and the IRS-related channel are given as and , respectively. The small-scale fading of the direct UDs-BS channel and the IRS-related channel are considered as Rayleigh fading and Rician fading, respectively. Assuming that all UEs have the same energy consumption limit, i.e., . For the statistical CSI error model, the variance of and are, respectively, defined as and , where and denote the normalized CSI error. In order to guarantee the communication quality, the outage probability is set to . In the simulation, we set , c = 12,000 cycle/sample, , , b = 200 KHZ, dBm/Hz and d = 25,000 nats.
In order to describe the advantages of our algorithm, the FL algorithm without IRS is compared, where the IRS-related channels is set to 0, and edge computation and communication resource allocation is optimized.
Figure 2 describes the delay versus the maximum transmit power with different energy consumption limits. It is shown that the delay of the FL algorithm decreases as the maximum power increases. This is because that the low transmit power leads to a narrow feasible set of the optimization problem and the feasible set increases as the maximum power increases. Compared with “FL algorithm without IRS”, the delay decrease in “FL algorithm with IRS” is up to 32%. In addition, we also found that the scheme with more relaxed energy consumption limits consumes less time.
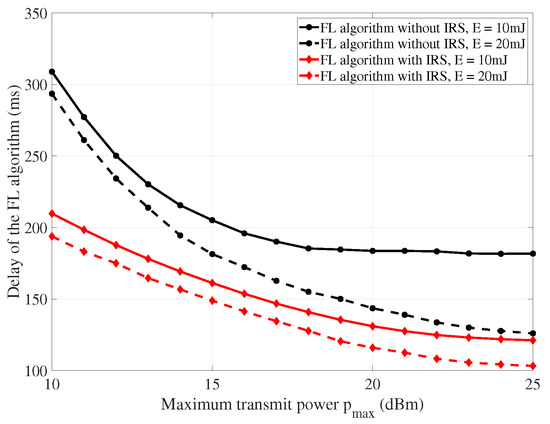
Figure 2.
The delay versus the maximum transmit power , where and .
Figure 3 presents the relationship between the delay and the outage probability. It is obvious that the delay of the FL algorithm decreases as the outage probability increases. This is because that the quality of service is sacrificed in order to increase the communication rate. As the communication rate increases, the energy consumption becomes less and less. Therefore, the delay gap between the algorithm with mJ and mJ becomes less.
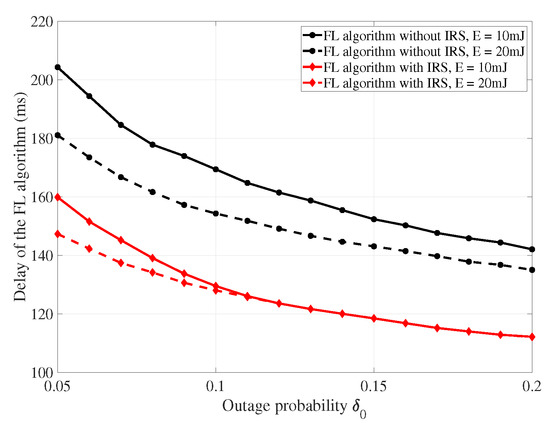
Figure 3.
The delay versus the outage probability , where and .
Figure 4 presents the relationship between the delay and the number of the IRS elements with different energy consumption limits. It is obvious that there is a performance gap between the “FL algorithm with IRS” and “FL algorithm without IRS”, and it increases with the number of the IRS elements increase. This is because that the IRS lead to a reflection-based beamforming gain, which increases as the number of IRS elements increases. Compared with “FL algorithm without IRS”, the time reduction by “FL algorithm with IRS” is up to 48% with mJ and .
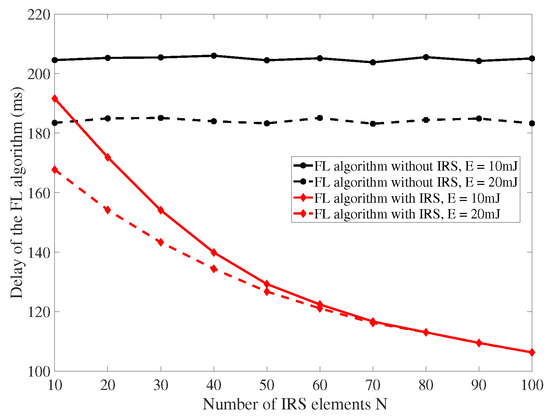
Figure 4.
The delay versus the number of IRS elements N, where and .
6. Conclusions
In this paper, we investigate the delay minimum problem in FL systems with IRS under imperfect CSI, and outage probability is introduced to characterize the impact of imperfect CSI. By using central chi-square distribution approximations, we transform the outage probability into tractable form. Then, the problem of minimizing delay was formulated in the IRS assisted FL framework, and it is a MINLP problem. Next, a low-complexity algorithm was developed base on the CCCP and SDR to solve the intractable problem. In various simulation environments, the benefits of the proposed algorithm are evaluated. Numerical results show that the effectiveness of proposed algorithm in reducing the training time of the FL system base on imperfect CSI.
Author Contributions
Conceptualization, W.H. and Z.H.; Investigation, L.Z.; Methodology, H.X.; Resources, Z.L.; Validation, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gündüz, D.; Kurka, D.B.; Jankowski, M.; Amiri, M.M.; Ozfatura, E.; Sreekumar, S. Communicate to Learn at the Edge. IEEE Commun. Mag. 2020, 58, 14–19. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Cheng, P.; Ding, M.; Lopez-Perez, D.; Pathirana, P.N.; Li, J.; Seneviratne, A.; Li, Y.; Poor, H.V. Enabling AI in Future Wireless Networks: A Data Life Cycle Perspective. IEEE Commun. Surv. Tutor. 2021, 23, 553–595. [Google Scholar] [CrossRef]
- Nguyen, M.N.H.; Tran, N.H.; Tun, Y.K.; Han, Z.; Hong, C.S. Toward Multiple Federated Learning Services Resource Sharing in Mobile Edge Networks. IEEE Trans. Mob. Comput. 2021. [Google Scholar] [CrossRef]
- Zaw, C.W.; Hong, C.S. Loss and Energy Tradeoff in Multi-access Edge Computing Enabled Federated Learning. In Proceedings of the 2021 International Conference on Information Networking (ICOIN), Jeju Island, Korea, 13–16 January 2021; pp. 597–602. [Google Scholar] [CrossRef]
- Zaw, C.W.; Pandey, S.R.; Kim, K.; Hong, C.S. Energy-Aware Resource Management for Federated Learning in Multi-Access Edge Computing Systems. IEEE Access 2021, 9, 34938–34950. [Google Scholar] [CrossRef]
- Pase, F.; Giordani, M.; Zorzi, M. On the Convergence Time of Federated Learning Over Wireless Networks Under Imperfect CSI. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Wadu, M.M.; Samarakoon, S.; Bennis, M. Federated Learning under Channel Uncertainty: Joint Client Scheduling and Resource Allocation. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards Smart and Reconfigurable Environment: Intelligent Reflecting Surface Aided Wireless Network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Chu, Z.; Xiao, P.; Shojafar, M.; Mi, D.; Mao, J.; Hao, W. Intelligent Reflecting Surface Assisted Mobile Edge Computing for Internet of Things. IEEE Wirel. Commun. Lett. 2021, 10, 619–623. [Google Scholar] [CrossRef]
- Zheng, J.; Ni, W.; Tian, H.; Wang, Y. QoS-Constrained Federated Learning Empowered by Intelligent Reflecting Surface. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; pp. 947–952. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, X.; Zhang, Y.J.A. Reconfigurable Intelligent Surface Enabled Federated Learning: A Unified Communication-Learning Design Approach. IEEE Trans. Wirel. Commun. 2021, 20, 7595–7609. [Google Scholar] [CrossRef]
- Ni, W.; Liu, Y.; Yang, Z.; Tian, H. Over-the-Air Federated Learning and Non-Orthogonal Multiple Access Unified by Reconfigurable Intelligent Surface. In Proceedings of the IEEE INFOCOM 2021-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Vancouver, BC, Canada, 10–13 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Taha, A.; Alrabeiah, M.; Alkhateeb, A. Enabling Large Intelligent Surfaces With Compressive Sensing and Deep Learning. IEEE Access 2021, 9, 44304–44321. [Google Scholar] [CrossRef]
- Mishra, D.; Johansson, H. Channel Estimation and Low-complexity Beamforming Design for Passive Intelligent Surface Assisted MISO Wireless Energy Transfer. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4659–4663. [Google Scholar] [CrossRef]
- Nadeem, Q.U.A.; Alwazani, H.; Kammoun, A.; Chaaban, A.; Debbah, M.; Alouini, M.S. Intelligent Reflecting Surface-Assisted Multi-User MISO Communication: Channel Estimation and Beamforming Design. IEEE Open J. Commun. Soc. 2020, 1, 661–680. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, R. Intelligent Reflecting Surface-Enhanced OFDM: Channel Estimation and Reflection Optimization. IEEE Wirel. Commun. Lett. 2020, 9, 518–522. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Pan, C.; Ren, H.; Wang, K.; Chai, K.K.; Nallanathan, A. Robust Transmission Design for Intelligent Reflecting Surface-Aided Secure Communication Systems With Imperfect Cascaded CSI. IEEE Trans. Wirel. Commun. 2021, 20, 2487–2501. [Google Scholar] [CrossRef]
- Zhou, G.; Pan, C.; Ren, H.; Wang, K.; Nallanathan, A. A Framework of Robust Transmission Design for IRS-Aided MISO Communications With Imperfect Cascaded Channels. IEEE Trans. Signal Process. 2020, 68, 5092–5106. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; Ding, G. Accelerating DNN Training in Wireless Federated Edge Learning Systems. IEEE J. Sel. Areas Commun. 2021, 39, 219–232. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Saad, W.; Hong, C.S.; Shikh-Bahaei, M. Energy Efficient Federated Learning Over Wireless Communication Networks. IEEE Trans. Wirel. Commun. 2021, 20, 1935–1949. [Google Scholar] [CrossRef]
- Luo, S.; Chen, X.; Wu, Q.; Zhou, Z.; Yu, S. HFEL: Joint Edge Association and Resource Allocation for Cost-Efficient Hierarchical Federated Edge Learning. IEEE Trans. Wirel. Commun. 2020, 19, 6535–6548. [Google Scholar] [CrossRef]
- Fang, F.; Wang, K.; Ding, Z.; Leung, V.C.M. Energy-Efficient Resource Allocation for NOMA-MEC Networks With Imperfect CSI. IEEE Trans. Commun. 2021, 69, 3436–3449. [Google Scholar] [CrossRef]
- Sun, Y.; Baricz, Á.; Zhou, S. On the Monotonicity, Log-Concavity, and Tight Bounds of the Generalized Marcum and Nuttall Q-Functions. IEEE Trans. Inf. Theory 2010, 56, 1166–1186. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Ng, D.W.K.; Ding, Z.; Schober, R. Optimal Joint Power and Subcarrier Allocation for MC-NOMA Systems. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Pesavento, M. Joint Optimization of Source Power Allocation and Distributed Relay Beamforming in Multiuser Peer-to-Peer Relay Networks. IEEE Trans. Signal Process. 2012, 60, 2962–2973. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2014. Available online: http://cvxr.com/cvx (accessed on 3 November 2021).
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef] [Green Version]
- Christopoulos, D.; Chatzinotas, S.; Ottersten, B. Weighted Fair Multicast Multigroup Beamforming Under Per-antenna Power Constraints. IEEE Trans. Signal Process. 2014, 62, 5132–5142. [Google Scholar] [CrossRef] [Green Version]
- Nemirovskii, A.S.; Nesterov, Y.E. Interior-Point Polynomial Algorithms in Convex Programming; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).