Adaptive Authentication Protocol Based on Zero-Knowledge Proof

Abstract

Authentication protocols are expanding their application scope in wireless information systems, among which are low-orbit satellite communication systems (LOSCS) for the OneWeb space Internet, automatic object identification systems using RFID, the Internet of Things, intelligent transportation systems (ITS), Vehicular Ad Hoc Network (VANET). This is due to the fact that authentication protocols effectively resist a number of attacks on wireless data transmission channels in these systems. The main disadvantage of most authentication protocols is the use of symmetric and asymmetric encryption systems to ensure high cryptographic strength. As a result, there is a problem in delivering keys to the sides of the prover and the verifier. At the same time, compromising of keys will lead to a decrease in the level of protection of the transmitted data. Zero-knowledge authentication protocols (ZKAP) are able to eliminate this disadvantage. However, most of these protocols use multiple rounds to authenticate the prover. Therefore, ZKAP, which has minimal time costs, is developed in the article. A scheme for adapting protocol parameters has been developed in this protocol to increase its efficiency. Reductions in the level of confidentiality allow us to reduce the time spent on the execution of the authentication protocol. This increases the volume of information traffic. At the same time, an increase in the confidentiality of the protocol entails an increase in the time needed for authentication of the prover, which reduces the volume of information traffic. The FPGA Artix-7 xc7a12ticsg325-1L was used to estimate the time spent implementing the adaptive ZKAP protocol. Testing was performed for 32- and 64-bit adaptive authentication protocols.

1. Introduction

Ensuring confidentiality in modern information systems is a very relevant topic at present. This is due to the expansion of the scope of wireless data-processing and transmission systems, in which an intruder can intercept, read, and modify the transmitted data. Therefore, the use of authentication protocols that effectively resist attacks on information systems has been proposed when projects such as low-orbit satellite communication systems (LOSCS) for the OneWeb global space Internet [1,2], automatic object identification systems using RFID [3,4,5,6], and the Internet of Things [7,8,9] are being developed.

A special place among information systems, on which the comfort of modern society largely depends, is occupied by intelligent transportation systems (ITS), particularly the automotive self-organizing network Vehicular Ad Hoc Network (VANET). The use of VANET makes it possible to increase the efficiency and comfort of vehicle movement by providing the vehicle owner with information about the current state of traffic, dangerous sections on the road, and relevant services [10]. This real-time management leads to a reduction in the number of road accidents.

As a rule, VANET consists of [11]:

• Roadside Units (RSU);
• On Board Unit (OBU);
• Certificate Authority (CA);
• Service Provider (SP).

OBU devices are placed on board the vehicles and used to transmit information about the vehicle’s speed of movement and its main parameters. In addition, the owner of the vehicle has access to the Internet and related services with the help of OBU. To carry out this data exchange, stationary RSU devices are used, and form a network. The Certificate Authority is a trusted party and designed to generate and deliver secret and public keys for OBUs and RSUs. The Service Provider provides them with the appropriate services using the appropriate OBU’s rights verification mechanism.

However, VANET has vulnerabilities, determined by the wireless data transmission channel [12,13,14], while providing the comfortable and safe movement of vehicles. Authentication protocols allow us to eliminate some of the vulnerabilities and attacks aiming to obtain confidential information. The analysis of works [15,16,17,18] showed that the authentication protocol should have the following properties:

• The protocol should have high cryptographic strength without the use of symmetric and asymmetric ciphers, with minimal time spent on its execution;
• The protocol should ensure the confidentiality of the vehicle’s route;
• The protocol should have a mechanism that allows the vehicle’s owner to change the level of confidentiality depending on the intensity of traffic.

Our Impact

• Based on the properties described above, an authentication protocol has been developed that can adapt its characteristics to the intensity of traffic on the road. Its basis is a zero-knowledge authentication protocol (ZKAP), which will ensure the high confidentiality of the route and anonymity of the vehicle owner. At the same time, this protocol spent minimal time on vehicle identification compared to other ZKAPs, which allows us to increase the volume of traffic and transmit useful information between OBUs and RSUs.
• A mechanism has been developed that allows the owner of the vehicle to change the parameters of the authentication protocol. If the traffic intensity on the road is low, then the OBU uses a maximal level of confidentiality. The vehicle’s owner reduces the level of confidentiality to a minimal value if the amount of network traffic between OBUs and RSUs increases in response to greater traffic intensity on the road. Since there is no exchange of useful information during OBU and RSU authentication, a reduction in the level of confidentiality reduces the time needed to determine the status of the vehicle. This will lead to an increase in the amount of transmitted useful information.

The structure of the article is as follows. Section 2 is devoted to the analysis of known authentication methods used to ensure VANET’s confidentiality. Section 3 is devoted to the analysis of zero-knowledge authentication protocols. Section 4 is devoted to the development of a scheme to adapt the level of confidentiality in the authentication protocol. Section 5 is devoted to the development of a scheme to verify the authority of the driver of the vehicle for the Service Provider. Section 6 is devoted to analysis of the research results.

2. Analysis of Authentication Protocols Used to Ensure Confidentiality in VANET

Since the computing power of the OBU is relatively small to ensure a high level of confidentiality in the authentication protocol, with minimal time spent on its execution, the use of Vehicular Cloud Computing (VCC) is proposed in a number of works [18,19,20,21,22]. The main advantage of this approach is the reduction in the time required for the authentication of OBU and RSU. In addition, VCC provides a number of services, such as data storage, vehicle maintenance, road condition and their loading in real-time, as well as vehicle traffic management, road accidents data, etc.

However, the use of multi-factor authentication proposed in [18] has a disadvantage, which is associated with an increase in the time spent on user identification, since this procedure uses several types of data. In references [19,20,21], the use of symmetric and asymmetric ciphers to increase the level of confidentiality is proposed. In [22] an authentication protocol is proposed that uses identifiers. However, this does not ensure the anonymity of the protocol participants.

In references [23,24,25], electronic digital signatures are used for authentication. However, the disadvantage of this authentication method is the need to deliver public and secret keys to each RSU and OBU.

In references [26], an approach was proposed in which vehicles located near one RSU form a single group. In this case, the OBUs data keys will be known to this RSU. The disadvantage of this solution is that if the RSU is compromised, OBUs keys will become available to an attacker.

In references [27,28,29], the authors justified the expediency of using encryption systems with secret keys in the authentication protocol. The purpose of these works is to increase the speed of the prover’s authentication. The disadvantages of such authentication protocols include the possibility of intercepting secret keys when they are delivered to RSUs and OBUs.

In reference [30], the message authentication code (MAC) is proposed for vehicle authentication. The prover generates a message authentication code (MAC) using a shared, secret key. The verifier verifies the prover using MAC and then receives the transmitted message. The advantage of this method is the minimal time spent on authentication. However, this method has low resistance to a number of attacks aiming to replace MAC. As a result, the intruder will be able to intercept all incoming and outgoing traffic passing through the user’s system and obtain the confidential data contained therein.

In references [31,32], ring signatures are proposed for authentication. In this case, the signatory must obtain the public keys of all other participants in order to generate a signature. Then, he uses all the public keys and his private key. As a result, the verifier does not know exactly who signed the message, but is aware that the signatory is included in the list of legal users. The disadvantage of this authentication method is the need for each legal owner to receive the keys of all vehicle owners.

The principles of building an authentication system that uses an optimized signature generation and verification scheme based on lattice-based cryptography are considered in [33]. This approach allows for signatures to be generated based on asymmetric encryption using lattice theory problems. The advantage of this approach is an 18% reduction in the length of the blind signature and 30% reduction in the signature generation time. However, the disadvantage of this authentication system is the lack of an accurate method to assess the complexity of lattice algorithms in relation to existing types of attack. Therefore, this authentication method has no formal proof of security.

The results of the analysis allow us to draw the following conclusions: 1. The use of encryption systems allows for a sufficiently high level of confidentiality when authenticating vehicles in VANET, but requires the creation of an additional key management system. At the same time, compromising the keys will lead to a decrease in the level of protection of the transmitted data in VANET. 2. The development of zero-knowledge authentication protocol, which ensures a high level of vehicle confidentiality without the use of encryption methods, is an urgent task.

3. Zero-Knowledge Authentication Protocols: Advantages and Disadvantages

The presence of the verifier (V) and the prover (P) is required for authentication using the zero-knowledge protocol. The prover must prove to the verifier that he owns a certain secret without disclosing it during the execution of the protocol. The protocol is built in such a way that the verifier can verify the truth of the prover’s answers without knowing its secret [34].

One of the first ZKAPs was the Fiat–Shamir protocol [35]. The protocol must be executed within 40 rounds to ensure high imitability. The Feige–Fiat–Shamir ZKAP can reduce the time spent on authentication. Increasing the number of questions to 5 bits reduces the number of rounds to 8 [34,36]. Feige–Fiat–Shamir protocols are used in smart cards [37,38], the Internet of Things [39], and RFID automatic object identification systems [40,41] due to their high imitability. In reference [42], it was shown that the use of Feige–Fiat–Shamir ZKAP in IoT devices provides high imitability with the use of a 20-bit key and 20 rounds of authentication.

The Schnorr ZKAP has a higher authentication speed [43]. This result was achieved by reducing the number of rounds in the protocol. However, this protocol does not provide a minimal authentication time. This is due to the fact that the considered protocols use high prime numbers, of 512 digits and more, to ensure a high level of confidentiality. This leads to an increase in the time spent performing the authentication procedure. This problem can be solved by developing the ZKAP, which uses session keys. This will reduce the number of authentication steps, providing a high level of confidentiality with a lower bit depth for the processed data.

4. ZKAP Using Session Keys

Assume that only OBUs and RSUs work in the VANET network. In reference [44], the authors proposed an authentication scheme in which OBUs fully trust RSUs. In this case, only the OBU needs to be authenticated. However, this scheme has a disadvantage. The RSU can control the vehicle’s route when this authentication scheme is used. Therefore, during the development of an authentication protocol, we proceed from the condition that both sides do not trust each other.

Assume that the vehicle manufacturer loads a secret key, $O_{private}^{}$, into each OBU. When the VANET network is deployed, every RSU has its own secret key $R_{private}^{}$, which is loaded into the appropriate RSU. These keys can be changed periodically using Certificate Authority.

Certificate Authority places a large prime number D and the number u (the primitive root modulo D) in the public domain to organize the authentication process.

OBU and RSU independently choose random numbers:

$$OBU: W<D-1, RSU: Y<D-1$$

(1)

These numbers are used to calculate the OBU and RSU session keys, respectively. The use of a pseudo-random function (PRF) is proposed [45] to obtain session keys. Then,

$$OBU: W(i)=u^{\frac{1}{W(i-1)+O_{\mathit{private}}^{}}}\mathrm{mod}D$$

(2)

$$RSU: Y(i)=u^{\frac{1}{Y(i-1)+R_{\mathit{private}}^{}}}\mathrm{mod}D$$

(3)

where $W(i-1), Y(i-1)$ are session keys, which were used on $(i-1)$-th authentication session: $W(0)=W, Y(0)=Y$.

Consider the ZKAP, which provides a maximal level of confidentiality. Assume that OBU is the prover and RSU is the verifier.

Authentication protocol $OBU\left(Prover\right)\to RSU\left(Verifer\right)$.

At the beginning of the authentication session, the prover calculates its true index:

$$1. OBU: X(i)=u_{}^{O_{private}^{}}{u}_{}^{W(i)}\mathrm{mod}D$$

(4)

where $X(i)$ is the true index of OBU; i is authentication session number.

Then, the OBU starts calculating its “noisy” index. To do this, it first generates numbers $\Delta O_{private}^{}(i), \Delta W(i)$:

$$2. OBU: \left\{\Delta O_{private}^{}(i), \Delta W(i)\right\}<D-1$$

(5)

where $\Delta O_{private}^{}(i), \Delta W(i)$ are random numbers for “noisy” keys.

“Noisy” keys are calculated using expressions (6):

$$\begin{array}{l}3. OBU: O_{private}^{*}(i)=\left(O_{private}^{}+ \Delta O_{private}^{}(i)\right)\mathrm{mod}\phi (D),\\ 4. OBU: W_{}^{*}(i)=\left(W(i)+\Delta W(i)\right)\mathrm{mod}\phi (D),\end{array}$$

(6)

where $O_{private}^{*}(i), W_{}^{*}(i)$ are “noisy” key values; $\phi (D)$ is Euler’s totient function of the prime number D.

After that, OBU calculates its “noisy” index:

$$5. OBU: X_{}^{*}(i)=u_{}^{O_{private}^{*}(i)}{u}_{}^{W_{}^{*}(i)}\mathrm{mod}D$$

(7)

where $X_{}^{*}(i)$—OBU’s “noisy” index; i is authentication session number.

The authentication process includes the following procedures. When an OBU appears in the range of the RSU, the latter generates a random number:

$$6. RSU: K(i)<D-1$$

(8)

This number serves as a question from the verifier in the developed protocol. The number K(i) is passed to the prover (OBU).

$$RSU\to OBU: K(i)$$

Having received the number–question K(i) from the verifier, the prover proceeds to calculate the answers. These answers depend on both the question and the secret and session keys.

$$7. G_1^{}(i)=(O_{private}^{*}(i)-K(i)O_{private}^{})\mathrm{mod}\phi (D).$$

(9)

$$8. G_2^{}(i)=(W_{}^{*}(i)-K(i)W(i))\mathrm{mod}\phi (D).$$

(10)

The true and “noisy” OBU’s indexes, as well as the answers to the questions, the prover transmits to the RSU in the form of a signal:

$$\begin{array}{l}9. OBU: S_{OBU}^{}(i)=(X(i)||X_{}^{*}(i)||G_1^{}(i)||G_2^{}(i)).\\ 10. OBU\to RSU: S_{OBU}^{}(i).\end{array}$$

After receiving a signal from the prover (OBU), RSU calculates the expression

$$11. RSU: S(i)=X_{}^{K(i)}(i)u_{}^{G_1^{}(i)}{u}_{}^{G_2^{}(i)}\mathrm{mod}D$$

(11)

If the answers to the question–number given by OBU are correct, then $S(i)=X_{}^{*}(i)$. This means that the OBU has passed authentication. After authentication, RSU can arrange a communication session with SP to provide the necessary service to the vehicle owner. At the same time, RSU cannot obtain information about the vehicle itself, or calculate its route, which ensures the confidentiality of the VANET network.

Since OBU and RSU do not trust each other, the authentication protocol must be executed in the other direction. In this case, RSU acts as a prover, and OBU acts as a verifier.

Authentication protocol $RSU\left(Prover\right)\to OBU\left(Verifer\right)$.

$$1. RSU: F(i)=u_{}^{R_{private}^{}}{u}_{}^{Y(i)}\mathrm{mod}D$$

(12)

where F(i) is the true index of RSU; i is authentication session number.

$$2. RSU: \left\{\Delta R_{private}^{}(i), \Delta Y(i)\right\}<D-1$$

(13)

$$\begin{array}{l}3. RSU: R_{private}^{*}(i)=\left(R_{private}^{}+ \Delta R_{private}^{}(i)\right)\mathrm{mod}\phi (D),\\ 4. RSU: Y_{}^{*}(i)=\left(Y(i)+\Delta Y(i),\right)\mathrm{mod}\phi (D).\end{array}$$

(14)

$$5. RSU: F_{}^{*}(i)=u_{}^{R_{private}^{*}(i)}{u}_{}^{Y_{}^{*}(i)}\mathrm{mod}D$$

(15)

where F*(i) is the “noisy” index of RSU.

$$6. OBU: Q(i)<D-1, OBU\to RSU: Q(i).$$

(16)

$$7. RSU: T_1^{}(i)=(R_{private}^{*}(i)-Q(i)R_{private}^{})\mathrm{mod}\phi (D),$$

(17)

where T₁(i) is the first answer to the posed question Q(i).

$$8. RSU: T_2^{}(i)=(Y_{}^{*}(i)-Q(i)Y_{}^{}(i))\mathrm{mod}\phi (D)$$

(18)

where T₂(i) is the second answer to the posed question Q(i).

$$\begin{array}{l}9. RSU: S_{RSU}^{}(i)=(F(i)||F_{}^{*}(i)||T_1^{}(i)||T_2^{}(i)).\\ 10. RSU\to OBU: S_{RSU}^{}(i).\end{array}$$

$$11. RSU: H(i)=F_{}^{Q(i)}(i)u_{}^{T_1^{}(i)}{u}_{}^{T_2^{}(i)}\mathrm{mod}D$$

(19)

If $H(i)=F_{}^{*}(i)$, then RSU is authenticated. After two-way authentication, RSU can receive information from OBU, bring the situation on the road to the vehicle, and provide warnings about dangerous areas, as well as accidents on the highway. In addition, RSU can provide a channel for communication with SP. This will allow the vehicle owner to receive the necessary service in real-time. Thanks to the developed protocol, RSU does not have the opportunity to obtain information about the vehicle, or calculate its route. This ensures VANET’s confidentiality. The authentication protocol can also be implemented between two OBUs. In this case, the roles of prover and verifier are performed by two different OBUs.

Analysis of the developed ZKAP shows that its cryptographic strength is determined by the computational complexity of solving the Diffie–Hellman problem (DHP). The use of a zero-knowledge authentication protocol allows us to ensure a level of confidentiality comparable to the confidentiality of encryption algorithms and electronic digital signatures. The authentication process takes place without the use of secret keys and a secure communication channel, unlike encryption algorithms and electronic digital signatures. Therefore, an open communication channel is used in VANET for authentication by the developed protocol. This channel will be used after authentication to transfer information packets between OBUs and RSU and provide various services.

5. Development of a Scheme for Adapting the Authentication Protocol to the Road Traffic Intensity

There is no exchange of information between RSU and OBU during the execution of the two-way authentication. As a result, the transmitted data traffic between OBU and RSU is reduced. At the same time, as the traffic flow increases, the time spent on authenticating all OBUs greatly increases. This has a negative impact on traffic safety, as the amount of information that OBUs receive from the RSU about the situation on the road and accidents on the highway is reduced. Therefore, the development of a scheme to adapt authentication protocol parameters to traffic intensity is an urgent task.

Analysis of the developed protocol shows that it has the potential to increase the authentication speed by reducing the level of confidentiality. This result is achieved by reducing the secret parameters in the authentication protocol. A maximal level of confidentiality is achieved by simultaneous use of secret and session keys for OBU and RSU. The implementation of authentication protocols was discussed earlier. A reduction in the confidentiality to a minimal level by rejecting session keys allows us to reduce the needed time to perform an authentication operation. This will increase the traffic of the messages transmitted between OBUs and RSUs.

Consider ZKAP, which provides a minimal level of confidentiality. Assume that OBU is the prover and RSU is the verifier.

Authentication protocol $OBU\left(Prover\right)\to RSU\left(Verifer\right)$.

$$1. OBU: X(i)=u_{}^{O_{private}^{}}\mathrm{mod}D$$

(20)

where $X(i)$ is the true index of OBU; i is authentication session number.

$$2. OBU: \left\{\Delta O_{private}^{}(i)\right\}<D-1$$

(21)

where $\Delta O_{private}^{}(i)$ is random number for “noisy” OBU’s secret key.

$$3. OBU: O_{private}^{*}(i)=\left(O_{private}^{}+ \Delta O_{private}^{}(i)\right)\mathrm{mod}\phi (D),$$

(22)

where $O_{private}^{*}(i)$ is the “noisy” value of OBU’s secret key; $\phi (D)$ is Euler’s totient function of the prime number D.

$$4. OBU: X_{}^{*}(i)=u_{}^{O_{private}^{*}(i)}\mathrm{mod}D$$

(23)

where $X_{}^{*}(i)$ is the “noisy” index of OBU.

When OBU appears in the range of RSU, the latter generates a random number and passes it to the OBU

$$5. RSU: K(i)<D-1$$

(24)

$$6. RSU\to OBU: K(i)$$

$$7. G_1^{}(i)=(O_{private}^{*}(i)-K(i)O_{private}^{})\mathrm{mod}\phi (D).$$

(25)

where G₁(i) is the answer to the posed question K(i).

$$\begin{array}{l}8. OBU: S_{OBU}^{}(i)=(X(i)||X_{}^{*}(i)||G_1^{}(i)).\\ 9. OBU\to RSU: S_{OBU}^{}(i).\end{array}$$

$$10. RSU: S(i)=X_{}^{K(i)}(i)u_{}^{G_1^{}(i)}\mathrm{mod}D$$

(26)

If the answers to the question–number given by OBU are correct, then $S(i)=X_{}^{*}(i)$. This means that OBU is authenticated.

Authentication protocol $RSU\left(Prover\right)\to OBU\left(Verifer\right)$.

$$1. RSU: F(i)=u_{}^{R_{private}^{}}\mathrm{mod}D$$

(27)

where F(i) is the true index of RSU; i is authentication session number.

$$2. RSU: \left\{\Delta R_{private}^{}(i)\right\}<D-1$$

(28)

where $\Delta R_{private}^{}(i)$ is random number for “noisy” RSU’s secret key.

$$3. RSU: R_{private}^{*}(i)=\left(R_{private}^{}+ \Delta R_{private}^{}(i)\right)\mathrm{mod}\phi (D).$$

(29)

where $R_{private}^{*}(i)$ is the “noisy” value of RSU’s secret key.

$$4. RSU: F_{}^{*}(i)=u_{}^{R_{private}^{*}(i)}\mathrm{mod}D$$

(30)

where F*(i) is the “noisy” index of RSU.

$$5. OBU: Q(i)<D-1, OBU\to RSU: Q(i),$$

(31)

where $Q(i)$ is a random question–number for the authentication of RSU.

$$6. RSU: T_1^{}(i)=(R_{private}^{*}(i)-Q(i)R_{private}^{})\mathrm{mod}\phi (D),$$

(32)

where T₁(i) is the answer to the posed question Q(i).

$$\begin{array}{l}7. RSU: S_{RSU}^{}(i)=(F(i)||F_{}^{*}(i)||T_1^{}(i)).\\ 8. RSU\to OBU: S_{RSU}^{}(i).\end{array}$$

$$9. RSU: H(i)=F_{}^{Q(i)}(i)u_{}^{T_1^{}(i)}\mathrm{mod}D,$$

(33)

If $H(i)=F_{}^{*}(i)$, then RSU is authenticated. The analysis of Equations (20)–(33) shows that a reduction in the time spent calculating the true and “noisy” RSU’s and OBU’s indexes to verify the correctness of the answer to the posed question, as well as a reduction in the number of answers themselves, can increase the speed of the authentication procedure. However, this reduces the confidentiality of the authentication protocol by reducing the bit depth of the signals $S_{OBU}^{}(i), S_{RSU}^{}(i)$. Thanks to this adaptation of the project, the efficiency of OBUs and RSUs increases with a high density of vehicles on the road.

As was described earlier, the strength of the developed authentication protocol is determined by the computational complexity of solving the Diffie–Hellman problem (DHP). The security of the scheme to reduce the level of confidentiality in the developed protocol is based on the reducibility of its exposure to, and solving of, computationally complex problems. According to the concept of evidence-based security, it is as difficult to solve the problem of exposing (security violation) the cryptographic schemes (algorithms, primitives) used in the protocol as it is to expose the protocol.

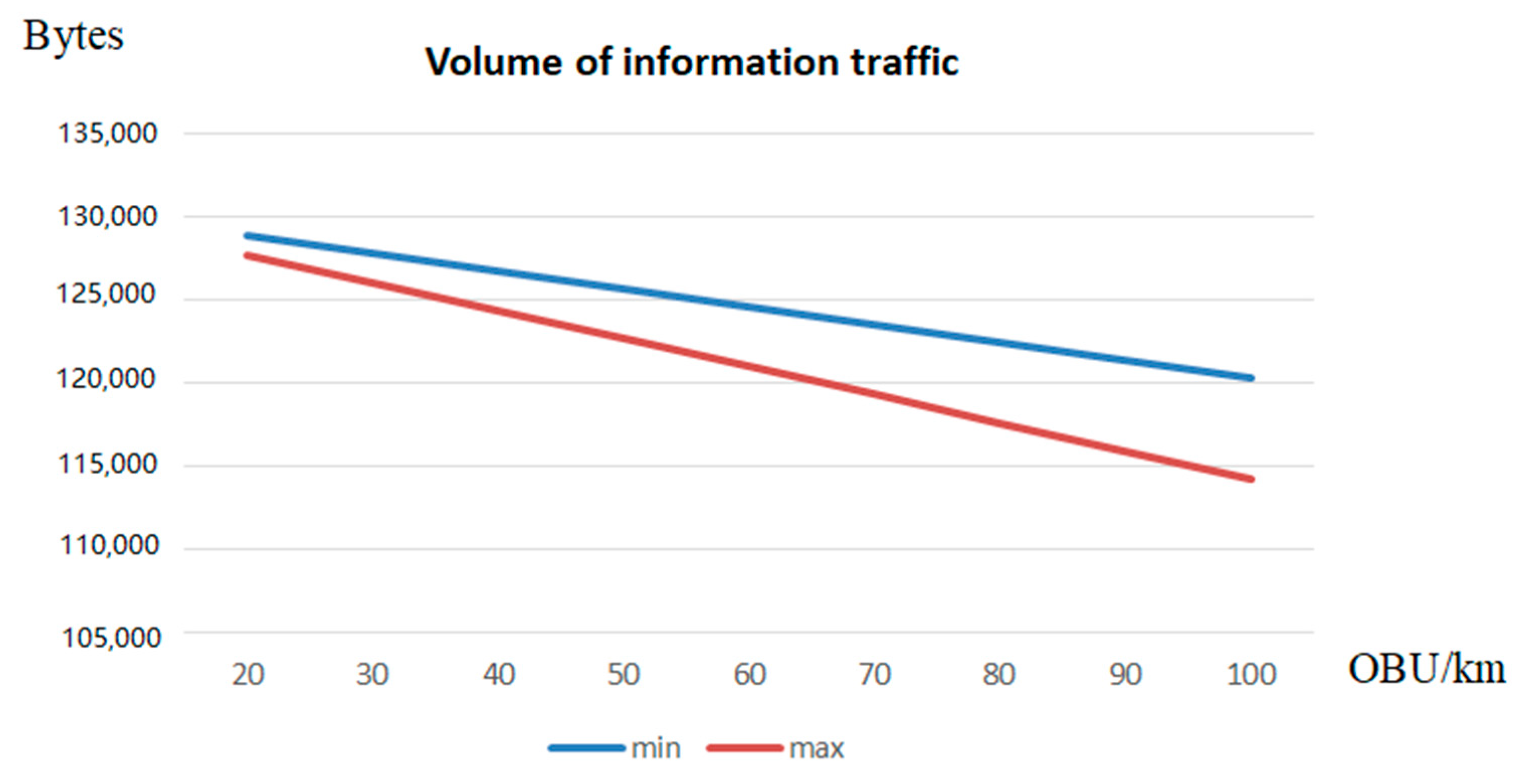
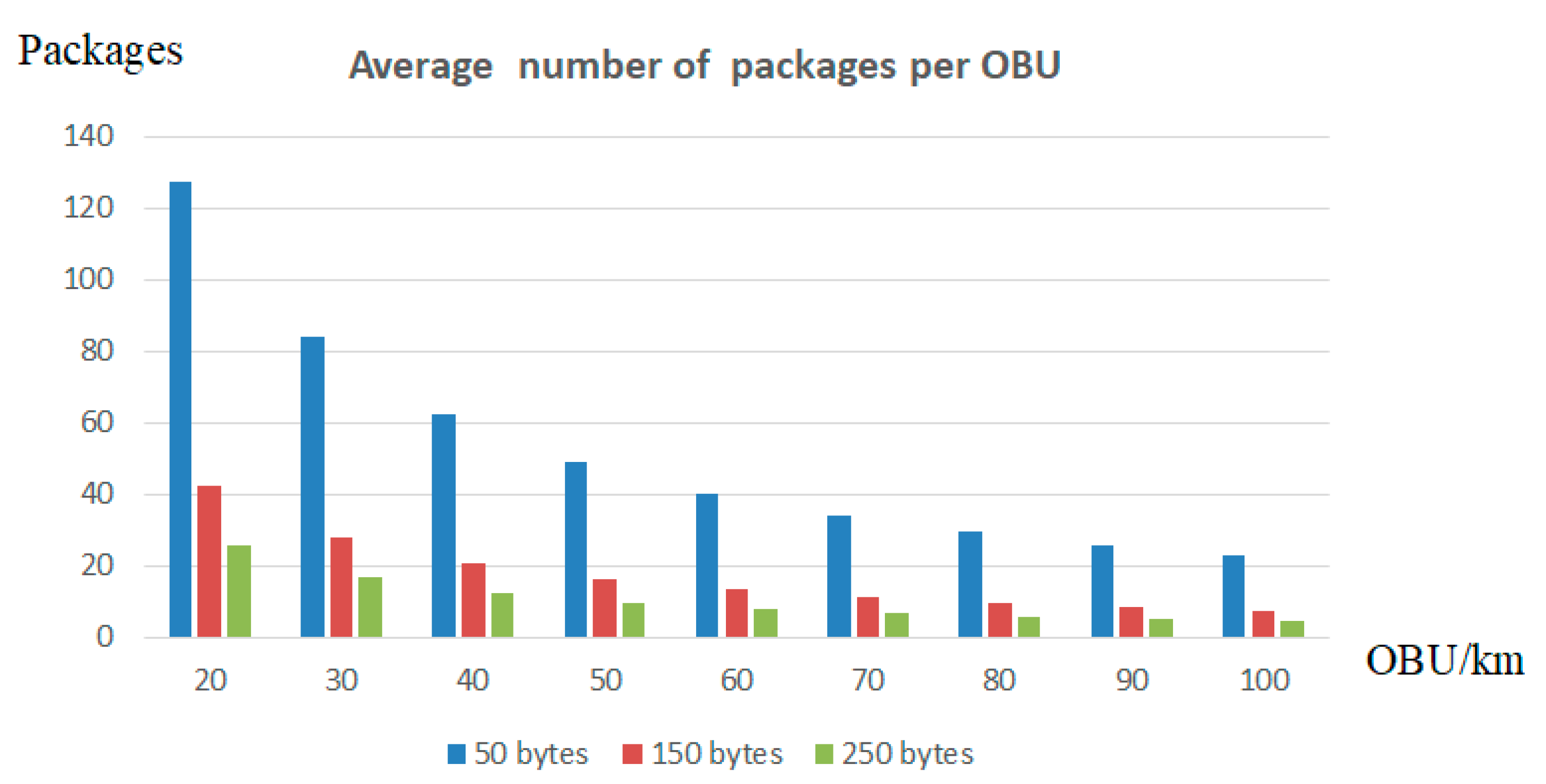
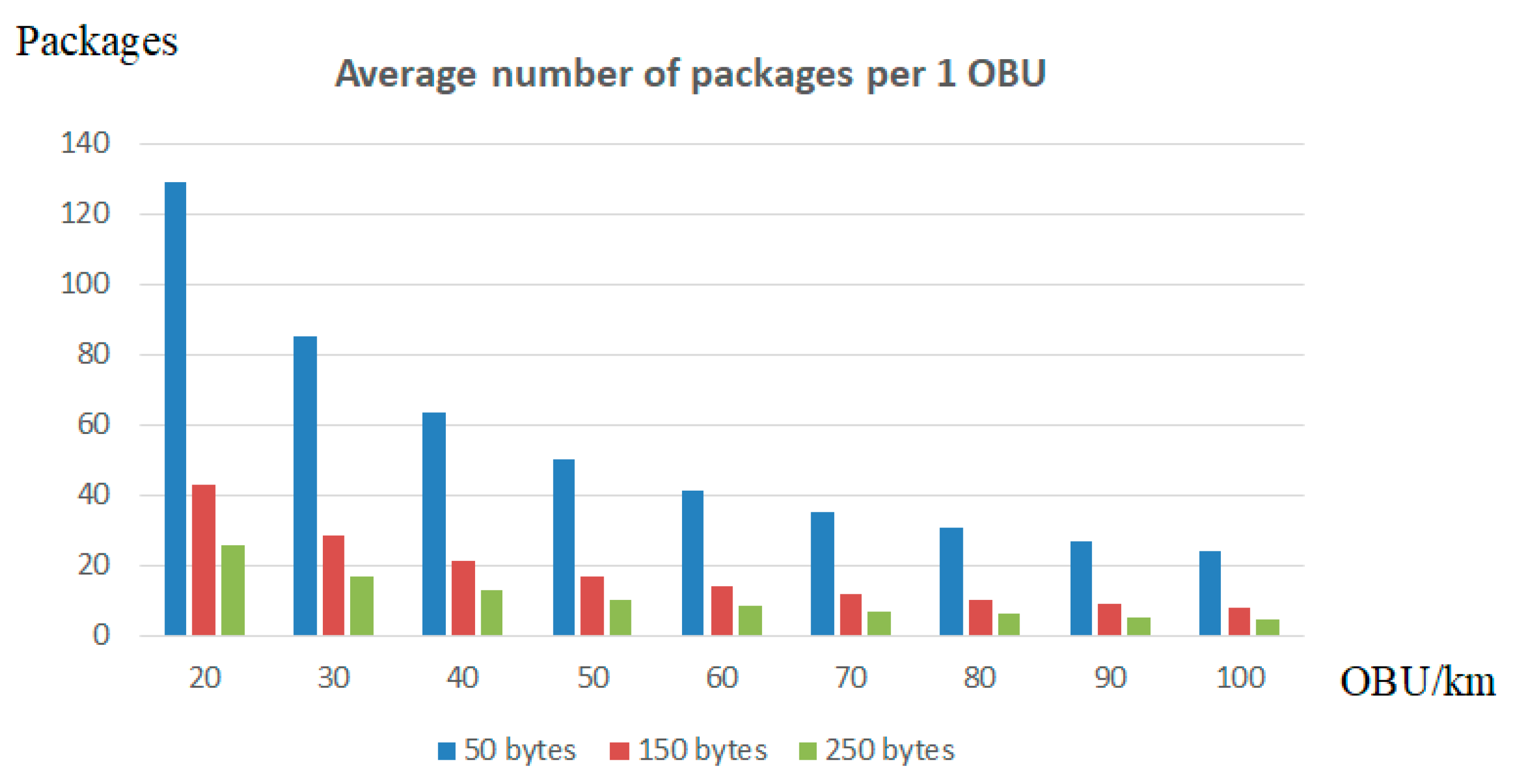
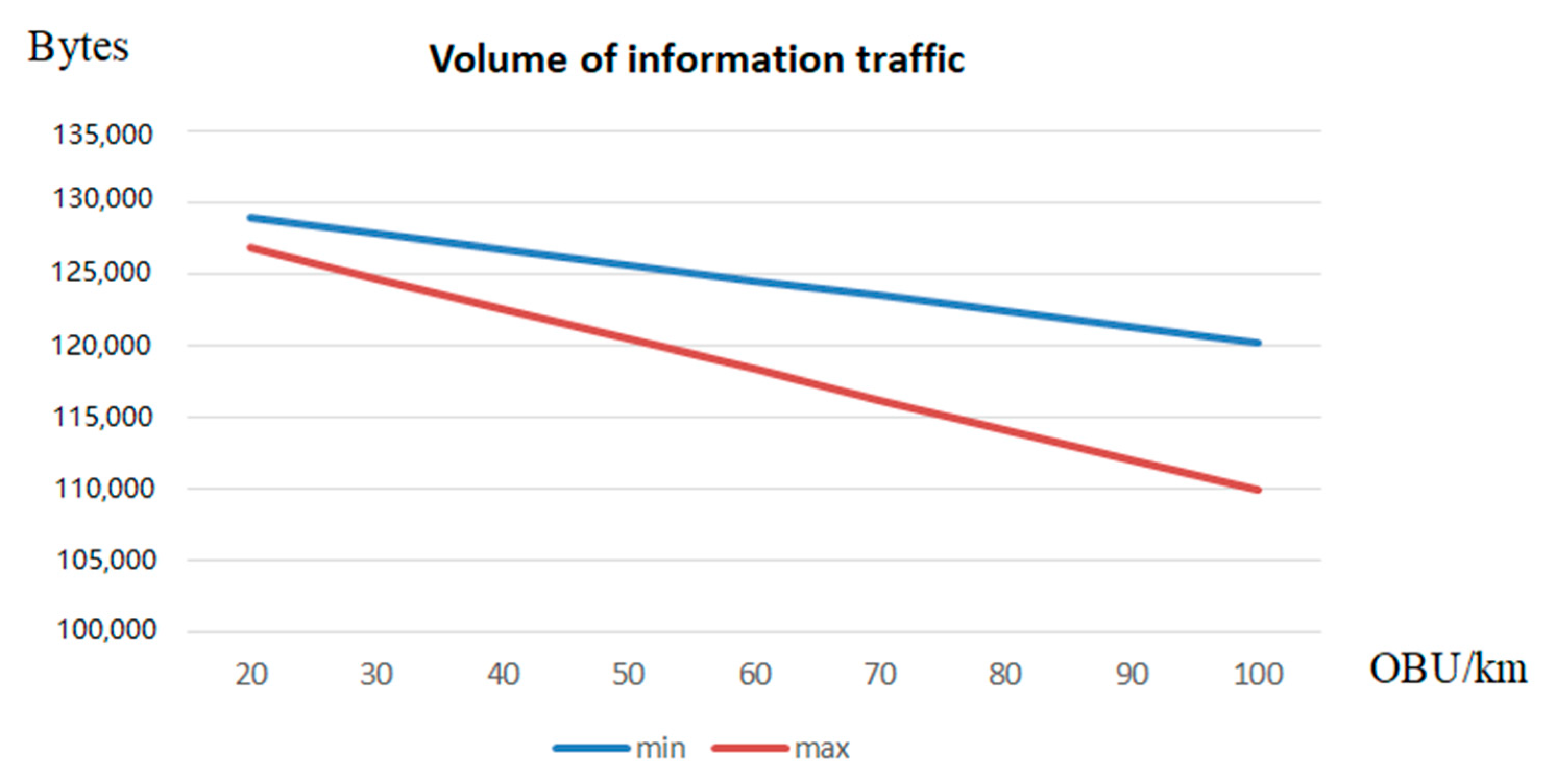
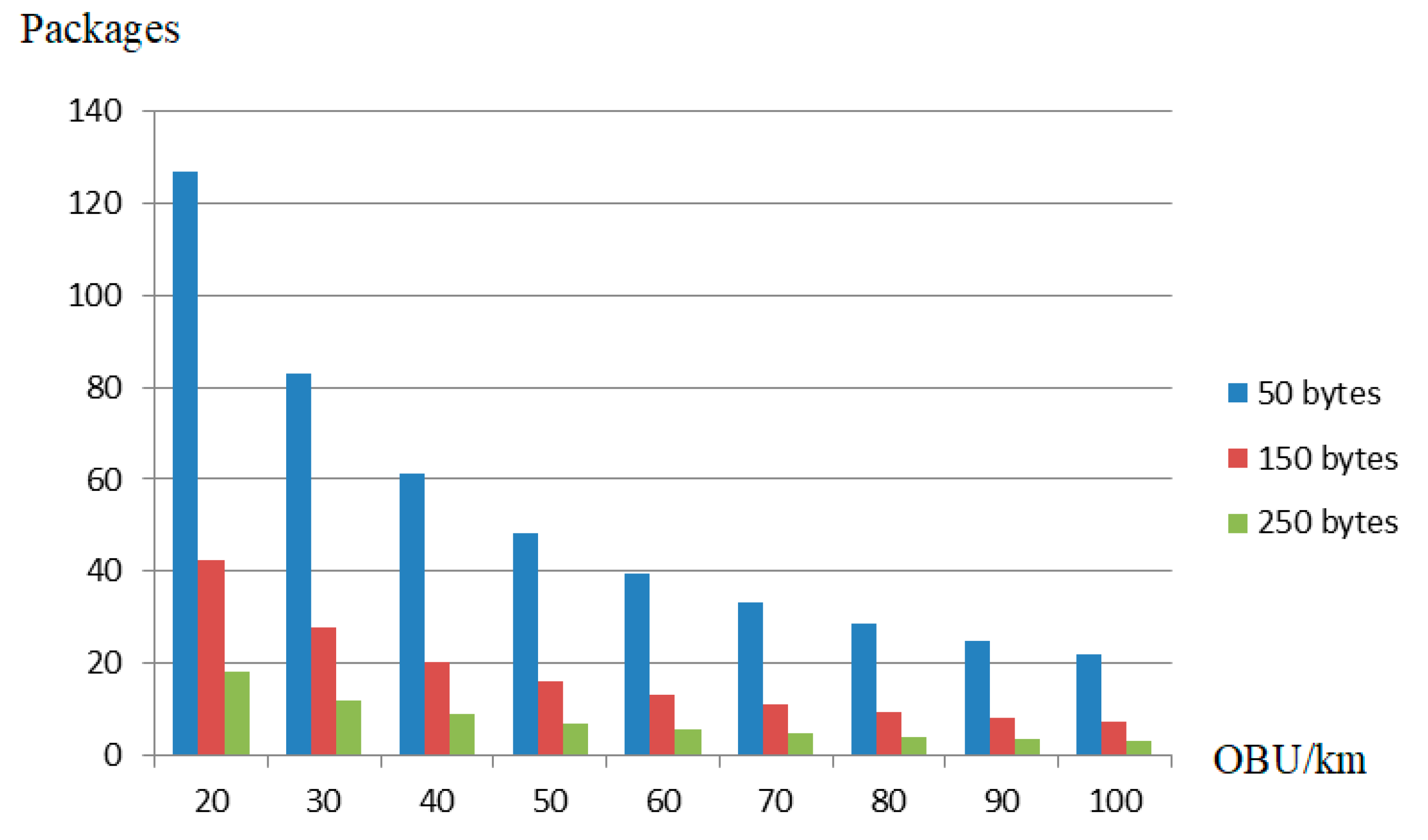
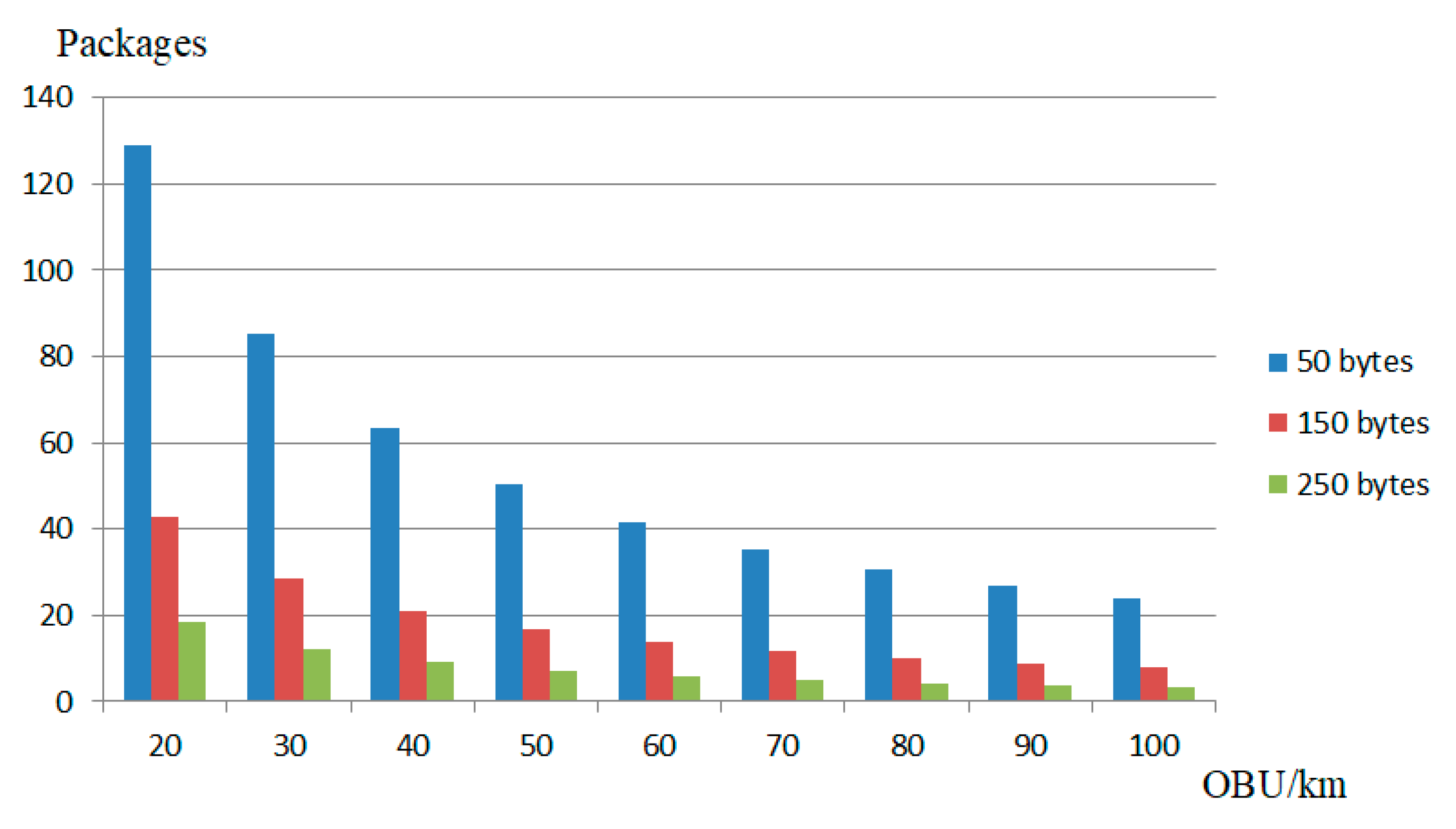
6. Analysis of the Results of the Conducted Research

The VANET model was developed to analyze the parameters of the developed adaptive authentication protocol. NS-2 was chosen as the simulation system, in which code modification is allowed. The VANET model consists of 10 RSUs. The maximal number of OBUs per RSU is 100. Each OBU and RSU uses the developed adaptive authentication protocol. Communication channel is a discrete communication channel without interference. The radius of the interaction zone of the OBU and RSU is 1 km. RSUs are 2 km apart to provide direct visibility. The data transfer rate between OBU and RSU is 1 Mbit/s. The time-to-live (TTL) of VANET network is 1. Minimal packet size is 50 bytes. Maximal packet size is 200 bytes.

The cryptographic strength of the developed adaptive authentication protocol will be determined by the bit depth of the signals $S_{OBU}^{}(i), S_{RSU}^{}(i)$ coming from the prover. We will use the probability of selecting the prover signal to assess the cryptographic strength of the adaptive protocol:

$$P=\frac{1}{M_j^{}{2}_{}^{{\log }_2^{}D}},$$

(34)

where $M_j^{}$ is the number of parts in signals $S_{OBU}^{}(i), S_{RSU}^{}(i)$.

Consider the use of a 32-bit modulus in the developed authentication protocol. The number of parts of $S_{OBU}^{}(i), S_{RSU}^{}(i)$ is $M_j^{}=4$ with a maximal level of confidentiality. Then, the probability of selecting the prover signal is $P_{\max }^{(32)}=5.82\cdot {10}^{-11}$. If the level of confidentiality is reduced to a minimum, the number of parts of $S_{OBU}^{}(i), S_{RSU}^{}(i)$ will be reduced to $M_j^{}=3$. In this case, the probability of selecting the prover signal is $P_{\min }^{(32)}=7.76\cdot {10}^{-11}$. Thus, the transition from maximal level of confidentiality to minimal one leads to a decrease in the cryptographic strength of the protocol by 1.33 times.

However, the authentication protocol using the 32-bit modulus D does not provide a high level of confidentiality. This is confirmed by a software implementation that allows us to determine the password’s resistance to brute force [46]. If a 56-bit password is used, it will be cracked after 2 h. If the password length is 64 bits, then the time interval required to crack the password increases to 2 days. Therefore, it is obvious that the bit depth of modulus D should not be less than 64 bits. Therefore, when using a 64-bit modulus and maximal level of confidentiality for the developed protocol, the probability of selecting the prover signal is $P_{\max }^{(64)}=1.35\cdot {10}^{-20}$. When the level of confidentiality is reduced to a minimum, the probability of selecting the prover signal is $P_{\min }^{(64)}=1.81\cdot {10}^{-20}$. Increasing the size of modulus D to 64 bits allowed for a confidentiality level that was more than eight orders of magnitude higher compared to the 32-bit authentication protocol.

The FPGA Artix-7 xc7a12ticsg325-1L was used to evaluate the effectiveness of the developed adaptive authentication protocol. The clock frequency was 100 MHz. Testing was conducted on the Vivado HLS 2019 platform. The bit depth of the modulus D used in the protocol was 32. The multiplicative operation was based on a binary algorithm, which was used to exponentiate an integer modulo D. The following parameters were selected to determine the maximal possible time spent on authentication: modulus D = 4,294,967,291, an exponent ranging from 20 to 30. With the use of a binary algorithm to exponentiate an integer, the calculation time of the true digest was T₁ = 14,200 ns and the calculation time of the noisy digest was T₂ = 15,650 ns. The transmission time of the question was T₃ = 32,000 ns. The calculation time of the answer to the question was T₄ = 400 ns. The transmission time of the answer to the question was T₅ = 96,000 ns. The answer check time was T₆ = 28,530 ns. The total execution time of the authentication protocol with a minimal level of confidentiality was $T_{\min }^{(32)}=185.780 \mathsf{\mu }\mathrm{s}$.

The figure shows the dependence of the volume of information traffic on the intensity of road traffic when using a 32-bit authentication protocol.

The analysis of Figure 1 allows us to draw the following conclusions. If the OBU density per 1 km is 30, then, for the authentication protocol with a maximal level of confidentiality, the volume of information traffic was 126,012.3 bytes. A reduction in the level of confidentiality to a minimal level allowed us to increase information traffic by 1.015 times, bringing its volume to the value of 127,816.3 bytes. If we increase the OBU density per 1 km three times, then the volume of information traffic is 115,892.8 bytes, with a maximal level of confidentiality. A reduction in the level of confidentiality to a minimal one allows us to increase information traffic by almost 5%, bringing its volume to 121,305 bytes.

Figure 2 shows the dependence of the average number of packets per OBU when using a 32-bit authentication protocol with a maximal level of confidentiality.

The analysis of Figure 2 allows us to draw the following conclusions. If the density of an OBU per 1 km does not exceed 30, then the average number of packets of 50 bytes per OBU is 84. When increasing a packet size to 150 bytes, the average number of packets per OBU is 27. We receive 16 packets with a packet size of 250 bytes. If the density of OBU per 1 km increases by three times, then the average number of packets per OBU will be 25 with a packet size of 50 bytes. The average number of packets per OBU is seven, with a packet size of 150 bytes. We receive four packets with a packet size of 250 bytes.

The average number of packets per OBU will be greater when a minimal level of confidentiality is used in the authentication protocol. Figure 3 shows the dependence of the average number of packets per OBU when using a 32-bit authentication protocol with a minimal level of confidentiality.

If the density of an OBU does not exceed 30 per 1 km, then the average number of 50-byte packets per OBU is 85. When the packet size is increased to 150 bytes, the average number of packets per OBU is 28. We obtain 17 packets with a packet size of 250 bytes. If the density of OBU per 1 km increases by three times, then the average number of packets per OBU will be 27, with a packet size of 50 bytes. The average number of packets per OBU is eight, with a packet size of 150 bytes. We obtain five packets with a packet size of 250 bytes.

The experimental results shown in Figure 2 and Figure 3, obtained using a 32-bit protocol, differ slightly from each other. This is because this protocol has a low computational complexity. Therefore, changing the protocol parameters (reducing modular exponentiation operations, the number of answers to the question and the bit depth of the prover’s signal) has a negligible effect on the authentication time in the case of a transition from a maximal confidentiality level to a minimal one. Therefore, the experimental results presented in Figure 2 and Figure 3 do not allow us to fully assess the effectiveness of the developed authentication protocol.

However, a 32-bit modulus cannot be used because it has low resistance to brute force attacks. At the same time, the implementation time of such an attack is very short. Let us increase the bit depth of the modulus used in the developed zero-knowledge authentication protocol. The time spent checking the status of the OBU and RSU increased with the transition to a 64-bit authentication protocol. For a minimal level of confidentiality, the calculation time of the true digest was T₁ = 54,000 ns, and the calculation time of the noisy digest was T₂ = 55,600 ns. The transmission time of the question was T₃ = 64,000 ns. The calculation time of the answer to the question was T₄ = 800 ns. The transmission time of the answer to the question was T₅ = 132,000 ns. The answer check time was T₆ = 108,180 ns. The total execution time of the authentication protocol with a minimal level of confidentiality is $T_{\min }^{(64)}=414.580 \mathsf{\mu }\mathrm{s}$.

When the level of confidentiality is switched to a maximal one, the time spent on protocol execution increases by 1.95 times, reaching the value of $T_{\min }^{(64)}=808.070 \mathsf{\mu }\mathrm{s}$. Figure 4 shows the volume of information traffic’s dependence on the road traffic intensity when executing a 64-bit protocol.

The analysis of Figure 4 allows us to draw the following conclusions. If the OBU density per 1 km is 30, then, for the authentication protocol with maximal level of confidentiality, the volume of information traffic is 124,702.9 bytes. A reduction in the level of confidentiality to a minimal one allows us to increase information traffic by 1.025 times, bringing its volume to the value of 127,811.6 bytes. If we increase the OBU density per 1 km by three times, then the volume of information traffic is 11,1964.8 bytes, with a maximal level of confidentiality. A reduction in the confidentiality level to a minimal one allows us to increase information traffic by 1.09 times, bringing its volume to 121,290 bytes.

Figure 5 shows the dependence of the average number of packets per OBU when using a 64-bit authentication protocol with a maximal level of confidentiality.

The analysis of Figure 5 allows us to draw the following conclusions. If the density of an OBU per 1 km does not exceed 30, then the average number of packets of 50 bytes per OBU is 81. When the packet size is increased to 150 bytes, the average number of packets per OBU is 25. We obtain 11 packets with a packet size of 250 bytes. If the density of OBU per 1 km increases by three times, then the average number of packets per OBU will be 22, with a packet size of 50 bytes. The average number of packets per OBU is five, with a packet size of 150 bytes. We obtain two packets, with a packet size of 250 bytes.

When a minimal confidentiality level is used for the authentication protocol, the average number of packets per OBU will be greater. Figure 6 shows the dependence of the average number of packets per OBU when using a 64-bit authentication protocol with a minimal level of confidentiality.

If the density of an OBU per 1 km does not exceed 30, then the average number of packets of 50 bytes per OBU is 83. When the packet size is increased to 150 bytes, the average number of packets per OBU is 27. We obtain 14 packets, with a packet size of 250 bytes. If the density of OBU per 1 km increases by three times, then the average number of packets per OBU will be 26, with a packet size of 50 bytes. The average number of packets per OBU is seven, with a packet size of 150 bytes. We obtain four packets, with a packet size of 250 bytes.

Analysis of the results showed that the time spent increases 1.048 times when switching from a 32-bit protocol to a 64-bit protocol. This is because when using 32- and 64-bit modulus, the time required to transmit the question and answer ranges from 0.68 (with a minimal level of confidentiality) to 0.25 (with a maximal level of confidentiality) of the entire protocol execution time. Obviously, it is possible to increase the volume of information traffic by changing the level of confidentiality with a modulus of size of 128 bits or more. This is the most promising future research direction. In addition, there is no scheme in the presented adaptive protocol that can authenticate the vehicle, to provide it with appropriate services using the Service Provider.

7. Conclusions

The article analyzes the main methods used to increase vehicles’ confidentiality when using VANET. Based on this research, it was concluded that it is advisable to use authentication protocols based on zero-knowledge proof, since they have a high cryptographic strength without the use of symmetric and asymmetric ciphers. The analysis of these protocols showed that they have a low authentication speed, since they have several rounds. To eliminate this disadvantage, an authentication protocol has been developed that requires a minimal number of operations to determine the prover’s status. A scheme was developed to adapt the level of confidentiality in the authentication protocol. The use of this scheme allows for a reduction in the level of confidentiality, to reduce the computational complexity of the protocol and increase the volume of information traffic when data exchanges occur between OBU and RSU. FPGA Artix-7 xc7a12ticsg325-1L was used to evaluate the effectiveness of the developed adaptive authentication protocol. The results showed that when a 64-bit modulus and maximal level of confidentiality are used for the developed protocol, the probability of selecting the verifier signal is $P_{\max }^{(64)}=1.35\cdot {10}^{-20}$.

The article presents the most promising methods to improve the efficiency of the developed adaptive authentication protocol. These include the use of a larger-sized modulus (128 bits), as well as the development of a scheme that would allow for authentication of the vehicle, to provide it with appropriate services by the Service Provider.