Outdoor Node Localization Using Random Neural Networks for Large-Scale Urban IoT LoRa Networks ^†

Abstract

Accurate localization for wireless sensor end devices is critical, particularly for Internet of Things (IoT) location-based applications such as remote healthcare, where there is a need for quick response to emergency or maintenance services. Global Positioning Systems (GPS) are widely known for outdoor localization services; however, high-power consumption and hardware cost become a significant hindrance to dense wireless sensor networks in large-scale urban areas. Therefore, wireless technologies such as Long-Range Wide-Area Networks (LoRaWAN) are being investigated in different location-aware IoT applications due to having more advantages with low-cost, long-range, and low-power characteristics. Furthermore, various localization methods, including fingerprint localization techniques, are present in the literature but with different limitations. This study uses LoRaWAN Received Signal Strength Indicator (RSSI) values to predict the unknown X and Y position coordinates on a publicly available LoRaWAN dataset for Antwerp in Belgium using Random Neural Networks (RNN). The proposed localization system achieves an improved high-level accuracy for outdoor dense urban areas and outperforms the present conventional LoRa-based localization systems in other work, with a minimum mean localization error of 0.29 m.

1. Introduction

Localization is a vital research subject that is gaining popularity and being applied in different IoT location-based applications, such as tracking. Moreover, various wireless technologies are being applied in localization. WiFi [1], Bluetooth [2], and Zigbee [3] are primarily applied in localization systems for indoor environments and only limited to a few meters. Furthermore, technologies based on satellites are the pioneers in the accurate localization systems for outdoor applications, with errors less than 4 m for Galileo’s Open Service and 10 m using GPS [4]. Satellite-based technologies provide continuous global coverage and play significant roles in a wide range of applications. However, Global Navigation Satellite System (GNSS) modules consume high energy, which rules them out for many low-power IoT end devices. Additionally, incorporating many stand-alone sensor nodes in dense sensor network applications with GPS modules would not be efficient due to high hardware cost, high power consumption, and failures due to non-line-of-sight communications [5]. Time-of-Arrival (ToA), RSSI ranging, and Time-Difference-of-Arrival (TDoA) algorithms are among the most researched range-based localization techniques in IoT and Wireless Sensor Networks (WSN). Trilateration or Triangulation approaches are used to calculate the location coordinates of the end device using multiple anchor end nodes with known location coordinates [6], whereby LoRaWAN gateways may be referred to as anchor points. A propagation model and the RSSI are used to compute the distance between receiver and transmitter in RSSI ranging. However, multipath and shadow fading lead to the loss profile with indoor RSSI ranging.

A scheduling algorithm with accurate end devices’ time synchronization is required for ToA, whereas accurate gateways time stamps for at least three distant gateways are only required for TDoA and make it more suitable for IoT end devices. The calculation of an end device location is made when at least three distant gateways received the same transmission signal from the same end device as, ideally, the signal trajectories to the gateways intersect at the location of the end device. However, any slight scheduling error may lead to inaccurate location predictions. The traditional Low-power Long-Range (LoRa)-based localization systems use TDoA [7] and fingerprint algorithms [8], all with limitations in dense, large urban areas and still under investigation. TDoA performance is poor in dense urban areas, though it performs well in open areas [9]. Fingerprinting localization uses end devices’ RSSI fingerprint values received by gateways to localize any end device in the network accurately. A fingerprint-based approach consists of an offline training phase and an online phase [10]. Data samples are collected from a considered service area where localization is to be predicted and used to train a fingerprint algorithm. The location of any end device can then be predicted using the trained algorithm in an online phase based on end-device RSSI characteristics. However, all existing fingerprint algorithms also have various challenges; among others are changing environments that affect fingerprint maps, fingerprint databases that require manpower to be created, and the complicated infrastructure layout, particularly in urban areas. Additionally, different RSSI fingerprint Low-Power Wide-Area Networks (LPWAN) such as LoRaWAN-based approaches using different machine learning algorithms and Artificial Neural Networks (ANN) are also present in the literature [11].

Furthermore, RNN has been used to develop robust models in different applications with considerable accuracy [12]. However, RNN applied to localization systems is a research topic yet to be fully explored. This research applies RNN to develop a low-power, large-scale localization system using LoRaWAN RSSI values to predict unknown 2D X and Y coordinates. Different RNN-based localization models are trained and tested using different learning rates and samples on the publicly available LoRaWAN dataset for Antwerp in Belgium and outperforms localization systems in other related work with the minimum mean localization error of 0.29 m. The main contributions of this paper are as follows:

• Developing a new LoRaWAN-based localization model using RNN for large, dense urban scenarios.
• Training and testing the different RNN-based localization systems with various learning rates.
• Training and testing the different RNN-based localization models with different data samples in Antwerp dataset publicly available and used in many research papers.
• Critically analyzing the results with other popular methods applied to the same dataset.

The organization of this paper is as follows: Section 2 gives an overview of LoRa and LoRaWAN; Section 3 summarizes the related work; Section 4 describes the methodology used; Section 5 discusses the obtained results and performance analysis; finally, conclusions are given in Section 6.

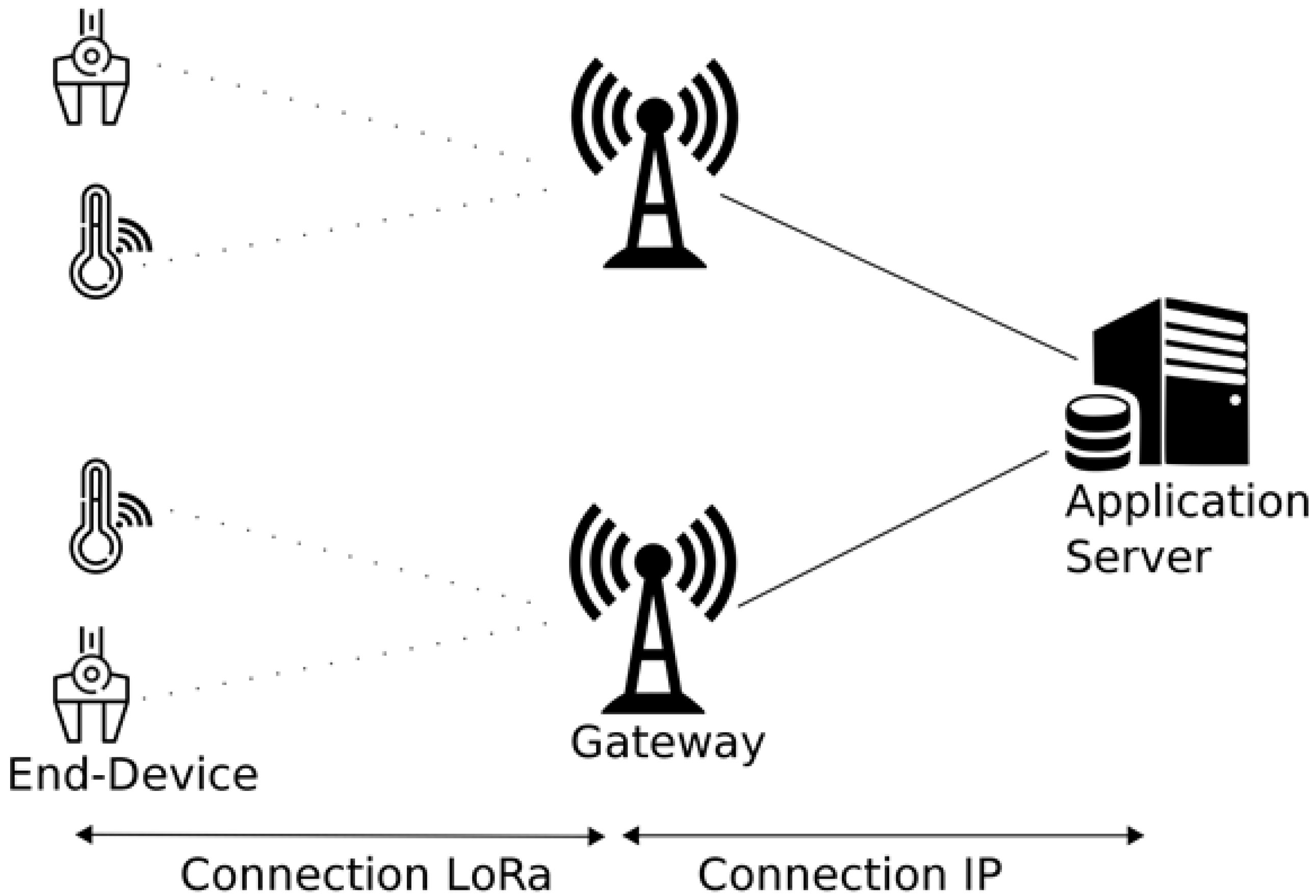
2. LoRa and LoRaWAN

LoRa is a physical layer with the Chirp Spread Spectrum (CSS) modulation technique operated by Semtech and usable within the license-free spectrum from 863 MHz to 870 MHz in Europe and from 902 MHz to 928 MHz in the USA [13]. The connection of the wide-area network of LoRa is called LoRaWAN and is a network protocol stack and offers the architecture of LoRa technology on the MAC layer. A LoRaWAN network is made up of LoRa end devices connected in a star topology that sends information to one or more LoRaWAN gateways, which, in turn, send the received message along with a recorded unique message’s metadata information to a network server, as shown in Figure 1. This metadata information is used for localization services in LoRaWAN networks, whereby gateways serve as anchor points to predict end device locations. LoRaWAN networks use RSSI values as a critical metric for fingerprint localization algorithms, whereas TDoA algorithms use timestamps at which gateways receive the same message. Furthermore, localization accuracy of any of the methods depends on more gateways receiving the same message [14].

3. Related Work

Several TDoA-based localization systems using LoRaWAN IoT networks are available in the literature [10,15]. An acceptable accuracy of less than 100 m in most of the published work was reported considering fixed nodes and gateways as anchor points on a small area. However, the performance degraded significantly when mobile nodes or large areas were considered. Fargas et al. in [16], used an iterative TDoA-based algorithm to locate static nodes and obtained a good accuracy with an error of around 100 m. A median error of 200 m was reported by Podevijn et al. in [7] by using a TDoA-based algorithm that considered map details such as roads. Aernouts. M. et al. in [17], via extensive simulations, used two gateways with combined TDoA and Angle of Arrival (AoA) using probabilistic algorithms. Their simulation results reported a mean error of 548 m with TDoA and managed to reduce the mean error to 399 m by combining the TDoA estimate with a single AoA estimate. Furthermore, range-based algorithms do not work in indoor scenarios due to multipath as a result of complicated radio environments. Hence, RSSI fingerprinting localization techniques also explored and proved to be potential candidates for harsh environments, including both indoor and outdoor dense urban areas. Different algorithms using RSSI fingerprint localization are available in the literature using various technologies; nevertheless, most of the present works investigated indoor scenarios because of many data needed for the training phase and tedious work in accumulating enough data for a large area. Wi-Fi has been used in fingerprint localization by different researchers [18,19,20,21], whereby a smartphone may be used to record its RSSI and calculate its location using the web. The authors in [22] compared the performance analyses of different wireless technologies based on RSSI localization. Furthermore, the authors in [23] used satellite images for LoRa-based outdoor fingerprint localization and achieved a median error of 47.1 m.

Different research works in the literature have evaluated ANN methods for sensor localization and confirmed them to be effective [24]. In addition, the authors investigated localization models using ANN for Low-Power Wide Area Networks (LPWAN) in [25], and they confirmed ANN as an objective approach, mainly for dense IoT networks. Furthermore, various studies are available in the literature on using ANN to develop LoRa-based [8,26,27] localization models with high accuracy. Different RSSI fingerprint LPWAN-based approaches using machine learning algorithms, particularly LoRaWAN, are also present in the literature [11]. Janssen. T. et al. in [17] conducted a comparative performance analysis of various machine learning algorithms for RSS–LPWAN-based localization models. The random forest regression method had the highest accuracy with a mean estimation error of 340 m, and the k-Nearest Neighbour (kNN) method had a similar accuracy with the least computational performance. Sallouha reported an error lower than 20 m in [28], while analyzing localization in ultra-narrow band IoT networks. Similarly, RSSI fingerprint localization methods based on deep learning algorithms have also been published in the literature [29,30,31,32]. Moreover, Carrino. F. et al. in [33] reported a root mean square estimation of error less than 9 m with a Long Short-Term Memory (LSTM) method compared with the accuracy of Random Forest and ANN methods.

Furthermore, RNN algorithms have been used in various applications including Heating, Ventilation, and Air Conditioning (HVAC) systems [34,35,36]; nonoccupied buildings’ energy prediction [37]; image pattern recognition [38]; and intrusion detection systems [12,39,40] all with significant results. Moreover, according to the results of Cerkez et al. [41] and Abdelbaki et al. [42], simple encounters can represent neurons in RNN and, hence, easy hardware implementation. In addition, RNN accurately predicted unseen patterns not included in the training data when compared with the conventional ANN performance [43]. RNN outperformed ANN during run-time though at the expense of a greater training time [44]; the authors also reported that RNN had a stronger generalization capacity for the training phase uncovered patterns. Furthermore, a performance analysis of different models of the proposed RNN-based localization system was evaluated in our previous published work [45]. Nevertheless, RNN application is still under investigation and yet to be fully applied in developing and evaluating end device localization systems in general, specifically using LoRaWAN in a large, dense urban environment.

4. Methodology

This section presents all the details and procedures used to collect and preprocess the dataset we used to develop the proposed LoRa-based localization system using RNN.

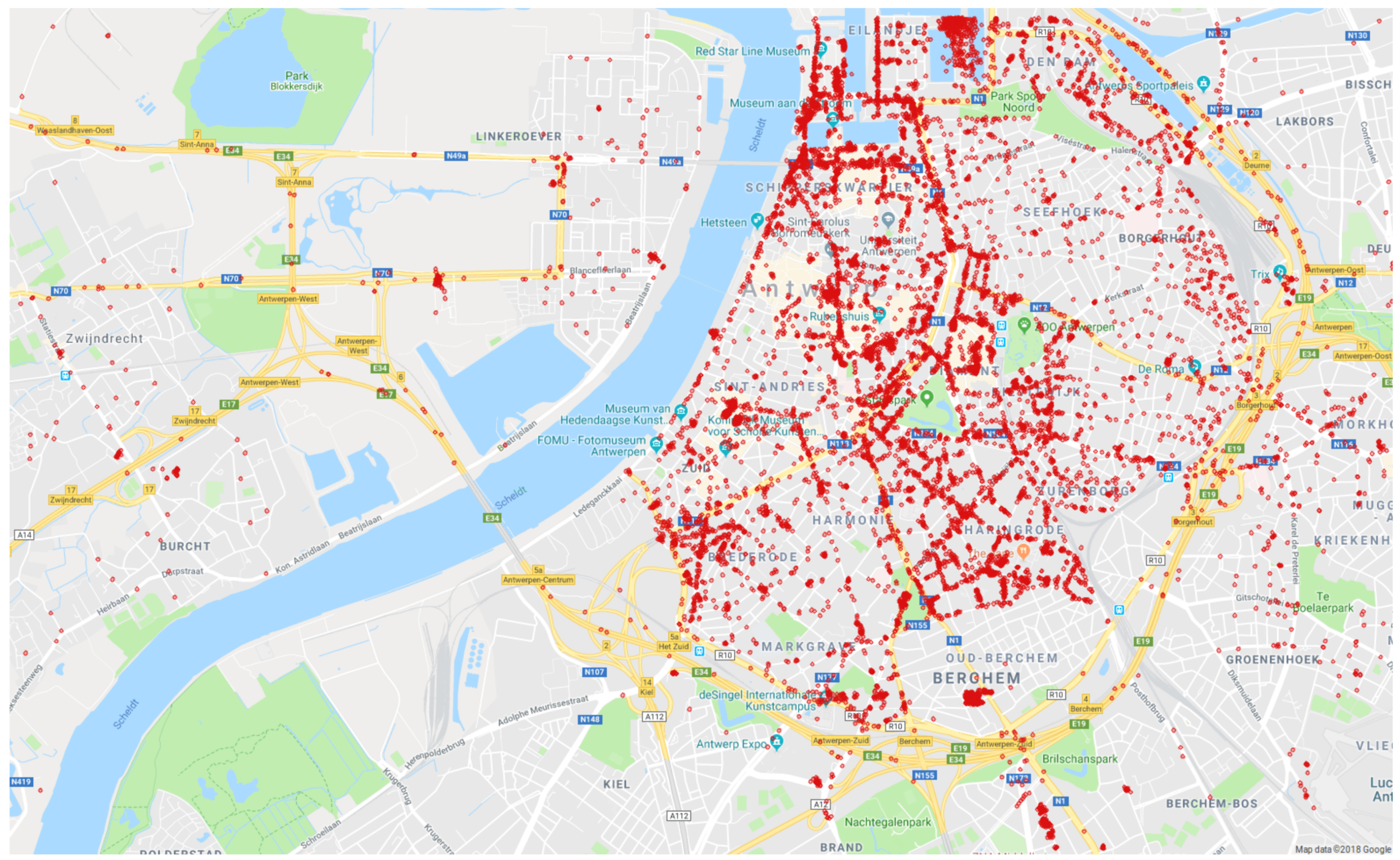
4.1. Dataset

Our study used the LoRaWAN dataset published by Aernouts et al. in [46], gathered in an area of 52 km${}^2$ in Antwerp in Belgium, and is publicly available. Data were collected by attaching LoRa modules to postal service vehicles, whereby a total of 130,343 data points were gathered from these nodes sending a message every minute to 72 LoRaWAN gateways deployed by a private company called Proximus for three months. A map showing a random sample of data points in Antwerp evenly distributed in the city streets is shown in Figure 2. For every data point or message, the authors recorded X and Y position coordinates of each LoRa node with its RSSI values received by 72 different gateways. If any of the gateways did not receive a particular message, a RSSI value of −200 was recorded. The distribution of RSSI values is presented in Figure 3 and varies between −122 dBm and −79 dBm.

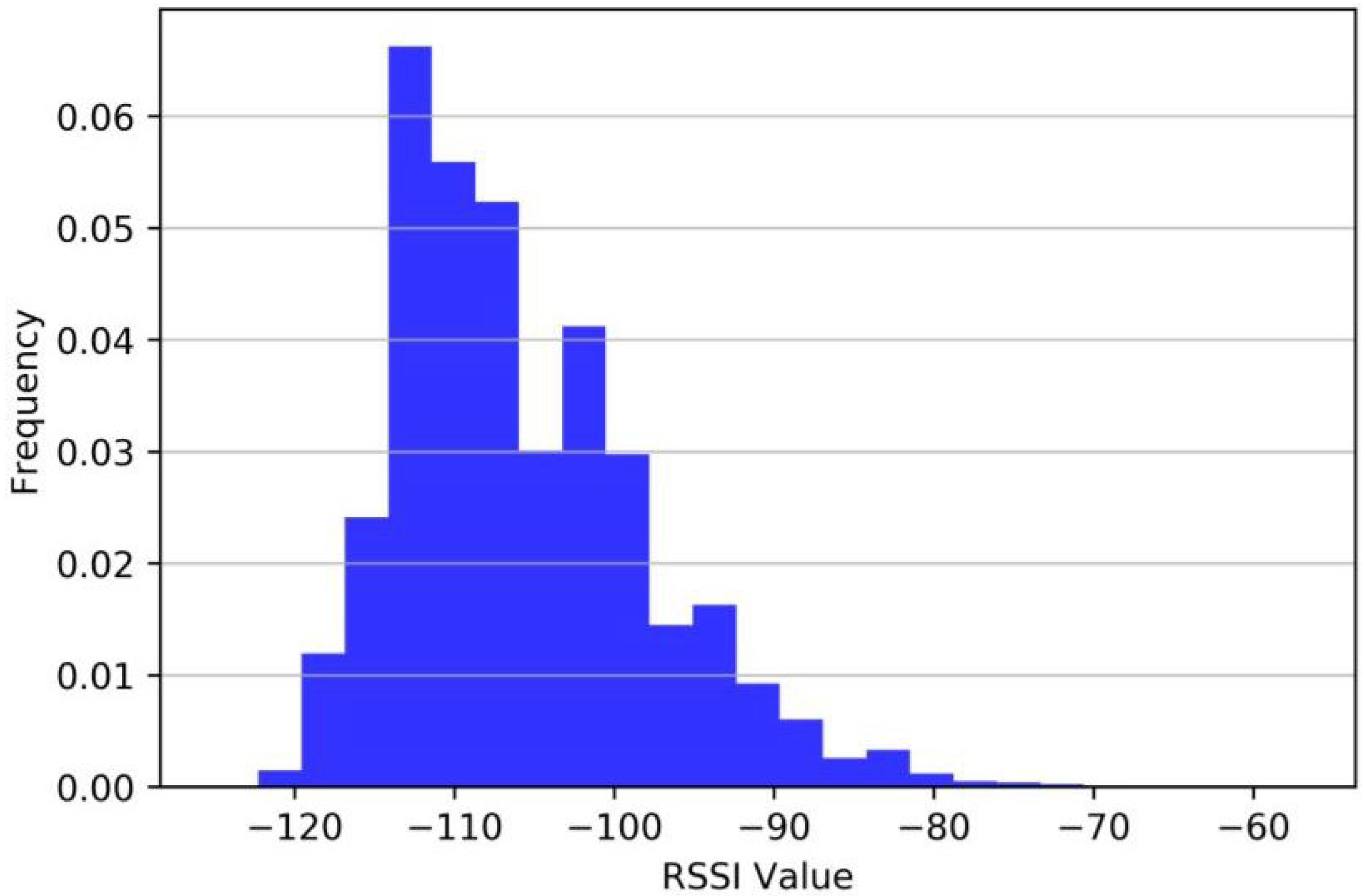
4.2. Data Normalization

The RSSI values of the used dataset are large and, due to large weights, the network becomes unstable. Therefore, we scaled the dataset using the Min-Max Normalization data preprocessing technique to the range of 0 to 1, with the formula that follows:

$$x_i=\frac{RSS{I}_i-min\left(RSSI\right)}{max\left(RSSI\right)-min\left(RSSI\right)},$$

(1)

whereby the raw RSSI input data is $RSSI=(RSS{I}_1,\dots ,RSS{I}_n)$ and the resultant normalized data are $x\left(i\right)$.

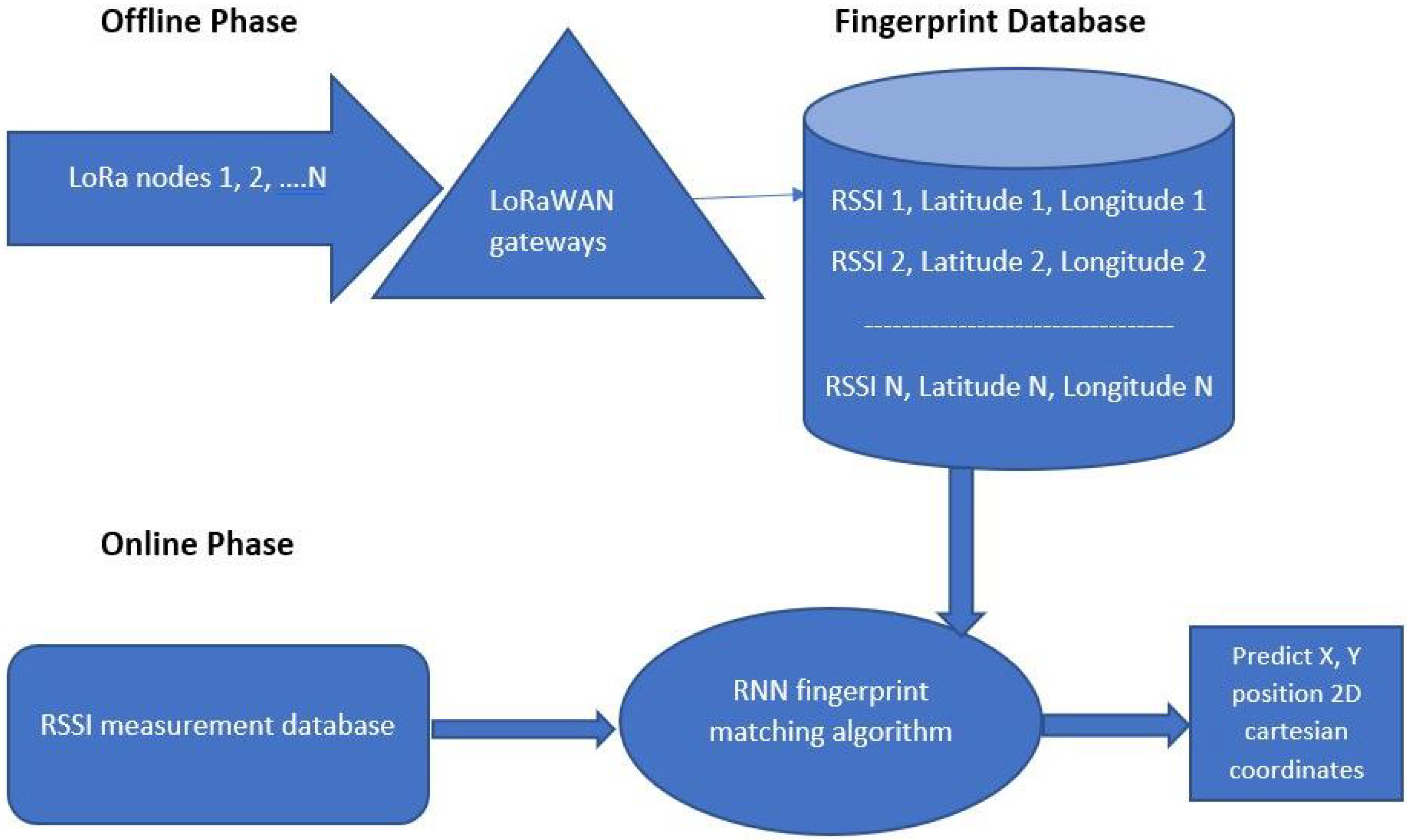
4.3. Proposed RNN-Based Localization System Using LoRaWAN

Gelenbe developed RNN as a novel class of ANN [47]. It is composed of N several layers of linked neurons that exchange information signals as impulses; a positive potential (+1) is used for an excited signal and a negative potential (−1) is used for inhibited signals to the next connected neuron. The potential of every neuron i at time t is represented by a nonnegative integer $K_i\left(t\right)$. The neuron i is in an excited state if $K_i\left(t\right)$ > 0 and I is in idle state if $K_i\left(t\right)$ = 0. If neuron i is excited, it transmits signal information to the next receiving neuron j at the Poisson rate $r_i$. The transmitted signal can reach neuron j as an impulse signal in an excited or inhibition state with probabilities $p^{+}(i,j)$ or $p^{-}(i,j)$, respectively. Furthermore, the transmitted signal can leave the network with a probability defined with the following mathematical formula:

$$c\left(i\right)+\sum _{j=1}^N{p}^{+}(i,j)+p^{-}(i,j)=1,\forall i,$$

(2)

$$w^{+}(i,j)=r_i{p}^{+}+(i,j)\ge 0,$$

(3)

Likewise

$$w^{-}(i,j)=r_i{p}^{-}+(i,j)\ge 0.$$

(4)

Equations (2)–(4) combined:

$$r\left(i\right)={(1-c\left(i\right))}^{-}1\sum _{j=1}^N[w^{+}(i,j)+w^{-}(i,j)]$$

(5)

The rate of transmission between neurons in Equation (5) is $r\left(i\right)$, and is defined as $r\left(i\right)={\displaystyle \sum _{j=1}^N}[w^{+}(i,j)+w^{-}(i,j)]$. Though “w” describes the matrices of weight updates from neurons, it is always positive as it is a product of probabilities and transmission rates.

If a signal arrives at neuron $\left(i\right)$ in excitation state with a positive potential, it is denoted by Poisson rate $\mathsf{\Lambda }\left(i\right)$, while a signal in inhibition with a negative potential reaches at a Poisson rate $\lambda \left(i\right)$. Hence, for each node “i”, the output activation function for that particular neuron is described by

$$q\left(i\right)=\frac{{\lambda }^{+}\left(i\right)}{r\left(i\right)+{\lambda }^{-}\left(i\right)},$$

(6)

where

$${\lambda }^{+}\left(i\right)=\sum _{j=1}^{n}q\left(j\right)r\left(j\right)p^{+}(j,i)+\mathsf{\Lambda }\left(i\right),$$

(7)

and

$${\lambda }^{-}\left(i\right)=\sum _{j=1}^{n}q\left(j\right)r\left(j\right)p^{-}(j,i)+\lambda \left(i\right).$$

(8)

In this study, the proposed RNN–LoRaWAN-based localization system is trained with Gradient Descent (GD) and the computed weights and biases are updated to the neurons as the algorithm calculates the error. GD is a first-order iterative optimization algorithm commonly considered by various researchers for training; it minimizes the cost function, and the error cost function is described by

$$E_p=\frac{1}{2}\sum _{i=1}^n{\gamma }_i{(q_j^p-q_j^p)}^2,{\gamma }_i\ge 0$$

(9)

where $\gamma \in (0,1)$ gives the status of output neuron i; similarly, $q_j^p$ is a real differential function, where $q_j^p$ is the estimated output value. As per Equation (9), to find the local minima and reduce the error value of the error cost function, the relationship between neurons y and z is used, where weights $w^{+}(y,z)$ and $w^{-}(y,z)$ are updated by

$$w_{y,z}^{+t}=w_{y,z}^{+(t-1)}-\eta \sum _{i=1}^n{\gamma }_i(q_j^p-y_j^p){\left[{\displaystyle \frac{\partial q_i}{\partial w_{y,z}^{+}}}\right]}^{t-1},$$

(10)

Moreover,

$$w_{y,z}^{-t}=w_{y,z}^{-(t-1)}-\eta \sum _{i=1}^n{\gamma }_i(q_j^p-y_j^p){\left[{\displaystyle \frac{\partial q_i}{\partial w_{y,z}^{-}}}\right]}^{t-1}.$$

(11)

More details about RNN and GD are reported in [37]. In this work, RNN is used to develop our proposed model to accurately map the input to the output using the LoRaWAN Antwerp dataset (RSSI values, Latitude, and Longitude coordinates), and the developed model is used to output any desired unknown X, Y position coordinates. This work considers deg2utm stand-alone function application to convert GPS coordinates to X, Y vector coordinates using MATLAB R2020b [48]. RNN supervised learning algorithm is considered for training the proposed model to locate each end device in the network service area, and then the trained model is extended further to predict the position of any other LoRa sensor nodes on the same network grid based on end-device RSSI values, as shown in Figure 4.

We used the LoRaWAN Antwerp dataset [46] to train and test our proposed RNN–LoRa-based localization using the gradient descent algorithm for regression. Different experiment setups are designed, whereby in the first instance, 80% of the available 130,343 total data points are used for training the model with the used LR in different epochs, and the remaining 20% of the dataset is used for testing the model. The proposed RNN model runs k-folds and uses seventy-two input layer neurons, seventy-two hidden layer neurons, and two output layer neurons. Algorithm 1 is the RNN-based localization algorithm used:

Algorithm 1: RNN-Based Localization.

Input: RSSIxt,yt in each time slot, M Output: Regression model based on RNN 1: Use 80% of the collected RSSI values from trajectory where the user moved and consider enough of the data in this trajectory. 2: Generate the RSSI database in each time slot. 3: Initialize the structure of RNN. 4: Train RNN and compute the RNN parameters. 5: Use 20% of the collected RSSI data for testing, then verify the trained RNN model in step 4. 6: Change the RNN parameters and estimate the best parameters for accurate localization using steps 5 and 6.

5. Results and Analysis

To analyze the performance and localization accuracy of our proposed RNN model, we used the MATLAB R2020b simulation-controlled environment. Figure 5 shows the system’s average mean localization error values with the used learning rates of 0.001, 0.01, 0.1, and 1 at different epochs. The developed RNN-based localization model was evaluated using the average localization error (AE) defined by the following formula:

$$AE=\sum _{i=1}^n{({(X_{real}-X_{pred})}^2+{(Y_{real}-Y_{pred})}^2)}^{0.5}$$

(12)

where $(X_{real},Y_{real})$ is the actual prerecorded position coordinates recorded using GPS; $(X_{pred},Y_{pred})$ is the estimated location of unknown location predicted by the developed localization system; and n represents the total number of data samples used in modeling.

From Figure 6, generally, the highest accuracy of the proposed model was obtained with lower learning rates than higher learning rates at the expense of longer training time. Additionally, with higher learning rates, the localization system tends to be more unstable during training. We trained our model with multiple learning rates to offset these issues. Increasing the learning rate from 0.001 to 0.1 did not improve the developed system’s accuracy by increasing the system’s mean localization error by 0.03 m, which may be significant or not depending on the application. Meanwhile, increasing the learning rate further to 1 improved the accuracy of the localization system by minimizing the mean localization error by 0.02 m. Our system achieved a minimum mean localization error of 0.291 m while using a learning rate of 0.001. More details about obtained mean localization error values obtained for all the used learning rates are presented in

Table 1. Average mean localization error (m) for used learning rates.

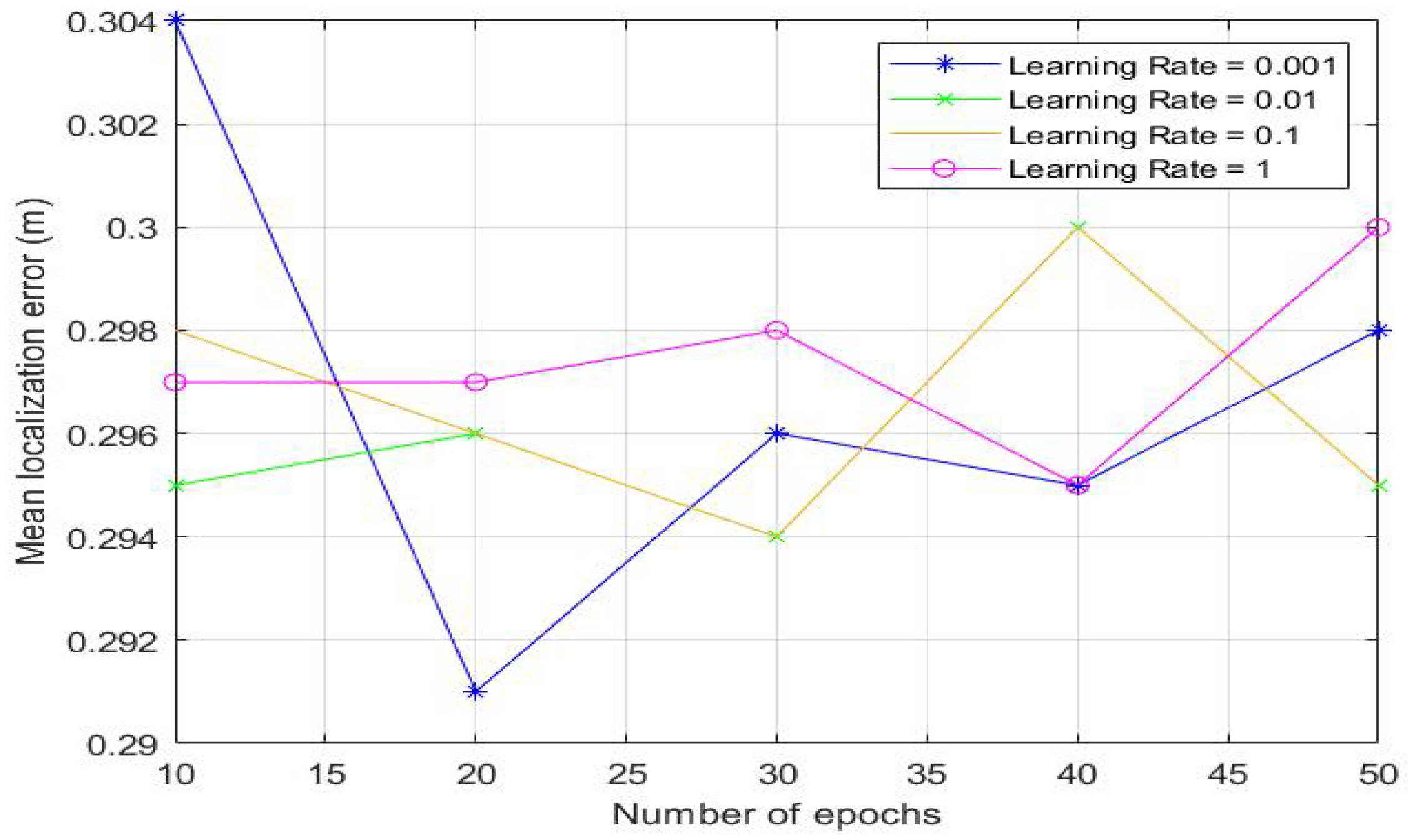
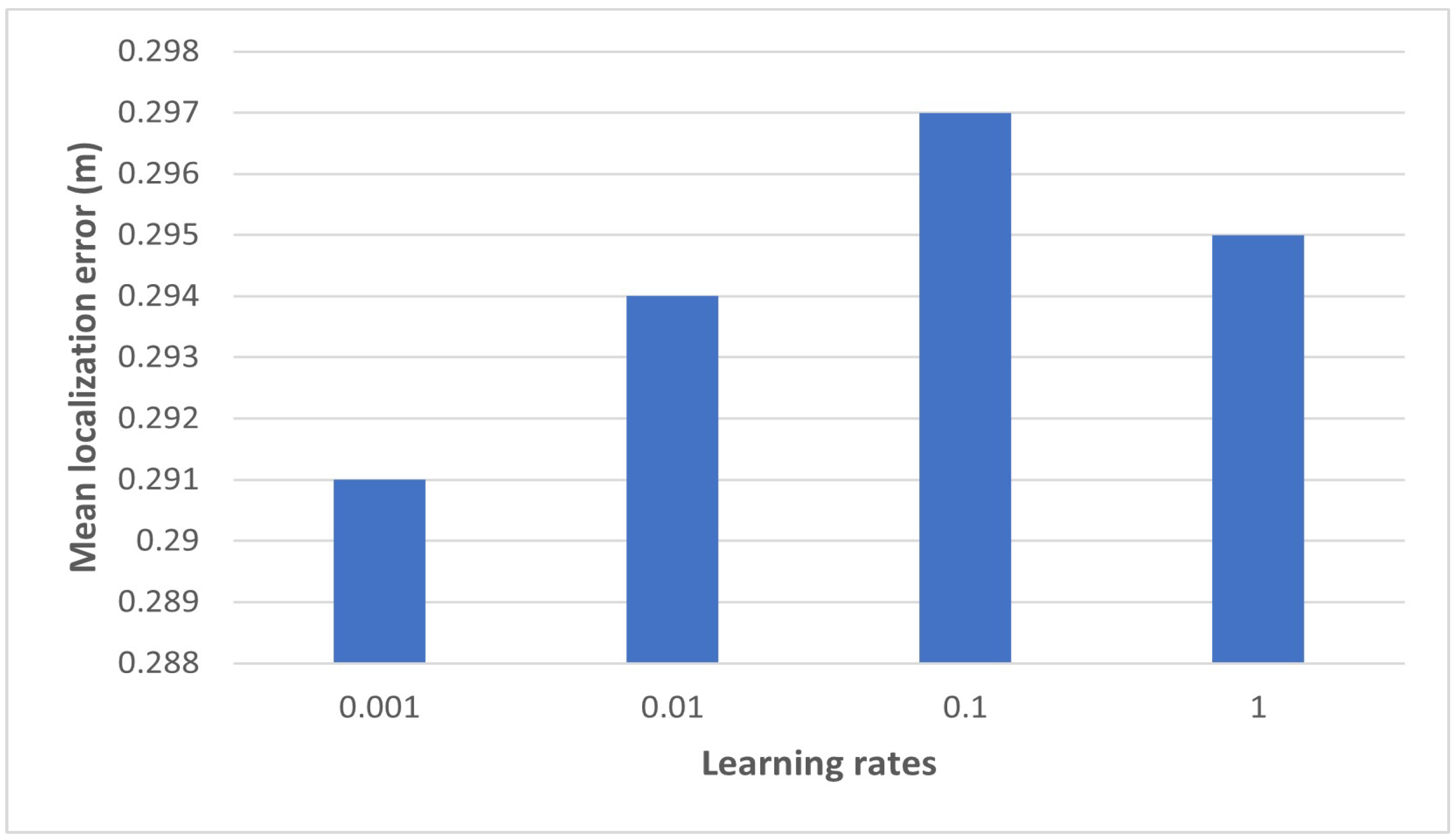
Learning Rate	Mean Localization Error (m)
0.001	0.291
0.01	0.294
0.1	0.297
1	0.295

. Additionally, a minimum mean square error (MSE) value of 0.09 m was obtained while training our model.

Next, we evaluated the impact of the different samples since we had a massive number of data points that took a very long training time, depending on the used learning rate. The mean localization error values of our system while using 1000, 3000, 5000, 10,000, and 15,000 data samples keeping the same RNN network architecture with the same used learning rates plus 0.0001 are shown in Figure 7. For 1000, 5000, and 10,000 data samples, increasing the learning rate from 0.0001 to 0.01 increased the mean localization error of the system, and when we increased further to 0.1 and 1, the system’s error decreased. Furthermore, for 3000 and 15,000 data samples, increasing the learning rate from 0.0001 to 1 improved the system’s performance by decreasing its mean localization error.

The minimum mean localization error of 0.3 m was achieved with 15,000 samples while using learning rates of 0.1 and 1. Consequently, we investigated the total RNN training time elapsed (in sec) for the used number of samples and learning rates, as shown in

Table 2. Average mean localization error (m) for used samples.

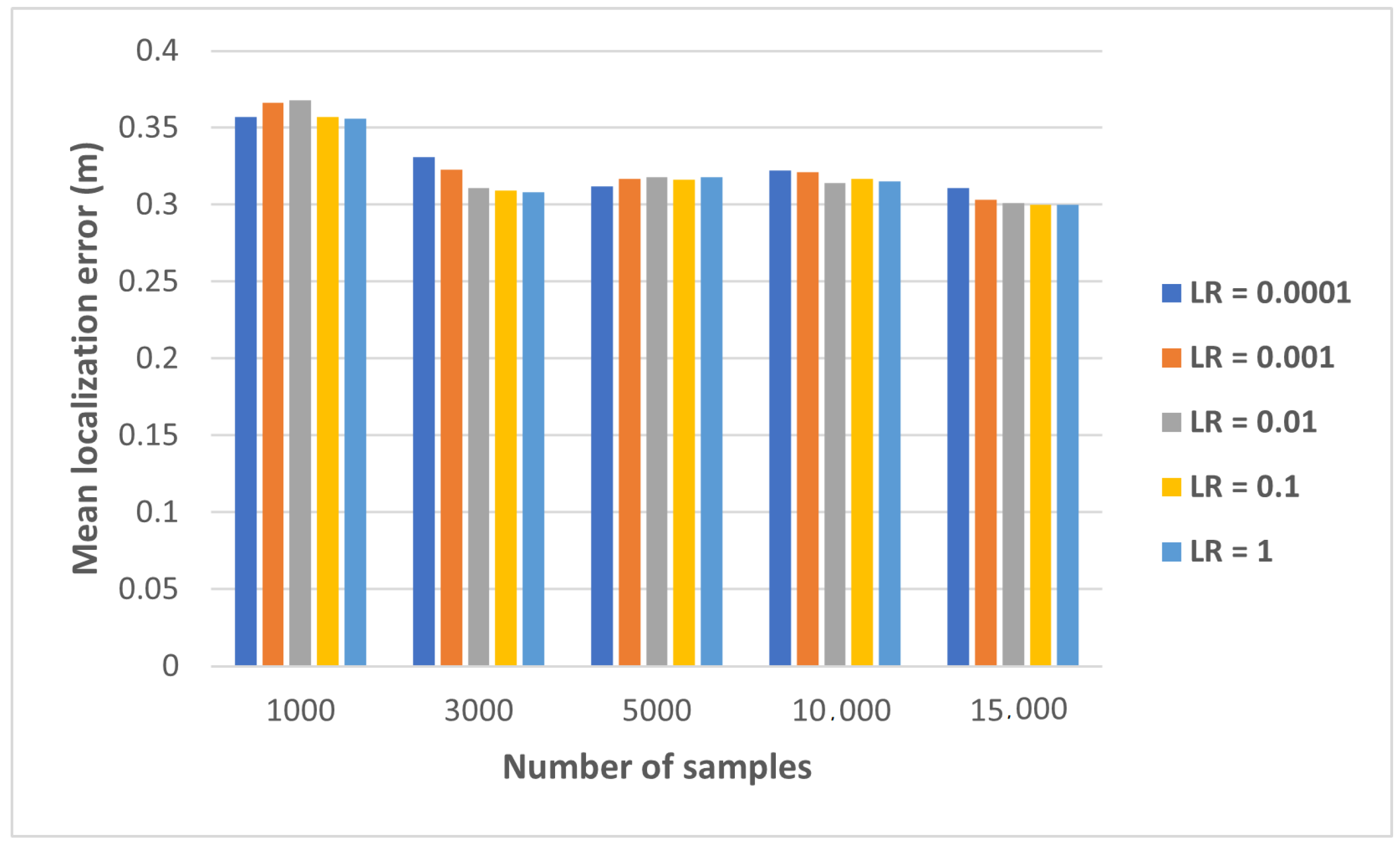
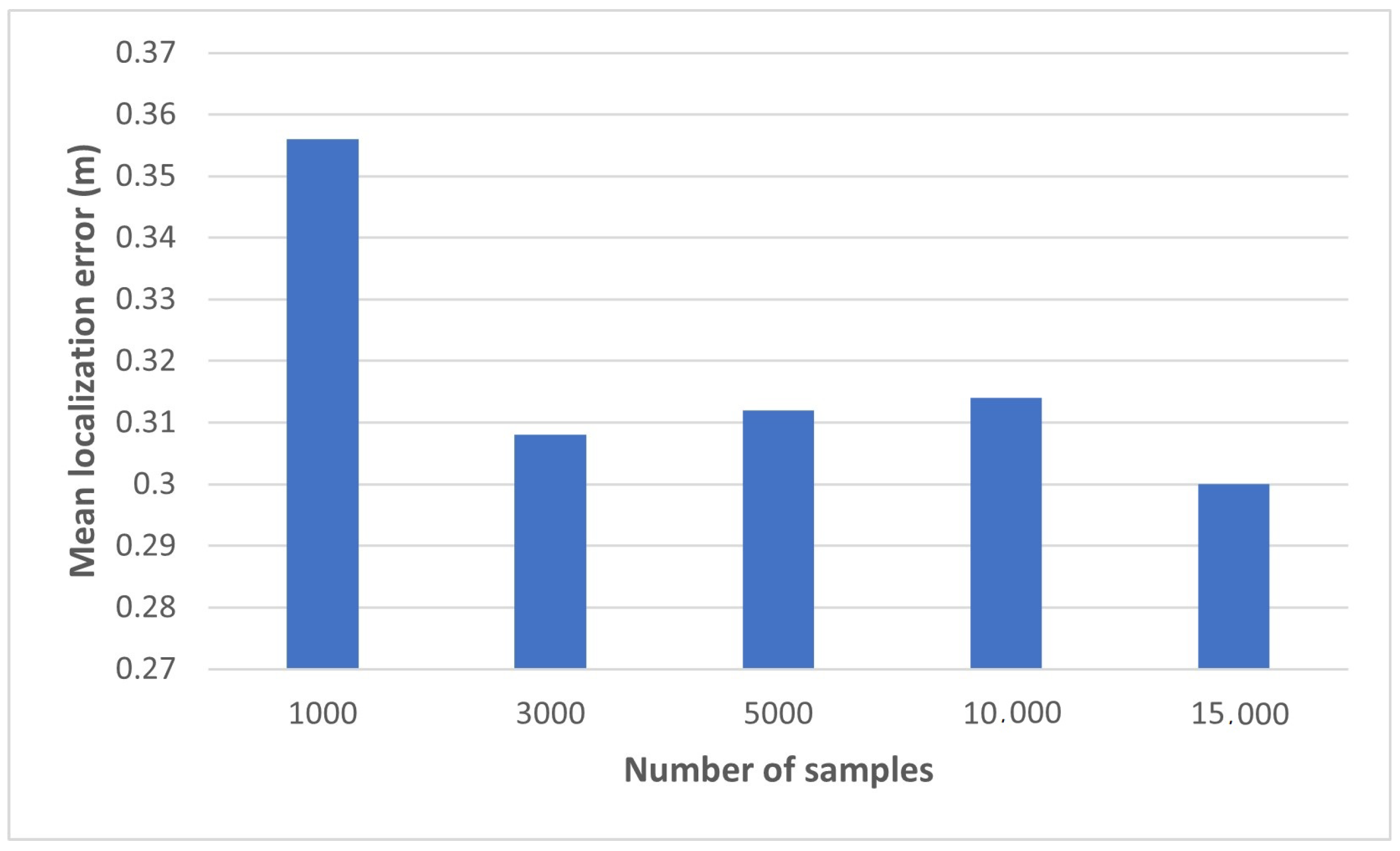
Samples	Mean Localization Error (m)
1000	0.356
3000	0.308
5000	0.312
10,000	0.314
15,000	0.3

. Hence, the highest system accuracy was achieved using the highest learning rate of one with the shortest training time of 4970 s and a training error of MSE equal to 0.1 m. Mean localization values obtained for all the used samples are presented in Figure 8 with more details given in Table 2. The obtained results about data samples show that increasing data samples from 1000 to 15,000 and further, to 130,343 samples, did not significantly impact the system’s accuracy as the difference is only 0.01 m at the expense of higher training times.

Comparative Performance Analysis

The localization accuracy of the proposed RNN-based localization approach is compared with traditional localization approaches presented in related research studies, and

Table 3. Accuracy of different RSSI fingerprinting approaches in outdoor LoRaWAN from different research studies.

Research Work	Mean Localization Error (m)	Approach
Proposed RNN-based localization system	0.29	RNN
Ingabire et al. [45]	0.39	RNN
Bonafini et al. [49]	6.2	Multilateration
Du et al. [50]	7.57	Hybrid
Shokry et al. [51]	18.8	Deep learning
Anjum et al. [52]	45.75	Linear
Purohit et al. [53]	191.52	ANN-Deep
Janssen et al. [54]	340	kNN
Aernouts et al. [46]	398.4	kNN
Anagnostopoulos et al. [8]	358	ANN
Nguyen [55]	500	ANN

summarizes the localization performance of each of the systems. A minimum mean localization error of 0.39 m was achieved for a small-scale urban area in our previously published work [45]. Bonafini et al. [49] used Multilateration algorithm and achieved a minimum localization error of 6.2 m while Du et al. [50] obtained a minimum localization error of 7.57 m. Shokry et al. [51] used deep learning and obtained a minimum localization error of 18.8 m, and Anjum et al. [52] used a linear regression model and achieved a localization error of 45.75 m. Purohit et al. [53] used deep neural networks and obtained a localization error of 191.52 m; Janssen et al. [54] also used kNN and obtained a localization error of 340 m. Aernouts et al. [46] used kNN method and achieved a localization error of 398.4 m; Anagnostopoulos et al. [8] also used ANN and obtained an error of 358 m, while Nguyen [55] used ANN approach and achieved a localization error of 500 m. From Table 3, it is clear that the proposed RNN-based localization model outperforms the other RSSI fingerprint LoRaWAN-based localization systems from related research with a minimum localization error of 0.29 m. The proposed RNN method has achieved 25%, 95%, 96%, 98.5%, 99.85%, 99.37%, 99.92%, 99.93%, and 99.94% improvements in mean localization error compared with our previous work [45], Bonafini et al. [49], Du et al. [50], Shokry et al. [51], Anjum et al. [52], Purohit et al. [53], Janssen et al. [54], Aernouts et al. [46], Anagnostopoulos et al. [8], and Nguyen [55], respectively.

6. Conclusions and Future Work

In this paper, we proposed a LoRa RSSI-based localization system using the RNN algorithm. The proposed method uses 0.001, 0.01, 0.1 learning rates and 1000, 3000, 5000, and 10,000 data samples to evaluate the performance of the proposed RNN–LoRa RSSI-based localization system in a large, dense urban area of Antwerp in Belgium. The proposed localization system is trained using 0.001, 0.01, 0.1, and 1 learning rates; 1000, 3000, 5000, 10,000, and 130,343 data samples; and about 1000 data samples were enough to evaluate our system’s performance with minimum training time. Furthermore, through extensive simulations and analysis, the proposed system tested and achieved a minimum mean localization error of 0.29 m. We plan to evaluate the performance of our proposed localization system in an indoor environment.