The Model Order Reduction Method as an Effective Way to Implement GPC Controller for Multidimensional Objects
Abstract
1. Introduction
2. GPC Problem Formulation
2.1. Predictive Controller Formulation
2.2. Construction of GPC Algorithm
3. Process Identification
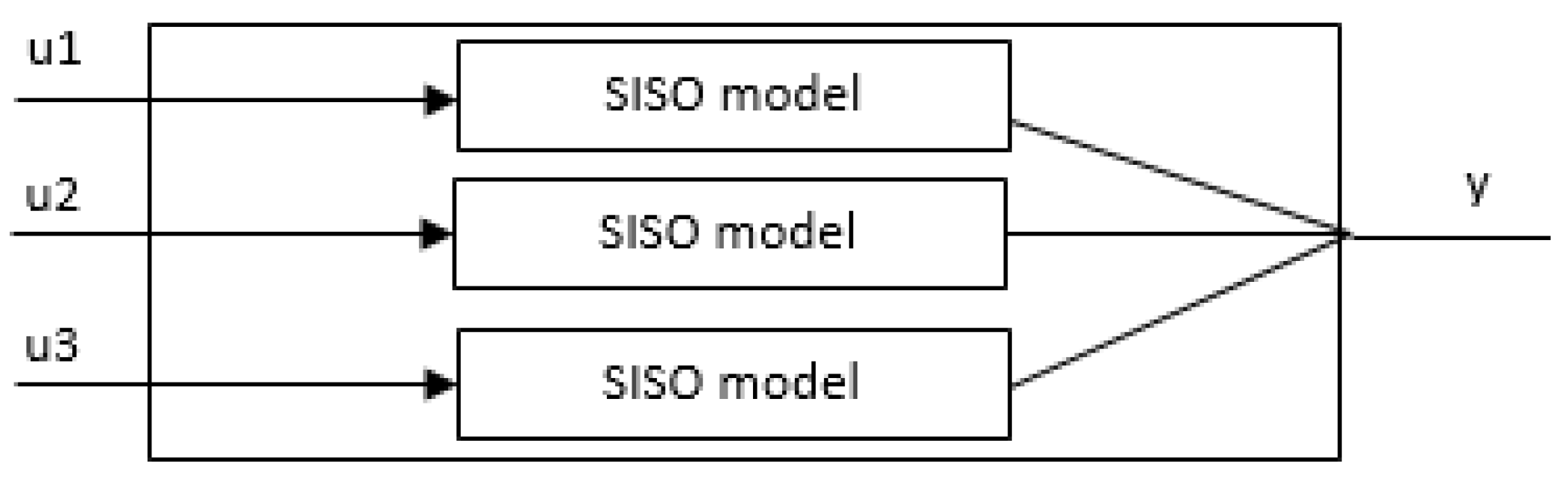
4. Example Models
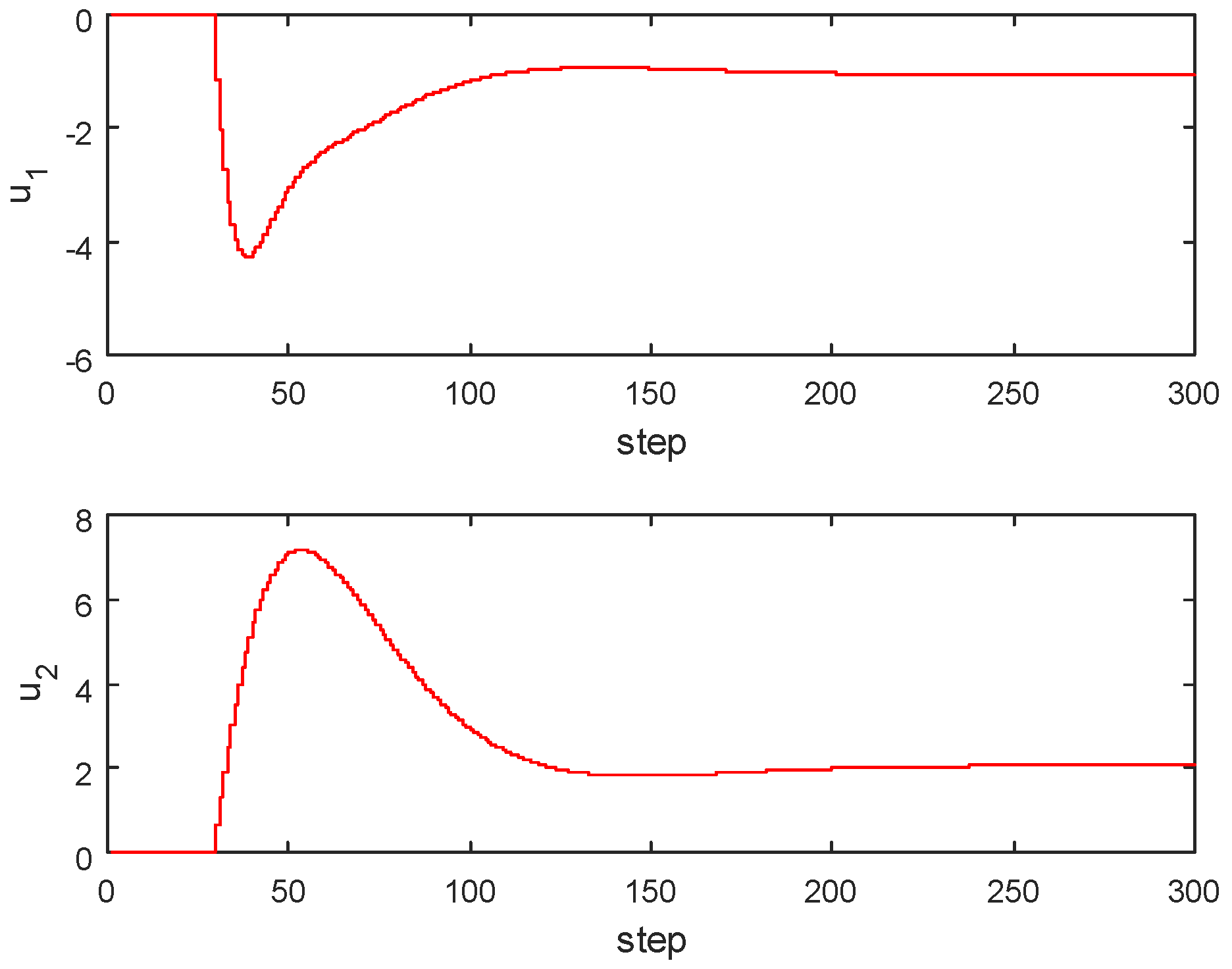
4.1. Two Input-Two Output Model
4.2. Transformation to GPC Internal Model Format
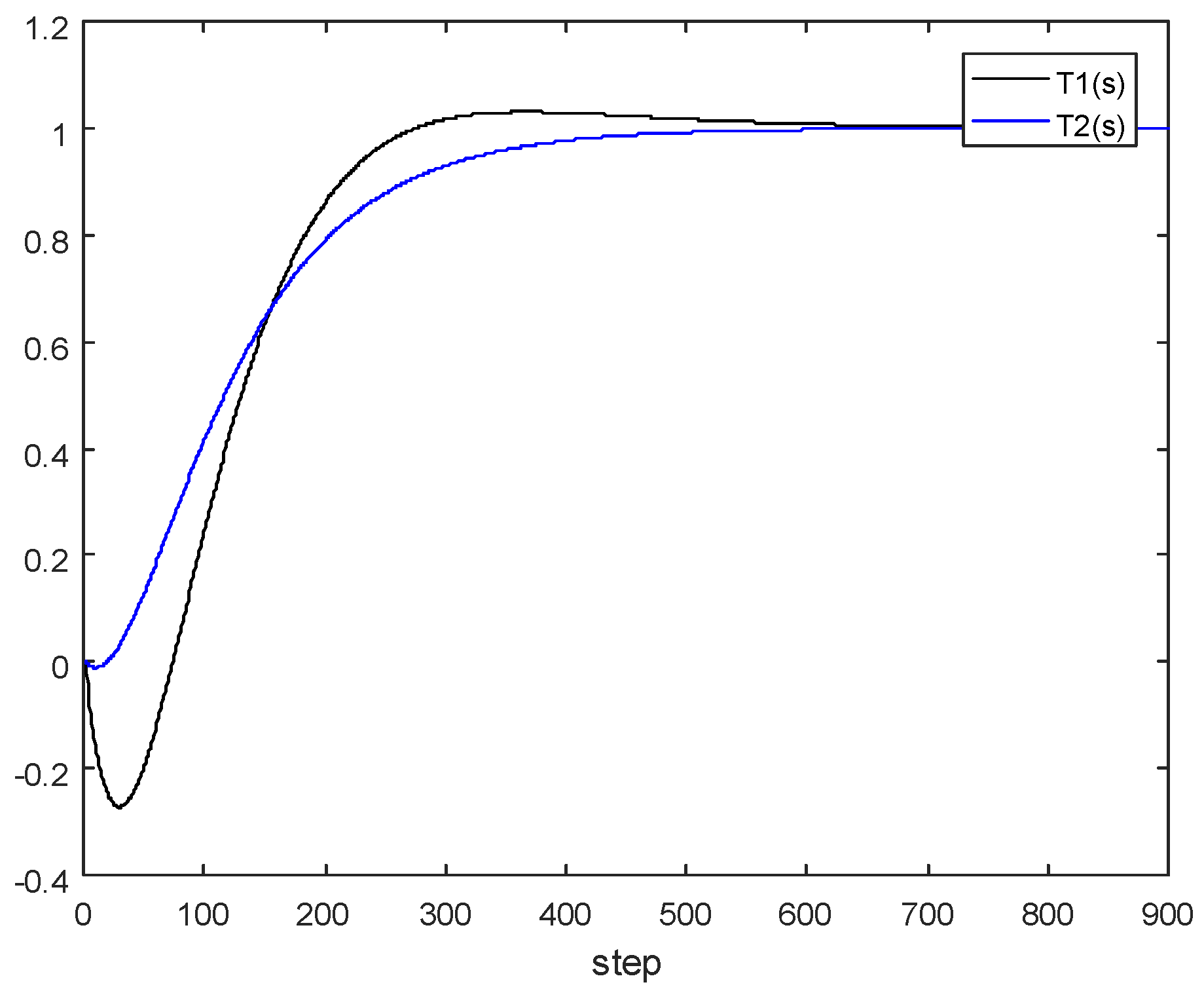
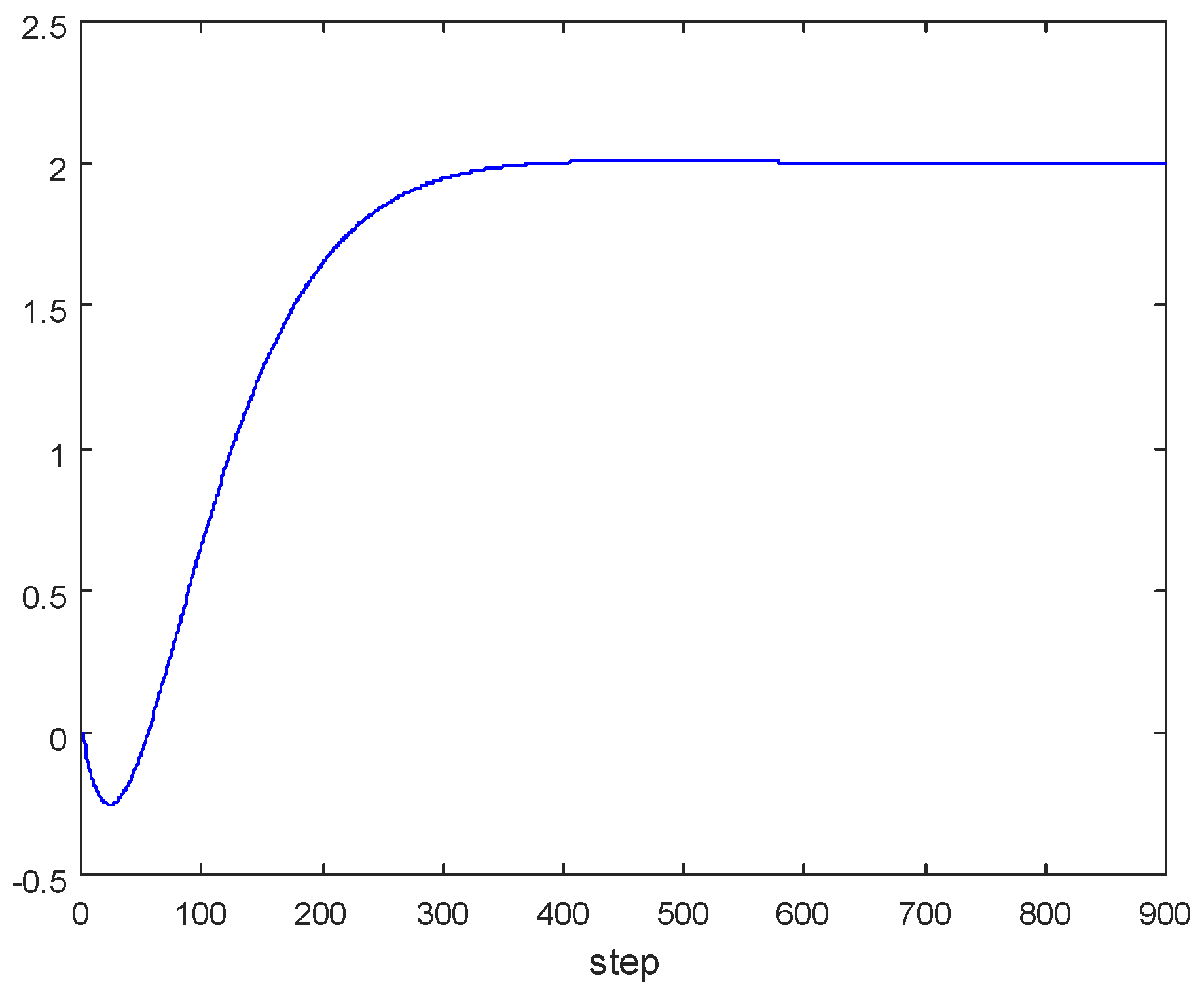
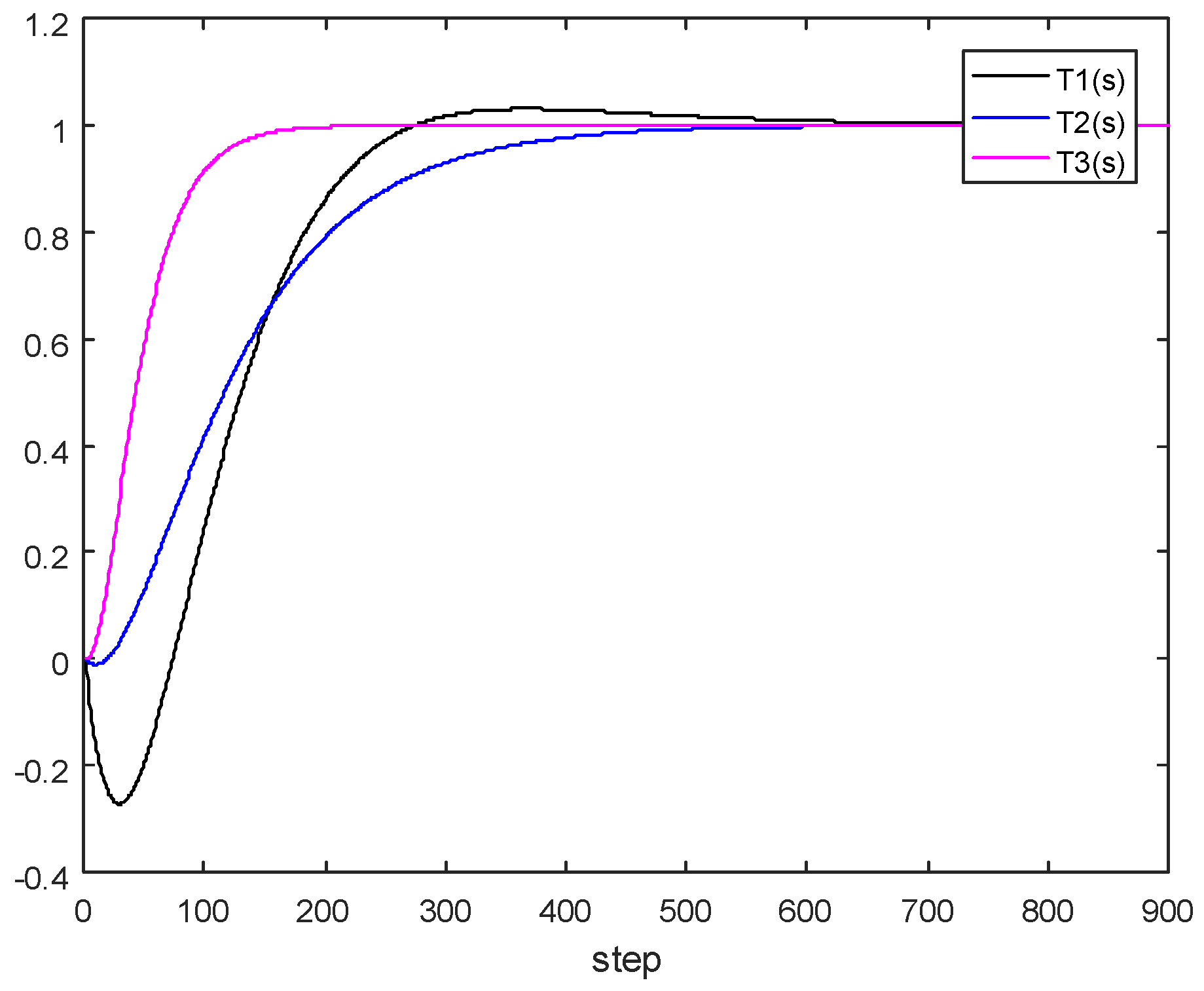
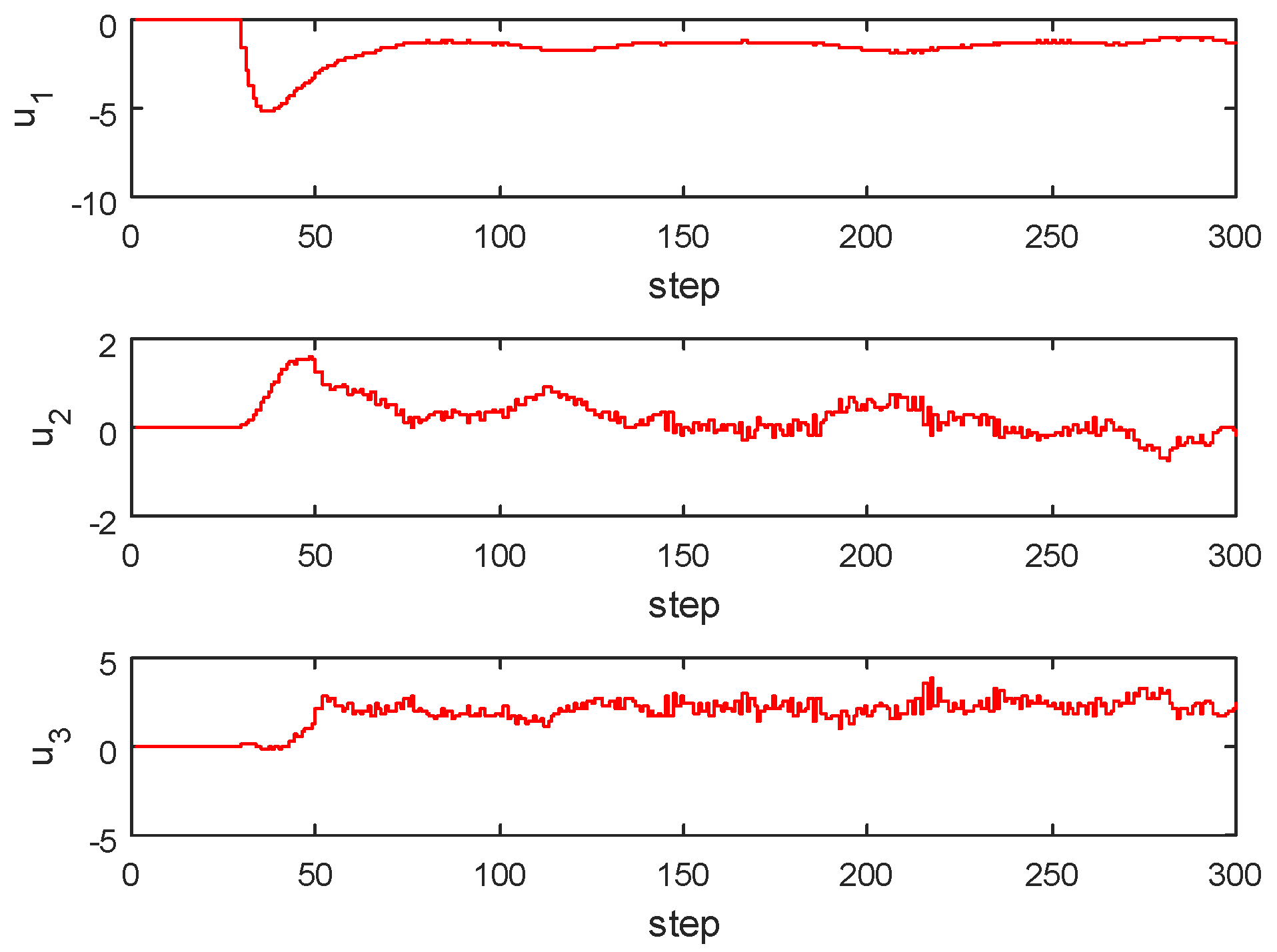
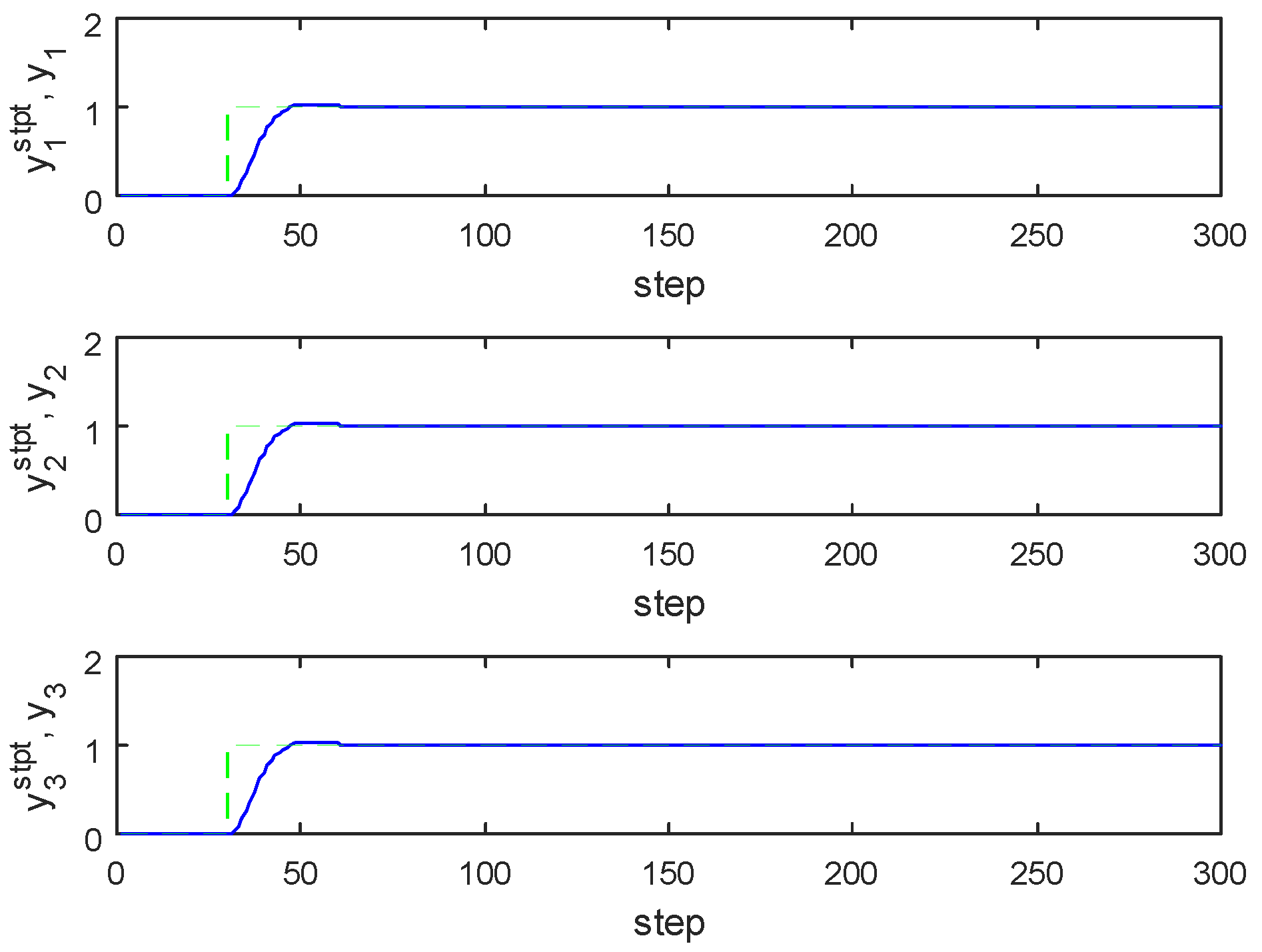
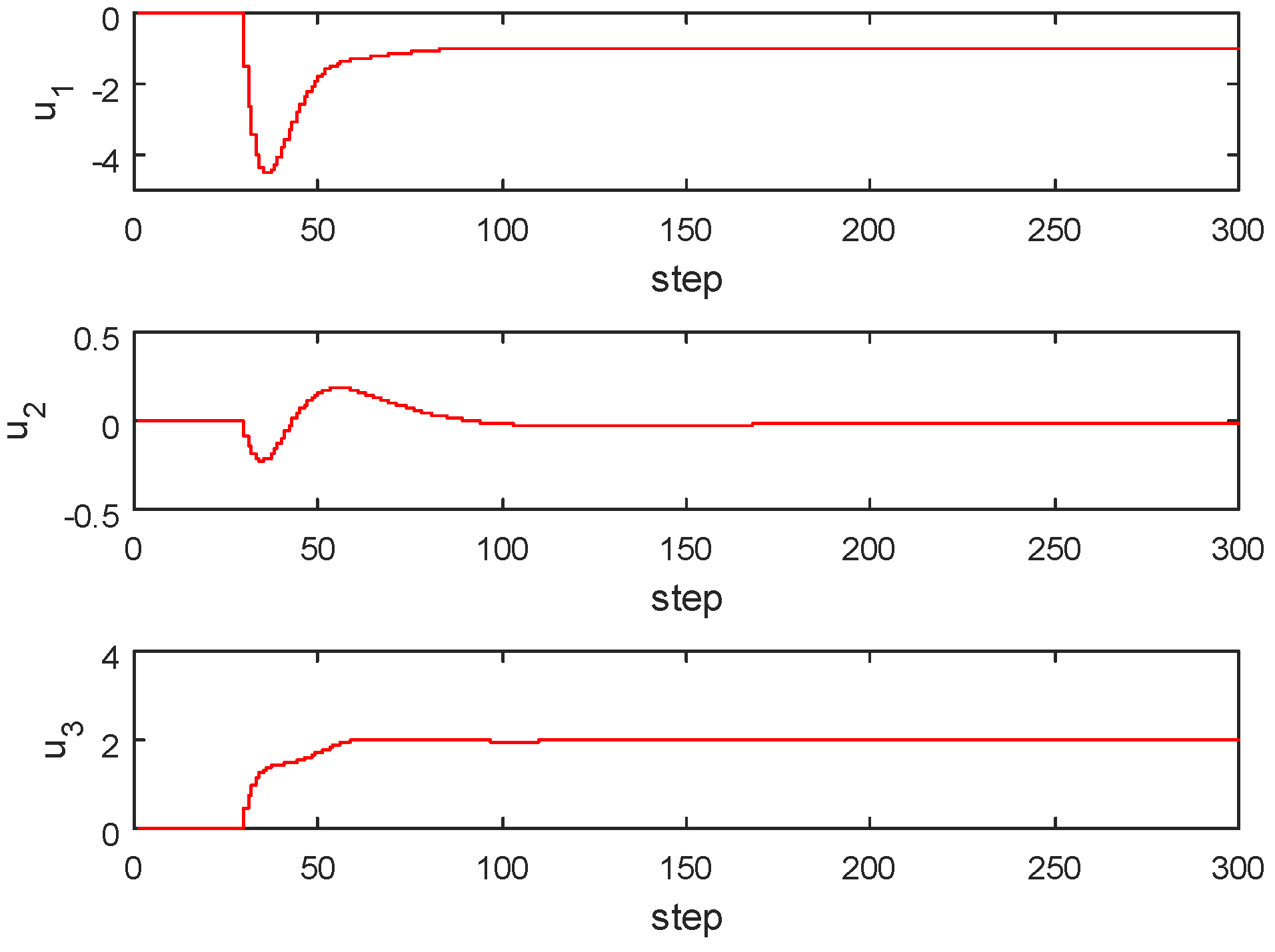
4.3. Three Input-Three Output Model
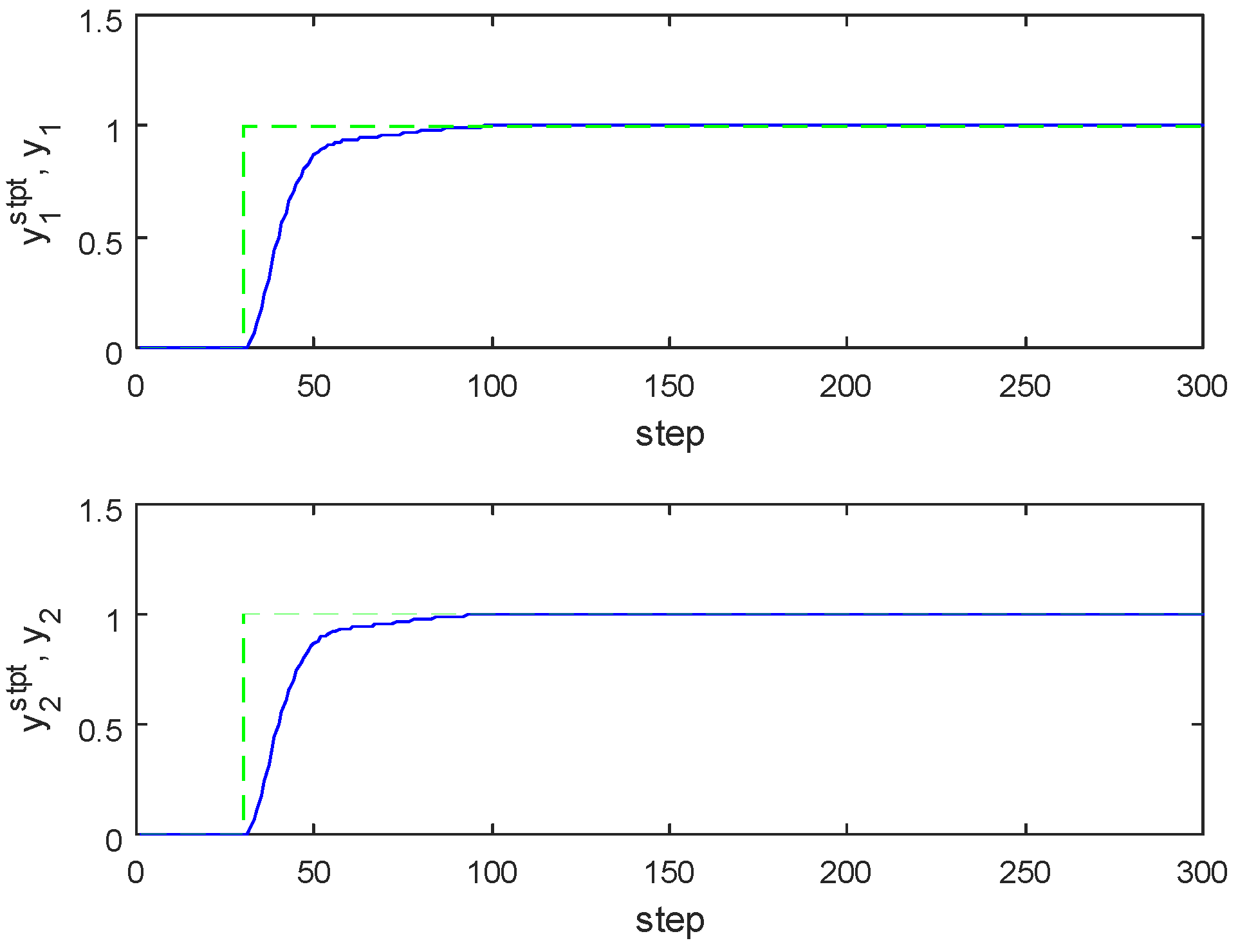
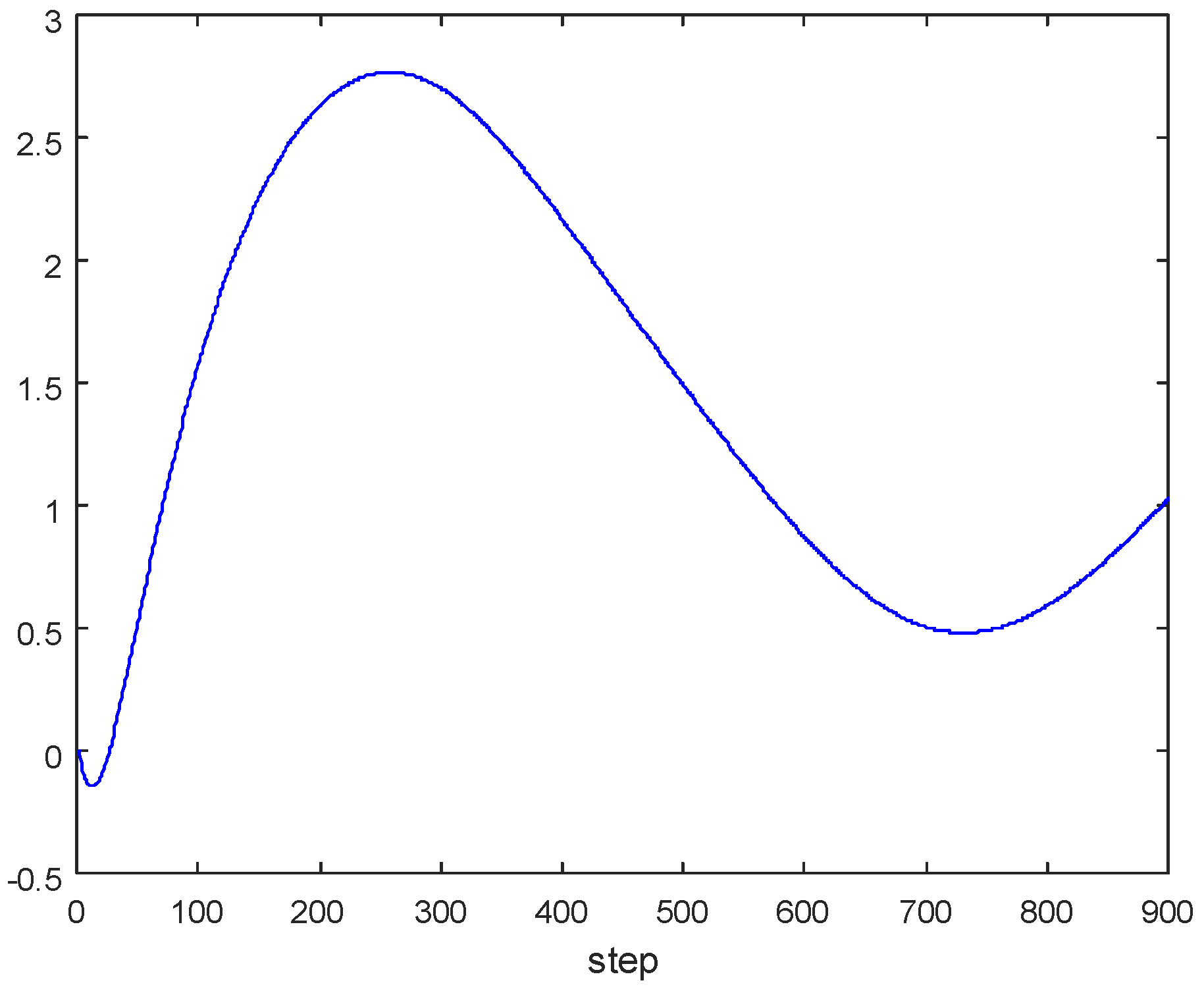
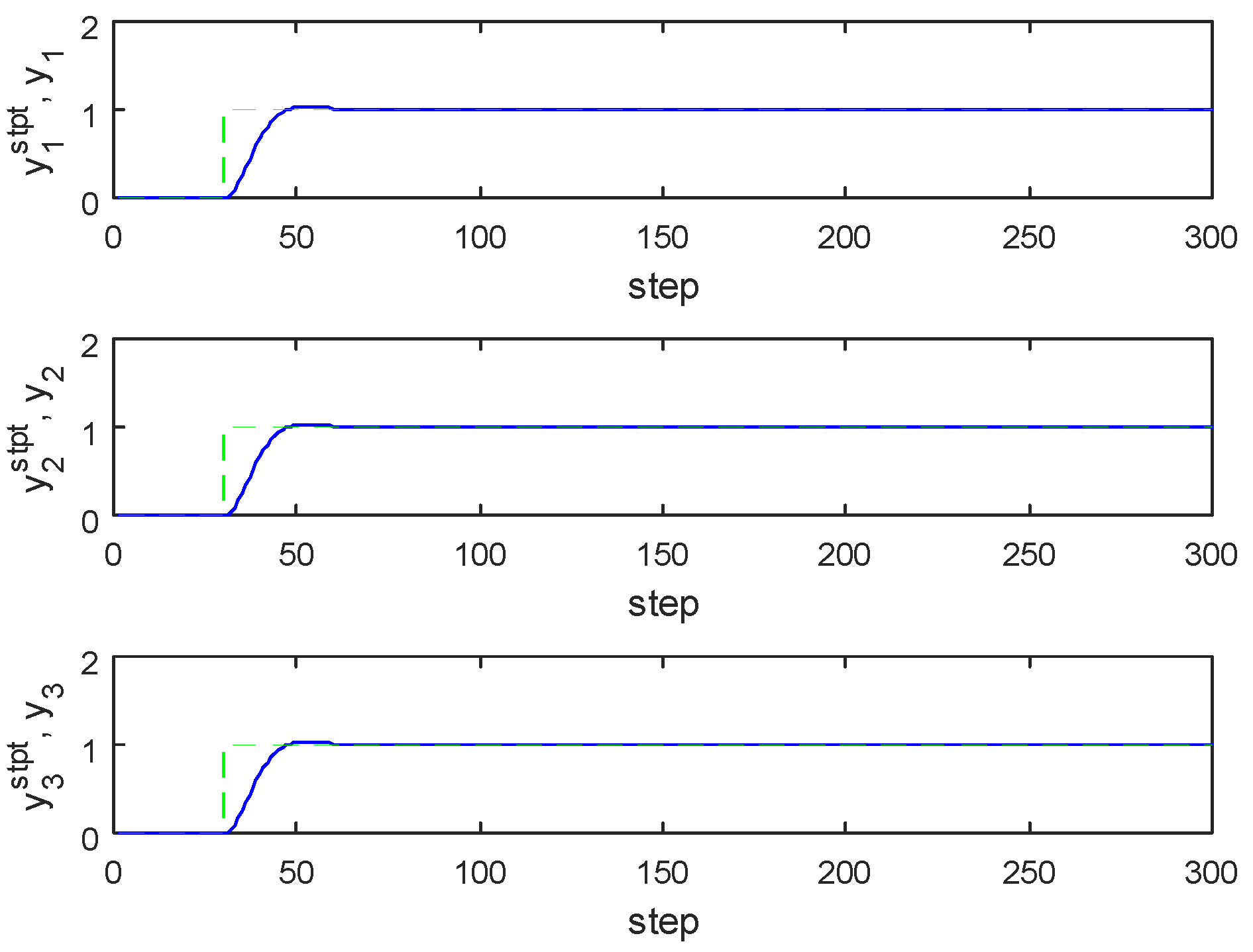
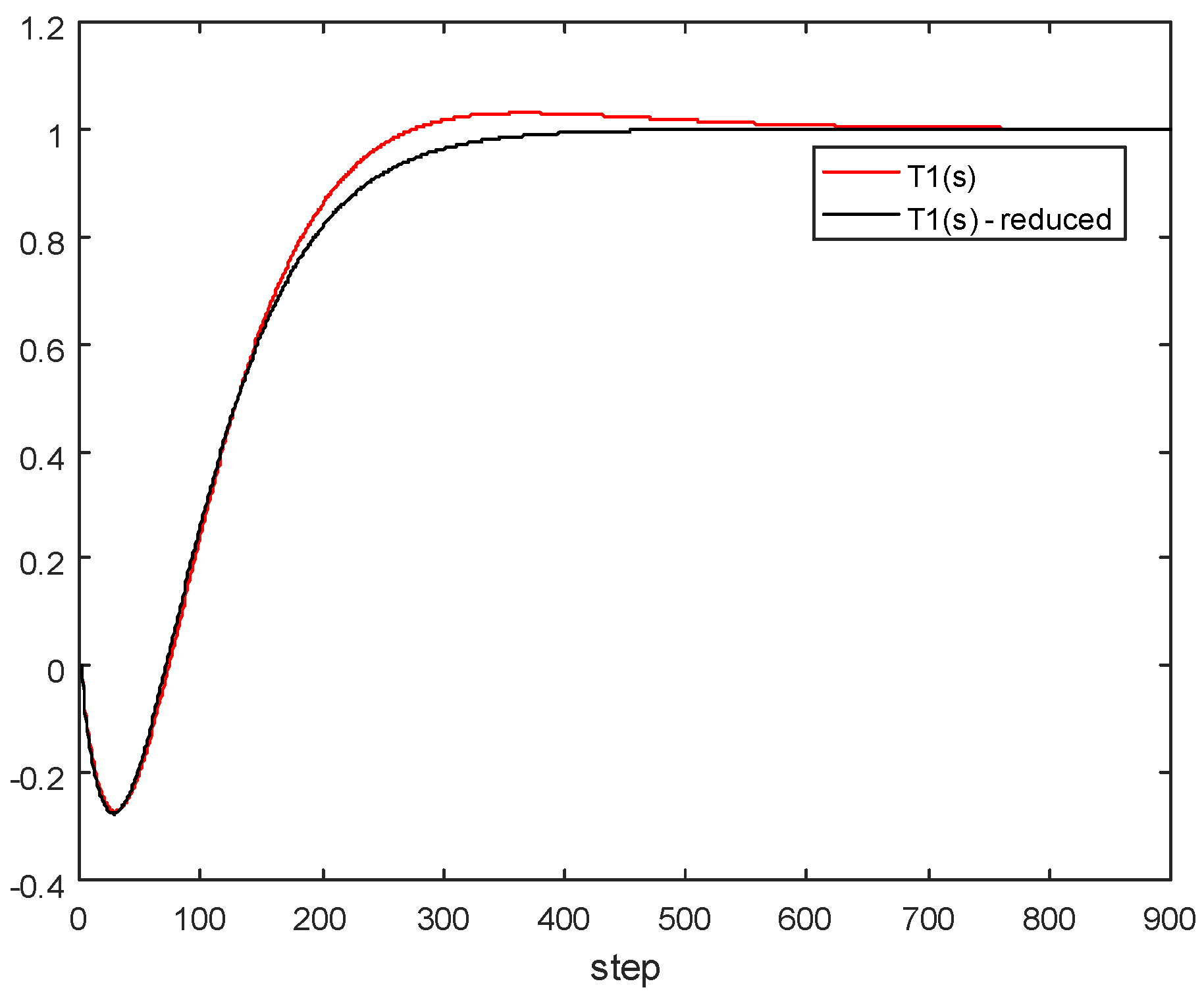
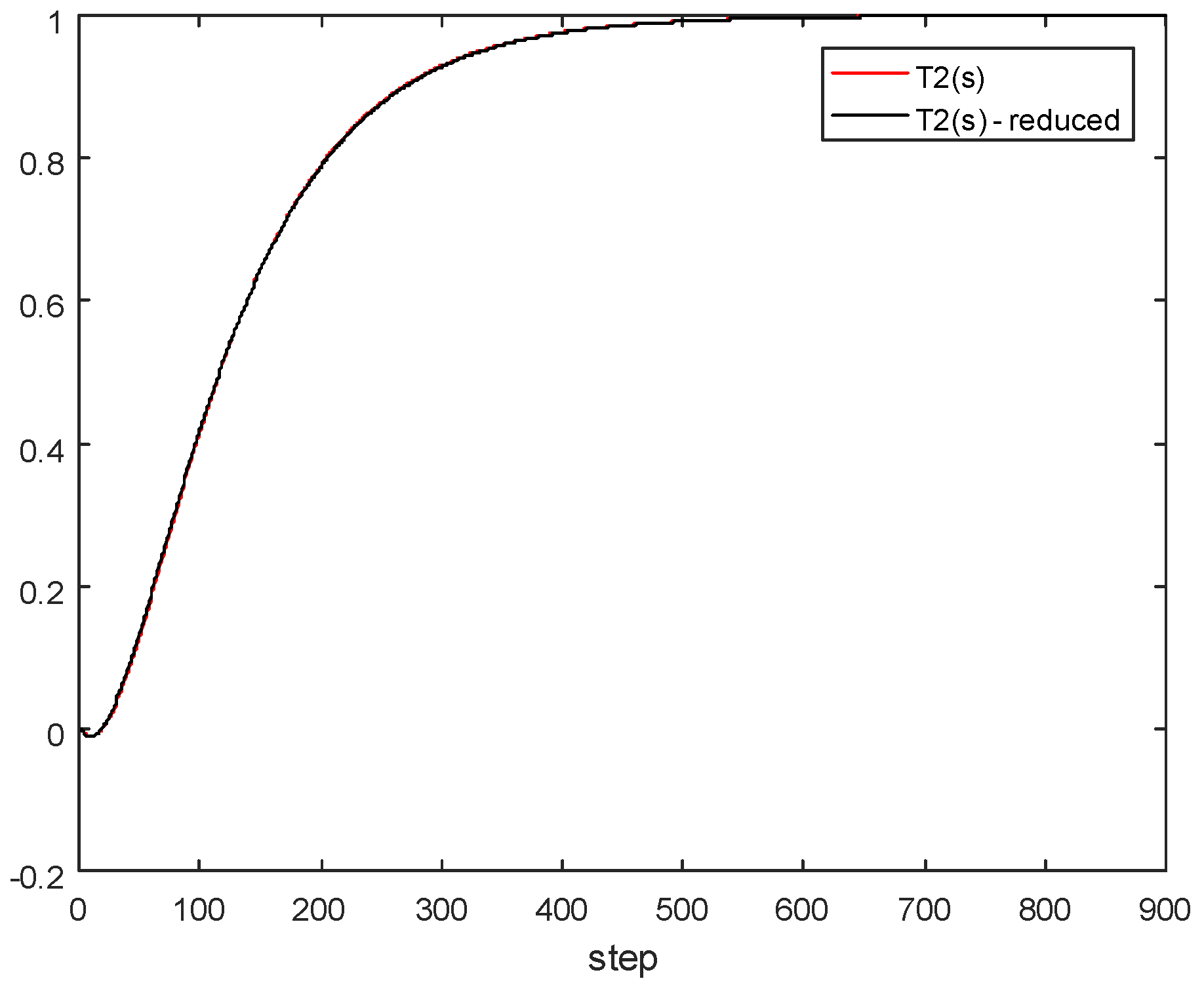
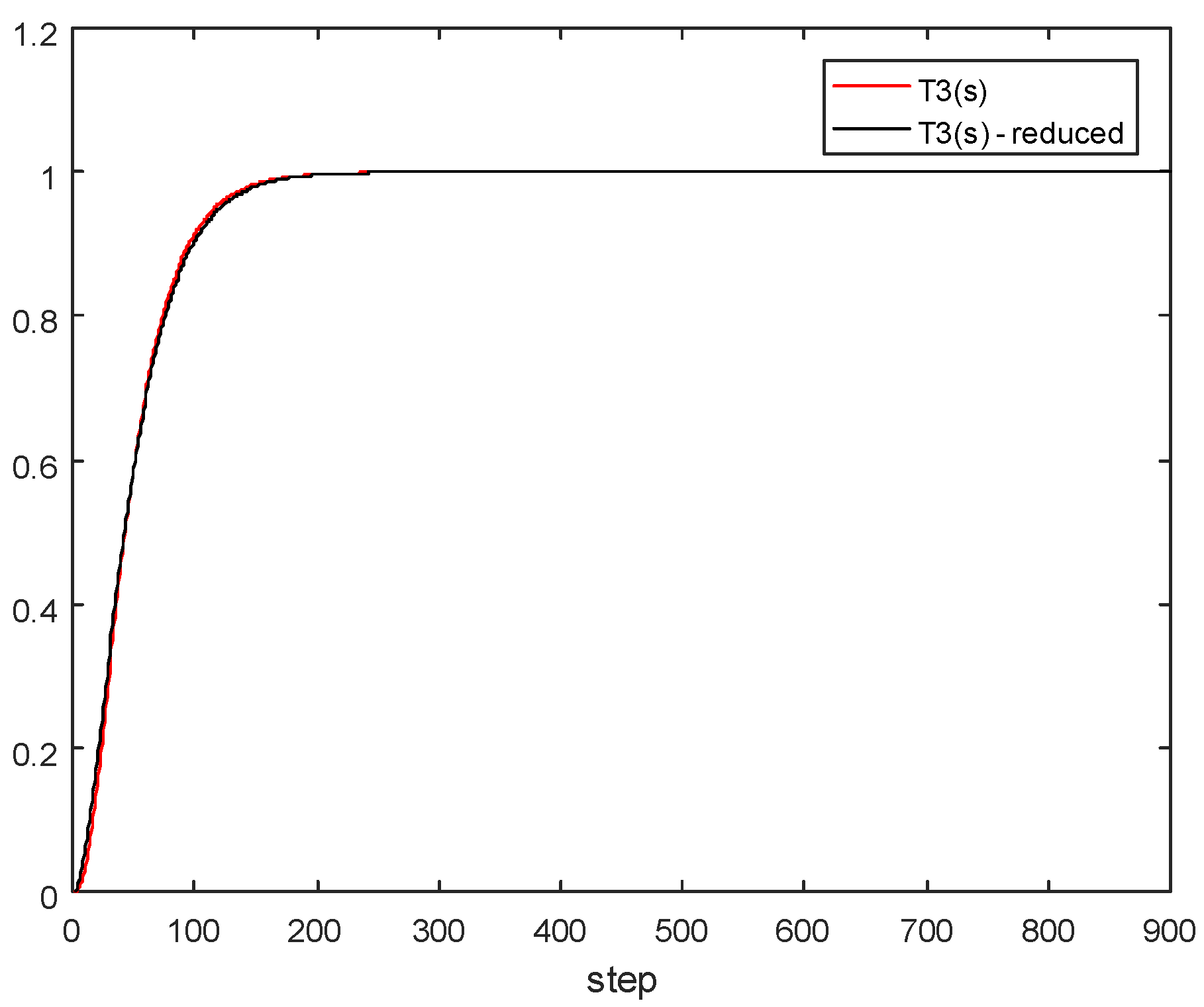
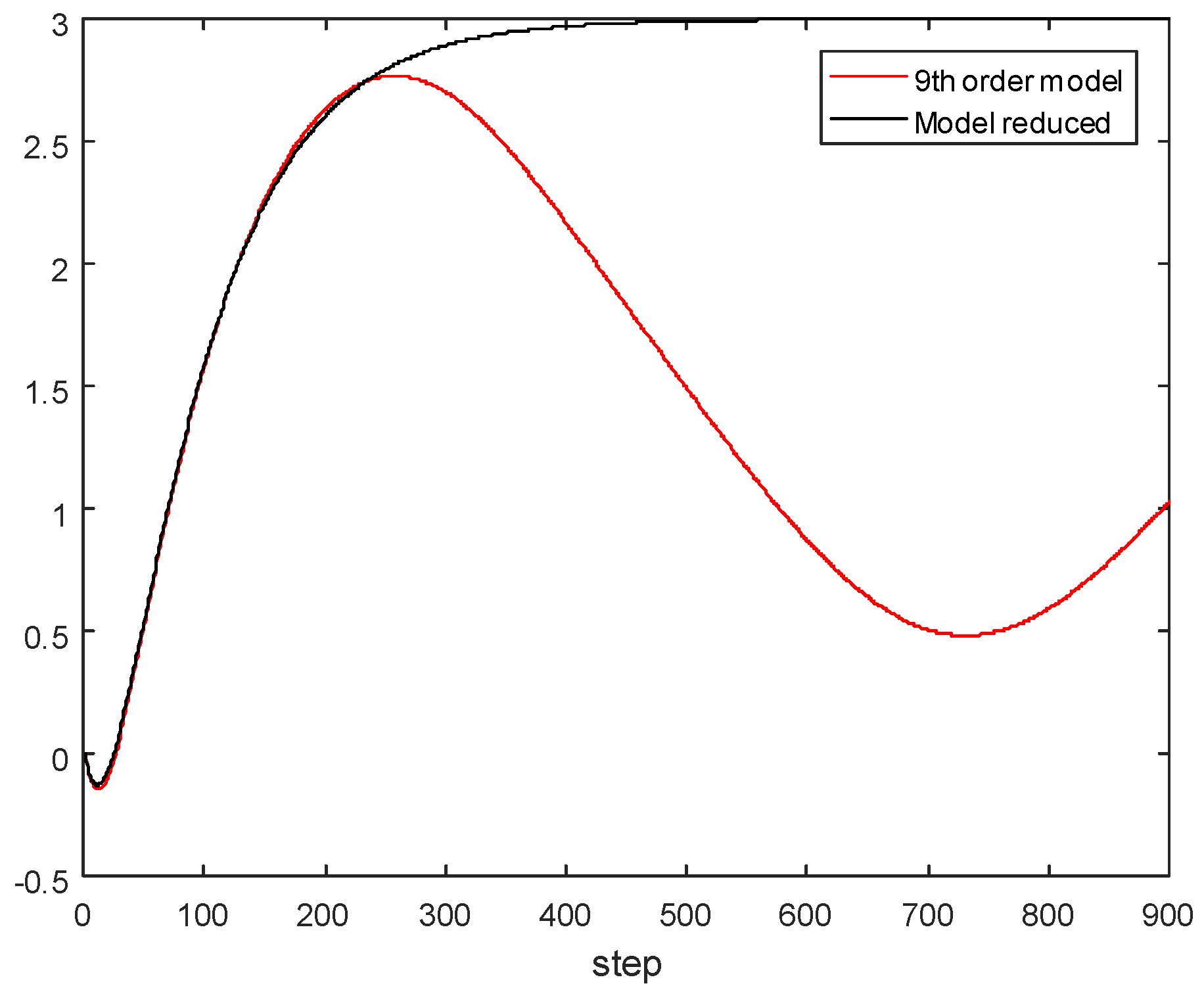
5. Model Order Reduction Method
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GPC | Generalized Predictive Control |
| MPC | Model Predictive Control |
| PID | Proportional, Integral and Derivative |
| MIMO | Multiple-Input Multiple-Output |
| SISO | Single-Input Single-Output |
| DCS | Distributed Control system |
| PLC | Programmable Logic Controllers |
| FPGA | Field Programmable Gate Arrays |
| MV | Manipulated Variable |
| CV | Controlled Variable |
| DV | Disturbance Variable |
| CRHPC | Constrained Receding Horizon Predictive Control |
| SIORHC | Stabilizing Input Output Receding Horizon Control |
| QP | Quadratic Programming |
| CPU | Central Processing Unit |
References
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 1999. [Google Scholar]
- Ławryńczuk, M. Computationally Efficient Model Predictive Control Algorithms: A Neural Network Approach, Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2014; Volume 3. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Domański, P. Performance Assessment of Predictive Control—A Survey. Algorithms 2020, 13, 97. [Google Scholar] [CrossRef]
- El Youssef, J.; Castle, J.; Ward, W.K. A Review of Closed–Loop Algorithms for Glycemic Control in the Treatment of Type 1 Diabetes. Algorithms 2009, 2, 518–532. [Google Scholar] [CrossRef]
- Sands, T. Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms 2019, 12, 232. [Google Scholar] [CrossRef]
- Forbes, M.G.; Patwardhan, R.; Hamadah, H.; Gopaluni, R. Model predictive control in in-dustry: Challenges and opportunities. IFAC PapersOnLine 2015, 48, 531–538. [Google Scholar] [CrossRef]
- Marusak, P.; Kuntanapreeda, S. A neural network-based implementation of an MPC algorithm applied in the control systems of electromechanical plants. In Proceedings of the 8th TSME–International Conference on Mechanical Engineering (TSME–ICoME), Bangkok, Thailand, 12–15 December 2017. [Google Scholar]
- Abdelaal, M.; Schön, S. Predictive Path Following and Collision Avoidance of Autonomous Connected Vehicles. Algorithms 2020, 13, 52. [Google Scholar] [CrossRef]
- Marusak, P. Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction—Application to a Chemical Reactor. Algorithms 2020, 13, 143. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Fuzzy modeling and predictive control of superheater steam temperature for power plant. ISA Trans. 2015, 56, 241–251. [Google Scholar] [CrossRef]
- Khooban, M.H.; Vafam, N.; Niknam, T. Optimal partitioning of a boiler–turbine unit for Fuzzy model predictive control. ISA Trans. 2016, 64, 231–240. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Disturbance–observer–based fuzzy model predictive control for nonlinear processes with disturbances and input constraints. ISA Trans. 2019, 90, 74–88. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Generalized Discrete–time Nonlinear Disturbance Observer Based Fuzzy Model Predictive Control for Boiler–Turbine Systems. ISA Trans. 2019, 90, 89–106. [Google Scholar] [CrossRef] [PubMed]
- Shen, D.; Lim, C.-C.; Shi, P. Robust fuzzy model predictive control for energy management systems in fuel cell vehicles. Control Eng. Pract. 2020, 98, 104364. [Google Scholar] [CrossRef]
- Killian, M.; Kozek, M. T–S fuzzy model predictive speed control of electrical vehicles. IFAC PapersOnLine 2017, 50, 2011–2016. [Google Scholar] [CrossRef]
- Marusak, P.; Tatjewski, P. Stability analysis of nonlinear control systems with unconstrained fuzzy predictive controllers. Arch. Control Sci. 2002, 12, 267–288. [Google Scholar]
- Boulkaibet, I.; Belarbi, K.; Bououden, S.; Marwala, T.; Chadli, M. A new T–S fuzzy model predictive control for nonlinear processes. Expert Syst. Appl. 2017, 88, 132–151. [Google Scholar] [CrossRef]
- Essien, E.; Ibrahim, H.; Mehrandezh, M.; Idem, R. Adaptive neuro-fuzzy inference system (ANFIS)—Based model predictive control (MPC) for carbon dioxide reforming of methane (CDRM) in a plug flow tubular reactor for hydrogen production. Therm. Sci. Eng. Prog. 2019, 9, 148–161. [Google Scholar] [CrossRef]
- Wojtulewicz, A.; Ławryńczuk, M. Computationally efficient implementation of dynamic matrix control algorithm for very fast processes using programmable logic controller. In Proceedings of the 23th IEEE International Conference on Methods and Models in Automation and Robotics (MMAR 2018), Międzyzdroje, Poland, 27–30 August 2018; pp. 579–584. [Google Scholar]
- Plamowski, S. Implementation of DMC algorithm in embedded controller—Resources, memory and numerical modifications. In Proceedings of the KKA 2017—The 19th Polish Control Conference, Kraków, Poland, 18–21 June 2017; pp. 335–343. [Google Scholar]
- Chaber, P.; Ławryńczuk, M. Fast analytical model predictive controllers and their implementation for STM32 ARM microcontroller. IEEE Trans. Ind. Inform. 2019, 15, 4580–4590. [Google Scholar] [CrossRef]
- Wojtulewicz, A.; Ławryńczuk, M. Implementation of Multiple-Input Multiple-Output Dynamic Matrix Control Algorithm for Fast Processes Using Field Programmable Gate Array. In Proceedings of the 15th IFAC Conference on Programmable Devices and Embedded Systems PDeS, Ostrava, Czech Republic, 23–25 May 2018; pp. 324–329. [Google Scholar]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Salez, D.; Cipriano, A.; Ordys, A.W. Optimisation of Industrial Processes at Supervisory Level; Springer: London, UK, 2002. [Google Scholar]
- Tatjewski, P. Advanced Control of Industrial Processes; Springer: London, UK, 2007. [Google Scholar]
- Findeisen, W. Control and Coordination in Hierarchical Systems, Chichester (Eng.); John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Kayacan, E.; Peschel, J. Robust Model Predictive Control of Systems by Modelling Mismatched Uncertainty. IFAC-PapersOnLine 2016, 49, 265–269. [Google Scholar] [CrossRef]
- Plamowski, S.; Tatjewski, P. Safe implementation of advanced control in a diagnostic-based switching structure. In Proceedings of the 6th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, Beijing, China, 30 August–1 September 2006; pp. 487–495. [Google Scholar]
- Clarke, D.W.; Mohtadi, C.; Tuffs, S. Generalized predictive control—Parts I and II. Automatica 1987, 23, 137–160. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mohtadi, C. Properties of generalized predictive control. Automatica 1989, 25, 859–875. [Google Scholar] [CrossRef]
- Gorez, R.; Wertz, V.; Zhu, K.Y. On a generalised predictive control algorithm. Syst. Control Lett. 1987, 9, 369–377. [Google Scholar] [CrossRef]
- Grimble, M.J. Generalized predictive optimal control: An introduction to the advantages and limitations. Int. J. Syst. Sci. 1992, 23, 85–98. [Google Scholar] [CrossRef]
- Clarke, D.W.; Scattolini, R. Constrained receding-horizon predictive control. IEE Proc. D 1991, 138, 347–354. [Google Scholar] [CrossRef]
- Bemporad, A.; Chisci, L.; Mosca, E. On the stabilizing property of SIORHC. Automatica 1994, 30, 2013–2015. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice Hall: London, UK, 2002. [Google Scholar]
- Hughes, P.C.; Skelton, R. Modal truncation for flexible spacecraft. J. Guid. Control 1981, 4, 291–297. [Google Scholar]
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Enns, D. Model reduction with balanced realizations: An error bound and a frequency weighted generalization. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; Volume 23, pp. 127–132. [Google Scholar]
- Anderson, B.; Liu, Y. Controller reduction: Concepts and approaches. IEEE Trans. Autom. Control 1989, 34, 802–812. [Google Scholar] [CrossRef]
- Astolfi, A. Model Reduction by Moment Matching for Linear and Nonlinear Systems. IEEE Trans. Autom. Control 2010, 55, 2321–2336. [Google Scholar] [CrossRef]
- Glover, K. All optimal Hankel-norm approximations of linear multivariable systems and their L∞-error bounds. Int. J. Control 1984, 39, 1115–1193. [Google Scholar] [CrossRef]
- Willcox, K.; Peraire, J. Balanced model reduction via the proper orthogonal decomposition. AIAA J. 2002, 40, 2323–2330. [Google Scholar] [CrossRef]
- Kubalčik, M.; Bobál, V. Predictive control of higher order systems approximated by lower order time-delay models. WSEAS Trans. Syst. 2012, 11, 607–616. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plamowski, S.; Kephart, R.W. The Model Order Reduction Method as an Effective Way to Implement GPC Controller for Multidimensional Objects. Algorithms 2020, 13, 178. https://doi.org/10.3390/a13080178
Plamowski S, Kephart RW. The Model Order Reduction Method as an Effective Way to Implement GPC Controller for Multidimensional Objects. Algorithms. 2020; 13(8):178. https://doi.org/10.3390/a13080178
Chicago/Turabian StylePlamowski, Sebastian, and Richard W Kephart. 2020. "The Model Order Reduction Method as an Effective Way to Implement GPC Controller for Multidimensional Objects" Algorithms 13, no. 8: 178. https://doi.org/10.3390/a13080178
APA StylePlamowski, S., & Kephart, R. W. (2020). The Model Order Reduction Method as an Effective Way to Implement GPC Controller for Multidimensional Objects. Algorithms, 13(8), 178. https://doi.org/10.3390/a13080178



