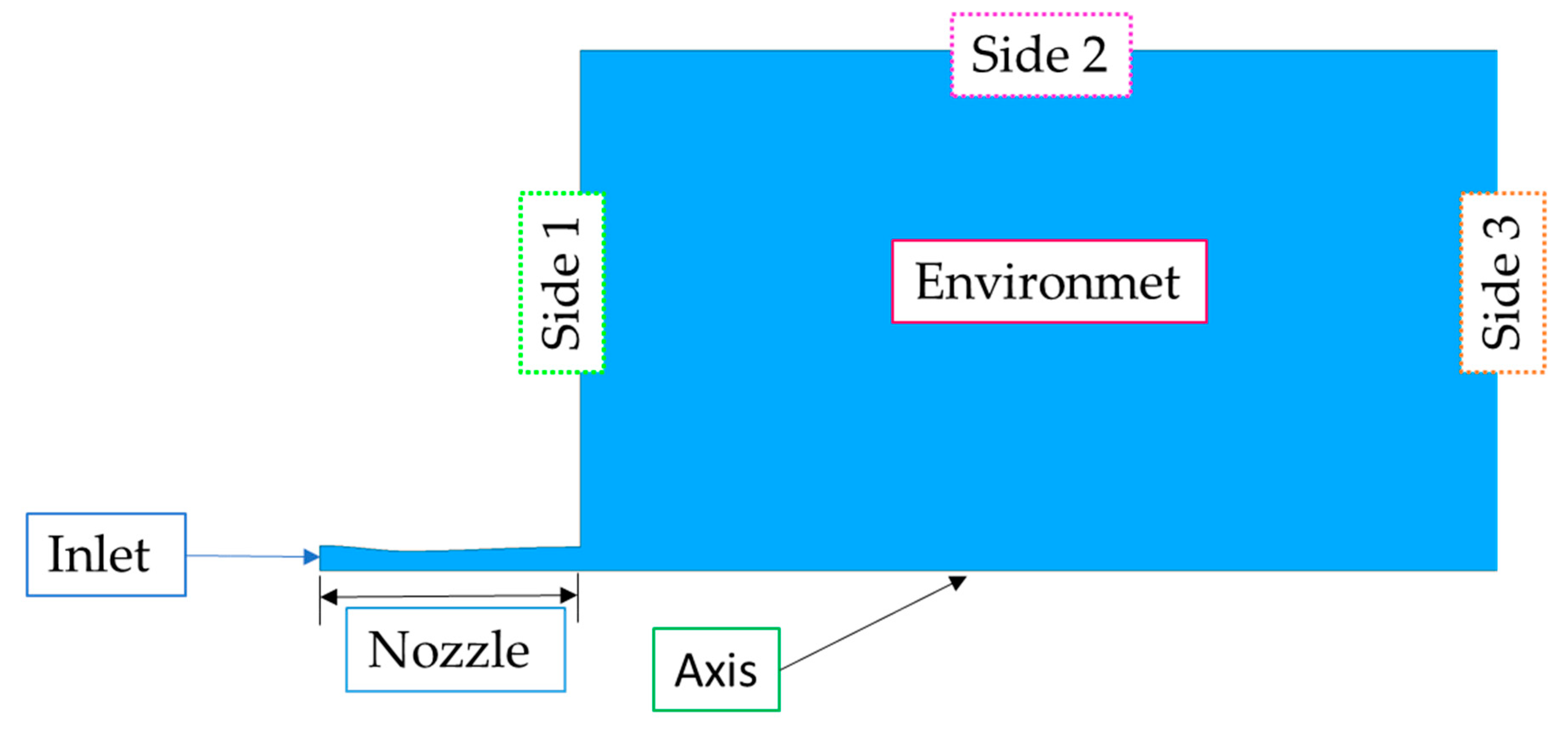
3.1. Sensitivity Analysis on Discharge Pressure
The value of the discharge pressure p
s has a remarkable impact on the nozzle flow structure, especially in determining the position and strength of the shock wave: this is evident referring to the ‘r2’ condition where the shock wave is positioned at the nozzle exit section [
8]. As a proof of the reliability of the CFD model, similar results have been obtained in similar conditions in the experimental case by Zapryagaev et al. [
22].
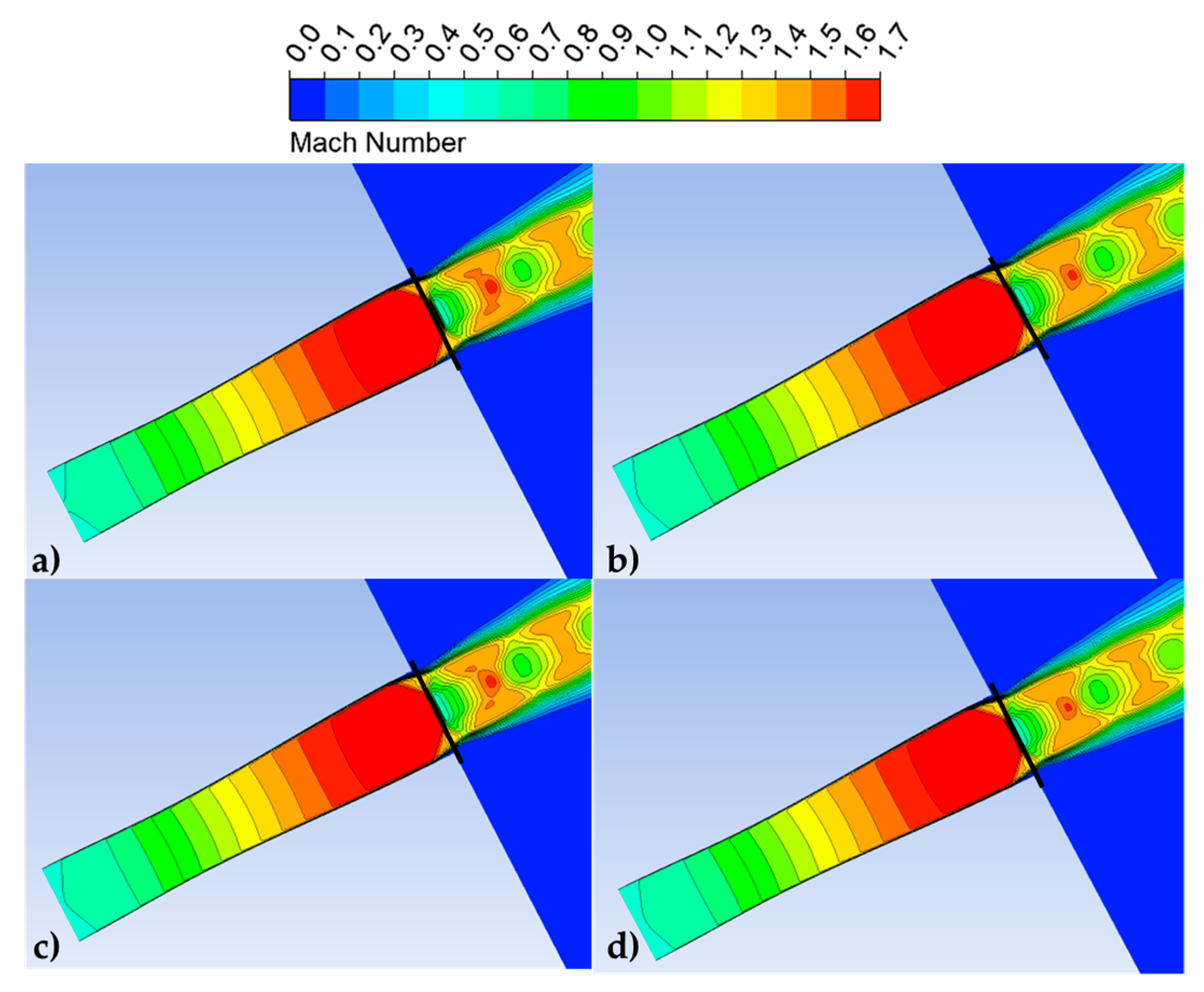
Figure 3 shows Mach number contours for five different p
s values (80 kPa ÷ 120 kPa) around the ‘r2’ condition. The flow structure and the shock wave location change significantly even with a small Δ of 10 kPa (about 10% of the pressure range mean value).
The performance variation of the nozzle within the above range is further confirmed by the charts in
Figure 4, which represent the Mach and the Pressure Ratio (PR) along the nozzle axis (Equation (2)).
It is evident that the position of the shock wave close to the nozzle exit is affected by the small change in the environment discharge static pressure. Another important parameter, which confirms the performance variation, is the Δp
t (Equation (3)) i.e., the total pressure drop through the nozzle that quantifies the mechanical losses due to viscous or compressible flow effects. In
Table 2, the large variation of this quantity was reported: losses tend to decrease with outlet static pressure in a non-linear way (see the difference between cases 1 and 2 compared to 2 and 3); this is related to the shock wave location (inside/outside the convergent–divergent).
This off-design behavior makes the UQ analysis useful to study the component response to a non-deterministic input variable.
3.2. Uncertainty Quantification Analysis
A UQ analysis was carried out considering the discharge pressure as the variable parameter. The Quantities of Interest (QoI) considered as output performance parameters are the Mach number at the nozzle exit (M
exit) and the total pressure drop (Δp
t). With a fully automated procedure implemented in the Dakota environment, a DoE for the two QoI based on LHS method was performed for the pressure range 80–120 [kPa]. The outlet static pressure values provided by Dakota, according to LHS scheme, were used as the input variable in Fluent CFD software, which allowed us to obtain the corresponding response functions values (see
Figure 5). In order to approximate the ‘physical’ (numerical) model, 121 samples were chosen inside the design space. Equations (4)–(6) show the response functions in the normalized form:
Kriging or ‘Gaussian Process’ Response Surface Methodology is considered and the response surfaces for the above functions were generated from the training points given by the DoE. The UQ analysis was then performed through Latin Hypercube sampling method, considering 1000 samples taken on the generated response surfaces.
In order to ensure the meta-model reliability, a cross-validation analysis was performed. In Dakota, the type of cross-validation which can be exploited is the k-fold cross-validation: at first, the DoE dataset is divided into k partitions and k meta-models are generated, each excluding the
k-th partition of training data. Each surrogate is tested at the points that were excluded in its generation and the user-specified diagnostic metrics are computed with respect to the held out data [
14]. In this work, a particular type of k-fold cross-validation was performed, i.e., the Leave-one-out cross-validation or Prediction Error Sum of Squares (PRESS). In this special case, the number of partitions is equal to the number of data points. The results obtained from this analysis, reported in
Table 3, include the Root Mean Squared, the Mean Absolute Value and the Maximum Absolute Value of the prediction error (calculated between the observed value and the surrogate model prediction for the training data points).
Moreover, three random operating points were selected from the UQ database of 1000 samples, and then, simulated with the CFD solver. The corresponding fluid dynamics results for the QoI were given in input to Dakota as a challenge set of data. The metrics calculated with respect to this dataset are reported in
Table 4.
The outcomes of the previous analyses were supplemented by the calculation of the relative percentage error (
Table 5) between the CFD and the surrogate model response function values. The obtained results certify the reliability of the meta-model.
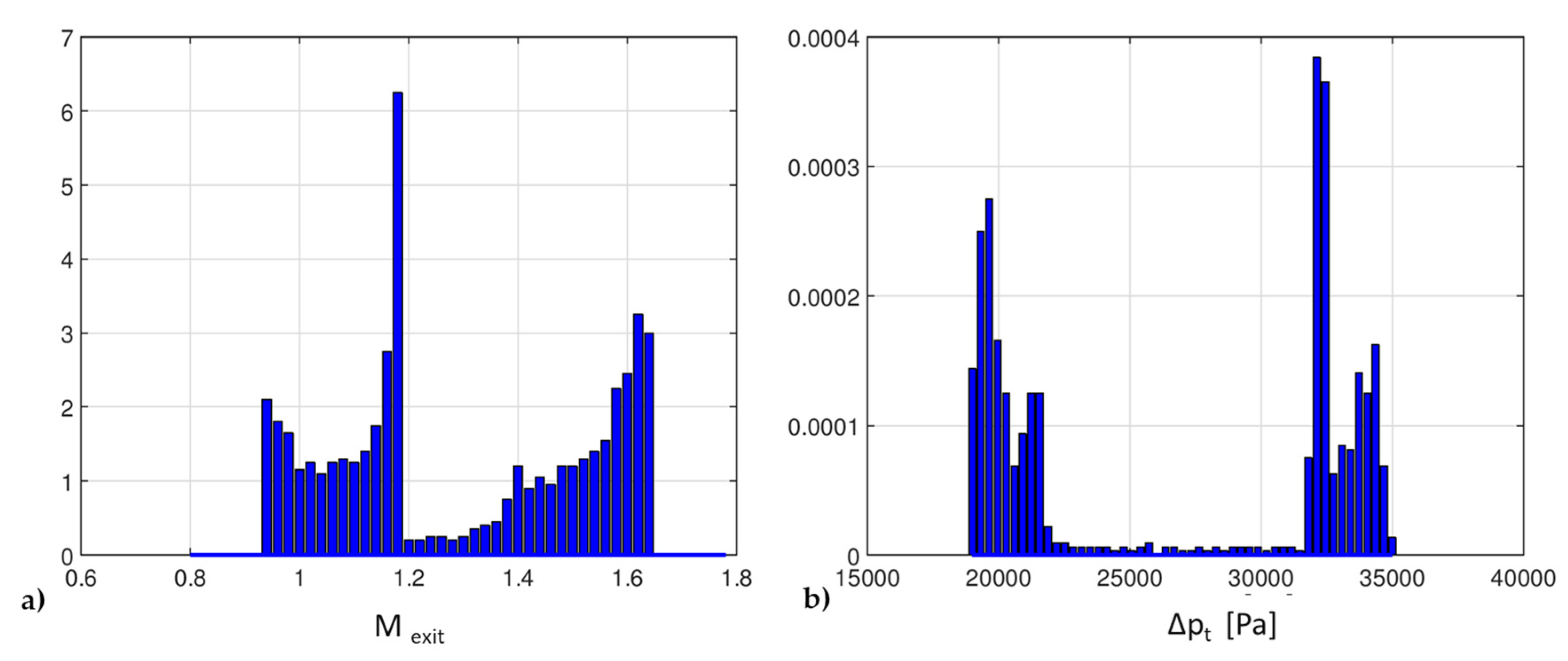
At first, a uniform distribution of the p
s variable were considered as the input probability density function (pdf): in this case, any pressure values within the established range have the same probability. Results of the uncertainty propagation through the surrogate model are the output functions (M
exit and Δp
t) discretized pdfs, reported in
Figure 6. It is evident that the pdfs of the QoI are very far from the uniform distribution of the input variable (p
s). The physical explanation of these non-uniform pdfs can be found, considering that the ‘r2’ state matches with the case p
s = 100 [kPa], i.e., the mean of the uncertain input variable distribution. Around this value, two kinds of solutions are highly probable, as evidenced by the exit Mach and Δp
t pdfs (
Figure 6):
This means that even with a large variation of the input variable, the most frequent flow structures can be restricted to two main ranges of M exit and Δpt.
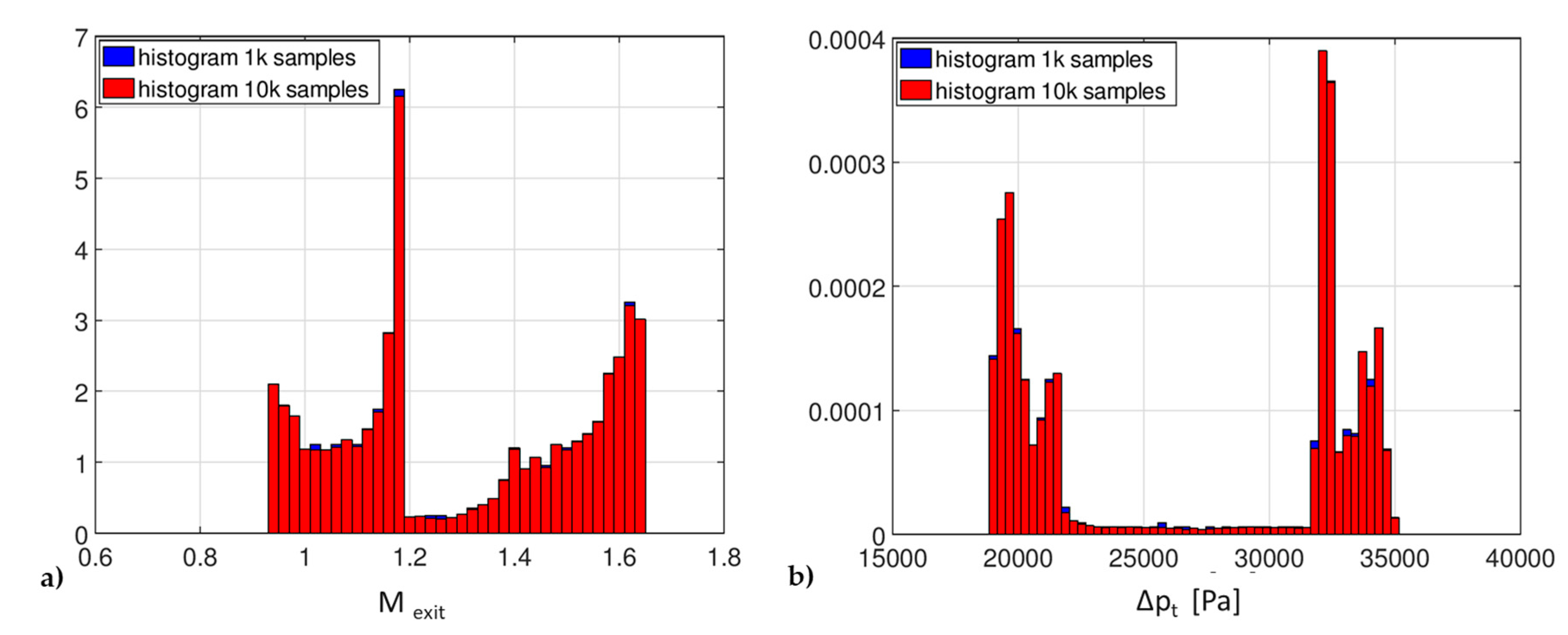
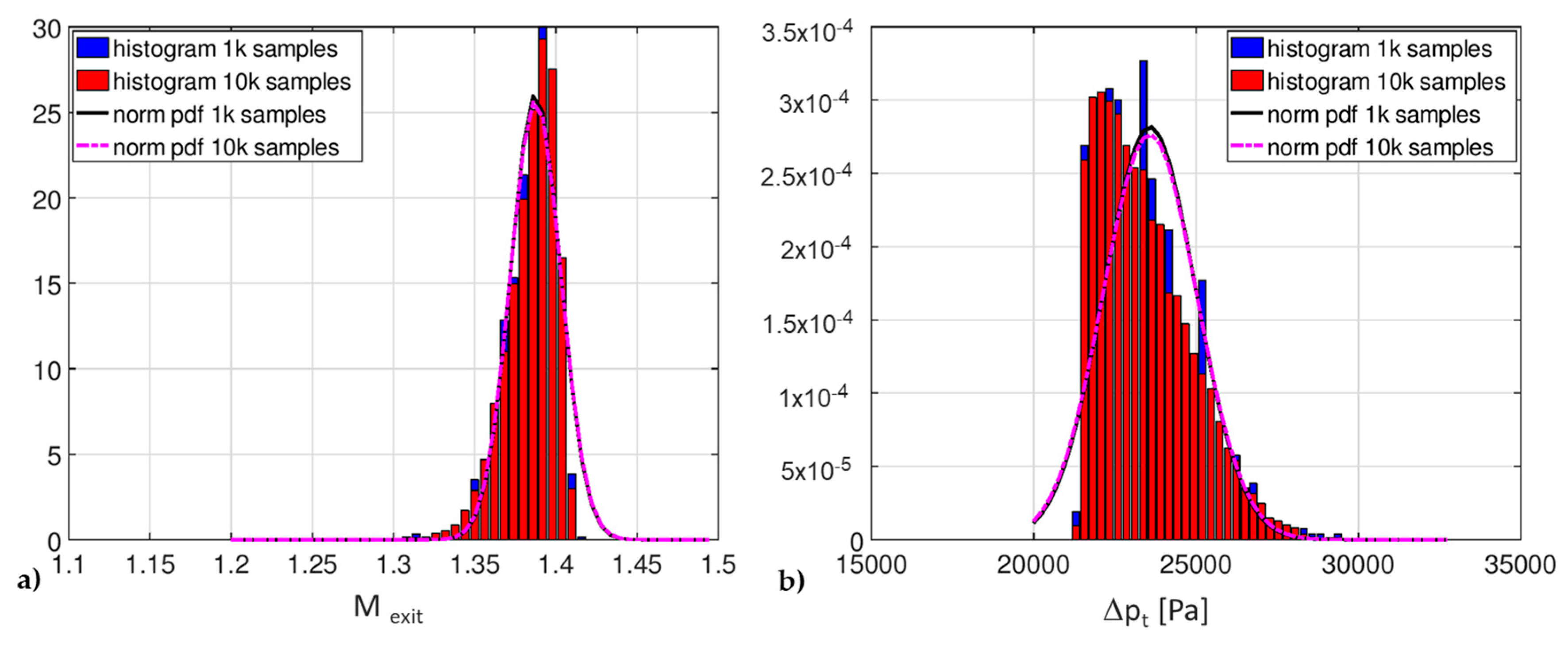
In order to provide more reliable results for the UQ analysis, a second case with an increased number of samples (10,000, one order of magnitude greater than the previous one) was considered. The comparison among the histograms obtained for the QoI is reported in
Figure 7: differences between the two distributions can be detected, but they are so small that the 1000 samples UQ analysis can be considered satisfactory.
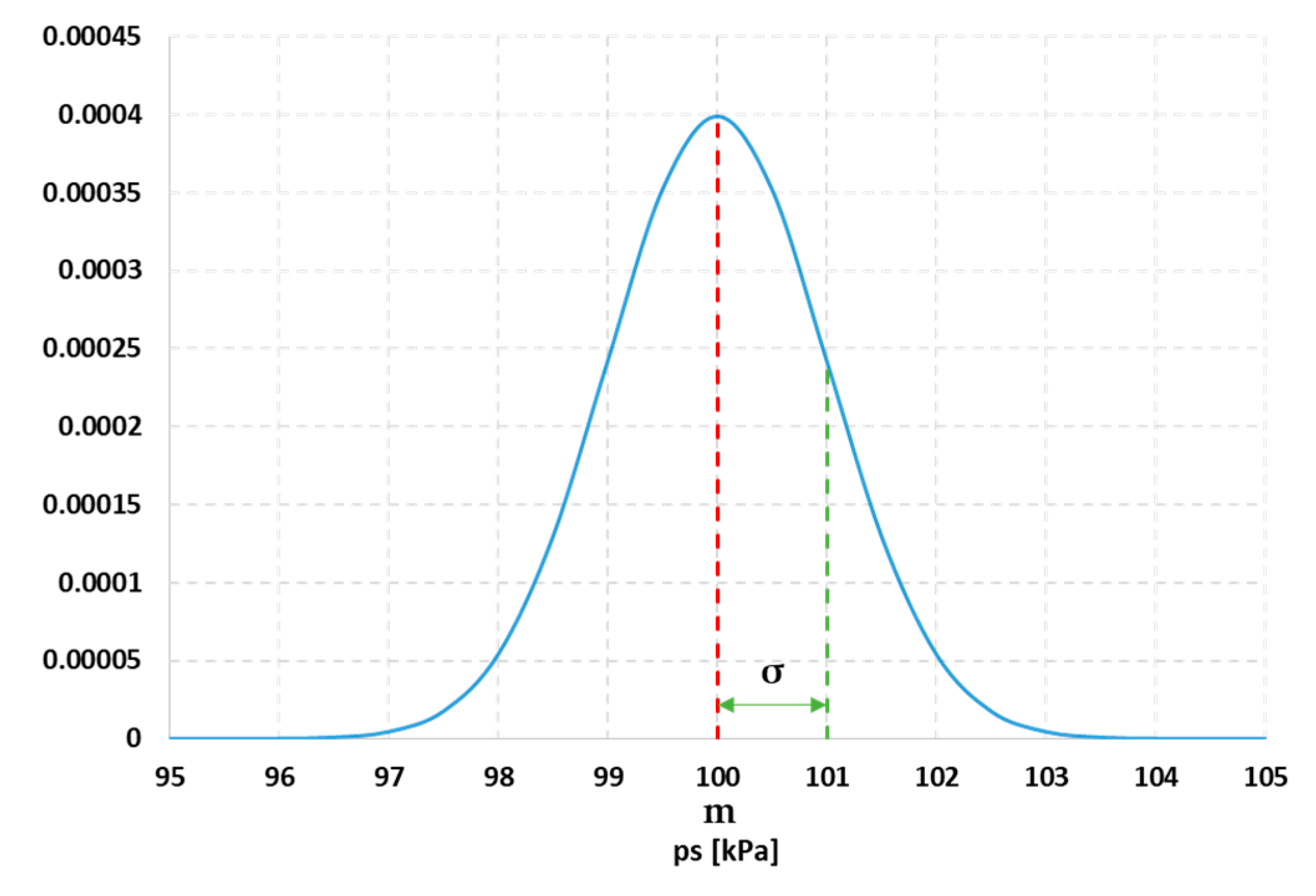
Another case was performed, assigning a normal distribution for the input pdf with a mean value ‘m’ (100 [kPa]) centered on the previously considered variation range and a standard deviation σ chosen in order to have a small perturbation of the pressure: e.g., σ ≈ 1% of the mean value. The resulting pdf for the input variable ps is shown in
Figure 8.
Using again the LHS method for the uncertainty quantification propagation (1000 samples as before), the distributions reported in
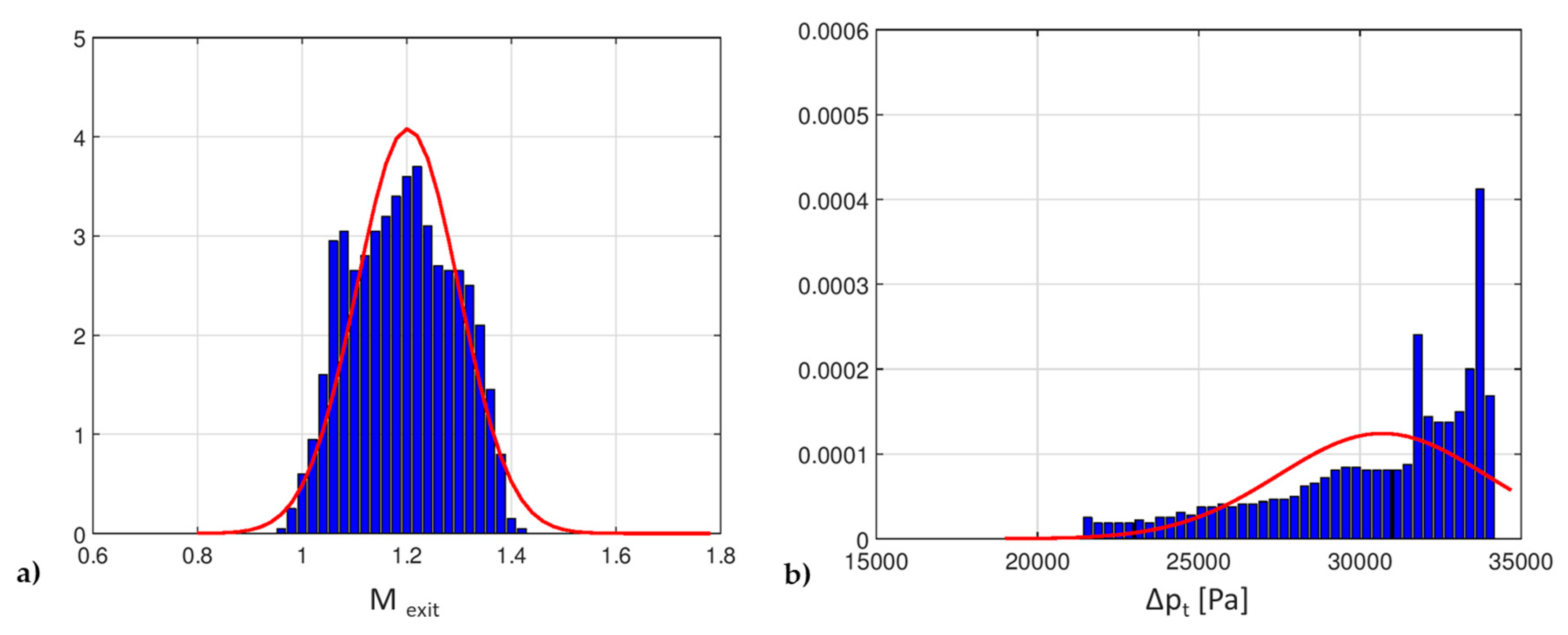
Figure 9 are obtained for the response functions. It is evident, especially for the losses, that even in this case, the output pdfs are different from the input one (normal distribution).
Table 6 summarizes the data of the statistical moments calculated for these distributions. The red curves over the histograms of
Figure 9 represent the reference Gaussian continuous distributions associated with the mean and standard deviation values of each discretized distribution obtained from Dakota. Comparing to the normal pdf (in red), the M
exit distribution is more flat (negative value of Kurtosis) and slightly asymmetrical. The distribution of the total pressure drop is shifted to the right (negative Skewness) and sharper (positive Kurtosis) with respect to the Gaussian pdf.
The results analysis suggests that in this case, the values of the QoI are spread over a wider range of values. Hence, a small variation in the input discharge pressure (with respect to r2 discharge pressure which is approximately 100 [kPa]) can change drastically the operative condition, and consequently, the nozzle performance.
The comparison between the pdf histograms for the QoI in both cases of 1000 and 10,000 samples is reported in
Figure 10. Even in this case, it can be observed that the increase in the number of samples used for the LHS method has no remarkable influence on the pdfs and on the corresponding normal distributions, which remain almost unchanged.