Image Resolution Enhancement of Highly Compressively Sensed CT/PET Signals
Abstract
1. Introduction
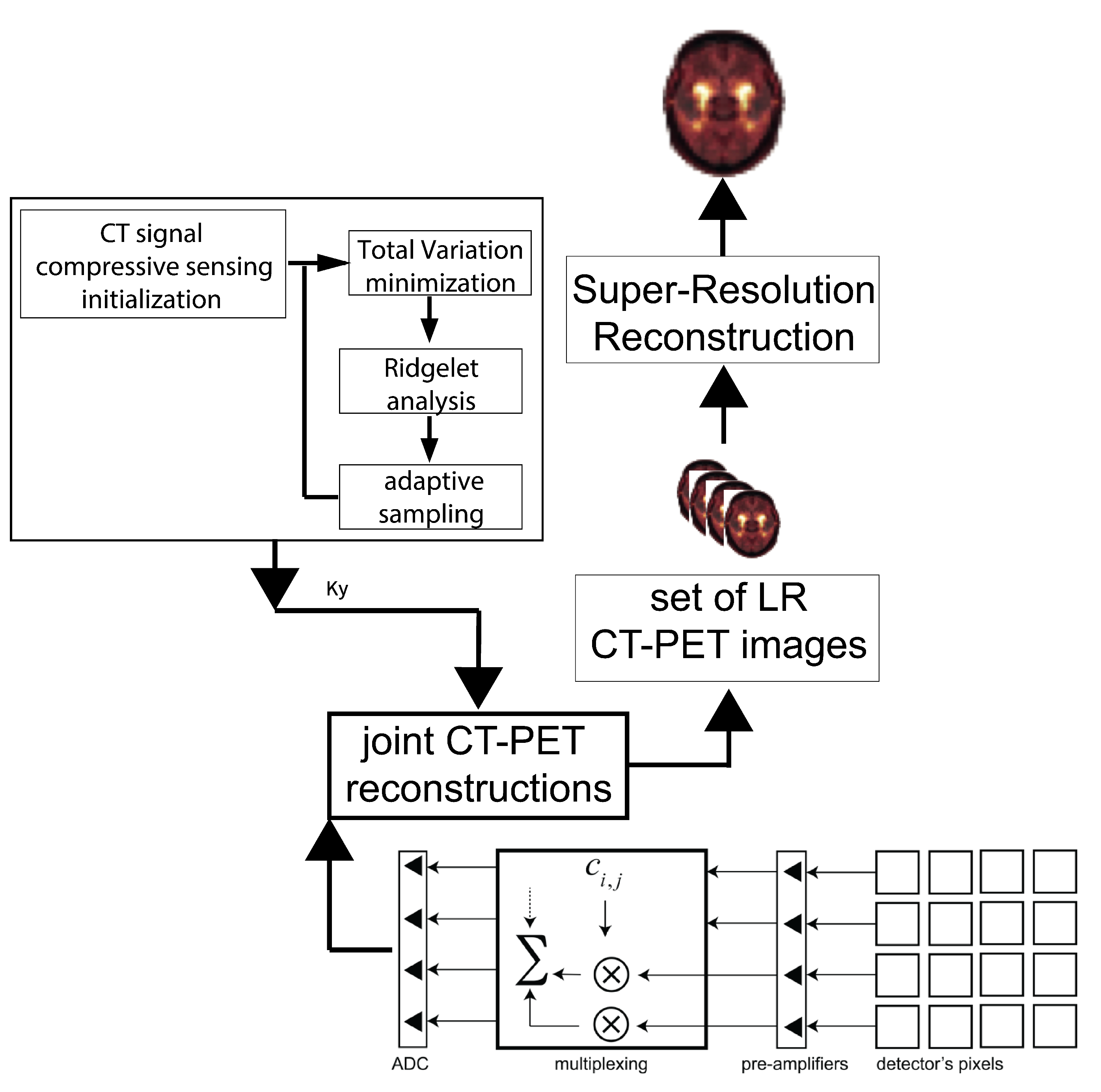
2. CT/PET Joint Sparsity
3. Computed Tomography Imaging Speeding Up
4. Compressively Sensed CT/PET Signals
5. The Super-Resolution Algorithm vs. Image Registration Issues
- high-resolution estimate.
- repeat until convergence
- Estimate noise parameters
- Calculate deformable image registration parameters and realign an image grid using them
- Estimate blur kernel operator
- Improve the High-Resolution estimate
- Repeat steps a-d until convergence, see Figure 2
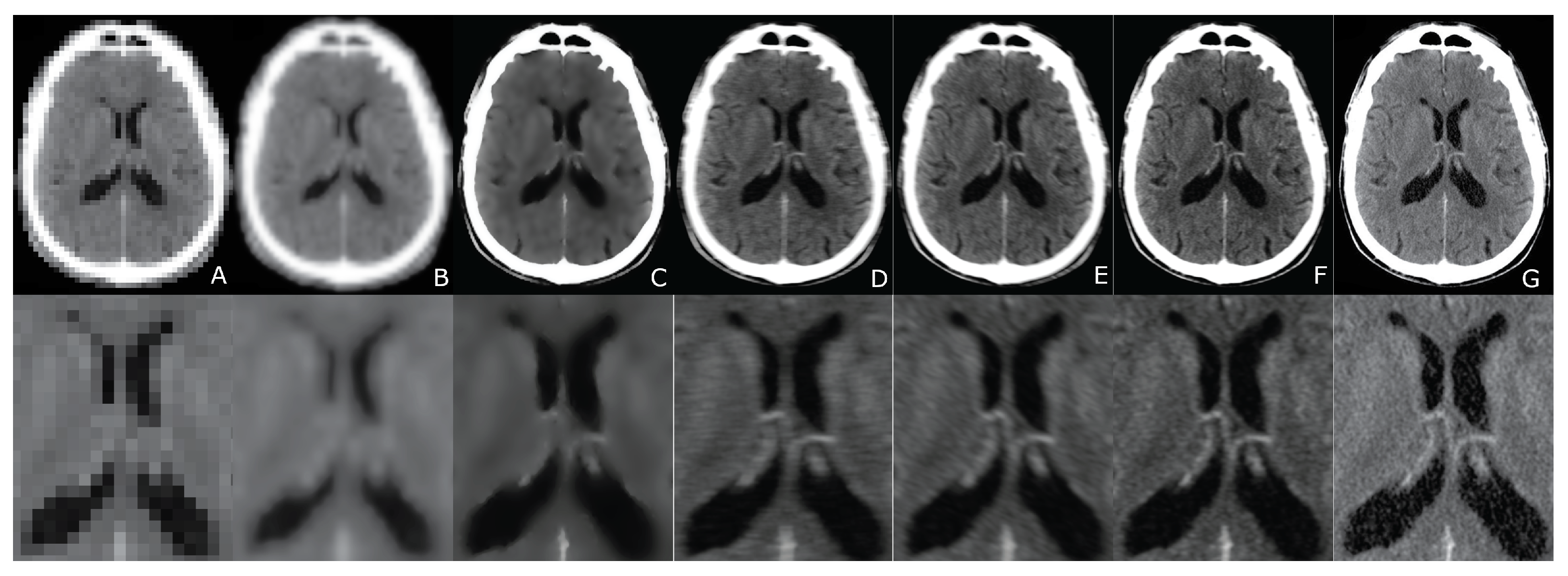
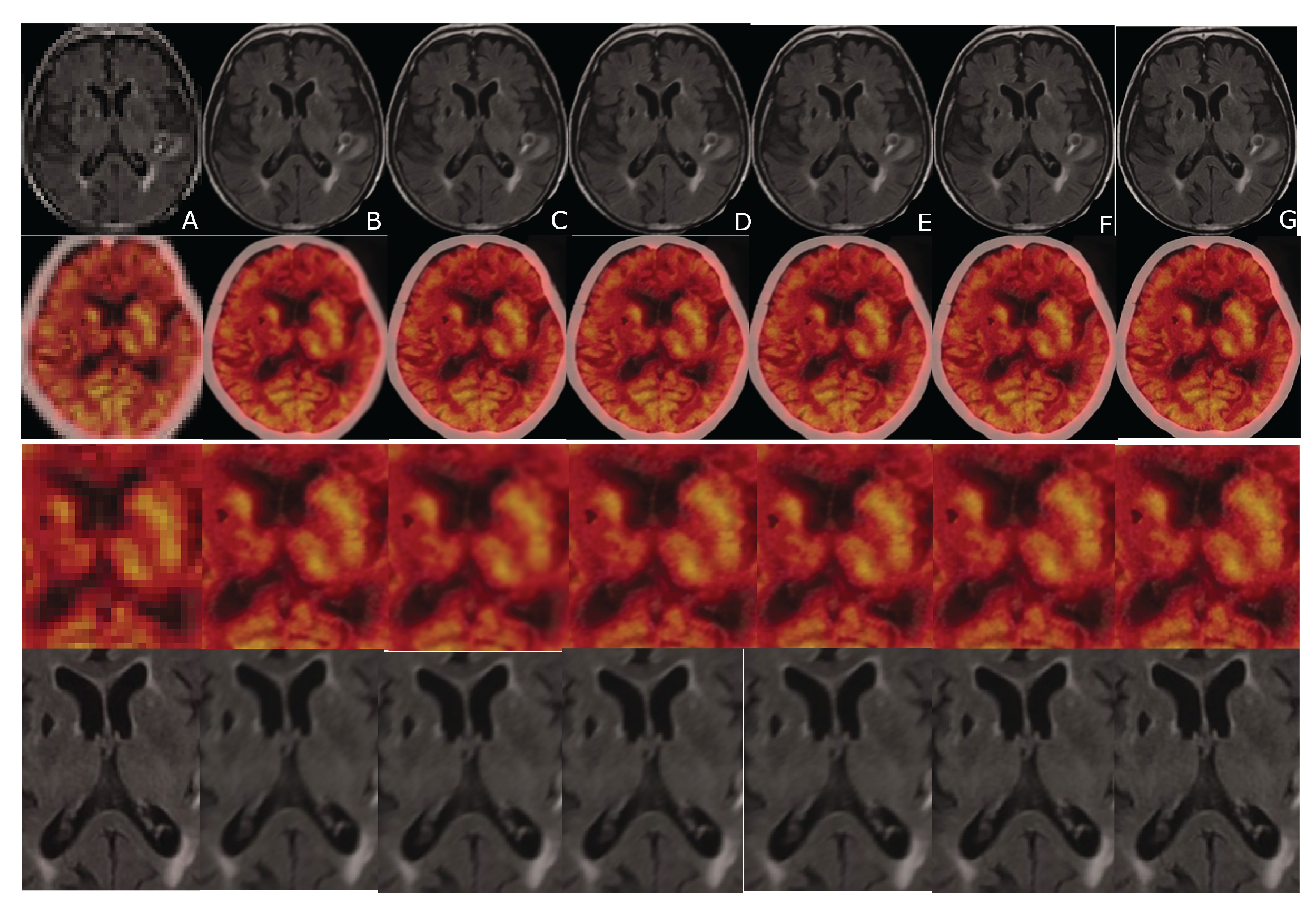
6. Evaluation
7. Results
8. Discussion
Funding
Conflicts of Interest
References
- Kinahan, P.E.; Townsend, D.W.; Beyer, T.; Sashin, D. Attenuation correction for a combined 3D PET/CT scanner. Med. Phys. 1998, 25, 2046–2053. [Google Scholar] [CrossRef] [PubMed]
- Beyer, T.; Townsend, D.W.; Brun, T.; Kinahan, P.E.; Charron, M.; Roddy, R.; Jerin, J.; Young, J.; Byars, L.; Nutt, R. A Combined PET/CT scanner for clinical oncology. J. Nucl. Med. 2000, 41, 1369–1379. [Google Scholar] [PubMed]
- Townsend, D.W.; Wensveen, M.; Byars, L.G.; Geissbuhler, A.; Tochon-Danguy, H.J.; Christin, A.; Defrise, M.; Bailey, D.L.; Grootoonk, S.; Donath, A.; et al. A rotating PET scanner using BGO block detectors: Design, performance and applications. J. Nucl. Med. 1993, 34, 1367–1376. [Google Scholar] [PubMed]
- Knoll, F.; Koesters, T.; Otazo, R.; Block, T.; Feng, L.; Vunckx, K.; Faul, D.; Nuyts, J.; Boada, F.; Sodickson, D.K. Joint reconstruction of simulwtaneously acquired MR-PET data with multi sensor compressed sensing based on a joint sparsity constraint. Ejnmmi Phys. 2014, 1, A26. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Antoch, G.; Bockisch, A. Combined PET/MRI: A new dimension in whole-body oncology imaging. EJNMI 2008, 36, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Fueger, B.J.; Czernin, J.; Hildebrandt, I.; Tran, C.; Halpern, B.S.; Stout, D.; Phelps, M.E.; Weber, W.A. Impact of animal handling on the results of 18F-FDG PET studies in mice. J. Nucl. Med. 2006, 47, 999–1006. [Google Scholar] [PubMed]
- Malczewski, K. Super-Resolution with compressively sensed MR/PET signals at its input. Inform. Med. Unlocked 2020, 18, 1–20. [Google Scholar] [CrossRef]
- Malczewski, K. Rapid Diffusion Weighted Imaging with Enhanced Resolution. Appl. Magn. Reson. 2020, 51, 221–239. [Google Scholar] [CrossRef]
- McGibney, G.; Smith, M.R.; Nichols, S.T.; Crawley, A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. MRM 1993, 30, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Cheryauka, A.B.; Lee, J.N.; Samsonov, A.A.; Defrise, M.; Gullberg, G.T. MRI diffusion tensor reconstruction with PROPELLER data acquisition. Magn. Reson. Imaging 2004, 22, 39–148. [Google Scholar] [CrossRef]
- Cuppen, J.; van Est, A. Reducing MR imaging time by one-sided reconstruction. MRI 1987, 5, 526–527. [Google Scholar] [CrossRef]
- Griswold, M.A.; Jakob, P.M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef] [PubMed]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, CVPR Workshops 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018; pp. 294–310. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar]
- Heinrich, M.P.; Jenkinson, M.; Brady, M.; Schnabel, J. Globally optimal deformable registration on a minimum spanning tree using dense displacement sampling. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2012, Nice, France, 1–5 October 2012; pp. 115–122. [Google Scholar]
- Brenner, D.; Ellison, C.; Hall, E.; Berdon, W. Estimatedrisks of radiation-induced fatal cancer from Pediatric CT. Am. J. Roentgenol. 2001, 176, 289–296. [Google Scholar] [CrossRef]
- Nelson, R. Thousands of New Cancers Predicted Due to Increased Use of CT. Available online: https://www.medscape.com/viewarticle/714025 (accessed on 20 April 2020).
- Shuryak, I.; Sachs, R.; Brenner, D. Cancer Risks after Radiation Exposure in Middle Age. J. Natl. Cancer Inst. 2010, 102, 1606–1609. [Google Scholar] [CrossRef] [PubMed]
- Kolditz, D.; Kyriakou, Y.; Kalender, W. Volume-of interest (VOI) imaging in C-arm flat-detector CT for high image quality at reduced dose. Med. Phys. 2010, 37, 2719–2730. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.; Barret, H.; Furenlid, L. Adaptive CT for highresolution, controlled-dose, region-of-interest imaging. IEEE Nucl. Sci. Symp. Conf. 2009, 2009, 4154–4157. [Google Scholar]
- Candes, E. Ridgelets: Theory and Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1998. [Google Scholar]
- Barkan, O.; Weill, J.; Averbuch, A.; Dekel, S. Adaptive Compressed Tomography Sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2013, Washington, DC, USA, 23–28 June 2013; pp. 2195–2202. [Google Scholar]
- Panta, R.K.; Segars, P.; Yin, F.F.; Cai, J. Establishing a framework to implement 4D XCAT Phantom for 4D radiotherapy research. J. Can. Res. Ther. 2012, 8, 565–570. [Google Scholar]
- Yang, F.; Ding, M.; Zhang, X. Non-Rigid Multi-Modal 3D Medical Image Registration Based on Foveated Modality Independent Neighborhood Descriptor. Sensors 2019, 19, 4675. [Google Scholar] [CrossRef] [PubMed]

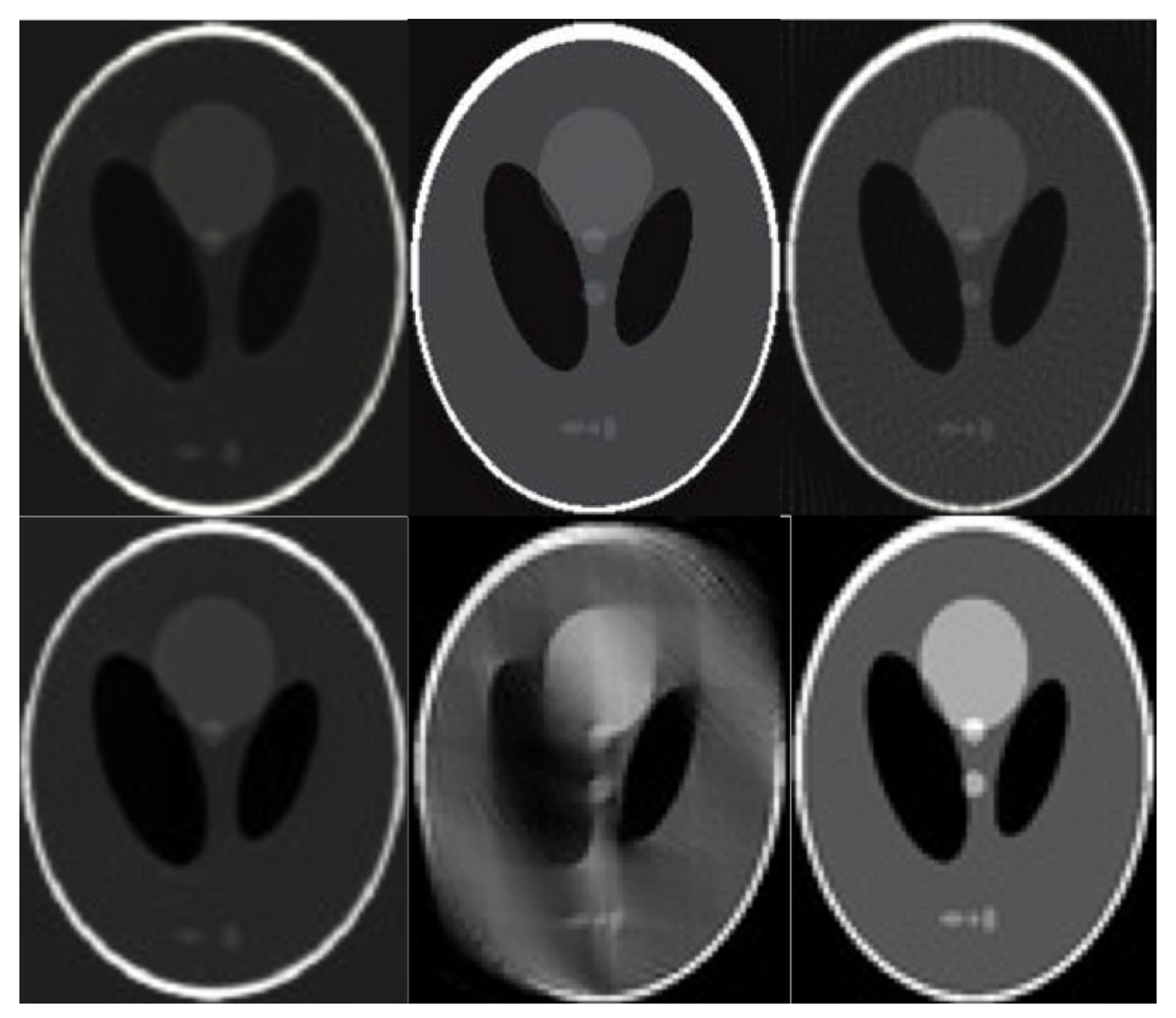
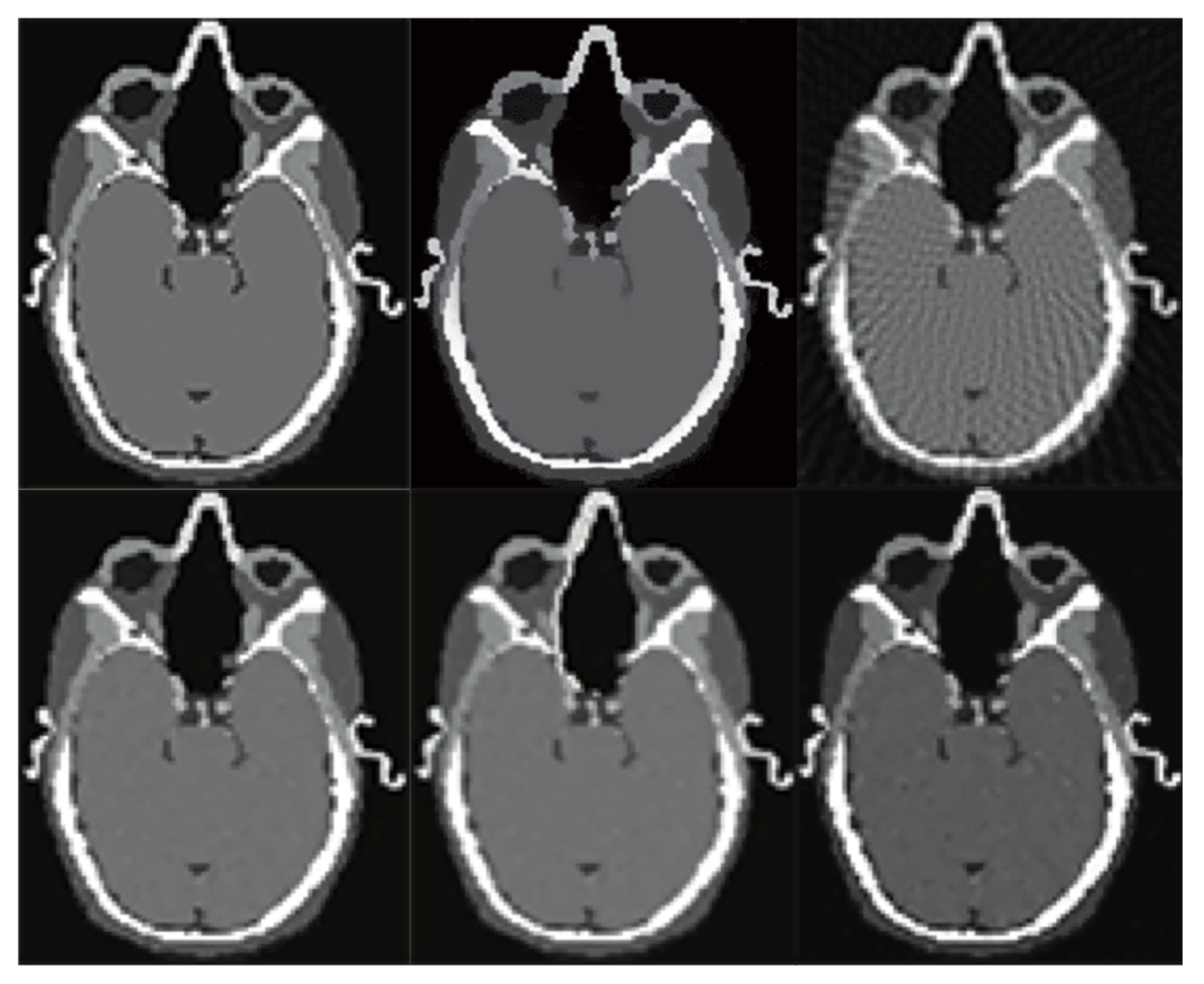

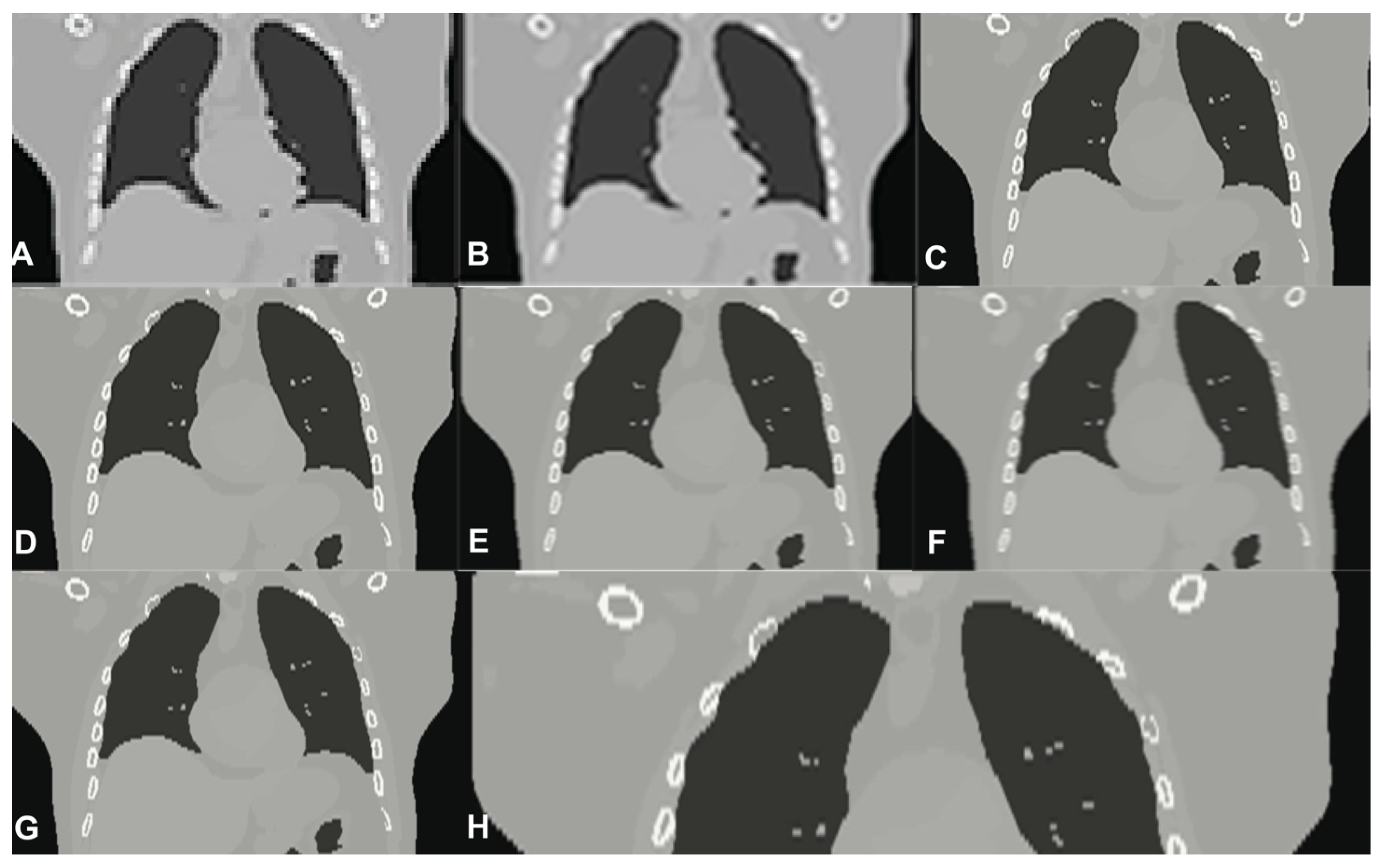

| Reconstruction Algorithm | Projection Lines [Coeff. No.] | MC | SRR | PSNR [dB] | MAE | N | SD | t(100) | p |
|---|---|---|---|---|---|---|---|---|---|
| ATA | 4096 | YES | NO | 29.96 | 14.22 | 100 | 0.03 | 0.383 | 0.551 |
| ATA | 4096 | YES | YES | 32.92 | 12.01 | 100 | 0.02 | −0.731 | 0.101 |
| FBP | 12,288 | YES | NO | 21.38 | 17.55 | 100 | 0.02 | −1.131 | 0.232 |
| NAUF | 4096 | YES | NO | 28.09 | 16.44 | 100 | 0.03 | −1.031 | 0.191 |
| ATA | 4096 | NO | NO | 27.36 | 17.01 | 100 | 0.03 | −1.231 | 0.231 |
| NAES | 2048 | YES | NO | 27.18 | 16.55 | 100 | 0.03 | −1.332 | 0.186 |
| Reconstruction Algorithm | Projection Lines [Coeff. No.] | MC | SRR | PSNR [dB] | MAE | N | SD | t(100) | p |
|---|---|---|---|---|---|---|---|---|---|
| ATA | 4096 | YES | NO | 29.96 | 14.22 | 100 | 0.03 | 0.383 | 0.551 |
| ATA | 4096 | YES | YES | 32.92 | 12.01 | 100 | 0.02 | −0.731 | 0.101 |
| FBP | 12,288 | YES | NO | 21.38 | 17.55 | 100 | 0.02 | −1.131 | 0.232 |
| NAUF | 4096 | YES | NO | 28.09 | 16.44 | 100 | 0.03 | −1.031 | 0.191 |
| ATA | 4096 | NO | NO | 27.36 | 17.01 | 100 | 0.03 | −1.231 | 0.231 |
| NAES | 2048 | YES | NO | 27.18 | 16.55 | 100 | 0.03 | −1.332 | 0.186 |
| Reconstruction Algorithm | Projection Lines [Coeff. No.] | MC | SRR | PSNR [dB] | MAE | N | SD | t(100) | p |
|---|---|---|---|---|---|---|---|---|---|
| ATA | 4096 | YES | NO | 32.16 | 14.25 | 100 | 0.04 | 0.024 | 0.500 |
| ATA | 4096 | YES | YES | 38.22 | 12.51 | 100 | 0.02 | −0.611 | 0.110 |
| FBP | 12,288 | YES | NO | 24.44 | 13.66 | 100 | 0.02 | −1.115 | 0.184 |
| NAUF | 4096 | YES | NO | 31.12 | 16.88 | 100 | 0.03 | −1.022 | 0.199 |
| ATA | 4096 | NO | NO | 32.18 | 16.61 | 100 | 0.03 | −1.251 | 0.263 |
| NAES | 2048 | YES | NO | 25.42 | 14.92 | 100 | 0.03 | −1.387 | 0.136 |
| Reconstruction Algorithm | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|
| LR input | 26.07 | 19.41 | 100 | 26.07 | 0.04 | 0.387 | 0.592 |
| B-spline Cubic interpolation | 26.31 | 18.42 | 100 | 26.31 | 0.02 | −0.721 | 0.361 |
| Non-Rigid Multi-Modal 3D Medical Image Registration Based on Foveated Modality Independent Neighbourhood Descriptor | 31.01 | 16.31 | 100 | 31.01 | 0.02 | −1.031 | 0.312 |
| Enhanced deep residual networks for single image super-resolution | 28.44 | 15.22 | 100 | 28.44 | 0.03 | −1.001 | 0.201 |
| Image super-resolution using very deep residual chanel attention networks | 30.21 | 14.66 | 100 | 30.21 | 0.03 | −1.071 | 0.232 |
| Residual dense network for image super-resolution | 31.44 | 14.30 | 100 | 31.44 | 0.03 | −1.112 | 0.206 |
| The presented algorithm | 33.39 | 12.02 | 100 | 33.39 | 0.03 | −1.211 | 0.129 |
| Compressed Sensing Quality * [%] | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|
| 20 | 18.76 | 21.43 | 100 | 18.76 | 0.03 | −1.490 | 0.139 |
| 40 | 25.62 | 20.01 | 100 | 25.62 | 0.03 | −1.440 | 0.153 |
| 50 | 33.39 | 18.40 | 100 | 33.39 | 0.03 | −1.211 | 0.129 |
| 80 | 31.16 | 17.02 | 100 | 31.16 | 0.03 | −1.692 | 0.094 |
| 100 | 35.19 | 13.01 | 100 | 35.19 | 0.03 | −1.692 | 0.094 |
| Input | CS [%] | MC | SRR | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|---|---|---|
| LR | 50 | NO | NO | 26.09 | 19.22 | 100 | 26.09 | 0.03 | −1.252 | 0.213 |
| LR | 50 | YES | NO | 27.93 | 18.43 | 100 | 27.93 | 0.03 | −1.075 | 0.285 |
| HR | 50 | YES | NO | 29.38 | 16.59 | 100 | 29.38 | 0.03 | −1.226 | 0.223 |
| SR | 50 | YES | YES | 33.19 | 14.21 | 100 | 33.19 | 0.03 | −1.692 | 0.129 |
| Reconstruction Algorithm | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|
| LR input | 26.01 | 19.35 | 100 | 26.01 | 0.04 | 0.387 | 0.591 |
| B-spline Cubic interpolation | 26.09 | 18.438 | 100 | 26.09 | 0.02 | −0.721 | 0.331 |
| Non-Rigid Multi-Modal 3D Medical Image Registration Based on Foveated Modality Independent Neighborhood Descriptor | 31.01 | 14.23 | 100 | 31.01 | 0.02 | −1.031 | 0.331 |
| Enhanced deep residual networks for single image super-resolution | 29.47 | 14.99 | 100 | 29.47 | 0.03 | −1.001 | 0.266 |
| Image super-resolution using very deep residual chanel attention networks | 28.55 | 14.81 | 100 | 28.55 | 0.03 | −1.071 | 0.219 |
| Residual dense network for image super-resolution | 29.01 | 14.31 | 100 | 29.01 | 0.03 | −1.102 | 0.194 |
| The presented algorithm | 35.42 | 11.01 | 100 | 35.42 | 0.03 | −1.201 | 0.109 |
| Compressed Sensing Quality * [%] | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|
| 20 | 19.31 | 20.01 | 100 | 19.31 | 0.03 | −1.510 | 0.101 |
| 40 | 21.77 | 19.34 | 100 | 21.77 | 0.02 | −1.014 | 0.321 |
| 50 | 35.42 | 11.01 | 100 | 35.42 | 0.03 | −1.201 | 0.109 |
| 80 | 36.01 | 14.05 | 100 | 36.01 | 0.03 | −1.211 | 0.103 |
| 100 | 36.69 | 13.09 | 100 | 36.69 | 0.03 | −1.310 | 0.109 |
| Reconstruction Algorithm | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|
| LR input | 21.11 | 20.33 | 100 | 21.11 | 0.03 | −1.282 | 0.193 |
| B-spline Cubic interpolation | 24.26 | 18.41 | 100 | 24.26 | 0.03 | −1.451 | 0.142 |
| Non-Rigid Multi-Modal 3D Medical Image Registration Based on Foveated Modality Independent Neighborhood Descriptor | 33.22 | 16.83 | 100 | 33.22 | 0.03 | −1.373 | 0.173 |
| Enhanced deep residual networks for single image super-resolution | 31.03 | 15.71 | 100 | 30.33 | 0.03 | −1.281 | 0.214 |
| Image super-resolution using very deep residual chanel attention networks | 32.21 | 14.62 | 100 | 32.21 | 0.03 | −1.282 | 0.216 |
| Residual dense network for image super-resolution | 32.44 | 14.60 | 100 | 32.44 | 0.03 | −1.311 | 0.213 |
| The presented algorithm | 34.59 | 13.37 | 100 | 34.59 | 0.03 | −1.284 | 0.102 |
| Compressed Sensing Quality * [%] | PSNR [dB] | MAE | N | M | SD | t(99) | p |
|---|---|---|---|---|---|---|---|
| 20 | 19.40 | 21.03 | 100 | 19.40 | 0.03 | −1.502 | 0.131 |
| 40 | 22.89 | 19.44 | 100 | 22.89 | 0.02 | −1.016 | 0.323 |
| 50 | 34.59 | 13.37 | 100 | 34.59 | 0.03 | −1.284 | 0.102 |
| 80 | 36.21 | 15.58 | 100 | 36.21 | 0.03 | −1.415 | 0.123 |
| 100 | 37.63 | 13.21 | 100 | 37.63 | 0.03 | −1.420 | 0.103 |
| Registration Algorithm | TRE [Voxels ] | ||
|---|---|---|---|
| Mean | Std | p-Value | |
| No registration applied | 4.8 | 2.7 | <0.002 |
| Entropy images based SSD | 2.5 | 0.7 | <0.002 |
| Non-rigid multi modal medical image registration by combining L-BFGS-B with cat swarm optimisation | 2.2 | 0.3 | <0.002 |
| Modality independent neighborhood descriptor | 1.8 | 0.1 | <0.002 |
| Globally optimal deformable registration | 1.6 | 0.1 | <0.002 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malczewski, K. Image Resolution Enhancement of Highly Compressively Sensed CT/PET Signals. Algorithms 2020, 13, 129. https://doi.org/10.3390/a13050129
Malczewski K. Image Resolution Enhancement of Highly Compressively Sensed CT/PET Signals. Algorithms. 2020; 13(5):129. https://doi.org/10.3390/a13050129
Chicago/Turabian StyleMalczewski, Krzysztof. 2020. "Image Resolution Enhancement of Highly Compressively Sensed CT/PET Signals" Algorithms 13, no. 5: 129. https://doi.org/10.3390/a13050129
APA StyleMalczewski, K. (2020). Image Resolution Enhancement of Highly Compressively Sensed CT/PET Signals. Algorithms, 13(5), 129. https://doi.org/10.3390/a13050129




