Distributional Reinforcement Learning with Ensembles
Abstract
1. Introduction
2. Background
2.1. Expected Reinforcement Learning
2.2. Distributional Reinforcement Learning
2.2.1. Evaluation
2.2.2. Control
2.2.3. Categorical Evaluation and Control
| Algorithm 1: Categorical Distributional Reinforcement Learning (CDRL) |
|
3. Learning with Ensembles
3.1. Ensembles
3.2. Ensemble Categorical Control
| Algorithm 2: Ensemble Categorical Control (ECC) |
|
4. Empirical Results on a Subset of Atari 2600 Games
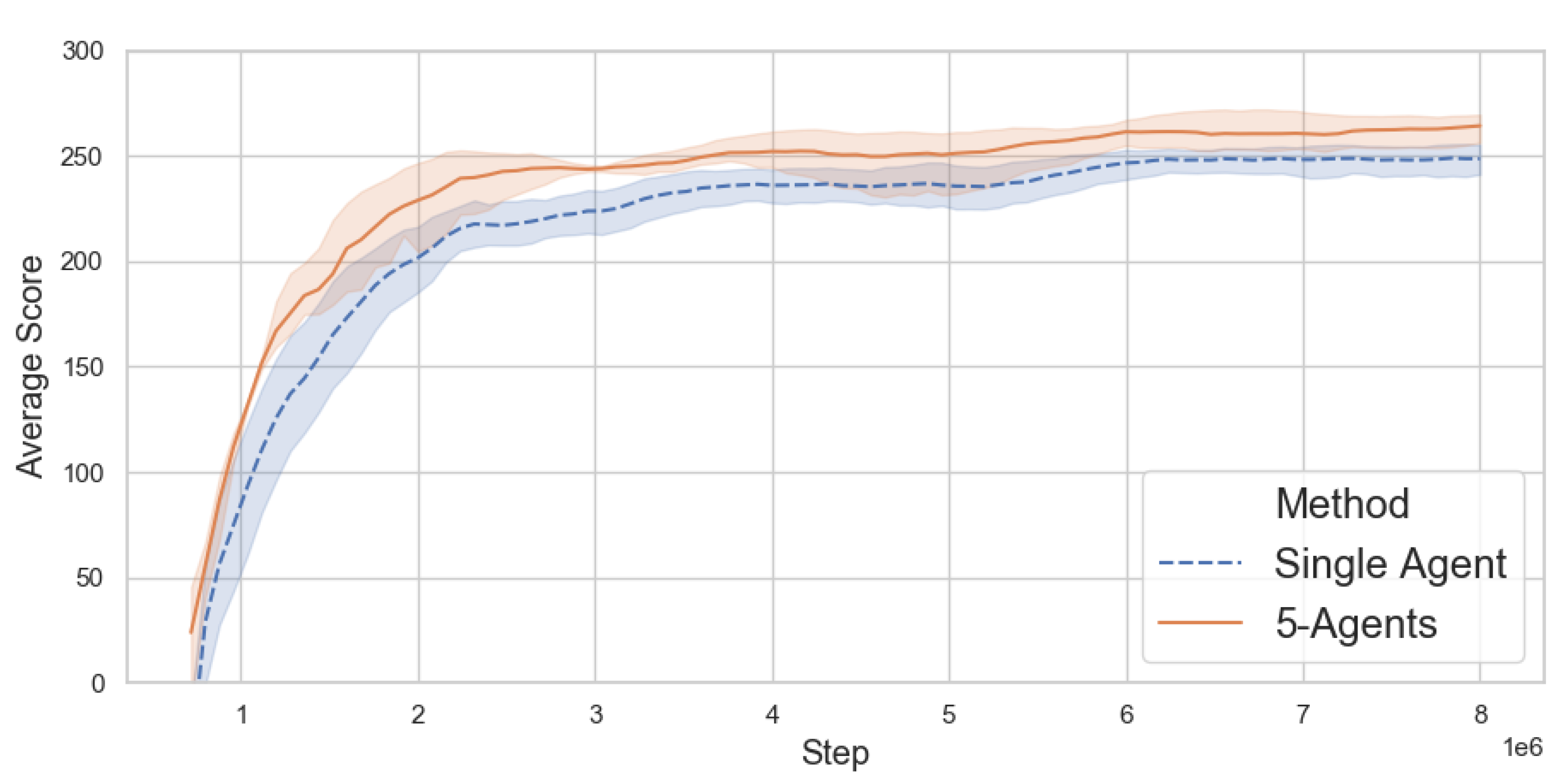
4.1. Online Performance
4.2. Relative Ensemble Sample Performance
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDRL | Categorical Distributional Reinforcement Learning |
| MDP | Markov Decision Process |
| ECC | Ensemble Categorical Control |
Appendix A
| Algorithm A1: Ensemble categorical control. |
| Input: Number of iteration steps N, ensemble size k, support |
| Initialize starting states in independent environments |
| Initialize agent networks with random parameters |
| Initialize target network with |
| Initialize replay buffers with the same size S |
| for N do |
| for all do |
| Set to be a uniform random action with probability |
| Otherwise, set |
| Execute , and store the transition in |
| Set |
| end for |
| if then |
| for all do |
| Initialize loss |
| Sample uniformly a minibatch |
| for all do |
| Set |
| Set |
| end for |
| Update by a gradient descent step on L |
| end for |
| end if |
| if then |
| for alldo |
| Update target network with |
| end for |
| end if |
| end for |
References
- Singh, S.P. The efficient learning of multiple task sequences. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1992; pp. 251–258. [Google Scholar]
- Sun, R.; Peterson, T. Multi-agent reinforcement learning: weighting and partitioning. Neural Netw. 1999, 12, 727–753. [Google Scholar] [CrossRef]
- Wiering, M.A.; Van Hasselt, H. Ensemble algorithms in reinforcement learning. IEEE Trans. Syst. Man, Cybern. Part B (Cybernetics) 2008, 38, 930–936. [Google Scholar] [CrossRef] [PubMed]
- Faußer, S.; Schwenker, F. Selective neural network ensembles in reinforcement learning: Taking the advantage of many agents. Neurocomputing 2015, 169, 350–357. [Google Scholar] [CrossRef]
- Bellemare, M.G.; Dabney, W.; Munos, R. A distributional perspective on reinforcement learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 449–458. [Google Scholar]
- Morimura, T.; Sugiyama, M.; Kashima, H.; Hachiya, H.; Tanaka, T. Parametric return density estimation for reinforcement learning. In Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence, Catalina Island, CA, USA, 8–11 July 2010; pp. 368–375. [Google Scholar]
- Dabney, W.; Rowland, M.; Bellemare, M.G.; Munos, R. Distributional reinforcement learning with quantile regression. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Dabney, W.; Ostrovski, G.; Silver, D.; Munos, R. Implicit Quantile Networks for Distributional Reinforcement Learning. Int. Conf. Mach. Learn. 2018, 80, 1096–1105. [Google Scholar]
- Lyle, C.; Bellemare, M.G.; Castro, P.S. A comparative analysis of expected and distributional reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4504–4511. [Google Scholar]
- Rowland, M.; Bellemare, M.; Dabney, W.; Munos, R.; Teh, Y.W. An Analysis of Categorical Distributional Reinforcement Learning. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Canary Islands, Spain, 9–11 April 2018; pp. 29–37. [Google Scholar]
- Bellemare, M.G.; Le Roux, N.; Castro, P.S.; Moitra, S. Distributional reinforcement learning with linear function approximation. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Okinawa, Japan, 16–18 April 2019; pp. 2203–2211. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The Arcade Learning Environment: An Evaluation Platform for General Agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Rizzo, M.L.; Székely, G.J. Energy distance. Wiley Interdiscip. Rev. Comput. Stat. 2016, 8, 27–38. [Google Scholar] [CrossRef]
- Bertsekas, D.P.; Tsitsiklis, J.N. Neuro-Dynamic Programming; Athena Scientific: Belmont, MA, USA, 1996. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin, Germany, 2008; Volume 338. [Google Scholar]
- Bellemare, M.G.; Danihelka, I.; Dabney, W.; Mohamed, S.; Lakshminarayanan, B.; Hoyer, S.; Munos, R. The Cramer Distance as a Solution to Biased Wasserstein Gradients. arXiv 2017, arXiv:1705.10743. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Clemen, R.T.; Winkler, R.L. Combining probability distributions from experts in risk analysis. Risk Anal. 1999, 19, 187–203. [Google Scholar] [CrossRef]
- Casarin, R.; Mantoan, G.; Ravazzolo, F. Bayesian calibration of generalized pools of predictive distributions. Econometrics 2016, 4, 17. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.V. Applied Multivariate Statistical Analysis; Pearson: Harlow, UK, 2014. [Google Scholar]
- Lindenberg, B.; Nordqvist, J.; Lindahl, K.O. bjliaa/ecc: ecc; (Version v0.3-alpha). Zenodo: 2020. Available online: https://zenodo.org/record/3760246#.XrP1Oi4za1U (accessed on 22 April 2020).
- Hill, A.; Raffin, A.; Ernestus, M.; Gleave, A.; Kanervisto, A.; Traore, R.; Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; et al. Stable Baselines. 2018. Available online: https://github.com/hill-a/stable-baselines (accessed on 22 April 2020).
- Horgan, D.; Quan, J.; Budden, D.; Barth-Maron, G.; Hessel, M.; van Hasselt, H.; Silver, D. Distributed Prioritized Experience Replay. arXiv 2018, arXiv:1803.00933. [Google Scholar]
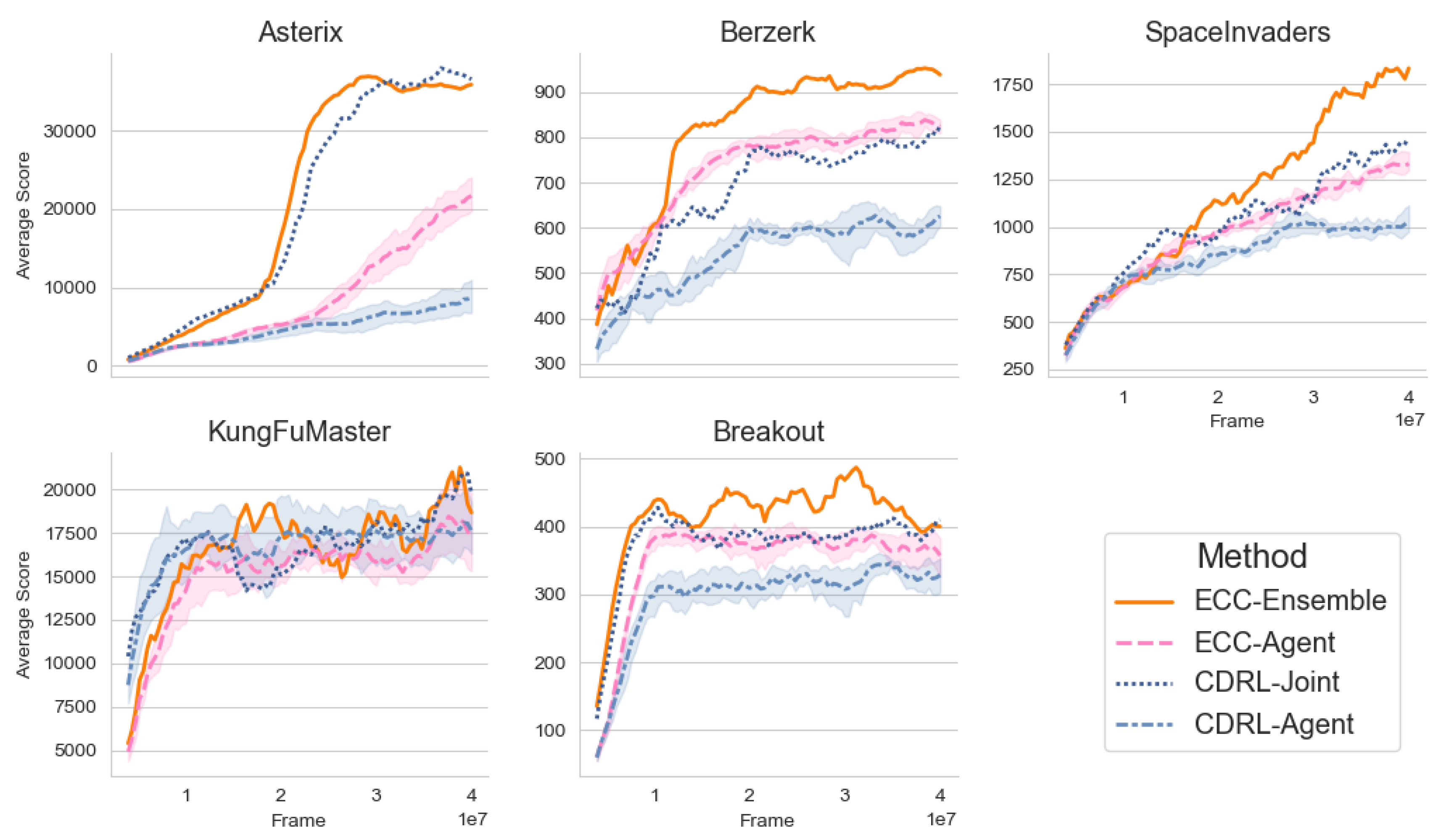
| Game | CDRL Agent | ECCAgent | CDRL Joint | ECCEnsemble |
|---|---|---|---|---|
| Asterix | 12,998 ± 3042 | 28,196 ± 903 | 39,413 | 38,938 |
| Berzerk | 795 ± 47 | 958 ± 12 | 890 | 1034 |
| SpaceInvaders | 1429 ± 91 | 1812 ± 87 | 1850 | 2395 |
| Breakout | 444 ± 44 | 546 ± 27 | 515 | 665 |
| KungFuMaster | 27,984 ± 1767 | 27,302 ± 2213 | 25,826 | 29,629 |
| Method | Asterix | Berzerk | Breakout | SpaceInvaders | KungFuMaster |
|---|---|---|---|---|---|
| ECCEnsemble | 47.7 % | 93.7 % | 93.7 % | 63.4 % | 66.9 % |
| CDRL Joint | 56.3 % | 86.7 % | 86.1 % | 67.2 % | 87.0 % |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindenberg, B.; Nordqvist, J.; Lindahl, K.-O. Distributional Reinforcement Learning with Ensembles. Algorithms 2020, 13, 118. https://doi.org/10.3390/a13050118
Lindenberg B, Nordqvist J, Lindahl K-O. Distributional Reinforcement Learning with Ensembles. Algorithms. 2020; 13(5):118. https://doi.org/10.3390/a13050118
Chicago/Turabian StyleLindenberg, Björn, Jonas Nordqvist, and Karl-Olof Lindahl. 2020. "Distributional Reinforcement Learning with Ensembles" Algorithms 13, no. 5: 118. https://doi.org/10.3390/a13050118
APA StyleLindenberg, B., Nordqvist, J., & Lindahl, K.-O. (2020). Distributional Reinforcement Learning with Ensembles. Algorithms, 13(5), 118. https://doi.org/10.3390/a13050118





