Abstract
Symbiotic organisms search (SOS) is a promising metaheuristic algorithm that has been studied recently by numerous researchers due to its capability to solve various hard and complex optimization problems. SOS is a powerful optimization technique that mimics the simulation of the typical symbiotic interactions among organisms in an ecosystem. This study presents a new SOS-based hybrid algorithm for solving the challenging construction site layout planning (CSLP) discrete problems. A new algorithm called the hybrid symbiotic organisms search with local operators (HSOS-LO) represents a combination of the canonical SOS and several local search mechanisms aimed at increasing the searching capability in discrete-based solution space. In this study, three CSLP problems that consist of single and multi-floor facility layout problems are tested, and the obtained results were compared with other widely used metaheuristic algorithms. The results indicate the robust performance of the HSOS-LO algorithm in handling discrete-based CSLP problems.
1. Introduction
Determining the best site and facility layout, especially for large construction projects, has always been a critical and challenging task for construction managers. Poor layout can lead to decreased workers’ productivity, overloading of material transportation and handling, longer queues, and ultimately an increased budget. Hence, layout planning is important for project success because it has a direct impact on different kinds of construction operation performance, such as transportation costs, the flow of work, and productivity [1]. An ineffective layout can increase material handling costs by over 35%. Studies have suggested that an effective layout can enhance the general effectiveness of operations and lower operating expenses between 20% to 50% [2]. Accordingly, an increasing number of studies has focused on facility layout planning in numerous areas, including industrial engineering, construction management, and architecture.
The construction site layout planning (CSLP) problem, from the perspective of an optimization problem, is commonly addressed as a quadratic assignment problem (QAP). In CSLP problem, n facilities are assigned to n locations with the assumption that every single facility requires the same space. Hence, it is possible to assign any facility to any site [3]. The CSLP is regarded as non-polynomial hard (NP-hard), where this kind of problem cannot be solved in polynomial time [4]. In the case of CSLP with a large number of facilities, it is hard to determine the optimal solution within an acceptable time frame [5]. Approximately, there are n! possible alternative solutions for CSLP with n facilities. For example, if the construction project has 10 facilities, there will be more than 3 million possible alternatives for the site layout.
Many studies have been conducted to develop the methods for obtaining an optimal solution within a limited computational time. Several mathematical exact approaches and heuristic methods were built in early attempts to address the CSLP problem, including the branch-and-bound [6], dynamic programming [7], and integer linear programming [8]. Nevertheless, the exact approaches are often inadequate in tackling large problems, while the heuristic search techniques appear reasonable since they are an inexact method for obtaining near-optimal solutions. Kumar et al. [9] have presented a greedy heuristic approach for handling a facility layout problem. However, the quality solution produced by heuristic methods is often poor. This situation, because the heuristic method on many occasions is too greedy, results from the inability to escape the local optima, and consequently, failing to propose the global solution.
The past decades have seen the rapid growth of metaheuristic algorithm applications in solving the CSLP problem due to their ability to solve complex and large optimization problems from various disciplines [10]. Most metaheuristic algorithms allow their searching mechanism to accept less preferable candidate solutions leading to a wider solution space coverage and possibly a better result in comparison to the traditional heuristic methods. Metaheuristic has been widely known as an effective tool for handling NP-hard problems [11,12]. Examples of metaheuristic techniques applied to CSLP problem include artificial bee colony (ABC) [13], tabu search [14], ant colony optimization (ACO) [15], particle swarm optimization (PSO) [16,17], and genetic algorithm (GA) [8,18,19]. As the project has become larger, more advanced technique development is needed to handle the complex layout design problem.
Recently, Cheng and Prayogo introduced a metaheuristic optimization algorithm, known as the symbiotic organisms search (SOS) [20]. It adopts the natural adaptive interactions among living organisms in one ecosystem. At first, the SOS was utilized for resolving the continuous optimization problems, such as engineering design problems and the complex benchmark functions. Its strong performance was compared to the other metaheuristic techniques [21]. The SOS algorithm is considered a new algorithm, hence, its ability to solve different types of a complex problem should be further investigated and explored. Furthermore, only a few studies have been carried out to explore the potential of SOS in solving a discrete problem such as the CSLP problem. Hence, there is space for research and experiments for enhancing the performance of SOS in exploiting and exploring the discrete solutions. Choosing a useful hybrid approach is a key determinant for achieving the best performance in solving a difficult problem [22,23].
This study proposes a novel hybrid metaheuristic algorithm called hybrid symbiotic organisms search with local operators (HSOS-LO) for solving the CSLP problem. The HSOS-LO presents the two-fold improvement in searching mechanism over the basic SOS. First, HSOS-LO transforms the original real-valued individual positions of SOS into a discrete-valued representation by sorting the values of the solutions and memorizing the index as discrete CSLP-based solutions. Second, HSOS-LO adopts three dynamic neighborhood local search mechanisms to refine the solution quality after the SOS searching routine is conducted. For validating the performance of HSOS-LO, three actual case studies from the construction CSLP problem are employed, which are a single floor facility layout problem and a multi-floor facility layout problem. Subsequently, the results received from other heuristic methods introduced by previous studies are examined and compared with the proposed method.
The remainder of this paper is structured as follows. Section 2 introduces the basic concept of the SOS algorithm. Section 3 presents the review of CSLP problem. Section 4 introduces the basic components and the procedure of the HSOS-LO for solving the CSLP problem. Section 5 shows the comparative performance analysis of the proposed algorithm and other methods. Section 6 presents the conclusion and future direction.
2. The Symbiotic Organisms Search Algorithm
SOS is first developed as a continuous-based optimization algorithm that adopts multiple relationships that exist between any two distinctive organisms that cohabit together [20]. The strong point of choosing SOS over other metaheuristic algorithms is that SOS does not include any algorithm-specific tuning parameter. Nonetheless, the SOS algorithm still delivers a strong performance as it has been proven on a variety of mathematical test functions in comparison to widely used metaheuristic algorithms [24].
In the real world situation, frequently, three symbiotic relationships usually exist between two or more distinctive organisms. Firstly, the relationship where two living organisms benefit reciprocatively is known as mutualism. Secondly, the relationship where one of the organisms derives all the benefit from the other organism while the other is not significantly affected by the immediate interaction is denoted as commensalism. Lastly, parasitism is a relationship where one of the organisms benefits at the detriment of the other organism. Those phenomena are accommodated into the movement formulation in the SOS method. SOS searching mechanism involves three main phases: mutualism phase, commensalism phase, and parasitism phase.
Algorithm 1 outlines the pseudo-code of the SOS algorithm. First, the initial population of solutions, denoted as organisms, is randomly generated in correspondence to the number of design variables and the population size. Then, the organisms are processed through three modifying operators. These operators are the mutualism phase, the commensalism phase, and parasitism phase. The trial population generated from each phase is then compared with the previous population in which the better one will survive. After undergoing all the phases, the whole procedure is repeated in another iteration until the stopping criteria are satisfied.
| Algorithm 1 Symbiotic Organism Search pseudo-code |
| Initialization: ecosystem |
| Input: population size: , the maximum number of evaluation number |
| Output: best solution |
| 1: For counter = 1 to (termination condition) |
| 2: For each organism in (maximum number of function evaluations) |
| 3: Update the current best organism |
| 4: Modify organism by |
| a. Mutualism phase |
| b. Commensalism phase |
| c. Parasitism phase |
| 5: End for |
| 6: End for |
Since its early inception, the SOS framework has been implemented to a wide variety of complex and hard problems in civil engineering, including optimization problems in resource levelling [22,25], time–cost–labor utilization trade-off [21], time–cost–quality–work continuity trade-off [26], and truss structure design [27,28,29,30]. Although many past studies have explored the potential of the SOS algorithm, developing advanced algorithms remains on the research agenda as the number of hard problems has steadily been increasing.
3. Construction Site Layout Planning Problem
The CSLP problem focuses on the physical arrangement of sites, machines, or departments in the scope of a predetermined configuration. In general, the layout problem refers to the issues of (i) identification of the size and shape of the facilities; (ii) identification of constraints between facilities; and (iii) determination of the facilities’ relative positions aimed at satisfying the constraints and enabling efficient functioning. CSLP problem consists of coordinating the restricted space in the city that should accommodate temporary facilities, such as the site office, equipment or materials, trailers, and fabrication shops. The purpose is to have an efficient functioning on the site.
An effective layout will assist any company in improving its project performance. Moreover, the facility layout is often a costly long-term investment. Hence, it is not possible to easily perform modifications as it requires significant time and budget. Relayouting facilities is time-consuming; moreover, it disrupts the flow of materials and activities of workers [31]. Thus, proper layout planning reduces construction costs (plant, labour, and material), increases labourer and equipment productivity (labour time and equipment time), and improves safety (hazardous materials, falling objects, and waste) on a construction site.
As discussed earlier, the CSLP can be formulated as a QAP. In this study, it is assumed that each facility occupies an identical area. Thus, it is feasible to assign any site to any facility. Currently, there are no general methods or techniques employed to handle these tasks. Each task is solved independently of the others based on project-specific assumptions and well-defined information. The purpose is to find suitable solutions that satisfy all the constraints outlined by the decision-maker. Thus, the objective of this QAP is to find the optimal assignment of n facilities to n sites. The objective function is minimizing the total travelling distance taken based on the product of distance and frequency of trips of the site workers. The total travelling distance of facilities layout can be defined as QAP optimization model as shown in the following equations:
where n is the number of facilities, and are members of facility–location assignment matrix ( = 1 if facility i is assigned to location j; = 0 otherwise; = 1 if facility k is assigned to location l, = 0 otherwise); is the frequencies of trips of construction personnel between facilities i and k; and is the distances between locations j and l.
4. Application of HSOS-LO to CSLP problem
Although the basic SOS algorithm has been successful in solving continuous mathematical problems [32], the SOS algorithm has not yet been tested for solving the CSLP problem. Since CLSP is a discrete optimization problem, SOS needs to adapt the solution representation from a continuous real number to a discrete value. Thus, to increase the solution quality, a method to transform the solution representation is proposed. Furthermore, several local search mechanisms are developed to enhance the solution quality.
The following section explains each component of the HSOS-LO method for CSLP problem. Section 4.1 explains the solution representation method. Section 4.2 presents three local search improvement procedures. Section 4.3 describes the parameters used in the HSOS-LO algorithm for the CSLP problem, while Section 4.4 describes the HSOS-LO framework for dealing with the CSLP problem.
4.1. Solution Representation
Adopting a proper solution representation of site layout in HSOS-LO for CSLP problem can increase the searching performance. This study employs the solution representation from Zhang et al. [17] that has been proven successful to solve the CSLP problem. It is a general decoding procedure to turn a continuous-based number into a sequence-based value. A layout plan is created based on the values in each index array sorted in ascending order. This solution representation is employed for solving the CSLP problem. The illustration of the solution representation can be seen in Figure 1. There are eight facilities and eight locations. The real-valued SOS-based solution is then transformed into an integer value by using the sort function. The sort function returns the sorted element in the ascending order.
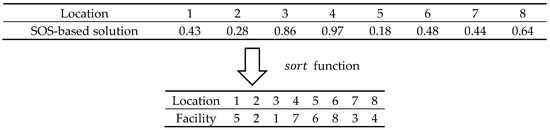
Figure 1.
Solution representation.
The sequence on this layout plan represents the one-to-one correspondence between locations and facilities. Each sequence consists of an index and value associated with the location and facility assigned to it.
4.2. Local Search Improvement
An additional local search procedure can improve the result of metaheuristic algorithms [33]. During the local search improvement phase, several neighbourhood operators are used to improve the solution quality. The term improvement is defined as a decrease in the current solution’s total distance. The procedure is as follows. First, the original real-valued based solution is decoded into the permutation-based solution. After finishing the local search improvement process, the permutation-based solution is then encoded into the real-valued based solution. At each iteration, each solution (Popi) is improved using the local search improvement by implementing a neighbourhood operator. The neighbourhood operator is randomly chosen, including swap, insert, and reverse.
- (1)
- SwapThis neighbourhood operator randomly selects two elements in the solution vectors, i and j, with i ≠ j, and swaps the customer located in position i with the customer at position j.
- (2)
- InsertionThis neighbourhood operator randomly selects positions i and j, where i ≠ j, and relocates the customer from position i to position j.
- (3)
- Random ReverseThis neighbourhood replaces a randomly chosen facility’s subsequence by its reversal.
The probability of performing the three operators above is set at 1/3 each. The pseudo-code for the local search improvement procedure is presented in Algorithm 2.
| Algorithm 2 Local search pseudo-code |
| Input: current solution , best solution |
| Output: updated solution |
| 1: Let the initial solution X = decode () |
| 2: Generate r = rand (0,1) |
| 3: If r <= 1/3 then |
| 4: Apply swap operator to X |
| 5: Else if r <= 2/3 then |
| 6: Apply insert operator to X |
| 7: Else |
| 8: Apply random reverse operator to X |
| 9: End If |
| 10: = encode (X) |
| 11: If f() < f() then |
| 12: = |
| 13: End if |
4.3. Parameter Used
The basic version of SOS encourages a primary advantage of using a less specific parameter in the algorithm. This study maintains the main advantage of having a less specific parameter of the original version of the SOS algorithm by not introducing extra parameters. The proposed HSOS-LO algorithm uses only two standard control parameters, namely a maximum number of function evaluations (maxFE) and a population size (pop_size). These two parameters are the only parameters that need to be set for the proposed HSOS-LO as well as the original SOS algorithm.
4.4. The HSOS-LO Procedure for CSLP Problem
The HSOS-LO procedure for CSLP problem is described as follows. First, the algorithm parameters are determined. Then, the algorithm starts by generating a random population or ecosystem Pop based on the population size and the number of design variables. One solution vector represents a solution, Popi, with a corresponding fitness value, f(Popi). The evaluation process is then conducted by calculating the objective function for the corresponding solution vector of each solution. The decoding method for calculating the fitness value is explained in Section 4.1. Next, the population of the solution is iteratively updated through the mutualism phase, commensalism phase, and parasitism phase.
This study used the sort function to transform each of the three basic SOS update phases into discrete variables. The sort function returns the sorted element of the real-valued variable X in ascending order. The mode of conversion for the SOS mutualism, commensalism, and parasitism phases adopted in this study are as follows:
where , is mutual vector and and denote the benefit factors.
The local search improvement is employed after finishing the movement in each phase to improve the performance of SOS. As explained in Section 4.2, the local search procedure involves three neighbourhood operators, namely swap, insertion, and reverse. Neighborhood local search operators play an important role in exploiting the search space around the current solution. The Popbest is updated if a new best solution has been found during SOS phases or local search improvement. Finally, the procedure is repeated until it meets the maximum number of function evaluations. Then the best result in that iteration, Popbest, is appointed as the final result of the optimization process.
5. Case Studies for Construction Site Layout Planning and Managerial Implication
In this study, three case studies are used to investigate the capability of the HSOS-LO in dealing with CSLP problems. Various metaheuristic algorithms are tested to present the comparative performance analysis between the proposed algorithm and other methods. All previously proposed metaheuristic algorithms in the related literature were adapted to search towards the optimal solutions of the construction site layout problem. However, since metaheuristic is not an exact approach, the obtained solution may or may not represent the optimal solution. This study uses the best-known solutions that are taken from the previous studies. The experimental results of those three case studies are then recorded and presented. The first case study is a classical layout problem with unequal-area characteristic, which is adapted from Li et al. [34]. The second case study is a storage layout plan design problem with the objective to minimize the entire transportation cost of moving material from storage cells to building floors obtained from Fung et al. [35]. The third case study is a layout problem with equal-area characteristic, which is adopted from recent work Prayogo et al. [36]. These datasets can be acessed at http://wiraredi.com/cslp-dataset/.
The algorithms are implemented using Matlab and executed on a computer with a specification of Intel I7-7700 at 3.6 GHz CPU and 8 GB RAM, running on a 64-bit platform under Windows 7 operating system. The total time complexity of the proposed HSOS-LO was O(MaxIter * pop_size * m * p), where MaxIter is the maximum number of generations, pop_size is the population size, m is the number of facilities, and p is the number of function evaluations in one iteration. In HSOS-LO, the number of function evaluations in one iteration is five; two times occurred in mutualism phase, and one time each in commensalism, parasitism, and neighbourhood local search phase.
5.1. Parameter Setting
This version of SOS and HSOS-LO only needs to set the parameter values for the maximum number of function evaluations (maxFE) and the population size (pop_size). The SOS and HSOS-LO parameter setting do not involve a complex procedure. The following combinations of parameters were tested on each case study.
pop_size: 30, 50, 100, 150.
maxFE: 1000, 3000, 6000, 12,000.
For the parameter setting, each parameter is changed one variable at a time to see the effect on the objective value and computational time. The effect and analysis of the parameter setting can be seen in Figure 2. Take an example of the effect of different pop_size on case study 1, larger pop_size shows a trade-off between objective value and computation time. However, the objective function value of using pop_size equal to 50, 100, and 150 is similar. Therefore, in this case, pop_size equals 50 is selected for case study 1. The same procedure is conducted for the rest of the parameter settings of each algorithm. Finally, the following combinations of parameters were selected in each case study.
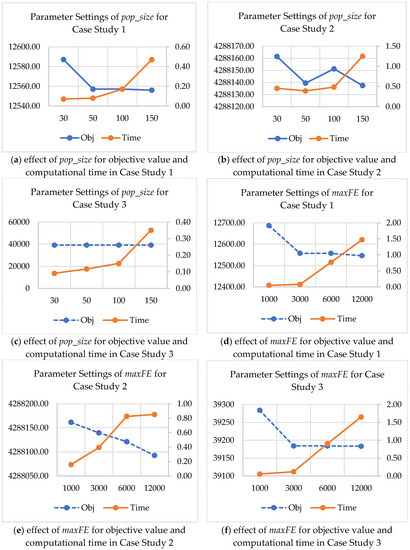
Figure 2.
Parameter settings result of pop_size and maxFE for SOS and HSOS-LS.
Case study 1: pop_size = 50, maxFe = 3000.
Case study 2: pop_size = 50, maxFe = 12,000.
Case study 3: pop_size = 30, maxFe = 3000.
5.2. Case Study 1
In this case, the primary objective is to design the temporary construction facilities layout aimed at minimizing the total travelling distance of site workers between different facilities. The site layout has 11 facilities and 11 locations, as can be seen in Figure 3. Side gate and main gate are fixed location while others are not. The list of facilities used in this case study is shown below:
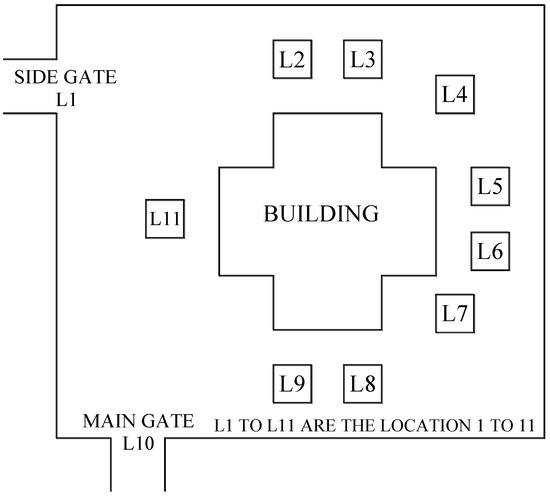
Figure 3.
Solution representation.
- Site office (F1)
- Falsework workshop (F2)
- Labour residence (F3)
- Storeroom 1 (F4)
- Storeroom 2 (F5)
- Carpentry workshop (F6)
- Reinforcement steel workshop (F7)
- Side gate (F8, fixed to L1)
- Electrical, water and other utilities control room (F9)
- Concrete batch workshop (F10)
- The main gate (F11, fixed to L10)
The objective is to design a temporary facilities layout to get the minimum travel distance, which is calculated by multiplying the frequency and distance between each facility. The daily frequency of trips and the distance between locations are shown in Table 1 and Table 2. The objective function is defined using Equations (1)–(4).

Table 1.
Frequencies of trips between facilities.

Table 2.
Travel distance between locations.
SOS, PSO, differential evolution (DE), and the proposed HSOS-LO were applied in the case study and were compared to each other. All previously mentioned metaheuristic algorithms were adapted to search towards the optimal solutions of construction site layout problem. Each algorithm was run for 100 simulations, and the mean of the best value was recorded. Numerical comparison results of each algorithm are discussed in this section. Each algorithm has 50 populations (pop_size). A maximum number of evaluations (maxFE) is 3000 for all algorithms (equal to 60 iterations for both PSO and DE; 30 iterations for SOS; and 20 iterations for HSOS-LO). The results of the comparisons are presented in Table 3. Table 3 shows the information regarding the best, average, worst, and standard deviations of objective value. Furthermore, the percentage difference between best to average, best to worst, and average computational time is reported. The obtained results have indicated that HSOS-LO manages to outperform the competing algorithms in fitness value and consistency. It can get the most optimum solution (minimum travel distance = 12,546) with the best average, worst, and standard deviation iteration (12,553.86, 12672, and 19.37, respectively). Also, the average computational time of each instance by HSOS-LO is 0.084 s.

Table 3.
Travel distance between locations.
This study also compares HSOS-LO with the outcome of previous research studies. The comparison results are shown in Table 4. Based on the simulation results, HSOS-LO is able to outperform other algorithms such as GA, TS, CBO, and ECBO. HSOS-LO manages to have the most consistent result with the least number of iterations and function evaluations. It can be seen that the number of search spaces of possible solution combinations is 9! (because two facilities are fixed). Hence, the possible layout arrangement is 362,880 possibilities. HSOS-LO only needs 3000 attempts on average to get the solution with the objective value equal to the best-known solution consistently, which is about 0.8267% of the total attempts. The convergence graphic of competing algorithms is shown in Figure 4. Therefore, the HSOS-LO proposed in this case study can be successfully used for resolving practical construction engineering problems for construction site layout.

Table 4.
Result comparison with previous research.
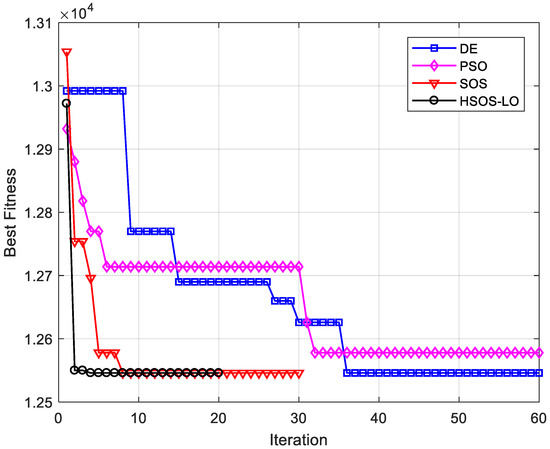
Figure 4.
Convergence graphic of metaheuristic algorithms for Case 1.
5.3. Case Study 2
Multi-storey building construction sites have limited space. Therefore, materials storage planning for the construction site is critical for construction management. Developing sufficient structural strength in the lower floors to temporarily store materials needed for construction is required to reduce the material transportation times and to enhance the general construction efficiency. A real case study obtained from Fung et al. [35] was used to validate the proposed method. The objective was to design a storage layout plan in the completed floors of a multi-storey building. It considered the horizontal movements between different storage cells and the hoist system. Also, it considered the vertical transportation of construction materials on different floors.
In this study, several assumptions related to the problem are listed as follows.
- The building has 30 floors and floors one to eight can be used as materials storage.
- There are 10 types of materials and each floor has five storage cells that can only be used by 1 type of material.
- There are three types of transportation costs: horizontal movement, vertical movement from the ground floor to the storage floor, and vertical movement from the storage floor to the demanding floor.
- There are fixed and predetermined physical and demand quantities.
- Only one lift used as the materials hoist.
- All storage cell areas are large enough to meet storage requirements.
- After being built, lower building floors can function as materials storages.
- There are no costs related to loading and unloading of materials in the hoist system.
- All details can be seen in Fung et al. [35].
Figure 5 and Figure 6 visualize the material distribution process from the side view of the building and from the floor plan, respectively.
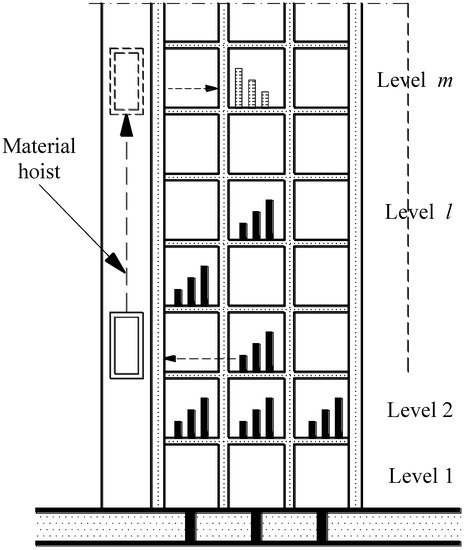
Figure 5.
Side view of the material hoist in multi-storey building construction.
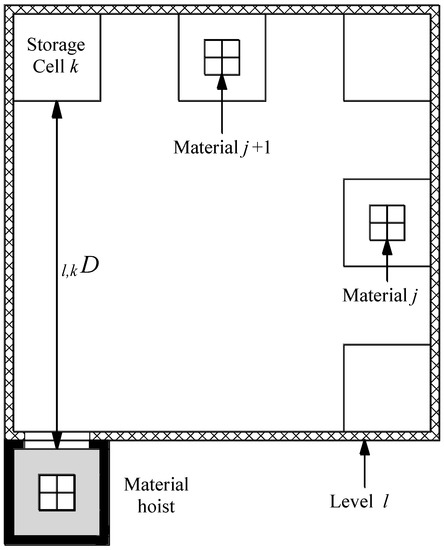
Figure 6.
Floor plan at floor l installing material storage cell.
The objective function is calculated using Equation (9):
where:
- j = Index of Material types.
- l = Index of a building’s floor used for material storage as supply sources.
- k = Index of storage cells on building floors.
- m = Index of a building floor requesting the materials.
- J = The total number of material.
- L = The total number of floors for storage.
- K = The total number of cells on the building level’s.
- M = The total number of levels.
- = Floor m’s demand in a building for material type j.
- = Cost of horizontal unit transportation of material type j.
- = Cost of vertical unit transportation of material type j to a building’s floor l from the ground.
- = Cost of vertical unit transportation of material type j to a building’s floor m from the ground.
- = Distance from the material hoist on level l to cell k.
- = Binary decision variable for storing material j on level l inside cell k.
- = Auxiliary binary-type variable where one means material j is transferred from floor l cell k to floor m, otherwise zero.
Equation (9) has two components used to calculate the total distribution and material transportation costs. The first component involves costing the usage of a hoist to move materials from the ground floor to one of the storage floors. Also included is the horizontal cost of transportation from the elevator to one of the storage cells. We defined a set of binary decision variables representing the location of the materials storage. The second component represents the total cost of material distribution from the floor of storage to each floor of the building requesting materials. The expectation is for requests for material type j, materials on every floor, and m to be presented for the calculation.
Four optimization algorithms were tested in this experiment, namely DE, PSO, SOS, and HSOS-LO. The control parameters for the optimization algorithms tested were set as follows: the population size (pop_size) for DE, PSO, SOS, and HSOS-LO was decided to be 50; the maximum number of function evaluations (maxFE) for DE, PSO, SOS, and HSOS-LO was decided to be 12,000 (equal to 240 iterations for both PSO and DE; 60 iterations for SOS; and 40 iterations for HSOS-LO); and the number of independent runs was set to 100.
Table 5 compares the performance of HSOS-LO with DE, PSO, and SOS. It was shown that HSOS-LO outperforms SOS, PSO, and DE in fitness value, consistency, number of iterations, and number of function evaluations. Table 6 compares the performance of HSOS-LO to the previous research. According to Table 6, HSOS-LO gave a better solution than the references result, saving $5024 in transportation costs. The result is obtained within the average computational time of 0.492 s. Finally, Figure 7 shows the convergence graphic of competing algorithms.

Table 5.
Comparative results of DE, PSO, SOS, and HSOS-LO for Case 2.

Table 6.
The comparative results between HSOS-LO and previous research.
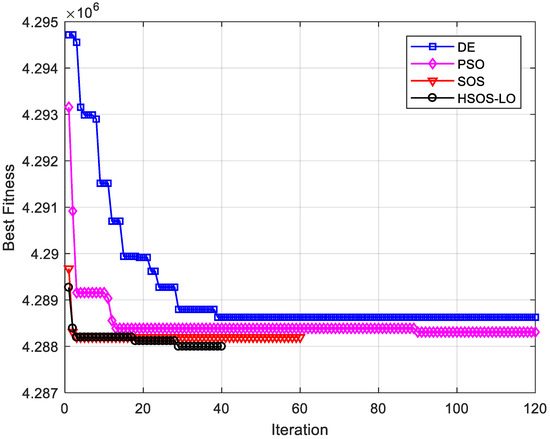
Figure 7.
Convergence graphic of metaheuristic algorithms for Case 2.
5.4. Case Study 3
Given that multi-storey building construction sites have limited space for materials storage, planning for the construction site is critical for construction management. Developing sufficient structural strength in the lower floors to temporarily store materials needed for construction is required for reducing the material transportation times and enhancing the general construction efficacy. A real case study obtained from Fung et al. [35] was used to validate the proposed method. The objective was to design a storage layout plan in the completed floors of a multi-storey building. It considered the horizontal movements between different storage cells and the hoist system. Also, it considered the vertical transportation of construction materials on different floors.
In this case study, the primary objective is to design the temporary construction facilities layout aimed at minimizing the total travelling distance of site workers between different facilities. The site layout has 10 facilities and 10 locations, as can be seen in Figure 8. Entrance gate and guard post are placed permanently at location 4 and 5, respectively, while others are not.
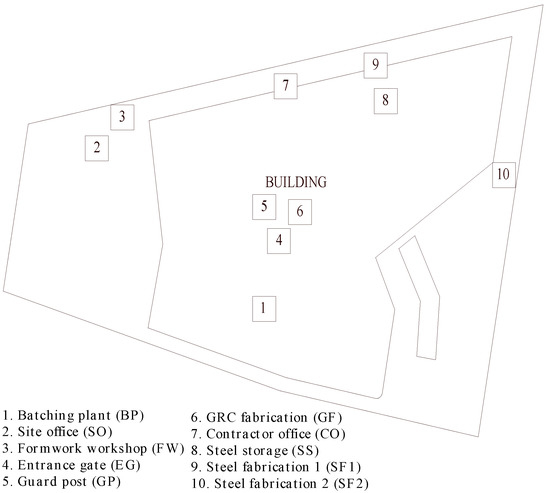
Figure 8.
Site Layout for Case 3.
The objective is to design the temporary facilities layout to get the minimum travel distance, which is calculated by multiplying the frequency and distance between each facility. The daily frequency of trips and the distance between locations are shown in Table 7 and Table 8. The objective function is defined using Equations (1)–(4).

Table 7.
Frequencies of trips between facilities.

Table 8.
Travel distance between locations.
The proposed HSOS-LO was applied in the case study and were compared to the outcome of previous research studies. HSOS-LO was run for 100 simulations and the mean of the best value was recorded. The parameter setting was adopted from previous work; pop_size was set to 30 and maximum number of iterations was set to 20. The results of comparisons are presented in Table 9. The mean best values, standard deviations, and maximum and minimum value are also given in Table 9. The average computational time of HSOS-LO for case 3 is 0.117s. The obtained results have indicated that HSOS-LO manages to outperform the competing algorithms in fitness value and consistency.

Table 9.
Comparative results of DE, PSO, SOS, and HSOS-LO for Case 3.
5.5. Managerial Implication
In this section, we discuss the managerial implication, as well as the limitation and consideration needed before using the HSOS-LO to solve the CSLP. The computational results have shown that the proposed HSOS-LO algorithm can support a decision-maker or project manager by providing a recommendation for the best site and facility layout plan, especially for a construction project. In practice, a project manager may need to re-check the result suggested by the algorithm with the real situation in the field. However, rather than going with a decision based on intuition, a well-analyzed and assessed solution provided by the algorithm can improve the quality of the decision. Furthermore, based on the results shown in case study 1, 2, and 3, which consist of single and multi-floor facility layout problems, there is some consideration needed. The proposed HSOS-LO includes several extra steps in the local search procedure to avoid being trapped in local optimal. Moreover, several real-life problems may involve more complex constraints and decision variables that make the HSOS-LO need to be further modified to solve the problem.
6. Conclusions and Future Research
This paper presented a novel optimization algorithm named hybrid symbiotic organisms search with local operators (HSOS-LO). It is proposed as an innovative search for solving the CSLP problem. As a hybrid of two algorithms, SOS and local operators, HSOS-LO combines the unique searching abilities of both. SOS focuses on global search, while local operators focus on neighbourhood local search. The combination of these advantages creates a new model with better consistency. The HSOS-LO was tested with three real case studies of the construction site layout and the material storage layout problems. Experimental results showed that HSOS-LO has good consistency and reliability in obtaining solutions with good quality within a reasonable time for those layout problems. According to the results, the HSOS-LO surpasses the performance of SOS, PSO, GA, and other optimization algorithms. We, thus, conclude that the novel HSOS-LO is a robust optimization tool for solving the CSLP problem.
Further research may consider the application of the proposed HSOS-LO to solve other problems in a similar setting or variants of the CSLP. The proposed HSOS-LO can be further developed to solve a problem with an extended characteristic of CSLP, such as the one that considers multi-objective optimization.
Author Contributions
Conceptualization, D.P., M.-Y.C., and Y.-W.W.; Methodology, D.P., M.-Y.C., and Y.-W.W., A.A.N.P.R. and V.F.Y.; Software, D.P.; Validation, D.P., M.-Y.C., Y.-W.W., A.A.N.P.R.; Formal analysis, D.P., M.-Y.C., Y.-W.W., A.A.N.P.R.; Investigation, D.P., M.-Y.C., Y.-W.W., A.A.N.P.R.; Resources, D.P., M.-Y.C., Y.-W.W., A.A.N.P.R.; Data curation, D.P. and A.A.N.P.R.; Writing—original draft preparation, D.P., M.-Y.C., and Y.-W.W., A.A.N.P.R. and V.F.Y.; Writing—review and editing, D.P., A.A.N.P.R., V.F.Y., S.F.P., and R.N.; Visualization, D.P., A.A.N.P.R., V.F.Y., S.F.P., and R.N.; Supervision, D.P., M.-Y.C., Y.-W.W. and V.F.Y.; Project administration, D.P.; Funding acquisition, D.P., A.A.N.P.R., S.F.P. and R.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Ministry of Research, grant number SP DIPA-042.06.1.401516/2018.
Acknowledgments
The authors gratefully acknowledge that The Ministry of Research financially supports the present research, Technology, and Higher Education of the Republic of Indonesia under the “World Class Professor” Research Grant Scheme (No: 123.58/D2.3/KP/2018) and partially under the “Penelitian Dasar Unggulan Perguruan Tinggi 2019” Research Grant Scheme (No: SP DIPA-042.06.1.401516/2018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kouvelis, P.; Kurawarwala, A.A.; Gutiérrez, G.J. Algorithms for robust single and multiple period layout planning for manufacturing systems. Eur. J. Oper. Res. 1992, 63, 287–303. [Google Scholar] [CrossRef]
- Tompkins, J.A.; White, J.A.; Bozer, Y.A.; Tanchoco, J.M.A. Facilities Planning, 4th ed.; Wiley: New York, NY, USA, 2010. [Google Scholar]
- Koopmans, T.; Beckmann, M. Assignment Problems and the Location of Economic Activities. Econometrica 1957, 25, 53–76. [Google Scholar] [CrossRef]
- Sahni, S.; Gonzalez, T. P-Complete Approximation Problems. J. ACM 1976, 23, 555–565. [Google Scholar] [CrossRef]
- Mak, K.L.; Wong, Y.S.; Chan, F.T.S. A genetic algorithm for facility layout problems. Comput. Integr. Manuf. Syst. 1998, 11, 113–127. [Google Scholar] [CrossRef]
- Simmons, D.M. One-Dimensional Space Allocation: An Ordering Algorithm. Oper. Res. 1969, 17, 812–826. [Google Scholar] [CrossRef]
- Picard, J.-C.; Queyranne, M. On the One-Dimensional Space Allocation Problem. Oper. Res. 1981, 29, 371–391. [Google Scholar] [CrossRef]
- Love, R.; Wong, J. On Solving A One-Dimensional Space Allocation Problem With Integer Programming. INFOR Inf. Syst. Oper. Res. 2016, 14, 139–143. [Google Scholar] [CrossRef]
- Kumar, R.; Hadjinicola, G.C.; Lin, T.-L. A heuristic procedure for the single-row facility layout problem. Eur. J. Oper. Res. 1995, 87, 65–73. [Google Scholar] [CrossRef]
- Adrian, A.M.; Utamima, A.; Wang, K.-J. A comparative study of GA, PSO and ACO for solving construction site layout optimization. KSCE J. Civ. Eng. 2015, 19, 520–527. [Google Scholar] [CrossRef]
- Ho, S.Y.; Shu, L.S.; Chen, J.H. Intelligent evolutionary algorithms for large parameter optimization problems. IEEE Trans. Evol. Comput. 2004, 8, 522–541. [Google Scholar] [CrossRef]
- Alaghebandha, M.; Hajipour, V.; Hemmati, M. Optimizing multi-objective sequencing problem in mixed-model assembly line on just-in-time: Particle swarm optimization algorithm. Int. J. Manag. Sci. Eng. Manag. 2017, 12, 288–298. [Google Scholar] [CrossRef]
- Yahya, M.; Saka, M.P. Construction site layout planning using multi-objective artificial bee colony algorithm with Levy flights. Autom. Constr. 2014, 38, 14–29. [Google Scholar] [CrossRef]
- Liang, L.Y.; Chao, W.C. The strategies of tabu search technique for facility layout optimization. Autom. Constr. 2008, 17, 657–669. [Google Scholar] [CrossRef]
- Lam, K.C.; Ning, X.; Ng, T. The application of the ant colony optimization algorithm to the construction site layout planning problem. Constr. Manag. Econ. 2007, 25, 359–374. [Google Scholar] [CrossRef]
- Önüt, S.; Tuzkaya, U.R.; Doğaç, B. A particle swarm optimization algorithm for the multiple-level warehouse layout design problem. Comput. Ind. Eng. 2008, 54, 783–799. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.Y. Particle Swarm Optimization for Construction Site Unequal-Area Layout. J. Constr. Eng. Manag. 2008, 134, 739–748. [Google Scholar] [CrossRef]
- Zouein, P.P.; Harmanani, H.; Hajar, A. Genetic Algorithm for Solving Site Layout Problem with Unequal-Size and Constrained Facilities. J. Comput. Civ. Eng. 2002, 16, 143–151. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Roh, M.-I.; Jeong, H.-S. An improved genetic algorithm for multi-floor facility layout problems having inner structure walls and passages. Comput. Oper. Res. 2005, 32, 879–899. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Tran, D.-H.; Cheng, M.-Y.; Prayogo, D. A novel Multiple Objective Symbiotic Organisms Search (MOSOS) for time–cost–labor utilization tradeoff problem. Knowl. Based Syst. 2016, 94, 132–145. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D.; Tran, D.-H. Optimizing Multiple-Resources Leveling in Multiple Projects Using Discrete Symbiotic Organisms Search. J. Comput. Civ. Eng. 2016, 30, 04015036. [Google Scholar] [CrossRef]
- Chagwiza, G.; Jones, B.C.; Hove-Musekwa, S.D.; Mtisi, S. A new hybrid matheuristic optimization algorithm for solving design and network engineering problems. Int. J. Manag. Sci. Eng. Manag. 2018, 13, 11–19. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Prayogo, D. Symbiotic Organisms Search Algorithm: Theory, recent advances and applications. Expert Syst. Appl. 2019, 119, 184–209. [Google Scholar] [CrossRef]
- Prayogo, D.; Cheng, M.-Y.; Wong, F.T.; Tjandra, D.; Tran, D.-H. Optimization model for construction project resource leveling using a novel modified symbiotic organisms search. Asian J. Civ. Eng. 2018, 19, 625–638. [Google Scholar] [CrossRef]
- Tran, D.-H.; Luong-Duc, L.; Duong, M.-T.; Le, T.-N.; Pham, A.-D. Opposition multiple objective symbiotic organisms search (OMOSOS) for time, cost, quality and work continuity tradeoff in repetitive projects. J. Comput. Des. Eng. 2018, 5, 160–172. [Google Scholar] [CrossRef]
- Tejani, G.G.; Pholdee, N.; Bureerat, S.; Prayogo, D. Multiobjective adaptive symbiotic organisms search for truss optimization problems. Knowl. Based Syst. 2018, 161, 398–414. [Google Scholar] [CrossRef]
- Tejani, G.G.; Savsani, V.J.; Patel, V.K. Adaptive symbiotic organisms search (SOS) algorithm for structural design optimization. J. Comput. Des. Eng. 2016, 3, 226–249. [Google Scholar] [CrossRef]
- Tejani, G.G.; Savsani, V.J.; Bureerat, S.; Patel, V.K. Topology and Size Optimization of Trusses with Static and Dynamic Bounds by Modified Symbiotic Organisms Search. J. Comput. Civ. Eng. 2018, 32, 04017085. [Google Scholar] [CrossRef]
- Tejani, G.G.; Savsani, V.J.; Patel, V.K.; Mirjalili, S. Truss optimization with natural frequency bounds using improved symbiotic organisms search. Knowl. Based Syst. 2018, 143, 162–178. [Google Scholar] [CrossRef]
- Sule, D.R. Manufacturing Facilities: Location, Planning, and Design; PWS-Kent Pub. Co.: Boston, MA, USA, 1988; p. 514. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Yu, V.F.; Redi, A.A.N.P.; Yang, C.-L.; Ruskartina, E.; Santosa, B. Symbiotic organisms search and two solution representations for solving the capacitated vehicle routing problem. Appl. Soft Comput. 2017, 52, 657–672. [Google Scholar] [CrossRef]
- Li, H.; Love, P.E.D. Site-Level Facilities Layout Using Genetic Algorithms. J. Comput. Civ. Eng. 1998, 12, 227–231. [Google Scholar] [CrossRef]
- Fung, I.W.H.; Wong, C.K.; Tam, C.M.; Tong, T.K.L. Optimizing Material Hoisting Operations and Storage Cells in Single Multi-storey Tower Block Construction by Genetic Algorithm. Int. J. Constr. Manag. 2008, 8, 53–64. [Google Scholar] [CrossRef]
- Prayogo, D.; Sutanto, J.C.; Suryo, H.E.; Eric, S. A Comparative Study on Bio-Inspired Algorithms in Layout Optimization of Construction Site Facilities. Civ. Eng. Dimens. 2018, 20, 102–110. [Google Scholar] [CrossRef]
- Kaveh, A. Construction Site Layout Planning Using Colliding Bodies Optimization and Enhanced Colliding Bodies Optimization. In Applications of Metaheuristic Optimization Algorithms in Civil Engineering; Springer International Publishing: Basel, Switzerland, 2016; pp. 351–373. [Google Scholar]
- Huang, C.; Wong, C.K.; Tam, C.M. Optimization of material hoisting operations and storage locations in multi-storey building construction by mixed-integer programming. Autom. Constr. 2010, 19, 656–663. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).