Two-Step Classification with SVD Preprocessing of Distributed Massive Datasets in Apache Spark
Abstract
1. Introduction
2. Related Work
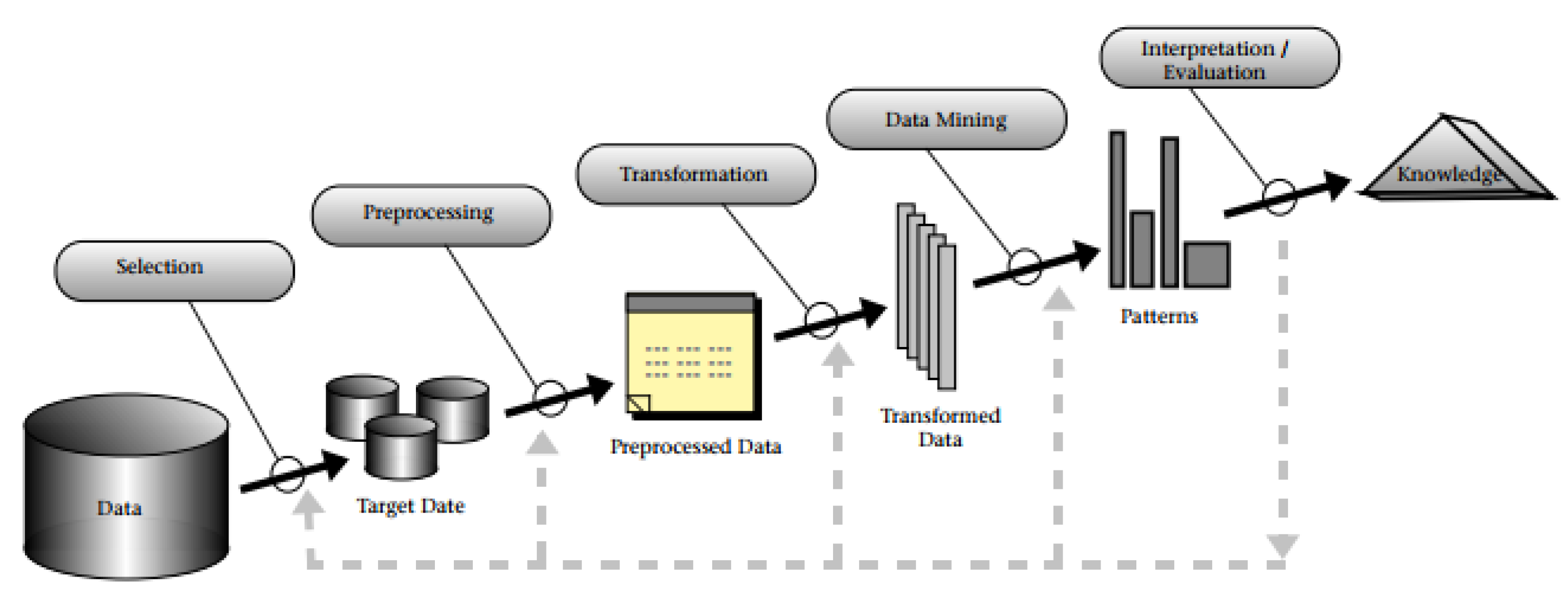
2.1. Data Mining and Two-Step Classification
2.2. Distributed Computing
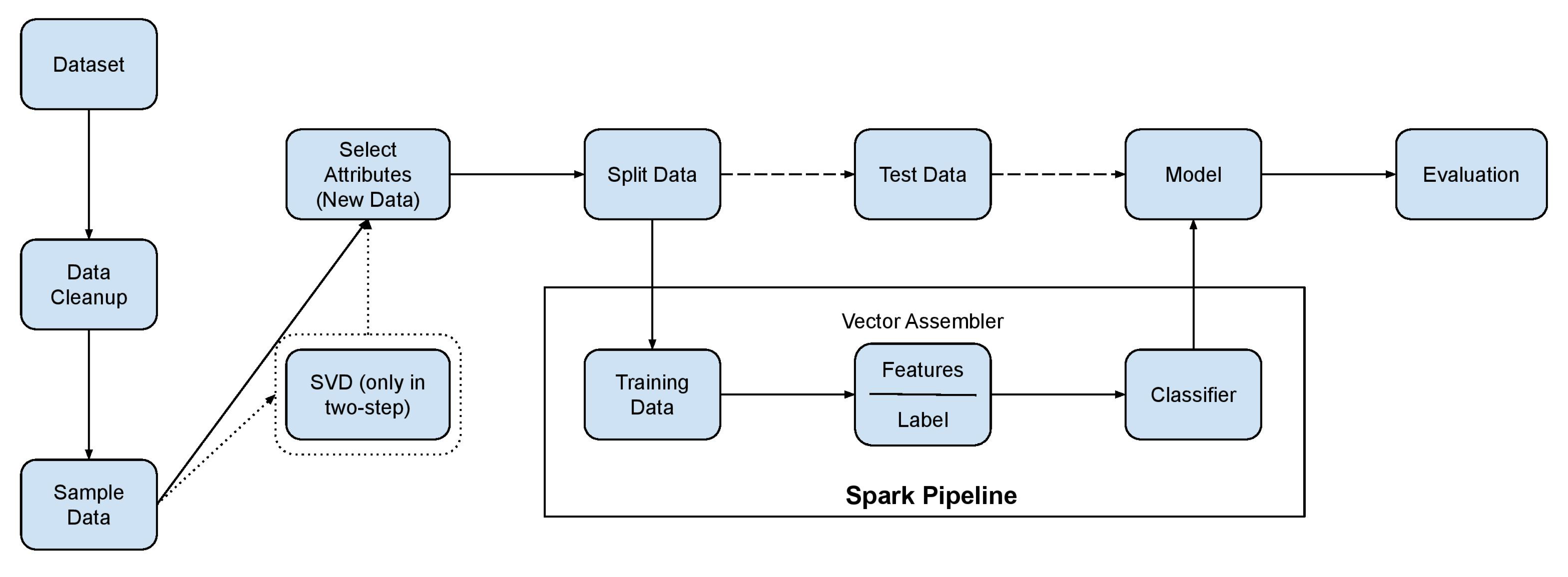
3. Proposed Method
3.1. 10V Data
- Volume: The volume of 10V data greatly exceeds the main memory capacity and, therefore, the data have to be moved to secondary memory and possibly across over a distributed system such as NFS, Minio, and HDFS. Thus, new computational strategies about moving the computations and not the data have to be developed.
- Velocity: This factor refers to the rate data are generated or refreshed. Data update rate depends on the application and ranges from milliseconds to hours. The larger the time scale, the bigger the need for a sizeable buffer zone.
- Variety: 10V collected data can well be structured in various formats, semistructured, or unstructured according to the collection policies. It is not unlikely the same dataset contains graphs, images, sound clips, maps, video, and text as well as raw measurements in binary blobs.
- Variability: Large datasets are bound to contain missing values and outliers, both of which need to be addressed with cleansing and anomaly discovery methods as appropriate. The latter are crucial in improving data quality and facilitate building more efficient pipelines.
- Volatility: This factor refers to the useful data life span. Before the advent of 10V data it was not uncommon to store everything in data warehouses. Now there is pressure for more selective strategies. Choosing which entries or which transformed attributes for long term storage is a major topic in data science.
- Visualization: Humans tend to understand better the “big picture” inherent in the processed and refined knowledge because of the way brain operates. Thus, information visualization may well be the key to successfully conveying a message. Although lately the importance of storytelling techniques has gained traction, visualization remains the best and easiest way to describe sizeable amounts of knowledge.
- Vulnerability: Each and every computing device nowadays is a potential security threat. The systems of a data processing pipeline are no exception, especially if they collect measurements with the outside world.
- Veracity: Creating ad hoc queries and small scale tests easily is an important parameter in data quality. Given the unstructured nature of 10V data, the development of ad hoc queries is paramount as invaluable insight can be gained from them.
- Validity: This factor refers to how relevant the dataset is to the questions which are to be answered. This includes among others how data are sampled and collected, how frequently are updated, how the collection methodology influences data integrity, and what transforms are appropriate.
- Value: The design of a specialized ML pipeline or the implementation of a generic one is an expensive action. Therefore, there should be at least some evidence that the knowledge contained in the raw data can be of tremendous benefit.
3.2. Classification Algorithms
3.2.1. Decision Trees
3.2.2. Random Forest
3.2.3. Logistic Regression
3.2.4. Gradient-Boosted Trees
3.2.5. Multilayer Perceptron
3.2.6. One-Vs-Rest
3.3. Feature Selection
- When n is smaller than 100 or when k exceeds , then the Gramian matrix is computed and its top eigenvectors are subsequently computed locally at the Spark driver.
- Otherwise, the Gramian matrix is computed in a distributed way and its top eigenvectors are again locally computed at the driver as in the previous case.
3.4. Complexities
4. Implementation
4.1. Databricks
4.2. Higgs Dataset
4.3. PAMAP Dataset
4.4. Analysis Cases
- Decision trees were optimized based on the depth of the trees with values ranging between 2 and 30.
- Random forest was optimized in terms of the number of trees in the forest with values ranging between 1 and 60, having a step equal to two and maximum tree height equal to 10.
- Logistic regression was implemented for binomial and multinomial.
- Gradient-boosted tree was optimized based on the depth of the trees with values ranging between 2 and 4 and the total number of trees equal to 150. It must be noted that this type of classifier was only used with the Higgs dataset because it is considered as a binomial classifier.
- Multilayer perceptron with two, three, and four levels of hidden layers. For the case of two levels, the numbers of nodes were , , respectively, whereas for case of three levels the numbers of nodes were , , , and for the case of four levels , , and . Moreover, the number of epochs was set equal to 1000.
- One-Vs-Rest was only used with the PAMAP dataset.
5. Evaluation
5.1. Higgs Dataset
5.1.1. Analysis with all Features
5.1.2. Analysis with Limited Number of Features
5.1.3. Discussion over Higgs Dataset
5.2. PAMAP Dataset
Discussion over PAMAP Dataset
6. Conclusions and Future Work
- SVD has been initially applied to the original data matrix in order to obtain a low dimensional representation with a smaller attribute set.
- The classifier has been subsequently applied to the new attribute set in order to obtain the final labellings.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alexopoulos, A.; Kanavos, A.; Giotopoulos, K.C.; Mohasseb, A.; Bader-El-Den, M.; Tsakalidis, A.K. Incremental Learning for Large Scale Classification Systems. In IFIP International Conference on Artificial Intelligence Applications and Innovations; Iliadis, L., Maglogiannis, I., Plagianakos, V., Eds.; Springer: Cham, Switzerland, 2018; Volume 520, pp. 112–122. [Google Scholar]
- Hand, D.J.; Mannila, H.; Smyth, P. Principles of Data Mining; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Fayyad, U.M.; Piatetsky-Shapiro, G.; Smyth, P. From Data Mining to Knowledge Discovery in Databases. AI Mag. 1996, 17, 37–54. [Google Scholar]
- Witten, I.H.; Eibe, F.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Candes, E.; Tao, T. The Dantzig Selector: Statistical Estimation when p is Much Larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar] [CrossRef]
- Koltchinskii, V. The Dantzig Selector and Sparsity Oracle Inequalities. Bernoulli 2009, 15, 799–828. [Google Scholar] [CrossRef]
- Koperski, K.; Han, J.; Stefanovic, N. An Efficient Two-Step Method for Classification of Spatial Data. In Proceedings of the International Symposium on Spatial Data Handling (SDH), Vancouver, BC, Canada, 11–15 July 1998; pp. 45–54. [Google Scholar]
- Christen, P. A Two-Step Classification Approach to Unsupervised Record Linkage. In Proceedings of the 6th Australasian Data Mining Conference (AusDM), Gold Coast, Australia, 3–4 December 2007; pp. 111–119. [Google Scholar]
- Lian, C.; Ruan, S.; Denoeux, T. An Evidential Classifier based on Feature Selection and Two-Step Classification Strategy. Pattern Recogn. 2015, 48, 2318–2327. [Google Scholar] [CrossRef]
- Drakopoulos, G.; Stathopoulou, F.; Kanavos, A.; Paraskevas, M.; Tzimas, G.; Mylonas, P.; Iliadis, L. A Genetic Algorithm for Spatiosocial Tensor Clustering: Exploiting TensorFlow Potential; Springer: Berlin, Germany, 2019; pp. 1–11. [Google Scholar]
- Alloghani, M.; Al-Jumeily, D.; Hussain, A.; Mustafina, J.; Baker, T.; Aljaaf, A.J. Implementation of Machine Learning and Data Mining to Improve Cybersecurity and Limit Vulnerabilities to Cyber Attacks. In Nature-Inspired Computation in Data Mining and Machine Learning; Yang, X.S., He, X.S., Eds.; Springer: Cham, Switzerland, 2020; Volume 855, pp. 47–76. [Google Scholar]
- Alloghani, M.; Baker, T.; Al-Jumeily, D.; Hussain, A.; Mustafina, J.; Aljaaf, A.J. Prospects of Machine and Deep Learning in Analysis of Vital Signs for the Improvement of Healthcare Services. In Nature-Inspired Computation in Data Mining and Machine Learning; Yang, X.S., He, X.S., Eds.; Springer: Cham, Switzerland, 2020; Volume 855, pp. 113–136. [Google Scholar]
- Moniruzzaman, A.B.M.; Hossain, S.A. NoSQL Database: New Era of Databases for Big data Analytics - Classification, Characteristics and Comparison. 2013. Available online: http://article.nadiapub.com/IJDTA/vol6_no4/1.pdf (accessed on 22 March 2020).
- Melnik, S.; Gubarev, A.; Long, J.J.; Romer, G.; Shivakumar, S.; Tolton, M.; Vassilakis, T. Dremel: Interactive Analysis of Web-Scale Datasets. Proc. VLDB Endow. 2010, 3, 330–339. [Google Scholar] [CrossRef]
- Malewicz, G.; Austern, M.H.; Bik, A.J.C.; Dehnert, J.C.; Horn, I.; Leiser, N.; Czajkowski, G. Pregel: A system for large-scale graph processing. In Proceedings of the ACM International Conference on Management of Data (SIGMOD), Indianapolis, IN, USA, 6–11 June 2010; pp. 135–146. [Google Scholar]
- Isard, M.; Budiu, M.; Yu, Y.; Birrell, A.; Fetterly, D. Dryad: Distributed Data-Parallel Programs from Sequential. Building Blocks. In Proceedings of the 2nd ACM SIGOPS/EuroSys European Conference on Computer Systems, New York, NA, USA, 21 March 2007; pp. 59–72. [Google Scholar]
- Low, Y.; Gonzalez, J.; Kyrola, A.; Bickson, D.; Guestrin, C.; Hellerstein, J.M. Distributed GraphLab: A Framework for Machine Learning in the Cloud. 2012. Available online: http://vldb.org/pvldb/vol5/p716_yuchenglow_vldb2012.pdf (accessed on 22 March 2020).
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache Spark: A Unified Engine for Big Data Processing. Comm. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Shvachko, K.; Kuang, H.; Radia, S.; Chansler, R. The Hadoop Distributed File System. In Proceedings of the IEEE 26th Symposium on Mass Storage Systems and Technologies (MSST), Incline Village, NV, USA, 3–7 May 2010; pp. 1–10. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified Data Processing on Large Clusters. Comm. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Shi, J.; Qiu, Y.; Minhas, U.F.; Jiao, L.; Wang, C.; Reinwald, B.; Özcan, F. Clash of the Titans: MapReduce vs. Spark for Large Scale Data Analytics. Proc. VLDB Endow. 2015, 8, 2110–2121. [Google Scholar] [CrossRef]
- Koliopoulos, A.; Yiapanis, P.; Tekiner, F.; Nenadic, G.; Keane, J.A. A Parallel Distributed Weka Framework for Big Data Mining Using Spark. In Proceedings of the IEEE International Congress on Big Data, New York, NY, USA, 27 June–2 July 2015; pp. 9–16. [Google Scholar]
- Hall, M.A.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Yang, L.; Shi, Z. An Efficient Data Mining Framework on Hadoop using Java Persistence API. In Proceedings of the 10th IEEE International Conference on Computer and Information Technology (CIT), Bradford, UK, 29 June–1 July 2010; pp. 203–209. [Google Scholar]
- Zhao, W.; Ma, H.; He, Q. Parallel K-Means Clustering Based on MapReduce; Springer: Berlin, Germany, 1 December 2009; pp. 674–679. [Google Scholar]
- Kang, U.; Faloutsos, C. Big Graph Mining: Algorithms and Discoveries. SIGKDD Explor. 2012, 14, 29–36. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kyriazidou, I.; Drakopoulos, G.; Kanavos, A.; Makris, C.; Mylonas, P. Towards Predicting Mentions to Verified Twitter Accounts: Building Prediction Models over MongoDB with Keras. 2019. Available online: https://www.researchgate.net/profile/Georgios_Drakopoulos/publication/334681267_Towards_Predicting_Mentions_To_Verified_Twitter_Accounts_Building_Prediction_Models_Over_MongoDB_With_Keras/links/5d39dfe792851cd046869a4c/Towards-Predicting-Mentions-To-Verified-Twitter-Accounts-Building-Prediction-Models-Over-MongoDB-With-Keras.pdf (accessed on 22 March 2020).
- Zhang, T. Solving Large Scale Linear Prediction Problems Using Stochastic Gradient Descent Algorithms. In Proceedings of the 21st International Conference on Machine Learning (ICML), Banff, AB, Canada, 4 July 2004. [Google Scholar]
- Younis, O.; Fahmy, S. Distributed Clustering in Ad-hoc Sensor Networks: A Hybrid, Energy-Efficient Approach. In Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM), Hong Kong, China, 7–11 March 2004. [Google Scholar]
- Januzaj, E.; Kriegel, H.; Pfeifle, M. DBDC: Density Based Distributed Clustering. In Advances in Database Technology - EDBT 2004; Bertino, E., Ed.; Springer: Berlin, Germany, 2004; Volume 2992, pp. 88–105. [Google Scholar]
- Gorodetsky, V.; Karsaev, O.; Samoilov, V. Multi-agent Technology for Distributed Data Mining and Classification. In Proceedings of the IEEE/WIC International Conference on Intelligent Agent Technology (IAT), Halifax, NS, Canada, 13–17 October 2003; pp. 438–441. [Google Scholar]
- Ghasemzadeh, H.; Loseu, V.; Jafari, R. Structural Action Recognition in Body Sensor Networks: Distributed Classification Based on String Matching. IEEE Trans. Inform. Tech. Biomed. 2010, 14, 425–435. [Google Scholar] [CrossRef] [PubMed]
- Kokiopoulou, E.; Frossard, P. Distributed Classification of Multiple Observation Sets by Consensus. IEEE Trans. Signal Process. 2011, 59, 104–114. [Google Scholar] [CrossRef]
- D’Costa, A.; Sayeed, A.M. Collaborative Signal Processing for Distributed Classification in Sensor Networks. In Information Processing in Sensor Networks; Zhao, F., Guibas, L., Eds.; Springer: Berlin, Germany, 2003; Volume 2634, pp. 193–208. [Google Scholar]
- Malhotra, B.; Nikolaidis, I.; Harms, J.J. Distributed Classification of Acoustic Targets in Wireless audio-sensor Networks. Comput. Netw. 2008, 52, 2582–2593. [Google Scholar] [CrossRef]
- Raychaudhuri, S. Introduction to Monte Carlo simulation. In Proceedings of the Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 91–100. [Google Scholar]
- Meng, X.; Bradley, J.K.; Yavuz, B.; Sparks, E.R.; Venkataraman, S.; Liu, D.; Freeman, J.; Tsai, D.B.; Amde, M.; Owen, S.; et al. MLlib: Machine Learning in Apache Spark. J. Mach. Learn. Res. 2016, 17, 1235–1241. [Google Scholar]
- Baltas, A.; Kanavos, A.; Tsakalidis, A. An Apache Spark Implementation for Sentiment Analysis on Twitter Data. In Algorithmic Aspects of Cloud Computing; Sellis, T., Oikonomou, K., Eds.; Springer: Cham, Switzerland, 2016; Volume 10230, pp. 15–25. [Google Scholar]
- Sioutas, S.; Mylonas, P.; Panaretos, A.; Gerolymatos, P.; Vogiatzis, D.; Karavaras, E.; Spitieris, T.; Kanavos, A. Survey of Machine Learning Algorithms on Spark Over DHT-based Structures. In Algorithmic Aspects of Cloud Computing; Sellis, T., Oikonomou, K., Eds.; Springer: Cham, Switzerland, 2016; Volume 10230, pp. 146–156. [Google Scholar]
- Kanavos, A.; Nodarakis, N.; Sioutas, S.; Tsakalidis, A.; Tsolis, D.; Tzimas, G. Large Scale Implementations for Twitter Sentiment Classification. Algorithms 2017, 10, 33. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Supervised Machine Learning: A Review of Classification Techniques. Inform. (Slovenia) 2007, 31, 249–268. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mohan, A.; Chen, Z.; Weinberger, K.Q. Web-Search Ranking with Initialized Gradient Boosted Regression Trees. 2011. Available online: http://proceedings.mlr.press/v14/mohan11a/mohan11a.pdf (accessed on 22 March 2020).
- Baldi, P.; Sadowski, P.; Whiteson, D. Searching for Exotic Particles in High-energy Physics with Deep Learning. Nat. Comm. 2014, 5, 4308. [Google Scholar] [CrossRef] [PubMed]
- Reiss, A.; Stricker, D. Introducing a New Benchmarked Dataset for Activity Monitoring. In Proceedings of the International Symposium on Wearable Computers (ISWC), Newcastle, UK, 18–22 June 2012; pp. 108–109. [Google Scholar]
| Dataset Size | Precision | Recall | Metric | Time | Depth | Number of Nodes |
|---|---|---|---|---|---|---|
| one-step classifier | ||||||
| 5.000 | 0.633 | 0.631 | 0.632 | 0:12:19 | 4 | 31 |
| 10.000 | 0.665 | 0.665 | 0.665 | 0:14:09 | 6 | 119 |
| 25.000 | 0.662 | 0.662 | 0.662 | 0:18:53 | 7 | 231 |
| 50.000 | 0.682 | 0.683 | 0.682 | 0:39:13 | 8 | 469 |
| 75.000 | 0.688 | 0.687 | 0.687 | 0:50:17 | 7 | 251 |
| 100.000 | 0.688 | 0.688 | 0.688 | 1:03:39 | 9 | 961 |
| 200.000 | 0.692 | 0.692 | 0.692 | 1:42:47 | 9 | 1001 |
| two-step classifier | ||||||
| 5.000 | 0.618 | 0.618 | 0.618 | 0:11:43 | 2 | 7 |
| 10.000 | 0.657 | 0.657 | 0.657 | 0:14:26 | 7 | 205 |
| 25.000 | 0.638 | 0.639 | 0.638 | 0:18:13 | 7 | 237 |
| 50.000 | 0.657 | 0.657 | 0.657 | 0:37:21 | 6 | 119 |
| 75.000 | 0.661 | 0.662 | 0.661 | 0:48:17 | 7 | 255 |
| 100.000 | 0.659 | 0.659 | 0.659 | 1:04:29 | 10 | 1667 |
| 200.000 | 0.663 | 0.663 | 0.663 | 1:39:18 | 9 | 963 |
| Dataset Size | Precision | Recall | Metric | Time | Number of Trees | Number of Nodes |
|---|---|---|---|---|---|---|
| one-step classifier | ||||||
| 5.000 | 0.683 | 0.682 | 0.682 | 0:18:04 | 58 | 32,662 |
| 10.000 | 0.698 | 0.697 | 0.697 | 0:24:52 | 52 | 40,712 |
| 25.000 | 0.699 | 0.700 | 0.699 | 0:38:09 | 46 | 50,044 |
| 50.000 | 0.704 | 0.704 | 0.704 | 1:32:04 | 38 | 48,974 |
| 75.000 | 0.713 | 0.713 | 0.713 | 2:02:18 | 54 | 75,846 |
| 100.000 | 0.713 | 0.713 | 0.713 | 2:28:50 | 44 | 65,826 |
| 200.000 | 0.710 | 0.711 | 0.710 | 4:10:07 | 54 | 90,658 |
| two-step classifier | ||||||
| 5.000 | 0.661 | 0.661 | 0.661 | 0:17:04 | 44 | 22,474 |
| 10.000 | 0.686 | 0.684 | 0.685 | 0:22:46 | 42 | 29,762 |
| 25.000 | 0.671 | 0.671 | 0.671 | 0:39:18 | 60 | 61,290 |
| 50.000 | 0.679 | 0.678 | 0.679 | 1:35:13 | 52 | 61,358 |
| 75.000 | 0.681 | 0.681 | 0.681 | 2:20:12 | 54 | 72,610 |
| 100.000 | 0.683 | 0.684 | 0.684 | 2:47:25 | 54 | 78,582 |
| 200.000 | 0.684 | 0.684 | 0.684 | 4:44:11 | 52 | 82,542 |
| Dataset Size | Precision | Recall | Metric | Time |
|---|---|---|---|---|
| one-step classifier | ||||
| 5.000 | 0.609 | 0.609 | 0.609 | 0:00:02 |
| 10.000 | 0.649 | 0.645 | 0.639 | 0:00:02 |
| 25.000 | 0.636 | 0.634 | 0.634 | 0:00:02 |
| 50.000 | 0.644 | 0.642 | 0.642 | 0:00:04 |
| 75.000 | 0.644 | 0.645 | 0.644 | 0:00:05 |
| 100.000 | 0.648 | 0.648 | 0.648 | 0:00:05 |
| 200.000 | 0.641 | 0.639 | 0.639 | 0:00:08 |
| two-step classifier | ||||
| 5.000 | 0.605 | 0.606 | 0.606 | 0:00:01 |
| 10.000 | 0.619 | 0.617 | 0.618 | 0:00:01 |
| 25.000 | 0.616 | 0.616 | 0.616 | 0:00:03 |
| 50.000 | 0.615 | 0.615 | 0.615 | 0:00:03 |
| 75.000 | 0.617 | 0.617 | 0.617 | 0:00:04 |
| 100.000 | 0.618 | 0.618 | 0.618 | 0:00:06 |
| 200.000 | 0.620 | 0.621 | 0.620 | 0:00:08 |
| Dataset Size | Precision | Recall | Metric | Time | Number of Trees | Number of Nodes | Depth |
|---|---|---|---|---|---|---|---|
| one-step classifier | |||||||
| 5.000 | 0.680 | 0.681 | 0.680 | 0:33:54 | 150 | 1050 | 2 |
| 10.000 | 0.707 | 0.707 | 0.707 | 0:45:17 | 150 | 2250 | 3 |
| 25.000 | 0.701 | 0.701 | 0.701 | 1:13:27 | 150 | 2250 | 3 |
| 50.000 | 0.714 | 0.714 | 0.714 | 1:24:24 | 150 | 4648 | 4 |
| 75.000 | 0.723 | 0.724 | 0.723 | 1:34:58 | 150 | 4650 | 4 |
| 100.000 | 0.723 | 0.723 | 0.723 | 1:42:02 | 150 | 4650 | 4 |
| 200.000 | 0.725 | 0.725 | 0.725 | 2:08:07 | 150 | 4650 | 4 |
| two-step classifier | |||||||
| 5.000 | 0.654 | 0.654 | 0.654 | 0:32:13 | 150 | 1050 | 2 |
| 10.000 | 0.684 | 0.684 | 0.684 | 0:40:36 | 150 | 2250 | 3 |
| 25.000 | 0.681 | 0.681 | 0.681 | 1:11:34 | 150 | 4646 | 4 |
| 50.000 | 0.691 | 0.691 | 0.691 | 1:14:43 | 150 | 4642 | 4 |
| 75.000 | 0.693 | 0.693 | 0.693 | 1:25:17 | 150 | 4648 | 4 |
| 100.000 | 0.694 | 0.694 | 0.694 | 1:34:30 | 150 | 4648 | 4 |
| 200.000 | 0.695 | 0.695 | 0.695 | 1:57:28 | 150 | 4650 | 4 |
| Dataset Size | Precision | Recall | Metric | Time | Best Layer |
|---|---|---|---|---|---|
| one-step classifier | |||||
| 5.000 | 0.595 | 0.595 | 0.595 | 0:06:51 | [28, 15, 14, 2] |
| 10.000 | 0.641 | 0.641 | 0.641 | 0:12:55 | [28, 15, 14, 2] |
| 25.000 | 0.688 | 0.688 | 0.688 | 0:27:49 | [28, 15, 14, 2] |
| 50.000 | 0.711 | 0.712 | 0.711 | 0:54:28 | [28, 15, 14, 2] |
| 75.000 | 0.726 | 0.726 | 0.726 | 1:17:05 | [28, 20, 15, 2] |
| 100.000 | 0.726 | 0.726 | 0.726 | 1:40:54 | [28, 25, 20, 15, 2] |
| 200.000 | 0.720 | 0.720 | 0.720 | 3:50:29 | [28, 25, 20, 2] |
| two-step classifier | |||||
| 5.000 | 0.551 | 0.551 | 0.551 | 0:08:45 | [21, 35, 25, 20, 2] |
| 10.000 | 0.569 | 0.571 | 0.570 | 0:12:45 | [21, 15, 14, 2] |
| 25.000 | 0.583 | 0.583 | 0.583 | 0:27:25 | [21, 15, 14, 2] |
| 50.000 | 0.627 | 0.627 | 0.627 | 0:52:05 | [21, 15, 14, 2] |
| 75.000 | 0.663 | 0.663 | 0.663 | 1:16:24 | [21, 35, 30, 25, 20, 2] |
| 100.000 | 0.693 | 0.693 | 0.693 | 1:41:06 | [21, 25, 20, 2] |
| 200.000 | 0.695 | 0.695 | 0.695 | 3:16:22 | [21, 40, 30, 20, 2] |
| Dataset Size | Precision | Recall | Metric | Time | Depth | Number of Nodes |
|---|---|---|---|---|---|---|
| one-step classifier | ||||||
| 5.000 | 0.581 | 0.583 | 0.581 | 0:12:23 | 10 | 443 |
| 10.000 | 0.594 | 0.593 | 0.593 | 0:13:33 | 7 | 215 |
| 25.000 | 0.593 | 0.592 | 0.592 | 0:17:01 | 8 | 327 |
| 50.000 | 0.589 | 0.59 | 0.589 | 0:32:32 | 8 | 357 |
| 75.000 | 0.606 | 0.607 | 0.607 | 0:40:26 | 9 | 749 |
| 100.000 | 0.602 | 0.603 | 0.602 | 0:48:19 | 9 | 745 |
| 200.000 | 0.609 | 0.609 | 0.609 | 1:21:53 | 10 | 1357 |
| two-step classifier | ||||||
| 5.000 | 0.57 | 0.568 | 0.569 | 0:11:31 | 8 | 263 |
| 10.000 | 0.589 | 0.589 | 0.589 | 0:13:37 | 7 | 189 |
| 25.000 | 0.593 | 0.593 | 0.593 | 0:16:25 | 8 | 331 |
| 50.000 | 0.593 | 0.593 | 0.593 | 0:51:13 | 8 | 353 |
| 75.000 | 0.608 | 0.61 | 0.609 | 0:53:45 | 9 | 757 |
| 100.000 | 0.61 | 0.61 | 0.61 | 1:05:24 | 9 | 739 |
| 200.000 | 0.611 | 0.611 | 0.611 | 1:48:17 | 10 | 1391 |
| Dataset Size | Precision | Recall | Metric | Time | Number of Trees | Number of Nodes |
|---|---|---|---|---|---|---|
| one-step classifier | ||||||
| 5.000 | 0.59 | 0.59 | 0.59 | 0:16:07 | 50 | 24,056 |
| 10.000 | 0.612 | 0.609 | 0.611 | 0:21:43 | 54 | 36,924 |
| 25.000 | 0.622 | 0.623 | 0.622 | 0:33:33 | 52 | 48,906 |
| 50.000 | 0.615 | 0.615 | 0.615 | 1:22:39 | 36 | 40,438 |
| 75.000 | 0.628 | 0.629 | 0.629 | 1:47:26 | 56 | 68,434 |
| 100.000 | 0.631 | 0.633 | 0.632 | 2:15:43 | 60 | 78,488 |
| 200.000 | 0.627 | 0.627 | 0.627 | 4:15:01 | 58 | 85,640 |
| two-step classifier | ||||||
| 5.000 | 0.597 | 0.596 | 0.597 | 0:16:07 | 46 | 22,682 |
| 10.000 | 0.622 | 0.62 | 0.621 | 0:21:18 | 54 | 37,778 |
| 25.000 | 0.62 | 0.62 | 0.62 | 0:33:02 | 60 | 57,682 |
| 50.000 | 0.625 | 0.626 | 0.626 | 1:36:53 | 56 | 63,868 |
| 75.000 | 0.63 | 0.632 | 0.631 | 2:06:27 | 46 | 57,202 |
| 100.000 | 0.631 | 0.632 | 0.632 | 2:36:19 | 60 | 80,748 |
| 200.000 | 0.628 | 0.628 | 0.628 | 4:26:49 | 56 | 84,224 |
| Dataset Size | Precision | Recall | Metric | Time |
|---|---|---|---|---|
| one-step classifier | ||||
| 5.000 | 0.551 | 0.555 | 0.553 | 0:00:02 |
| 10.000 | 0.574 | 0.572 | 0.573 | 0:00:02 |
| 25.000 | 0.561 | 0.56 | 0.56 | 0:00:02 |
| 50.000 | 0.563 | 0.563 | 0.563 | 0:00:02 |
| 75.000 | 0.567 | 0.566 | 0.566 | 0:00:02 |
| 100.000 | 0.567 | 0.567 | 0.567 | 0:00:02 |
| 200.000 | 0.563 | 0.564 | 0.563 | 0:00:04 |
| two-step classifier | ||||
| 5.000 | 0.605 | 0.606 | 0.606 | 0:00:01 |
| 10.000 | 0.619 | 0.617 | 0.618 | 0:00:01 |
| 25.000 | 0.616 | 0.616 | 0.616 | 0:00:01 |
| 50.000 | 0.615 | 0.615 | 0.615 | 0:00:01 |
| 75.000 | 0.617 | 0.617 | 0.617 | 0:00:01 |
| 100.000 | 0.618 | 0.618 | 0.618 | 0:00:02 |
| 200.000 | 0.620 | 0.621 | 0.620 | 0:00:04 |
| Dataset Size | Precision | Recall | Metric | Time | Number of Trees | Number of Nodes | Depth |
|---|---|---|---|---|---|---|---|
| one-step classifier | |||||||
| 5.000 | 0.587 | 0.589 | 0.588 | 0:30:48 | 150 | 1050 | 2 |
| 10.000 | 0.611 | 0.612 | 0.611 | 0:38:21 | 150 | 2250 | 3 |
| 25.000 | 0.623 | 0.622 | 0.622 | 1:00:27 | 150 | 4646 | 4 |
| 50.000 | 0.628 | 0.629 | 0.629 | 1:10:17 | 150 | 4644 | 4 |
| 75.000 | 0.642 | 0.644 | 0.643 | 1:13:24 | 150 | 4636 | 4 |
| 100.000 | 0.638 | 0.64 | 0.639 | 1:21:09 | 150 | 4646 | 4 |
| 200.000 | 0.64 | 0.641 | 0.64 | 1:49:08 | 150 | 4650 | 4 |
| two-step classifier | |||||||
| 5.000 | 0.595 | 0.596 | 0.596 | 0:30:27 | 150 | 1050 | 2 |
| 10.000 | 0.603 | 0.602 | 0.603 | 0:36:13 | 150 | 2250 | 3 |
| 25.000 | 0.617 | 0.618 | 0.618 | 0:43:43 | 150 | 2250 | 3 |
| 50.000 | 0.627 | 0.629 | 0.628 | 1:22:24 | 150 | 4646 | 4 |
| 75.000 | 0.643 | 0.644 | 0.644 | 1:20:34 | 150 | 4648 | 4 |
| 100.000 | 0.64 | 0.641 | 0.64 | 1:29:18 | 150 | 4650 | 4 |
| 200.000 | 0.638 | 0.64 | 0.639 | 2:04:26 | 150 | 4650 | 4 |
| Dataset Size | Precision | Recall | Metric | Time | Best Layer |
|---|---|---|---|---|---|
| one-step classifier | |||||
| 5.000 | 0.552 | 0.551 | 0.551 | 0:06:52 | [21, 40, 30, 20, 2] |
| 10.000 | 0.569 | 0.568 | 0.568 | 0:12:53 | [21, 35, 30, 25, 20, 2] |
| 25.000 | 0.552 | 0.552 | 0.552 | 0:27:51 | [21, 15, 14, 2] |
| 50.000 | 0.553 | 0.553 | 0.553 | 0:52:27 | [21, 15, 14, 2] |
| 75.000 | 0.563 | 0.564 | 0.564 | 1:16:54 | [21, 35, 30, 25, 20, 2] |
| 100.000 | 0.601 | 0.602 | 0.602 | 1:42:20 | [21, 30, 25, 20, 15, 2] |
| 200.000 | 0.645 | 0.643 | 0.644 | 3:20:58 | [21, 40, 35, 30, 25, 2] |
| two-step classifier | |||||
| 5.000 | 0.516 | 0.518 | 0.517 | 0:06:56 | [16, 35, 25, 20, 2] |
| 10.000 | 0.524 | 0.524 | 0.524 | 0:11:14 | [16, 35, 30, 25, 20, 2] |
| 25.000 | 0.543 | 0.542 | 0.543 | 0:24:02 | [16, 15, 14, 2] |
| 50.000 | 0.546 | 0.547 | 0.547 | 0:46:20 | [16, 25, 20, 2] |
| 75.000 | 0.553 | 0.553 | 0.553 | 1:06:16 | [16, 35, 25, 20, 2] |
| 100.000 | 0.563 | 0.564 | 0.564 | 1:27:21 | [16, 35, 25, 20, 2] |
| 200.000 | 0.578 | 0.579 | 0.579 | 2:50:38 | [16, 40, 30, 20, 2] |
| Dataset Size | Precision | Recall | Metric | Time | Depth | Number of Nodes |
|---|---|---|---|---|---|---|
| one-step classifier | ||||||
| 5.000 | 0.862 | 0.859 | 0.860 | 0:15:25 | 17 | 731 |
| 10.000 | 0.923 | 0.923 | 0.923 | 0:17:21 | 16 | 1007 |
| 25.000 | 0.954 | 0.954 | 0.954 | 0:21:09 | 18 | 1625 |
| 50.000 | 0.966 | 0.966 | 0.966 | 0:24:44 | 25 | 2441 |
| 75.000 | 0.968 | 0.968 | 0.968 | 0:39:55 | 27 | 3363 |
| 100.000 | 0.981 | 0.981 | 0.981 | 0:41:43 | 27 | 3139 |
| 200.000 | 0.989 | 0.989 | 0.989 | 0:57:26 | 30 | 4083 |
| two-step classifier | ||||||
| 5.000 | 0.879 | 0.881 | 0.879 | 0:14:42 | 17 | 765 |
| 10.000 | 0.921 | 0.921 | 0.921 | 0:15:37 | 19 | 1013 |
| 25.000 | 0.955 | 0.955 | 0.955 | 0:18:39 | 26 | 1773 |
| 50.000 | 0.976 | 0.976 | 0.976 | 0:21:54 | 27 | 2299 |
| 75.000 | 0.974 | 0.974 | 0.974 | 0:34:25 | 24 | 2839 |
| 100.000 | 0.984 | 0.984 | 0.984 | 0:36:31 | 26 | 2951 |
| 200.000 | 0.991 | 0.991 | 0.991 | 0:52:08 | 30 | 3861 |
| Dataset Size | Precision | Recall | Metric | Time | Number of Trees | Number of Nodes |
|---|---|---|---|---|---|---|
| one-step classifier | ||||||
| 5.000 | 0.907 | 0.907 | 0.907 | 0:29:27 | 60 | 28,908 |
| 10.000 | 0.927 | 0.925 | 0.926 | 0:36:01 | 50 | 28,522 |
| 25.000 | 0.945 | 0.945 | 0.945 | 0:49:12 | 44 | 31,618 |
| 50.000 | 0.953 | 0.953 | 0.953 | 1:04:11 | 42 | 35,836 |
| 75.000 | 0.950 | 0.949 | 0.949 | 2:01:05 | 44 | 38,600 |
| 100.000 | 0.958 | 0.958 | 0.958 | 2:28:11 | 48 | 45,134 |
| 200.000 | 0.951 | 0.950 | 0.950 | 3:42:04 | 56 | 56,274 |
| two-step classifier | ||||||
| 5.000 | 0.918 | 0.915 | 0.916 | 0:25:53 | 38 | 17,730 |
| 10.000 | 0.936 | 0.935 | 0.935 | 0:31:19 | 56 | 31,786 |
| 25000 | 0.941 | 0.939 | 0.939 | 0:43:14 | 38 | 27,384 |
| 50.000 | 0.942 | 0.940 | 0.941 | 1:01:23 | 60 | 48,250 |
| 75.000 | 0.942 | 0.940 | 0.941 | 1:52:59 | 40 | 33,402 |
| 100.000 | 0.956 | 0.955 | 0.955 | 2:18:01 | 56 | 48,278 |
| 200.000 | 0.947 | 0.945 | 0.946 | 3:45:36 | 60 | 58,190 |
| Dataset Size | Precision | Recall | Metric | Time |
|---|---|---|---|---|
| one-step classifier | ||||
| 5.000 | 0.858 | 0.861 | 0.860 | 0:00:26 |
| 10.000 | 0.861 | 0.862 | 0.861 | 0:00:26 |
| 25.000 | 0.814 | 0.818 | 0.816 | 0:00:32 |
| 50.000 | 0.803 | 0.807 | 0.804 | 0:00:42 |
| 75.000 | 0.802 | 0.806 | 0.803 | 0:01:00 |
| 100.000 | 0.825 | 0.828 | 0.826 | 0:01:14 |
| 200.000 | 0.800 | 0.804 | 0.802 | 0:01:56 |
| two-step classifier | ||||
| 5.000 | 0.805 | 0.805 | 0.805 | 0:00:21 |
| 10.000 | 0.821 | 0.822 | 0.821 | 0:00:23 |
| 25.000 | 0.772 | 0.774 | 0.776 | 0:00:29 |
| 50.000 | 0.758 | 0.762 | 0.761 | 0:00:42 |
| 75.000 | 0.747 | 0.751 | 0.749 | 0:00:52 |
| 100.000 | 0.787 | 0.789 | 0.788 | 0:01:04 |
| 200.000 | 0.762 | 0.766 | 0.763 | 0:01:45 |
| Dataset Size | Precision | Recall | Metric | Time | Best Layer |
|---|---|---|---|---|---|
| one-step classifier | |||||
| 5.000 | 0.639 | 0.646 | 0.641 | 0:09:20 | [31, 35, 25, 20, 12] |
| 10.000 | 0.691 | 0.708 | 0.697 | 0:14:27 | [31, 35, 25, 20, 12] |
| 25.000 | 0.720 | 0.719 | 0.719 | 0:32:22 | [31, 40, 30, 20, 12] |
| 50.000 | 0.707 | 0.732 | 0.721 | 1:01:55 | [31, 40, 30, 20, 12] |
| 75.000 | 0.724 | 0.738 | 0.727 | 1:30:39 | [31, 40, 30, 20, 12] |
| 100.000 | 0.755 | 0.776 | 0.759 | 1:55:59 | [31, 35, 25, 20, 12] |
| 200.000 | 0.775 | 0.778 | 0.775 | 3:59:41 | [31, 35, 25, 20, 12] |
| two-step classifier | |||||
| 5.000 | 0.631 | 0.646 | 0.637 | 0:09:00 | [24, 25, 20, 12] |
| 10.000 | 0.717 | 0.723 | 0.719 | 0:14:15 | [24, 25, 20, 12] |
| 25.000 | 0.723 | 0.734 | 0.725 | 0:32:41 | [24, 40, 30, 20, 12] |
| 50.000 | 0.784 | 0.788 | 0.787 | 1:02:01 | [24, 40, 30, 20, 12] |
| 75.000 | 0.753 | 0.746 | 0.751 | 1:29:44 | [24, 40, 30, 20, 12 |
| 100.000 | 0.762 | 0.768 | 0.765 | 1:54:06 | [24, 40, 30, 20, 12] |
| 200.000 | 0.764 | 0.776 | 0.772 | 3:59:29 | [24, 25, 20, 12] |
| Dataset Size | Precision | Recall | Metric | Time |
|---|---|---|---|---|
| one-step classifier | ||||
| 5.000 | 0.755 | 0.755 | 0.749 | 0:02:03 |
| 10.000 | 0.789 | 0.791 | 0.789 | 0:02:15 |
| 25.000 | 0.788 | 0.792 | 0.789 | 0:02:29 |
| 50.000 | 0.781 | 0.784 | 0.781 | 0:02:56 |
| 75.000 | 0.770 | 0.773 | 0.771 | 0:04:56 |
| 100.000 | 0.796 | 0.798 | 0.796 | 0:07:17 |
| 200.000 | 0.774 | 0.778 | 0.775 | 0:11:16 |
| two-step classifier | ||||
| 5.000 | 0.699 | 0.703 | 0.702 | 0:01:29 |
| 10.000 | 0.725 | 0.724 | 0.725 | 0:01:45 |
| 25.000 | 0.706 | 0.708 | 0.708 | 0:02:10 |
| 50.000 | 0.714 | 0.717 | 0.716 | 0:03:24 |
| 75.000 | 0.703 | 0.705 | 0.704 | 0:04:05 |
| 100.000 | 0.744 | 0.744 | 0.744 | 0:05:48 |
| 200.000 | 0.715 | 0.718 | 0.717 | 0:09:14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexopoulos, A.; Drakopoulos, G.; Kanavos, A.; Mylonas, P.; Vonitsanos, G. Two-Step Classification with SVD Preprocessing of Distributed Massive Datasets in Apache Spark. Algorithms 2020, 13, 71. https://doi.org/10.3390/a13030071
Alexopoulos A, Drakopoulos G, Kanavos A, Mylonas P, Vonitsanos G. Two-Step Classification with SVD Preprocessing of Distributed Massive Datasets in Apache Spark. Algorithms. 2020; 13(3):71. https://doi.org/10.3390/a13030071
Chicago/Turabian StyleAlexopoulos, Athanasios, Georgios Drakopoulos, Andreas Kanavos, Phivos Mylonas, and Gerasimos Vonitsanos. 2020. "Two-Step Classification with SVD Preprocessing of Distributed Massive Datasets in Apache Spark" Algorithms 13, no. 3: 71. https://doi.org/10.3390/a13030071
APA StyleAlexopoulos, A., Drakopoulos, G., Kanavos, A., Mylonas, P., & Vonitsanos, G. (2020). Two-Step Classification with SVD Preprocessing of Distributed Massive Datasets in Apache Spark. Algorithms, 13(3), 71. https://doi.org/10.3390/a13030071









