Abstract
Flying robots have gained great interest because of their numerous applications. For this reason, the control of Unmanned Aerial Vehicles (UAVs) is one of the most important challenges in mobile robotics. These kinds of robots are commonly controlled with Proportional-Integral-Derivative (PID) controllers; however, traditional linear controllers have limitations when controlling highly nonlinear and uncertain systems such as UAVs. In this paper, a control scheme for the pose of a quadrotor is presented. The scheme presented has the behavior of a PD controller and it is based on a Multilayer Perceptron trained with an Extended Kalman Filter. The Neural Network is trained online in order to ensure adaptation to changes in the presence of dynamics and uncertainties. The control scheme is tested in real time experiments in order to show its effectiveness.
1. Introduction
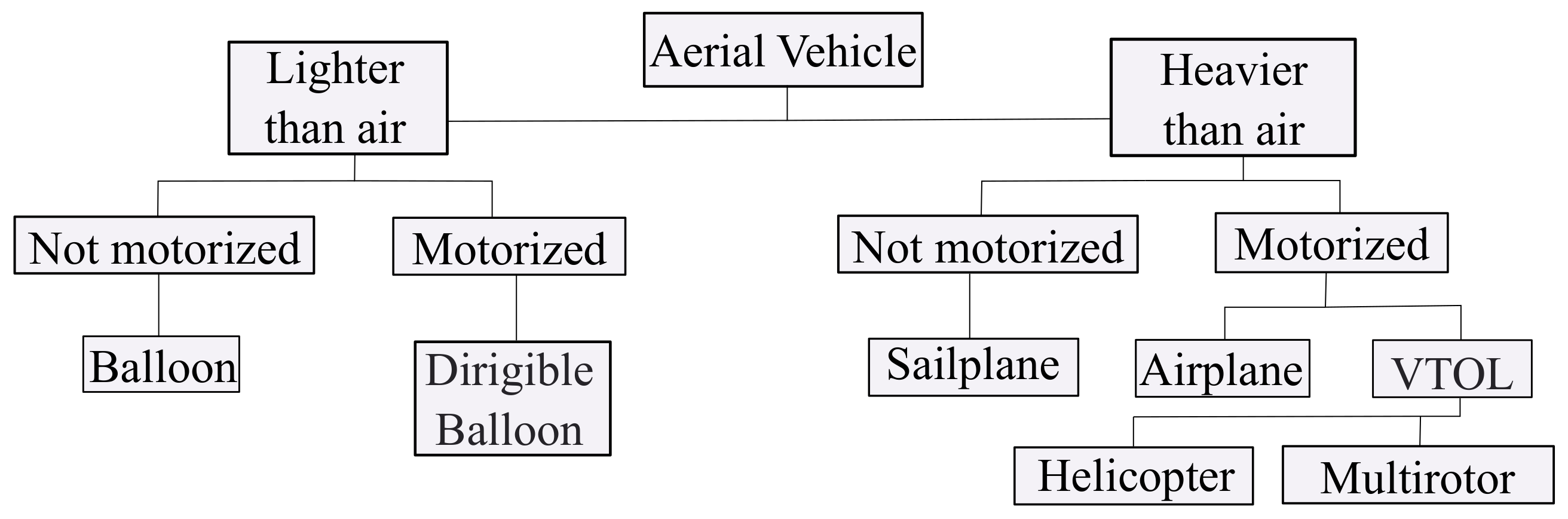
Unmanned Aerial Vehicles (UAVs) have become very popular thanks to recent progress in propulsion technologies and small sensors with low power consumption [1]. These kinds of vehicles surpass other types of robotics platforms in both military [2] and civilian applications [3], including surveillance, agriculture, traffic monitoring, fire detection and high social impact activities, such as search and rescue in disaster zones. Figure 1 shows the classification of several types of aerial vehicles based on [4]. This paper is focused on Vertical Take-Off and Landing (VTOL) vehicles, such as multirotors.
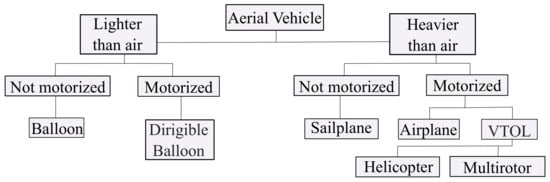
Figure 1.
Aerial vehicles classification. This work is focused on multirotors.
VTOL vehicles are more cost-efficient than bigger drones like Medium Altitude Long Endurance (MALE) or High Altitude Long Endurance (HALE) and present the ability to hover above a reference position [5]. In contrast, multirotors have limited energy consumption and payload; consequently, light and compact sensors are required for the navigation, and in most of the cases, inertial sensors are not enough to obtain some states of the system, such as its position. Usually, multirotors are teleoperated by a ground station with a limited operational range, but when autonomous tasks are required, the positional feedback is crucial to control the UAV [5].
Drones are equipped with a Global Positioning System (GPS) to solve the problem of the estimation of the position. However, depending on the accuracy of the assignment, a GPS sensor may not be suitable; besides, the GPS signal is lost when working in indoor environments. For indoor flight control, the positional feedback is commonly carried out by motion capture systems, which each consist of a set of fixed cameras in a room. Unfortunately, approaches like this require previous knowledge of the scene and assembly and calibration of the motion capture system, which, in practice, would not be possible in search and rescue tasks. Generally, a combination of visual and inertial information is used to solve the problem of Simultaneous Localization and Mapping (SLAM) [6]. In this paper, a vision sensor is used; cameras are compact and lightweight sensors with low power consumption. These characteristics make them suitable for drones flying in unknown, GPS-denied environments.
Once the SLAM problem has been solved, it is possible to control the position of the vehicle. Proportional-Integral-Derivative (PID) controllers are widely applied in industry because of their simplicity, and they are usually used to control these kinds of UAVs. Nevertheless, multirotors are highly nonlinear, underactuated systems with six Degrees of Freedom (Dof) and four control inputs—torque in x, y and z, and thrust—and therefore, they are difficult to control with conventional methods [7,8]. To overcome the limitations of conventional controllers, direct control using a neural network is proposed. In this work, a Multilayer Perceptron (MLP) is implemented to adapt the gains of a PD controller. As reported in [9], Artificial Neural Networks (ANN) have shown satisfactory results when controlling nonlinear systems, and despite the limitations of conventional controllers, the approach presented in this paper can cover most of the disadvantages of PID, even if the multirotor changes its parameters during the flight.
The MLP is trained with the Extended Kalman Filter (EKF). The Kalman filter is an optimal estimator which deduces parameters based on noisy measurements. Its solution is recursive; therefore, the filter processes data as soon as it arrives and predicts the next value without the need for having the complete data set of observations [10]. This feature makes it faster and convenient for online applications, in contrast with other methods such as batch processing [11]. The idea behind the use of the EKF to train the ANN is that other training algorithms, such as gradient descent, recursive least squares and backpropagation, are particular cases of the Kalman filter; for this reason, the EKF is suitable for training [12,13]. When using the EKF for training, the weights of the neural network are the states that the filter estimates, and the output of the neural network is the measurement used by the Kalman filter. Then, the training of the ANN can be seen as an optimal filtering problem. The EKF has been successfully applied to estimate parameters of an ANN in [14,15,16].
Although several PID tuning algorithms have been proposed, those approaches are mostly offline applications [17,18] or simulation-only experiments [19]. The main contribution of this work is the control of both position and orientation of a quadrotor in real-time experimental tests using direct control; i.e., the output of the neural network is the control action for the UAV. The neural networks are trained online in order to adapt to changes in the dynamics and uncertainties. The objective is to find a robust solution to real applications [20] in which UAVs are capable of grabbing or deliver objects. This approach also uses a solution for the SLAM problem, to control the position using only onboard sensors, making it able to fly in unknown environments.
The remainder of this paper is organized as follows: in Section 2, some previous and related works are presented. The dynamic model of the platform used is described in Section 3. Section 4 presents the architecture of the neural network trained with EKF. In Section 5, the algorithm of localization is described. The quadrotor control scheme is shown in Section 6. Finally, simulation and experimental results are shown in Section 7. The conclusions of this work are discussed in Section 8.
2. Related work
Multirotors are commonly controlled by PID [21]. PID controllers have been widely used in industry, mainly because of the trade-off between efficiency and simplicity [22], and numerous offline tuning techniques have been reported in the literature [19]. The main problem with conventional approaches is that physical systems present parametric changes and uncertainties, and they are perturbed by external disturbances; consequently, an online, continuous tuning approach is needed.
Another common approach is the Linear Quadratic Regulator (LQR) for attitude stabilization [23,24,25]. While this may be applicable for some configurations, multirotors are non-linear systems that present uncertainties, such as unknown physical parameters, actuator degradation, unknown delays in-process communication and unmodeled dynamics [26]. Hence, an approach considering these characteristics must be used [27,28]. Nonlinear control techniques provide better performance [29], and one of the most applied methods is feedback linearization, which relies on cancellation of all nonlinearities to convert the non-linear system into a system with linear dynamics [30,31,32]. In [33,34,35], the authors use a backstepping control, which is designed to stabilize the whole system based on the Lyapunov stability theory, showing good results. However, backstepping requires the analytic calculation of the partial derivatives of the stabilizing functions, which becomes impractical as the order of the system grows [36], and in general, most of the nonlinear techniques require complete knowledge of the nonlinearities present in the plant and are vulnerable to modeling errors or parametric uncertainty [29]. In this paper, an adaptive controller based on an Artificial Neural Network (ANN) is proposed. The ANN has been used to control complex nonlinear systems [9,37,38,39]. The controller used in this scheme has the same simple structure and easy implementation of a PD controller but with the adaptability and learning capabilities of a neural network [9]. The system will be able to adapt to actuator faults, such as loss of effectiveness [40] and solve the principal disadvantages of traditional PID [41].
On the other hand, there is no onboard sensor to read the absolute position of the UAV. There are two common solutions to solve this; the first one consists of an external motion detection system, which has to be mounted, thereby limiting the applications to known indoor environments.
The second approach is based on solving the SLAM problem. For this, different sensors can be used, such as laser range scanners [42], stereo vision systems [43,44], RGB-Depth sensors [45,46,47] and monocular cameras [48,49,50]. In this work, a monocular vision system is preferred because of its lower power consumption and compact size, compared to the amount of information it delivers. The advantage is that the range of a camera is virtually unlimited [6], making it possible flying in both small and large environments. Despite the advantages of monocular vision, it is impossible to determine the scale of the environment using only one view, and it is necessary to fuse this information with inertial information provided by an Inertial Measurement Unit (IMU). To solve this, Parallel Tracking and Mapping (PTAM) for robot localization (introduced in [6,51,52]) will be implemented.
3. Multirotor Dynamic Model
The multirotor used for this work was the quadcopter. There are two principal configurations for quadcopters; in this case, the configuration selected is described in Figure 2.

Figure 2.
Illustration of the concept of the motion of a quadrotor. Let the propeller rotation speed be proportional to the width of the arrow on the propeller; the movement of the UAV is denoted with the dashed arrow at the center of the quadrotor. (a) Upward movement, (b) horizontal movement, (c) downward movement, (d) left turning movement and (e) right turning movement.
The robotic platform where the algorithm was tested is the Parrot AR.Drone 2.0 ® quadrotor. Multirotor systems have an even number of rotors divided into two groups rotating in opposite directions. The configuration of the selected platform is depicted in Figure 2. For this specific configuration, where the robot structure does not match with the x and y axis from the body frame (Figure 3), the movement of the vehicle is given by the following combination of rotor actions: increasing or decreasing the speed of the four rotors in the same proportion changes the altitude of the system. Then, because the multirotor is an underactuated system, there is no actuator that generates movement in x and y directions directly; instead, these displacements are achieved by changes in the attitude due to combinations of the two pairs of propellers: the rotation in y axis (pitch ) results in translational movement in x; contrarily, a rotation in x (roll ) results in translational movement in y. Similarly, the orientation (yaw ) needs a combination of the four propellers and it is the result of the difference of the counter-torque between both pairs.
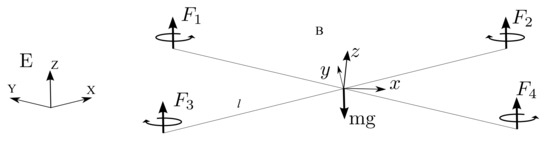
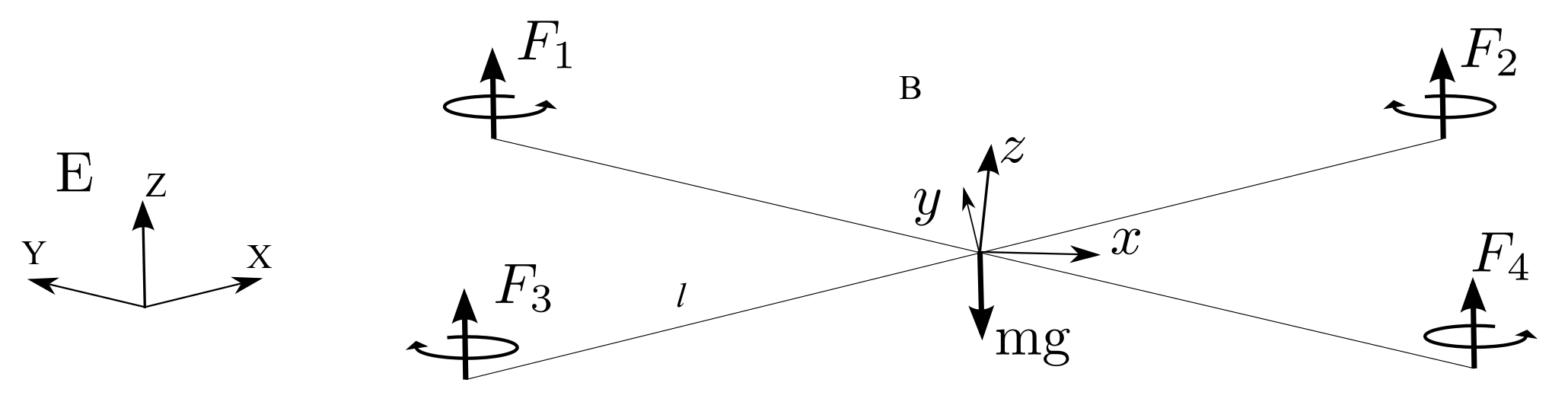
Figure 3.
Quadrotor configuration. B represents the quadrotor fixed frame and E the inertial frame.
In general, the center of mass is considered to be at the origin of the body fixed frame. The quadrotor orientation in space is given by a rotation matrix from the quadrotor to the inertial frame . As in [4], the dynamics of the quadrotor may be expressed as follows
where is the inertia matrix, is the body linear speed vector and is the angular speed.
The quadrotor equations of motion can be expressed as
where the gravity g is acting on z axis (), is the linear velocity vector, the rotation matrix is represented by , is the skew symmetric matrix of the vector of angular velocity and represents the speed of rotor i. and are the body and the rotor inertia respectively. m is the mass of the system, b is the thrust factor, l is the distance from the center of mass to the rotor (it is assumed the same distance to all rotors) and represents the torque applied to the quadrotor. For this configuration, is denoted as follows
with a drag factor d.
The quadrotor dynamics, as described in [4], are given by
where represents the gyroscopic effects induced by the propellers, which are usually neglected [53], and they are given by
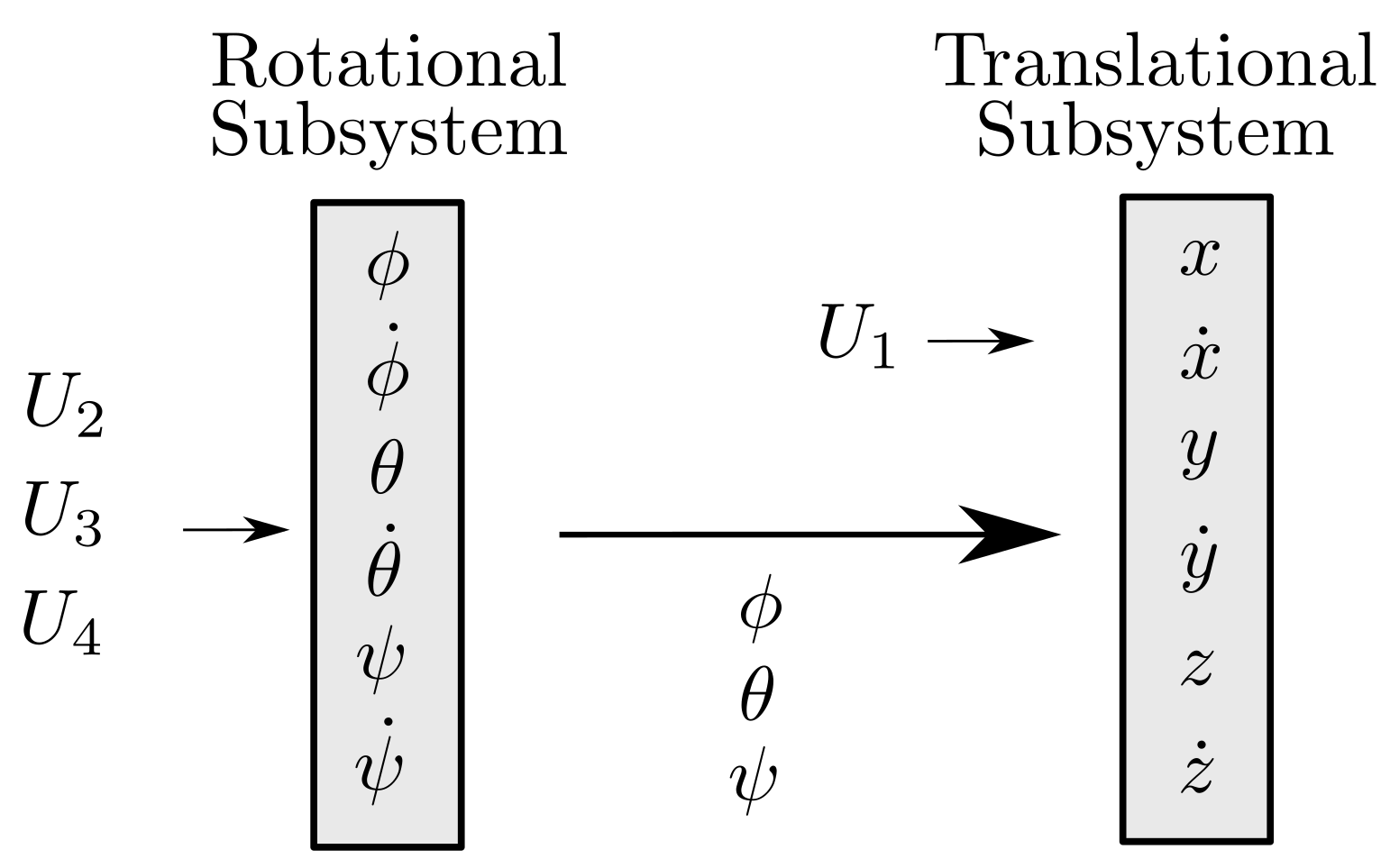
are the system inputs: is related to its translation and to are related to its attitude and orientation. The relation between both subsystems can be seen in Figure 4. The inputs for this specific configuration of multirotor are given by
and they are calculated by the neural network. In this work, a Multilayer Perceptron trained with the Extended Kalman Filter is selected.
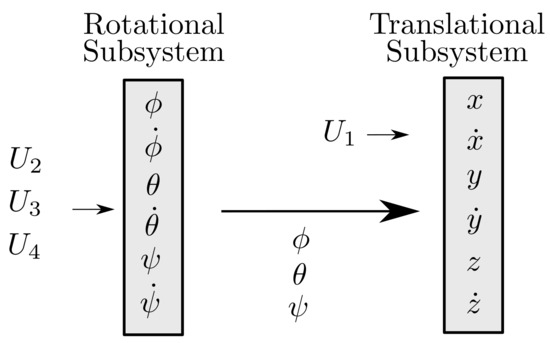
Figure 4.
, and are inputs for the rotational subsystem; , roll, pitch and yaw are inputs for the following translation subsystem.
4. MLP trained with the EKF
The architecture of an ANN was inspired by biological neurons. Like synaptic connection in a regular biological neuron, each node in an ANN receives a signal from an adjacent node and its output is computed by some nonlinear function of the sum of the inputs. These connections between adjacent neurons have weights that adjusts as the network learns [19].
The training process of the MLP can be seen as an estimation problem for a nonlinear system that can be solved with the EKF [54,55,56]. Neural networks trained with the EKF have demonstrated faster learning speeds and convergence times than networks trained with algorithms based on backpropagation, which is ideal for real time applications [57,58]. The objective is to find the optimal weights that minimize the prediction error [59].
Consider an MLP with L weights and m output nodes. The neural network can be modeled as follows
where is the state vector, is the input vector, is the output vector and h is the nonlinear output function. From Kalman Filter equations, it is known that
where L is the total number of weights, is the learning rate, and are the prediction error covariance matrices in k and . is the Kalman gain matrix. is the system output, and is the network output. is the process noise covariance matrix, and represents the measurement covariance error. is the weights (state) vector, and contains the partial derivatives of each output of the neural network with respect to each weight and it is defined as
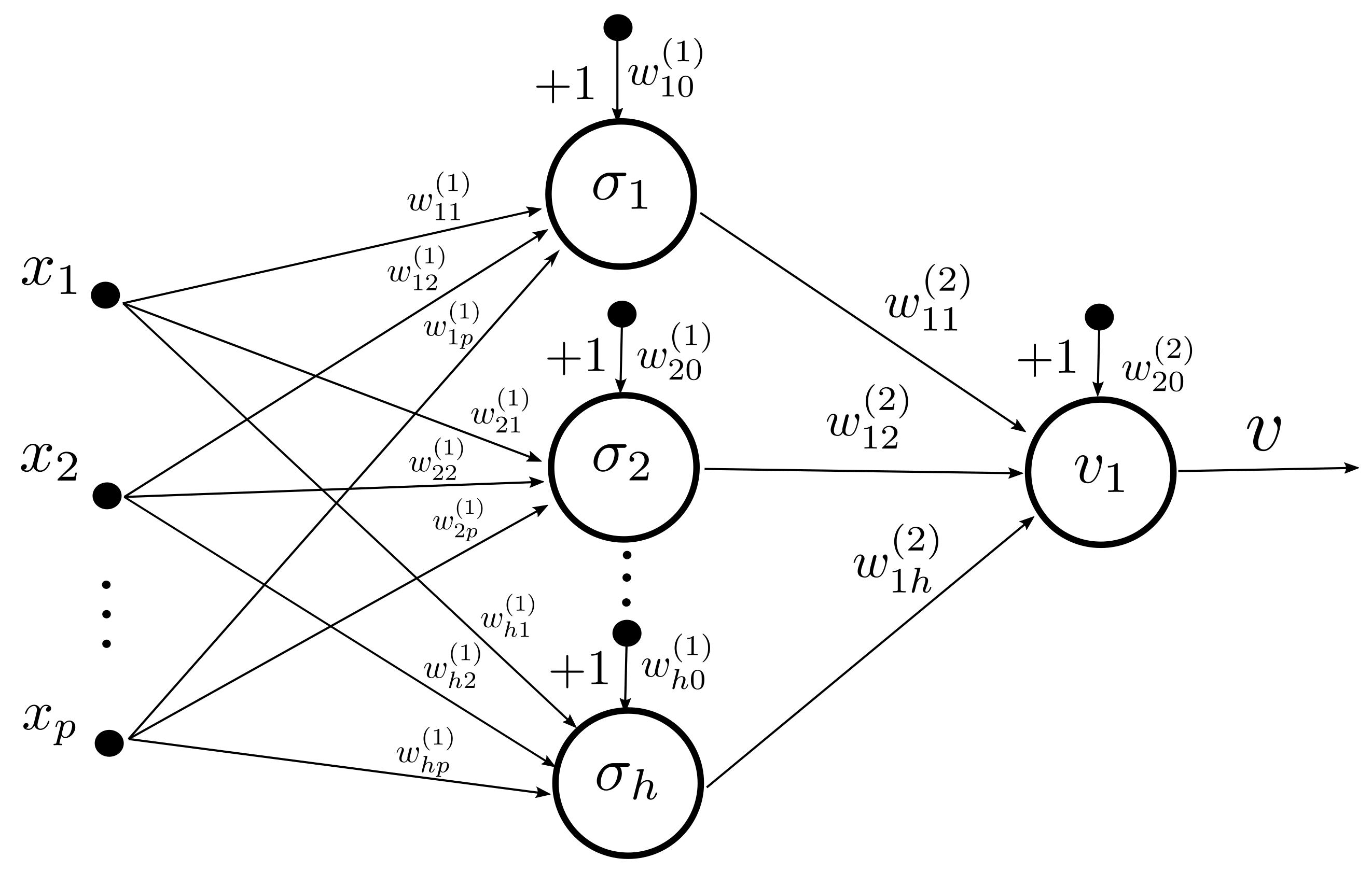
Consider the MLP in Figure 5 with one hidden layer and one node at the output layer, where p denotes the number of inputs to the network and h the number of nodes in the hidden layer. The output of the neural network is defined by
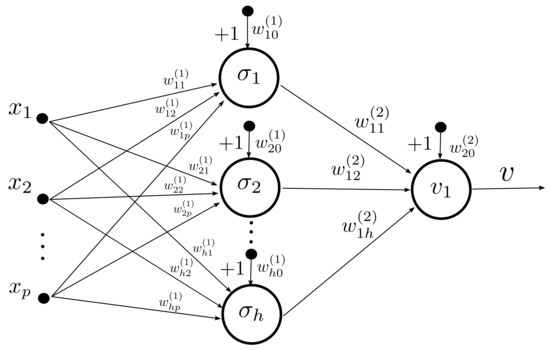
Figure 5.
Multilayer Perceptron architecture. The networks has p inputs and h nodes in the hidden layer. the weights from the input layer to the hidden layer are denoted by while the weights from the hidden layer to the output layer are described by
Finally, vector can be expressed as
where
Let us define a new variable as follows
then, the vector H for the MLP shown in Figure 5 with sigmoid activation functions for the hidden layers and linear function for the output node can be expressed as follows
The network designed for this work has two inputs which are the error and the derivative of the error between the desired pose and the pose of the system which is calculated using monocular visual odometry.
5. Monocular Visual Odometry
Multirotors are equipped with inertial sensors which are capable of measuring the attitude and orientation of the system. Unfortunately, most of the quadrotors do not have any onboard sensors to measure position in indoor environments; in contrast, position is usually measured by a GPS sensor which has an error between 1 and 5 meters depending on the quality of the GPS signal.
This approach is based on Parallel Tracking and Mapping (PTAM) algorithm [60] to solve the localization problem. The algorithm is named this way because tracking and mapping are separated and run in parallel; it creates a keyframe based map using Bundle Adjustment (BA). This map is initialized from a stereo pair, and new points are initialized with epipolar searches.
It is well known that the scale of the environment cannot be determined using only monocular vision [52]. Once the map is initialized, the visual map is rotated such that the plane corresponds to the horizontal plane according to the accelerometer, and it is scaled with an average keypoint depth of 1. During the tracking, the scale of the map must be estimated as in [52].
The quadrotor measures in regular intervals, the distance traveled according to the visual SLAM , and uses the metric sensors available, denoted by . To each interval, a pair is given, where is scaled according to the visual map and is in metric units. Both and measure motion of the UAV, and they are related by . If Gaussian noise in the measurements is assumed, then a set of sample pairs is given with
where are the unknown distances, are the variances of the measurements error and I is the identity matrix of dimension d. To estimate the unknown parameters, maximum-likelihood estimation is used, minimizing the negative log-likelihood.
The global minimum of (23) is unique; its derivation can be found in [52,61], and it is stated as follows
with
Assuming and are known, (24) gives a closed solution for the estimation of . For the estimation of the measurement variances, the authors refer to [52]. To generate the sample pairs, for each visual altitude measurement there is a corresponding metric altitude measurement over a window of sensor measurements, and then a visual and metric distance traveled within a period is computed as follows.
For visual odometry, EKF is used to identify and reject falsely tracked frames and compensate for time delays [6]. The filter includes the motion model of the quadrotor; the state space of the EKF is given by
where is the position of the quadrotor; its velocity; are the roll, pitch and yaw angle respectively (in degrees); and is the yaw rotational speed. For each sensor, an observation function is defined as below
and the respective observation vector, derived from sensor measurements is defined as shown
where and are velocities in plane directly measured by the quadrotor. The velocity in z direction can be computed since the altitude is given by an ultrasonic or an air pressure sensor and is the time from time step t and . Equally, for rotation readings, roll and pitch are directly measured and the yaw rotation speed can be calculated since is given by the IMU.
If PTAM tracks a video frame, the pose estimation is scaled with and transformed to the coordinate system of the quadrotor, leading to direct observation of its pose as follows.
where is the estimated camera pose scaled with , is the rigid transformation from the camera to the quadrotor coordinate system and f is the function that maps from to roll-pitch-yaw representation.
The Kalman filter predicts how the state vector evolves to the next time step. The horizontal acceleration is proportional to the horizontal force and is given by
where is the drag force and denotes the accelerating force which is proportional to the projection of the z axis of the quadrotor onto the horizontal plane, which leads to
where coefficients and are estimated from data collected from test flights. The influence of the control inputs is described by
where coefficients are estimated from flight tests. The overall state transition is given by
For a complete derivation of the state transition and delay compensation for a quickly reacting system to avoid oscillations and unstable behavior, the authors refer to [52].
6. Quadrotor Control Scheme
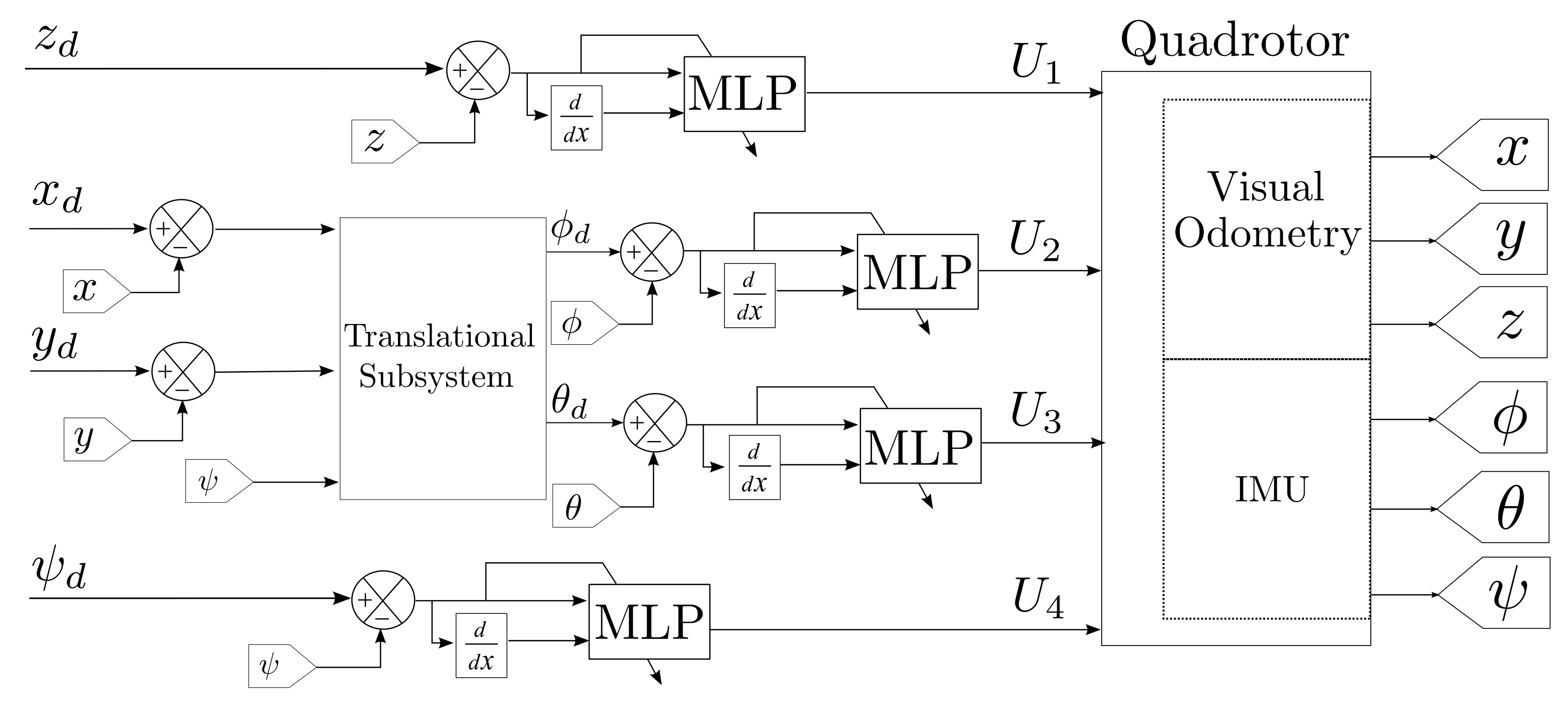
In this section, the control scheme is described. An MLP is used with an architecture as shown in Figure 5. The ANN has two inputs: the error between the desired value and the output measured from the system, and the derivative of this error to get information about the rate of change of the process output. PTAM estimates the positional observations (x, y, z), and the yaw angle can be directly measured by the IMU.
The network has one hidden layer with four nodes and one neuron at the output layer, and there are four MLP modules, one for each controllable Degree of Freedom (Figure 6). The weights are randomly selected and uniformly distributed between . The outputs of the four MLPs represent the control inputs from (6). Despite all Degrees of Freedom being internally coupled, the advantage of using the MLP modules separately (one for every DoF) is an easier implementation and interpretation of the control scheme behavior.
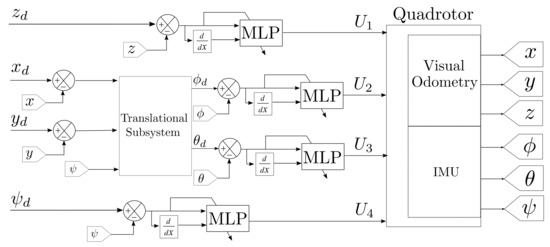
Figure 6.
Control of quadrotor with MLP. There is one MLP module for each Degree of Freedom to control.
7. Results
The platform selected to test the algorithm was the Parrot Ar.Drone 2.0, which is a quadrotor equipped with a 3-axis gyroscope, 3-axis accelerometer, a magnetic compass, an ultrasound altimeter, one camera looking in x direction and another camera looking downward. For these experiments, the camera looking forward was used; it has a field of view of and a resolution of . Its video is streamed at 30 fps to the ground station. Sensor measurements of the Ar.Drone 2.0 can be sent to the ground station at a frequency of 200 Hz; however, due to integration of the ANN training, control, localization and mapping, this transmission rate is decreased to 30 Hz in the following experiments.
7.1. Simulation Results
Simulation experiments were carried out in Linux Ubuntu with Gazebo, which is an open-source simulator with easy integration with a Robot Operating System (ROS). The world scene used for the test and the camera view are shown in Figure 7.
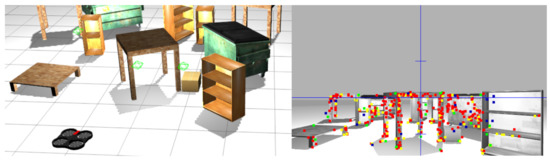
Figure 7.
World Scene of Gazebo used for simulation and the camera view.
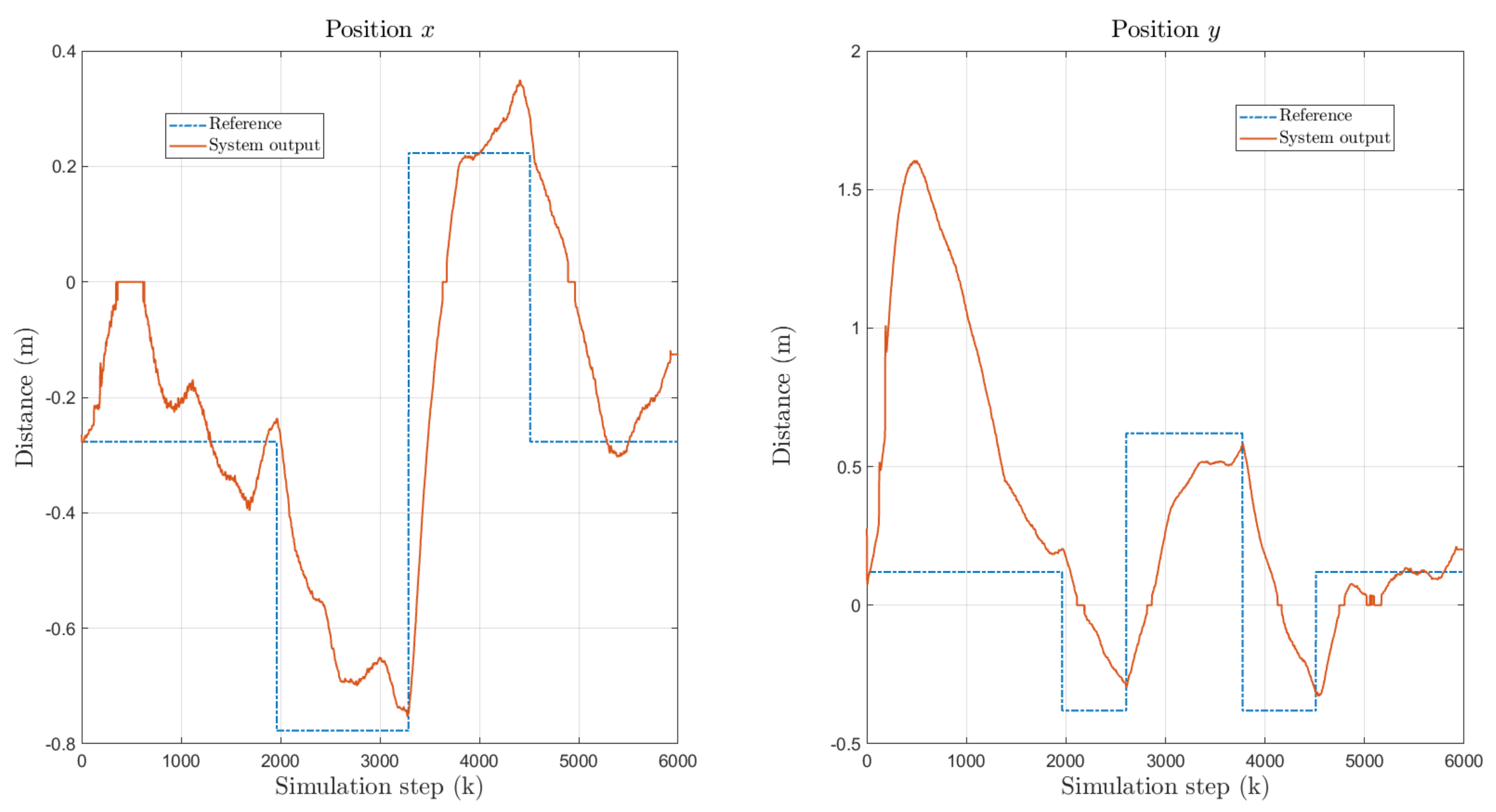
In the first experiment, a trajectory in the plane is selected to train weights for both directions at the same time. For each degree, all the weights of an MLP module with ten nodes in the hidden layer are selected. As can be seen in Figure 8, the overshoot is reduced and eventually eliminated after some iterations.
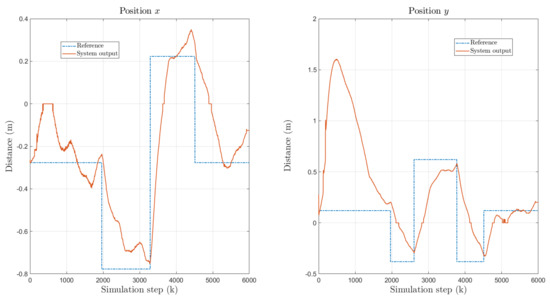
Figure 8.
First simulation experiment with random initial weights. Dashed line represents the desired value and solid lines represent the system output. As can be seen, overshoot is reduced after some iterations.
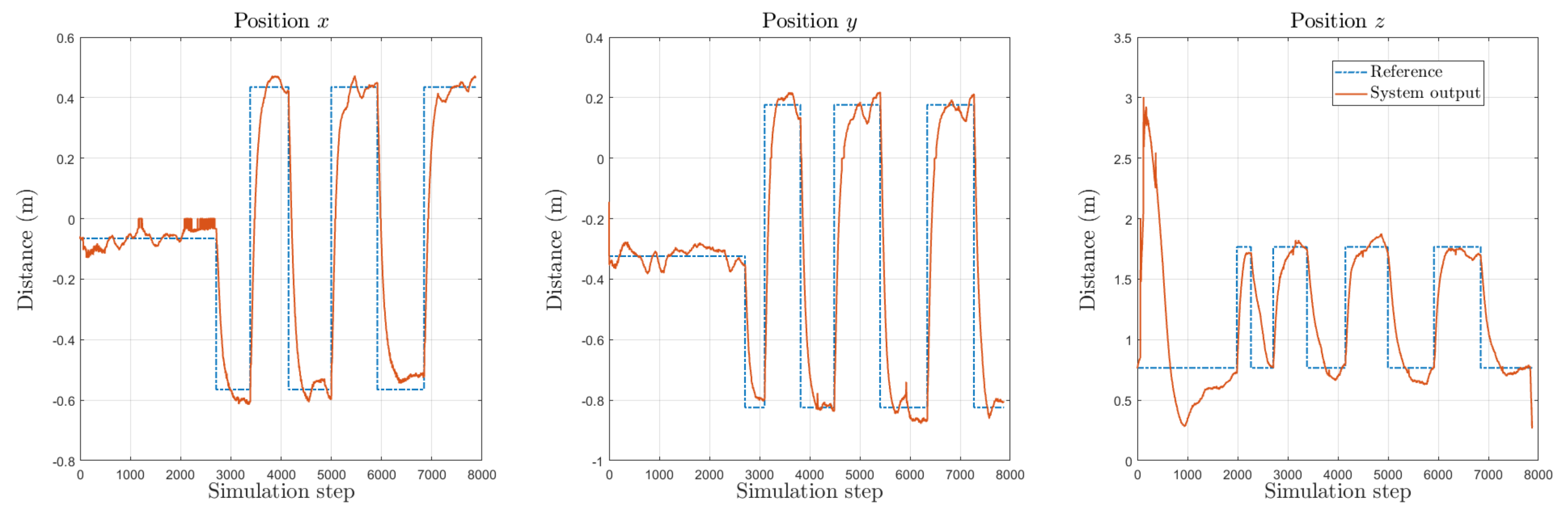
After some iterations of x and y training, the z axis is added and a new test is performed training the three Degrees of Freedom. Again, the z axis MLP module is initialized with random weights. The results of these tests are shown in Figure 9. In Figure 10 the PTAM output can be seen. It can be seen that the overshoot in z is reduced after some iterations, and eventually, the path is followed correctly. Table 1 shows the Root Mean Squared Error (RMSE) for each axis.
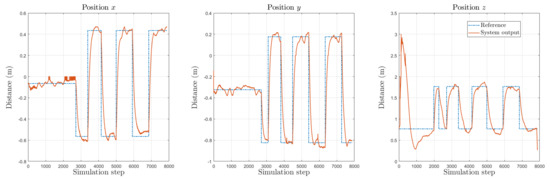
Figure 9.
Second simulation: x and y axis were trained beforehand. Now z axis is added and initialized with random weights. Dashed line represents the reference and solid lines describe the output of the system.
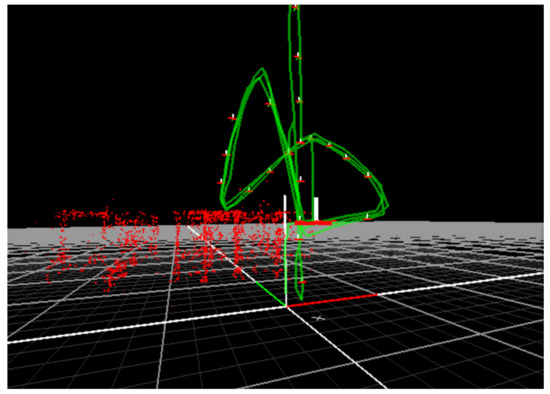
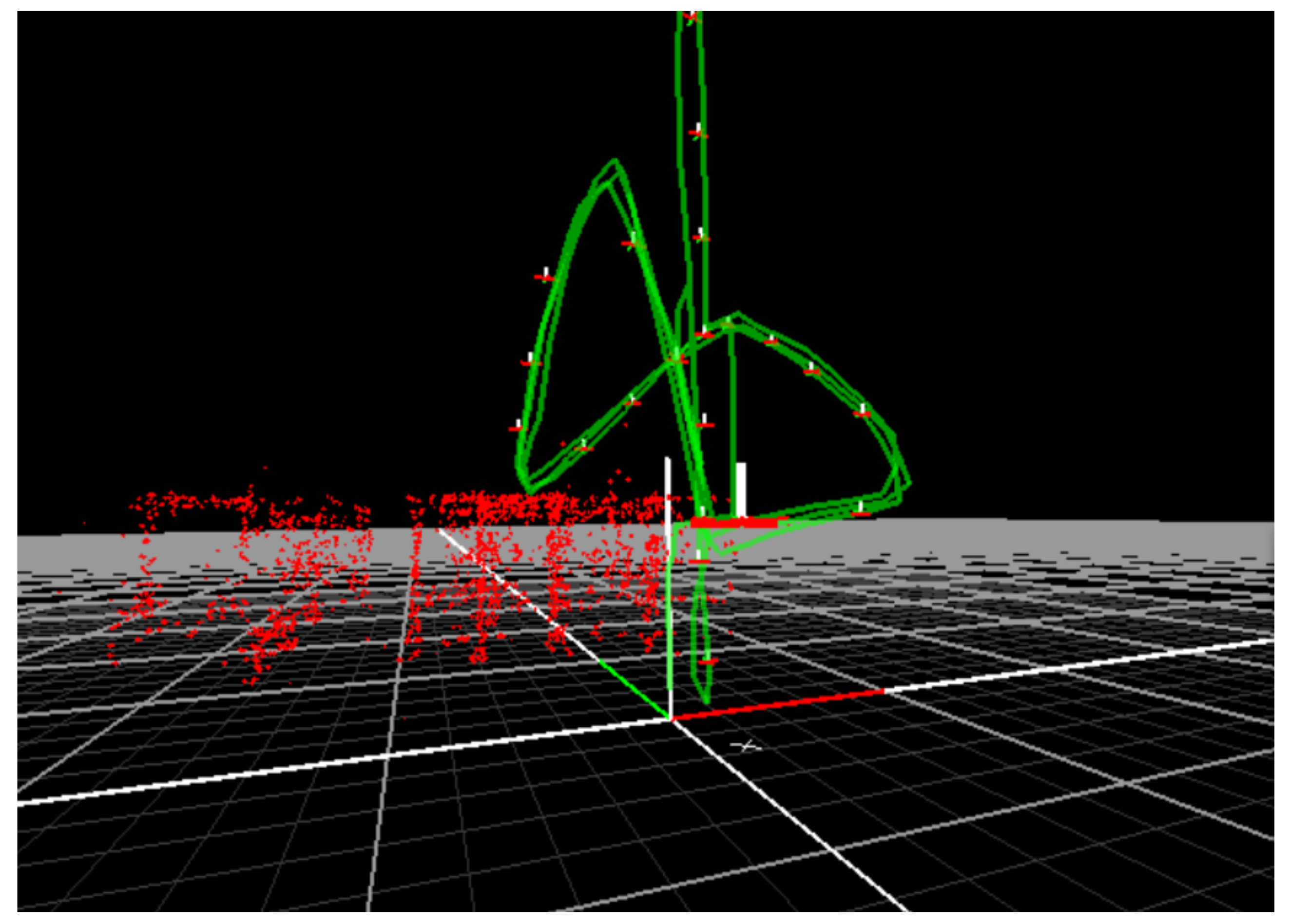
Figure 10.
Parallel Tracking and Mapping (PTAM) output for the first trajectory. x, y and z axes are denoted red, green and white respectively. It can be seen that the quadrotor follows the reference correctly.

Table 1.
Root Mean Squared Error (RMSE) for each axis from simulation from Figure 10.
7.2. Experimental Results
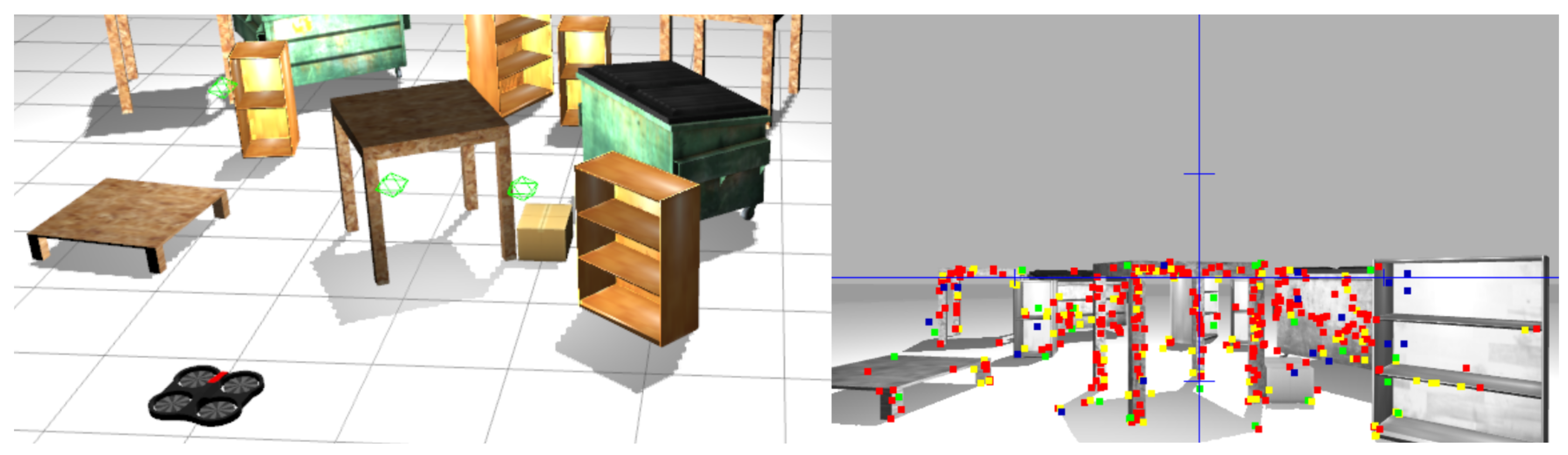
The experimental tests were carried out in indoor unknown environment; however, since the localization of the system is estimated using only onboard sensors, it can also navigate in outdoor conditions. It is preferable that the scene includes sufficient objects (features) to be seen by the camera in a range of 0–7 m. The weights were initialized with the last value of the simulation. Since the Ar.Drone 2.0 driver for ROS was used, the parameters should be close to the real system. The data were received at 30 Hz (the time interval of each iteration was 1/30 s). Figure 11 shows the camera view and mapping output of the experiment. In Figure 12 are the results of controlling the quadrotor using the MLP using online training. As shown, oscillations and overshot were eliminated.
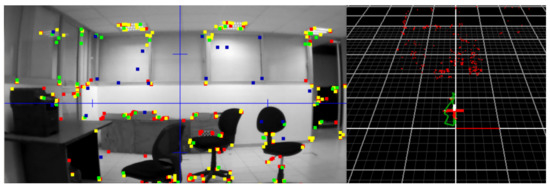
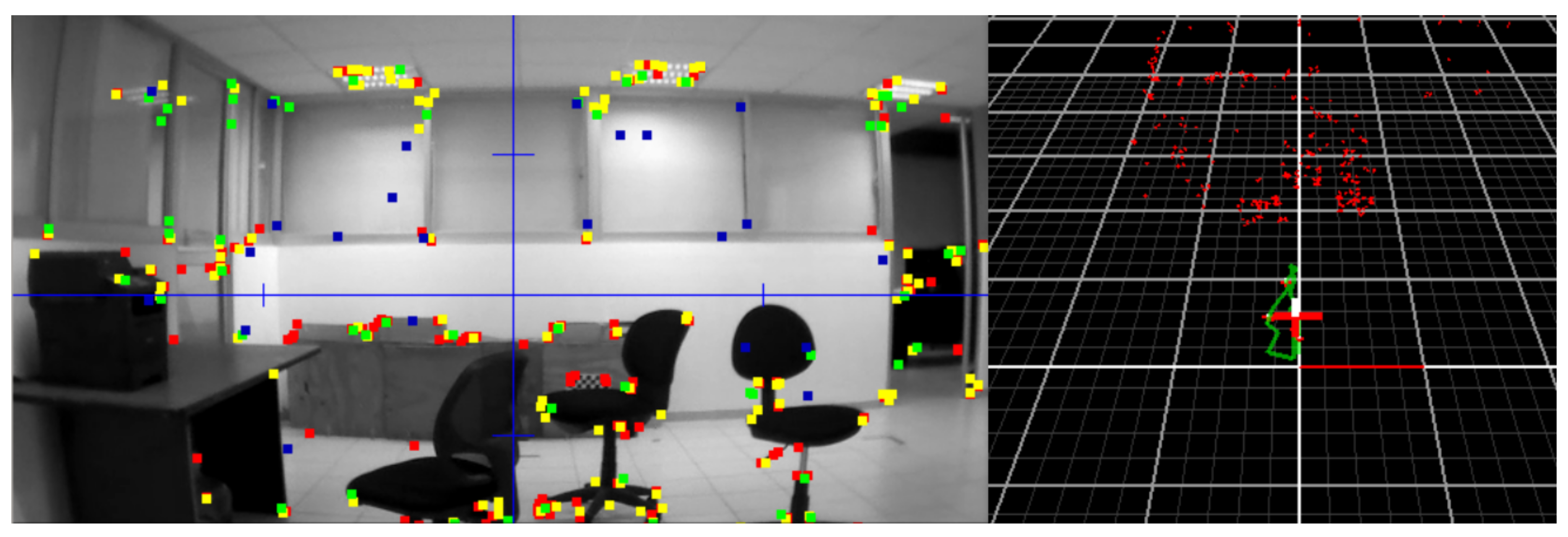
Figure 11.
Camera view and map generated with PTAM for experimental tests.
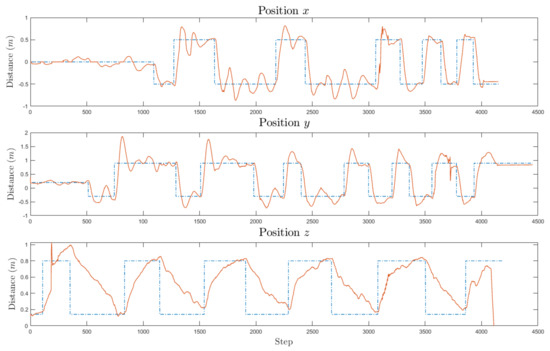
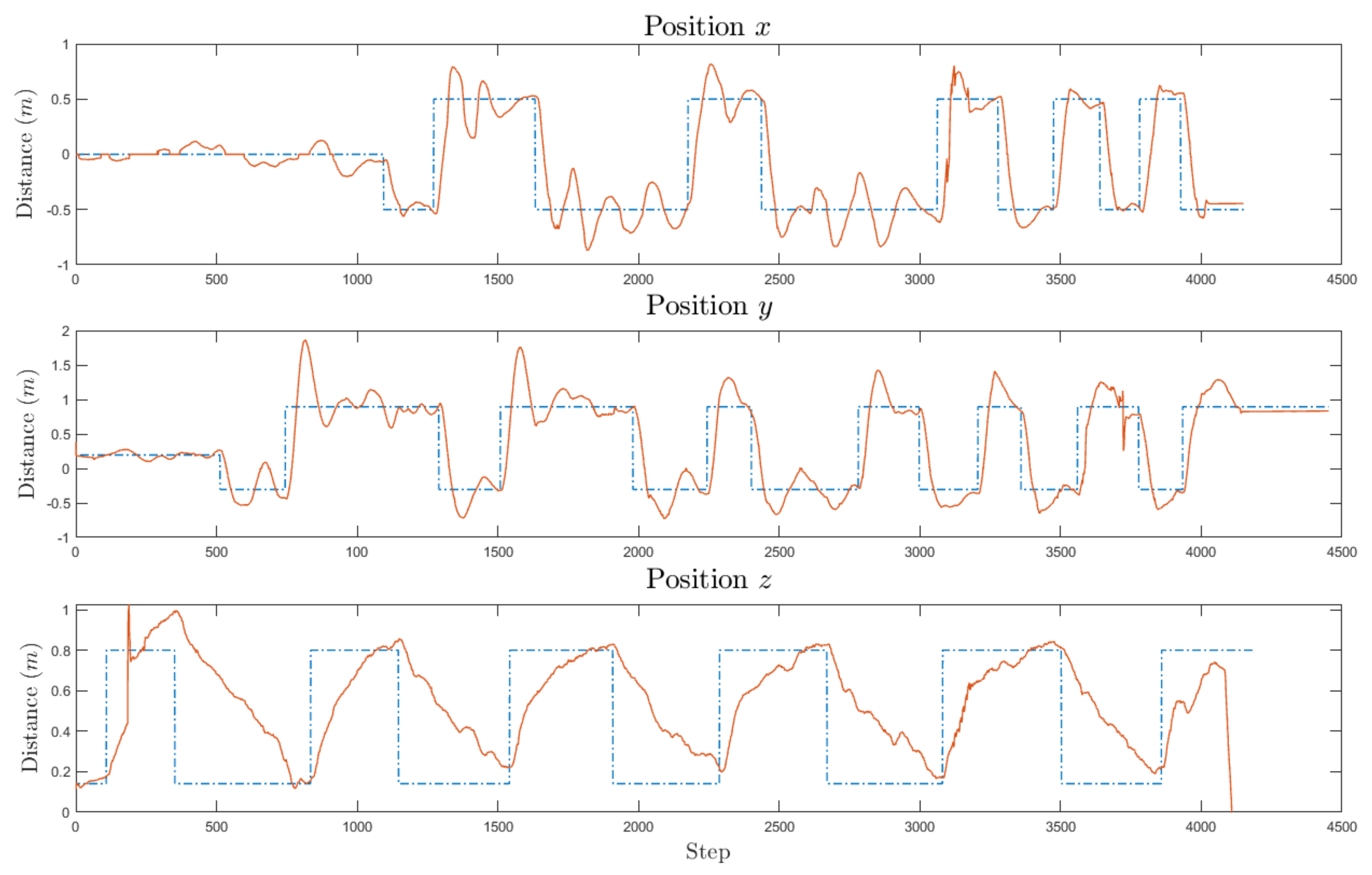
Figure 12.
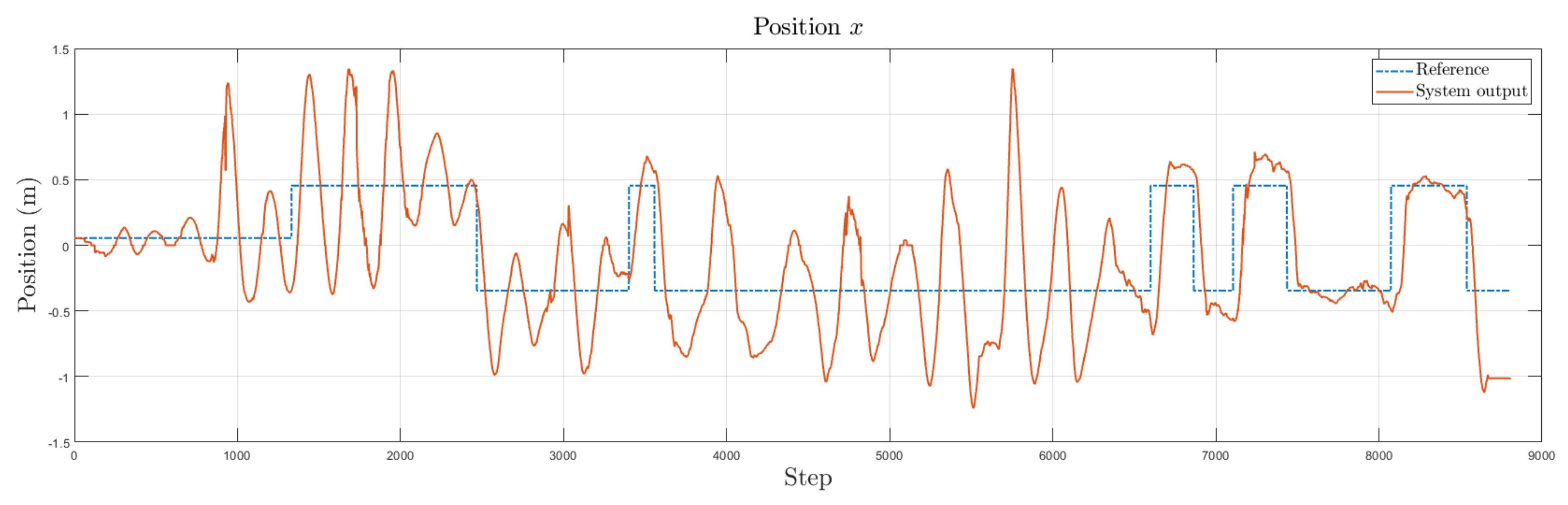
Experimental results for position of the UAV. One MLP module for each axis is used and they are trained online. The desired value is represented by the dashed line and the output of the system with the solid line.
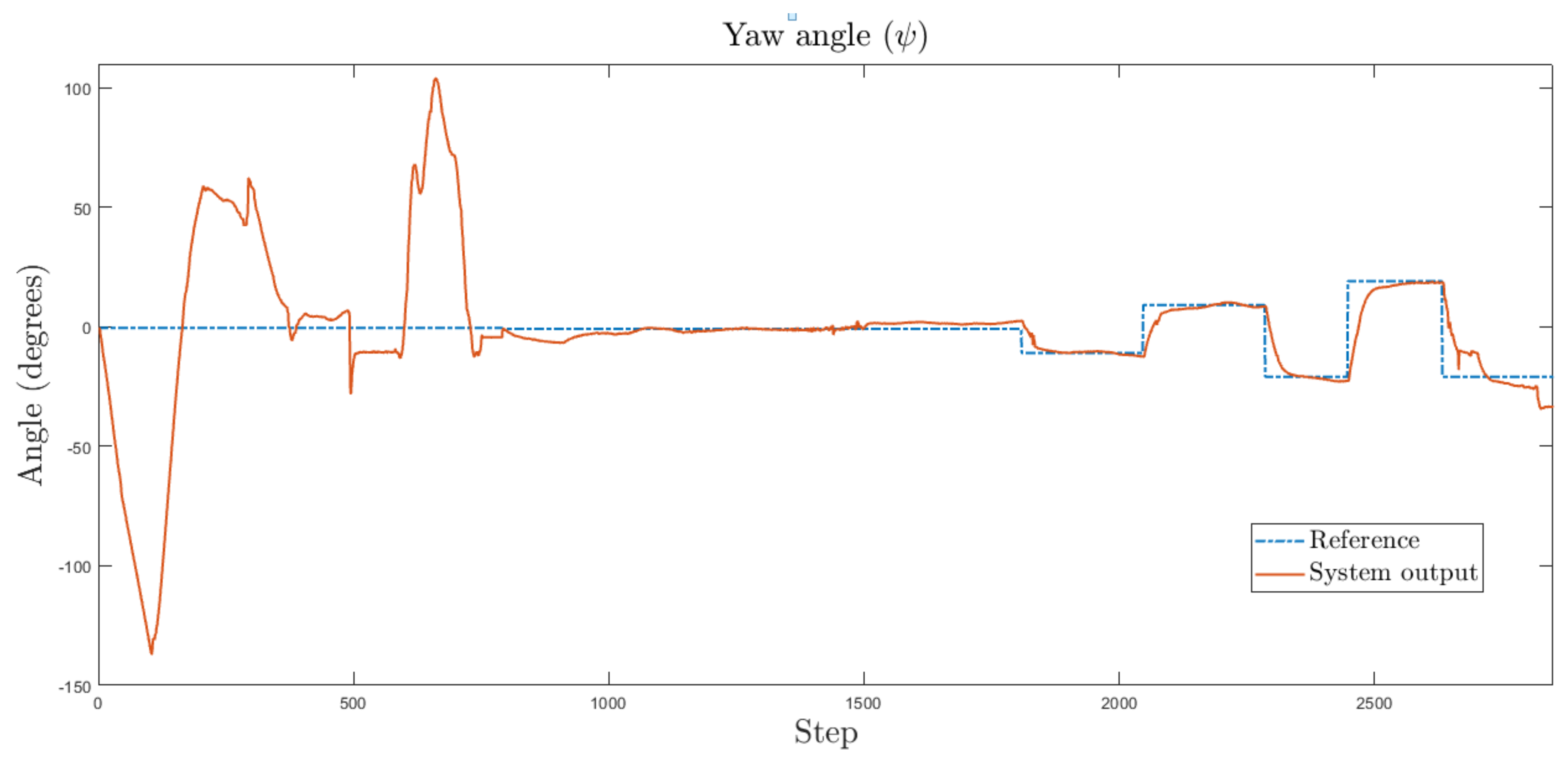
For the yaw angle , in contrast with the other three modules, the weights were initialized randomly. The fourth MLP module was trained online to control the yaw angle, and the results are shown in Figure 13. As can be seen, the neural network adapts its weights to follow the reference.
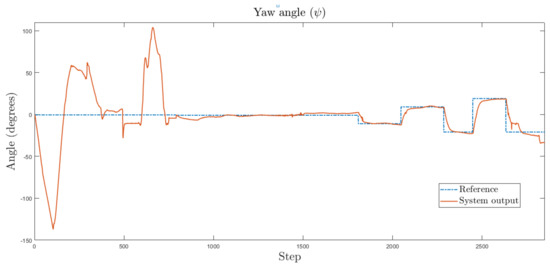
Figure 13.
Experimental results for yaw angle of the UAV. Dashed line represents the reference and the solid line represents the system output.
For a second experiment, a mass is added to the system during the flight in order to test its adaptability; the mass has a value of 45 g, which represents, approximately, 1/3 of the maximum payload of the Ar.Drone 2.0. The results of this experiment are shown in Figure 14. As can be seen, at iteration 750 approximately, the mass is added on the x axis of the quadrotor. After some iterations, the oscillations are eliminated.
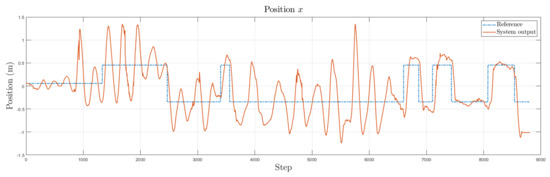
Figure 14.
Experimental results for x axis changing the dynamics. Dashed line represents the reference and the solid line represents the system output.
8. Conclusions
In this paper, a direct control approach for a quadrotor was presented. The controller was based in a Multilayer Perceptron trained with the Extended Kalman Filter. Each MLP module consists of two inputs, ten nodes in the hidden layer and one output, which is the control action. Each controllable degree of freedom required an MLP module that was trained online to adapt its control law to uncertainties, loss of rotor efficiency, time delays and changes in the dynamic model of the system. The results were first validated via simulation using the Ar.Drone 2.0 ROS driver with Gazebo simulator. The neural network was initialized with random weights for x, y and z axes, and once the overshoot and oscillations were reduced, the weights were used to initialize the MLP modules in the real system. In the simulation, every degree of freedom was separately trained. For experimental tests, x, y, and z were initialized with the weights calculated in simulation, and all of them continued their training online. As can be seen in Figure 12, even using the simulation results, the neural networks must continue the training, since they present oscillations around the reference location. After some iteration steps, the oscillations were eliminated. For the experimental tests on the yaw angle , the weights were initialized randomly; that is, without previous training in a simulation. Figure 13 can be seen as the erratic behavior at the beginning of the experiment, and it is shown that the MLP adapt its weights to control the yaw of the quadrotor. Finally, in Figure 14, it has been shown that the controller adapts its weights when changing the dynamics during the flight.
Author Contributions
Project administration, N.A.-D.; neural network formal analysis, A.Y.A.; neural network code, C.V.; ROS simulations and implementations, J.H.-B.; methodology, N.A.-D and C.L.-F.; real-time experiments, J.G.-A. and C.V.; writing—original draft preparation, J.G.-A. and C.V.; writing—review and editing, N.A.-D. and C.L.-F. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the support of Council of Sciences and Technology (CONACYT), Mexico, for financially supporting the following projects: CB-256769, CB-258068 and PN-2016-4107.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial Neural Network |
| BA | Bundle Adjustment |
| EKF | Extended Kalman Filter |
| GPS | Global Positioning System |
| HALE | High Altitude Long Endurance |
| LQR | Linear Quadratic Regulator |
| MALE | Medium Altitude Long Endurance |
| MLP | Multilayer Perceptron |
| PID | Proportional Integral Derivative |
| PTAM | Parallel Tracking and Mapping |
| ROS | Robot Operating System |
| SLAM | Simultaneous Localization and Mapping |
| UAV | Unmanned Aerial Vehicle |
| VTOL | Vertical Take-Off and Landing |
References
- Nebiker, S.; Annen, A.; Scherrer, M.; Oesch, D. A light-weight multispectral sensor for micro UAV—Opportunities for very high resolution airborne remote sensing. Int. Arch. Photogramme. Remote Sens. Spat. Inf. Sci. 2008, 37, 1193–1199. [Google Scholar]
- Bento, M.d.F. Unmanned aerial vehicles: An overview. Inside GNSS 2008, 3, 54–61. [Google Scholar]
- Eugster, H.; Nebiker, S. UAV-based augmented monitoring-real-time georeferencing and integration of video imagery with virtual globes. IAPRSSIS 2008, 37, 1229–1235. [Google Scholar]
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Design and control of an indoor micro quadrotor. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4393–4398. [Google Scholar]
- Bürkle, A.; Segor, F.; Kollmann, M. Towards autonomous micro uav swarms. J. Intell. Robot. Syst. 2011, 61, 339–353. [Google Scholar] [CrossRef]
- Engel, J.; Sturm, J.; Cremers, D. Accurate figure flying with a quadrocopter using onboard visual and inertial sensing. Imu 2012, 320. [Google Scholar] [CrossRef]
- Rivera-Mejía, J.; Léon-Rubio, A.; Arzabala-Contreras, E. PID based on a single artificial neural network algorithm for intelligent sensors. J. Appl. Res. Technol. 2012, 10, 262–282. [Google Scholar] [CrossRef]
- Lu, W.; Yang, J.; Liu, X. The PID Controller Based on the Artificial Neural Network and the Differential Evolution Algorithm. JCP 2012, 7, 2368–2375. [Google Scholar] [CrossRef]
- Ge, S.S.; Zhang, J.; Lee, T.H. Adaptive neural network control for a class of MIMO nonlinear systems with disturbances in discrete-time. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 1630–1645. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Sánchez Camperos, E.; Alanís García, A. Redes Neuronales: Conceptos fundamentales y aplicaciones a control automático; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Leung, H.; Haykin, S. The complex backpropagation algorithm. IEEE Trans. Signal Process. 1991, 39, 2101–2104. [Google Scholar] [CrossRef]
- Ruck, D.W.; Rogers, S.K.; Kabrisky, M.; Maybeck, P.S.; Oxley, M.E. Comparative analysis of backpropagation and the extended Kalman filter for training multilayer perceptrons. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 686–691. [Google Scholar] [CrossRef]
- De Freitas, J.F.; Niranjan, M.; Gee, A.H. Hierarchical Bayesian models for regularization in sequential learning. Neural Comput. 2000, 12, 933–953. [Google Scholar] [CrossRef] [PubMed]
- Singhal, S.; Wu, L. Training feed-forward networks with the extended Kalman algorithm. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 23–26 May 1989; pp. 1187–1190. [Google Scholar]
- Williams, R.J. Some Observations on the Use of the Extended Kalman Filter as A Recurrent Network Learning Algorithm; Citeseer: University Park, PA, USA, 1992. [Google Scholar]
- Latt, Z.K.K.; Si, H.; Kaneko, O. Controller Parameter Tuning of a Hexacopter with Fictitious Reference Iterative Tuning. In Proceedings of the 2019 SICE International Symposium on Control Systems (SICE ISCS), Kumamoto, Japan, 7–9 March 2019; pp. 96–101. [Google Scholar]
- Serrano-Pérez, O.; Villarreal-Cervantes, M.G.; González-Robles, J.C.; Rodríguez-Molina, A. Meta-heuristic algorithms for the control tuning of omnidirectional mobile robots. Eng. Optim. 2019, 52, 325–342. [Google Scholar] [CrossRef]
- Bari, S.; Hamdani, S.S.Z.; Khan, H.U.; ur Rehman, M.; Khan, H. Artificial Neural Network Based Self-Tuned PID Controller for Flight Control of Quadcopter. In Proceedings of the 2019 International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 21–22 February 2019; pp. 1–5. [Google Scholar]
- Radiansyah, S.; Kusrini, M.; Prasetyo, L. Quadcopter Applications for Wildlife Monitoring; IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2017; Volume 54, p. 012066. [Google Scholar]
- Antonio-Toledo, M.E.; Sanchez, E.N.; Alanis, A.Y.; Florez, J.; Perez-Cisneros, M.A. Real-time integral backstepping with sliding mode control for a quadrotor UAV. IFAC-PapersOnLine 2018, 51, 549–554. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Yi, Y.; Xin, J.; Liu, D. Nonlinear tracking control methods applied to qball-x4 quadrotor uav against actuator faults. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 3478–3483. [Google Scholar]
- Reyes-Valeria, E.; Enriquez-Caldera, R.; Camacho-Lara, S.; Guichard, J. LQR control for a quadrotor using unit quaternions: Modeling and simulation. In Proceedings of the CONIELECOMP 2013, 23rd International Conference on Electronics, Communications and Computing, Cholula, Mexico, 11–13 March 2013; pp. 172–178. [Google Scholar]
- Cowling, I.D.; Whidborne, J.F.; Cooke, A.K. Optimal trajectory planning and LQR control for a quadrotor UAV. In Proceedings of the International Conference on Control, Glasgow, UK, 2 September 2006. [Google Scholar]
- Khatoon, S.; Gupta, D.; Das, L. PID & LQR control for a quadrotor: Modeling and simulation. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), New Delhi, India, 24–27 September 2014; pp. 796–802. [Google Scholar]
- Lin, Q.; Cai, Z.; Wang, Y.; Yang, J.; Chen, L. Adaptive flight control design for quadrotor UAV based on dynamic inversion and neural networks. In Proceedings of the 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control, Shenyang, China, 21–23 September 2013; pp. 1461–1466. [Google Scholar]
- Bouabdallah, S.; Siegwart, R. Full control of a quadrotor. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 153–158. [Google Scholar]
- Madani, T.; Benallegue, A. Backstepping sliding mode control applied to a miniature quadrotor flying robot. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 700–705. [Google Scholar]
- Swarnkar, S.; Kothari, M. A simplified adaptive backstepping control of aircraft lateral directional dynamics. IFAC PapersOnLine 2016, 49, 579–584. [Google Scholar] [CrossRef]
- Meyer, G.; Su, R.; Hunt, L.R. Application of nonlinear transformations to automatic flight control. Automatica 1984, 20, 103–107. [Google Scholar] [CrossRef]
- Lane, S.H.; Stengel, R.F. Flight control design using non-linear inverse dynamics. Automatica 1988, 24, 471–483. [Google Scholar] [CrossRef]
- Ochi, Y.; Kanai, K. Design of restructurable flight control systems using feedback linearization. J. Guid. Control Dyn. 1991, 14, 903–911. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. Backstepping/nonlinear Hinf control for path tracking of a quadrotor unmanned aerial vehicle. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3356–3361. [Google Scholar]
- Zhang, Y.; Chamseddine, A. Fault tolerant flight control techniques with application to a quadrotor UAV testbed. In Automatic Flight Control Systems-Latest Developments; IntechOpen: London, UK, 2012; pp. 119–150. [Google Scholar]
- Li, T.; Zhang, Y.; Gordon, B.W. Nonlinear fault-tolerant control of a quadrotor uav based on sliding mode control technique. IFAC Proc. Vol. 2012, 45, 1317–1322. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A.; Polycarpou, M.M.; Djapic, V.; Sharma, M. Command filtered adaptive backstepping. IEEE Trans. Control Syst. Technol. 2011, 20, 566–580. [Google Scholar] [CrossRef]
- Guo, D.; Hu, H.; Yi, J. Neural network control for a semi-active vehicle suspension with a magnetorheological damper. Modal Anal. 2004, 10, 461–471. [Google Scholar] [CrossRef]
- Lee, M.; Choi, H.S. A robust neural controller for underwater robot manipulators. IEEE Trans. Neural Netw. 2000, 11, 1465–1470. [Google Scholar] [PubMed]
- Yuh, J. A neural net controller for underwater robotic vehicles. IEEE J. Ocean. Eng. 1990, 15, 161–166. [Google Scholar] [CrossRef]
- Freddi, A.; Longhi, S.; Monteriù, A.; Prist, M. Actuator fault detection and isolation system for an hexacopter. In Proceedings of the 2014 IEEE/ASME 10th International Conference on Mechatronic and Embedded Systems and Applications (MESA), Senigallia, Italy, 10–12 September 2014; pp. 1–6. [Google Scholar]
- Sheng, Q.; Xianyi, Z.; Changhong, W.; Gao, X.; Zilong, L. Design and implementation of an adaptive PID controller using single neuron learning algorithm. In Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, China, 10–14 June 2002; Volume 3, pp. 2279–2283. [Google Scholar]
- Grzonka, S.; Grisetti, G.; Burgard, W. Towards a navigation system for autonomous indoor flying. In Proceedings of the 2009 IEEE international conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2878–2883. [Google Scholar]
- Achtelik, M.; Bachrach, A.; He, R.; Prentice, S.; Roy, N. Stereo vision and laser odometry for autonomous helicopters in GPS-denied indoor environments. In Unmanned Systems Technology XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; Volume 7332, p. 733219. [Google Scholar]
- Strydom, R.; Thurrowgood, S.; Srinivasan, M.V. Visual odometry: Autonomous uav navigation using optic flow and stereo. In Proceedings of the Australasian Conference on Robotics and Automation, Melbourne, Australia, 2–4 December 2014. [Google Scholar]
- Huang, A.S.; Bachrach, A.; Henry, P.; Krainin, M.; Maturana, D.; Fox, D.; Roy, N. Visual odometry and mapping for autonomous flight using an RGB-D camera. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2017; pp. 235–252. [Google Scholar]
- Whelan, T.; Johannsson, H.; Kaess, M.; Leonard, J.J.; McDonald, J. Robust real-time visual odometry for dense RGB-D mapping. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Dryanovski, I.; Valenti, R.G.; Xiao, J. Fast visual odometry and mapping from RGB-D data. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2305–2310. [Google Scholar]
- Blösch, M.; Weiss, S.; Scaramuzza, D.; Siegwart, R. Vision based MAV navigation in unknown and unstructured environments. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 21–28. [Google Scholar]
- Achtelik, M.; Achtelik, M.; Weiss, S.; Siegwart, R. Onboard IMU and monocular vision based control for MAVs in unknown in-and outdoor environments. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3056–3063. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE international conference on robotics and automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Engel, J.; Sturm, J.; Cremers, D. Camera-based navigation of a low-cost quadrocopter. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 2815–2821. [Google Scholar]
- Engel, J.; Sturm, J.; Cremers, D. Scale-aware navigation of a low-cost quadrocopter with a monocular camera. Robot. Auton. Syst. 2014, 62, 1646–1656. [Google Scholar] [CrossRef]
- Schmidt, M.D. Simulation and Control of a Quadrotor Unmanned Aerial Vehicle. Master ’s Thesis, University of Kentucky, Lexington, KY, USA, 2011. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Puskorius, G.V.; Feldkamp, L.A. Parameter-based Kalman filter training: Theory and implementation. Kalman Filter. Neural Netw. 2001, 23. [Google Scholar] [CrossRef]
- Williams, R.J. Training recurrent networks using the extended Kalman filter. In Proceedings of the IJCNN International Joint Conference on Neural Networks, Baltimore, MD, USA, 7–11 June 1992; Volume 4, pp. 241–246. [Google Scholar]
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 47. [Google Scholar]
- Alanis, A.Y.; Sanchez, E.N. Discrete-Time Neural Observers: Analysis and Applications; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Camperos, E.N.S.; García, A.Y.A. Redes neuronales: conceptos fundamentales y aplicaciones a control automático; Pearson Educación: London, UK, 2006. [Google Scholar]
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 1–10. [Google Scholar]
- Engel, J. Autonomous Camera-Based Navigation of a Quadrocopter. Master’s Thesis, TUM University, Munich, Germany, December 2011. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).