PD Steering Controller Utilizing the Predicted Position on Track for Autonomous Vehicles Driven on Slippery Roads
Abstract
1. Introduction
2. Materials and Methods
2.1. Environment and the Car Simulator TORCS
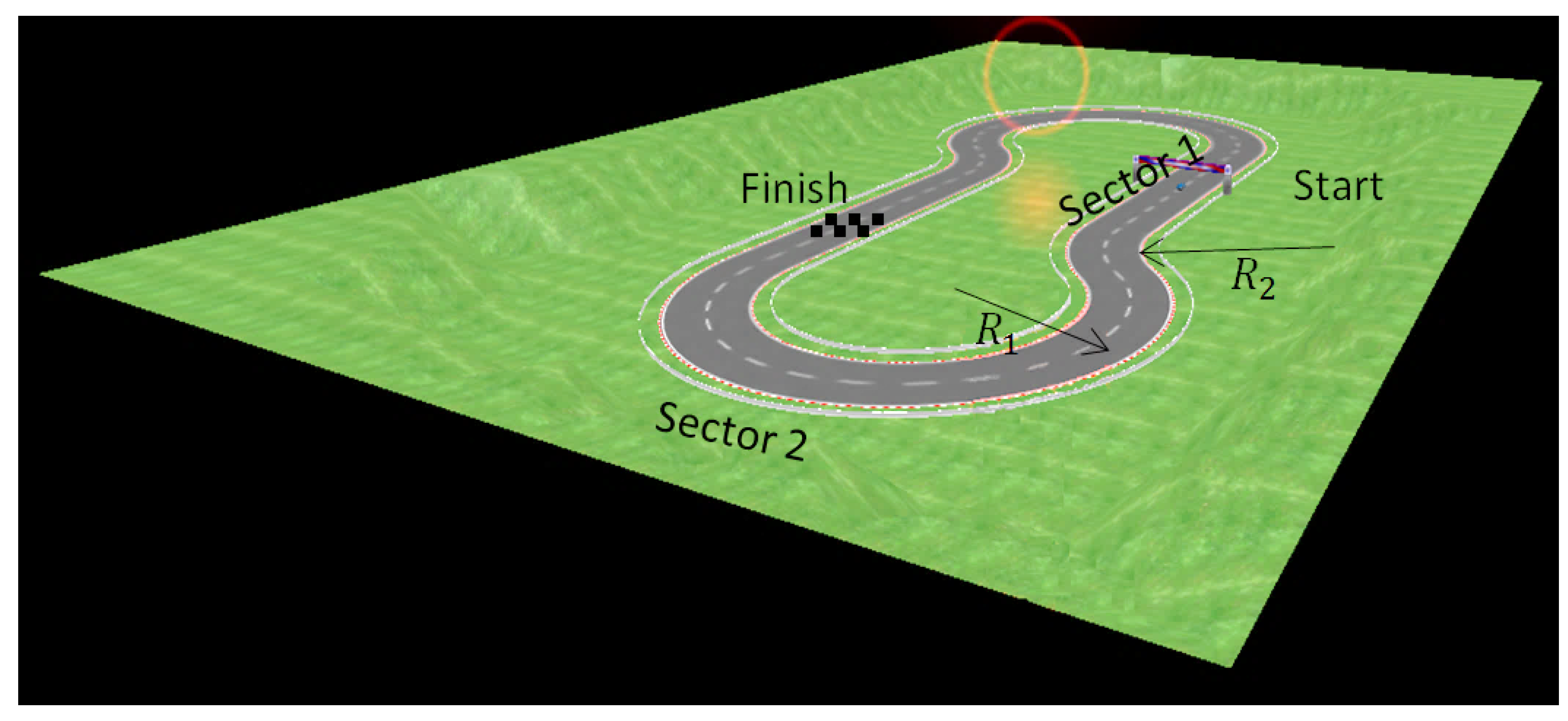
2.2. The Track
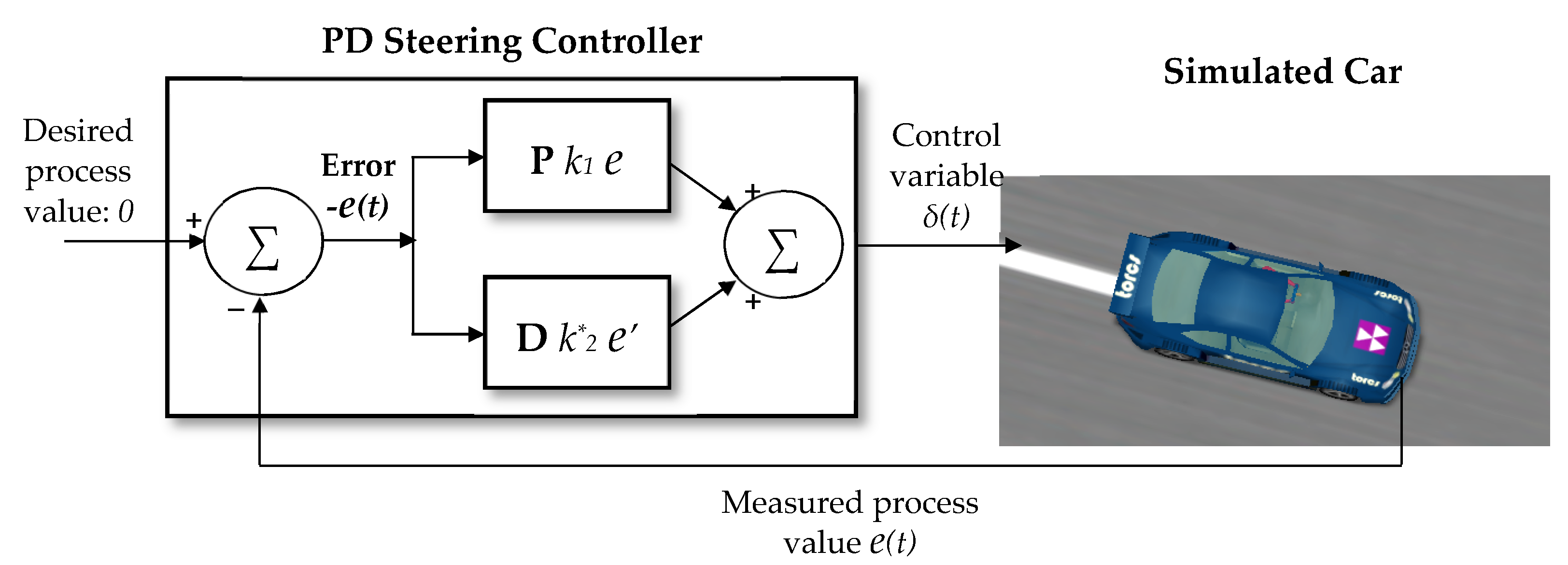
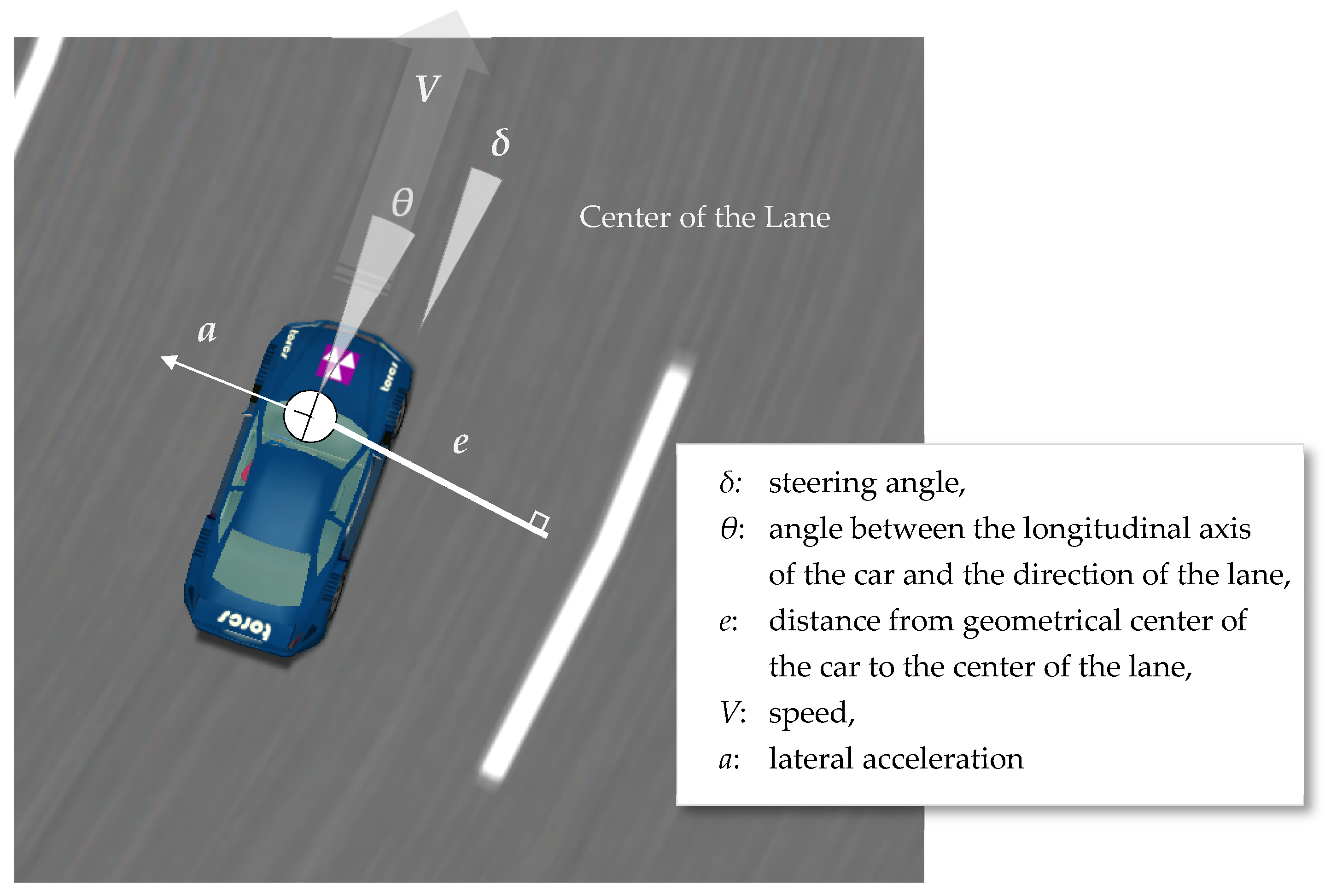
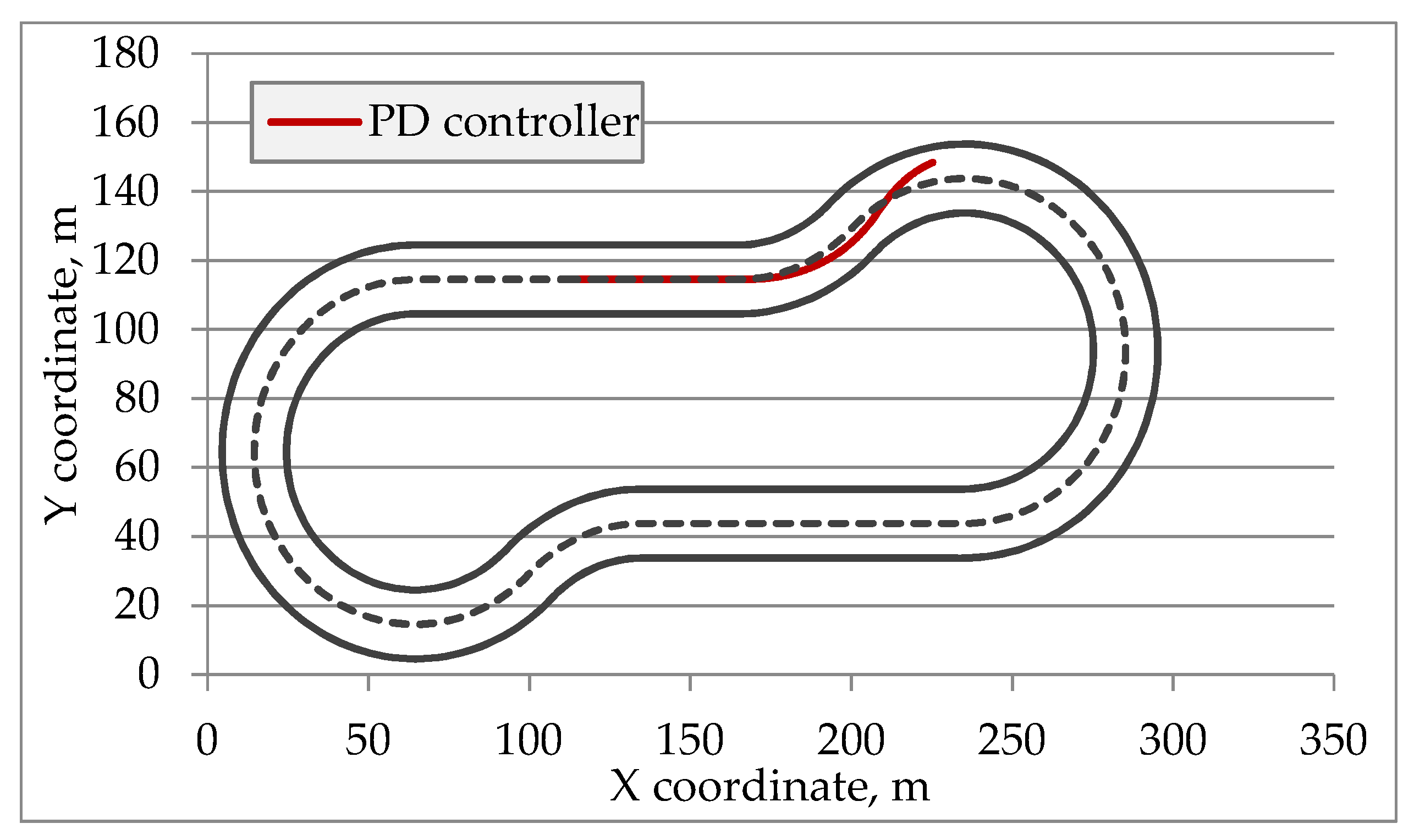
2.3. Servo Control as a PD Controller
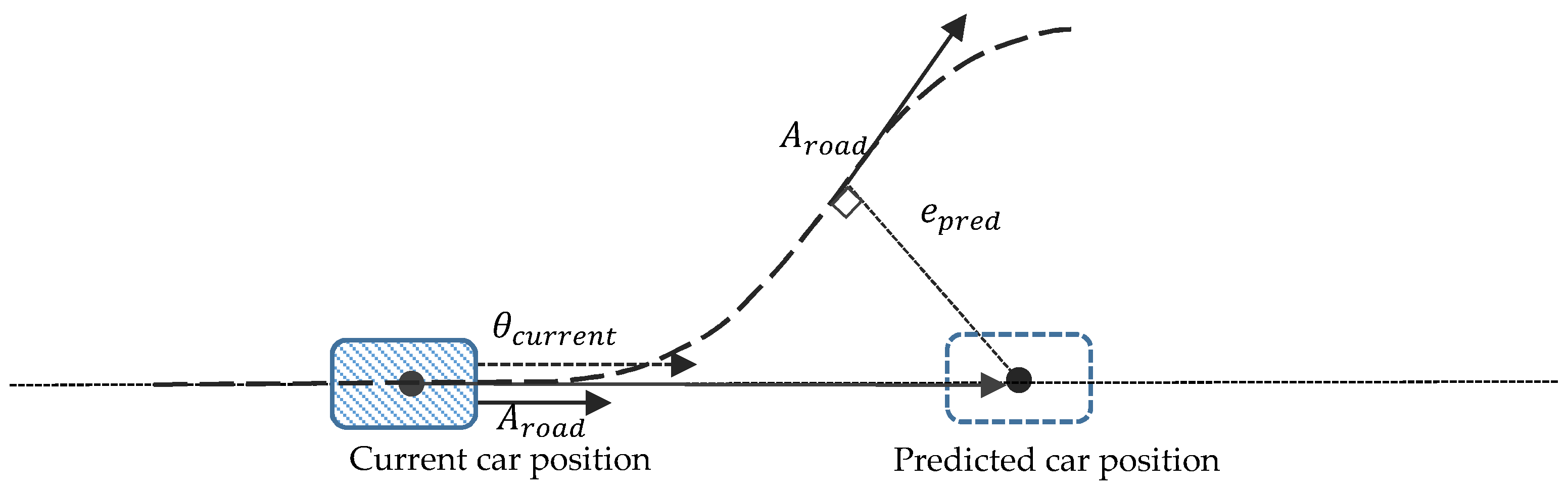
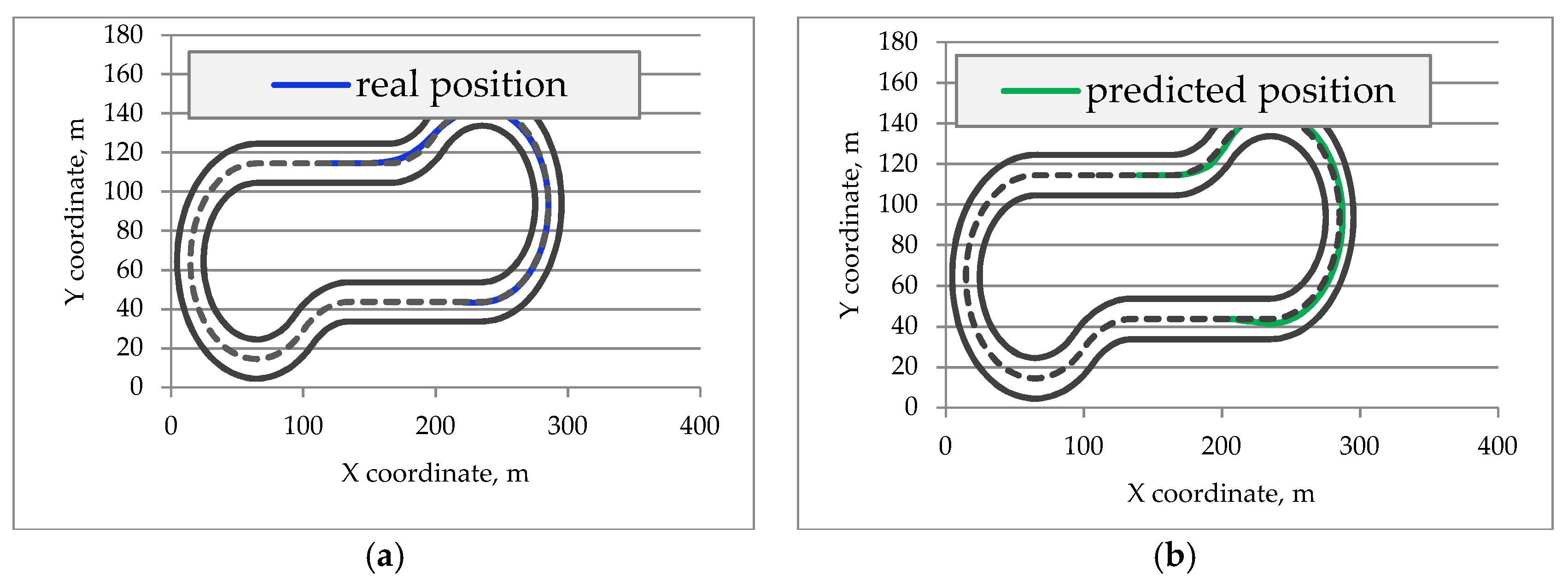
2.4. Extending the Servo-Control Model: A PD Steering Controller with Prediction
2.5. Steering Controller Obtained by Genetic Programming (GP)
2.6. Target Quality Function Evaluation
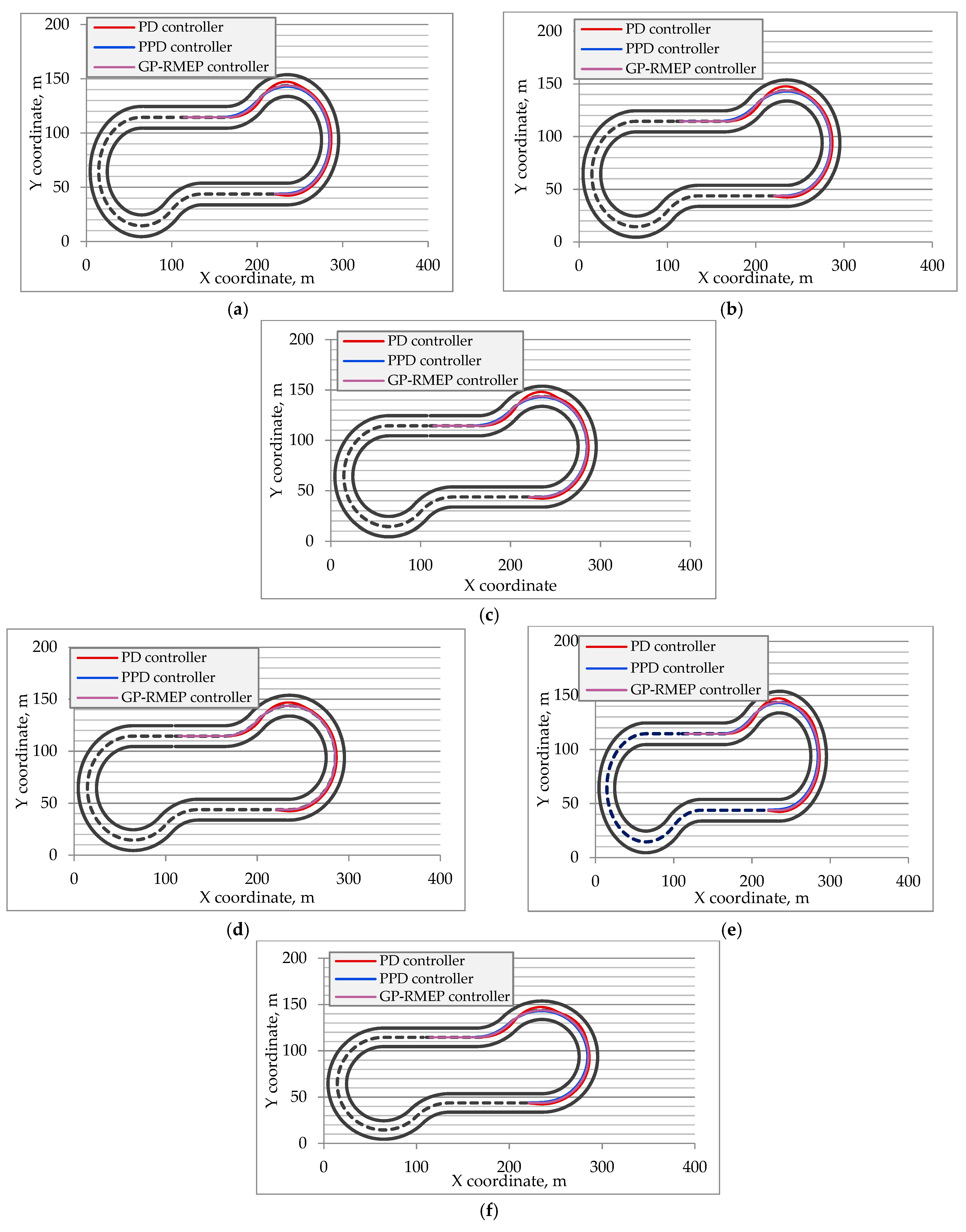
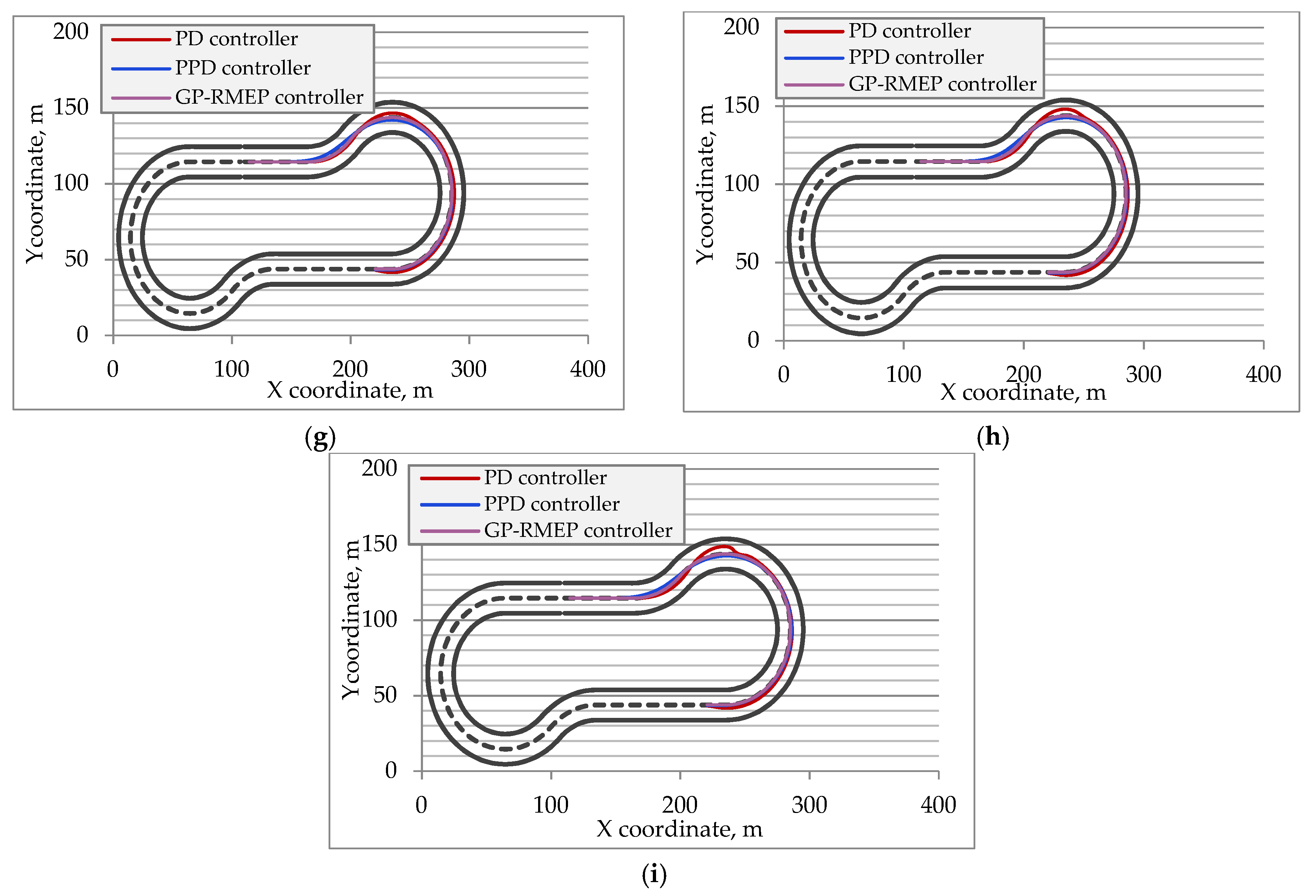
3. Experimental Results
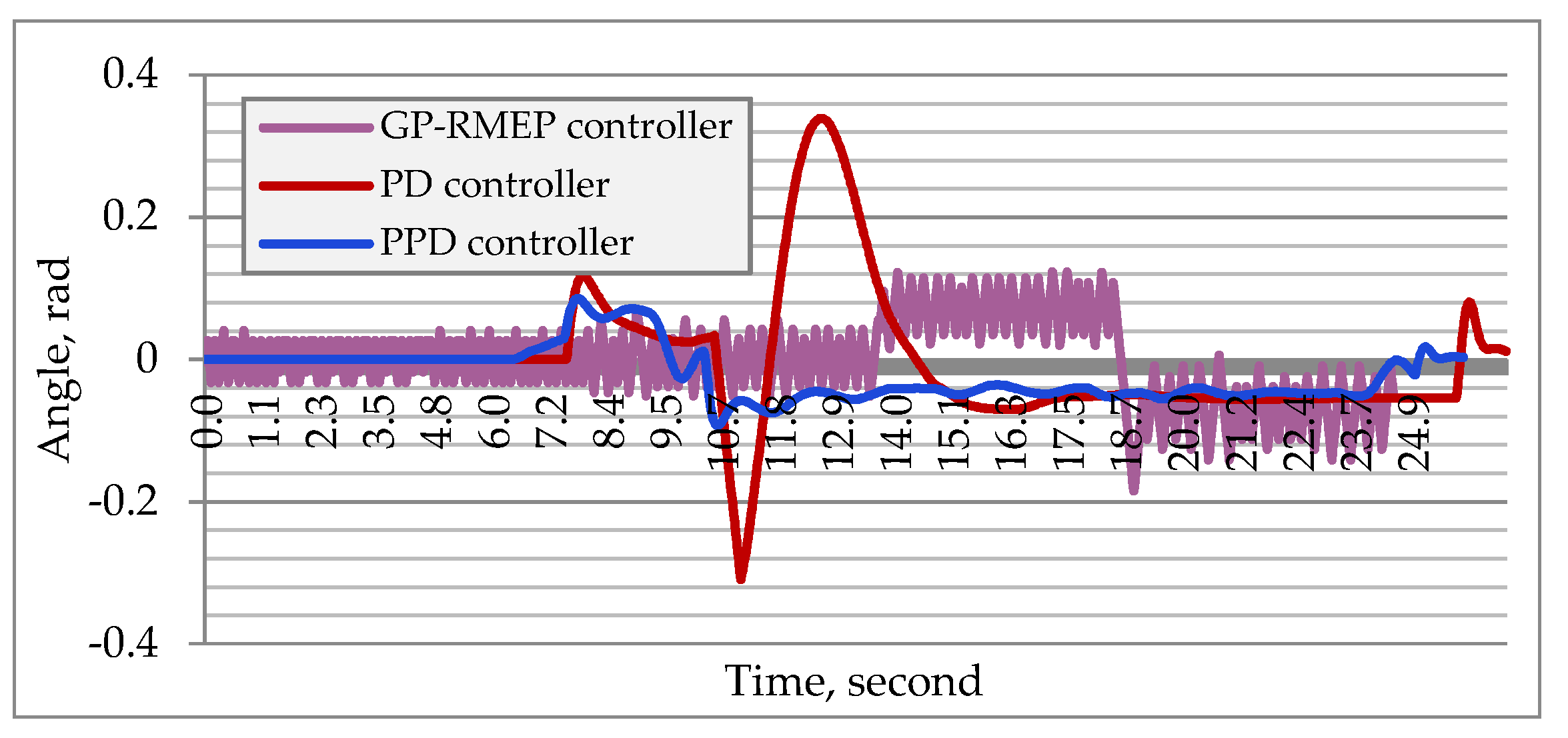
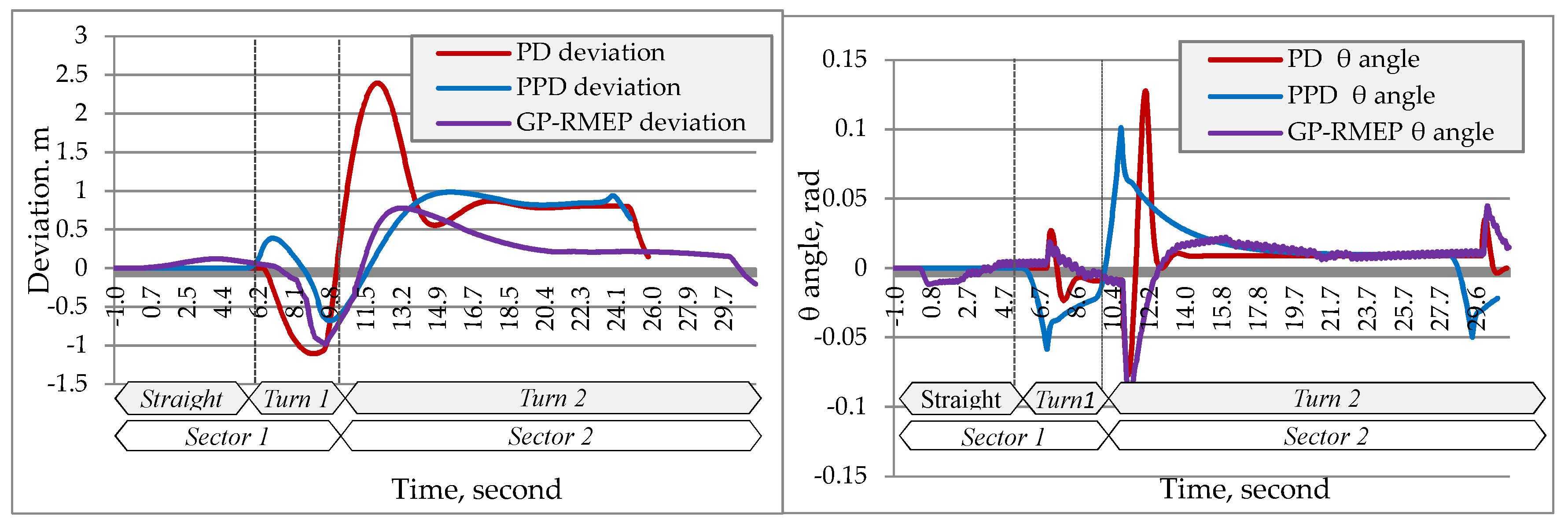
3.1. Time Needed to Return on Desired Trajectory
3.2. Critical Speed Rising
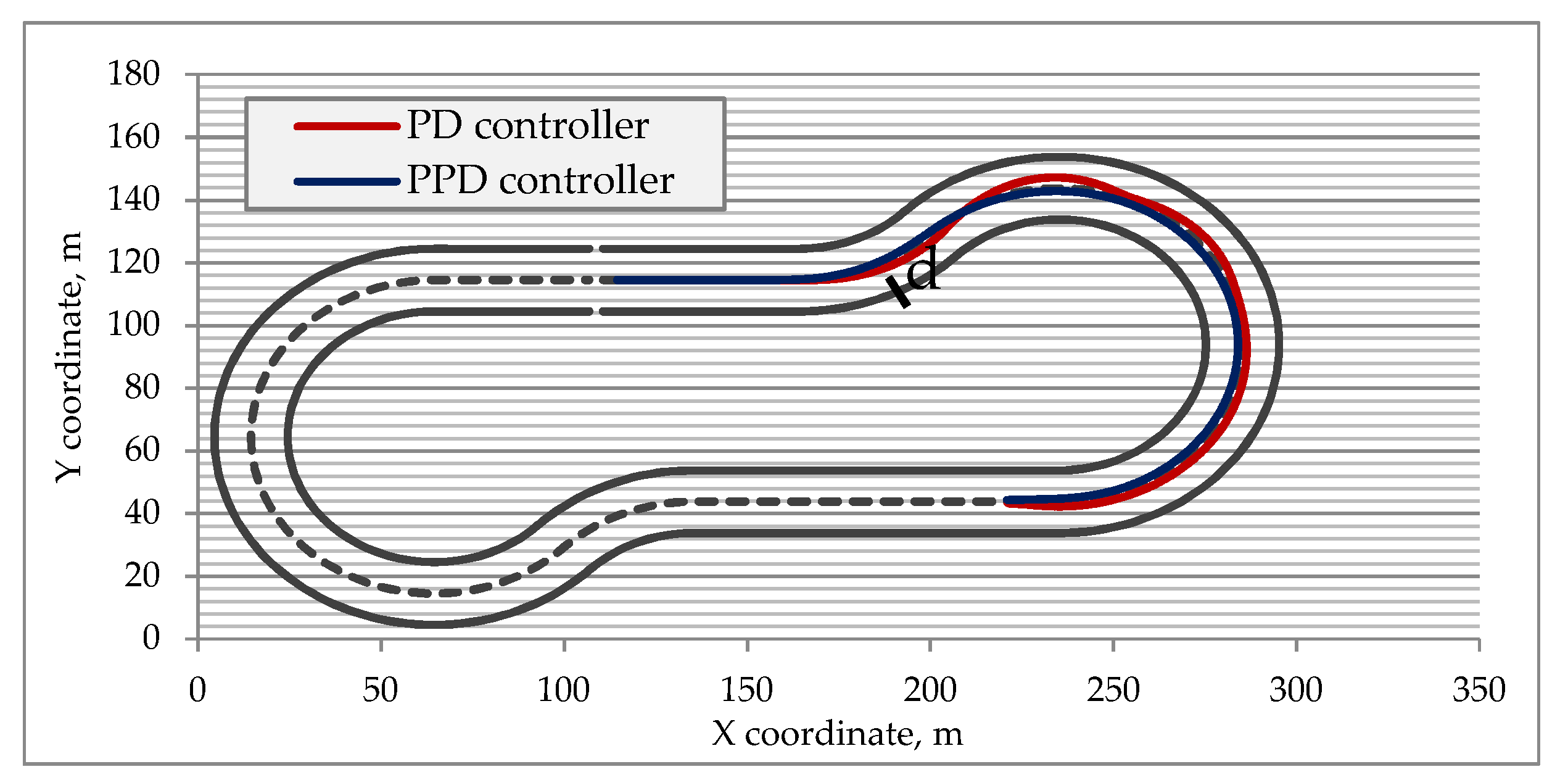
3.3. Safe Distance
4. Discussion
- Coordinates and heading at which it starts: ();
- Its length L;
- Its linear curvature function, which is determined by the two coefficients ().
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stone, P.; Brooks, R.; Brynjolfsson, E.; Calo, R.; Etzioni, O.; Hager, G.; Hirschberg, J.; Kalyanakrishnan, S.; Kamar, E.; Kraus, S.; et al. Artificial Intelligence and Life in 2030. In Proceedings of the One Hundred Year Study on Artificial Intelligence: Report of the 2015-2016 Study Panel, Stanford, CA, USA, 6 September 2016; p. 52. [Google Scholar]
- Le-Anh, T.; De Koster, M.B. A Review of Design and Control of Automated Guided Vehicle Systems. Eur. J. Oper. Res. 2006, 171, 1–23. [Google Scholar] [CrossRef]
- Cheein, F.; De La Cruz, C.; Bastos, T.; Carelli, R. SLAM-based Cross-a-Door Solution Approach for a Robotic Wheelchair. Int. J. Adv. Robot. Syst. 2010, 7, 155–164. [Google Scholar] [CrossRef]
- Alekseeva, K.S.N.; Tanev, I. Evolving a Single-variable Controller for Automated Steering of a Car on Slippery Roads. In Proceedings of the SICE Annual Conference 2018: SCIE 2018, Nara, Japan, 11–14 September 2018; pp. 680–685. [Google Scholar]
- Huang, J.; Tanev, I.; Shimohara, K. Evolving a general electronic stability program for car simulated in TORCS. In Proceedings of the 2015 IEEE Conference Computational Intelligence and Games (CIG), Tainan, Taiwan, 31 August–2 September 2015; pp. 446–453. [Google Scholar]
- Alekseeva, N.; Tanev, I.; Shimohara, K. Evolving the Controller of Automated Steering of a Car in Slippery Road Conditions. Algorithms 2018, 11, 108. [Google Scholar] [CrossRef]
- Wymann, B.C.R.; Dimitrakakis, C.; Sumner, A.; Espié, E.; Guionneau, C. TORCS, the Open Racing Car Simulator, v1.3.5. 2013. Available online: http://www.torcs.org (accessed on 20 February 2020).
- Komoriya, K.; Tanie, K. Trajectory Design and Control of a Wheel-type Mobile Robot Using B-spline Curve. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems ‘(IROS ’89)’ the Autonomous Mobile Robots and Its Applications, Tsukuba, Japan, 4–6 September 1989; pp. 398–405. [Google Scholar]
- Marzbani, H.; Jazar, R.; Fard, M. Better Road Design Using Clothoids. In Sustainable Automotive Technologies; Springer: Cham, Switzerland, 2015; pp. 25–40. [Google Scholar]
- Lamm, R.; Psarianos, B.; Choueiri, E.M. A practical safety approach to highway geometric design International case studies: Germany, Greece, Lebanon, and the United States. In Proceedings of the International Symposium on Highway Geometric Design Practices, Boston, MA, USA, 30 August–1 September 1995. [Google Scholar]
- Melder, N.; Tomlinson, S. Racing Vehicle Control Systems using PID Controllers. Game AI Pro 2014, 491–500. [Google Scholar]
- Zeeb, K.; Buchner, A.; Schrauf, M. Is take-over time all that matters? The impact of visual-cognitive load on driver take-over quality after conditionally automated driving. Accid. Anal. Prev. 2016, 92, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Alekseeva, N.; Tanev, I.; Shimohara, K. On the Emergence of Oscillations in the Evolved Autosteering of a Car on Slippery Roads. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 1371–1378. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: New York, NY, USA, 2007. [Google Scholar]
- Frère, P. Sports Car and Competition Driving; Pickle Partners Publishing: Auckland, New Zealand, 2016. [Google Scholar]
- Marzbani, H.; Simic, M.; Fard, M.; Jazar, R. Better Road Design for Autonomous Vehicles Using Clothoids. In Intelligent Interactive Multimedia Systems and Services; Springer: Cham, Switzerland, 2015; pp. 265–278. [Google Scholar]


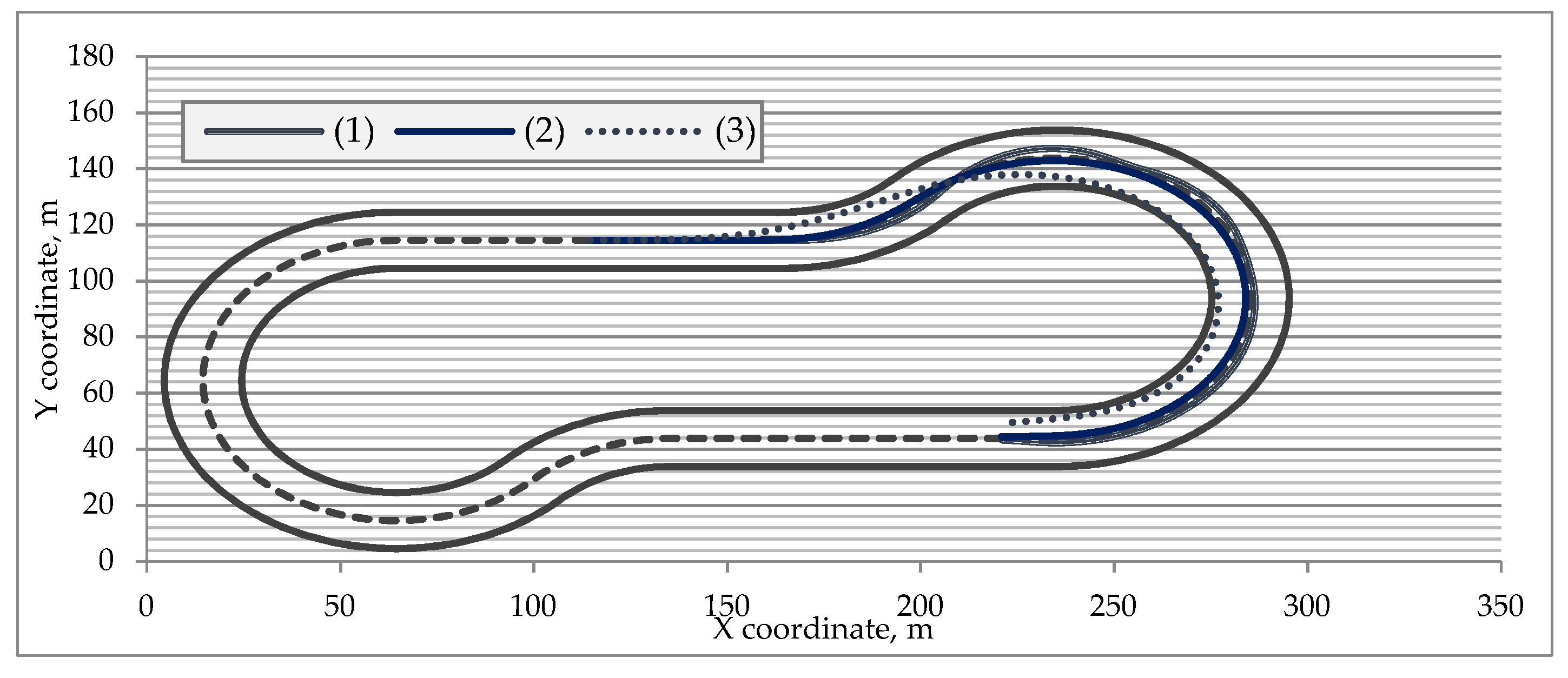
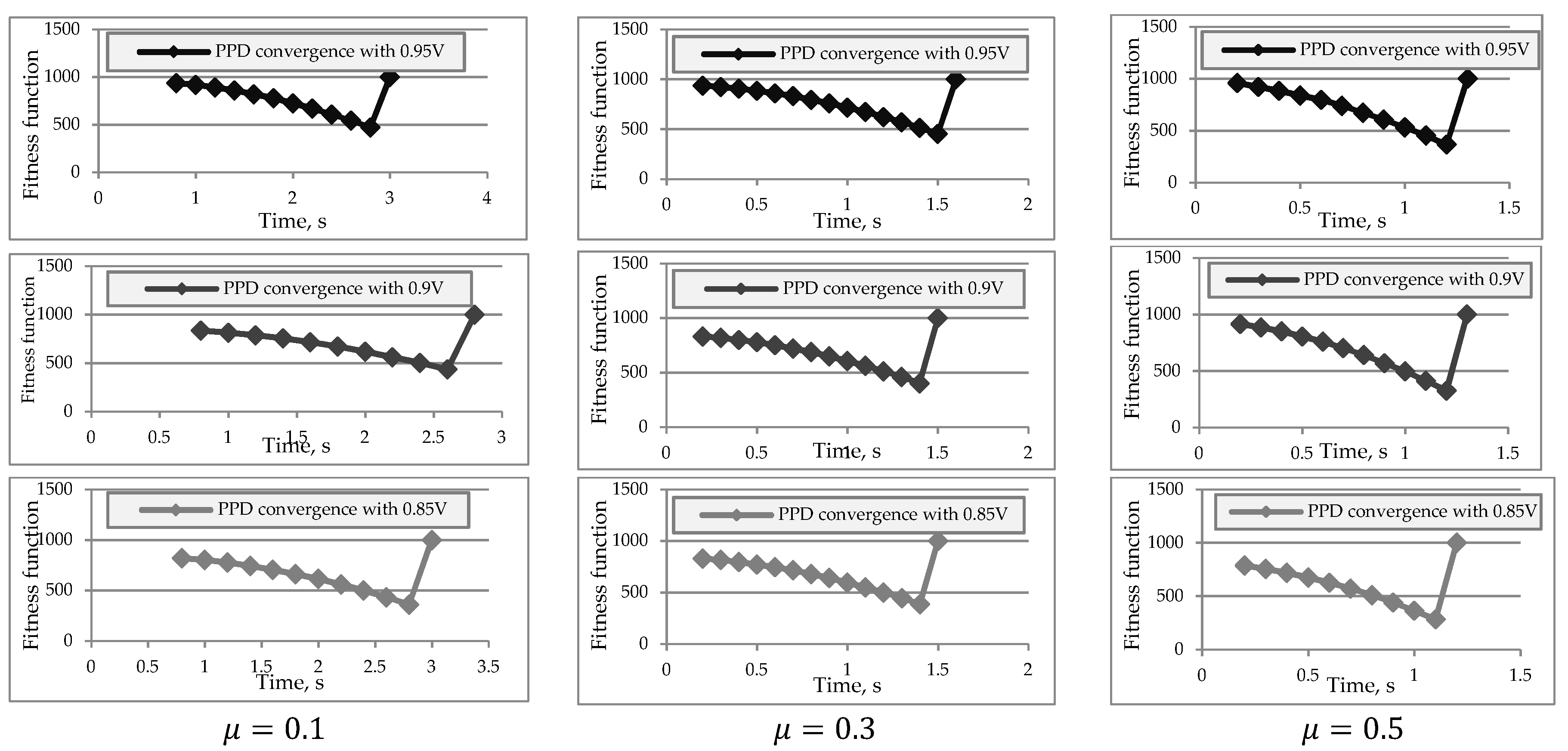
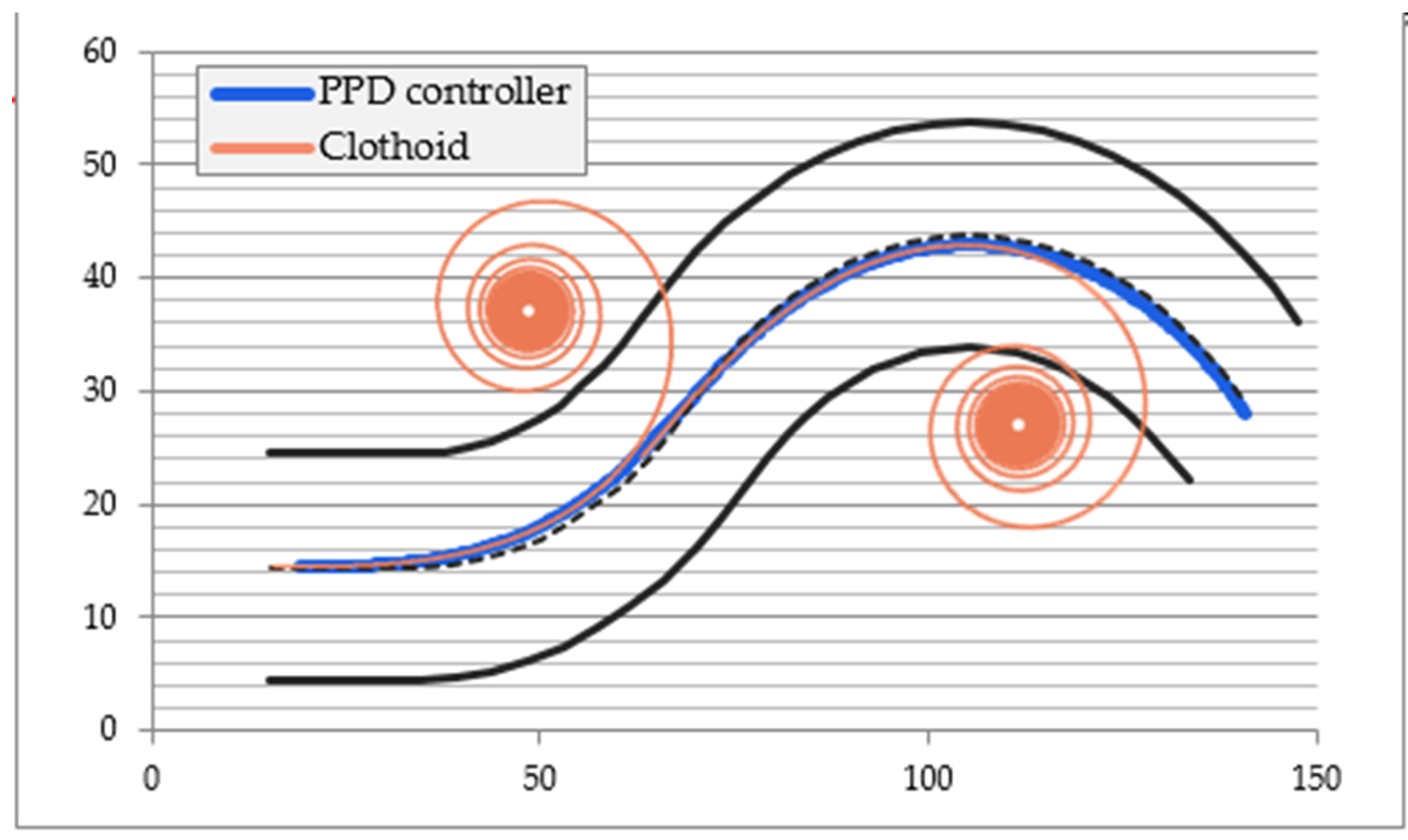
| Feature | Value |
|---|---|
| Model | CLK DTM |
| Length, m | 4.76 |
| Width, m | 1.96 |
| Height, m | 1.17 |
| Mass, kg | 1050 |
| Front/rear weight repartition | 0.5/0.5 |
| Height of center of gravity, m | 0.25 |
| Coefficient of friction of tires | 1.0 |
| Drivetrain | Front engine, rear wheels drive |
| Feature | Value |
|---|---|
| Total length, m | 300 |
| Lane width, m | 20 |
| Length of sector 1, m | 90 |
| Radius of turn 1, R1 m | 50 |
| Length of sector 2, m | 210 |
| Radius of turn 2, R2, m | 50 |
| Parameter | Value |
|---|---|
| Evolved individuals | SAF δ |
| Genetic representation | Parse tree |
| Set of non-terminals (functions) | {+, −, *, /} |
| Set of terminals | Variables pertinent to the state of the car, and their derivatives: lateral deviation (e, e’), speed (V), steering angle(δ), lateral acceleration (a, a’) angular deviation (θ, θ’), and a random constant (C) |
| Population size | 200 individuals |
| Selection | Binary tournament, ratio 0.1 |
| Elitism | Best 4 individuals |
| Crossover | Single point, random, ratio 0.9 |
| Mutation | Single point, random, ratio 0.05 |
| Fitness value | Sum of (i) the area under the trajectory of the car around the center of the lane and (ii) the average of its lateral velocity. |
| Termination criteria | (#Generations > 200) or (no improvement of fitness during 16 consecutive generations) |
| #Road Condition | Friction of Tires, µt | Friction of Road Surface, µs | Overall Friction, µ = µt × µs | Critical Speed, VCR, m/s | Speed of the Car (0.85 VCR), m/s | Speed of the Car (0.9 VCR), m/s | Speed of the Car (0.95 VCR), m/s |
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 0.5 (rainy) | 0.5 | 15.65 | 13.3 | 14.2 | 15 |
| 2 | 1.0 | 0.3 (icy and snowy) | 0.3 | 14 | 10.4 | 11 | 11.6 |
| 1.0 | 0.1 (icy) | 0.1 | 12.12 | 6 | 6.3 | 6.7 |
| #Road Condition | Overall Friction µ | 0.85 of Critical | 0.9 of Critical | 0.95 of Critical | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PD | PPD | GP-RMEP | PD | PPD | GP-RMEP | PD | PPD | GP-RMEP | ||
| 1 | 0.5 | 685 | 298 | 373 | 711 | 334 | 318 | 843 | 364 | 385 |
| 2 | 0.3 | 1693 | 383 | 374 | 1801 | 417 | 399 | 1854 | 458 | 413 |
| 3 | 0.1 | 1659 | 408 | 381 | 1717 | 432 | 420 | 1782 | 471 | 461 |
| #Road Condition | Overall Friction µ | 0.85 of Critical | 0.9 of Critical | 0.95 of Critical | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PD | PPD | GP-RMEP | PD | PPD | GP-RMEP | PD | PPD | GP-RMEP | ||
| 1 | 0.5 | 14.72 | 13.71 | 14.18 | 14.56 | 13.57 | 12.81 | 14.44 | 13.35 | 13.52 |
| 2 | 0.3 | 18.47 | 17.59 | 17.18 | 18.3 | 17.89 | 17.19 | 18.19 | 17.1 | 16.9 |
| 3 | 0.1 | 37.51 | 34.58 | 33.14 | 35.59 | 32.17 | 31.42 | 34.31 | 30.48 | 30.16 |
| #Road Condition | Overall Friction µ | 0.85 of Critical | 0.9 of Critical | 0.95 of Critical | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PD | PPD | GP-RMEP | PD | PPD | GP-RMEP | PD | PPD | GP-RMEP | ||
| 1 | 0.5 | 8.88 | 12.14 | 12.33 | 8.73 | 11.81 | 12.07 | 8.34 | 11.4 | 11.84 |
| 2 | 0.3 | 8.09 | 10.81 | 11.6 | 7.93 | 10.79 | 11.38 | 7.91 | 10.74 | 11.14 |
| 3 | 0.1 | 8.03 | 10.87 | 11.23 | 7.89 | 10.8 | 11.16 | 7.86 | 10.07 | 10.9 |
| #Road Condition | Overall Friction µ | 0.85 of Critical Speed | 0.9 of Critical Speed | 0.95 of Critical Speed | |||
|---|---|---|---|---|---|---|---|
| PD | PPD | PD | PPD | PD | PPD | ||
| 1 | 0.5 | 239 + 446 | 79 + 219 | 255 + 456 | 103 + 231 | 288 + 555 | 110 + 254 |
| 2 | 0.3 | 779 + 914 | 186 + 196 | 823 + 978 | 215 + 201 | 870 + 984 | 252 + 206 |
| 3 | 0.1 | 1241 + 418 | 346 + 62 | 1291 + 426 | 367 + 65 | 1305 + 477 | 405 + 66 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alekseeva, N.; Tanev, I.; Shimohara, K. PD Steering Controller Utilizing the Predicted Position on Track for Autonomous Vehicles Driven on Slippery Roads. Algorithms 2020, 13, 48. https://doi.org/10.3390/a13020048
Alekseeva N, Tanev I, Shimohara K. PD Steering Controller Utilizing the Predicted Position on Track for Autonomous Vehicles Driven on Slippery Roads. Algorithms. 2020; 13(2):48. https://doi.org/10.3390/a13020048
Chicago/Turabian StyleAlekseeva, Natalia, Ivan Tanev, and Katsunori Shimohara. 2020. "PD Steering Controller Utilizing the Predicted Position on Track for Autonomous Vehicles Driven on Slippery Roads" Algorithms 13, no. 2: 48. https://doi.org/10.3390/a13020048
APA StyleAlekseeva, N., Tanev, I., & Shimohara, K. (2020). PD Steering Controller Utilizing the Predicted Position on Track for Autonomous Vehicles Driven on Slippery Roads. Algorithms, 13(2), 48. https://doi.org/10.3390/a13020048





