Kernel Identification of Non-Linear Systems with General Structure
Abstract
1. Introduction
- proposed identification algorithm is run without any prior knowledge about the system structure and parametric representation of nonlinearity,
- non-parametric multi-dimensional kernel regression estimate was generalized for modeling of non-linear dynamic systems, and the dimensionality problem was solved by using special input sequences,
- the scheme elaborated in the paper was successfully applied in Differential Scanning Calorimeter for testing parameters of chalcogenide glasses.
2. Problem Statement
2.1. Class of Systems
2.2. Examples
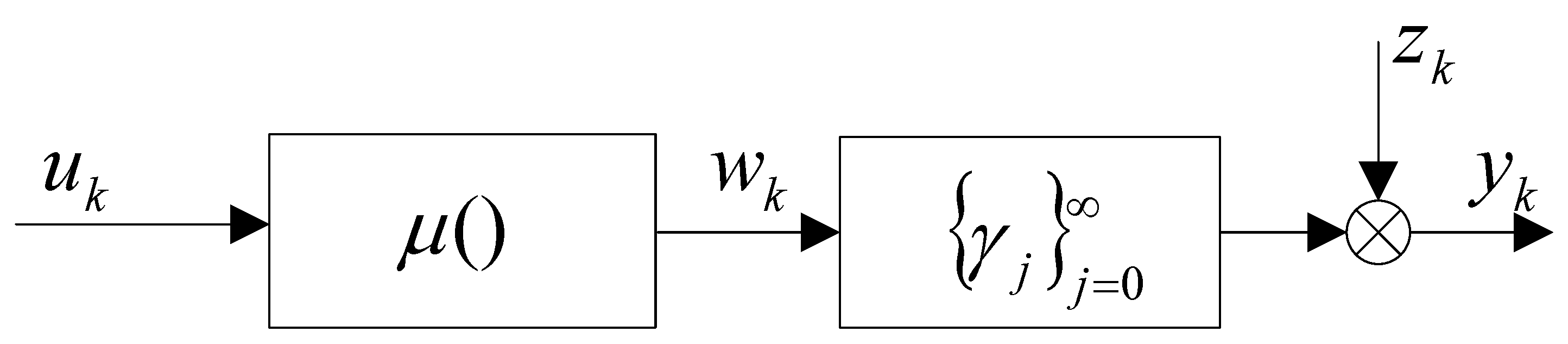
2.2.1. Hammerstein System
2.2.2. Wiener System
2.2.3. Finite Memory Bilinear System
3. Non-Parametric Regression
3.1. General Overview
3.2. Dimension Reduction
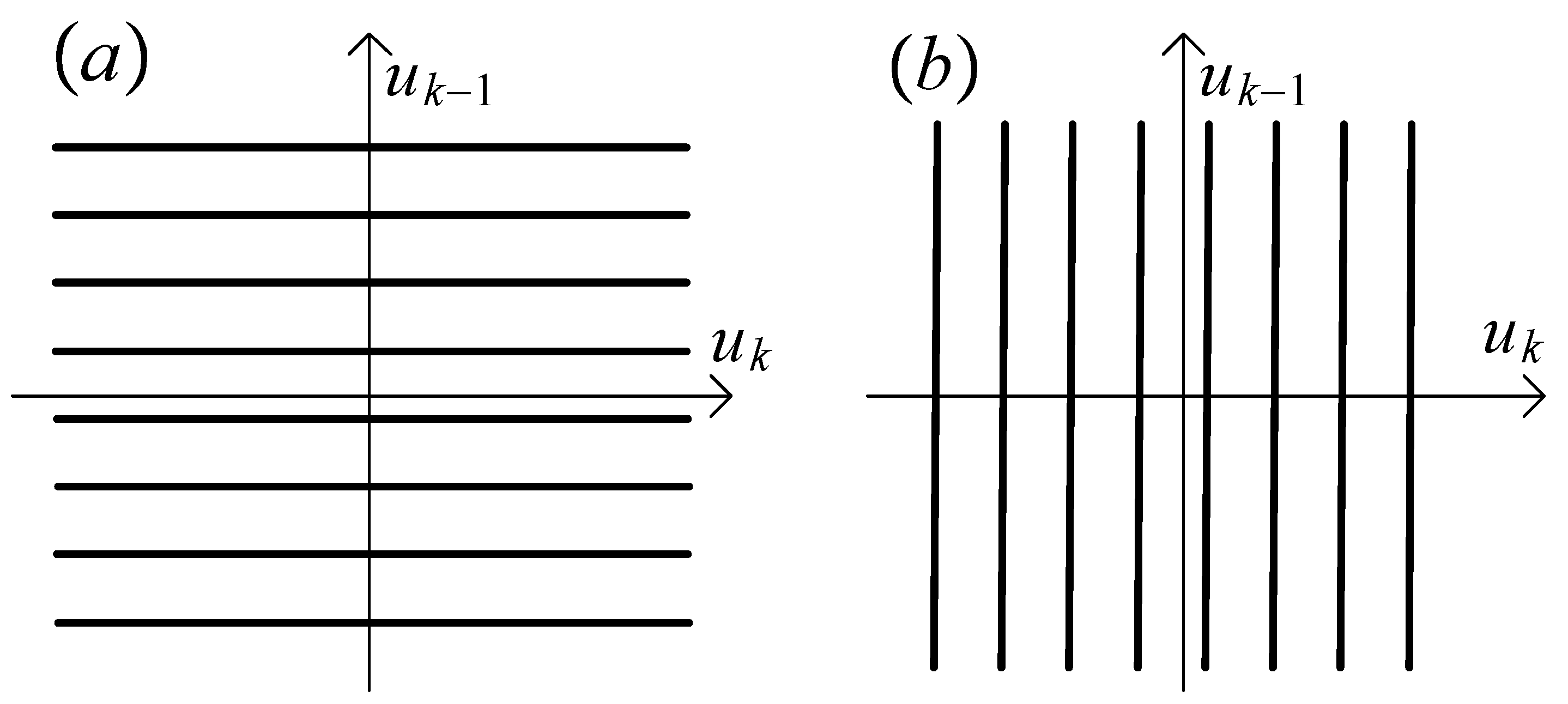
3.2.1. Discrete Input
3.2.2. Periodic Input
4. Hybrid/Combined Parametric-Non-Parametric Approach
5. Simulation Example
6. Application in Testing of Chalcogenide Glasses with the Use of DSC Method
6.1. Chalcogenide Glasses
6.2. Results of Experiment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Giannakis, G.; Serpedin, E. A bibliography on nonlinear system identification. Signal Process. 2001, 81, 533–580. [Google Scholar] [CrossRef]
- Schetzen, M. The Volterra and Wiener Theories of Nonlinear Systems; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Batselier, K.; Chen, Z.; Wong, N. Tensor Network alternating linear scheme for MIMO Volterra system identification. Automatica 2017, 84, 26–35. [Google Scholar] [CrossRef]
- Birpoutsoukis, G.; Marconato, A.; Lataire, J.; Schoukens, J. Regularized non-parametric Volterra kernel estimation. Automatica 2017, 82, 324–327. [Google Scholar] [CrossRef]
- Narendra, K.; Gallman, P.G. An iterative method for the identification of nonlinear systems using the Hammerstein model. IEEE Trans. Autom. Control 1966, 11, 546–550. [Google Scholar] [CrossRef]
- Giri, F.; Bai, E.W. Block-Oriented Nonlinear System Identification; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bai, E.; Li, D. Convergence of the iterative Hammerstein system identification algorithm. IEEE Trans. Autom. Control 2004, 49, 1929–1940. [Google Scholar] [CrossRef]
- Billings, S.; Fakhouri, S. Identification of systems containing linear dynamic and static nonlinear elements. Automatica 1982, 18, 15–26. [Google Scholar] [CrossRef]
- Chang, F.; Luus, R. A noniterative method for identification using Hammerstein model. IEEE Trans. Autom. Control 1971, 16, 464–468. [Google Scholar] [CrossRef]
- Giri, F.; Rochdi, Y.; Chaoui, F. Parameter identification of Hammerstein systems containing backlash operators with arbitrary-shape parametric borders. Automatica 2011, 47, 1827–1833. [Google Scholar] [CrossRef]
- Śliwiński, P. Lecture Notes in Statistics. In Nonlinear System Identification by Haar Wavelets; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Stoica, P.; Söderström, T. Instrumental-variable methods for identification of Hammerstein systems. Int. J. Control 1982, 35, 459–476. [Google Scholar] [CrossRef]
- Bershad, N.; Celka, P.; Vesin, J. Analysis of stochastic gradient tracking of time-varying polynomial Wiener systems. IEEE Trans. Signal Process. 2000, 48, 1676–1686. [Google Scholar] [CrossRef]
- Chen, H.F. Recursive identification for Wiener model with discontinuous piece-wise linear function. IEEE Trans. Autom. Control 2006, 51, 390–400. [Google Scholar] [CrossRef]
- Hagenblad, A.; Ljung, L.; Wills, A. Maximum likelihood identification of Wiener models. Automatica 2008, 44, 2697–2705. [Google Scholar] [CrossRef]
- Lacy, S.; Bernstein, D. Identification of FIR Wiener systems with unknown, non-invertible, polynomial non-linearities. Int. J. Control 2003, 76, 1500–1507. [Google Scholar] [CrossRef]
- Vörös, J. Parameter identification of Wiener systems with multisegment piecewise-linear nonlinearities. Syst. Control Lett. 2007, 56, 99–105. [Google Scholar] [CrossRef]
- Wigren, T. Convergence analysis of recursive identification algorithms based on the nonlinear Wiener model. IEEE Trans. Autom. Control 1994, 39, 2191–2206. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; Wiley-IEEE Press: Hoboken, NJ, USA, 2004. [Google Scholar]
- Greblicki, W.; Pawlak, M. Nonparametric System Identification; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Györfi, L.; Kohler, M.; Krzyżak, A.; Walk, H. A Distribution-Free Theory of Nonparametric Regression; Springer: New York, NY, USA, 2002. [Google Scholar]
- Härdle, W. Applied Nonparametric Regression; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Wand, M.; Jones, H. Kernel Smoothing; Chapman and Hall: London, UK, 1995. [Google Scholar]
- Hasiewicz, Z.; Mzyk, G. Combined parametric-nonparametric identification of Hammerstein systems. IEEE Trans. Autom. Control 2004, 48, 1370–1376. [Google Scholar] [CrossRef]
- Hasiewicz, Z.; Mzyk, G. Hammerstein system identification by non-parametric instrumental variables. Int. J. Control 2009, 82, 440–455. [Google Scholar] [CrossRef]
- Mzyk, G. A censored sample mean approach to nonparametric identification of nonlinearities in Wiener systems. IEEE Trans. Circuits Syst. 2007, 54, 897–901. [Google Scholar] [CrossRef]
- Mzyk, G. Combined Parametric-Nonparametric Identification of Block-Oriented Systems; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Mzyk, G.; Wachel, P. Kernel-based identification of Wiener-Hammerstein system. Automatica 2017, 83, 275–281. [Google Scholar] [CrossRef]
- Mzyk, G.; Wachel, P. Wiener system identification by input injection method. Int. J. Adapt. Control Signal Process. 2020, 34, 1105–1119. [Google Scholar] [CrossRef]
- Wachel, P.; Mzyk, G. Direct identification of the linear block in Wiener system. Int. J. Adapt. Control Signal Process. 2016, 30, 93–105. [Google Scholar] [CrossRef]
- Kozdraś, B.; Mzyk, G.; Mielcarek, P. Identification of the heating process in Differential Scanning Calorimetry with the use of Hammerstein model. In Proceedings of the 2020 21st International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 27–29 October 2020. [Google Scholar]
- Boyd, S.; Chua, L. Fading memory and the problem of approximating nonlinear operators with Volterra series. IEEE Trans. Circuits Syst. 1985, 32, 1150–1161. [Google Scholar] [CrossRef]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
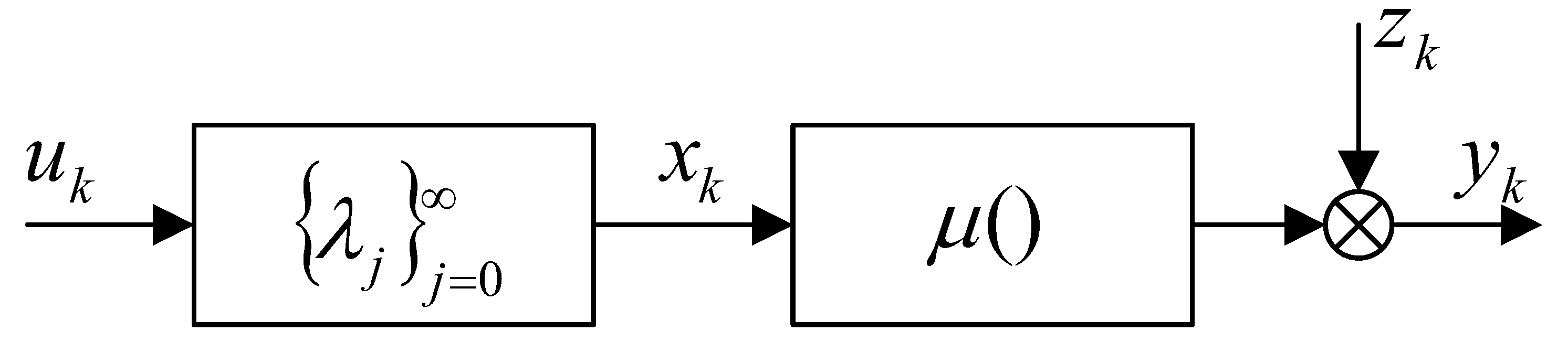
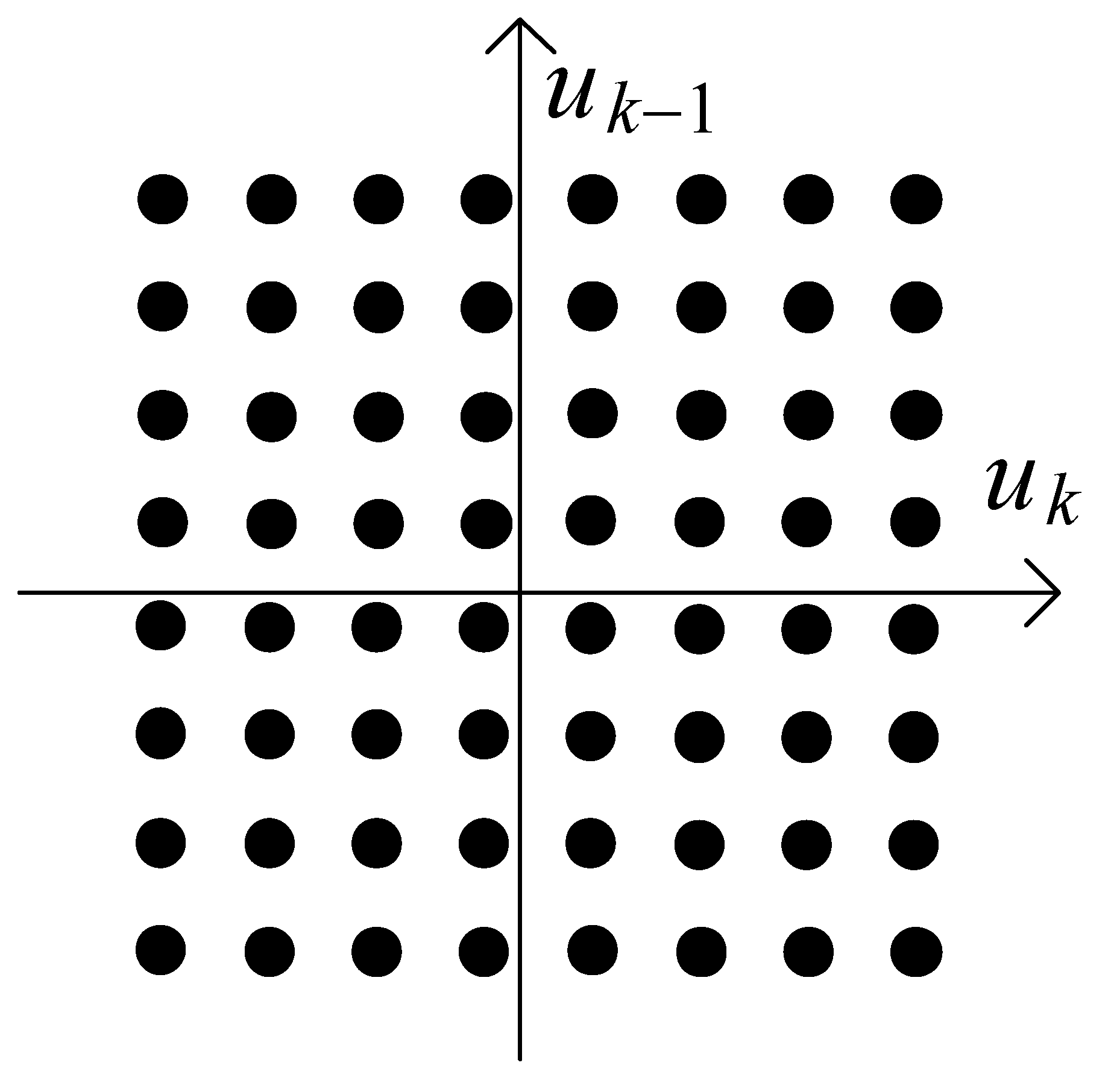
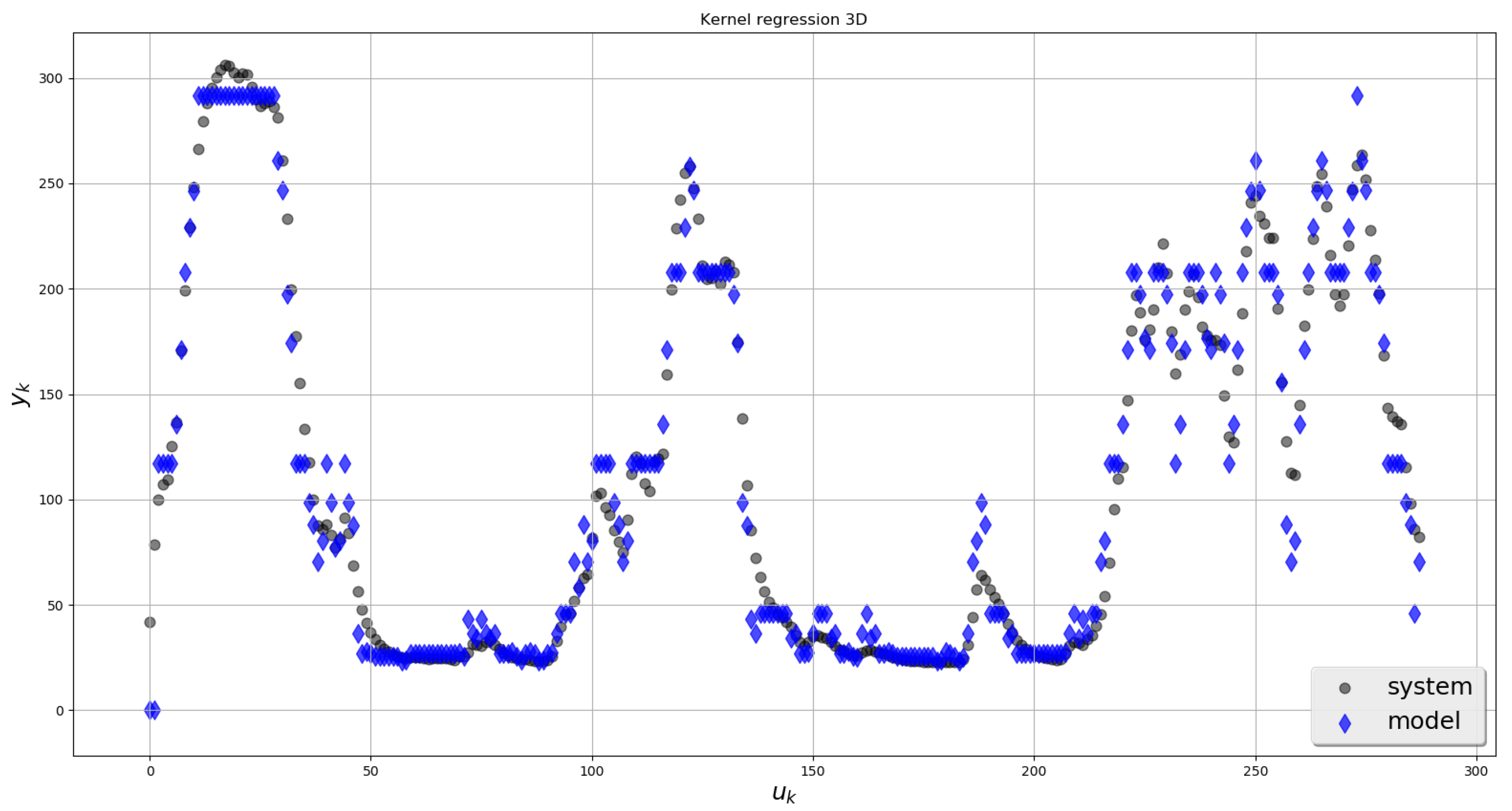
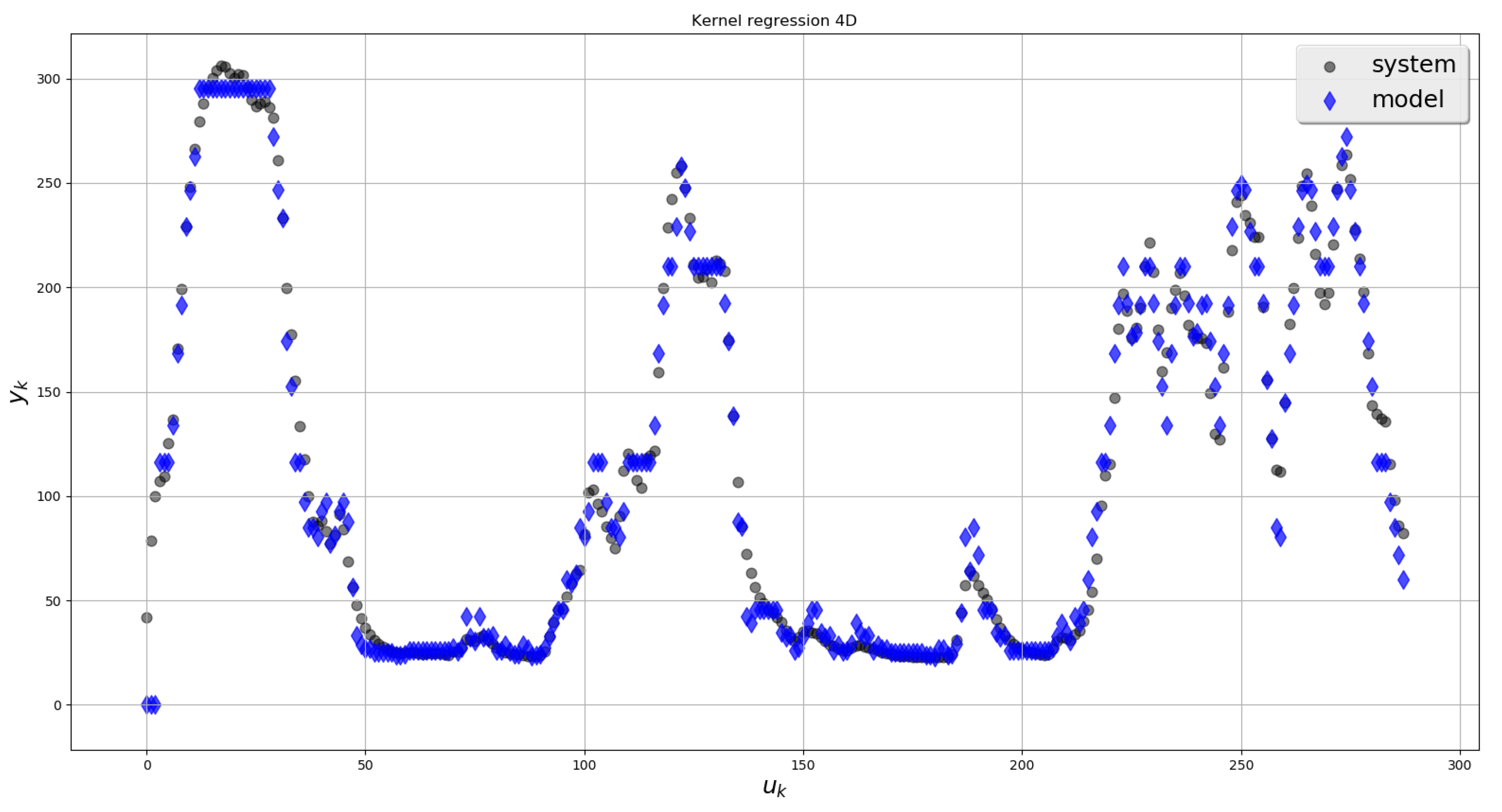
| 0.0656 | 0.0279 | 0.0137 | |
| BLA | 0.0660 | 0.0304 | 0.0176 |
| (presented method) | 1017 | 477 | 232 | 169 |
| BLA (Linear FIR(s)) | 1710 | 1331 | 1165 | 1114 |
| Hammerstein polynomial (3rd order + FIR(s)) | 1102 | 553 | 296 | 202 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mzyk, G.; Hasiewicz, Z.; Mielcarek, P. Kernel Identification of Non-Linear Systems with General Structure. Algorithms 2020, 13, 328. https://doi.org/10.3390/a13120328
Mzyk G, Hasiewicz Z, Mielcarek P. Kernel Identification of Non-Linear Systems with General Structure. Algorithms. 2020; 13(12):328. https://doi.org/10.3390/a13120328
Chicago/Turabian StyleMzyk, Grzegorz, Zygmunt Hasiewicz, and Paweł Mielcarek. 2020. "Kernel Identification of Non-Linear Systems with General Structure" Algorithms 13, no. 12: 328. https://doi.org/10.3390/a13120328
APA StyleMzyk, G., Hasiewicz, Z., & Mielcarek, P. (2020). Kernel Identification of Non-Linear Systems with General Structure. Algorithms, 13(12), 328. https://doi.org/10.3390/a13120328





