Feasibility of Kd-Trees in Gaussian Process Regression to Partition Test Points in High Resolution Input Space
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
- showing that the kd-tree approximation can lead to considerable time savings without sacrificing much accuracy.
- proposing a cut-off rule by combining criteria that are easy to interpret and that can be tailored for different computational budgets.
- applying our method in a sequential analysis setting on two types of generated toy data: a 3D point cloud with hotspots and a simulated 2D laser Doppler vibrometry example.
1.3. Outline of the Paper
2. Gaussian Processes
2.1. Gaussian Process Regression
2.2. Covariance Functions
2.3. Computational and Memory Requirements
3. Kd-Trees
3.1. Construction
- label(root) = X, the whole set
- label(leaf) = , one point
- label(internal node) = label(left child) ⊔ label(right child), the disjoint union of the sets below
3.2. Cut-Off Rule
| Algorithm 1 Get Nodes In Kd-Tree | |
| 1: | ▹ start with an empty list of tree nodes |
| 2: | ▹ start recursion |
| 3: return | |
| 4: procedure GetNodesInBranch(node) | |
| 5: | ▹ empty list of branch nodes |
| 6: if node.isLeaf then | |
| 7: | |
| 8: return | |
| 9: else | |
| 10: if node.mustVisitChildren then | ▹ if flag set in previous iteration |
| 11: | |
| 12: | |
| 13: return | |
| 14: else | |
| 15: for all do | ▹ evaluate every training point |
| 16: if then | ▹ node too wide |
| 17: node.mustVisitChildren ← True | |
| 18: | ▹ no need to evaluate other training points |
| 19: else if then | ▹ node too close |
| 20: node.mustVisitChildren ← True | |
| 21: | ▹ no need to evaluate other training points |
| 22: else if then | |
| 23: node.mustVisitChildren ← True | |
| 24: | ▹ no need to evaluate other training points |
| 25: end if | |
| 26: end for | |
| 27: if node.mustVisitChildren then | ▹ recursion continues |
| 28: | |
| 29: | |
| 30: else | ▹ recursion is cut off |
| 31: | |
| 32: end if | |
| 33: return | |
| 34: end if | |
| 35: end if | |
| 36: end procedure |
- references to the left and right child nodes which are also objects of the class KDNode
- a boolean indicating the node is a leaf or not
- for the leaves the position of the point
- the position of the nearest neighbour in the node to the average position, i.e., the representative point
- a boolean whether the child nodes should be visited by the algorithm
- the pre-calculated covariance between the two most distant points in the node
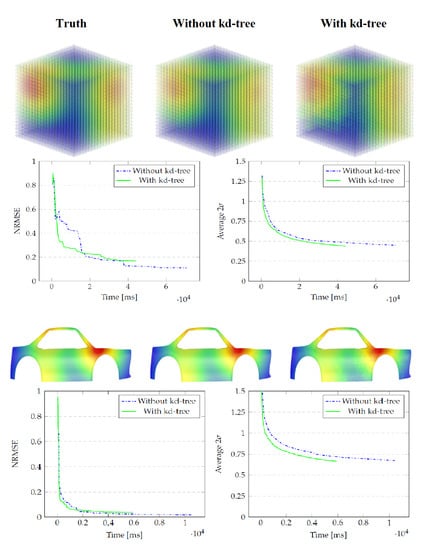
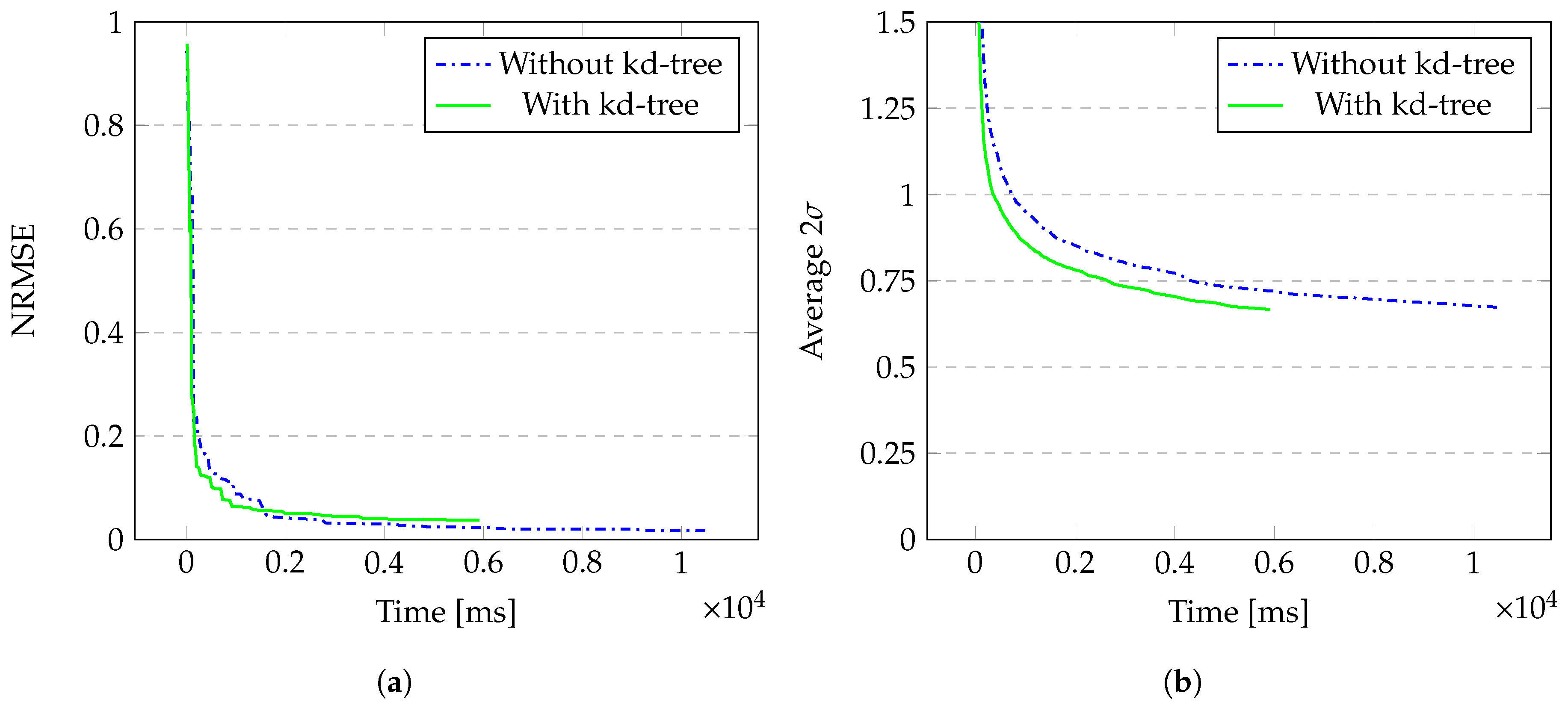
4. Results
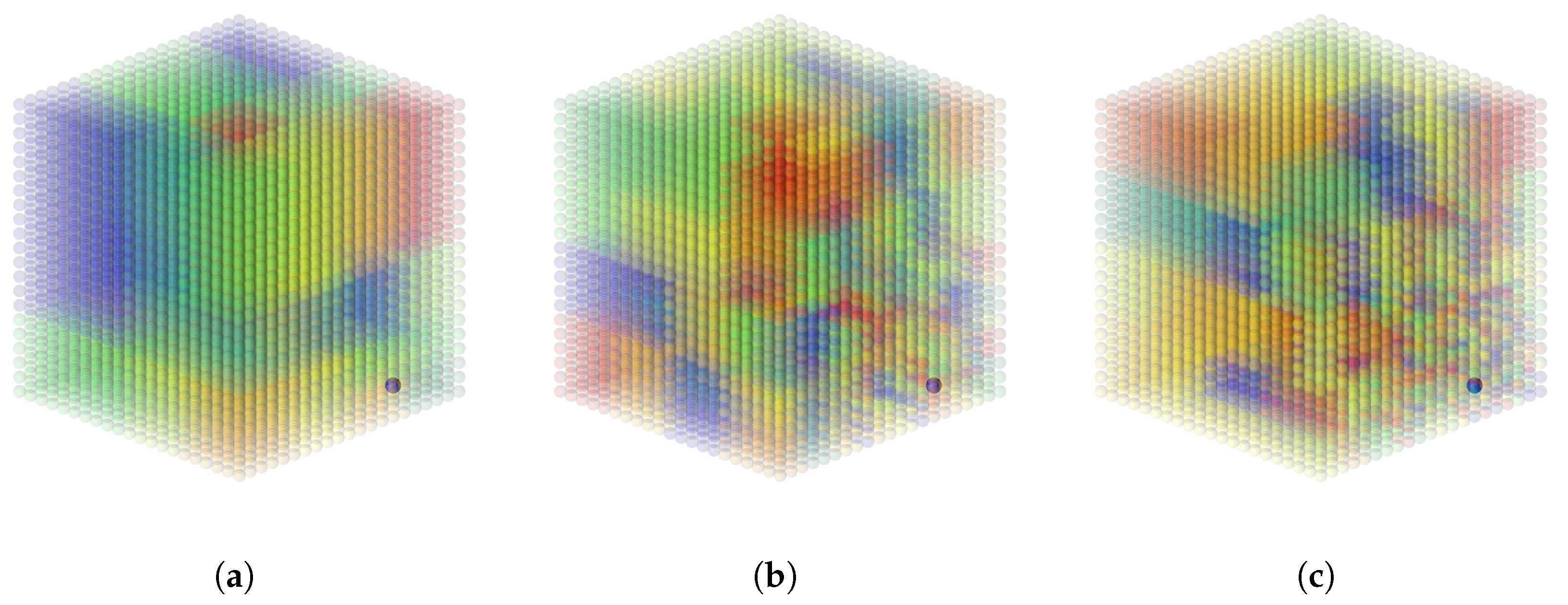
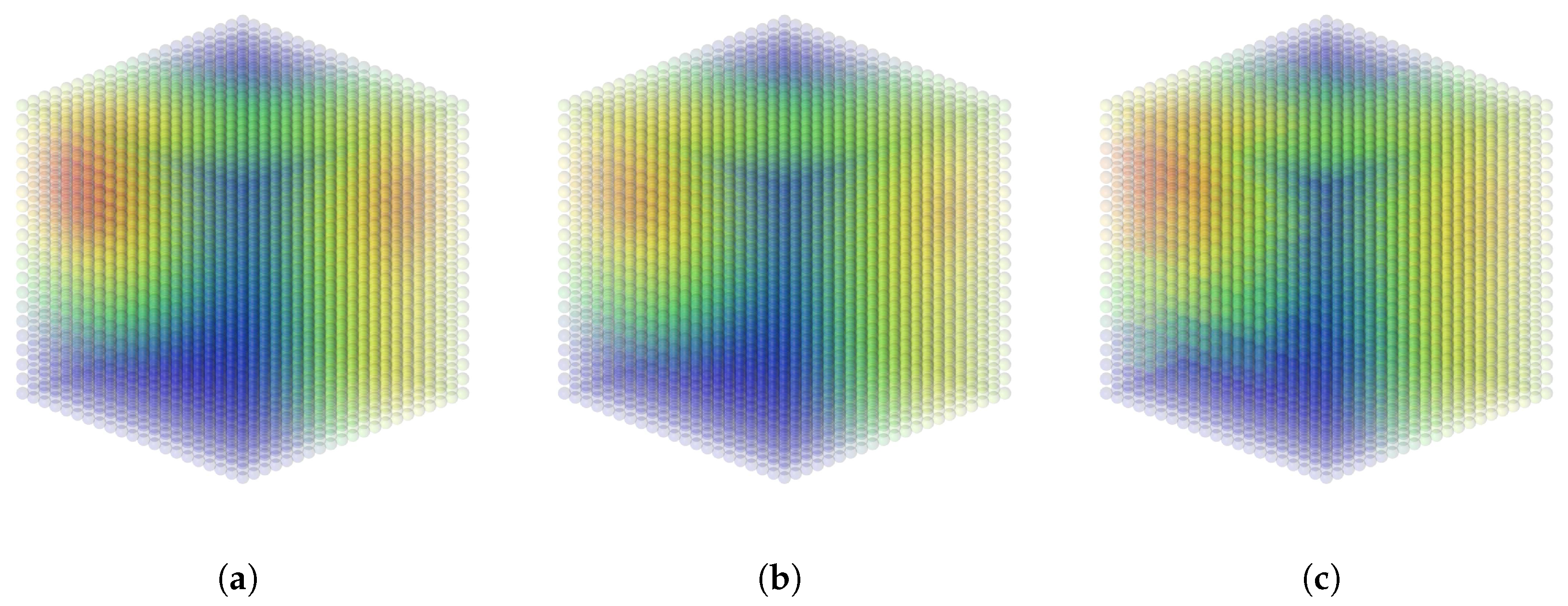
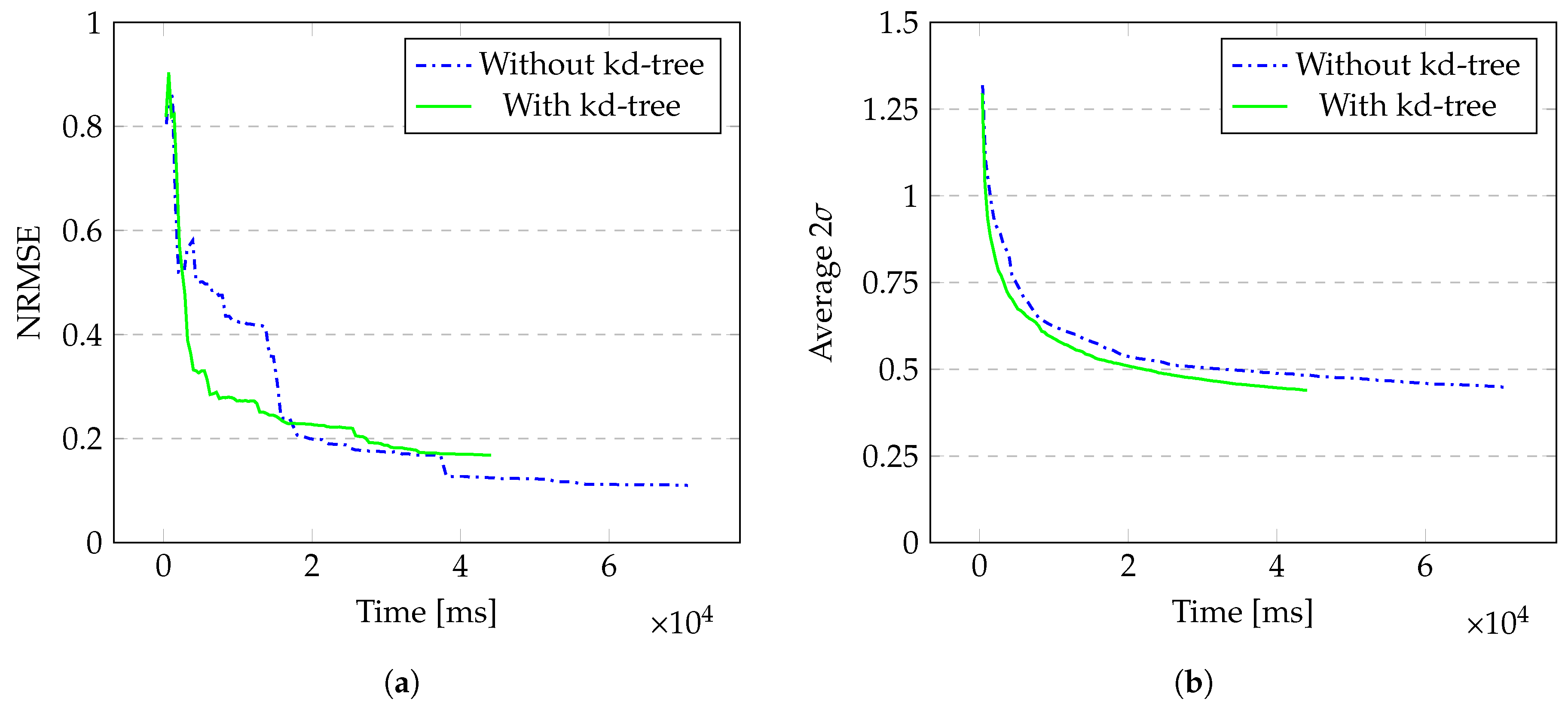
4.1. Generated Data on a 3D Point Cloud
4.2. Laser Doppler Vibrometry Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Jaquier, N.; Rozo, L.; Calinon, S.; Bürger, M. Bayesian optimization meets Riemannian manifolds in robot learning. In Proceedings of the Conference on Robot Learning, Cambridge MA, USA, 16–18 November 2020; pp. 233–246. [Google Scholar]
- Tiger, M.; Heintz, F. Gaussian Process Based Motion Pattern Recognition with Sequential Local Models. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1143–1149. [Google Scholar]
- Mojaddady, M.; Nabi, M.; Khadivi, S. Stock market prediction using twin Gaussian process regression. Int. J. Adv. Comput. Res. (JACR) Preprint 2011. Available online: http://disi.unitn.it/~nabi/files/stock.pdf (accessed on 4 December 2020).
- Wang, X.; Wang, X.; Mao, S.; Zhang, J.; Periaswamy, S.C.; Patton, J. Indoor Radio Map Construction and Localization with Deep Gaussian Processes. IEEE Internet Things J. 2020, 7, 11238–11249. [Google Scholar] [CrossRef]
- Brochu, E.; Cora, V.M.; De Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv 2010, arXiv:1012.2599. [Google Scholar]
- Zhu, J.; Hoi, S.C.; Lyu, M.R. Nonrigid shape recovery by gaussian process regression. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1319–1326. [Google Scholar]
- Hachino, T.; Kadirkamanathan, V. Multiple Gaussian process models for direct time series forecasting. IEEJ Trans. Electr. Electron. Eng. 2011, 6, 245–252. [Google Scholar] [CrossRef]
- Plate, T.A. Accuracy versus interpretability in flexible modeling: Implementing a trade-off using gaussian process models. Behaviormetrika 1999, 26, 29–50. [Google Scholar] [CrossRef]
- Lasko, T.A. Efficient inference of Gaussian-process-modulated renewal processes with application to medical event data. In Uncertainty in Artificial Intelligence: Proceedings of the Conference on Uncertainty in Artificial Intelligence; NIH Public Access: Bethesda, MD, USA, 2014; Volume 2014, p. 469. [Google Scholar]
- Aye, S.; Heyns, P. An integrated Gaussian process regression for prediction of remaining useful life of slow speed bearings based on acoustic emission. Mech. Syst. Signal Process. 2017, 84, 485–498. [Google Scholar] [CrossRef]
- Mohammed, R.O.; Cawley, G.C. Over-fitting in model selection with gaussian process regression. In Proceedings of the International Conference on Machine Learning and Data Mining in Pattern Recognition, New York, NY, USA, 15–20 July 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 192–205. [Google Scholar]
- Liu, H.; Ong, Y.S.; Shen, X.; Cai, J. When Gaussian process meets big data: A review of scalable GPs. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4405–4423. [Google Scholar] [CrossRef]
- Wilson, A.G.; Dann, C.; Nickisch, H. Thoughts on massively scalable Gaussian processes. arXiv 2015, arXiv:1511.01870. [Google Scholar]
- Rothberg, S.; Allen, M.; Castellini, P.; Di Maio, D.; Dirckx, J.; Ewins, D.; Halkon, B.J.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2017, 99, 11–22. [Google Scholar] [CrossRef]
- Spinhirne, J.D. Micro pulse lidar. IEEE Trans. Geosci. Remote. Sens. 1993, 31, 48–55. [Google Scholar] [CrossRef]
- Shi, S.; Wang, Z.; Shi, J.; Wang, X.; Li, H. From points to parts: 3d object detection from point cloud with part-aware and part-aggregation network. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef] [PubMed]
- Chadalavada, R.T.; Andreasson, H.; Schindler, M.; Palm, R.; Lilienthal, A.J. Bi-directional navigation intent communication using spatial augmented reality and eye-tracking glasses for improved safety in human–robot interaction. Robot. Comput. Integr. Manuf. 2020, 61, 101830. [Google Scholar] [CrossRef]
- Paone, N.; Scalise, L.; Stavrakakis, G.; Pouliezos, A. Fault detection for quality control of household appliances by non-invasive laser Doppler technique and likelihood classifier. Measurement 1999, 25, 237–247. [Google Scholar] [CrossRef]
- Ramasubramanian, V.; Paliwal, K.K. A generalized optimization of the K-d tree for fast nearest-neighbour search. In Proceedings of the Fourth IEEE Region 10 International Conference TENCON, Bombay, India, 22–24 November 1989; pp. 565–568. [Google Scholar]
- Fox, E.; Dunson, D.B. Multiresolution gaussian processes. Adv. Neural Inf. Process. Syst. 2012, 25, 737–745. [Google Scholar]
- Kim, H.M.; Mallick, B.K.; Holmes, C. Analyzing nonstationary spatial data using piecewise Gaussian processes. J. Am. Stat. Assoc. 2005, 100, 653–668. [Google Scholar] [CrossRef]
- Shen, Y.; Seeger, M.; Ng, A.Y. Fast gaussian process regression using kd-trees. Adv. Neural Inf. Process. Syst. 2006, 18, 1225–1232. [Google Scholar]
- Moore, D.A.; Russell, S.J. Fast Gaussian Process Posteriors with Product Trees. In Proceedings of the UAI, Quebec City, QC, Canada, 23–27 July 2014; pp. 613–622. [Google Scholar]
- Vasudevan, S.; Ramos, F.; Nettleton, E.; Durrant-Whyte, H. Gaussian process modeling of large-scale terrain. J. Field Robot. 2009, 26, 812–840. [Google Scholar] [CrossRef]
- Deisenroth, M.; Ng, J.W. Distributed gaussian processes. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1481–1490. [Google Scholar]
- Yamaguchi, K.; Kunii, T.; Fujimura, K.; Toriya, H. Octree-related data structures and algorithms. IEEE Comput. Graph. Appl. 1984, 53–59. [Google Scholar] [CrossRef]
- Omohundro, S.M. Five Balltree Construction Algorithms; International Computer Science Institute: Berkeley, CA, USA, 1989. [Google Scholar]
- Beygelzimer, A.; Kakade, S.; Langford, J. Cover trees for nearest neighbour. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 97–104. [Google Scholar]
- De Ath, G.; Fieldsend, J.E.; Everson, R.M. What Do You Mean? The Role of the Mean Function in Bayesian Optimisation. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion (GECCO ’20), Cancún, Mexico, 8–12 July 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1623–1631. [Google Scholar] [CrossRef]
- Duvenaud, D. Automatic Model Construction with Gaussian Processes. Ph.D. Thesis, Computational and Biological Learning Laboratory, University of Cambridge, Cambridge, UK, 2014. [Google Scholar]
- Rasmussen, C.; Ghahramani, Z. Occam’s Razor. In Advances in Neural Information Processing Systems 13; Max-Planck-Gesellschaft, MIT Press: Cambridge, MA, USA, 2001; pp. 294–300. [Google Scholar]
- Blum, M.; Riedmiller, M.A. Optimization of Gaussian process hyperparameters using Rprop. In Proceedings of the ESANN, Bruges, Belgium, 24–26 April 2013; pp. 339–344. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Genton, M.G. Classes of Kernels for Machine Learning: A Statistics Perspective. J. Mach. Learn. Res. 2002, 2, 299–312. [Google Scholar]
- Preparata, F.P.; Shamos, M.I. Computational Geometry: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhou, K.; Hou, Q.; Wang, R.; Guo, B. Real-Time KD-Tree Construction on Graphics Hardware. ACM Trans. Graph. 2008, 27. [Google Scholar] [CrossRef]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An Algorithm for Finding Best Matches in Logarithmic Expected Time. ACM Trans. Math. Softw. 1977, 3, 209–226. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Sproull, R. Refinements to nearest-neighbour searching ink-dimensional trees. Algorithmica 1991, 6, 579–589. [Google Scholar] [CrossRef]
- Sample, N.; Haines, M.; Arnold, M.; Purcell, T. Optimizing Search Strategies in k-d Trees. Available online: http://infolab.stanford.edu/~nsample/pubs/samplehaines.pdf (accessed on 4 December 2020).
- Deng, K.; Moore, A. Multiresolution Instance-Based Learning. In Proceedings of the IJCAI, Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Haas, J.K. A History of the Unity Game Engine. 2014. Available online: https://web.wpi.edu/Pubs/E-project/Available/E-project-030614-143124/unrestricted/Haas_IQP_Final.pdf (accessed on 4 December 2020).
- Ruegg, C.; Cuda, M.; Van Gael, J. Math .NET Numerics. 2016. Available online: http://numerics.mathdotnet.com (accessed on 4 December 2020).
- Ram, R.; Müller, S.; Pfreundt, F.; Gauger, N.R.; Keuper, J. Scalable Hyperparameter Optimization with Lazy Gaussian Processes. In Proceedings of the 2019 IEEE/ACM Workshop on Machine Learning in High Performance Computing Environments (MLHPC), Denver, CO, USA, 18 November 2019; pp. 56–65. [Google Scholar]
- Crane, K.; Weischedel, C.; Wardetzky, M. Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow. ACM Trans. Graph. 2013, 32. [Google Scholar] [CrossRef]
- Sarkka, S.; Solin, A.; Hartikainen, J. Spatiotemporal Learning via Infinite-Dimensional Bayesian Filtering and Smoothing: A Look at Gaussian Process Regression Through Kalman Filtering. IEEE Signal Process. Mag. 2013, 30, 51–61. [Google Scholar] [CrossRef]
- Schürch, M.; Azzimonti, D.; Benavoli, A.; Zaffalon, M. Recursive estimation for sparse Gaussian process regression. Automatica 2020, 120, 109127. [Google Scholar] [CrossRef]


| Model | Without kd-Tree | With kd-Tree | % Gain |
|---|---|---|---|
| Cube | 70,596 | 44,075 | 37.6 |
| Car | 10,497 | 5914 | 43.7 |
| Model | Without kd-Tree | With kd-Tree | Difference |
|---|---|---|---|
| Cube | 0.110 | 0.168 | 0.058 |
| Car | 0.017 | 0.037 | 0.020 |
| Model | Without kd-Tree | With kd-Tree | Difference |
|---|---|---|---|
| Cube | 0.449 | 0.439 | 0.010 |
| Car | 0.673 | 0.666 | 0.007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Boi, I.; Ribbens, B.; Jorissen, P.; Penne, R. Feasibility of Kd-Trees in Gaussian Process Regression to Partition Test Points in High Resolution Input Space. Algorithms 2020, 13, 327. https://doi.org/10.3390/a13120327
De Boi I, Ribbens B, Jorissen P, Penne R. Feasibility of Kd-Trees in Gaussian Process Regression to Partition Test Points in High Resolution Input Space. Algorithms. 2020; 13(12):327. https://doi.org/10.3390/a13120327
Chicago/Turabian StyleDe Boi, Ivan, Bart Ribbens, Pieter Jorissen, and Rudi Penne. 2020. "Feasibility of Kd-Trees in Gaussian Process Regression to Partition Test Points in High Resolution Input Space" Algorithms 13, no. 12: 327. https://doi.org/10.3390/a13120327
APA StyleDe Boi, I., Ribbens, B., Jorissen, P., & Penne, R. (2020). Feasibility of Kd-Trees in Gaussian Process Regression to Partition Test Points in High Resolution Input Space. Algorithms, 13(12), 327. https://doi.org/10.3390/a13120327