1. Introduction
The performance of machine learning models is highly dependent on the quality of the data that are available to train them: the more information they contain, the better the insights we can obtain from them. Incomplete data contain, by construction, less useful information to model the phenomenon we are studying because there are fewer complete observations from which to learn the distribution of the variables and their interplay. Therefore, it is important to make the best possible use of such data by incorporating incomplete observations and the stochastic mechanism that leads to certain variables not being observed in the analysis.
There is ample literature on the statistical modelling of incomplete data. While it is tempting to simply replace missing values as a separate preprocessing step, it has long been known that even fairly sophisticated techniques like hot-deck imputation are problematic [
1]. Just deleting incomplete samples can also bias learning, depending on how missing data are missing [
2]. Therefore, modern probabilistic approaches have followed the lead of Rubin [
3,
4] and modelled missing values along with the stochastic mechanism of missingness. This class of approaches introduces one auxiliary variable for each experimental variable that is not completely observed in order to model the distribution of missingness; that is, the binary pattern of values being observed or not for that specific experimental variable. These auxiliary variables are then integrated out in order to compute the expected values of the parameters of the model. The most common approach to learn machine learning models that build on this idea is the
Expectation-Maximisation (EM) algorithm [
5]; other approaches such as variational inference [
6] have seen substantial applications but are beyond the scope of this paper and we will not discuss them further. The EM algorithm comprises two steps that are performed iteratively until convergence: the “expectation” (E) step computes the expected values of the sufficient statistics given the current model, and the “Maximisation” (M) step updates the model with new parameter estimates. (A statistic is called
sufficient for a parameter in a given model if no other statistic computed from the data, including the data themselves, provides any additional information to the parameter’s estimation.)
A natural way of representing experimental variables, auxiliary variables and their relationships is through graphical models, and in particular Bayesian networks (BNs) [
7]. BNs represent variables as nodes in a directed acyclic graph in which arcs encode probabilistic dependencies. The graphical component of BNs allows for automated probabilistic manipulations via belief propagation, which in turn makes it possible to compute the marginal and conditional distributions of experimental variables in the presence of incomplete data. However, learning a BN from data, that is, learning its graphical structure and parameters, is a challenging problem; we refer the reader to [
8] for a recent review on the topic.
The EM algorithm can be used in its original form to learn the parameters of a BN. The Structural EM algorithm [
9,
10] builds on the EM algorithm to implement structure learning: it computes the sufficient statistics required to score candidate BNs in the E-step. However, the Structural EM is computationally demanding due to the large number of candidate models that are evaluated in the search for the optimal BN. Using EM for parameter learning can be computationally demanding as well for medium and large BNs. Hence, practical implementations, e.g., [
11,
12], of both often replace belief propagation with single imputation: each missing value is replaced with its expected value conditional on the values observed for the other variables in the same observation. This is a form of
hard EM because we are making hard assignments of values; whereas using belief propagation would be a form of
soft EM. This change has the effect of voiding the theoretical guarantees for the Structural EM in [
9,
10], such as the consistency of the algorithm. Hard EM, being a form of single imputation, is also known to be problematic for learning the parameters of statistical models [
13].
In this paper, we investigate the impact of learning the parameters and the structure of a BN using hard EM instead of soft EM with a comprehensive simulation study covering incomplete data with a wide array of different characteristics. All the code used in the paper is available as an R [
14] package (
https://github.com/madlabunimib/Expectation-Maximisation).
The rest of the paper is organised as follows. In
Section 2, we will introduce BNs (
Section 2.1); missing data (
Section 2.2); imputation (
Section 2.3); and the EM algorithm (
Section 2.4). We describe the experimental setup we use to evaluate different EM algorithms in the context of BN learning in
Section 3, and we report on the results in
Section 4. Finally, we provide practical recommendations on when to use each EM algorithm in BN structure learning in
Section 5. Additional details on the experimental setup are provided in the appendix.
2. Methods
This section introduces the notation and key definitions for BNs and incomplete data. We then discuss possible approaches to learn BNs from incomplete data, focusing on the EM and Structural EM algorithms.
2.1. Bayesian Networks
A Bayesian network BN [
7] is a probabilistic graphical model that consists of a directed acyclic graph (DAG)
and a set of random variables over
with parameters
. Each node in
is associated with a random variable in
, and the two are usually referred to interchangeably. The directed arcs
E in
encode the conditional independence relationships between the random variables using graphical separation, which is called
d-separation in this context. As a result,
leads to the decomposition
in which the global (joint) distribution of
factorises in a local distribution for each
that is conditional on its parents
in
and has parameters
. In this paper, we assume that all random variables are categorical: both
and the
follow multinomial distributions, and the parameters
are conditional probability tables (CPTs) containing the probability of each value of
given each configuration of the values of its parents
. In other words,
where
. This class of BNs is called
discrete BNs [
15]. Other classes commonly found in the literature include Gaussian BNs (GBNs) [
16], in which
is a multivariate normal random variable and the
are univariate normals linked by linear dependencies; and conditional Gaussian BNs (CLGBNs) [
17], which combine categorical and normal random variables in a mixture model.
The task of learning a BN from a data set
containing
n observations is performed in two steps:
Structure learning consists of finding the DAG
that encodes the dependence structure of the data, thus maximising
or some alternative goodness-of-fit measure;
parameter learning consists in estimating the parameters
given the
obtained from structure learning. If we assume that different
are independent and that data are complete [
15], we can perform parameter learning independently for each node following (
1) because
Furthermore, if
is sufficiently sparse, each node will have a small number of parents; and
will have a low-dimensional parameter space, making parameter learning computationally efficient. Both structure and parameter learning involve
, which can be estimated as using maximum likelihood
or Bayesian posterior estimates
where the
are hyperparameters of the (conjugate) Dirichlet prior for
and the
are the corresponding counts computed from the data. Estimating the
is the focus of parameter learning but they are also estimated in structure learning. Directly, when
is approximated with the Bayesian Information Criterion (BIC) [
18]:
Indirectly, through the
, we are computing
as
The expression on the right is the marginal probability of the data given a DAG
averaging over all possible
, and is known as the Bayesian Dirichlet score (BD) [
15]. In all of (
3)–(
6) depends on the data only through the counts
, which are the
minimal sufficient statistics for estimating all the quantities above.
Once both
and
have been learned, we can use the BN to answer queries about our quantities of interest using either
exact or
approximate inference algorithms that work directly on the BN [
19]. Common choices are
conditional probability queries, in which we compute the posterior probability of one or more variables given the values of other variables; and
most probable explanation queries, in which we identify the configuration of values of some variables that has the highest posterior probability given the values of some other variables. The latter are especially suited to implement both prediction and imputation of missing data, which we will discuss below.
2.2. Missing Data
A data set
comprising samples from the random variables in
is called
complete when the values of all
are known, that is, observed, for all samples. On the other hand, if
is
incomplete, some samples will be completely observed while others will contain missing values for some
. The patterns with which data are missing are called the
missing data mechanism. Modelling these mechanisms is crucial because the properties of missing data depend on their nature, and in particular, on whether the fact that values are missing is related to the underlying values of the variables in the data set. The literature groups missing data mechanisms in three classes [
4]:
Missing completely at random (MCAR): missingness does not depend on the values of the data, missing or observed.
Missing at random (MAR): missingness depends on the variables in only through the observed values in the data.
Missing not at random (MNAR): the missingness depends on both the observed and the missing values in the data.
MAR is a sufficient condition for likelihood and Bayesian inference to be the valid without modelling the missing data mechanism explicitly; hence, MCAR and MAR are said to be ignorable patterns of missingness.
In the context of BNs, we can represent the missing data mechanism for each
with a binary latent variable
taking value 0 for an observation if
is missing and 1 otherwise.
is included in the BN as an additional parent of
, so that the local distribution of
in (
1) can be written as
In the case of MCAR,
will be independent from all the variables in
except
; in the case of MAR,
can depend on
(
) but not on
(
) for all
. In both cases, the data missingness is ignorable, meaning that
However, this is not the case for MNAR, where the missing data mechanism must be modelled explicitly for the model to be learned correctly and for any inference to be valid. As a result, different approaches to handle missing data will be effective depending on which missing data mechanism we assume for the data.
2.3. Missing Data Imputation
A possible approach to handle missing data is to transform an incomplete data set into a complete one. The easiest way to achieve this is to just remove all the observations containing at least one missing value. However, this can markedly reduce the amount of data and it is widely documented to introduce bias in both learning and inference, see, for instance [
2,
20]. A more principled approach is to perform
imputation; that is, to predict missing values based on the observed ones. Two groups of imputation approaches have been explored in the literature:
single imputation and
multiple imputation. We provide a quick overview of both below, and we refer the reader to [
4] for a more comprehensive theoretical treatment.
Single imputation approaches impute one value for each missing value in the data set. As a result, they can potentially introduce bias in subsequent inference because the imputed values naturally have a smaller variability than the observed values. Furthermore, it is impossible to assess imputation uncertainty from that single value. Two examples of this type of approach are mean imputation (replacing each missing value with the sample mean or mode) or k-NN imputation [
21,
22] (replacing each missing value with the most common value from similar cases identified via
k-nearest neighbours).
Multiple imputation replaces each missing value by
B possible values to create
B complete data sets, usually with
. Standard complete-data probabilistic methods are then used to analyse each completed data set, and the
B completed-data inferences are combined to form a single inference that properly reflects uncertainty due to missingness under that model [
13]. A popular example is multiple imputation by chained equation [
23], which has seen widespread use in the medical and life sciences fields.
It is important to note that there are limits to the amount of missing data that can be effectively managed. While there is no common guideline on that, since each method and missing data mechanism are different in that respect, suggested limits found in the literature range from 5% [
13] to 10% [
24].
2.4. The Expectation-Maximisation (EM) Algorithm
The imputation methods described above focus on completing individual missing values with predictions from the observed data without considering what probabilistic models will be estimated from the completed data. The Expectation-Maximisation (EM) [
5] algorithm takes the opposite view: starting from the model we would like to estimate, it identifies the sufficient statistics we need to estimate its parameters and it completes those sufficient statistics by averaging over the missing values. The general nature of this formulation makes EM applicable to a wide range of probabilistic models, as discussed in [
25,
26] as well as [
4].
EM (Algorithm 1) is an iterative algorithm consisting of the following two steps:
the Expectation step (E-step) consists in computing the expected values of the sufficient statistics for the parameters using the previous parameter estimates ;
the Maximisation step (M-step) takes the sufficient statistics from the E-step and uses them to update the parameters estimates.
Both maximum likelihood and Bayesian posterior parameter estimates are allowed in the M-Step. The E-step and the M-step are repeated until convergence. Each iteration increases marginal likelihood function for the observed data, so the EM algorithm is guaranteed to converge because the marginal likelihood of the (unobservable) complete data is finite and bounds above that of the current model.
| Algorithm 1: The (Soft) Expectation-Maximisation Algorithm (Soft EM) |
![Algorithms 13 00329 i001 Algorithms 13 00329 i001]() |
One key limitation of EM as described in Algorithm 1 is that the estimation of the expected sufficient statistics may be computationally unfeasible or very costly, thus making EM impractical for use in real-world applications. As an alternative, we can use what is called hard EM, which is shown in Algorithm 2. Unlike the standard EM, hard EM computes the expected sufficient statistics by imputing the missing data with their most likely completion , and then using the completed data to compute the sufficient statistics. Hence the name, we replace the missing data with hard assignments. In contrast, the standard EM in Algorithm 1 is sometimes called soft EM because it averages over the missing values, that is, it considers all its possible values weighted by their probability distribution.
| Algorithm 2: The Hard EM Algorithm. |
![Algorithms 13 00329 i002 Algorithms 13 00329 i002]() |
It is important to note that hard EM and soft EM, while being both formally correct, may display very different behaviour and convergence rates. Both algorithms behave similarly when the random variables that are not completely observed have a skewed distribution [
7].
2.5. The EM Algorithm and Bayesian Networks
In the context of BNs, EM can be applied to both parameter learning and structure learning. For the parameter learning, the E-step and M-step become:
the Expectation (E) step consists of computing the expected values of the sufficient statistics (the counts ) using exact inference along the lines described above to make use of incomplete as well as complete samples;
the Maximisation (M) step takes the sufficient statistics from the E-step and estimates the parameters of the BN.
As for structure learning, the Structural EM algorithm [
9] implements EM as follows:
in the E-step, we complete the data by computing the expected sufficient statistics using the current network structure;
in the M-step, we find the structure that maximises the expected score function for the completed data.
This approach is computationally feasible because it searches for the best structure inside of the EM, instead of embedding EM inside a structure learning algorithm; and it maintains the convergence guarantees of the original both in its maximum likelihood [
9] and Bayesian [
10] formulations. However, the Structural EM is still quite expensive because of the large number and the dimensionality of the sufficient statistics that are computed in each iteration. [
9] notes: “Most of the running time during the execution of our procedure is spent in the computations of expected statistics. This is where our procedure differs from parametric EM. In parametric EM, we know in advance which expected statistics are required. […] In our procedure, we cannot determine in advance which statistics will be required. Thus, we have to handle each query separately. Moreover, when we consider different structures, we are bound to evaluate a larger number of queries than parametric EM.” Even if we explore candidate DAGs using a local search algorithm such as hill-climbing, and even if we only score DAGs that differ from the current candidate by a single arc, this means computing
sets of sufficient statistics. Furthermore, the size of each of these sufficient statistics increases combinatorially with the size of the
of the corresponding
.
As a result, practical software implementations of the Structural EM such as those found in [
11,
12] often replace the soft EM approach described in Algorithm 1 with the hard EM from Algorithm 2. The same can be true for applications of EM to parameter learning, for similar reasons: the cost of using exact inference can become prohibitive if
is large or if there is a large number of missing values. Furthermore, the decomposition in (
2) no longer holds because the expected sufficient statistics depend on all
. In practice this means that, instead of computing the expected values of the
as weighted average over all possible imputations of the missing values, we perform a single imputation of each missing value and use the completed observation to tally up
.
This leads us to the key question we address in this paper: what is the impact of replacing soft EM with hard EM on learning BNs?
3. Materials
In order to address the question above, we perform a simulation study to compare soft and hard EMs. We limit ourselves to discrete BNs, for which we explore both parameter learning (using a fixed gold-standard network structure) and structure learning (using network structures with high that would be likely candidate BNs during learning). In addition, we consider a variant of soft EM in which we use early stopping to match its running time with that of hard EM. We will call it soft-forced EM, meaning that we force it to stop without waiting for it to converge. In particular, soft-forced EM stops after 3, 4 and 6 iterations, respectively, for small, medium and large networks.
The study investigates the following experimental factors:
Network size: small (from 2 to 20 nodes), medium (from 21 to 50 nodes) and large (more than 50 nodes).
Missingness balancing: whether the distribution of the missing values over the possible values taken by a node is balanced or unbalanced (that is, some values are missing more often than others).
Missingness severity: low (⩽1% missing values), medium (1% to 5% missing values) and high (5% to 20% missing values).
Missingness pattern: whether missing values appear only in root nodes (labelled “root”), only in leaf nodes (“leaf”), in nodes with large number of neighbours (“high degree”) or uniformly on all node types (“fair”). We also consider specific target nodes that represent the variables of interest in the BN (“target”).
Missing data mechanism: the
ampute function of the
mice R package [
27] has been applied to generated data sets to simulate MCAR, MAR and MNAR missing data mechanisms as described in
Section 2.2.
We recognise that these are but a small selection of the characteristics of the data and of the missingness patterns that might determine differences in the behaviour of soft EM and hard EM. We focus on these particular experimental factors because either they can be empirically verified from data, or they must be assumed in order to learn any probabilistic model at all, and therefore provide a good foundation for making practical recommendations for real-world data analyses.
The simulation study is based on seven reference BNs from
The Bayesys data and Bayesian network repository [
28], which are summarised in
Table 1. We generate incomplete data from each of them as follows:
We generate a complete data set from the BN.
We introduce missing values in the data from step 1 by hiding a random selection of observed values in a pattern that satisfies the relevant experimental factors (missingness balancing, missingness severity, missingness pattern and missing data mechanism). We perform this step 10 times for each complete data set.
We check that the proportion of missing values in each incomplete data set from step 2 is within a factor of 0.01 of the missingness severity.
We perform parameter learning with each EM algorithm and each incomplete data set to estimate the for each node , which we then use to impute the missing values in those same data sets. As for the network structure, we consider both the DAG of the reference BN and a set network structures with high .
The complete list of simulation scenarios is included
Appendix A.
We measure the performance of the EM algorithms with:
These three measures compare the performance of different EM algorithms at different levels of detail. PCR provides a rough indication about the overall performance in terms of how often the EM algorithm correctly imputes a missing value, but it does not give any insight on how incorrect imputations occur. Hence, we also consider APD and KLD, which measure how different are the produced by each EM algorithm from the corresponding in the reference BN. These two measures have a very similar behaviour in our simulation study, so for brevity we will only discuss KLD.
As mentioned in step 4, we compute the performance measures using both the network structure of the reference BN and a set of network structures with high . When using the former, which can be taken as an “optimal” structure, we are focusing on the performance of EM as it would be used in parameter learning. When using the latter, we are instead focusing on EM as it would be used in the context of a structure learning algorithm like the Structural EM. Such an algorithm will necessarily visit other network structures with high while looking for an optimal one. Such networks will be similar to that of the reference BN; hence, we generate them by perturbing its structure by removing, adding or reversing a number of arcs. In particular:
we choose to perturb 15% of nodes in small BNs and 10% of nodes in medium and large BNs, to ensure a fair amount of perturbation across BNs of different size;
we sample the nodes to perturb;
and then we apply, to each node, a perturbation chosen at random among single arc removal, single arc addition and single arc reversal.
We evaluate the performance of the EM algorithms with the perturbed networks using
that is, the difference in KLD divergence between the BN learned by EM from the perturbed networks and reference BN, and the KLD divergence between the BN learned by EM from the network structure of the reference BN and the reference BN itself. The difference is evaluated on 10 times for each combination of experimental factors on 10 different incomplete data sets. Lower values are better because they suggest a good level agreement between
and
and a small level of information loss.
4. Results
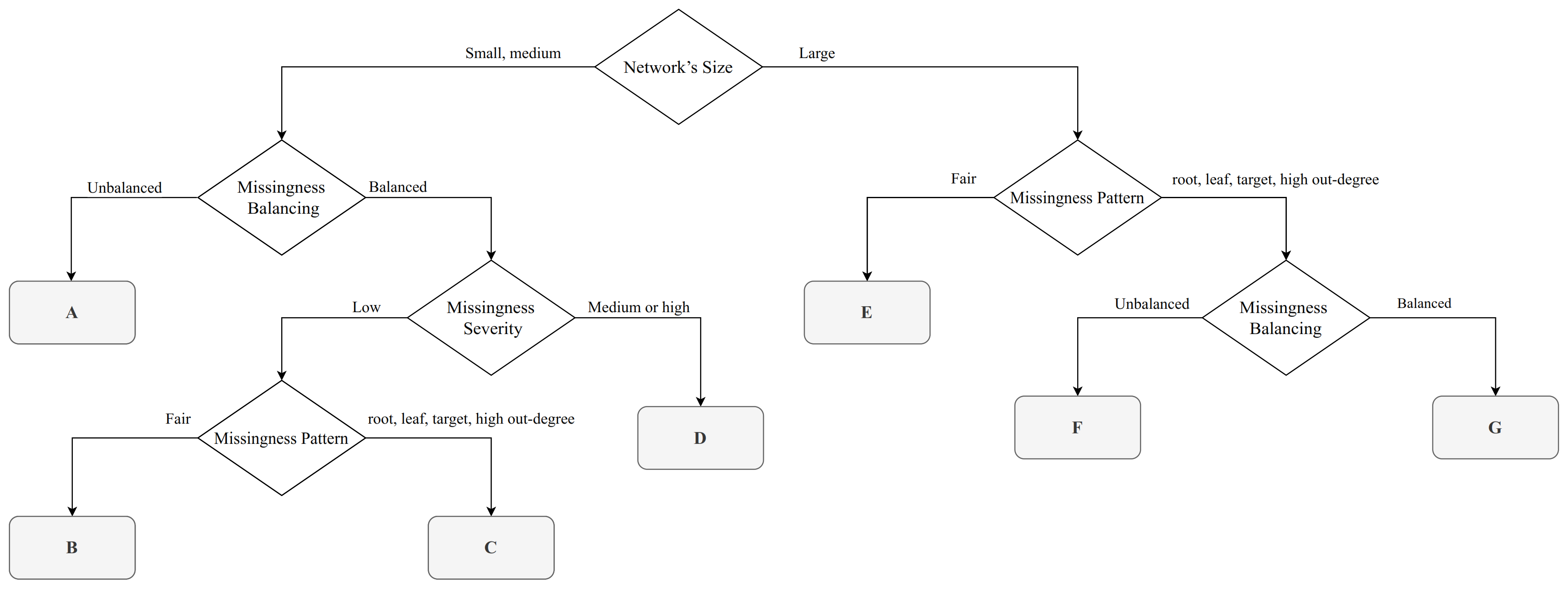
The results, comprising 5520 incomplete data sets and the resulting BNs, are summarised in
Figure 1 for the simulations in which we are using the network structure of the reference BNs. The decision tree shown in the Figure is intended to provide guidance to practitioners on which imputation algorithm appears to provide the best performance depending on the characteristics of their incomplete data problem. Each leaf in the decision tree corresponds to a subset of the scenarios we examined, grouped by the values of the experimental factors, and to a recommendation which EM algorithm has the best average KLD values. (Recommendations are also shown in
Table 2 for convenience, along with the leaf label corresponding the reference BNs). For brevity, we will discuss in detail on leaves A, B, E and G, which result into different recommended algorithms (
Table 2).
The 95% confidence intervals for KLD are shown in
Figure 2,
Figure 3,
Figure 4 and
Figure 5, respectively. We use those confidence intervals to rank the performance of various EM algorithms: we say an algorithm is better than another if it has a lower average KLD and their confidence intervals do not overlap.
Leaf A covers small and medium BNs in which variables have unbalanced missingness distributions. In these cases no EM algorithm dominates the others, hence no specific algorithm is recommended. As expected, KLD decreases as the sample size increases for all algorithms.
Leaf B covers small and medium BNs as well, but in this case random variables have balanced missingness distributions, the frequency of missing values is low and the pattern of missingness is fair. In these cases, hard EM is the recommended algorithm (
Figure 3). It is important to note that hard EM consistently has the lowest KLD value and has low variance, while soft EM and soft-forced EM have a much greater variance even for large samples sizes.
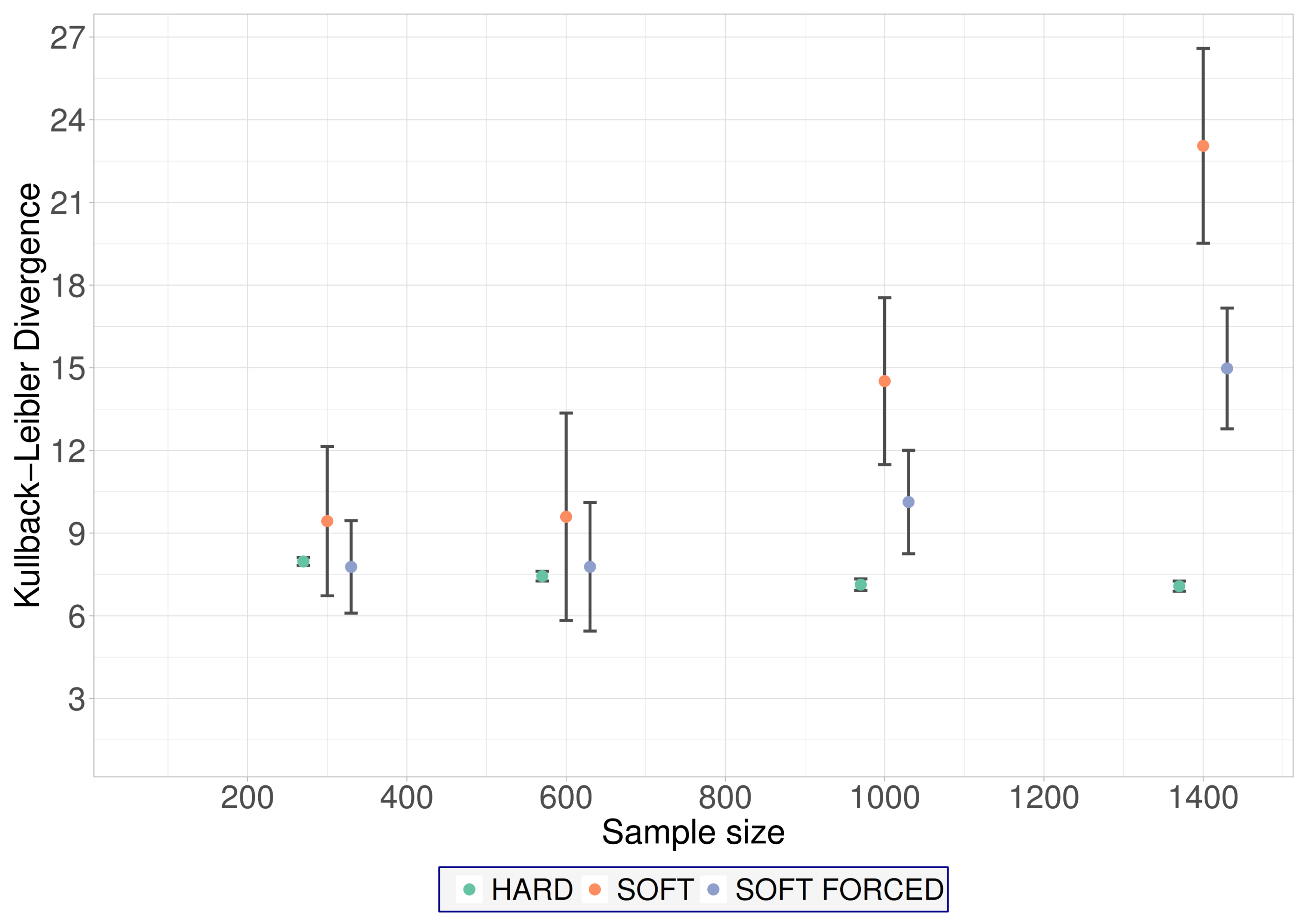
Leaf E covers large BNs where the pattern of missingness is fair. In these cases, hard EM is the recommended algorithm (
Figure 4). Note that the performance of both the soft EM and the soft-forced EM algorithms markedly degrades as the sample size increases. However, the performance of hard EM remains constant as the sample size increases.
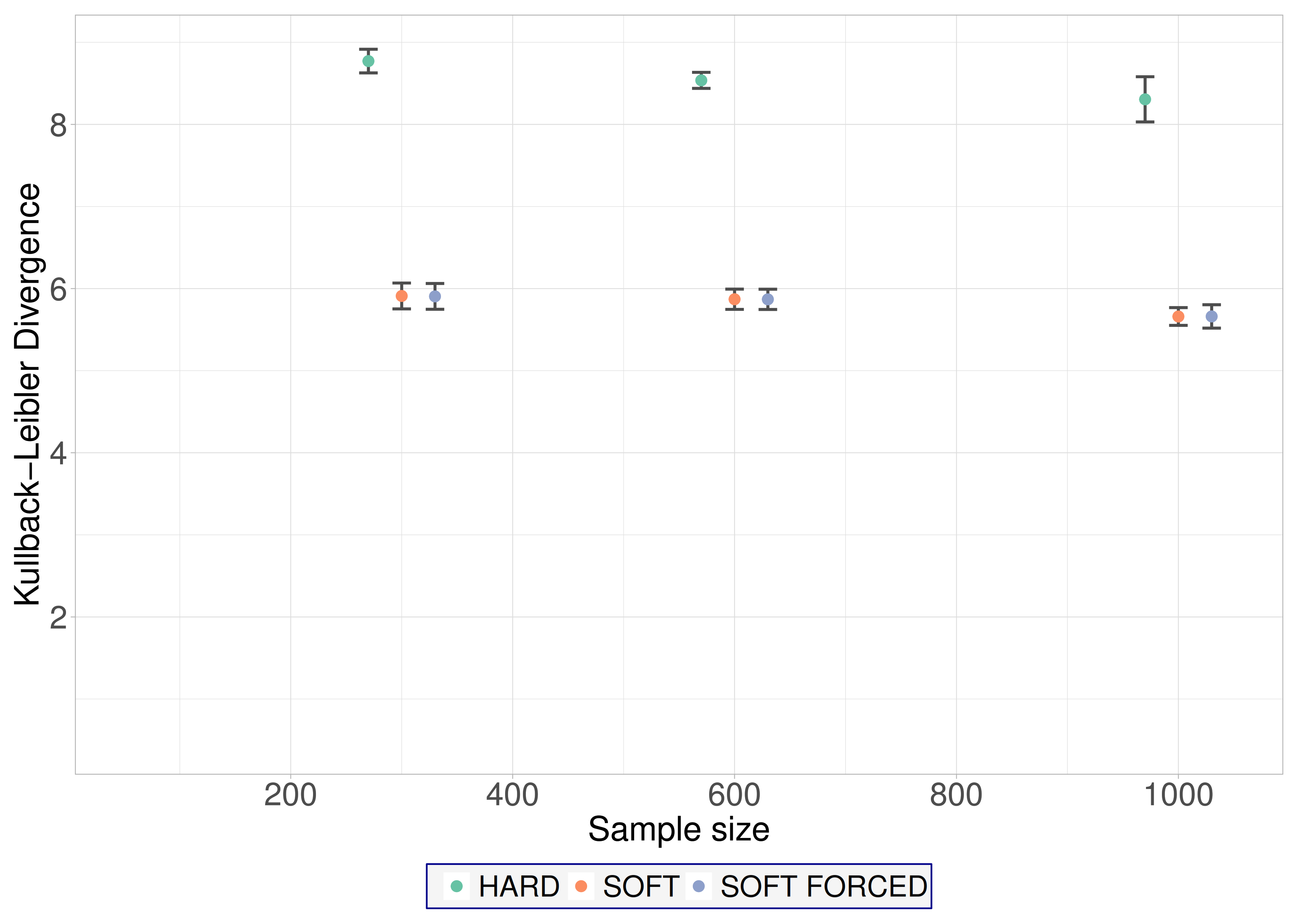
Leaf G covers large BNs where the pattern of missingness is not fair (the missingness pattern is one of “root”, “leaf”, “target”, “high degree”}), and the random variables have balanced missingness distributions. In these cases, soft EM is the recommended algorithm (
Figure 5). The performance of all EM algorithms shows only marginal improvements as the sample size increases, but low variance.
As for the remaining leaves, we recommend the hard EM algorithm for leafs D and F. Leaf D covers small and medium BNs with balanced missingness distributions and medium or high missingness severity; leaf F covers only large BNs and unbalanced missingness. Finally, leaf C recommends soft and soft-forced EM for small and medium BNs with balanced missingness distributions, low missingness severity and a pattern of missingness that is not fair.
As for the simulations that are based on the perturbed networks, the increased heterogeneity of the results makes it difficult to give recommendations as detailed as those above. We note, however, some overall trends:
Hard EM has the lowest in 44/67 scenarios, compared to 16/67 (soft EM) and 7/67 (soft-forced EM). Soft EM has the highest in 30/67 triplets, compared to 24/67 (soft-forced) and 13/67 (hard EM). Hence, hard EM can often outperform soft EM in the quality of estimated , and it appears to be the worst-performing only in a minority of simulations. The opposite seems to be true for soft EM, possibly because it converges very slowly or it fails to converge completely in some simulations. The performance of soft-forced EM appears to be not as good as that of hard EM, but not as often the worst as that of soft EM.
We observe some negative values for all EM algorithms: 7/67 (hard EM), 8/67 (soft EM), 5/67 (soft-forced). They highlight how all EM algorithms can sometimes fail to converge and produce good parameter estimates for the network structure of the reference BN, but not for the perturbed network structures.
Hard EM has the lowest 13/30 times in small networks, 9/14 in medium networks and 21/23 in large networks in a monotonically increasing trend. At the same time, hard EM has the highest in 8/30 times in small networks, 4/14 in medium networks and 0/23 in large networks, in a monotonically decreasing trend. This suggests that the performance of hard EM improves as the BNs increase in size: it provides the best more and more frequently, and it is never the worst performer in large networks.
Soft EM has the lowest in 12/30 times in small networks, 5/14 in medium networks and 0/23 in large networks in a monotonically increasing trend. At the same time, soft EM has the highest in 7/30 times in small networks, 6/14 in medium networks and 17/23 in large networks, in a monotonically increasing trend. Hence, we observe that soft EM is increasingly unlikely to be the worst performer as the size of the BN increases, but it is also increasingly likely outperformed by hard EM.
Soft-forced EM never has the lowest in medium and large networks. It has the highest 15/30 times in small networks, 4/14 in medium networks and 4/23 in large networks, in a monotonically decreasing trend (with a large step between small and medium networks, and comparable values for medium and large networks). Again, this suggests that the behaviour of soft-forced EM is an average of that of hard EM and soft EM, occupying the middle ground for medium and large networks.
5. Discussion and Conclusions
BN parameter learning from incomplete data is typically performed using the EM algorithm. Likewise, structure learning with the Structural EM algorithm embeds the search for the optimal network structure within EM. Practical applications of BN learning often choose to implement learning using the hard EM approach (which is based on single imputation) instead of the soft EM approach (which is based on belief propagation) for computational reasons despite the known limitations of the former. To the best of the authors’ knowledge, no previous work has systematically compared hard EM to soft EM when applied to BN learning, despite their popularity in several application fields. Hence, we investigated the following question: what is the impact of using hard EM instead of soft EM on the quality of the BNs learned from incomplete data? In addition, we also considered an early-stopping variant of soft EM, which we called soft-forced EM. However, we find that it does not outperform hard EM or soft EM in any simulation scenario.
Based on a comprehensive simulation study, we find that in the case of parameter learning:
Hard EM performs well across BNs of different sizes when the missing pattern is fair; that is, missing data occur independently on the structure of the BN.
Soft EM should be preferred to hard EM, across BNs of different sizes, when the missing pattern is not fair; that is, missing data occur at nodes of the BN with specific graphical characteristics (root, leaf, high-degree nodes); and when the missingness distribution of nodes is balanced.
Hard and soft EM perform similarly for medium-size BNs when missing data are unbalanced.
In the case of structure learning, which we explore by investigating a set of candidate networks with high posterior probability, we find that:
Hard EM achieves the lowest value of in most simulation scenarios, reliably outperforming other EM algorithms.
In terms of robustness, we find no marked difference between soft EM and hard EM for small to medium BNs. On the other hand, hard EM consistently outperforms soft EM for large BNs. In fact, for large BNs hard EM achieves the lowest value of in all simulations, and it never achieves the highest value of .
Sometimes all EM algorithms fail to converge and to provide good parameter estimates for the network structure of the true BN, but not for the corresponding perturbed networks.
However, it is important to note that this study presents two limitations. Firstly, a wider variety of numerical experiments should be performed to further validate conclusions. The complexity of capturing the key characteristics of both BNs and missing data mechanisms make it extremely difficult to provide comprehensive answers while limiting ourselves to a feasible set of experimental factors. Secondly, we limited the scope of this paper to discrete BN: but Gaussian BNs have seen wide applications in life sciences applications, and it would worthwhile to investigate to what extent our conclusions apply to them. Nevertheless, we believe the recommendations we have collected in
Section 4 and discussed here can be of use to practitioners using BNs with incomplete data.