Abstract
The general assignment problem is a classical NP-hard (non-deterministic polynomial-time) problem. In a warehouse, the constraints on the equipment and the characteristics of consecutive processes make it even more complicated. To overcome the difficulty in calculating the benefit of an assignment and in finding the optimal assignment plan, a simulation-based optimization method is introduced. We first built a simulation model of the warehouse with the object-oriented discrete-event simulation (O2DES) framework, and then implemented a random neighborhood search method utilizing the simulation output. With this method, the throughput and service level of the warehouse can be improved, while keeping the number of workers constant. Numerical results with real data demonstrate the reduction of discrepancy between inbound and outbound service level performance. With a less than reduction in inbound service level, we can achieve an over increase in outbound service level. The proposed decision support tool assists the warehouse manager in dealing with warehouse worker allocation problem under conditions of random daily workload.
1. Introduction
Workforce planning has been reported to be a persistent problem for a variety of process-centered industries [1]. These include healthcare operations—in particular, emergency departments, service industries, and warehouse management—whose performances are dependent on swift and even flows of resources and customers [2,3,4]. As the theory of swift and even flow suggests, the bottleneck management and process standardization are key to the speed and variance of the process flow [2]. The productivity of any process increases with the speed at which the materials (or information) flow through the process [5]. This indicates the importance of workforce planning for improving productivity.
Warehousing is a vital component of the supply chain, where the optimal planning of its workforce is a prerequisite towards achieving its global efficiency [6]. In a warehouse, a sequence of multiple processes is performed, starting from shipment arrivals and ending in shipment releases. These processes are usually constrained by space and workforce capacity. The main focus of the current study is the workforce planning system implemented in a warehouse. As the labor resources represent a significant cost item in a labor-short country such as Singapore; this poses new challenges for cost minimization and efficiency improvements via innovations in workforce planning and optimization. The preliminary analysis of the warehouse operations, and specifically worker allocation, revealed an unbalanced utilization of workers across different warehouse activities. It was identified that one of the critical bottlenecks affecting overall service level of the warehouse was the need to optimize worker assignment to each task/workstation while balancing the workload of each workstation.
In the traditional assignment optimization problem, the benefit can be directly calculated given a fixed worker–task pairing. Even with this assumption, the assignment problem is NP-hard [7]. The problem in the warehouse is more complicated due to the precedence constraints, whereby the succeeding activity cannot start until the preceding activity is completed. Another related problem is the assembly line balancing, which considers the precedence constraints. However, oftentimes such problems do not consider worker capability and capacity factors, which are critical to human resource allocation problems [8].
Discrete-event simulation (DES) is one of the popular modeling techniques in which a model changes only at a discrete random set of time points [9]. Nowadays, many commercial simulation software packages such as Arena integrate optimization techniques with DES [10,11]. Although such commercial software packages are designed to provide users with functionality to create their desired simulation models based on processes, oftentimes the users are not allowed to customize the event logic, which is an integral part of each DES model [10]. In this study, we adopt the object-oriented discrete-event simulation (O2DES in ) framework developed by Li et al. [12]. This novel framework features a flexible simulation modeling environment, which allows the user to customize the event logic, configure simulation parameters, and incorporate add-on algorithms, including optimization models.
Our research aim was to develop a simulation-based optimization method to improve the warehouse service level, i.e., daily productivity, by optimally allocating warehouse workers into inbound and outbound activities, while at the same time considering all operational constraints of the warehouse’s operation. In addressing this aim, a warehouse manpower planning tool was developed based on the simulation-based optimization method, which combines the O2DES simulation framework and a random neighborhood search method. Our study is the first in the operations research domain to introduce a decision support tool for warehouse worker allocation using a simulation-based optimization method.
The manpower allocation tool was tested in a warehouse located at Singapore. It is now used to support the warehouse managers’ decisions on a weekly and/or daily basis.
The rest of the paper is organized as follows. In Section 2, a literature review on the related topics is presented. Next, the worker assignment problem in the warehouse is described in Section 3. Section 4 outlines the simulation-based optimization method. The O2DES framework and the warehouse simulation model are introduced in Section 5, followed by the simulation-based optimization algorithm specifications in Section 6. Section 7 presents the numerical results.
2. Literature Review
Customer satisfaction via effective resource utilization, the shipment of the right product in good condition and within the target shipment time, is the key objective of warehousing [13,14,15,16]. Warehousing aims to address the differences in time and space between suppliers and customers, while adapting to the fluctuating market conditions [17]. Warehouses execute a broad range of process-based functions, including temporary storage, protecting goods, service support in customer order fulfillment, goods packaging, after sales service support, quality inspections, testing, assembly, and repairs [18,19].
In the current global economic environment, the warehouses face an unprecedented level of competitive and economic pressures [20], including a high level of uncertainty and risk of supply chain disruptions due to the COVID-19 pandemic [21,22]. The pressures from competitors and customers result in the reduction of profit margins [23,24]. Under this situation, efficient resource utilization becomes more critical than ever.
Humans are the central and most critical elements of the resource base in warehousing [25]. Due to the high fluctuations (both predictable and unexpected) in workload demand [18], research has advocated the need for the implementation of manpower planning strategies [20,26]. For example, Edwards et al. [27] distinguishes three phases of manpower planning, which include the prediction of manpower demand, the prediction of the future supply of manpower, and reconciliation of the discrepancies between supply and demand via workforce scheduling and staffing. Considering the above, workforce scheduling—and specifically personnel work assignments that deal with the allocation of personnel to tasks and work stations—is crucial to warehouse operational efficiency [6,28,29]. Optimal staffing, or allocation of workers to tasks, is the key to tackling the challenges of high demand fluctuations on a daily basis. In the warehouse, this problem is dependent on workers; qualifications, i.e., skill sets, which are very specific to each employee.
The most relevant problem to our topic is the mixed-model assembly line balancing problem (MALBP), which tries to assign the tasks of different models to the workstations. It is called a mixed-model as multiple models are assembled on the same assembly line. As summarized in Becker et al. [8], there are three types of MALBP problems, categorized according to the constraint and objective:
- MALBP-I: given the cycle time to minimize the number of workstations;
- MALBP-II: given the number of workstations to minimize the cycle time;
- MALBP-III: minimize both the cycle time and the number of workstations.
However, our target is to maximize the service level, i.e., the ratio between the number of completed tasks and the number of arriving tasks, given a fixed number of workers. Our research problem is different from the above-mentioned three problems by Becker et al. [8], except for the MALBP-II which can be considered the most relevant to our problem. The major points that differentiate our problem are:
- In our problem, each worker is only capable of performing a subset of operations.
- The processing time of each task is stochastic.
- The objective is to maximize the service level.
In Dou et al. [30], a machine deployment problem is considered, where the objective is to minimize the cost of setting up all the machines, while satisfying the precedence and space constraints. This involves also assignments of the machines to the tasks, and a GA-based optimization approach was designed to identify a set of best solutions. The machines in Dou et al.’s [30] model can be considered as workers in our model. However, in our problem the number of workers is fixed, while the objective is to maximize the service level. In contrast, in Dou et al.’s [30] model the number of machines in different stages (tasks) are independent.
Simulation-based optimization has been used for a number of decades for problem solving in logistics. For example, Azadivar [31] showed that the discrete rack systems can be better optimized through simulations rather than approximating with mathematical models. Later on, Ding et al. [32] extended this idea to the supply chain context. They developed a simulation-based optimization method for the selection of potential suppliers. To obtain an optimal design of the cold supply chain, Saif and Elheldhli [33] developed an innovative simulation-based optimization approach to minimize the total cost that includes the logistics costs and the global warming impact. More recently, Ghasemi and Khalili-Damghani [34] developed a novel simulation-based optimization approach to solve a multi-period inventory planning problem for the supply chain of a company in Iran.
3. Problem Description
Warehouses typically handle a variety of stock-keeping units (SKUs), which require a range of activities to be executed. Different products may require different activities. Considering the space and workforce constraints, the warehouse aims to maximize its productivity with via appropriate worker assignment. As warehouse workers may have different skills, it is not only the number of the workers that count, but also every specific worker–activity pairing becomes critical. Under the conditions of high fluctuations in daily workload, it is important for the warehouse planner to obtain an optimal worker assignment in a rather short period of time. To address this problem, a simulation-based optimization method was developed. Specifically, the optimal worker assignment to warehouse activities/tasks should be achieved while satisfying all operational and worker skill set constraints.
In our showcase, the following operational assumptions are considered:
- Product types: We chose to consider all product types, i.e., franchises, that the warehouse handles. There are in total nine franchises being handled in the warehouse. Different franchises require different processing times for different activities. More details are provided in Section 5.
- Inbound activities: Inbound activities start with the arrival of shipments at the warehouse. Immediately after the dock-in, the products in pallets are unloaded at the inbound staging area and later moved to the sorting workstation. After manual counting and checking for defects and damage, the products are moved to the goods receipt (GR) workstation. At the GR station, workers scan the barcode on each item and register the items in the warehouse management system (WMS), while putaway slips with storage bins are generated for each pallet load. After the GR, they are ready for putaway to the storage area(s). The putaway worker puts away the pallet in its designated storage area following the storage bin information printed on the putaway slip. Putaway activity is denoted as the terminal inbound activity. Figure 1 shows the entity flow diagram for inbound shipments.
 Figure 1. Inbound entity flow diagram.
Figure 1. Inbound entity flow diagram. - Outbound activities: Outbound activities start when order information arrives into the WMS and a pick slip is generated. One order is assigned to one picker. After the order picking is completed, depending on the labeling requirements, the items need to be labeled before scanning starts. Otherwise, the picked items are sent to the scanning station. There are two types of scanning, each for a certain type of product, i.e., manual scanning and scanning via auto-scanning tunnel (AST). The scanning activity makes sure that all the items are picked against the order lists, and it generates slips that denote items which need to be packed together based on pallet or case dimension constraints. Then the items are packed into pallets and cases accordingly. A release worker moves the order to the outbound staging, from where the order is shipped out with an outbound truck. Figure 2 describes the outbound entity flow diagram.
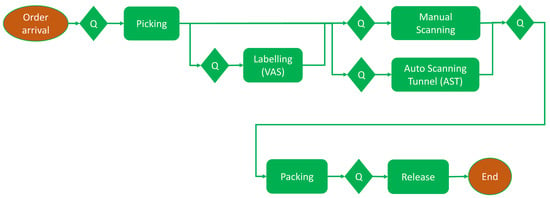 Figure 2. Outbound entity flow diagram.
Figure 2. Outbound entity flow diagram. - Three types of storage areas: There are three storage areas in the warehouse, i.e., racking, long-span shelving (LSS), and vertical lift modules (VLMs). Racking is designed to store SKUs in full pallets, LSS contains SKUs in loose boxes, and VLMs are for loose boxes. Each storage type is dedicated to one or more product types.
- Shift configuration and working days: There are two shifts operating during business days (excluding weekends and holidays): the morning shift operates from 8:00 a.m. to 6:00 p.m. with a one-hour break during 12:00–1:00 p.m., and the night shift operates from 9:00 p.m. to 7:00 a.m. (next day) with a one-hour break during 1:00–2:00 a.m.
- Worker numbers and shift assignment: The total number of workers is fixed (31 workers in total). Worker numbers assigned to each shift are pre-fixed; 21 workers are assigned to the morning shift and 5 workers are assigned to the night shift. Additionally, 5 outsourced workers are assigned to value-added service (VAS) activity for labeling upon request.
- Worker skill set matrix: We assume that each worker has his/her own unique skill set. If the worker is trained to conduct an activity, “yes” is put in the respective activity cell. Table 1 shows the worker skill set matrix assumed in our model.
 Table 1. Worker skill set.
Table 1. Worker skill set. - Workload demand for one-week period is known upfront.
To tackle the problem, the constraints on the workforce should be dealt with. These constraints may be worker-specific, such as the skill set, or arise from the resource limits and operational rules in the warehouse. For example, due to the warehouse equipment capacity, there is an upper bound on the number of workers allowed to be assigned to some activities. Namely, there is a limited amount of the material handling equipment (MHE) and a limited number of scanning computers at a workstation, thereby determining the maximum number of workers allowed to work at each workstation or activity at the same time. In our showcase in Section 7, it is assumed that GR allows up to two workers, putaway three workers, VLM two workers, picking six workers, AST either two or zero workers, and scanning up to three workers. However, we do not impose any constraints on sorting, packing, and release activities regarding the maximum number of workers, as such activities do not require any specific equipment. Moreover, following the warehouse operation requirements, we assume that the night shift can perform only putaway, picking, scanning, and packing activities.
Worker skill set is an important constraint in the assignment problem, which is also considered here. As shown in Table 1, each worker owns a distinct set of skills that allows the worker to perform the corresponding warehouse activities. If the worker is not trained to perform an activity, that worker cannot be considered as a candidate for assignment to this activity.
Nonetheless, we do not impose any constraints on warehouse storage capacity, working areas, and buffer zones between activities.
In the following sections, we will show how the simulation-based optimization method can be used to solve this problem. As the situation in reality may vary day by day, and also from one warehouse to another, our tool will provide the solution for the specific settings of the warehouse, including flexibility of both products and workers.
First of all, inbound and outbound workload information should be defined. For example, the inbound shipment arrival and/or outbound order start time-stamp, product name, workload in terms of number of pallets, and target completion time-stamp information, are all handled by the warehouse planners. This information is dependent on the forecast or expectation. Hence, this information may vary. Moreover, we allow the model to capture the pending workload from the previous day in pallet quantity, and by each type of inbound and outbound activity. Besides, the more detailed information, such as the product type and processing time for each activity, can also be customized by the user. Here we specify product name, designated storage area, whether the product requires AST for scanning or not, and per-pallet processing time (mean, standard deviation) by all inbound and outbound activities needed by each product type.
The tool also allows variability in the worker parameters. The number of workers assigned to a shift and the shift duration can vary. As an example, we consider two shifts in the showcase of Section 7, i.e., morning and night, operating from 8 a.m. to 6 p.m. and from 9 p.m. to 7 a.m. (next day), respectively, with a one-hour break in each shift. Besides, the information on national holidays can also be captured by our tool to specify the non-working days.
The worker skill set matrix is another important parameter. As defined in Table 1, each worker has a skill set (“Yes” if the worker owns the skill for the activity) with respect to each type of activity conducted in the warehouse.
To measure the performances of different worker assignment options in the warehouse, the hourly and daily KPIs are generated. The hourly KPIs include worker utilization by each activity in each hour, inbound and outbound throughput in terms of the number of completed pallets by each hour, and overall inbound and outbound team utilization rate by each hour. Overall daily KPIs include inbound and outbound team overall daily utilization, total work-in-progress (WIP) pallet quantity in inbound and outbound activities, total quantity of completed pallets by inbound and outbound teams, inbound and outbound service levels, and per-worker average productivity rate in terms of number of completed pallets.
To express the KPIs formally, we define the following notation:
- : number of occupied workers;
- : total number of available workers;
- : number of completed pallets;
- : number of arrived pallets;
- : number of completed inbound pallets;
- : number of completed outbound pallets;
- : number of inbound workers;
- : number of outbound workers.
We define as the average function over the simulation days. The KPIs can be calculated with the following formula:
In our simulation-based optimization model we consider service level as the target KPI, as communicated by the warehouse team. The warehouse operations team measures their service level performance as the ratio of total number of completed pallets (output) to total number of arrived pallets (input) on a given day, which is oftentimes denoted as throughput productivity in the warehouse literature. Additionally, it is considered to be one of the frequently used direct warehouse performance indicators [35,36].
For the purpose of parsimony, we further concentrate on the service level performance as per our target optimization objective of the simulation-based optimization tool.
4. Methodology
Ladier et al. [6] considered the staff scheduling in the warehouse on both weekly and daily granularity levels. They built three mixed integer programming (MIP) models and solved the models to obtain the optimal staff assignment and shift pattern. Their objective was to minimize the cost, while assuming that all the tasks should be completed by hiring sufficient number of staff. However, in the daily operations of the warehouse, the number of available workers may not be enough to complete all the tasks. In this situation, the objective is to finish as many tasks, with an optimal worker assignment.
The selected warehouse in this study serves as a distribution center with variations in product types and demands. There are different teams working on different activities. The warehouse operates as one single processing unit, which consists of sequence of activities. The major concern of the warehouse is to assign the optimal number of workers to each team. Moreover, under uncertainty in demand and processing time, this may require reallocation of worker(s) to other teams. This adds an additional layer of complexity to the problem and requires a methodology that can solve the problem. Given these requirements, following Amorim et al. [37], we devised a simulation–based optimization model that explores both simulation and optimization methods to improve the service level performance, by suggesting appropriate manpower assignment to different activities. First of all, the discrete-event simulation model was developed, considering the relationship between different activities. Then, the processing time of each activity was defined along with an initial assignment of manpower. Due to uncertainty in daily workload, the initial solution is not always optimal. Therefore, additional effort is required to optimally assign the manpower. As the assignment of workers to different activities is a complex task, a heuristic algorithm instead of exact algorithm was developed to find the optimal worker assignment. With each iteration, the new assignment of workers is input to the simulation model until the model output achieves the highest service level performance.
5. O2DES Framework and Warehouse Simulation
For the worker assignment problem in the warehouse, it is difficult to obtain a direct calculation for the worker assignment problem. In this case the simulation comes into play. With the simulation modeling of the warehouse, we can replicate the real system in a computer environment. The systems performance can be evaluated in a simulation, and additional features of system can be tested before its deployment. The simulation outcome allows the decision maker to fine tune a set of parameters to improve the operational performance. However, configuring these parameters for a complex system, such as warehouses, can be challenging. Therefore, the simulation-based optimization approach, which integrates the best of optimization with discrete-event simulation (DES) techniques, can be used to handle this complexity.
The object-oriented discrete-event simulation (O2DES) was adopted from Li et al. [12] and implemented as a core simulation engine in our simulation-based optimization tool to achieve the main objective of our research, i.e., the development of a decision support tool that can optimally assign workers to the warehouse activities.
5.1. O2DES
The main features of O2DES are as follows:
- Events are described in modules and they interact with each other.
- Simplified syntax for:
- (a)
- Event execution;
- (b)
- Event scheduling;
- (c)
- Input/output event interfacing.
- Automated warm-up induction.
5.2. Simulation Modeling
Any process system consists of a sequence of steps, i.e., activities. Entities move through the activities. Similarly, in the simulation modeling, the real life situation can be represented using an entity flow diagram (EFD), a logical flow diagram of entities between the activities. The resources required for the different activities are mapped in the EFD.
As described in Section 3, the warehouse operations consist of two main types, i.e., inbound and outbound, while the pallet is the entity that flows through inbound and outbound activities. To build the simulation model, an EFD based on the warehouse operational processes needs to be developed, as shown in Figure 3.
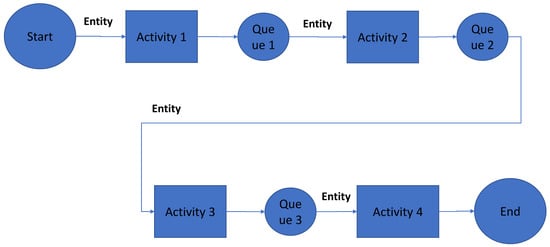
Figure 3.
Entity flow diagram (EFD).
With certain assumptions, the simulation model was built using these EFDs in code and simple heuristics integrated with simulation were used to assign the manpower.
Input information on inbound and outbound workload has been provided by the warehouse for simulation. On top of incoming inbound shipment load and customer order volume, leftover workload information was also considered.
Due to possible uncertainties in warehouse operations, we assumed the processing time of each activity follows a gamma distribution. The characteristics and advantages of gamma distribution can be found in several previous studies [38,39,40,41]. For example, in a study by Song [39], the Poisson distribution was considered to be inappropriate to describe the lead time, as the uncertainty may arise due to several reasons, which makes a more centralized distribution like the gamma distribution a preferred method.
The values of mean and standard deviation for each activity are calculated based on the time-motion study conducted in the warehouse. Gamma distribution can be characterized by and , where the density probability function:
with As the mean and squared deviation , we can derive and as following:
Table 2 shows the processing time data used in the simulation model.

Table 2.
Processing times of different franchises and processes. GR represents goods receipt; VAS value added service.
All simulation experiments were performed on an Intel Core™ i7-8550U CPU 1.80 GHz 1.99 GHz with 16 GB RAM and a 64-bit operating system. First of all, it was necessary to determine the simulation settings: initial conditions, warm-up length, and number of replications [10]. Preliminary tests were performed to evaluate the simulation duration and the number of replications necessary to achieve the steady-state results. Upon the initiation, the simulation tool reads input data and adjusts for the real simulation start time by running a single replication. As a warm-up, this process does not generate any statistics. Using real forecast data of the workload with arrival times, the simulation results indicate that one replication is sufficient to achieve steady output.
Once the model was validated, simulation iterations were run for each possible scenario, in combination with the optimization algorithm. This will be explained in the next section.
6. Simulation-Based Optimization
The objective is to maximize service level for both inbound and outbound operations, where service level .
Considering the constraints, the model is defined as follows:
where and represent inbound and outbound service levels, respectively; is a weight factor to control the trade-off between inbound and outbound. X is an assignment matrix, where means that the worker i is assigned to the activity i, otherwise . indicates that worker i has the skill j. In practice, the outbound service level performance is considered to be of a high priority as it is directly related to the customer satisfaction. Hence, a higher weight is set for the outbound service level .
The constraint part of the model is an assignment problem, where multiple workers can be assigned to the same task. As the objective is not an explicit function of the assignment scheme, but some metric given by the simulation output, it is not easy to solve the problem by an exact algorithm. In the context of a similar problem, i.e., the assembly line worker assignment, the neighborhood search method was shown to be effective in Polat et al. [42] and to outperform other heuristic methods. Motivated by this, we adopted a neighborhood search method in our model.
For a binary vector of matrix, the Hamming distance is the number of bit positions in which the two corresponding bits are different. For two assignment matrices and ; is denoted as the Hamming distance between them. For each worker , if the worker is assigned to different tasks in and , the difference will be two in row i. Thus is called a c-neighbor of if . In our problem, due to predetermined upper bounds for the number of workers in each activity, a c-neighbor may not be feasible.
We propose a random neighborhood search algorithm to solve the problem, which is described in Algorithm 1. Accordingly, every time a 1-neighborhood of the current solution is built randomly. If the new solution is feasible, the simulation will run with this assignment and generate the output statistics. The metric used for our objective is the service level. If the service level of the new solution is better than the incumbent solution, we will update the incumbent as this new solution. Usually, a random 1-neighborhood is not feasible, in the sense that the number of workers assigned to a task may be larger than . In this case, a 1-neighborhood of will be built and checked again. This procedure will be repeated until a feasible solution is found, or the number of solutions we have generated is larger than a determined threshold.
Note that our method is different from the 1-step neighborhood search. Before a new feasible solution is found, several workers may have been reassigned to other task(s). This can help to avoid the local optimum. As the random search is in a broader neighborhood, the probability of reaching a global optimum is higher. From the practical perspective, the number of new solutions and the number of simulation runs are both bounded, to make the total time reasonable for the industry application.
| Algorithm 1 The random neighborhood search algorithm. |
 |
7. Numerical Results
Using the simulation-based optimization method, the software tool was developed. The graphical user interface (GUI) design of the software is shown in Figure 4. The warehouse planner can select the workload data as an input and run the tool. The output includes the service level, along with other metrics.
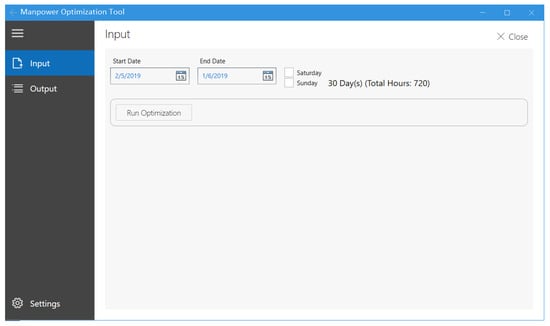
Figure 4.
The GUI of the manpower allocation tool.
In a set of experiments, we tested different values of for inbound and outbound service levels, with the input data sampled from different months of years 2018 and 2019. The simulation-based optimization was run with different values of the coefficient .
We used the historical data provided by the warehouse. Specifically, inbound shipment arrival and outbound shipment order information for the following months were chosen: July 2018, January 2019 and March 2019. For each month, we conducted the assignment optimization week by week, and calculated the summation over all weeks of the month. The value of coefficient ranges from 1.0 to 2.0, with a step of 0.1. Data analyses of historical workload demand suggest that the outbound order volume generally prevails the inbound one. To diversify our sample pools, the sampling was done in the following way:
- In July 2018, the outbound pallet number was nearly less than inbound pallet number;
- In January 2019, the outbound pallet number was nearly larger than the inbound one;
- In May 2019, the outbound pallet number was nearly larger than the inbound one.
For the warehouse, outbound service level is considered to be more critical than the inbound service level. As shown in Figure 5, Figure 6 and Figure 7, the results suggest that the optimized worker assignment can always achieve a better performance for the outbound service level, compared to the current assignment shown in Table 3. Regarding the inbound service level, the performance may be better when the value of is relatively small, that is, when the priority of outbound service level performance is not considered to be so high. Generally, with a decrease of less than for the inbound service level, an increase of more than can be obtained in the outbound service level performance. This indicates that our assignment can achieve a higher utilization of workers and a higher level of customer satisfaction.
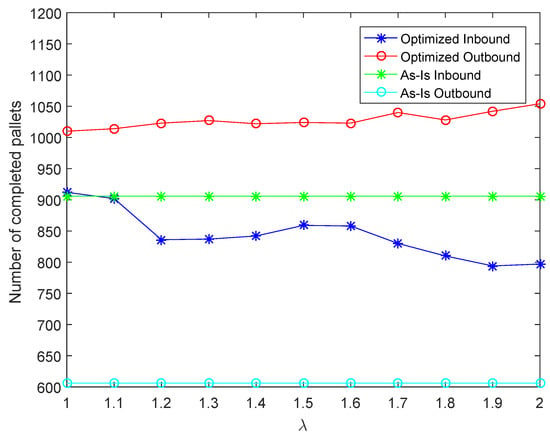
Figure 5.
Numerical results for January 2019 data, given the total numbers of inbound/outbound pallets of 1508/1702, and the numbers of completed pallets with the current worker allocation are 906/606.
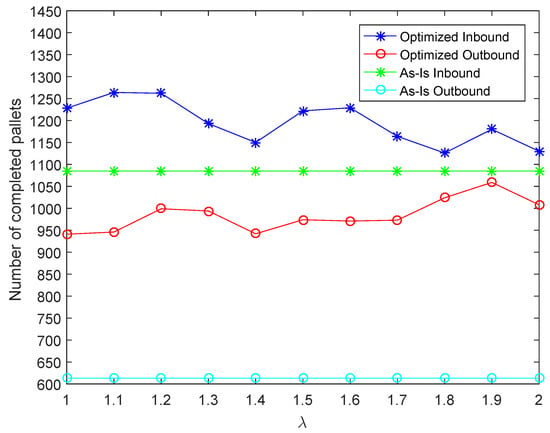
Figure 6.
Numerical results for May 2019 data, given the numbers total inbound/outbound pallets of 1541/1981, and the numbers of completed pallets with the current worker allocation are 1085/613.
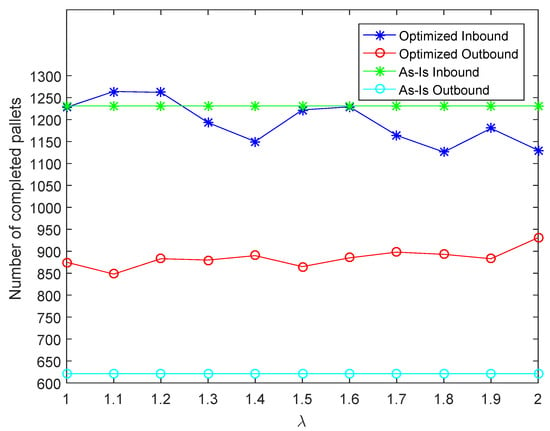
Figure 7.
Numerical results for July 2018 data, given the total numbers of inbound/outbound pallets of 1656/1529, and the numbers of completed pallets with the current worker allocation are 1231/621.

Table 3.
The current assignment used in the warehouse.
As seen from the reported results, when the value of increases, the outbound service level increases, while the inbound service level decreases. This indicates that the parameter can be used to control the trade-off between inbound and outbound service level performance metrics.
To demonstrate the improvements via the simulation-based optimization method, we generated additional service level outputs for a benchmark worker allocation case under the same workload scenarios. This benchmark worker allocation refers to the worker allocation matrix previously used by the warehouse manager prior to the implementation of our simulation-based optimization tool. In generating the service level statistics for the benchmark worker allocation, we preset the worker allocation and conducted simulations without any optimization. The comparisons of performance outputs from the optimized and non-optimized (benchmark) manpower allocations are shown in Figure 5, Figure 6 and Figure 7, indicating that with less than 10% decrease for the inbound service level, on average, the outbound service level can be increased by 30% across all three scenarios considered.
8. Conclusions
As a real-life complex system, the warehouse is characterized by high variability in workload arrival. Thus, the optimal worker assignment in such a dynamic system is a non-trivial task. Since the workload may vary on a daily basis, it is important for the warehouse planner to have a decision support tool that can optimally assign workers to different activities. As the exact method is impossible for this problem, we proposed the simulation-based optimization method, which combines the O2DES framework with a random neighborhood search method. Under dynamic daily workload conditions, the random neighborhood search model was shown to efficiently identify an improved manpower assignment strategy based on the simulation output. A decision support tool based on the proposed method was then verified and validated using the real data from a warehouse located in Singapore. The results show that with a slight decrease of the inbound service level, we can improve the outbound service level by more than 30%.
This study provides a practical contribution to the problem of workforce planning in a warehouse. Warehouse planners and managers can benefit from the use of such a manpower allocation tool. The managers or users of the tool will need to provide the upcoming workload forecast as the input, while the tool automatically generates the optimal manpower allocation to activities.
On the theoretical side, although the literature has advocated the need for implementation of strategies for manpower planning [20,26], the reported solutions have not been numerous. One of the few examples is from Ladier et al. [6], who proposed a two-step mixed integer linear programming model which optimizes worker allocation to activities and different shifts daily. Said optimization model does not capture the arrival time of the daily workload, and assumes that the human resources are always sufficient. Hence, such a model is not capable pf effectively accounting for the industry circumstances. In contrast, our simulation-based optimization model accounts for the workload arrival and queuing, and allows one to achieve a higher service level with the available manpower.
Future studies may further improve the flexibility of the proposed method by integrating a better selection of initial solution to accelerate the neighborhood search. This method can also be applied to other resource allocation problems in supply chains and logistics.
Author Contributions
Conceptualization, H.L. and O.G.; methodology, K.K. and W.Z.; software, H.L. and K.K.; validation, O.G.; resources, H.L.; data curation, O.G.; writing–original draft preparation, O.G., K.K., and W.Z.; writing–review and editing, O.G. and K.K.; visualization, W.Z. and O.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been made possible by the funding support from the Centre for Next Generation of Logistics (C4NGL), Department of Industrial Systems Engineering and Management, Faculty of Engineering, National University of Singapore. The work has been also supported by Singapore A*STAR IAF-PP fund (Grant No. A1895a0033) under the project “Digital Twin for Next Generation Warehouse”. The authors appreciate our researchers for their great contributions to the centre and projects.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Schmenner, R.W. Looking ahead by looking back: Swift, even flow in the history of manufacturing. Prod. Oper. Manag. 2001, 10, 87–96. [Google Scholar] [CrossRef]
- Fredendall, L.D.; Craig, J.B.; Fowler, P.J.; Damali, U. Barriers to swift, even flow in the internal supply chain of perioperative surgical services department: A case study. Decis. Sci. 2009, 40, 327–349. [Google Scholar] [CrossRef]
- Devaraj, S.; Ow, T.T.; Kohli, R. Examining the impact of information technology and patient flow on healthcare performance: A Theory of Swift and Even Flow (TSEF) perspective. J. Oper. Manag. 2013, 31, 181–192. [Google Scholar] [CrossRef]
- Garn, W.; Aitken, J.; Schmenner, R. Smoothly Pass the Parcel: Implementing the Theory of Swift, Even Flow. ResearchGate 2020. [Google Scholar] [CrossRef]
- Schmenner, R.W. Service businesses and productivity. Decis. Sci. 2004, 35, 333–347. [Google Scholar] [CrossRef]
- Ladier, A.L.; Alpan, G.; Penz, B. Barriers to swift, Joint employee weekly timetabling and daily rostering: A decision-support tool for a logistics platform. Eur. J. Oper. Res. 2014, 234, 278–291. [Google Scholar] [CrossRef]
- Nauss, R.M. Solving the generalized assignment problem: An optimizing and heuristic approach. INFORMS J. Comput. 2003, 15, 249–266. [Google Scholar] [CrossRef]
- Becker, C.; Scholl, A. A survey on problems and methods in generalized assembly line balancing. Eur. J. Oper. Res. 2006, 168, 694–715. [Google Scholar] [CrossRef]
- Burinskiene, A.; Lorenc, A.; Lerher, T. A simulation study for the sustainability and reduction of waste in warehouse logistics. Int. J. Simul. Model. 2018, 17, 485–497. [Google Scholar] [CrossRef]
- Kelton, W.D.; Sadowski, R.P.; Sadowski, D.P. Simulation with Arena; McGraw-Hill: New York NY, USA, 1998. [Google Scholar]
- Muller, D. Automod™-providing simulation solutions for over 25 years. In Proceedings of the 2011 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 11–14 December 2011; pp. 39–51. [Google Scholar]
- Li, H.; Zhu, Y.; Chen, Y.; Pedrielli, G.; Pujowidianto, N.A. The object-oriented discrete event simulation modeling: A case study on aircraft spare part management. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; pp. 3514–3525. [Google Scholar]
- Frazelle, E. The title of the cited contribution. In Supply Chain Strategy: The Logistics of Supply Chain Management; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Abushaikha, I.; Salhieh, L.; Towers, N. Improving distribution and business performance through lean warehousing. Int. J. Retail. Distrib. Manag. 2018, 46, 780–800. [Google Scholar] [CrossRef]
- Guthrie, B.; Parikh, P.J.; Kong, N. Evaluating warehouse strategies for two-product class distribution planning. Int. J. Prod. Res. 2017, 55, 6470–6484. [Google Scholar] [CrossRef]
- Ahmed, D.; Hyder, M. Improving Distribution and Business Performance through Lean Warehousing. Int. J. Bus. Stud. 2020, 1, 35–37. [Google Scholar]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Van Den Berg, J.P. Integral Warehouse Management; Management Outlook Publications: Utrecht, The Netherlands, 2007. [Google Scholar]
- Heragu, S.S.; Du, L.; Mantel, R.J.; Schuur, P.C. Mathematical model for warehouse design and product allocation. Int. J. Prod. Res. 2005, 43, 327–338. [Google Scholar] [CrossRef]
- De Leeuw, S.; Wiers, V.C.S. Warehouse manpower planning strategies in times of financial crisis: Evidence from logistics service providers and retailers in The Netherlands. Prod. Plan. Control 2015, 26, 328–337. [Google Scholar] [CrossRef]
- Ivanov, D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101922. [Google Scholar] [CrossRef]
- Nikolopoulos, K.; Punia, S.; Schäfers, A.; Tsinopoulos, C.; Vasilakis, C. Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions. Eur. J. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Klaus, P. The assessment of competitive intensity in logistics markets. Logist. Res. 2011, 3, 49–65. [Google Scholar] [CrossRef]
- Rebitzer, D.W. The European logistics market. In Europe Real Estate Yearbook; Real Estate Publishers BV: VC Den Haag, The Netherlands, 2007; Available online: www.europe-re.com (accessed on 18 November 2020).
- Graham Douglas, D. Warehouse of the future. Frontline Solut. 2003, 4, 20–26. [Google Scholar]
- Pooya, A.; Pakdaman, M. A new continuous time optimal control model for manpower planning with promotion from inside the system. Oper. Res. 2018, 1–16. [Google Scholar] [CrossRef]
- Edwards, J.S. A survey of manpower planning models and their application. J. Oper. Res. Soc. 1983, 34, 1031–1040. [Google Scholar] [CrossRef] [PubMed]
- Parker, S.C.; Malstrom, E.J.; Usmani, T. Computer-assisted warehouse personnel scheduling. Intell. Robot. Comput. Vis. Algorithms Tech. Int. Soc. Opt. Photonics 1992, 1607, 636–645. [Google Scholar]
- Sanders, N.R.; Ritzman, L.P. Using warehouse workforce flexibility to offset forecast errors. J. Bus. Logist. 2004, 25, 251–269. [Google Scholar] [CrossRef]
- Dou, J.; Dai, X.; Meng, Z. A GA-based approach for optimizing single-part flow-line configurations of RMS. J. Intell. Manuf. 2011, 22, 301–317. [Google Scholar] [CrossRef]
- Azadivar, F. A simulation optimization approach to optimum storage and retrieval policies in an automated warehousing system. In Proceedings of the 1984 Winter Simulation Conference (WSC), Dallas, TX, USA, 28–30 November 1984; pp. 207–214. [Google Scholar]
- Ding, H.; Benyoucef, L.; Xie, X. A simulation-optimization approach using genetic search for supplier selection. In Proceedings of the 2003 Winter Simulation Conference (WSC), New Orleans, LA, USA, 7–10 December 2003; pp. 1260–1267. [Google Scholar]
- Saif, A.; Elhedhli, S. Cold supply chain design with environmental considerations: A simulation-optimization approach. Eur. J. Oper. Res. 2016, 252, 274–287. [Google Scholar] [CrossRef]
- Ghasemi, P.; Khalili-Damghani, K. A robust simulation-optimization approach for pre-disaster multi-period location–allocation–inventory planning. Math. Comput. Simul. 2020, 179, 69–95. [Google Scholar] [CrossRef]
- De Marco, A.; Mangano, G. Relationship between logistic service and maintenance costs of warehouses. Facilities 2011, 29, 411–421. [Google Scholar] [CrossRef]
- Staudt, F.H.; Alpan, G.; Di Mascolo, M.; Rodriguez, C.M.T. Warehouse performance measurement: A literature review. Int. J. Prod. Res. 2015, 53, 5524–5544. [Google Scholar] [CrossRef]
- Amorim-Lopes, M.; Guimarães, L.; Alves, J.; Almada-Lobo, B. Improving picking performance at a large retailer warehouse by combining probabilistic simulation, optimization, and discrete-event simulation. Int. Trans. Oper. Res. 2020, 28, 687–715. [Google Scholar] [CrossRef]
- Zhang, C.W.; Xie, M.; Liu, J.Y.; Goh, T.N. A control chart for the Gamma distribution as a model of time between events. Int. J. Prod. Res. 2007, 45, 5649–5666. [Google Scholar] [CrossRef]
- Song, D.P. Optimal integrated ordering and production policy in a supply chain with stochastic lead-time, processing-time, and demand. IEEE Trans. Automat. Contr. 2009, 54, 2027–2041. [Google Scholar] [CrossRef]
- Guasch, A.; Piera, M.A.; Figueras, J. Automatic warehouse modelling and simulation. Int. J. Simul. Process. Model. 2011, 6, 288–296. [Google Scholar] [CrossRef]
- Andriansyah, R.; Etman, P.; Rooda, J. Simulation model of a single-server order picking workstation using aggregate process times. In Proceedings of the First International Conference on Advances in System Simulation, Porto, Portugal, 20–25 September 2009; pp. 23–31. [Google Scholar]
- Polat, O.; Kalayci, C.B.; Mutlu, Ö.; Gupta, S.M. A two-phase variable neighbourhood search algorithm for assembly line worker assignment and balancing problem type-II: An industrial case study. Int. J. Prod. Res. 2016, 54, 722–741. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).