Cross-Entropy Method in Application to the SIRC Model
Abstract
1. Introduction
1.1. Sequential Monte Carlo Methods
1.2. Importance Sampling
1.3. Cross-Entropy Method
- Generating random data samples (trajectories, vectors, etc.) according to a specific random mechanism.
- Updating parameters of the random mechanism based on data to obtain a “better” sample in the next iteration.
1.4. Application to Optimization Problems
1.5. Goal and Organization of This Paper
2. Optimization of Control for SIRC Model
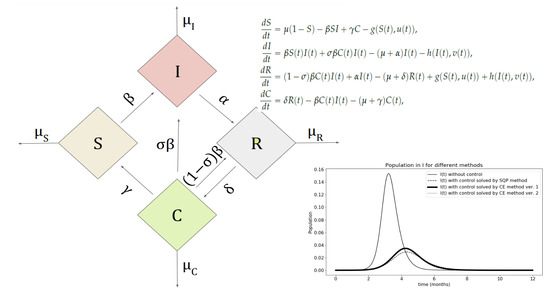
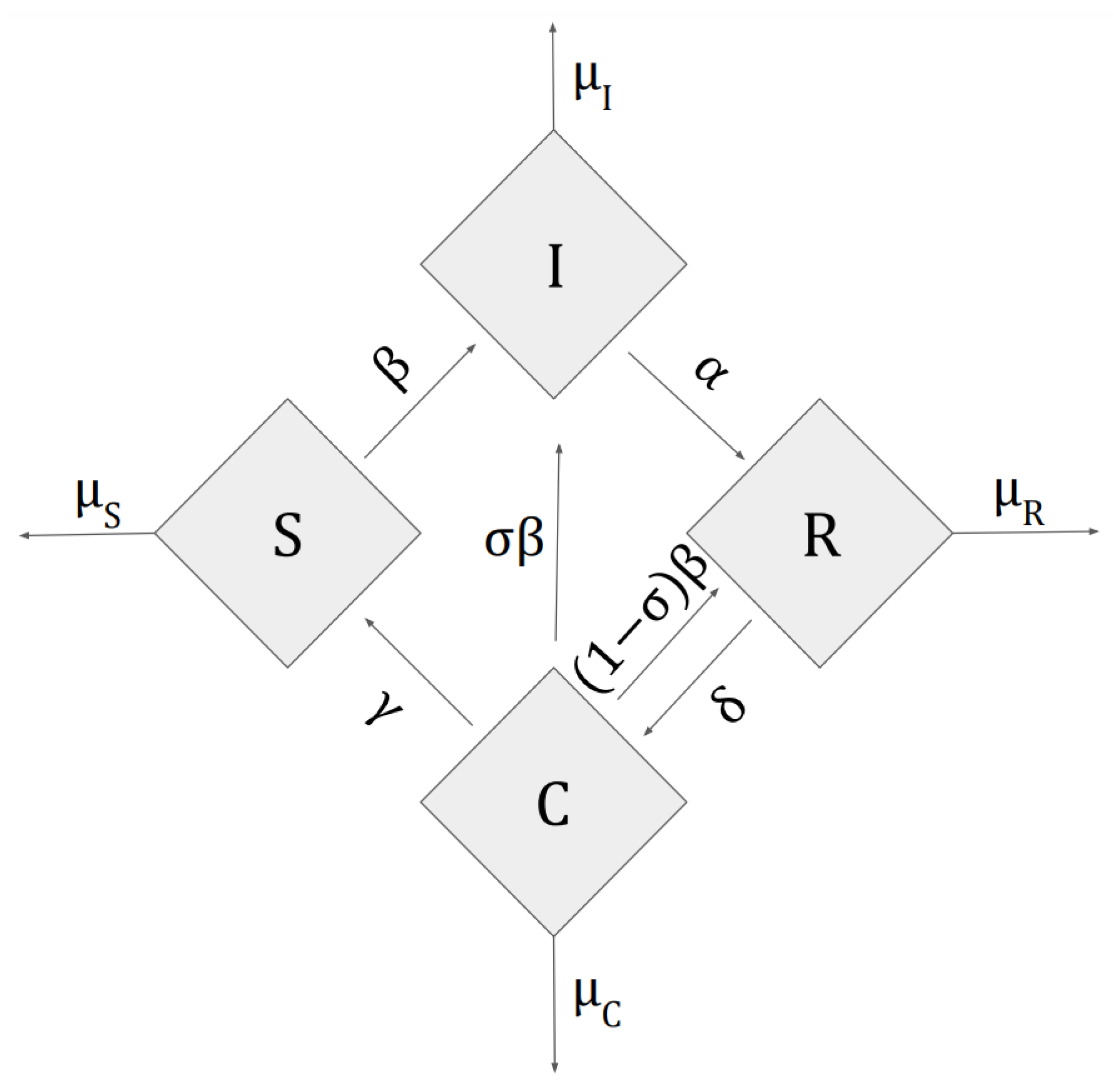
2.1. SIRC Model
- ▪
- S—persons susceptible to infection, who have not previously had contact with this disease and have no immune defense against this strain
- ▪
- I—people infected with the current disease
- ▪
- R—people who have had this disease and are completely immune to this strain
- ▪
- C—people partially resistant to the current strain (e.g., vaccinated or those who have had a different strain)
2.2. Derivation of Optimization Functions
2.3. Optimization of the Epistemological Model by the CE Method
| Algorithm 1: (Modification of the Sani and Kroese’s algorthm (v. [6]) to two optimal functions case): |
|
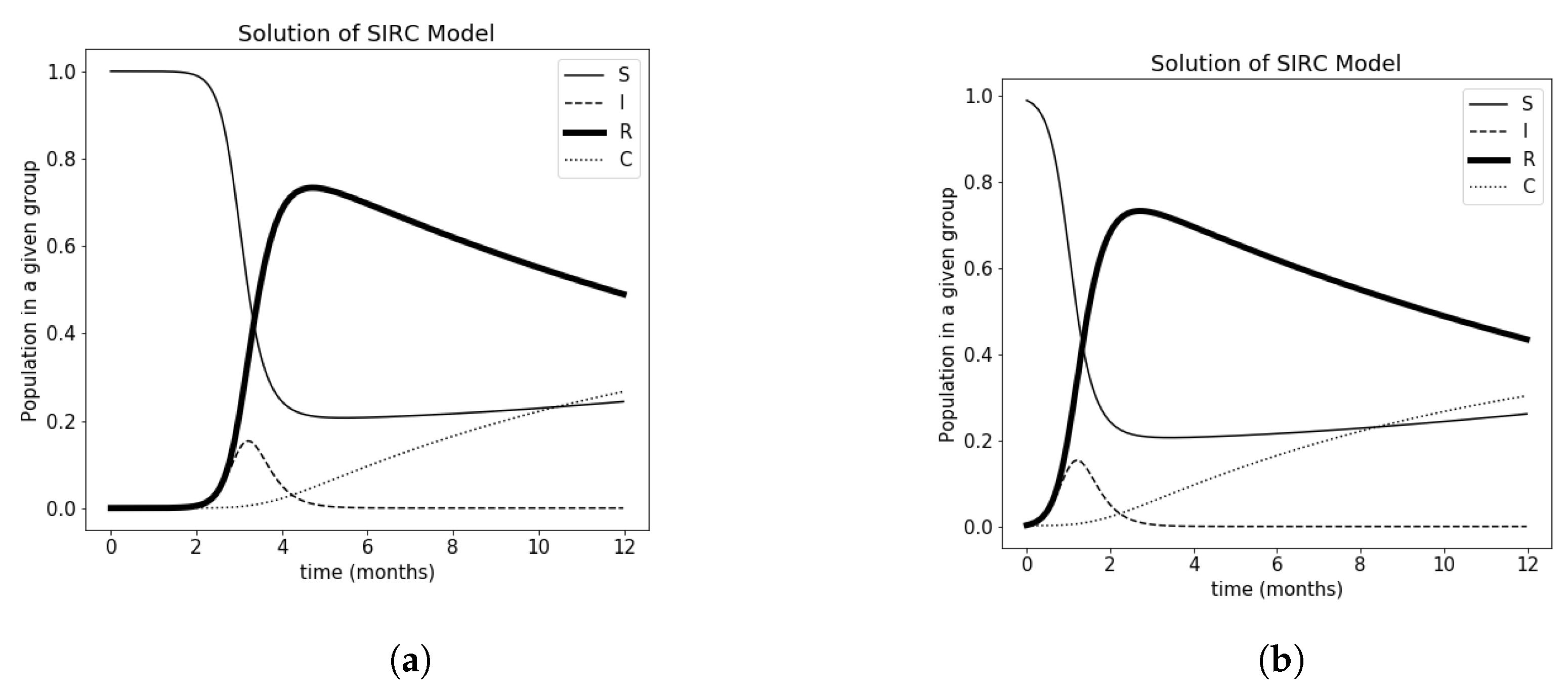
3. Description of the Numerical Results
3.1. A Remark about Adjusting the Parameters of the Control Determination Procedure
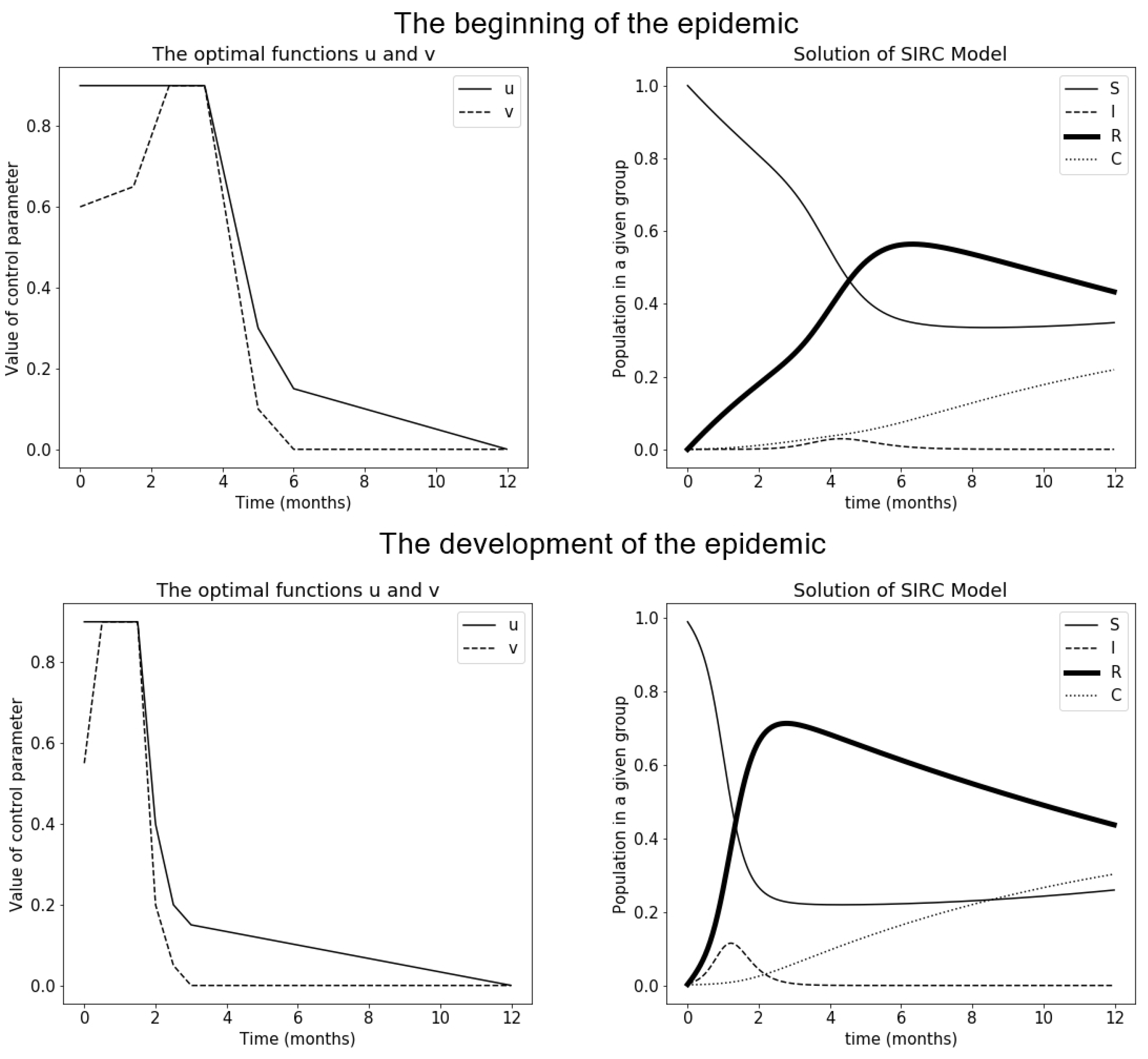
3.2. Proposed Optimization Methods in the Model Analysis
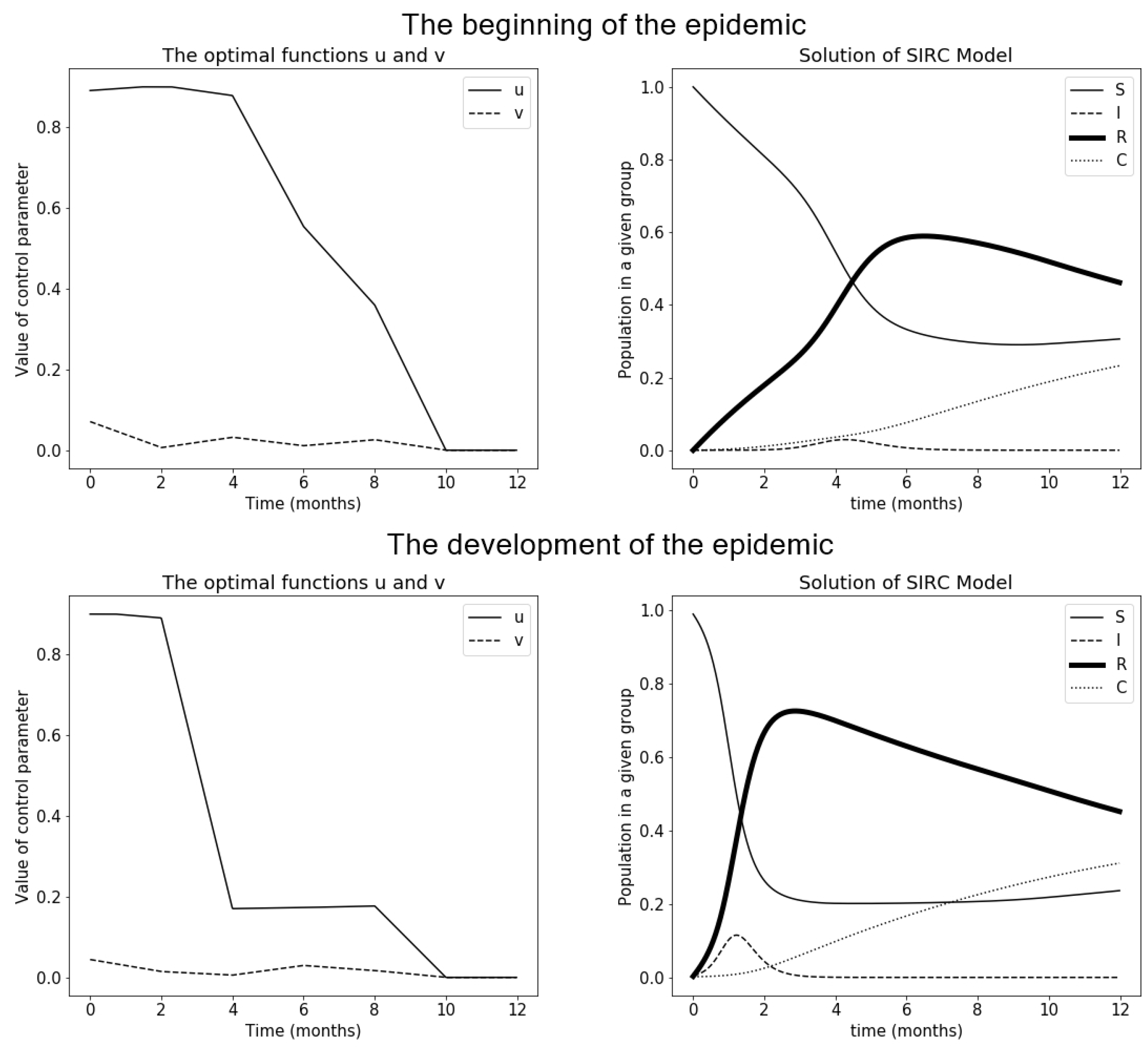
3.3. CE Method Version 1
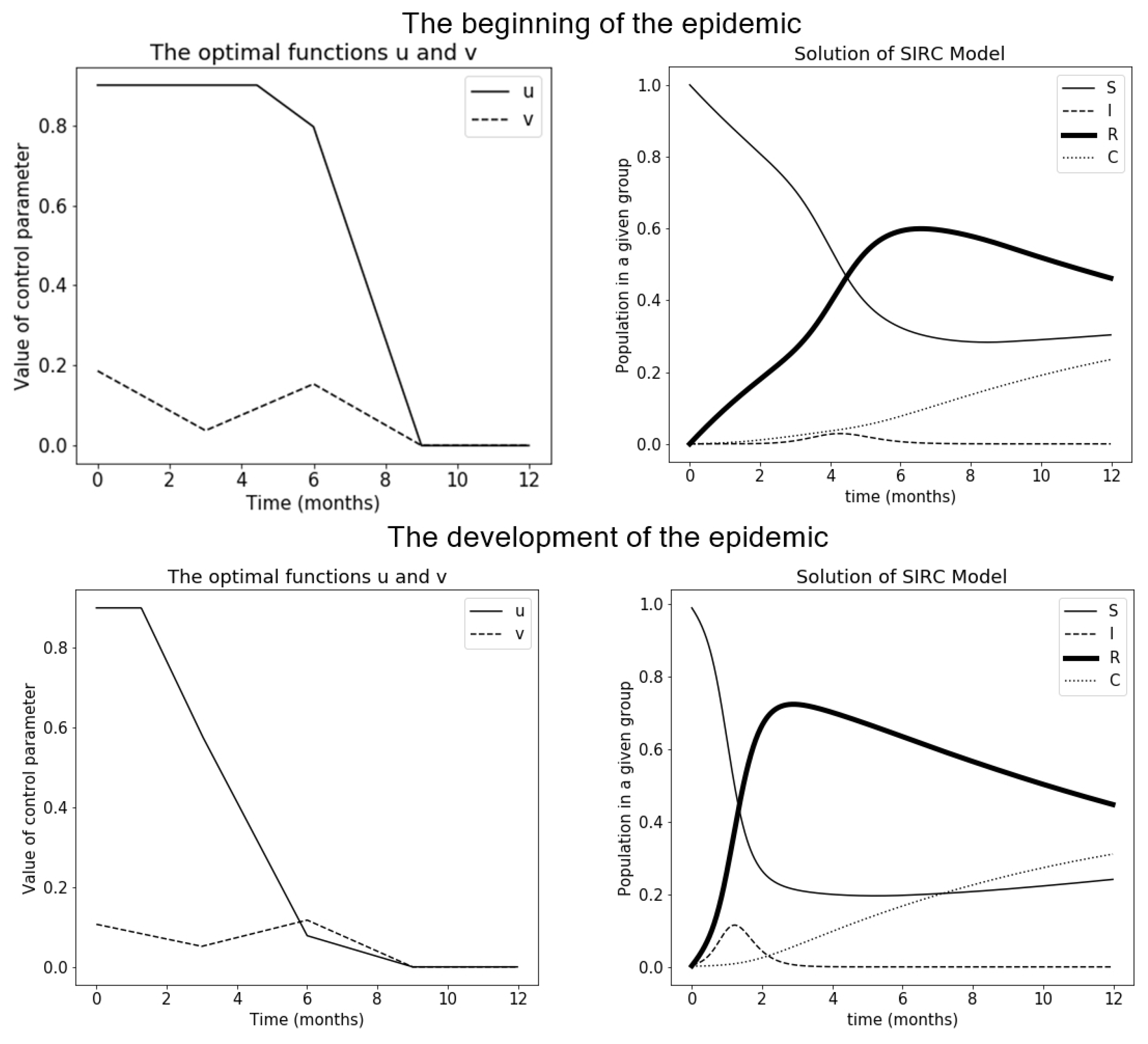
3.4. CE Method Version 2
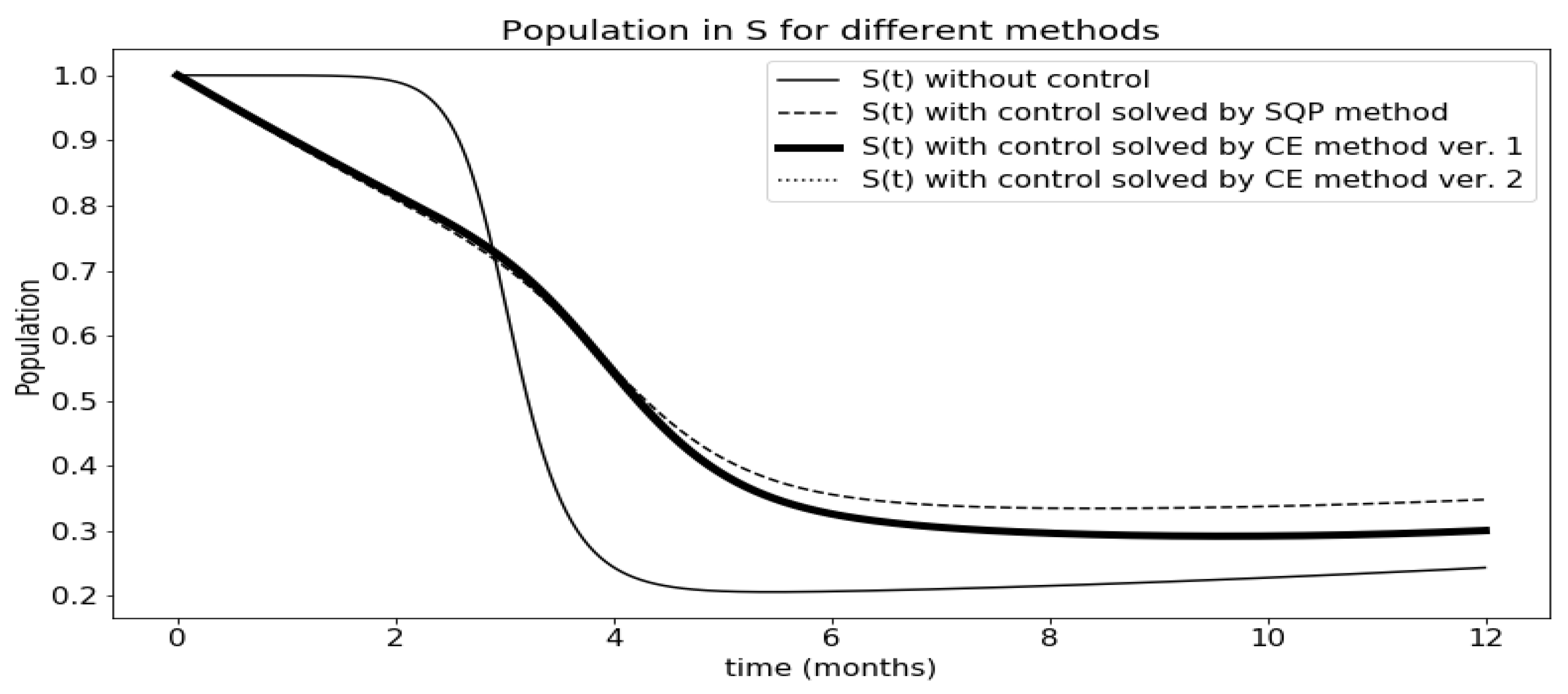
3.5. Comparison of Results
4. Summary
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CE | Cross-entropy method (v. page 2) |
| FEM | the finite element methods (v. page 6) |
| GOF | a goodness-of-fit (v. page 8) |
| IS | the importance sampling (v. page 2) |
| SIR | The SIR model is one of the simplest compartmental models. The letters means the number of Susceptible–Infected–Removed (and immune) or deceased individuals. (v. [43,44,45,46]). |
| SIRC | The SIR model with the additional group of partially resistant to the current strain people: Susceptible–Infectious–Recovered–Cross-immune (v. page 4). |
Appendix A. Optimization by the Method of Cross-Entropy
Appendix A.1. Multiple Selection to Minimize the Sum of Ranks
Appendix A.2. Minimization of Mean Sum of Ranks
- (1)
- Updating Generate a sample from . Calculate and sort in ascending order. For choose
- (2)
- Updating obtain from the Kullback–Leibler distance, that is, from maximizationsoAs in [49], here a three-dimensional matrix of parameters is consider.It seems thatand then after some transformationswhere , is a random variable from , corresponding to the Formula (A4). Instead of updating a parameter use the following smoothed version
- (3)
- Stopping Criterion The criterion is from [16], which stop the algorithm when (T is last step) has reached stationarity. To identify the stopping point of T, consider the following moving average processwhere K is fixed.Then let us defineandwhere R is fixed.Then the stopping criterion is defined as followswhere K and R are fixed and is not too small.
Appendix A.3. The Vehicle Routing Problem
References
- Martino, L.; Luengo, D.; Míguez, J. Introduction. In Independent Random Sampling Methods; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–26. [Google Scholar] [CrossRef]
- Metropolis, N. The beginning of the Monte Carlo method. Los Alamos Sci. 1987, 15, 125–130. [Google Scholar]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Marshall, A. The use of multistage sampling schemes in Monte Carlo computations. In Symposium on Monte Carlo; Wiley: New York, NY, USA, 1956; pp. 123–140. [Google Scholar]
- Rubinstein, R.Y. Optimization of computer simulation models with rare events. Eur. J. Oper. Res. 1997, 99, 89–112. [Google Scholar] [CrossRef]
- Sani, A.; Kroese, D. Optimal Epidemic Intervention of HIV Spread Using Cross-Entropy Method. In Proceedings of the International Congress on Modelling and Simulation (MODSIM); Oxley, L., Kulasiri, D., Eds.; Modelling and Simulation Society of Australia and New Zeeland: Christchurch, New Zeeland, 2007; pp. 448–454. [Google Scholar]
- Asamoah, J.; Nyabadza, F.; Seidu, B.; Chand, M.; Dutta, H. Mathematical Modelling of Bacterial Meningitis Transmission Dynamics with Control Measures. Comput. Math. Methods Med. 2018, A2657461, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Vereen, K. An SCIR Model of Meningococcal Meningitis. Master’s Thesis, Virginia Commonwealth University, Richmond, VI, USA, 2008. [Google Scholar]
- Casagrandi, R.; Bolzoni, L.; Levin, S.A.; Andreasen, V. The SIRC model and influenza A. Math. Biosci. 2006, 200, 152–169. [Google Scholar] [CrossRef] [PubMed]
- Parry, W. Entropy and Generators in Ergodic Theory; Mathematics Lecture Note Series; W. A. Benjamin, Inc.: Amsterdam, NY, USA, 1969; Volume xii, 124p. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience [John Wiley & Sons]: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Inglot, T. Teoria informacji a statystyka matematyczna. Math. Appl. 2014, 42, 115–174. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Amari, S.I. Differential-geometrical methods in statistics. In Lecture Notes in Statistics; Springer: New York, NY, USA, 1985; Volume 28. [Google Scholar] [CrossRef]
- Rubinstein, R. The cross-entropy method for combinatorial and continuous optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Ferguson, T.S. Who solved the secretary problem? Stat. Sci. 1989, 4, 282–296. [Google Scholar] [CrossRef]
- Szajowski, K. Optimal choice problem of a-th object. Matem. Stos. 1982, 19, 51–65. (In Polish) [Google Scholar] [CrossRef]
- Polushina, T.V. Estimating Optimal Stopping Rules in the Multiple Best Choice Problem with Minimal Summarized Rank via the Cross-Entropy Method. In Exploitation of Linkage Learning in Evolutionary Algorithms; Chen, Y.-P., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 227–241. [Google Scholar] [CrossRef]
- Stachowiak, M. The Cross-Entropy Method and Its Applications. Master’s Thesis, Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, Wroclaw, Poland, 2019; 33p. [Google Scholar]
- Dror, M. Vehicle Routing with Stochastic Demands: Models & Computational Methods. In Modeling Uncertainty; International Series in Operations Research & Management Science; Dror, M., L’ Ecuyer, P., Szidarovszky, F., Eds.; Springer: New York, NY, USA, 2002; Volume 46, pp. 625–649. [Google Scholar] [CrossRef]
- Chepuri, K.; Homem-de Mello, T. Solving the vehicle routing problem with stochastic demands using the cross-entropy method. Ann. Oper. Res. 2005, 134, 153–181. [Google Scholar] [CrossRef]
- Ekeland, I.; Temam, R. Convex Analysis and Variational Problems; Volume 28 of Classics in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Glowinski, R. Lectures on Numerical Methods for Non-Linear Variational Problems; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mumford, D.; Shah, J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef]
- Klimov, A.; Simonsen, L.; Fukuda, K.; Cox, N. Surveillance and impact of influenza in the United States. Vaccine 1999, 17, S42–S46. [Google Scholar] [CrossRef]
- Simonsen, L.; Clarke, M.J.; Williamson, G.D.; Stroup, D.F.; Arden, N.H.; Schonberger, L.B. The impact of influenza epidemics on mortality: Introducing a severity index. Am. J. Public Health 1997, 87, 1944–1950. [Google Scholar] [CrossRef]
- Earn, D.J.; Dushoff, J.; Levin, S.A. Ecology and evolution of the flu. Trends Ecol. Evol. 2002, 17, 334–340. [Google Scholar] [CrossRef]
- Andreasen, V.; Lin, J.; Levin, S.A. The dynamics of cocirculating influenza strains conferring partial cross-immunity. J. Math. Biol. 1997, 35, 825–842. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Andreasen, V.; Levin, S.A. Dynamics of influenza A drift: The linear three-strain model. Math. Biosci. 1999, 162, 33–51. [Google Scholar] [CrossRef]
- Iacoviello, D.; Stasio, N. Optimal control for SIRC epidemic outbreak. Comput. Methods Programs Biomed. 2013, 110, 333–342. [Google Scholar] [CrossRef]
- Zaman, G.; Kang, Y.H.; Jung, I.H. Stability analysis and optimal vaccination of an SIR epidemic model. BioSystems 2008, 93, 240–249. [Google Scholar] [CrossRef]
- Kamien, M.I.; Schwartz, N.L. Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management, 2nd ed.; Advanced Textbooks in Economics; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1991; Volume 31. [Google Scholar]
- Fang, Q.; Tsuchiya, T.; Yamamoto, T. Finite difference, finite element and finite volume methods applied to two-point boundary value problems. J. Comput. Appl. Math. 2002, 139, 9–19. [Google Scholar] [CrossRef]
- Caglar, H.; Caglar, N.; Elfaituri, K. B-spline interpolation compared with finite difference, finite element and finite volume methods which applied to two-point boundary value problems. Appl. Math. Comput. 2006, 175, 72–79. [Google Scholar] [CrossRef]
- Papadopoulos, V.; Giovanis, D.G. An introduction. In Stochastic Finite Element Methods; Mathematical Engineering; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar] [CrossRef]
- Hazelbag, C.M.; Dushoff, J.; Dominic, E.M.; Mthombothi, Z.E.; Delva, W. Calibration of individual-based models to epidemiological data: A systematic review. PLoS Comput. Biol. 2020, 16, e1007893. [Google Scholar] [CrossRef]
- Taylor, D.C.; Pawar, V.; Kruzikas, D.; Gilmore, K.E.; Pandya, A.; Iskandar, R.; Weinstein, M.C. Methods of model calibration. Pharmacoeconomics 2010, 28, 995–1000. [Google Scholar] [CrossRef]
- Taynitskiy, V.; Gubar, E.; Zhu, Q. Optimal Impulsive Control of Epidemic Spreading of Heterogeneous Malware. IFAC-PapersOnLine 2017, 50, 15038–15043. [Google Scholar] [CrossRef]
- Gubar, E.; Taynitskiy, V.; Zhu, Q. Optimal Control of Heterogeneous Mutating Viruses. Games 2018, 9, 103. [Google Scholar] [CrossRef]
- Kochańczyk, M.; Grabowski, F.; Lipniacki, T. Dynamics of COVID-19 pandemic at constant and time-dependent contact rates. Math. Model. Nat. Phenom. 2020, 15, 28. [Google Scholar] [CrossRef]
- Kermack, W.; McKendrick, A. Contributions to the mathematical theory of epidemics–I. 1927. Bull. Math. Biol. 1991, 53, 35–55, Reprint of the Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Kermack, W.; McKendrick, A. Contributions to the mathematical theory of epidemics–II. The problem of endemicity. 1932. Bull Math Biol. 1991, 53, 57–87, Reprint of the Proc. R. Soc. Lond. Ser. A 1932, 138, 55–83. [Google Scholar] [CrossRef]
- Kermack, W.; McKendrick, A. Contributions to the mathematical theory of epidemics–III. Further studies of the problem of endemicity. 1933. Bull Math Biol. 1991, 53, 89–118, Reprint of the Proc. R. Soc. Lond. Ser. A 1933, 141, 94–122. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K. Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates. Appl. Math. Comput. 2014, 236, 184–194. [Google Scholar] [CrossRef]
- Nikolaev, M.L. On optimal multiple stopping of Markov sequences. Theory Probab. Appl. 1998, 43, 298–306, Translation from Teor. Veroyatn. Primen. 1998, 43, 374–382. [Google Scholar] [CrossRef]
- Nikolaev, M.L. Optimal multi-stopping rules. Obozr. Prikl. Prom. Mat. 1998, 5, 309–348. [Google Scholar]
- Safronov, G.Y.; Kroese, D.P.; Keith, J.M.; Nikolaev, M.L. Simulations of thresholds in multiple best choice problem. Obozr. Prikl. Prom. Mat. 2006, 13, 975–982. [Google Scholar]
- Secomandi, N. Comparing neuro-dynamic programming algorithms for the vehicle routing problem with stochastic demands. Comput. Oper. Res. 2000, 27, 1201–1225. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. Cross-entropy and rare events for maximal cut and partition problems. ACM Trans. Model. Comput. Simul. 2002, 12, 27–53. [Google Scholar] [CrossRef]
- De Boer, P.T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
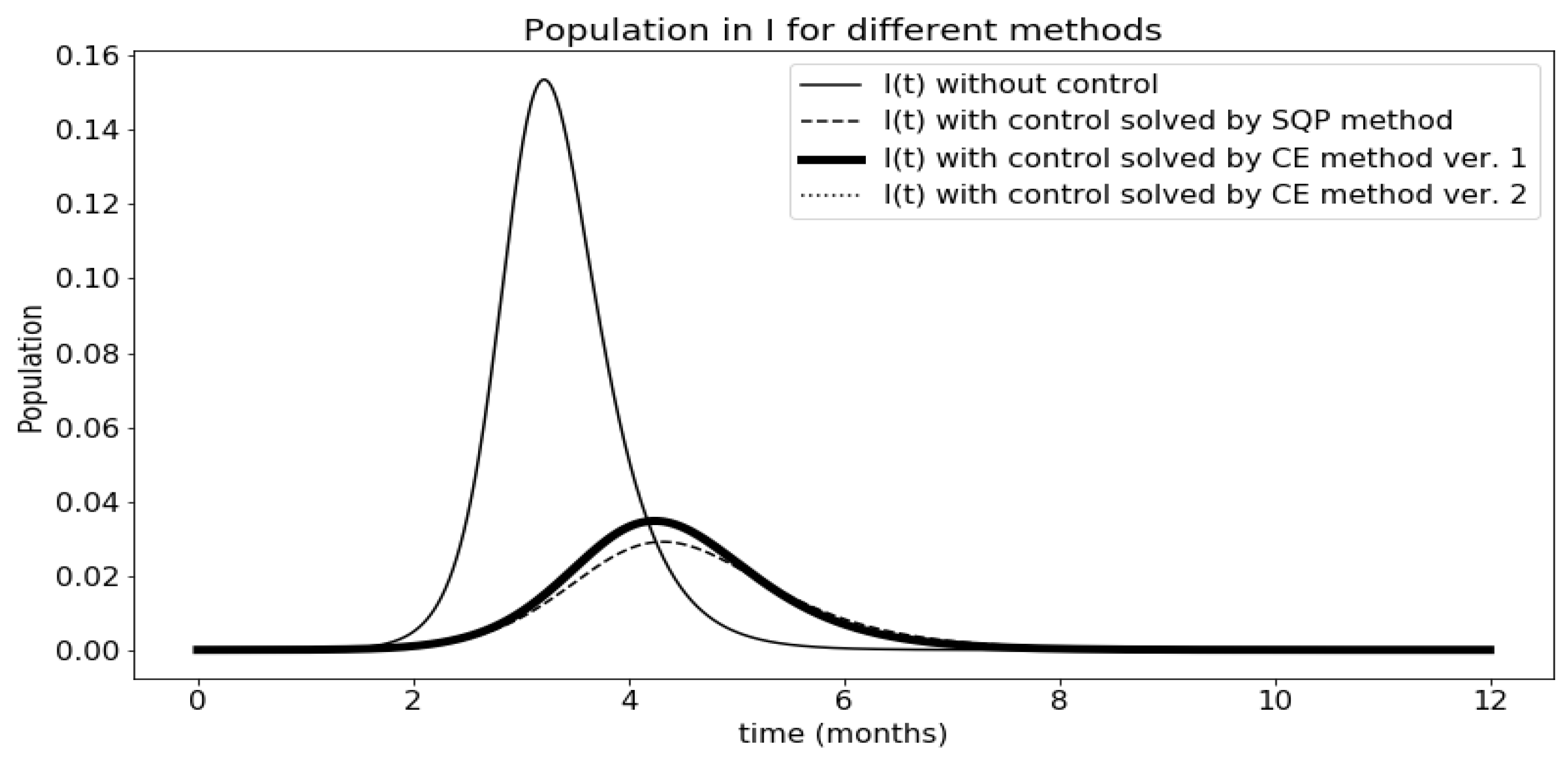
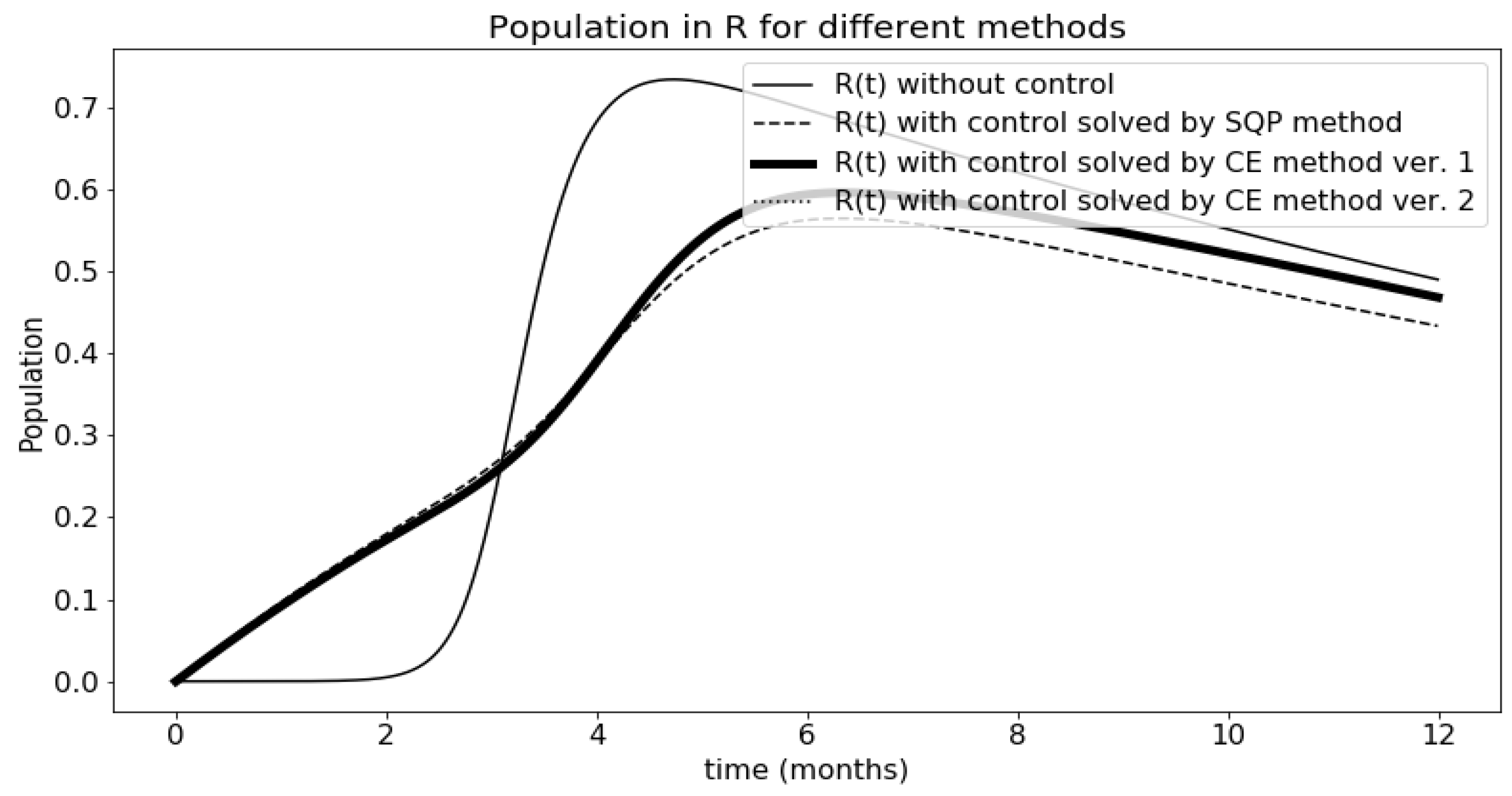
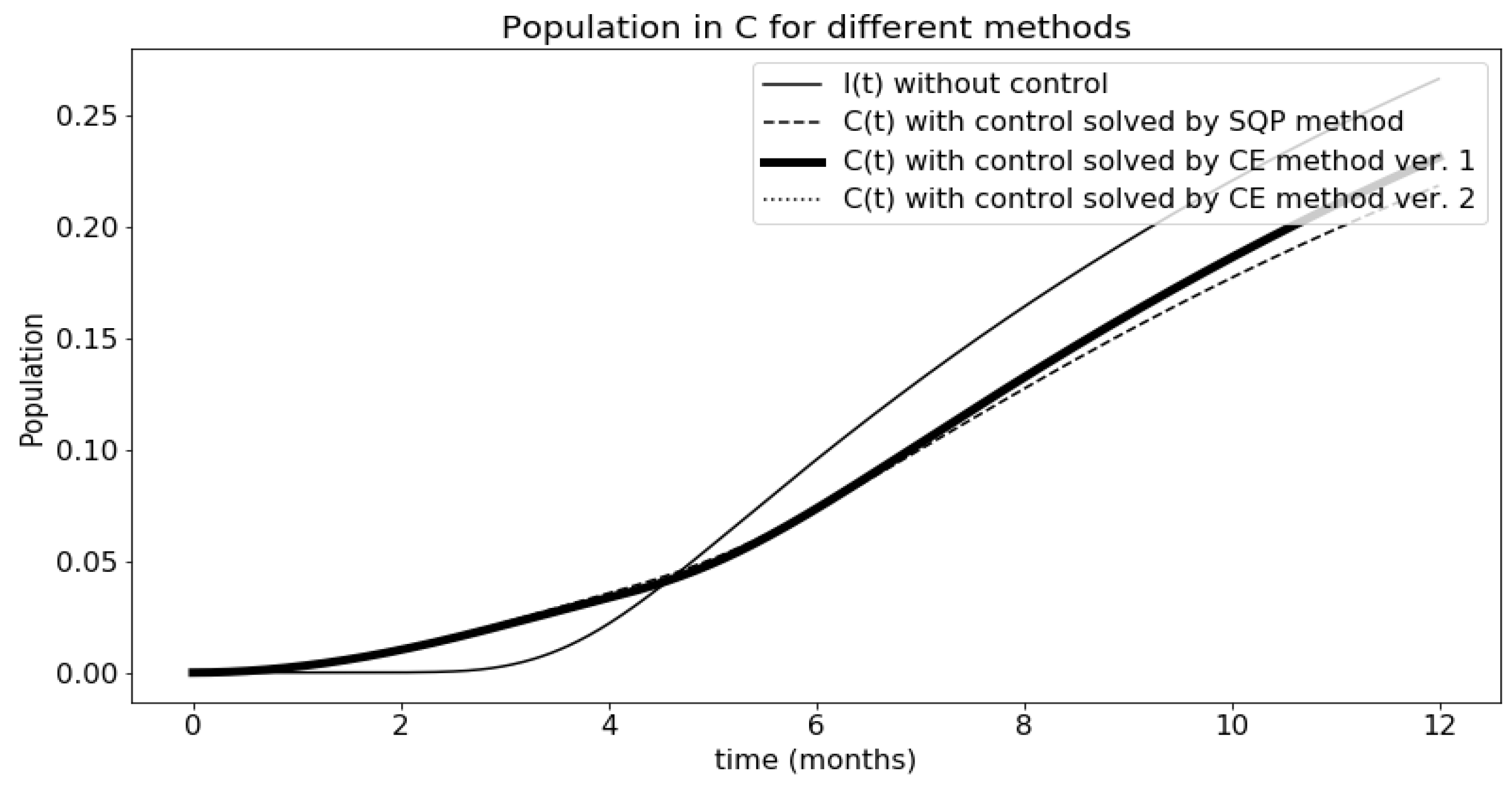
| Method | Cost Index | Time |
|---|---|---|
| Results without control functions | 0.00799 | - |
| 0.00789 | ||
| Sequential quadratic programming method | 0.003308 | - |
| 0.006489 | ||
| Cross-entropy method version 1 | 0.003086 | 30 s |
| 0.006443 | ||
| Cross-entropy method version 2 | 0.003044 | 4 min 54 s |
| 0.006451 |
Sample Availability: The implementation codes for the algorithms used in the examples are available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stachowiak, M.K.; Szajowski, K.J. Cross-Entropy Method in Application to the SIRC Model. Algorithms 2020, 13, 281. https://doi.org/10.3390/a13110281
Stachowiak MK, Szajowski KJ. Cross-Entropy Method in Application to the SIRC Model. Algorithms. 2020; 13(11):281. https://doi.org/10.3390/a13110281
Chicago/Turabian StyleStachowiak, Maria Katarzyna, and Krzysztof Józef Szajowski. 2020. "Cross-Entropy Method in Application to the SIRC Model" Algorithms 13, no. 11: 281. https://doi.org/10.3390/a13110281
APA StyleStachowiak, M. K., & Szajowski, K. J. (2020). Cross-Entropy Method in Application to the SIRC Model. Algorithms, 13(11), 281. https://doi.org/10.3390/a13110281