Generative Model for Skeletal Human Movements Based on Conditional DC-GAN Applied to Pseudo-Images
Abstract
1. Introduction
- spatial information: strong correlations between adjacent joints, which makes it possible to learn about body structural information within a single frame (intra-frame);
- temporal information: makes it possible to learn about temporal correlation between frames (inter-frame); and
- cooccurrence relationship between spatial and temporal domains when taking joints and bones into account.
2. Related Works
2.1. Generative Models for Skeletal Human Movements
2.2. Pseudo-Image Representation for Skeletal Pose Sequences
3. Materials and Methods
3.1. NTU_RGB+D Dataset
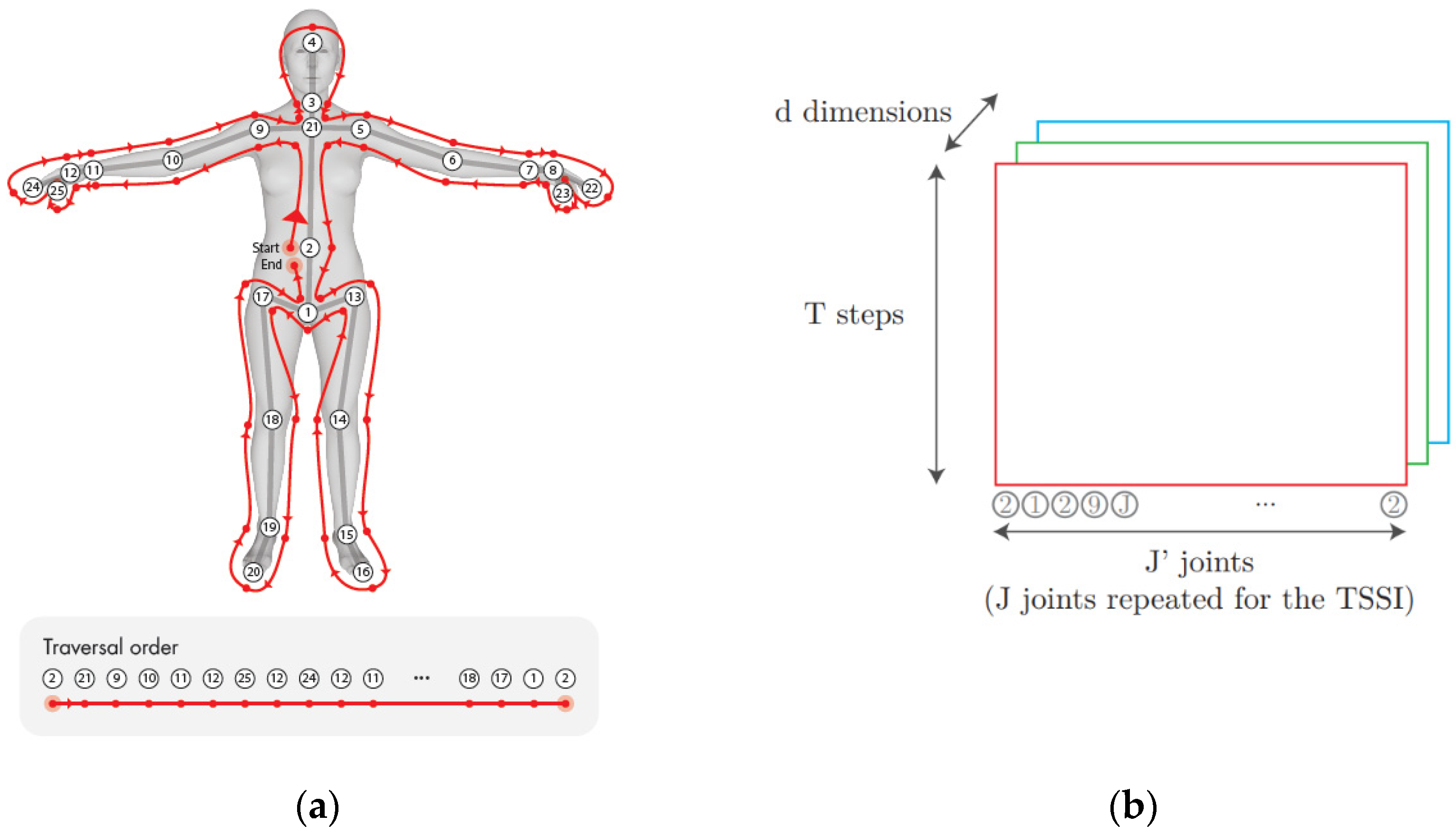
3.2. Tree Structure Skeleton Image (TSSI)
3.3. Data Preparation
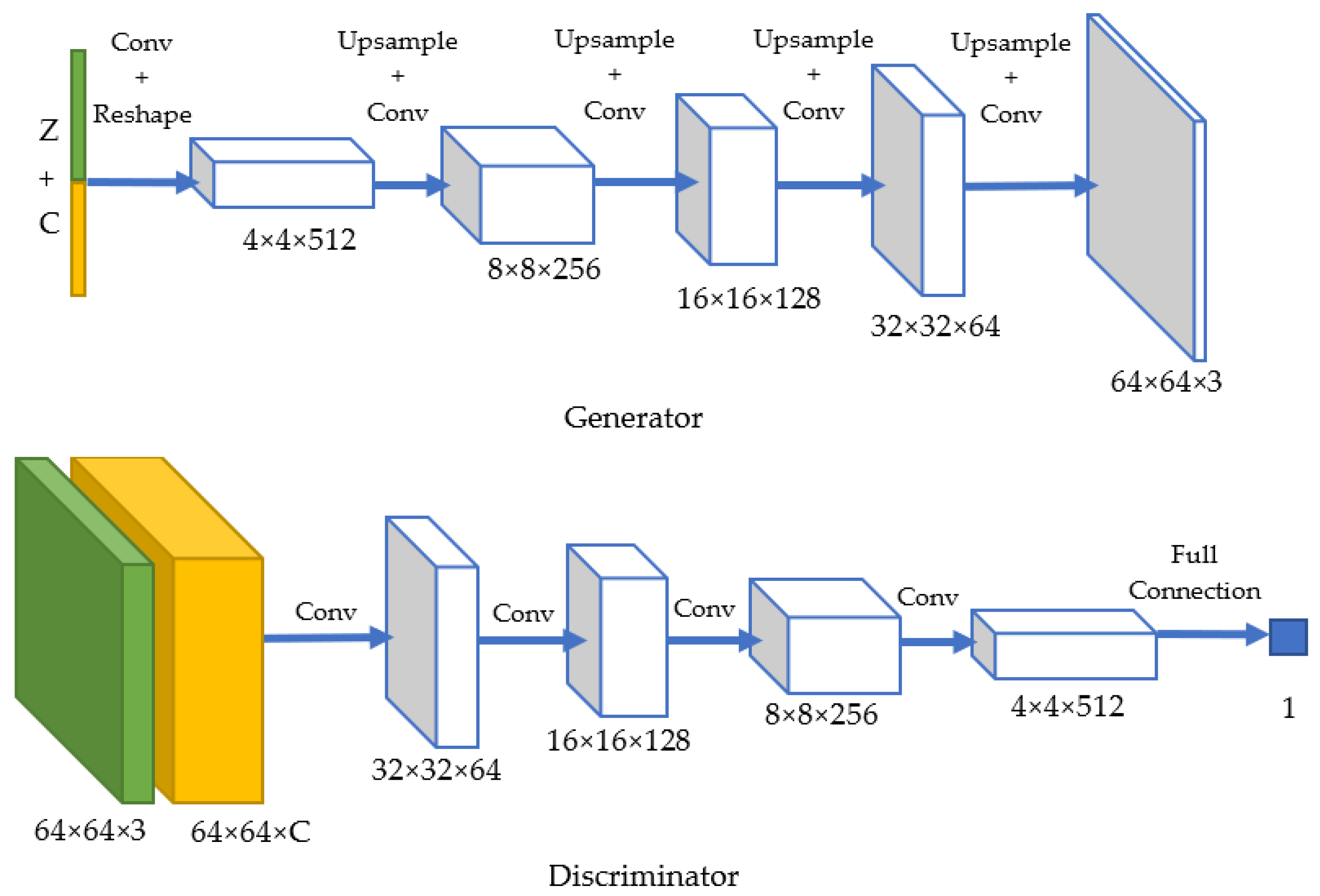
3.4. Conditional Deep Convolution Generative Adversarial Network (Conditional DC-GAN)
3.5. Loss Function and Training Process
3.6. Transformation of Generated Pseudo-Images into Skeletal Sequences
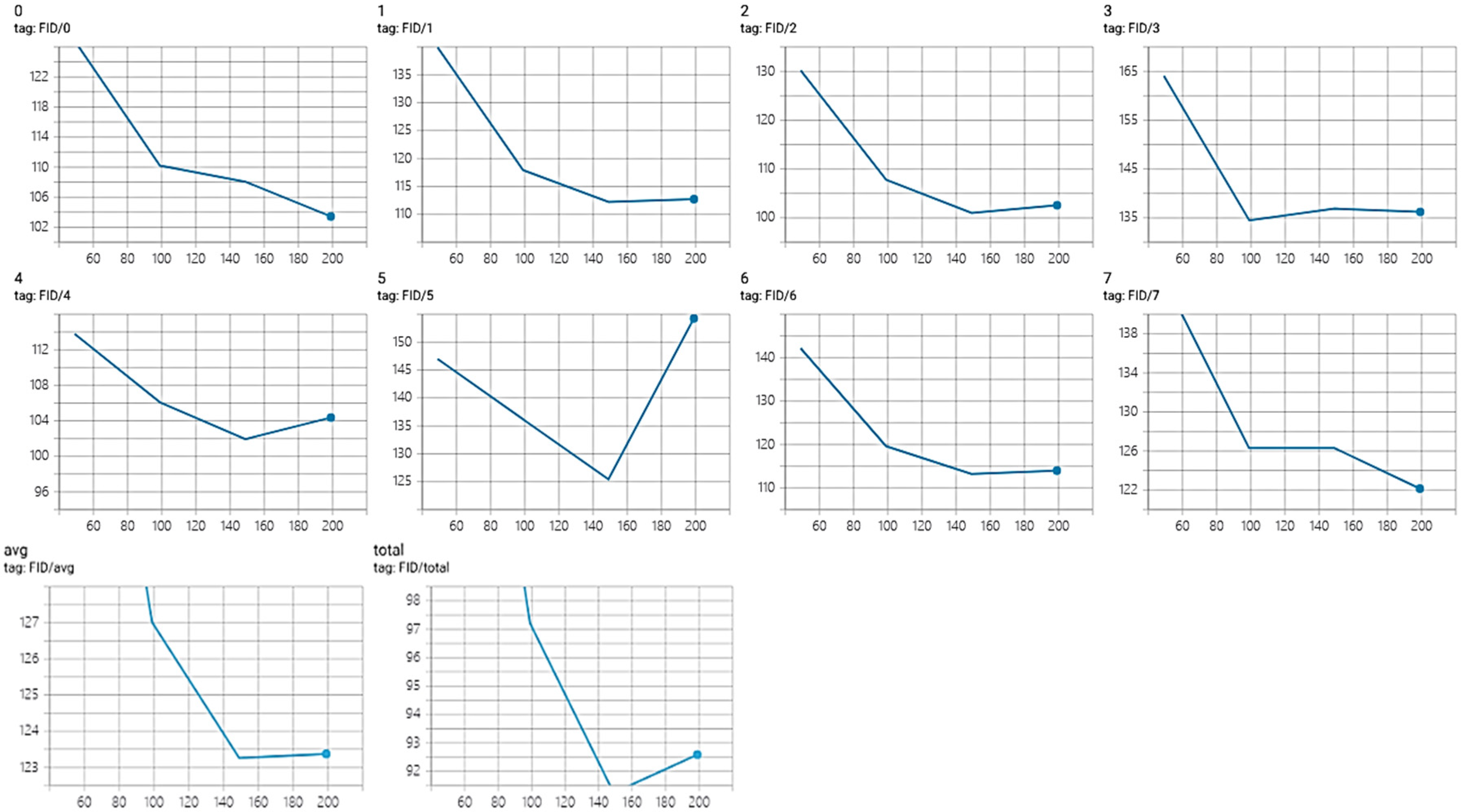
3.7. Model Evaluation—Fréchet Inception Distance (FID)
4. Results
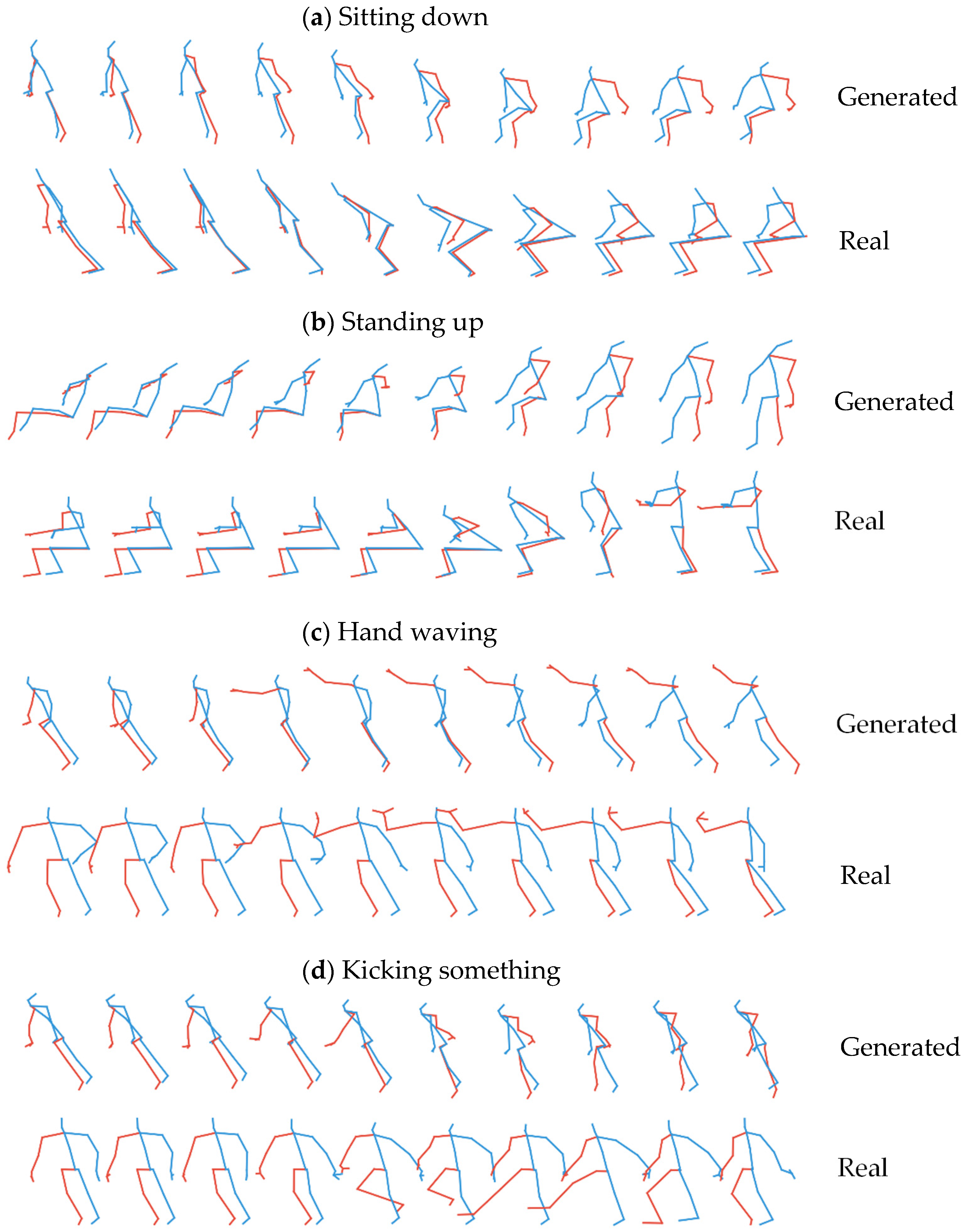
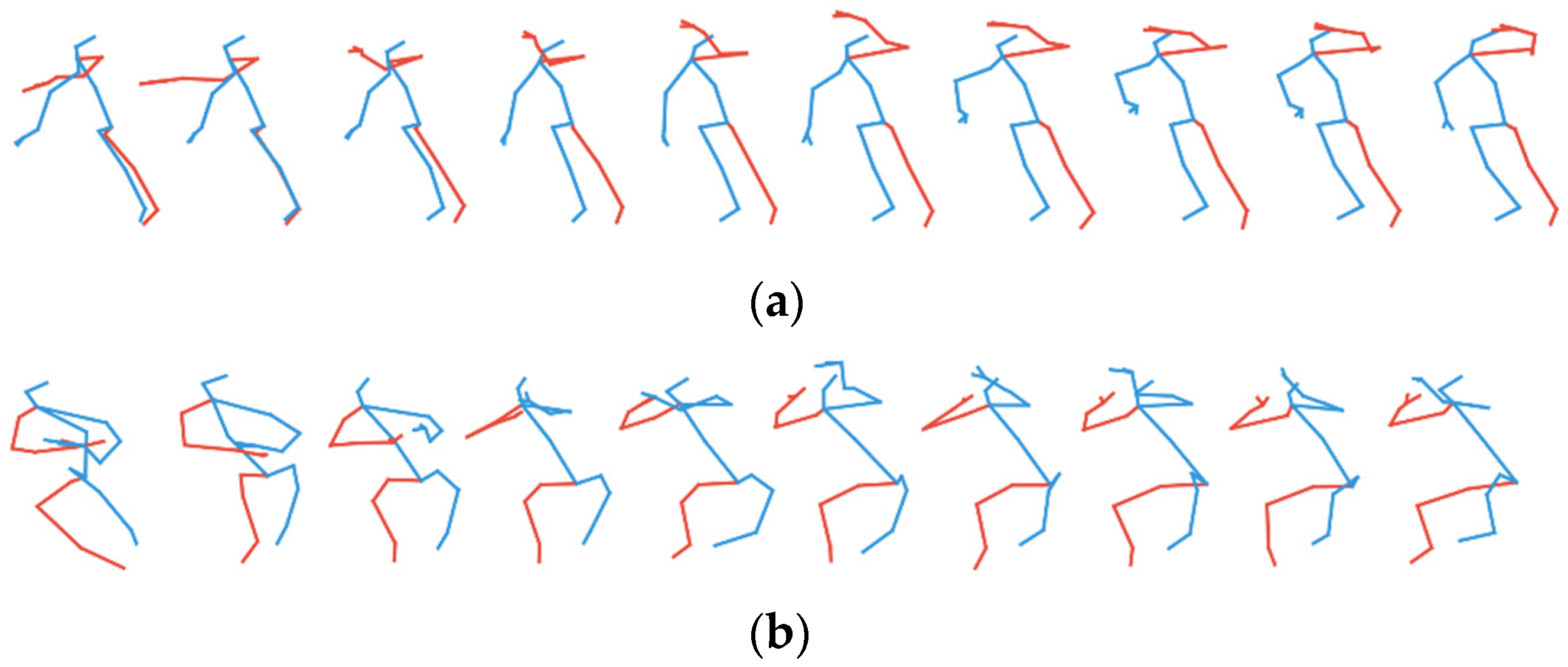
4.1. Qualitative Result for Generated Skeletal Actions
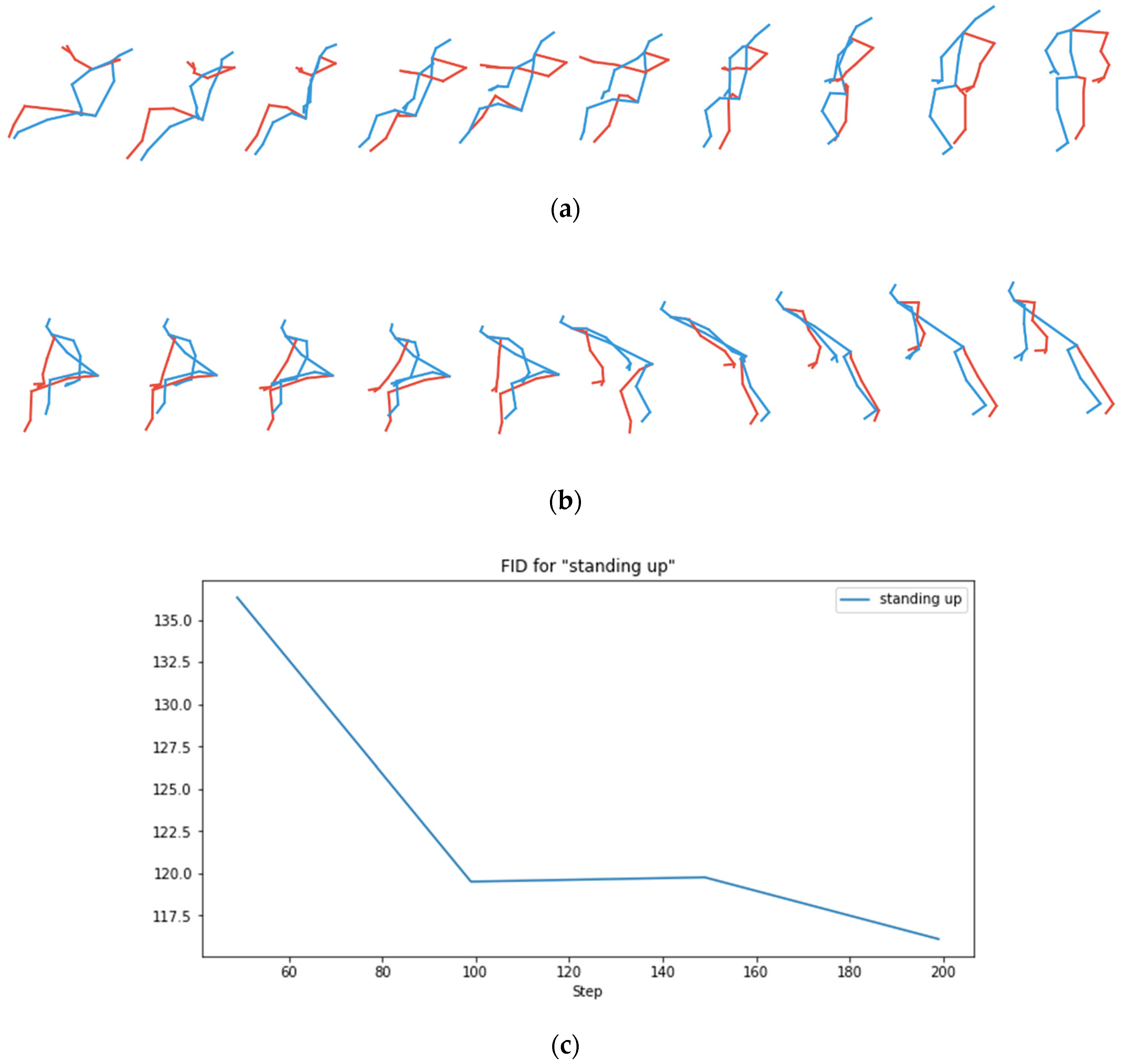
4.2. Quantitative Model Evaluation Using Fréchet Inception Distance (FID)
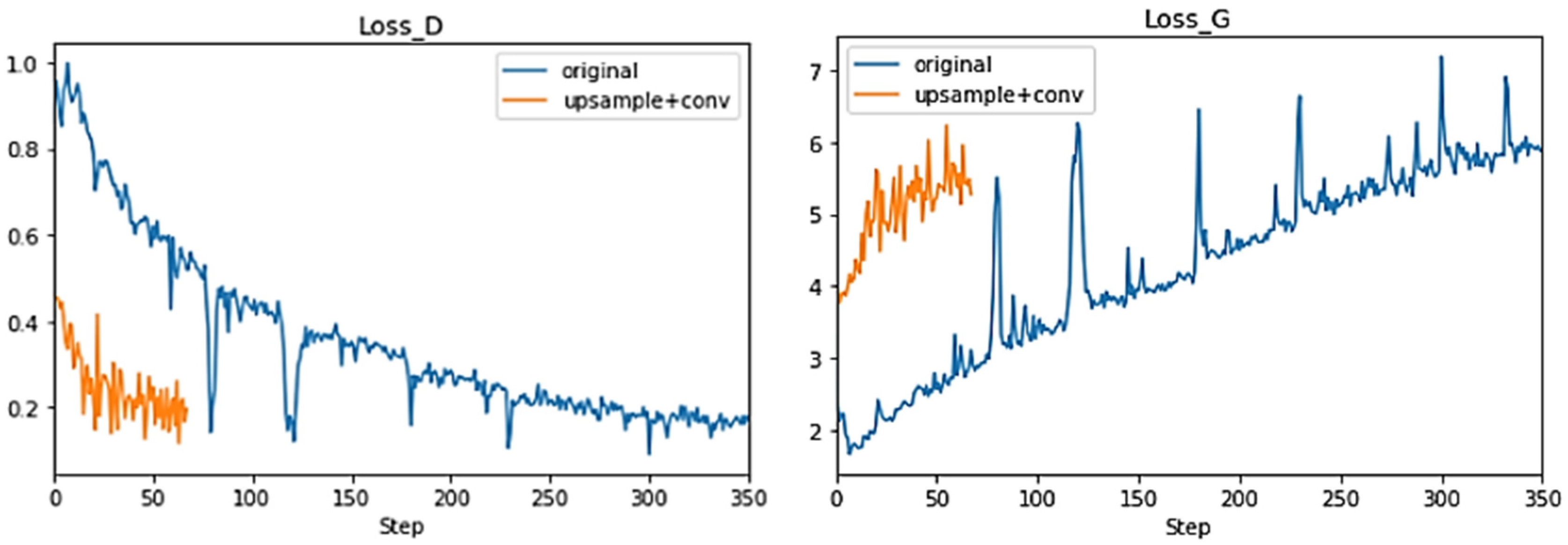
4.3. Importance of the Modification of Generator Using Upsample + Convolutional Layers
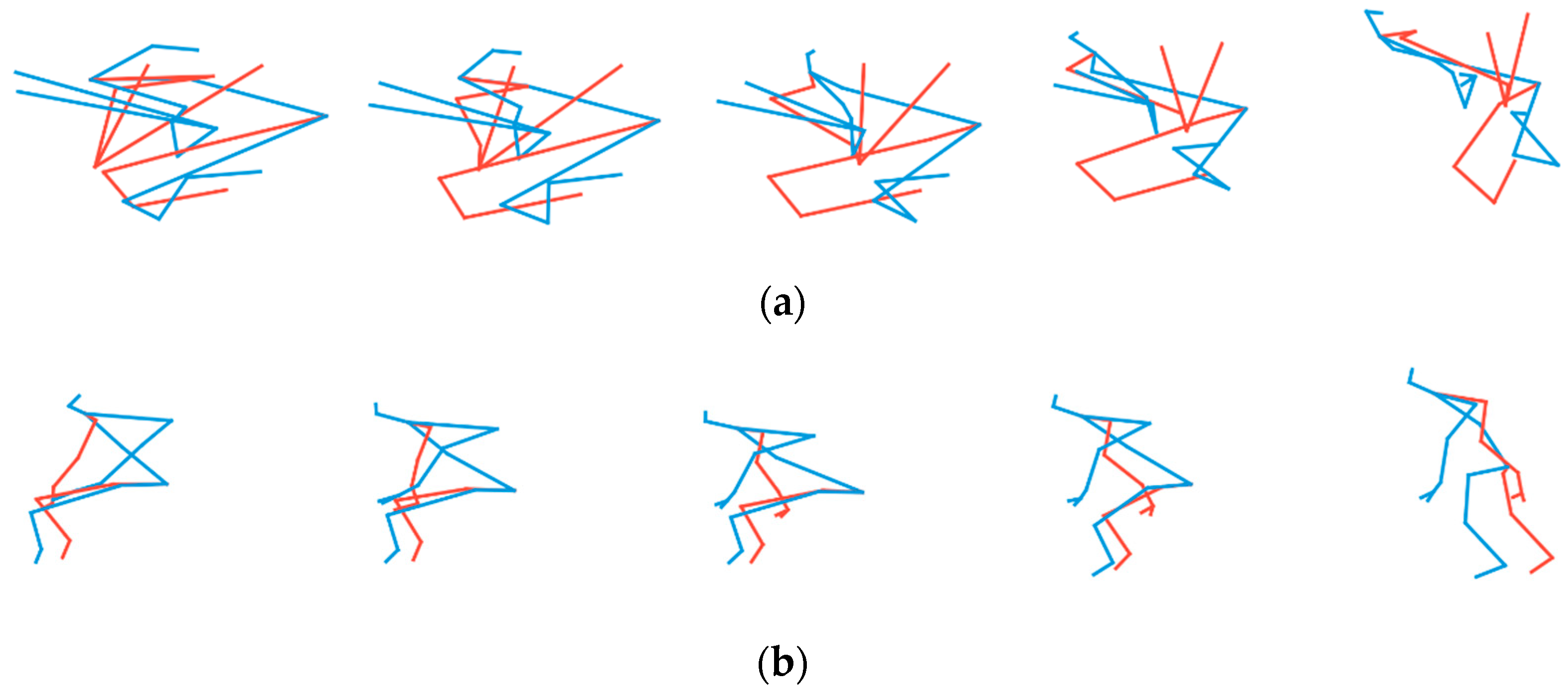
4.4. Importance of Reordering Joints in TSSI Spatiotemporal Images
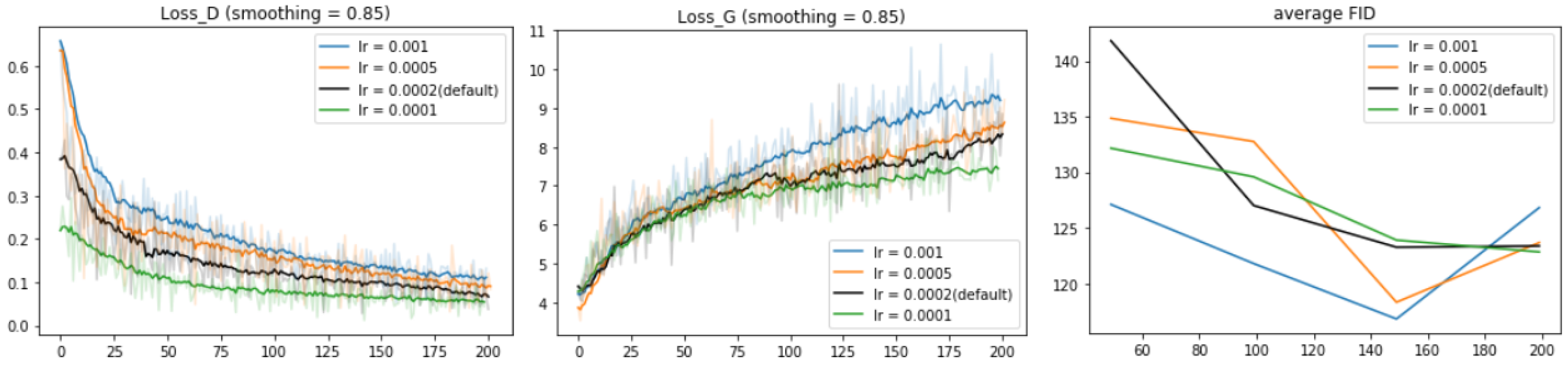
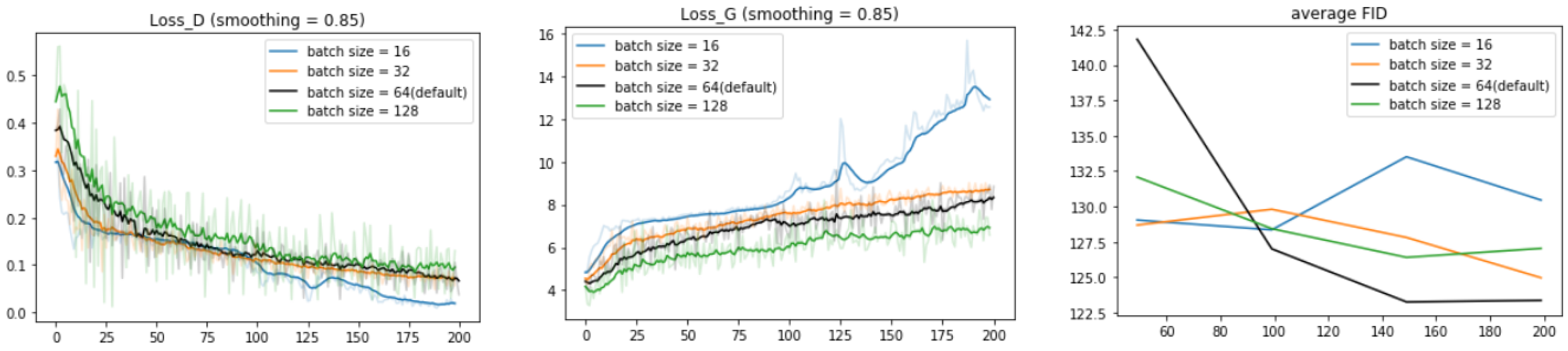
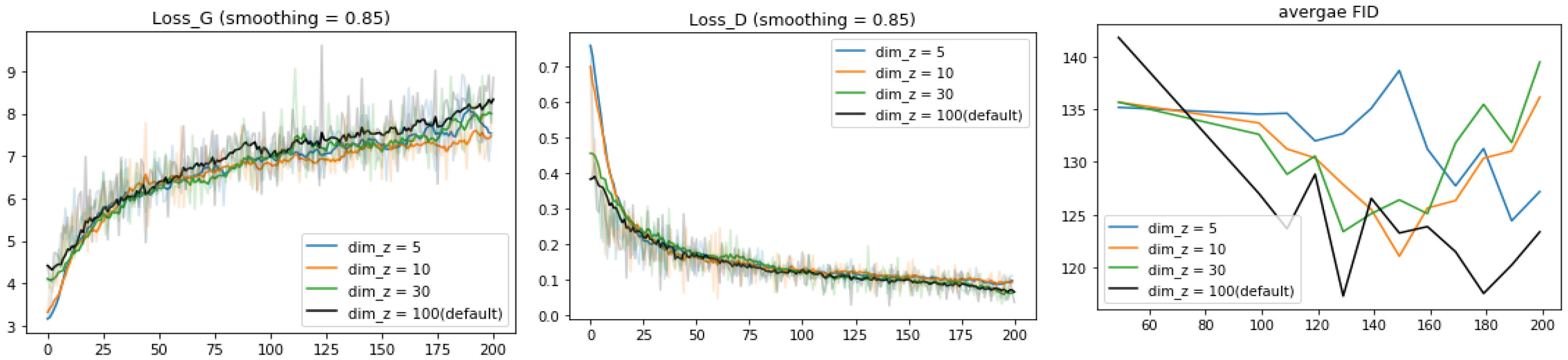
4.5. Hyperparameter Tuning
4.6. Analysis of Latent Space
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Martinez, J.; Black, M.J.; Romero, J.; IEEE. On human motion prediction using recurrent neural networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4674–4683. [Google Scholar]
- Ren, B.; Liu, M.; Ding, R.; Liu, H. A survey on 3D skeleton-based action recognition using learning method. arXiv 2020, arXiv:2002.05907. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2016, arXiv:1511.06434. [Google Scholar]
- Fragkiadaki, K.; Levine, S.; Felsen, P.; Malik, J. Recurrent network models for human dynamics. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; pp. 4346–4354. [Google Scholar]
- Jain, A.; Zamir, A.R.; Savarese, S.; Saxena, A. Structural-RNN: Deep learning on spatio-temporal graphs. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 5308–5317. [Google Scholar]
- Chung, J.; Kastner, K.; Dinh, L.; Goel, K.; Courville, A.; Bengio, Y. A recurrent latent variable model for sequential data. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2015. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2014. [Google Scholar]
- van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Barsoum, E.; Kender, J.; Liu, Z.; IEEE. HP-GAN: Probabilistic 3D human motion prediction via GAN. In Proceedings of the 2018 IEEE/cvf Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1499–1508. [Google Scholar]
- Ishaan, G.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of Wasserstein GANs. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2017. [Google Scholar]
- Kiasari, M.A.; Moirangthem, D.S.; Lee, M. Human action generation with generative adversarial networks. arXiv 2018, arXiv:1805.10416. [Google Scholar]
- Wang, P.; Li, W.; Li, C.; Hou, Y. Action recognition based on joint trajectory maps with convolutional neural networks. Knowl. Based Syst. 2018, 158, 43–53. [Google Scholar] [CrossRef]
- Li, B.; Dai, Y.; Cheng, X.; Chen, H.; Lin, Y.; He, M. Skeleton based action recognition using translation-scale invariant image mapping and multi-scale deep CNN. In Proceedings of the 2017 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Hong Kong, China, 10–14 July 2017; pp. 601–604. [Google Scholar]
- Li, Y.; Xia, R.; Liu, X.; Huang, Q. Learning shape-motion representations from geometric algebra spatio-temporal model for skeleton-based action recognition. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 1066–1071. [Google Scholar]
- Liu, M.; Liu, H.; Chen, C. Enhanced skeleton visualization for view invariant human action recognition. Pattern Recognit. 2017, 68, 346–362. [Google Scholar] [CrossRef]
- Caetano, C.; Sena, J.; Bremond, F.; Dos Santos, J.A.; Schwartz, W.R. Skelemotion: A New Representation of Skeleton Joint Sequences Based on Motion Information for 3D Action Recognition. In Proceedings of the 16th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Taipei, Taiwan, 18–21 September 2019. [Google Scholar]
- Caetano, C.; Bremond, F.; Schwartz, W.R.; IEEE. Skeleton image representation for 3D action recognition based on tree structure and reference joints. In Proceedings of the 2019 32nd Sibgrapi Conference on Graphics, Patterns and Images, Rio de Janeiro, Brazil, 28–30 October 2019; pp. 16–23. [Google Scholar]
- Li, C.; Zhong, Q.; Xie, D.; Pu, S. Co-occurrence feature learning from skeleton data for action recognition and detection with hierarchical aggregation. arXiv 2018, arXiv:1804.06055. [Google Scholar]
- Shahroudy, A.; Liu, J.; Ng, T.-T.; Wang, G. NTU RGB+D: A large scale dataset for 3D human activity analysis. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1010–1019. [Google Scholar]
- Yang, Z.; Li, Y.; Yang, J.; Luo, J. Action recognition with spatio-temporal visual attention on skeleton image sequences. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2405–2415. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Sugawara, Y.; Shiota, S.; Kiya, H. Checkerboard artifacts free convolutional neural networks. APSIPA Trans. Signal Inf. Process. 2019, 8. [Google Scholar] [CrossRef]
- Dowson, D.; Landau, B. The Fréchet distance between multivariate normal distributions. J. Multivar. Anal. 1982, 12, 450–455. [Google Scholar] [CrossRef]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Advances in Neural Information Processing Systems 30; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2017. [Google Scholar]
- Salimans, T.; Goodfellow, I.J.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training GANs. Adv. Neural Inf. Process. Syst. 2016, 29, 2234–2242. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]
- Giuffrida, M.; Scharr, H.; Tsaftaris, S. Arigan: Synthetic arabidopsis plants using generative adversarial network. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 21–26 July 2017; pp. 2064–2071. [Google Scholar]


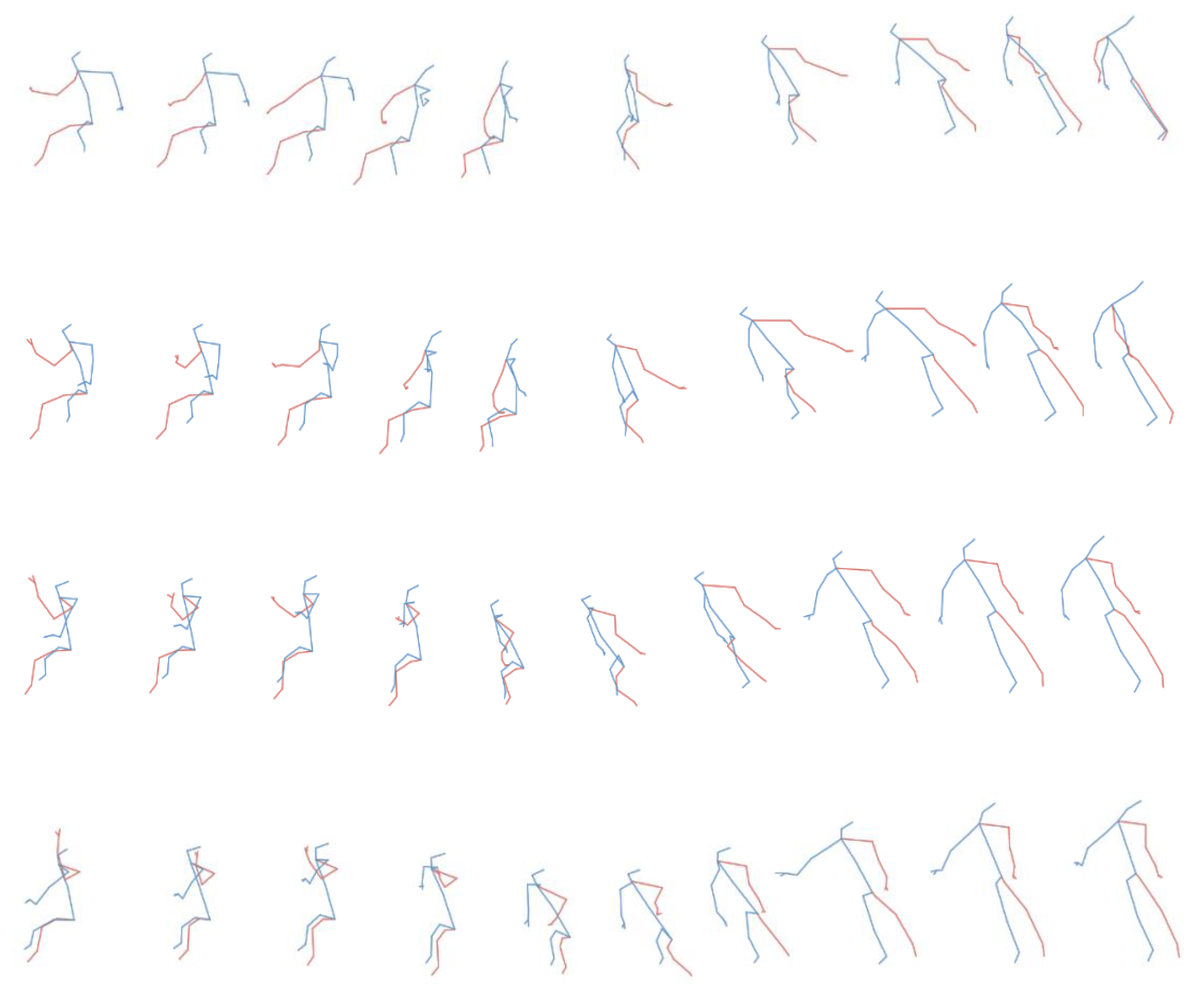
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, W.; Devineau, G.; Moutarde, F.; Yang, J. Generative Model for Skeletal Human Movements Based on Conditional DC-GAN Applied to Pseudo-Images. Algorithms 2020, 13, 319. https://doi.org/10.3390/a13120319
Xi W, Devineau G, Moutarde F, Yang J. Generative Model for Skeletal Human Movements Based on Conditional DC-GAN Applied to Pseudo-Images. Algorithms. 2020; 13(12):319. https://doi.org/10.3390/a13120319
Chicago/Turabian StyleXi, Wang, Guillaume Devineau, Fabien Moutarde, and Jie Yang. 2020. "Generative Model for Skeletal Human Movements Based on Conditional DC-GAN Applied to Pseudo-Images" Algorithms 13, no. 12: 319. https://doi.org/10.3390/a13120319
APA StyleXi, W., Devineau, G., Moutarde, F., & Yang, J. (2020). Generative Model for Skeletal Human Movements Based on Conditional DC-GAN Applied to Pseudo-Images. Algorithms, 13(12), 319. https://doi.org/10.3390/a13120319






