A Dynamic Route-Planning System Based on Industry 4.0 Technology
Abstract
1. Introduction
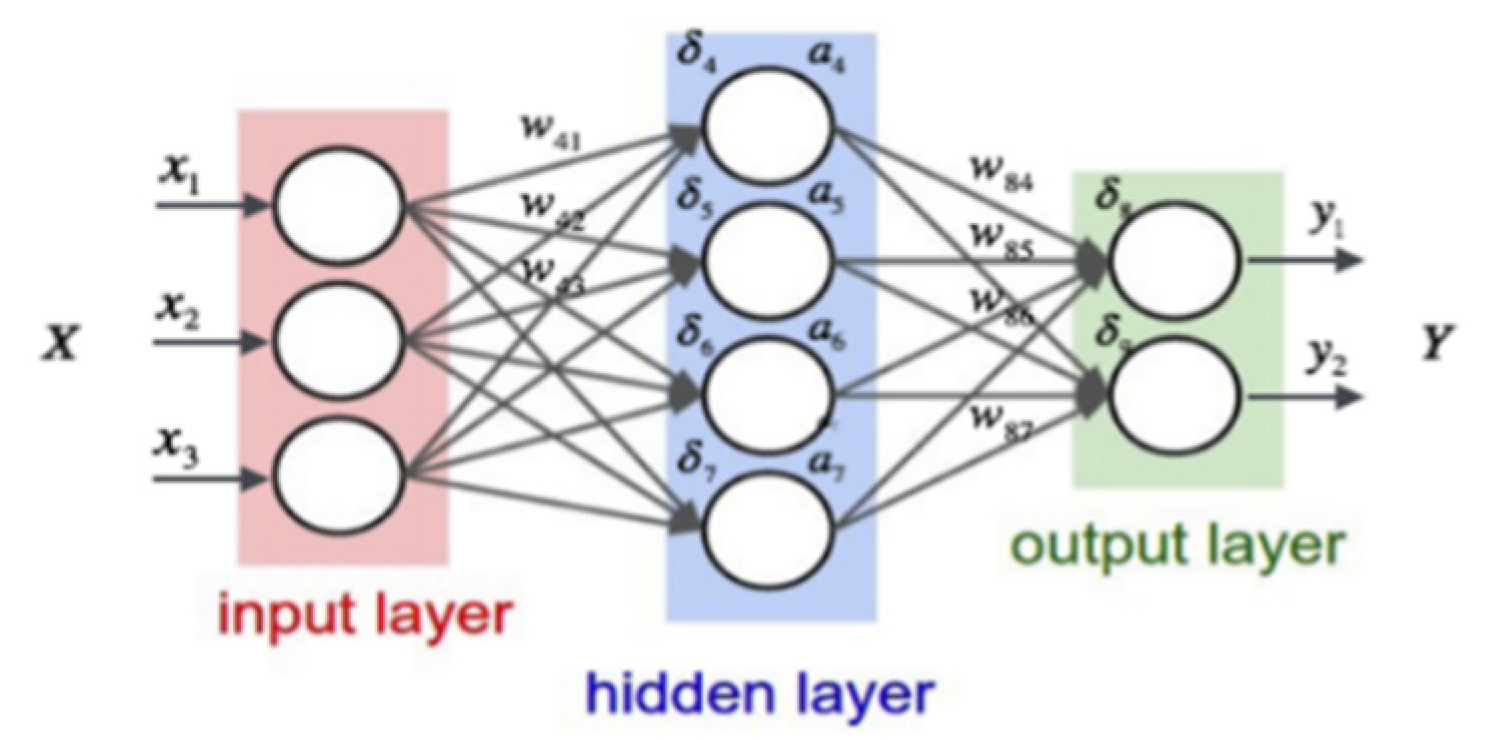
- This research presents a route-planning methodology based on an ANN. The ANN can be implemented on automated guided vehicles (AGVs) with limited computing resources. Once an ANN is trained, it can generate a route with minimal computational effort and runtime (less than a second).
- The considered route-planning problem is based on a practical warehouse environment that considers real-time obstacles.
- A route-planning system that collects the data for training an ANN and generates routes on the basis of real-time positions of obstacles is introduced.
- The proposed methodology is adaptive and scalable. It can be applied to other routing problems with different requirements. Heuristic methods can be used for generating routes for large-scale problems.
- This research presents managerial insights into how the configuration of an ANN affects the accuracy, and how the best configuration can be chosen.
2. Literature Review
2.1. Motion Planning
2.2. Route Planning
3. Models and Algorithms for Route Planning
3.1. An Optimization Model for Route Planning
- Indices
- i, j, and k: indices representing nodes in G
- A: a set of arcs from G
- Parameters
- cij: distance from node i to j, (i, j) ∈ A
- Z: the total distance
- Decision variables
- xij is equals to 1 if (i,j) is chosen and 0 otherwise.
3.2. A Heuristic Algorithm for Path Planning (A-Star Algorithm)
- The start node is removed from the “OPENED” list. The cost function f(n) is calculated; note that h(n) = 0 and g(n) are calculated on the basis of the distance between the start position and the destination (f(n) = g(n)).
- A node with the smallest cost function is removed from the “OPENED” list and inserted into the “CLOSED” list. The node is set as node n (break ties arbitrarily, if two or more nodes have the same cost function). If one of the nodes is the destination node, then the destination node is selected.
- If n is the destination node, the algorithm is terminated; otherwise, it continues.
- The cost function for each successor of n that is not on the “CLOSED” list is computed.
- Each successor not on the “OPENED” list or CLOSED list is associated with the calculated cost and put on the “OPENED” list.
- Any successor already on the “OPENED” list is associated with the minimum cost (min(new(f(n)), old(f(n)))).
- Return to step 2.
4. Results
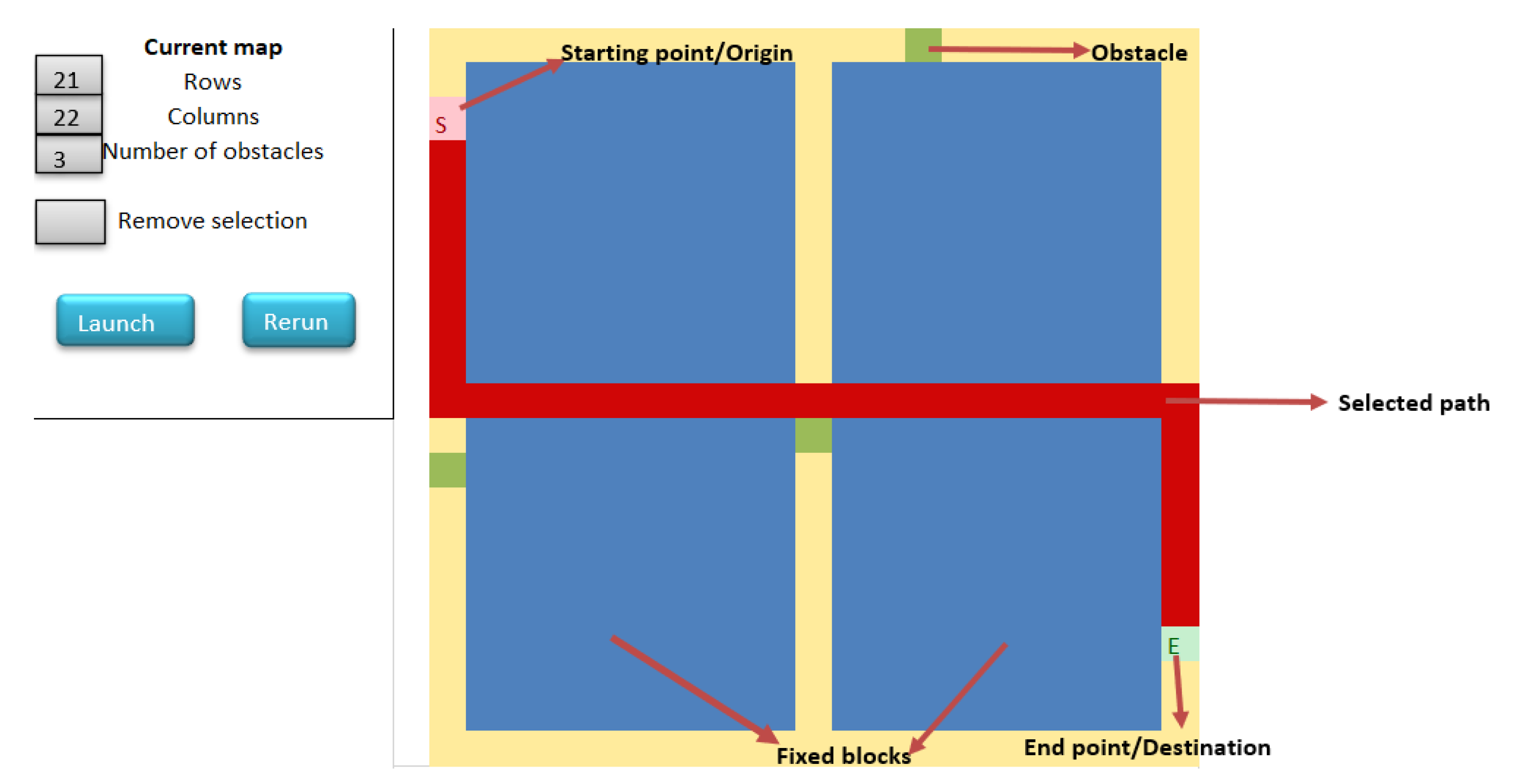
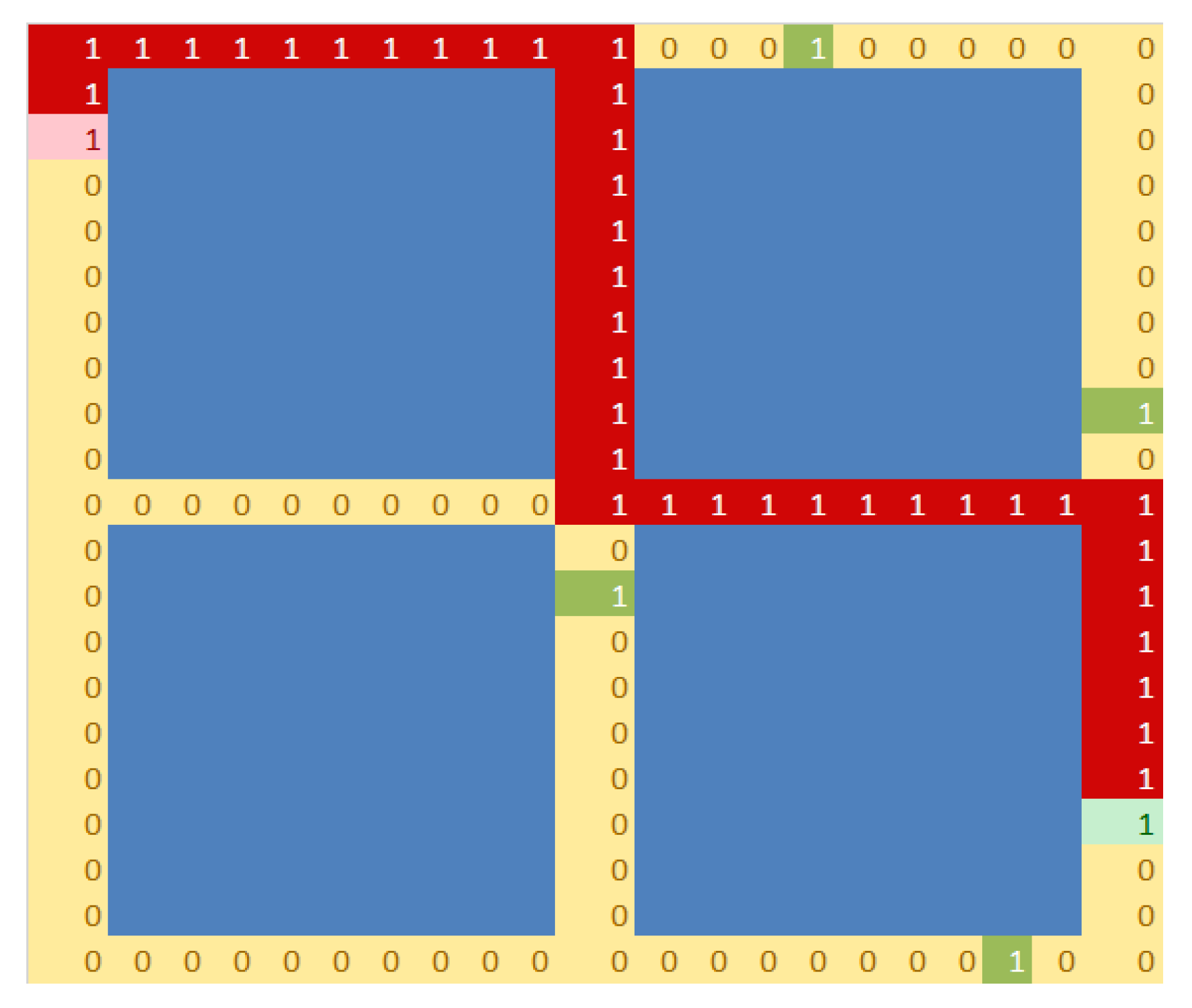
5. Transportation Environment
6. Dynamic Route-Planning System and Computational Results with Managerial Insights
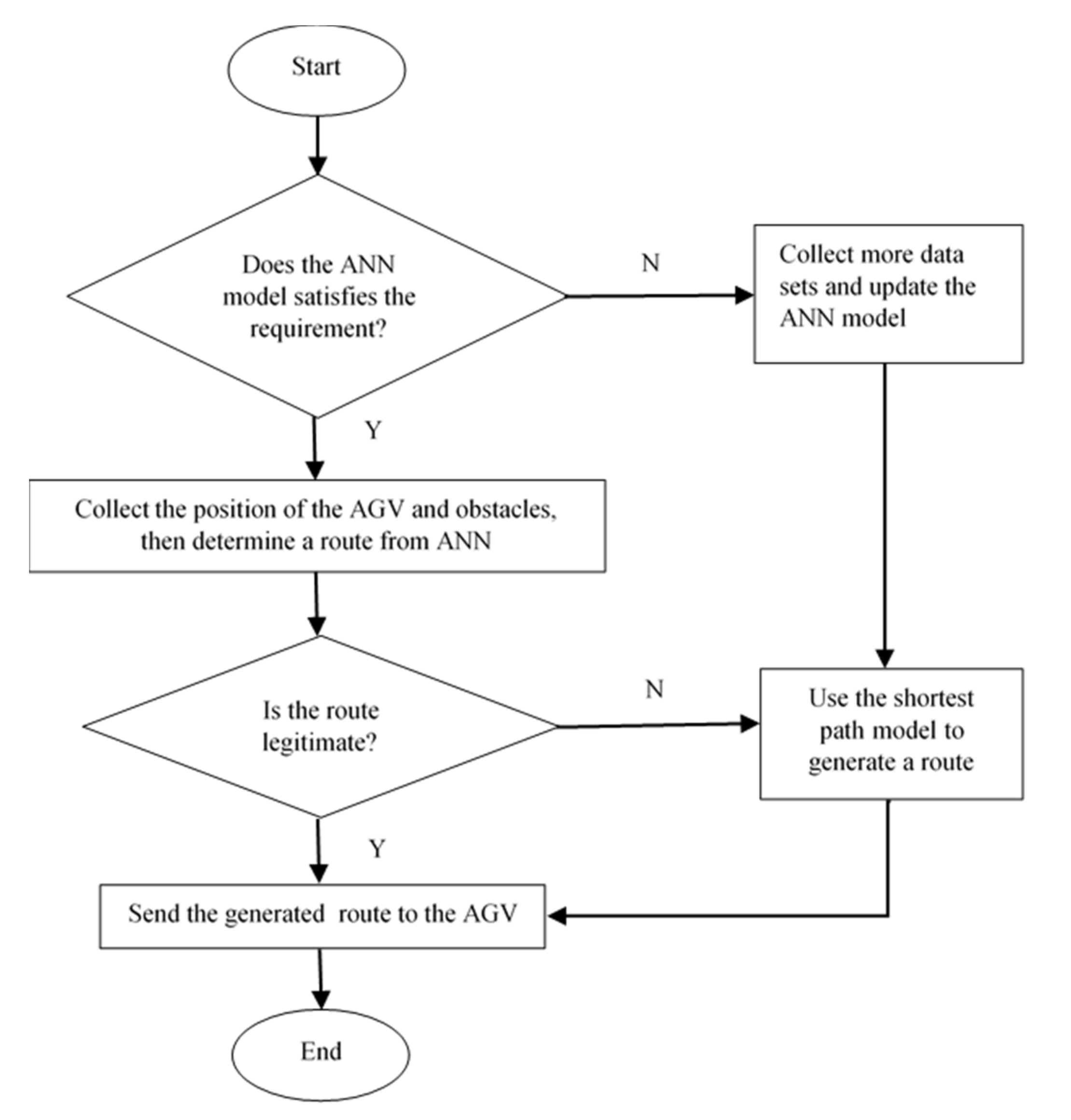
6.1. Dynamic Route-Planning System
6.2. Computational Results and Managerial Insight
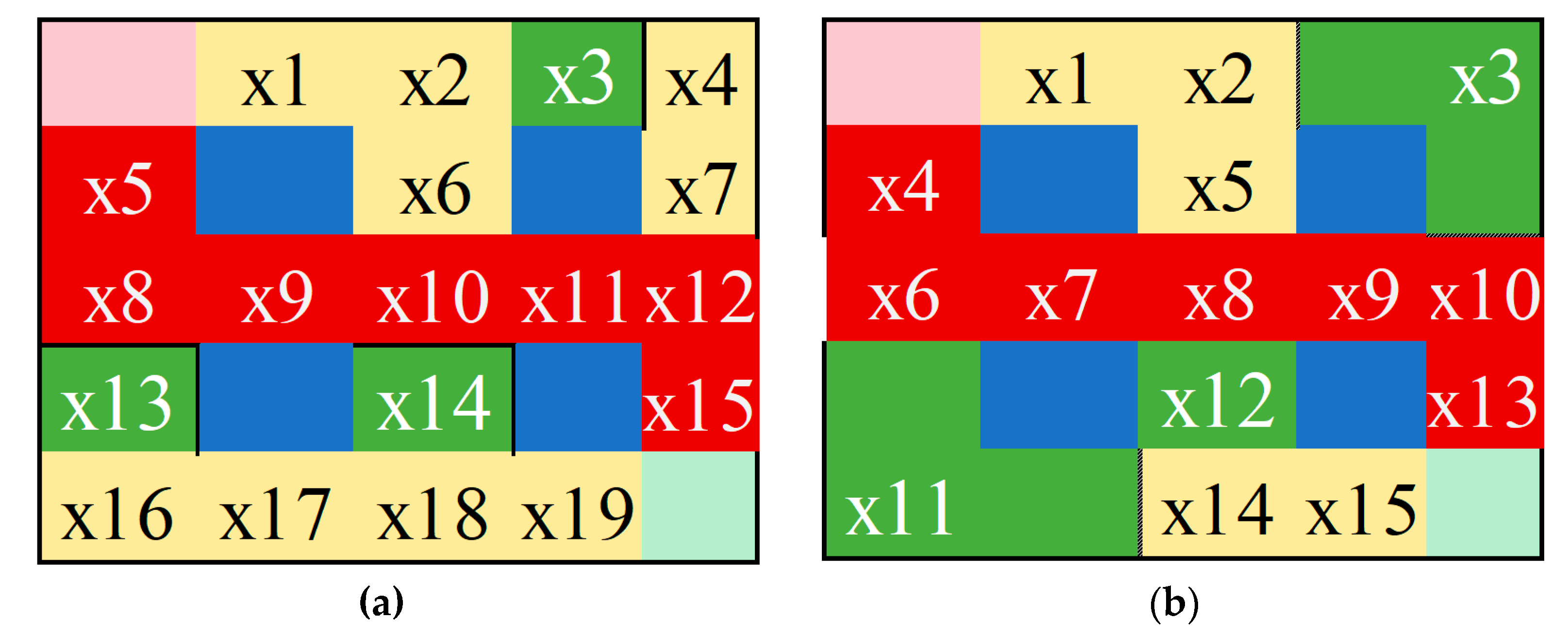
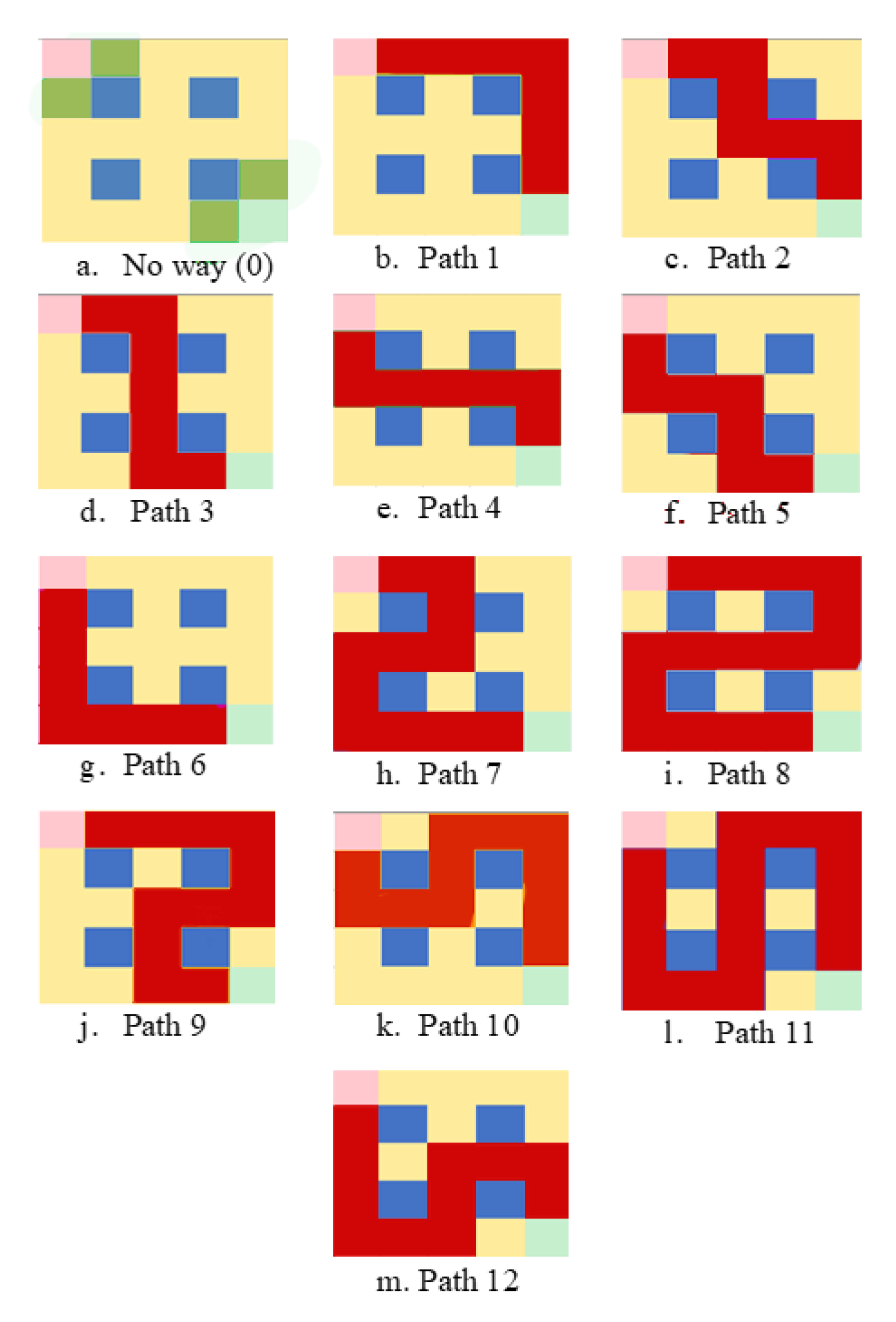
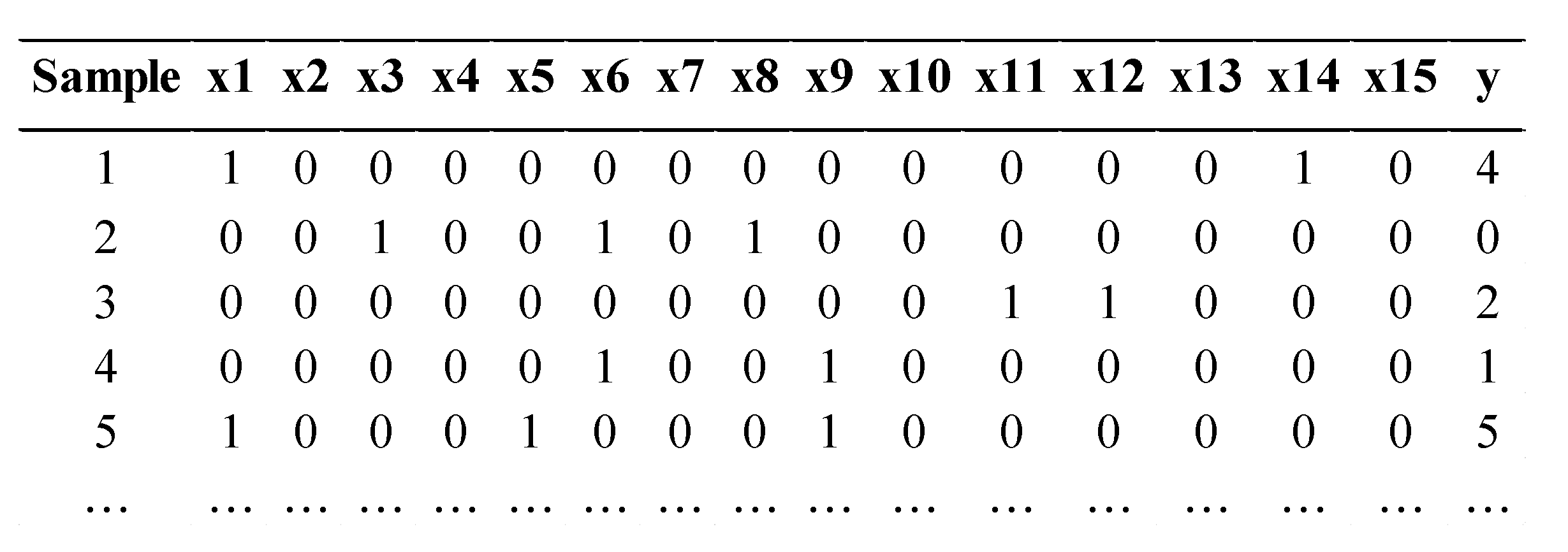
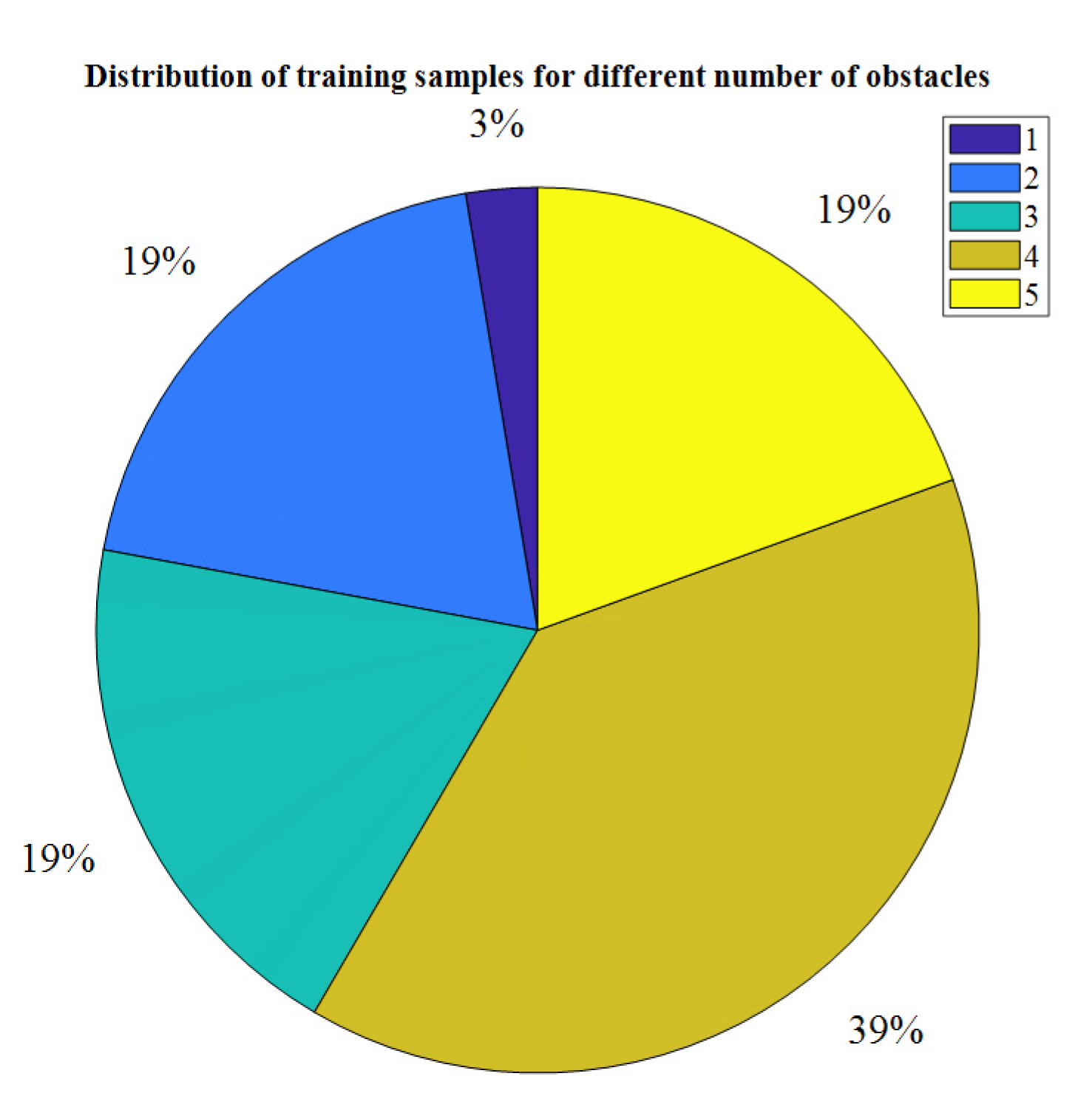
6.2.1. Computational Results from a Layout with Four Storage Racks and 15 Segments
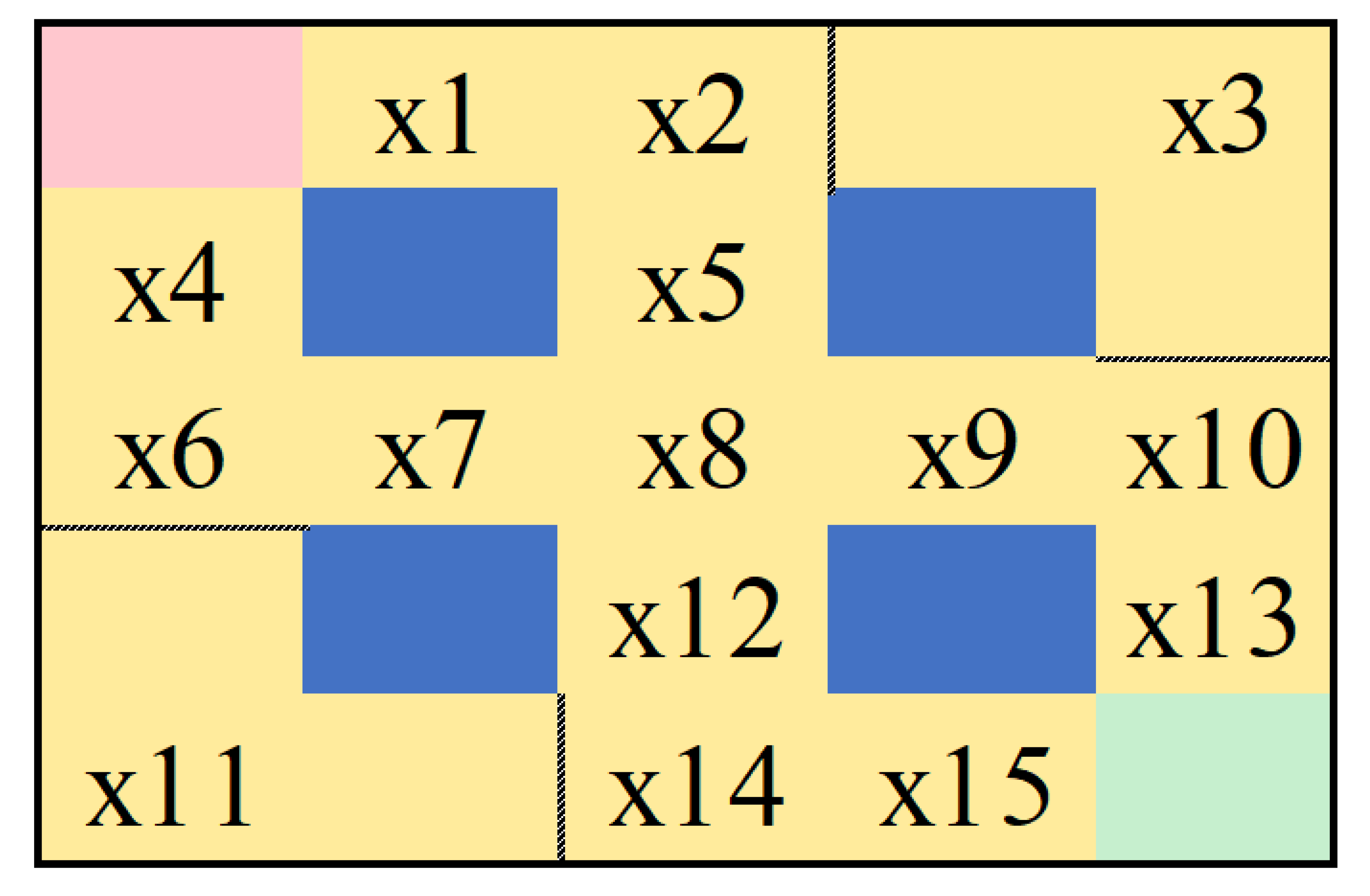
6.2.2. Computational Results from a Layout with 18 Storage Racks and 67 Segments
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Palka, D.; Ciukaj, J. Prospects for development movement in the industry concept 4.0. Multidiscip. Asp. Prod. Eng. 2019, 2, 315–326. [Google Scholar] [CrossRef][Green Version]
- AI and Robotics Automation in Consumer—Driven Supply Chains: A Rapidly Evolving Source of Competitive Advantage. PA Consulting Group and the Consumer Goods Forum. 2018. Available online: https://www.theconsumergoodsforum.com/wp-content/uploads/2018/04/201805-CGF-AI-Robotics-Report-with-PA-Consulting.pdf (accessed on 1 June 2018).
- D’Andrea, R.; Wurman, P. Future challenges of coordinating hundreds of autonomous vehicles in distribution facilities. In Proceedings of the 2008 IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 10–11 November 2008; pp. 80–83. [Google Scholar]
- Liu, X.; Gong, D. A comparative study of A-star algorithms for search and rescue in perfect maze. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 25–27 March 2011; pp. 24–27. [Google Scholar]
- ElHalawany, B.M.; Abdel-Kader, H.M.; TagEldeen, A.; Elsayed, A.E.; Nossair, Z.B. Modified a* algorithm for safer mobile robot navigation. In Proceedings of the 2013 5th International Conference on Modelling, Identification and Control (ICMIC), Tianjin, China, 13–15 July 2019; pp. 74–78. [Google Scholar]
- Contreras-González, A.-F.; Hernández-Vega, J.-I.; Hernández-Santos, C.; Palomares-Gorham, D.-G. A method to verify a path planning by a back-propagation articial neural network. In Proceedings of the LANMR, Puebla, Mexico, 15 August 2016; pp. 98–105. [Google Scholar]
- Zhang, Y.; Li, L.-l.; Lin, H.-C.; Ma, Z.; Zhao, J. Development of Path Planning Approach Based on Improved A-star Algorithm in AGV System. In Proceedings of the International Conference on Internet of Things as a Service, Taichung, Taiwan, 20–22 September 2017; pp. 276–279. [Google Scholar]
- Gochev, I.; Nadzinski, G.; Stankovski, M. Path Planning and Collision Avoidance Regime for a Multi-Agent System in Industrial Robotics. Mach. Technol. Mater. 2017, 11, 519–522. [Google Scholar]
- Mohan, L.J.; Ignatious, J. Navigation of Mobile Robot in a Warehouse Environment. In Proceedings of the 2018 International Conference on Emerging Trends and Innovations In Engineering And Technological Research (ICETIETR), Arakkunnam, India, 11–13 July 2018; pp. 1–5. [Google Scholar]
- Kurdi, M.M.; Dadykin, A.K.; Elzein, I.; Ahmad, I.S. Proposed system of artificial Neural Network for positioning and navigation of UAV-UGV. In Proceedings of the 2018 Electric Electronics, Computer Science, Biomedical Engineerings’ Meeting (EBBT), Istanbul, Turkey, 18–19 April 2018; pp. 1–6. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Liu, Z.; Yu, Z.; Qu, Y. Line-of-Sight Path Following Control on UAV with Sideslip Estimation and Compensation. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 4711–4716. [Google Scholar]
- Flórez, C.A.C.; Rosário, J.M.; Amaya, D. Control structure for a car-like robot using artificial neural networks and genetic algorithms. Neural Comput. Appl. 2018, 32, 1–14. [Google Scholar]
- Zhong, X.; Tian, J.; Hu, H.; Peng, X. Hybrid Path Planning Based on Safe A* Algorithm and Adaptive Window Approach for Mobile Robot in Large-Scale Dynamic Environment. J. Intell. Robot. Syst. 2020, 99, 1–13. [Google Scholar] [CrossRef]
- Bhadoria, A.; Singh, R.K. Optimized angular a star algorithm for global path search based on neighbor node evaluation. Int. J. Intell. Syst. Appl. 2014, 6, 46. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Zhao, Z. A multiple mobile robots path planning algorithm based on A-star and Dijkstra algorithm. Int. J. Smart Home 2014, 8, 75–86. [Google Scholar] [CrossRef]
- Kusuma, M.; Machbub, C. Humanoid robot path planning and rerouting using A-Star search algorithm. In Proceedings of the 2019 IEEE International Conference on Signals and Systems (ICSigSys), Bandung, Indonesia, 16–18 July 2019; pp. 110–115. [Google Scholar]
- Ruiz, E.; Soto-Mendoza, V.; Barbosa, A.E.R.; Reyes, R. Solving the open vehicle routing problem with capacity and distance constraints with a biased random key genetic algorithm. Comput. Ind. Eng. 2019, 133, 207–219. [Google Scholar] [CrossRef]
- Salavati-Khoshghalb, M.; Gendreau, M.; Jabali, O.; Rei, W. An exact algorithm to solve the vehicle routing problem with stochastic demands under an optimal restocking policy. Eur. J. Oper. Res. 2019, 273, 175–189. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Ma, L.; Zhang, Z.; Liu, Y. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Inf. Sci. 2019, 490, 166–190. [Google Scholar] [CrossRef]
- Sung, I.; Choi, B.; Nielsen, P. On the training of a neural network for online path planning with offline path planning algorithms. Int. J. Inf. Manag. 2020. [Google Scholar] [CrossRef]
- Pasha, J.; Dulebenets, M.A.; Kavoosi, M.; Abioye, O.F.; Wang, H.; Guo, W. An Optimization Model and Solution Algorithms for the Vehicle Routing Problem With a “Factory-in-a-Box”. IEEE Access 2020, 8, 134743–134763. [Google Scholar] [CrossRef]
- Trachanatzi, D.; Rigakis, M.; Marinaki, M.; Marinakis, Y. A Firefly Algorithm for the Environmental Prize-Collecting Vehicle Routing Problem. Swarm Evol. Comput. 2020, 57, 100712. [Google Scholar] [CrossRef]
- Taccari, L. Integer programming formulations for the elementary shortest path problem. Eur. J. Oper. Res. 2016, 252, 122–130. [Google Scholar] [CrossRef]
- Klancar, G.; Zdesar, A.; Blazic, S.; Skrjanc, I. Wheeled Mobile Robotics: From Fundamentals towards Autonomous Systems; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Baptista, F.D.; Rodrigues, S.; Morgado-Dias, F. Performance comparison of ANN training algorithms for classification. In Proceedings of the 2013 IEEE 8th International Symposium on Intelligent Signal Processing, Funchal, Portugal, 16–18 September 2013; pp. 115–120. [Google Scholar]
- Panchal, G.; Ganatra, A.; Kosta, Y.; Panchal, D. Behaviour analysis of multilayer perceptrons with multiple hidden neurons and hidden layers. Int. J. Comput. Theory Eng. 2011, 3, 332–337. [Google Scholar] [CrossRef]



| No. | Authors | Year | Route Planning | Motion Planning | Automated Robot | Warehouse Application | Use of ANN | Realtime Obstacle |
|---|---|---|---|---|---|---|---|---|
| 1 | Liu and Gong [4] | 2011 | x | x | x | |||
| 2 | ElHalawany et al. [5] | 2013 | x | x | ||||
| 3 | Bhadoria and Singh [14] | 2014 | x | x | x | |||
| 4 | Zhang and Zhao [15] | 2014 | x | x | x | |||
| 5 | Contreras-González et al. [6] | 2016 | x | x | x | |||
| 6 | Zhang et al. [7] | 2017 | x | x | ||||
| 7 | Gochev et al. [8] | 2017 | x | x | x | |||
| 8 | Mohan and Ignatious [9] | 2018 | x | x | x | |||
| 9 | Kurdi et al. [10] | 2018 | x | x | x | x | ||
| 10 | Zhang et al. [11] | 2018 | x | x | x | |||
| 11 | Flórez et al. [12] | 2018 | x | x | x | x | ||
| 12 | Kusuma and Machbub [16] | 2019 | x | x | x | |||
| 13 | Ruiz et al. [17] | 2019 | x | x | ||||
| 14 | Salavati-Khoshghalb et al. [18] | 2019 | x | x | ||||
| 15 | Zhang et al. [19] | 2019 | x | x | ||||
| 16 | Zhong et al. [13] | 2020 | x | x | x | |||
| 17 | Sung et al. [20] | 2020 | x | x | x | |||
| 18 | Pasha et al. [21] | 2020 | x | x | ||||
| 19 | Trachanatzi et al. [22] | 2020 | x | x | ||||
| 20 | This research | 2020 | x | x | x | x | x |
| ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | Others |
|---|---|---|---|---|---|---|---|---|
| Count | 91 | 32 | 61 | 28 | 67 | 40 | 49 | 7 |
| 200 Samples | 300 Samples | |||
|---|---|---|---|---|
| ANN’s Hidden Layer Topology | Training Accuracy (%) | Testing Accuracy (%) | Training Accuracy (%) | Testing Accuracy (%) |
| 15-5-7 | 93.3 | 70 | 92.5 | 85 |
| 15-8-7 | 100 | 85 | 100 | 96.7 |
| 15-10-7 | 100 | 75 | 100 | 91.7 |
| 15-8-7-7 | 100 | 95 | 100 | 98.3 |
| 15-8-10-7 | 100 | 90 | 100 | 93.3 |
| ANNs | 1000 | 1448 | ||
|---|---|---|---|---|
| Training | Testing | Training | Testing | |
| 67-60-21 | 99.7 | 94.00 | 99.7 | 94.83 |
| 67-67-21 | 99.7 | 93.50 | 99.7 | 95.52 |
| 67-70-21 | 99.7 | 96.00 | 99.7 | 96.90 |
| 67-73-21 | 99.7 | 93.50 | 99.7 | 93.79 |
| 67-67-21-21 | 99.7 | 95.50 | 99.7 | 97.93 |
| 67-67-30-21 | 99.7 | 96.00 | 99.7 | 97.24 |
| 67-70-30-21 | 99.7 | 96.50 | 99.7 | 97.93 |
| 67-70-40-21 | 99.25 | 96.00 | 99.65 | 96.55 |
| 67-67-21-10-21 | 90.00 | 91.50 | 91.19 | 88.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen Duc, D.; Tran Huu, T.; Nananukul, N. A Dynamic Route-Planning System Based on Industry 4.0 Technology. Algorithms 2020, 13, 308. https://doi.org/10.3390/a13120308
Nguyen Duc D, Tran Huu T, Nananukul N. A Dynamic Route-Planning System Based on Industry 4.0 Technology. Algorithms. 2020; 13(12):308. https://doi.org/10.3390/a13120308
Chicago/Turabian StyleNguyen Duc, Duy, Thong Tran Huu, and Narameth Nananukul. 2020. "A Dynamic Route-Planning System Based on Industry 4.0 Technology" Algorithms 13, no. 12: 308. https://doi.org/10.3390/a13120308
APA StyleNguyen Duc, D., Tran Huu, T., & Nananukul, N. (2020). A Dynamic Route-Planning System Based on Industry 4.0 Technology. Algorithms, 13(12), 308. https://doi.org/10.3390/a13120308






