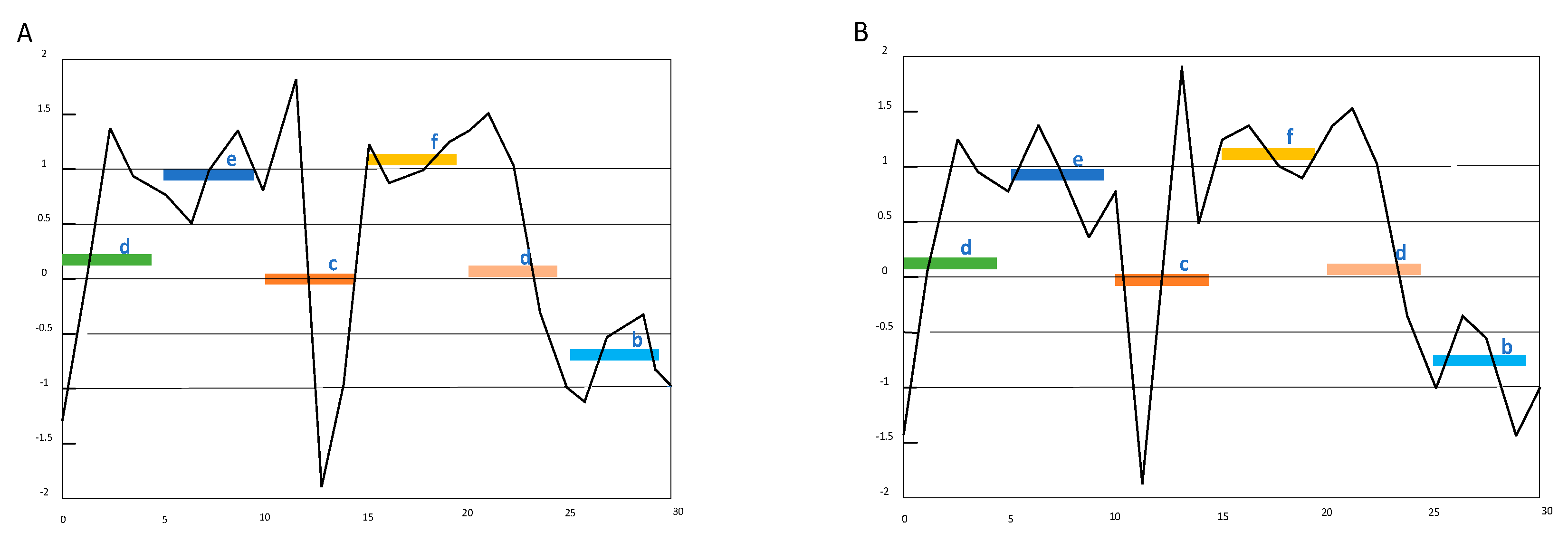A Boundary Distance-Based Symbolic Aggregate Approximation Method for Time Series Data

Abstract

A large amount of time series data is being generated every day in a wide range of sensor application domains. The symbolic aggregate approximation (SAX) is a well-known time series representation method, which has a lower bound to Euclidean distance and may discretize continuous time series. SAX has been widely used for applications in various domains, such as mobile data management, financial investment, and shape discovery. However, the SAX representation has a limitation: Symbols are mapped from the average values of segments, but SAX does not consider the boundary distance in the segments. Different segments with similar average values may be mapped to the same symbols, and the SAX distance between them is 0. In this paper, we propose a novel representation named SAX-BD (boundary distance) by integrating the SAX distance with a weighted boundary distance. The experimental results show that SAX-BD significantly outperforms the SAX representation, ESAX representation, and SAX-TD representation.

1. Introduction

Time series data are being generated every day in a wide range of application domains [1], such as bioinformatics, finance, engineering, etc. [2]. The parallel explosions of interest in streaming data and data mining of time series [3,4,5,6,7,8,9] have had little intersection. Time series classification methods can be divided into three main categories [10]: feature based, model based and distance based. There are many methods for feature extraction, for example: (1) spectral analysis such as discrete Fourier transform (DFT) [11], (2) discrete wavelet transform (DWT) [12], where features of the frequency domain are considered, and (3) singular value decomposition (SVD) [13], where eigenvalue analysis is carried out in order to find an optimal set of features. The model-based classification methods include auto-regressive models [14,15] or hidden Markov models [16], among others. In distance-based methods, 1-NN [1] has been a widely used method due to its simplicity and good performance.

Until now, almost all the research in distance-based classification has been oriented to defining different types of distance measures and then exploiting them within the 1-NN classifiers. The 1-NN classifier is probably the simplest classifier among all classifiers, while its performance is also good. Dynamic Time Warping(DTW) [17] as a distance method used for 1-NN classifier makes the classification accuracy reach the maximum at that time. However, due to the high dimensions, high volume, high feature correlation, and multiple noises, it has brought great challenges to the classification of time series, and even makes the DTW unusable. In fact, all non-trivial data mining and indexing algorithms decrease exponentially with dimensions. For example, above 16–20 dimensions, the index structure will be degraded to sequential scanning [18]. In order to reduce the time series dimensions and have a low bound to the Euclidean distance. The Piecewise Aggregate Approximation(PAA) [19] and Symbolic Aggregate Approximate(SAX) [20] were brought up. The distance in the SAX representation has a lower bound to the Euclidean distance. Therefore, the SAX representation speeds up the data mining process of time series data while maintaining the quality of the data mining results. SAX has been widely used in mobile data management [21], financial investment [22], feature extraction [23]. In recent years, with the popularity of deep learning, applying deep learning methods to multivariate time series classification has also received attention [24].

SAX allows a time series of arbitrary length n to be reduced to a string of arbitrary length w [20] (w < n, typically w << n). The alphabet size α is also an arbitrary integer. The SAX representation has a major limitation. In the SAX representation, symbols are mapped from the average values of segments, and some important features may loss. For example, in Figure 1, if w = 6 and α = 6, time series a represented as ‘decfdb’.

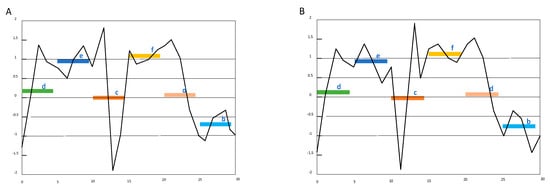
Figure 1. Financial time series A and B have the same SAX symbolic representation ‘decfdb’ in the same condition where the length of time series is 30, the number of segments is 6 and the size of symbols is 6. However, they are different time series.

However, it can be clearly seen from the Figure 1 that the time series changes drastically. Therefore, a compromise is needed to reduce the dimension of time series while improving the accuracy. ESAX representation can express the characteristics of time series in more detail [25]. It chooses a maximum, a minimum and the average value in each time series segment as the new feature, then map the new feature to strings according to the SAX method. For the same time series, in Figure 1 time series a can be represented as ‘adfeeffcaefffdaabc’.

SAX-TD (trend distance) method improves the accuracy of ESAX and reduce the complexity of symbol representation [26]. It uses fewer values than ESAX due to the strategy that one segment only needs one trend distance. In the Figure 1, the time series a is represented as’ _−1.4d_0.13e_0.75c_0.13f_1.25d_−0.25b_−0.25′.

In this paper we propose a new method SAX-BD, in which BD means the boundary distance. For each divided time series segment, they have the maximum point and minimum point, the distance from them to average value named boundary distance. Time series a and b in Figure 1 have a high probability of being identified as the same if SAX-TD is used. However, in our method, time series A is represented as ’ d_{(−1.4,0.63)}e_{(−0.38,0.38)}c_{(1.36,−1.39)}f_{(−0.25,0.36)}d_(1.5,−1)b_{(−0.38,0.38)}’ and time series B is represented as ‘d_(−1.4,1.2)e_{(0.38,−0.5)}c_(−1.8,1.9)f_{(0.38,−0.25)}d_(1.5,−1.0)b_{(0.45,−0.55)}‘. Obviously, there is a big difference between the two representations.

In our work, there are three main contributions. First, we prove an intuitive boundary distance measure on time series segments. The average value of the segment and its boundary distance help measure different trends of time series more accurately. Our representation captures the trends in time series better than the SAX, ESAX, and the SAX-TD representations. Second, we discussed the SAX-TD algorithm and the ESAX algorithm and explained that our method is actually a generalization of these two methods. For their poorly performing data, our method has improved the result to a certain extent. For the data they outperform, we can basically keep the reduced accuracy rate in a very small range. Third, we proved that our improved distance measure not only keeps a lower-bound to the Euclidean distance, but also achieves a tighter lower bound than that of the original SAX distance.

2. Related Work

Given that the normalized time series have highly Gaussian distribution, we can simply determine the “breakpoints” that will produce equal-sized areas under Gaussian curve. The idea of the SAX algorithm is to assume that the average value of each segment has the equal probability in ${\beta }_i to {\beta }_{i+1}=1/a$ Each segment is projected into its own specified area. While w determines how many dimensions to reduce for the n-dimension time series. The smaller w is, the larger n/w, indicating that more information will be compressed.

2.1. The Distance Calculation by SAX

For example, a sequence data of length n is converted into w symbols. The specific steps are as follows:

Divides time series data into w segments of the same size according to the Piecewise Aggregate Approximation (PAA) algorithm. The average value of each time segment for example $\overline{C}=\overline{C_1},\overline{C_2},\dots ,\overline{C_w}$ the $i_{th }$element of $\overline{\overline{C}}$ is the average of the $i_{th }$ segment and is calculated by the following equation:

$$\overline{C_i}=\frac{w}{n}{\displaystyle \sum }_{j=\left(n/w\right)\left(i+1\right)+1}^{\left(n/w\right)i}{C}_j$$

(1)

where $C_j$is one time point of time series C, using breakpoints to divide space into α equiprobable regions are determined

These breakpoints are arranged in list order as $B={\beta }_1,{\beta }_2,\dots ,{\beta }_{\mathsf{\alpha }-1}$, They satisfy Gaussian distribution, and the spacing between ${\beta }_i$ and ${\beta }_{i+1}$ is 1/α.

Finally, the divided s time series segments are represented by these breakpoints. The SAX algorithm can map segments’ average values to alphabetic symbols. The mapping rule of SAX is as follows, if it is smaller than the lower limit of the minimum breakpoints, it is mapped to ‘a’, and then greater than a bit smaller than the second breakpoints lower limit is mapped to ‘b’. The symbols after these mappings can roughly indicate a time series.

Given two time series Q and C, the two time series are of the same length n, which is divided into w time segments.$\widehat{Q}$ and $\widehat{C}$ are the symbol strings after they are transformed into SAX algorithm representation, then the SAX distance between Q and C can be expressed as follows:

$$\mathrm{MINDIST}\left(\widehat{Q},\widehat{C}\right)=\sqrt{\frac{n}{w}}\sqrt{{\displaystyle \sum }_{i=1}^w{(dist\left(\widehat{q},\widehat{c}\right))}^2}$$

(2)

Among them, the$\mathrm{dist}\left(\widehat{q},\widehat{c}\right)$ can be obtained according to Table 1, the query method can be expressed as the following equation:

$$\mathrm{dist}\left(\widehat{q},\widehat{c}\right)=\{\begin{array}{c}0\\ {\beta }_{max\left(\widehat{q},\widehat{c}\right)-1}-{\beta }_{min\left(\widehat{q},\widehat{c}\right)}\end{array}\begin{array}{cc}& \mathrm{if}\left|\widehat{q}-\widehat{c}\right|\le 1\\ & \mathrm{otherwise}\end{array}$$

(3)

Table 1. A lookup table for breakpoints with the alphabet size from 3 to 10.

${\mathit{\beta }}_{\mathit{i}}$	3	2	5	6	7	8	9	10
${\beta }_1$	−0.43	−0.67	−0.84	−0.97	−1.07	−1.15	−1.22	−1.28
${\beta }_2$	−0.43	0	−0.25	−0.43	−0.57	−0.67	−0.76	−0.84
${\beta }_3$		0.67	0.25	0	−0.18	−0.32	−0.43	−0.52
${\beta }_4$			0.84	0.43	0.18	0	−0.14	−0.25
${\beta }_5$				0.97	0.57	0.32	0.14	0
${\beta }_6$					1.07	0.67	0.43	0.25
${\beta }_7$						1.15	0.76	0.52
${\beta }_8$							1.22	0.84
${\beta }_9$								1.28

2.2. An Improvement of SAX Distance Measure for Time Series

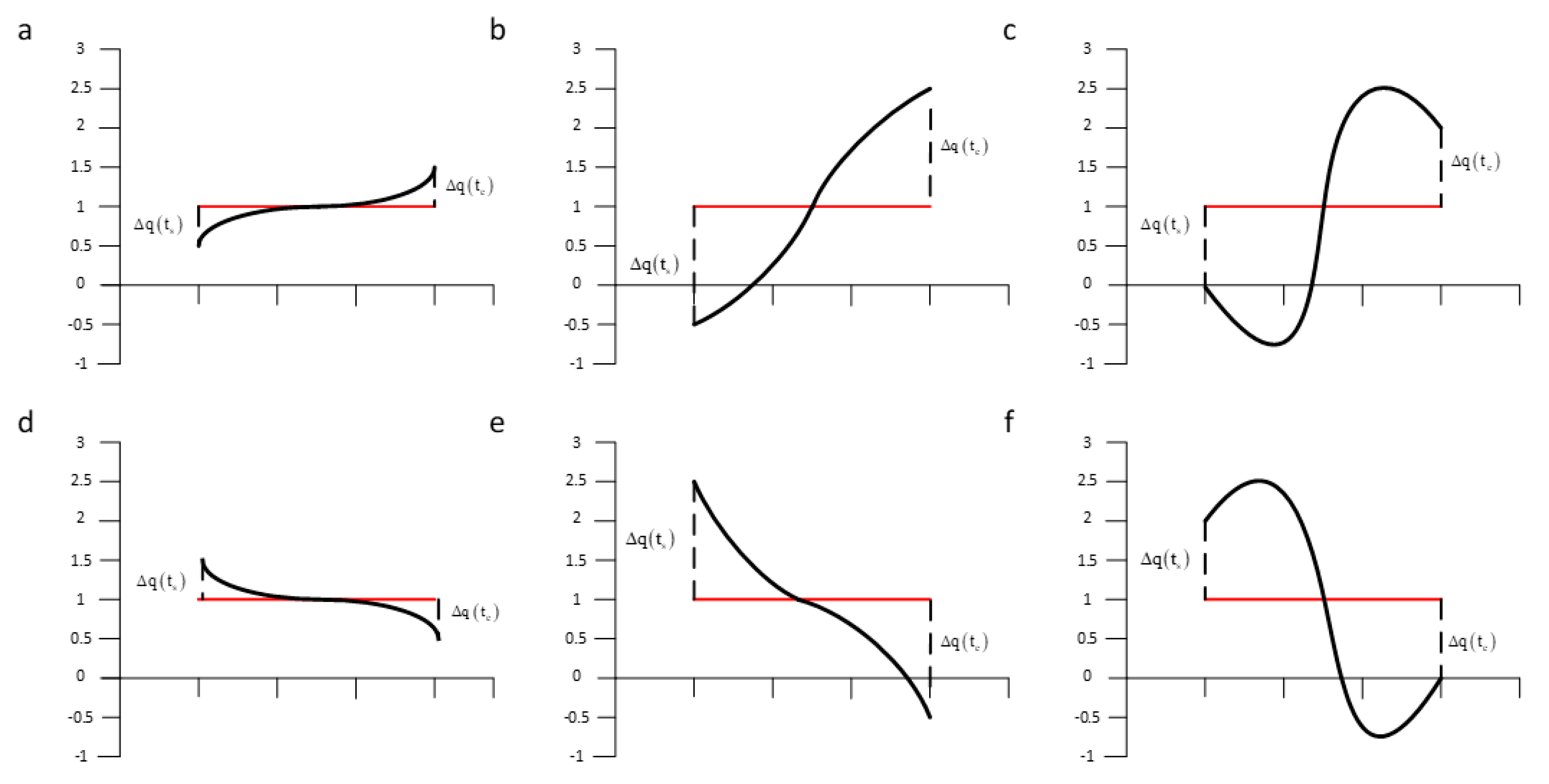
As the first to symbolize time series and can be effectively applied to time series classification, SAX has been recognized by many experts and scholars, however the shortcoming is also obviously to see. The larger w and smaller α, the more features will be lost for time series. To keep as much important information as possible, time series trend needed to be kept in the process of SAX dimensionality reduction. For example, in reference [26], some limitations of using SAX algorithm on the classification for time series were discussed. In this paper, these cases are listed separately in Figure 2.

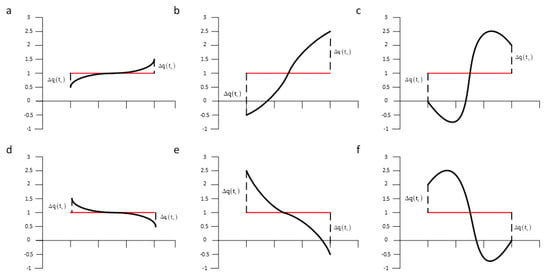
Figure 2. Several typical segments with the same average value but different trends [26]. Segment a and d, b and e, c and f are in opposite directions while all in same mean value.

In Figure 2, the average value of a and d, b and e, c, and f correspond to the same, but it is very clear that their time series tend to be significantly different. In order to correctly describe this difference, the author proposes using the SAX-TD method. According to the calculation rules of SAX-TD, the trend distance td (q, c) of two time series q and c is first calculated. The specific definition is as follows:

$$\mathrm{td}\left(\mathrm{q},\mathrm{c}\right)=\sqrt{{\left(\Delta q\left(t_s\right)-\Delta q\left(c_s\right)\right)}^2+{\left(\Delta q\left(t_e\right)-\Delta q\left(c_e\right)\right)}^2}$$

(4)

where $t_s$ and $t_e$ are the start point and end point of a time segment for the time series q and c. Respectively, the specific definition of $\Delta q\left(t\right)$ is as follows:

$$\Delta q\left(t\right)=q\left(t\right)-\overline{q}$$

(5)

$\Delta c\left(t\right)$ will be calculated in the same way, in article the author refers to this method as the tendency of time segments.

With the SAX method description, the time series Q and C respectively represented as follows:

$$\mathrm{Q}: \Delta q\left(1\right)\widehat{q_1} \Delta q\left(2\right)\widehat{q_2} \dots \Delta q\left(w\right)\widehat{q_w}\Delta q\left(w+1\right)$$

$$\mathrm{C}:\Delta c\left(1\right)\widehat{c_1} \Delta c\left(2\right)\widehat{c_2} \dots \Delta c\left(w\right)\widehat{c_w}\Delta c\left(w+1\right)$$

$\widehat{q_1},\widehat{q_2}\dots \widehat{q_w}$ is a sequence symbolized by SAX, $\Delta q\left(1\right), \Delta q\left(2\right) ,\dots ,\Delta q\left(w\right)$ are the trend variations, and$\Delta q\left(W+1\right)$ is the change of the last point.

The distance between two time series can be defined based on the trend distance as follows:

$$TDIST\left(\widehat{Q},\widehat{C}\right)=\sqrt{\frac{n}{w}}\sqrt{{\displaystyle \sum }_{i=1}^w({\left(dist\left(\widehat{q_i},\widehat{c_i}\right)\right)}^2+\frac{w}{n}{\left(td\left(q_i,c_i\right)\right)}^2}$$

(6)

where $\widehat{Q}$ and $\widehat{C},$ respectively, denote the time series Q and C, n is the length of Q and C, and w is the number of time segments. The distance between time series Q and C can be calculated by Equation (6). In this paper, the author proved that this method has a low bound to Euclidean distance, and the experimental results also showed that this method improves classification accuracy compared with ESAX.

3. SAX-BD: Boundary Distance-Based Method For Time Series

3.1. An Analysis of SAX-TD

First, in Figure 3, we select the b, c, e, f curve features from Figure 2.

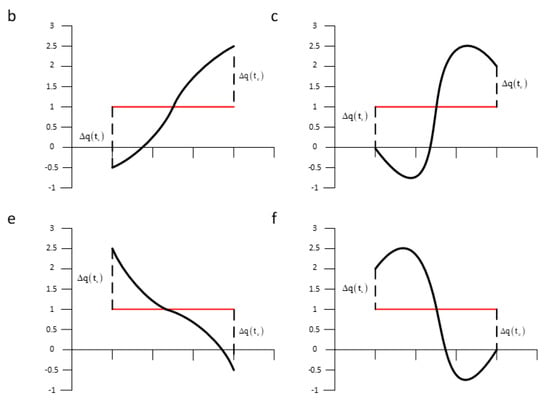
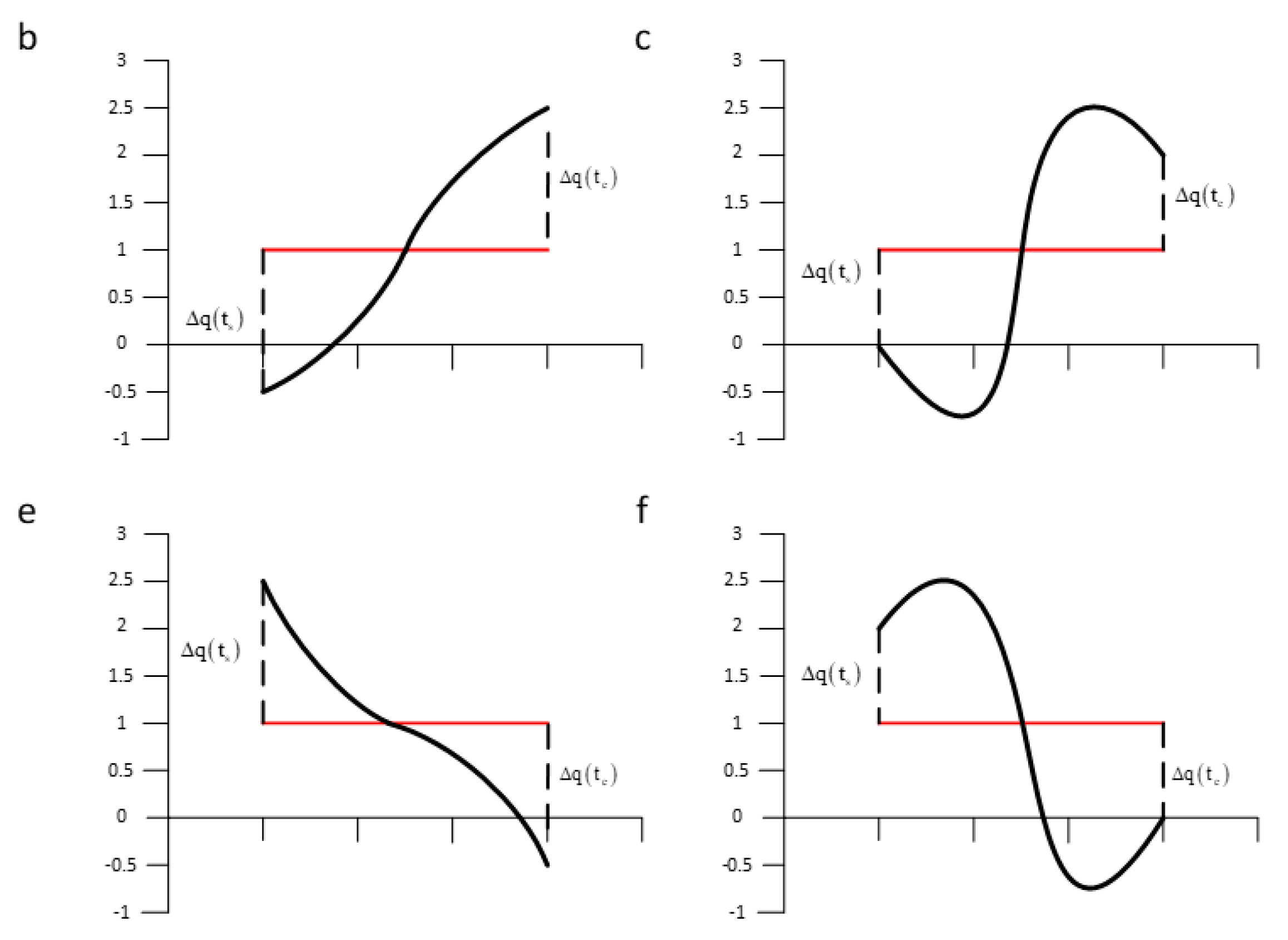
Figure 3. Several typical segments with the same average value and same trends but different boundary distance. Segment b and c, e and f with the same SAX representation and trend distance while they are different segments.

The difference between b and e, c and f can be identified by using the SAX-TD algorithm, because, for b, the trend distance is $\Delta q\left(t\right)$, and for the e is $-\Delta q\left(t\right)$, the final calculation results can distinguish these time series. However, if you want to identify the difference between a and c, e and f, there is a great possibility that you will fail. The trend distance for b and c, e and f are both the same value $\Delta q\left(t\right)$ or $-\Delta q\left(t\right)$, according to the calculation rules of SAX-TD, they will be judged as the same time series.

3.2. Our Method SAX-BD

In order to solve these problems, we propose to increase the boundary distance as a new reference instead of the trend distance. The details are as follows:

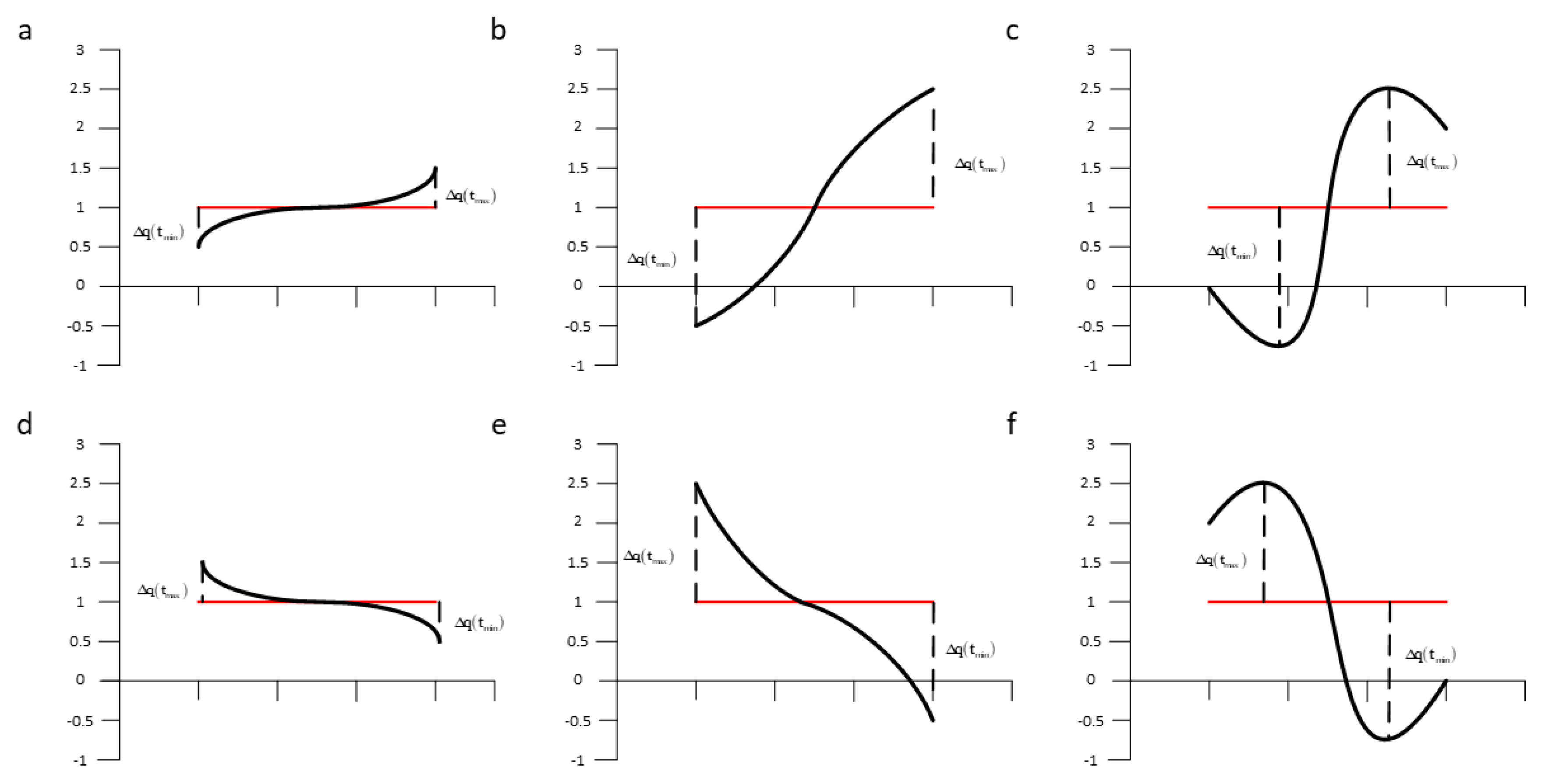
From Figure 4, we can see that this method is somewhat the same as ESAX, but it is different from ESAX.

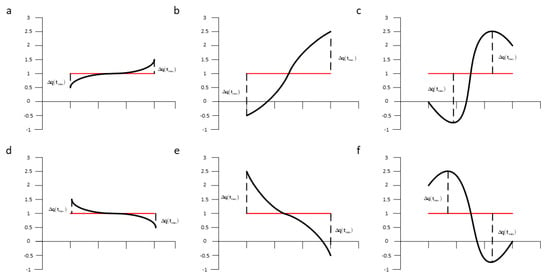
Figure 4. Several typical segments with the same average value but boundary distance. Segment a and d, b and e, c and f are in opposite directions while all in same mean value. The trend distance is replaced by boundary distance.

The maximum and minimum value of each time segment is the boundary. The boundary distance of c is$\Delta q\left(t\right)$and for f is$-\Delta q\left(t\right)$, shown in Equations (7) and (8):

$$\Delta q{\left(t\right)}_{max}=q{\left(t\right)}_{max} -\overline{q}$$

(7)

$$\Delta q{\left(t\right)}_{min}=q{\left(t\right)}_{min}-\overline{q}$$

(8)

The tendency change of c calculated by SAX-BD algorithm is $\Delta q\left(t_{max}\right)$, and the tendency change of f is $-\Delta q\left(t_{max}\right)$. It can be seen that our method can also distinguish well. For b and c, the distance calculated using SAX-TD is the same, but in our method, SAX-BD, the equation is not equal to 0, indicating that there is a possibility of distinction between the time series. For the cases of g and h, according to our method, it is as follows:

$$\Delta q\left(t_s\right)=\Delta q\left(t_{max}^h\right)and a and \Delta q\left(t_e\right)=\Delta q\left(t_{min}^h\right)$$

(9)

$$\Delta q\left(t_{max}^g\right)-\Delta q\left(t_s\right)\ne 0 and \Delta q\left(t_{min}^g\right)-\Delta q\left(t_e\right)\ne 0$$

(10)

3.3. Difference from ESAX

In the ESAX method, the maximum, minimum, and mean values in each time segment are mapped and arranged according to the following formula:

$$<S_1,S_2,S_3>=\{\begin{array}{l}<S_{\max },S_{mid},S_{\min }>if{\mathrm{P}}_{\max }>{\mathrm{P}}_{\mathrm{m}id}>{\mathrm{P}}_{\min }\\ <S_{\max },S_{\min },S_{mid}>if{\mathrm{P}}_{\max }>{\mathrm{P}}_{\min }>{\mathrm{P}}_{mid}\\ <S_{mid},S_{\min },S_{\max }>if{\mathrm{P}}_{mid}>{\mathrm{P}}_{\min }>{\mathrm{P}}_{\max }\\ <S_{mid},S_{\max },S_{\min }>if{\mathrm{P}}_{mid}>{\mathrm{P}}_{\max }>{\mathrm{P}}_{\min }\\ <S_{\min },S_{mid},S_{\max }>if{\mathrm{P}}_{\min }>{\mathrm{P}}_{mid}>{\mathrm{P}}_{\max }\\ <S_{\min },S_{\max },S_{mid}>Otherwise\end{array}$$

(11)

However, for the same feature points, we did not directly map these points in the same way as the ESAX method, mainly due to the following two reasons:

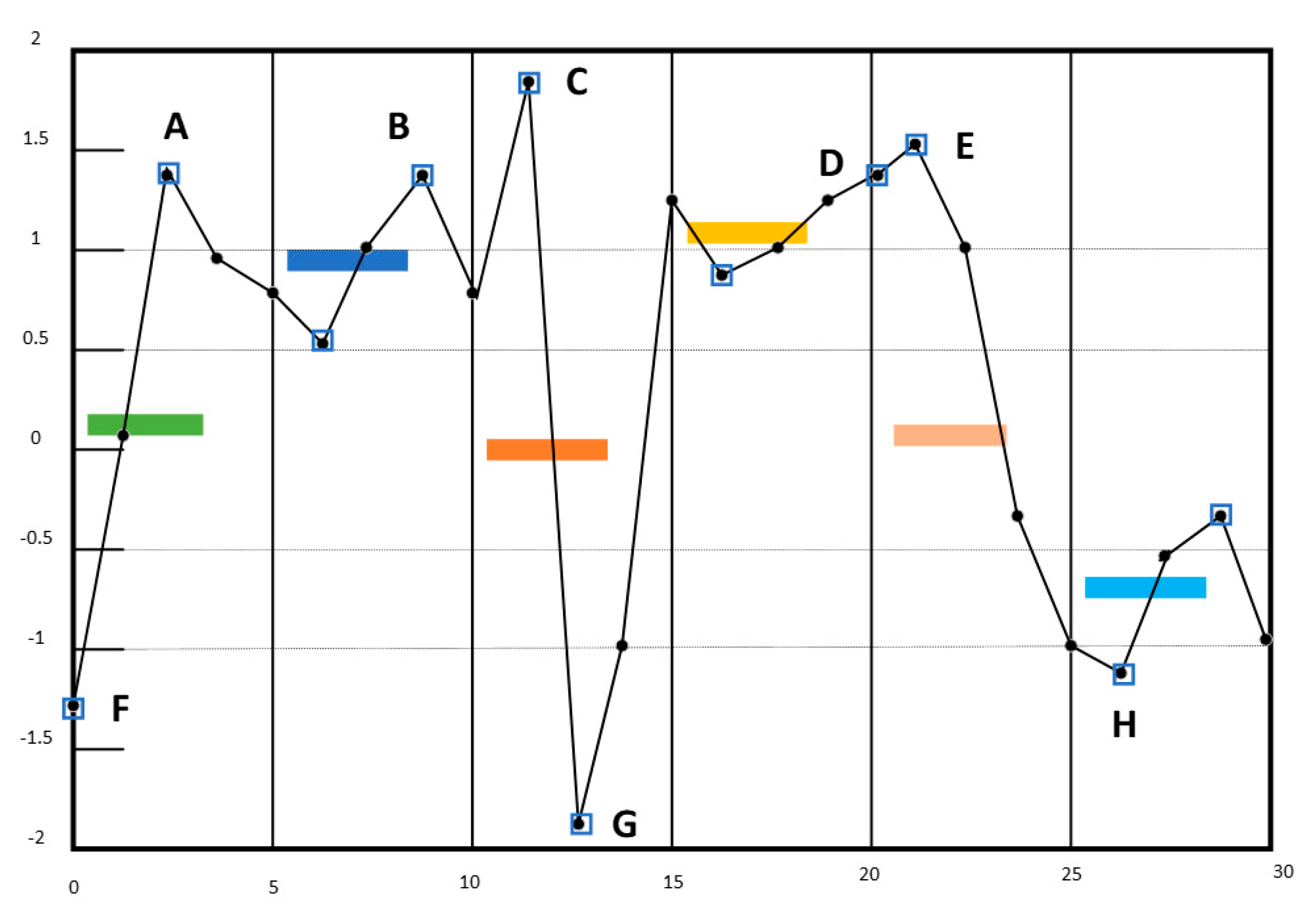
Firstly, in Figure 5, if you follow these points in the ESAX method diagram, for example, for A, B, C, D, E, they will all be mapped to the same character ‘f’ for α = 6 and F, G, H will be mapped to ‘a’. We directly retain these feature points and calculate the boundary distance. At this time, the specific values of A, B, C, D, E, and F, G, H can have a better discrimination.

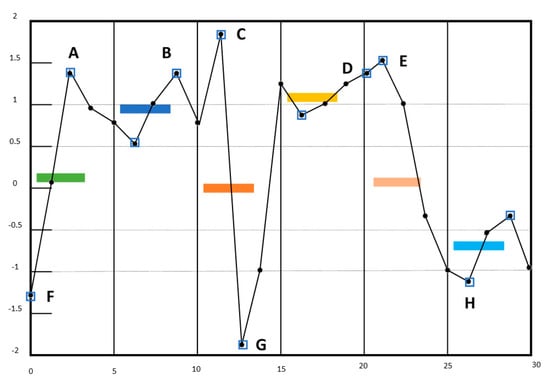
Figure 5. Time series represented as ‘adfeeffcaefffdaabc’ by ESAX [25]. Where the length of time series is 30, the number of segments is 6 and the size of symbols is 6. The capital letters A–H represent the maximum and minimum values in every segment.

Secondly, if we follow the ESAX method, we can see from Equation (11) that there may be a total of 6 comparisons. In fact, according to our method, only two comparisons are needed. Since our distance measurement is consistent with SXA-TD, the low correlation between Equation (13) and Euclidean distance has also been proven in the SAX-TD paper.

$$<\Delta {\mathrm{S}}_1,\Delta S_2>=\{\begin{array}{l}<\Delta S_{\min },\Delta S_{\max }>if{\mathrm{P}}_{\max }>{\mathrm{P}}_{\min }\\ <\Delta S_{\max },\Delta S_{\min }>if{\mathrm{P}}_{\min }>{\mathrm{P}}_{\min }\end{array}$$

(12)

Finally, time series Q and C can be expressed as follows according to our method SAX-BD:

$$\begin{gathered} \mathrm{Q}:\widehat{q_1}\Delta S_1^1\Delta S_2^1 \widehat{q_2} S_1^2{S}_2^2 \dots \widehat{q_w} \Delta S_1^w\Delta S_2^w \\ \mathrm{C}: \widehat{c_1}\Delta C_1^1\Delta C_2^1 \widehat{c_2}\Delta C_1^2\Delta C_2^2 \dots \widehat{c_w}\Delta C_1^w\Delta C_2^w \end{gathered}$$

The equation for calculating the distance between Q and C can be expressed as follows:

$$\mathrm{bd}\left(\mathrm{q},\mathrm{c}\right)=\sqrt{{\left(\Delta q{\left(t\right)}_1-\Delta C{\left(t\right)}_1\right)}^2+{\left(\Delta q{\left(t\right)}_2-\Delta C{\left(t\right)}_2\right)}^2}$$

(13)

$$BDIST\left(\widehat{Q},\widehat{C}\right)=\sqrt{\frac{n}{w}}\sqrt{{\displaystyle \sum }_{i=1}^w({\left(dist\left(\widehat{q},\widehat{c}\right)\right)}^2+\frac{w}{n}{\left(bd\left(q_i,c_i\right)\right)}^2}$$

(14)

3.4. Lower Bound

One of the most important characteristics of the SAX is that it provides a lower bounding distance measure. Lower bound is very useful for controlling errors and speeding up the computation. Below, we will show that our proposed distance also lower bounds the Euclidean distance.

According to [19,20], we have proved that the PAA distance lower bounds the Euclidean distance as follows:

$$\sqrt{{\displaystyle \sum }_{i=1}^n{\left(q_i-c_i\right)}^2}\ge \sqrt{\frac{n}{w}} \sqrt{{\displaystyle \sum }_{i=1}^w{(\overline{q_i},\overline{c_i})}^2}$$

(15)

For proving the TDIST also lower bounds the Euclidean distance, we repeat some of the proofs here. Let Q and C be the means of time series Q and C respectively. We first consider only the single frame case (i.e., w = 1), Equation (14) can be rewritten as follows:

$${\displaystyle \sum }_{i=1}^n{\left(q_i-c_i\right)}^2\ge n{\left(\overline{Q}-\overline{C}\right)}^2$$

(16)

Recall that Q is the average of the time series, so $q_i$ can be represented in terms of $q_i=\overline{Q}-\Delta q_i$. The same applies to each point $c_i$ in C, Equation (15) can be rewritten as follows:

$$n{\left(\overline{Q}-\overline{C}\right)}^2+{\displaystyle \sum }_{i=1}^n{\left(\Delta q_i-\Delta c_i\right)}^2\ge n{\left(\overline{Q}-\overline{C}\right)}^2$$

(17)

Because ${\displaystyle \sum }_{i=1}^n{\left(\Delta q_i-\Delta c_i\right)}^2\ge 0$, Recall the definition in Equation (9) and Equation (12), ${\left(\Delta q{\left(t\right)}_1-\Delta C{\left(t\right)}_1\right)}^2+{\left(\Delta q{\left(t\right)}_2-\Delta C{\left(t\right)}_2\right)}^2$, we can obtain an inequality as follows (its’ obviously exists that the boundary distance in $\Delta q_i$):

$${\displaystyle \sum }_{i=1}^n{\left(q_i-c_i\right)}^2\ge {\left(\Delta q{\left(t\right)}_1-\Delta C{\left(t\right)}_1\right)}^2+{\left(\Delta q{\left(t\right)}_2-\Delta C{\left(t\right)}_2\right)}^2$$

(18)

Substituting Equation (16) into Equation (17), we get:

$$n{\left(\overline{Q}-\overline{C}\right)}^2+{\displaystyle \sum }_{i=1}^n{\left(q_i-c_i\right)}^2\ge n{\left(\overline{Q}-\overline{C}\right)}^2+{\left(bd\left(q_i,c_i\right)\right)}^2$$

(19)

According to [20], the MINDIST lower bounds the PAA distance, that is:

$$n{\left(\overline{Q}-\overline{C}\right)}^2\ge n{\left(\widehat{Q}-\widehat{C}\right)}^2$$

(20)

where$\widehat{Q}$ and $\widehat{C}$ are symbolic representations of Q and C in the original SAX, respectively. By transitivity, the following inequality is true

$${\left(\overline{Q}-\overline{C}\right)}^2+{\displaystyle \sum }_{i=1}^n{\left(\Delta q_i-\Delta c_i\right)}^2\ge n{\left(dist\left(\widehat{Q}-\widehat{C}\right)\right)}^2+{\left(bd\left(q_i,c_i\right)\right)}^2$$

(21)

Recall Equation (15), this means

$${\displaystyle \sum }_{i=1}^n{\left(\Delta q_i-\Delta c_i\right)}^2\ge n\left({\left(dist\left(\widehat{Q}-\widehat{C}\right)\right)}^2+\frac{1}{n}{\left(bd\left(q_i,c_i\right)\right)}^2 \right)$$

(22)

N frames can be obtained by applying the single-frame proof on every frame, that is

$$\sqrt{{\displaystyle \sum }_{i=1}^n{\left(q_i-c_i\right)}^2} \ge \sqrt{\frac{n}{w}} \sqrt{{\displaystyle \sum }_{i=1}^w({\left(dist\left(\widehat{q},\widehat{c}\right)\right)}^2+\frac{w}{n}{\left(bd\left(q_i,c_i\right)\right)}^2}$$

(23)

The quality of a lower bounding distance is usually measured by the tightness of lower bounding (TLB).

$$TL=\frac{Lower Bounding Distance\left(Q,C\right)}{Euclidean Distance\left(Q,C\right)}$$

The value of TLB is in the range [0, 1]. The larger the TLB value, the better the quality. Recall the distance measure in Equation (13), we can obtain that$TLB\left(BDIST\right)\ge TLB\left(MINIDIST\right)$ which means the SAX-BD distance has a tighter lower bound than the original SAX distance.

4. Experimental Validation

In this section, we will present the results of our experimental validation. We used a stand-alone desktop computer, Inter(R) Core(TM) i5-4440 CPU @ 3.10 GHz.

Firstly, we introduce the data sets used, the comparison methods and parameter settings. Then, in order to show experimental results more conveniently, we evaluate the performances of the proposed method in terms of classification accuracy rate shown in figures and classification error rate shown in tables.

4.1. Data Sets

According to the latest time series database UCRArchive2018, in order to make the experimental results more credible, 100 data sets were obtained on the basis of removing null values in the data and show in Table 2. Each data set is divided into a training set and a testing set and a detailed documentation of the data. The datasets contain classes ranging from 2 to 60 and have the lengths of time series varying from 15 to 2844. In addition, the types of the data sets are also diverse, including image, sensor, motion, ECG, etc. [27].

Table 2. 100 different types of time series datasets.

ID	Type	Name	Train	Test	Class	Length
1	Device	ACSF1	100	100	10	1460
2	Image	Adiac	390	391	37	176
3	Image	ArrowHead	36	175	3	251
4	Spectro	Beef	30	30	5	470
5	Image	BeetleFly	20	20	2	512
6	Image	BirdChicken	20	20	2	512
7	Simulated	BME	30	150	3	128
8	Sensor	Car	60	60	4	577
9	Simulated	CBF	30	900	3	128
10	Traffic	Chinatown	20	343	2	24
11	Sensor	CinCECGTorso	40	1380	4	1639
12	Spectro	Coffee	28	28	2	286
13	Device	Computers	250	250	2	720
14	Motion	CricketX	390	390	12	300
15	Motion	CricketY	390	390	12	300
16	Motion	CricketZ	390	390	12	300
17	Image	DiatomSizeReduction	16	306	4	345
18	Image	DistalPhalanxOutlineAgeGroup	400	139	3	80
19	Image	DistalPhalanxOutlineCorrect	600	276	2	80
20	Image	DistalPhalanxTW	400	139	6	80
21	Sensor	Earthquakes	322	139	2	512
22	ECG	ECG200	100	100	2	96
23	ECG	ECGFiveDays	23	861	2	136
24	EOG	EOGHorizontalSignal	362	362	12	1250
25	EOG	EOGVerticalSignal	362	362	12	1250
26	Spectro	EthanolLevel	504	500	4	1751
27	Image	FaceAll	560	1690	14	131
28	Image	FaceFour	24	88	4	350
29	Image	FacesUCR	200	2050	14	131
30	Image	FiftyWords	450	455	50	270
31	Image	Fish	175	175	7	463
32	Sensor	FordA	3601	1320	2	500
33	Sensor	FordB	3636	810	2	500
34	HRM	Fungi	18	186	18	201
35	Motion	GunPoint	50	150	2	150
36	Motion	GunPointAgeSpan	135	316	2	150
37	Motion	GunPointMaleVersusFemale	135	316	2	150
38	Motion	GunPointOldVersusYoung	136	315	2	150
39	Spectro	Ham	109	105	2	431
40	Image	HandOutlines	1000	370	2	2709
41	Motion	Haptics	155	308	5	1092
42	Image	Herring	64	64	2	512
43	Device	HouseTwenty	40	119	2	2000
44	Motion	InlineSkate	100	550	7	1882
45	EPG	InsectEPGRegularTrain	62	249	3	601
46	EPG	InsectEPGSmallTrain	17	249	3	601
47	Sensor	InsectWingbeatSound	220	1980	11	256
48	Sensor	ItalyPowerDemand	67	1029	2	24
49	Device	LargeKitchenAppliances	375	375	3	720
50	Sensor	Lightning2	60	61	2	637
51	Sensor	Lightning7	70	73	7	319
52	Spectro	Meat	60	60	3	448
53	Image	MedicalImages	381	760	10	99
54	Traffic	MelbournePedestrian	1194	2439	10	24
55	Image	MiddlePhalanxOutlineAgeGroup	400	154	3	80
56	Image	MiddlePhalanxOutlineCorrect	600	291	2	80
57	Image	MiddlePhalanxTW	399	154	6	80
58	Sensor	MoteStrain	20	1252	2	84
59	ECG	NonInvasiveFetalECGThorax1	1800	1965	42	750
60	ECG	NonInvasiveFetalECGThorax2	1800	1965	42	750
61	Spectro	OliveOil	30	30	4	570
62	Image	OSULeaf	200	242	6	427
63	Image	PhalangesOutlinesCorrect	1800	858	2	80
64	Sensor	Phoneme	214	1896	39	1024
65	Hemodynamics	PigAirwayPressure	104	208	52	2000
66	Hemodynamics	PigArtPressure	104	208	52	2000
67	Hemodynamics	PigCVP	104	208	52	2000
68	Sensor	Plane	105	105	7	144
69	Power	PowerCons	180	180	2	144
70	Image	ProximalPhalanxOutlineAgeGroup	400	205	3	80
71	Image	ProximalPhalanxOutlineCorrect	600	291	2	80
72	Image	ProximalPhalanxTW	400	205	6	80
73	Device	RefrigerationDevices	375	375	3	720
74	Spectrum	Rock	20	50	4	2844
75	Device	ScreenType	375	375	3	720
76	Spectrum	SemgHandGenderCh2	300	600	2	1500
77	Spectrum	SemgHandMovementCh2	450	450	6	1500
78	Spectrum	SemgHandSubjectCh2	450	450	5	1500
79	Simulated	ShapeletSim	20	180	2	500
80	Image	ShapesAll	600	600	60	512
81	Device	SmallKitchenAppliances	375	375	3	720
82	Simulated	SmoothSubspace	150	150	3	15
83	Sensor	SonyAIBORobotSurface1	20	601	2	70
84	Sensor	SonyAIBORobotSurface2	27	953	2	65
85	Spectro	Strawberry	613	370	2	235
86	Image	SwedishLeaf	500	625	15	128
87	Image	Symbols	25	995	6	398
88	Simulated	SyntheticControl	300	300	6	60
89	Motion	ToeSegmentation1	40	228	2	277
90	Motion	ToeSegmentation2	36	130	2	343
91	Sensor	Trace	100	100	4	275
92	ECG	TwoLeadECG	23	1139	2	82
93	Simulated	TwoPatterns	1000	4000	4	128
94	Simulated	UMD	36	144	3	150
95	Sensor	Wafer	1000	6164	2	152
96	Spectro	Wine	57	54	2	234
97	Image	WordSynonyms	267	638	25	270
98	Motion	Worms	181	77	5	900
99	Motion	WormsTwoClass	181	77	2	900
100	Image	Yoga	300	3000	2	426

4.2. Comparison Methods and Parameter Settings

We compare the result with the above-mentioned ESAX and SAX. We also compare with SAX-TD, which is another latest research improving SAX based on the trend distance. We do the evaluation on the classification task, of which the accuracy is determined by the distance measure. In this way, it is well proved that our method improves the SAX-TD method. To compare the classification accuracy, we conduct the experiments using the 1 nearest neighbor (1-NN) classifier by reading the sun’s paper [26].

To make it fairer for each method, we use the testing data to search for the best parameters w and α. For a given timeseries of length n, w and α are picked using the following criteria [28]):

For w, we search for the value from 2 up ton = 2 and double the value of w each time.

For α, we search for the value from 3 up to 10.

If two sets of parameter settings produce the same classification error rate, we choose the smaller parameters.

The dimensionality reduction ratios are defined as follows:

$$Dimensionality Reduction Ratio=\frac{Number of the reduced data points}{Number of the Original data points}$$

4.3. Result Analysis

To make the table fit all the data, we abbreviate SAX-TD for SAXTD and SAX-BD for SAXBD. The overall classification results are listed in Table 3, where entries with the lowest classification error rates are highlighted. SAX-BD has the lowest error in the most of the data sets (69/100), followed by SAX-TD (22/100), EU (15/100). In some cases, it performs much better than the other two methods, and even achieves a 0 classification error rate.

Table 3. 1-NN classification error rates of different methods.

ID	EU Error	SAX Error	SAX w	SAX Ratio	SAX α	ESAX Error	ESAX w	ESAX Ratio	ESAX α	SAXTD Error	SAXTD w	SAXTD Ratio	SAXTD α	SAXBD Error	SAXBD w	SAXBD Ratio	SAXBD α
1	0.460	0.580	256	0.175	8	0.760	256	0.526	3	0.380	4	0.005	3	0.400	2	0.004	3
2	0.389	0.895	64	0.364	9	0.890	32	0.545	7	0.284	32	0.364	3	0.263	32	0.545	4
3	0.200	0.309	32	0.127	10	0.349	64	0.765	10	0.183	32	0.255	3	0.160	16	0.191	5
4	0.333	0.467	128	0.272	7	0.400	128	0.817	7	0.167	128	0.545	4	0.200	128	0.817	6
5	0.250	0.150	64	0.125	4	0.100	16	0.094	4	0.150	16	0.063	5	0.100	2	0.012	3
6	0.450	0.300	256	0.500	4	0.200	128	0.750	5	0.200	4	0.016	4	0.200	2	0.012	3
7	0.173	0.153	16	0.125	7	0.160	8	0.188	7	0.147	16	0.250	3	0.060	4	0.094	4
8	0.267	0.283	256	0.444	10	0.283	128	0.666	6	0.133	32	0.111	4	0.117	16	0.083	3
9	0.148	0.084	16	0.125	8	0.250	4	0.094	9	0.088	8	0.125	5	0.027	4	0.094	4
10	0.058	0.467	16	0.667	7	0.125	8	1.000	7	0.041	8	0.667	3	0.041	4	0.500	3
11	0.103	0.097	128	0.078	9	0.108	64	0.117	10	0.072	128	0.156	9	0.062	64	0.117	8
12	0.000	0.429	256	0.895	4	0.321	4	0.042	6	0.000	16	0.112	3	0.000	16	0.168	3
13	0.424	0.480	16	0.022	6	0.432	16	0.067	4	0.404	256	0.711	3	0.380	128	0.533	3
14	0.423	0.385	128	0.427	9	0.444	64	0.640	10	0.400	32	0.213	6	0.331	16	0.160	5
15	0.433	0.441	64	0.213	8	0.523	64	0.640	8	0.441	16	0.107	7	0.372	16	0.160	6
16	0.413	0.387	64	0.213	10	0.426	64	0.640	10	0.387	32	0.213	6	0.323	16	0.160	7
17	0.065	0.062	4	0.012	6	0.232	2	0.017	4	0.039	8	0.046	4	0.029	2	0.017	3
18	0.374	0.317	32	0.400	4	0.381	8	0.300	4	0.331	16	0.400	4	0.273	4	0.150	3
19	0.283	0.348	64	0.800	6	0.308	2	0.075	8	0.264	32	0.800	4	0.246	16	0.600	4
20	0.367	0.432	16	0.200	6	0.439	16	0.600	9	0.360	32	0.800	4	0.367	32	1.200	5
21	0.288	0.245	256	0.500	6	0.259	64	0.375	5	0.252	16	0.063	3	0.295	8	0.047	3
22	0.120	0.080	32	0.333	6	0.140	32	1.000	5	0.070	32	0.667	4	0.090	64	2.000	5
23	0.203	0.114	64	0.471	8	0.211	16	0.353	8	0.081	16	0.235	4	0.117	2	0.044	3
24	0.558	0.616	32	0.026	9	0.619	16	0.038	8	0.638	16	0.026	4	0.599	4	0.010	6
25	0.638	0.599	256	0.205	9	0.575	8	0.019	8	0.530	16	0.026	4	0.602	8	0.019	6
26	0.726	0.732	256	0.146	5	0.748	2	0.003	3	0.694	32	0.037	4	0.702	512	0.877	4
27	0.286	0.320	32	0.244	9	0.250	32	0.733	8	0.227	16	0.244	5	0.206	32	0.733	3
28	0.216	0.159	32	0.091	8	0.205	64	0.549	9	0.136	32	0.183	5	0.125	16	0.137	3
29	0.231	0.252	32	0.244	10	0.334	32	0.733	10	0.251	16	0.244	9	0.173	16	0.366	5
30	0.369	0.327	64	0.237	9	0.319	32	0.356	8	0.334	256	1.896	7	0.325	128	1.422	5
31	0.217	0.451	256	0.553	8	0.623	128	0.829	8	0.143	64	0.276	4	0.166	32	0.207	5
32	0.335	0.327	256	0.512	7	0.336	128	0.768	8	0.304	64	0.256	3	0.315	64	0.384	3
33	0.394	0.428	128	0.256	6	0.436	128	0.768	6	0.399	128	0.512	5	0.394	128	0.768	5
34	0.161	0.118	32	0.159	6	0.210	16	0.239	7	0.172	16	0.159	3	0.140	16	0.239	3
35	0.087	0.207	128	0.853	5	0.013	8	0.160	6	0.073	4	0.053	5	0.040	4	0.080	5
36	0.032	0.111	64	0.427	8	0.051	8	0.160	7	0.076	64	0.853	3	0.063	4	0.080	4
37	0.006	0.044	32	0.213	9	0.025	32	0.640	9	0.003	128	1.707	3	0.009	8	0.160	3
38	0.000	0.108	64	0.427	9	0.063	32	0.640	9	0.000	4	0.053	3	0.000	2	0.040	3
39	0.400	0.324	128	0.297	7	0.343	128	0.891	6	0.305	16	0.074	4	0.324	32	0.223	4
40	0.138	0.162	32	0.012	7	0.176	128	0.142	8	0.130	8	0.006	4	0.119	8	0.009	3
41	0.630	0.620	1024	0.938	6	0.597	128	0.352	7	0.584	1024	1.875	7	0.568	32	0.088	3
42	0.484	0.375	8	0.016	5	0.375	128	0.750	5	0.375	32	0.125	3	0.375	16	0.094	4
43	0.319	0.235	512	0.256	7	0.210	512	0.768	7	0.303	2	0.002	3	0.202	64	0.096	3
44	0.658	0.678	128	0.068	10	0.671	128	0.204	9	0.664	4	0.004	4	0.653	4	0.006	7
45	0.000	0.329	128	0.213	5	0.333	128	0.639	6	0.317	4	0.013	5	0.225	4	0.020	4
46	0.000	0.317	8	0.013	8	0.382	32	0.160	5	0.325	32	0.106	4	0.317	32	0.160	4
47	0.438	0.432	32	0.125	8	0.458	64	0.750	7	0.420	128	1.000	5	0.416	128	1.500	4
48	0.045	0.077	16	0.667	9	0.109	8	1.000	8	0.044	16	1.333	3	0.047	16	2.000	4
49	0.507	0.528	512	0.711	8	0.541	16	0.067	8	0.456	16	0.044	4	0.419	16	0.067	4
50	0.246	0.148	64	0.100	7	0.197	128	0.603	5	0.197	16	0.050	6	0.148	8	0.038	4
51	0.425	0.370	256	0.803	6	0.329	8	0.075	6	0.356	8	0.050	6	0.274	16	0.150	4
52	0.067	0.667	2	0.004	3	0.667	2	0.013	3	0.067	16	0.071	3	0.067	2	0.013	3
53	0.316	0.322	64	0.646	7	0.309	32	0.970	9	0.325	32	0.646	5	0.325	64	1.939	6
54	0.055	0.592	16	0.667	10	0.665	8	1.000	9	0.089	16	1.333	3	0.087	16	2.000	3
55	0.481	0.429	2	0.025	3	0.429	4	0.150	3	0.435	2	0.050	3	0.468	32	1.200	3
56	0.234	0.368	64	0.800	8	0.419	16	0.600	4	0.237	64	1.600	5	0.265	16	0.600	5
57	0.487	0.597	64	0.800	6	0.565	8	0.300	7	0.494	8	0.200	3	0.481	8	0.300	3
58	0.121	0.149	16	0.190	5	0.215	16	0.571	6	0.118	32	0.762	5	0.125	32	1.143	6
59	0.171	0.448	512	0.683	10	0.792	128	0.512	10	0.183	32	0.085	4	0.181	16	0.064	5
60	0.120	0.408	512	0.683	10	0.673	128	0.512	10	0.115	128	0.341	5	0.117	16	0.064	8
61	0.133	0.833	2	0.004	3	0.833	2	0.011	3	0.100	128	0.449	3	0.100	64	0.337	3
62	0.479	0.455	32	0.075	6	0.438	64	0.450	8	0.455	256	1.199	5	0.442	16	0.112	3
63	0.239	0.357	32	0.400	5	0.383	4	0.150	3	0.220	64	1.600	4	0.227	32	1.200	4
64	0.891	0.908	64	0.063	8	0.905	4	0.012	6	0.905	128	0.250	8	0.878	4	0.012	3
65	0.909	0.933	128	0.064	8	0.933	64	0.096	6	0.928	8	0.008	3	0.817	2	0.003	3
66	0.712	0.861	64	0.032	5	0.875	512	0.768	3	0.841	32	0.032	4	0.649	2	0.003	3
67	0.861	0.904	1024	0.512	5	0.923	64	0.096	4	0.904	64	0.064	3	0.861	2	0.003	3
68	0.038	0.048	128	0.889	9	0.105	16	0.333	8	0.029	32	0.444	3	0.000	8	0.167	3
69	0.022	0.072	128	0.889	6	0.072	32	0.667	6	0.044	32	0.444	5	0.033	32	0.667	6
70	0.215	0.537	32	0.400	6	0.424	2	0.075	6	0.180	64	1.600	3	0.176	16	0.600	3
71	0.192	0.292	8	0.100	6	0.289	16	0.600	4	0.144	64	1.600	3	0.131	32	1.200	3
72	0.293	0.976	64	0.800	4	0.746	2	0.075	7	0.278	64	1.600	3	0.244	8	0.300	3
73	0.605	0.608	16	0.022	5	0.632	32	0.133	5	0.581	2	0.006	3	0.520	8	0.033	3
74	0.360	0.180	1024	0.360	4	0.220	256	0.270	4	0.160	32	0.023	3	0.140	1024	1.080	4
75	0.640	0.597	16	0.022	6	0.573	32	0.133	8	0.576	16	0.044	3	0.555	2	0.008	3
76	0.102	0.193	32	0.021	8	0.310	4	0.008	7	0.278	4	0.005	5	0.053	32	0.064	5
77	0.402	0.471	64	0.043	9	0.669	4	0.008	10	0.511	4	0.005	7	0.211	32	0.064	7
78	0.209	0.287	64	0.043	9	0.529	4	0.008	9	0.476	4	0.005	6	0.116	32	0.064	5
79	0.461	0.428	8	0.016	4	0.411	64	0.384	5	0.406	128	0.512	6	0.361	128	0.768	4
80	0.248	0.278	512	1.000	10	0.290	64	0.375	9	0.247	16	0.063	4	0.232	32	0.188	3
81	0.659	0.533	64	0.089	7	0.547	16	0.067	5	0.347	4	0.011	6	0.365	4	0.017	6
82	0.047	0.240	8	0.533	8	0.273	4	0.800	7	0.167	2	0.267	3	0.060	4	0.800	3
83	0.304	0.306	64	0.914	6	0.146	8	0.343	4	0.303	64	1.829	4	0.243	8	0.343	3
84	0.141	0.120	64	0.985	6	0.188	16	0.738	5	0.143	32	0.985	5	0.136	16	0.738	10
85	0.054	0.354	128	0.545	4	0.354	64	0.817	4	0.038	64	0.545	3	0.043	32	0.409	3
86	0.211	0.408	128	1.000	10	0.440	32	0.750	10	0.208	32	0.500	4	0.125	16	0.375	5
87	0.101	0.137	128	0.322	9	0.192	128	0.965	8	0.104	16	0.080	5	0.095	8	0.060	7
88	0.120	0.047	16	0.267	8	0.147	16	0.800	8	0.100	8	0.267	8	0.050	16	0.800	8
89	0.320	0.311	64	0.231	6	0.373	8	0.087	5	0.307	8	0.058	4	0.246	4	0.043	3
90	0.192	0.123	128	0.373	7	0.177	64	0.560	4	0.138	16	0.093	5	0.123	64	0.560	5
91	0.240	0.380	32	0.116	6	0.240	4	0.044	7	0.160	64	0.465	3	0.000	2	0.022	3
92	0.253	0.311	8	0.098	7	0.254	8	0.293	7	0.166	64	1.561	4	0.057	4	0.146	3
93	0.093	0.039	16	0.125	9	0.217	4	0.094	10	0.063	16	0.250	8	0.048	8	0.188	6
94	0.194	0.194	16	0.107	9	0.160	8	0.160	6	0.208	16	0.213	4	0.014	4	0.080	3
95	0.005	0.002	128	0.842	6	0.002	32	0.632	7	0.003	32	0.421	5	0.003	32	0.632	7
96	0.389	0.500	2	0.009	3	0.500	2	0.026	3	0.407	64	0.547	3	0.426	16	0.205	3
97	0.382	0.381	64	0.237	8	0.384	64	0.711	10	0.382	16	0.119	7	0.381	16	0.178	4
98	0.545	0.481	256	0.284	4	0.558	128	0.427	4	0.468	32	0.071	4	0.442	32	0.107	4
99	0.390	0.351	512	0.569	4	0.338	128	0.427	5	0.312	512	1.138	4	0.312	8	0.027	4
100	0.170	0.198	64	0.150	10	0.174	64	0.451	10	0.176	64	0.300	6	0.166	16	0.113	5

We use the Wilcoxon signed ranks test to test the significance of our method against other methods. The test results are displayed in Table 4. Where $n^{+},$ $n^{\_}$, and $n^0$ denote the numbers of data sets where the error rates of the SAX-BD are lower, larger than and equal to those of another method respectively. The p-values (the smaller a p-value, the more significant the improvement) demonstrate that our distance measure achieves a significant improvement over the other four methods on classification accuracy.

Table 4. The Wilcoxon signed ranks test results of the SAX-BD vs. other methods. A p-value less than or equal to 0.05 indicates a significant improvement. n* means positive, n means equal and n⁰ means negative. The larger the value of n*, the better performance of SAX-TD.

Methods	n*	n	n0	p-Value
SAX-BD vs. Euclidean	79	15	6	p < 0.05
SAX-BD vs. SAX	83	11	6	p < 0.05
SAX-BD vs. ESAX	87	10	3	p < 0.05
SAX-BD vs. SAX-TD	69	22	10	p < 0.05

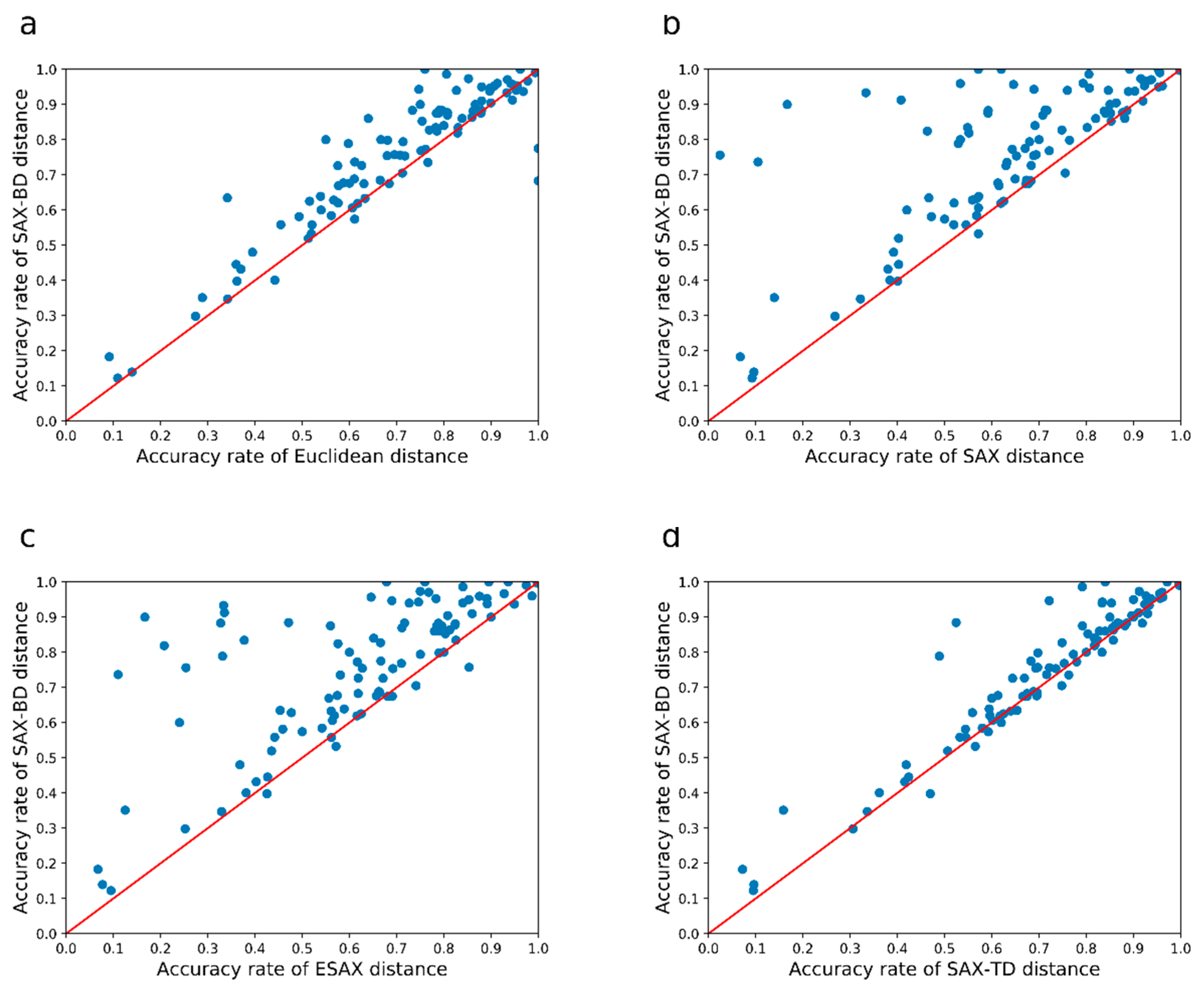
To provide a more intuitive illustration of the performance of the different measures compared in Table 3 and Table 4, we use scatter plots for pairwise comparisons. In a scatter plot, the accuracy rates of two measures under comparison are used as the x and y coordinates of a dot, where a dot represents a data set. When a dot above the diagonal line, the ‘y’ method performs better than the ‘x’ method. In addition, the further a dot is from the diagonal line, the greater the margin of an accuracy improvement. The region with more dots indicates a better method than the other.

In the following, we explain the results in Figure 6.

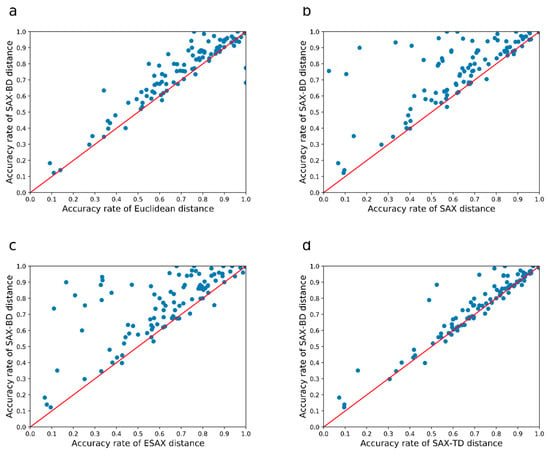
Figure 6. The SAX-BD algorithm is compared with other algorithms for accuracy. (a–d) represents a comparison between SAX-BD with Euclidean, SAX, ESAX, SAX-TD. The more dots above the red slash, the better performs of SAX-BD.

We illustrate the performance of our distance measure against the Euclidean distance, SAX distance, ESAX distance, SAX-TD distance in Figure 6a–d, respectively. Our method outperforms the other four methods by a large margin, both in the number of points and the distance of these points from the diagonals. From these figures, we can see that most of the points are far away from the diagonals, which indicates that our method has much lower error rates on most of the data sets.

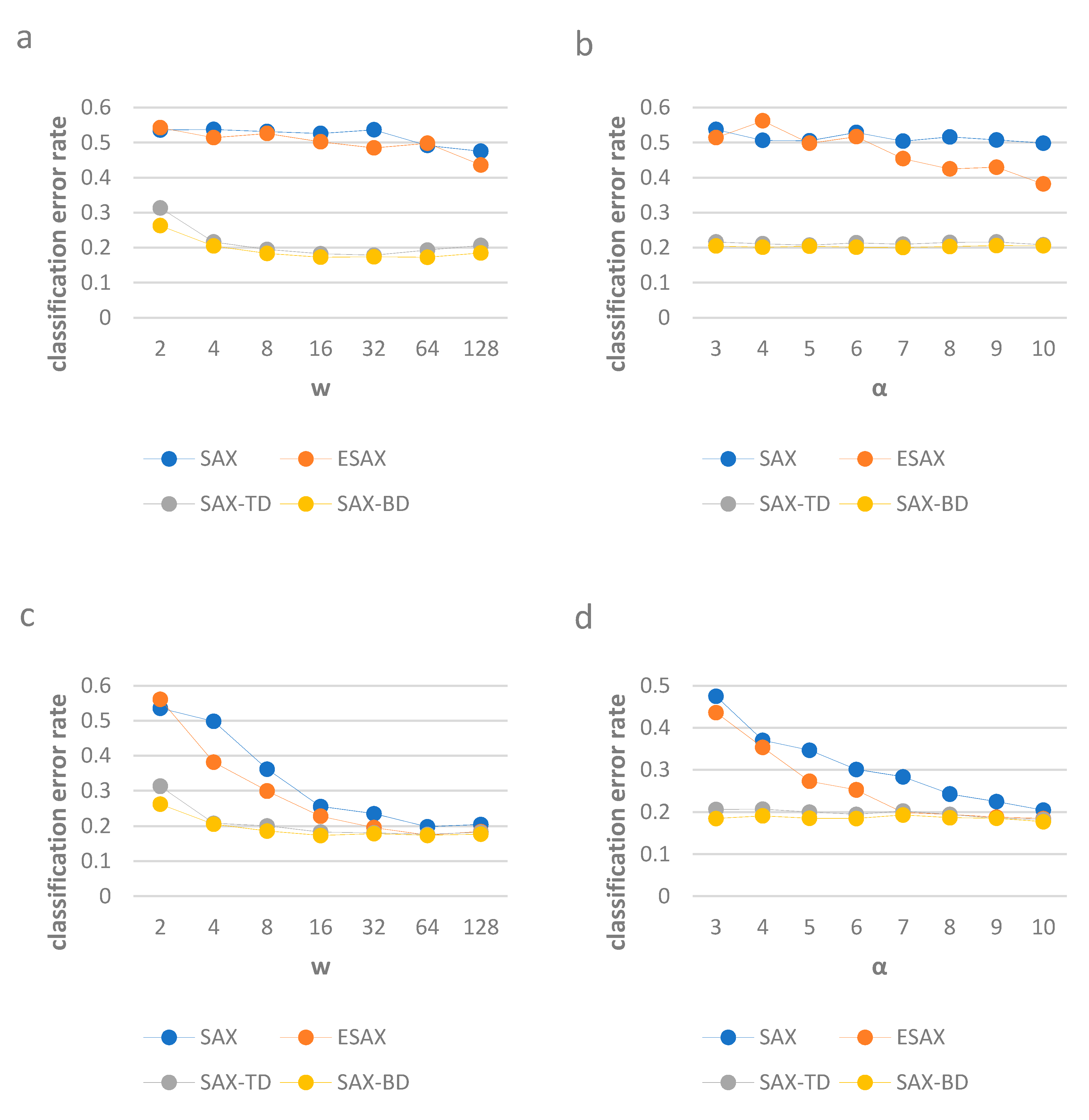
To show the continuity performance of our method and other three methods, we run the experiments on data set Yoga. We firstly compare the classification error rates with different w while α is fixed at 3, and then with different α while w is fixed at 4 (to illustrate the classification error rates using small parameters). Secondly, we use w, which varies, while α is fixed at 10, and then α varies while w is fixed at 128 (to illustrate the classification error rates using large parameters).

SAX-TD and SAX-BD has lower error rates than the other two methods when the parameters are small and large, SAX-BD has lower error rates than the SAX-TD. The results are shown in Figure 7.

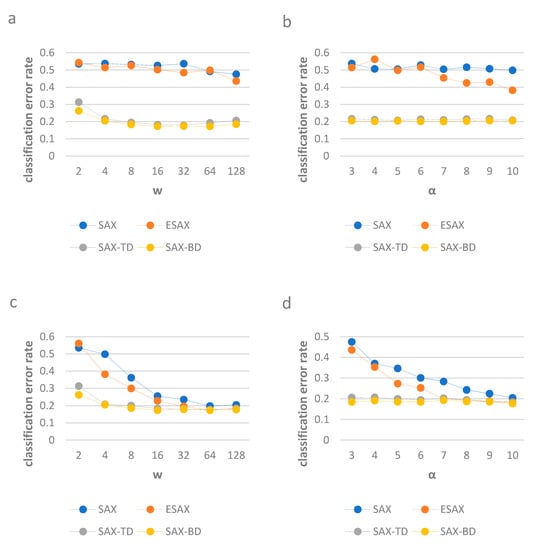
Figure 7. The classification error rates of SAX, ESAX, SAX-TD and SAX-BD with different parameters w and α. For (a), on Gun-Point, w varies while α is fixed at 3, for (b), on Gun-Point, varies while w is fixed at 4. For (c), on Yoga, w varies while α is fixed at 10, for (d), on Yoga, varies while w is fixed at 128.

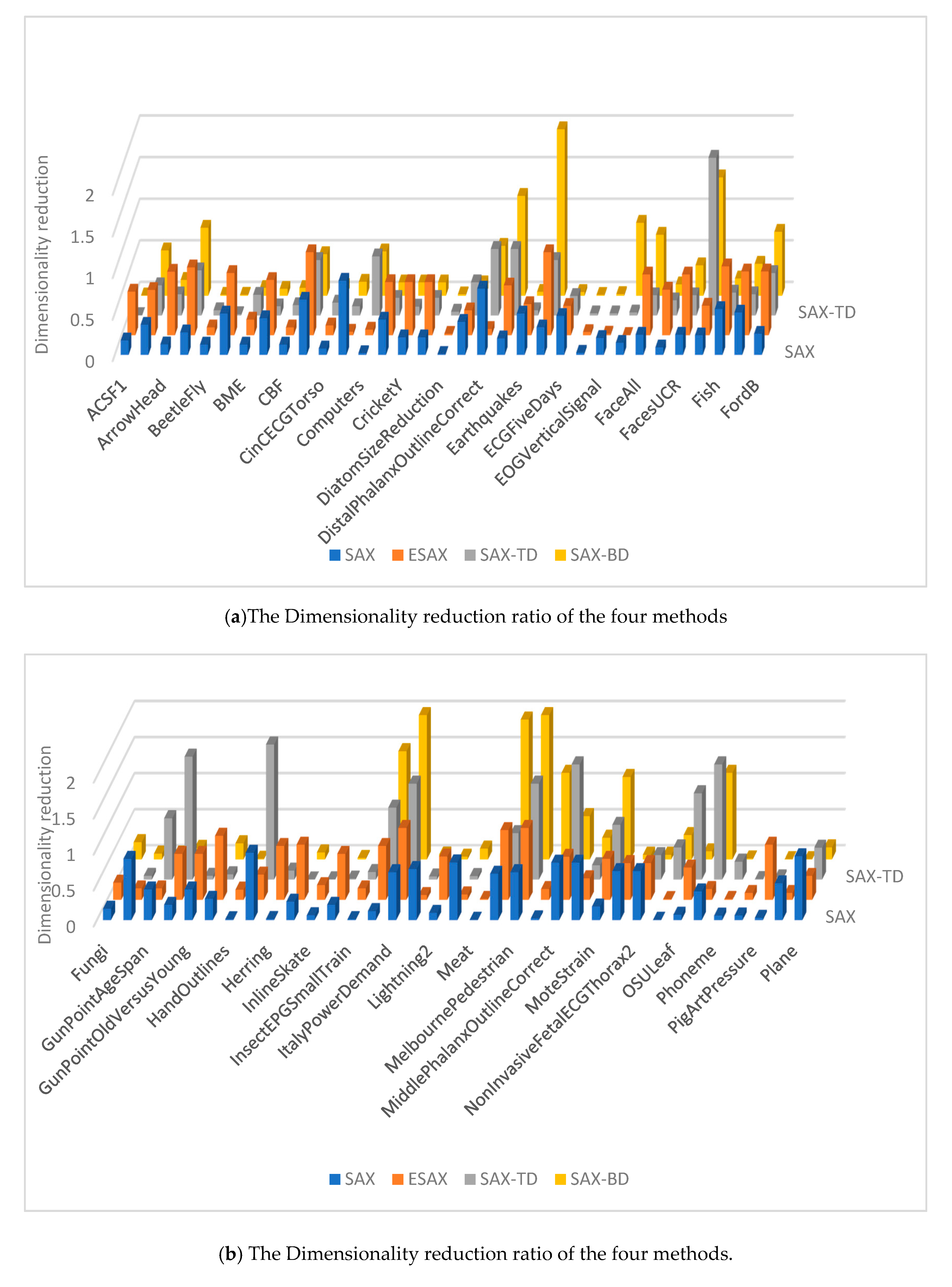
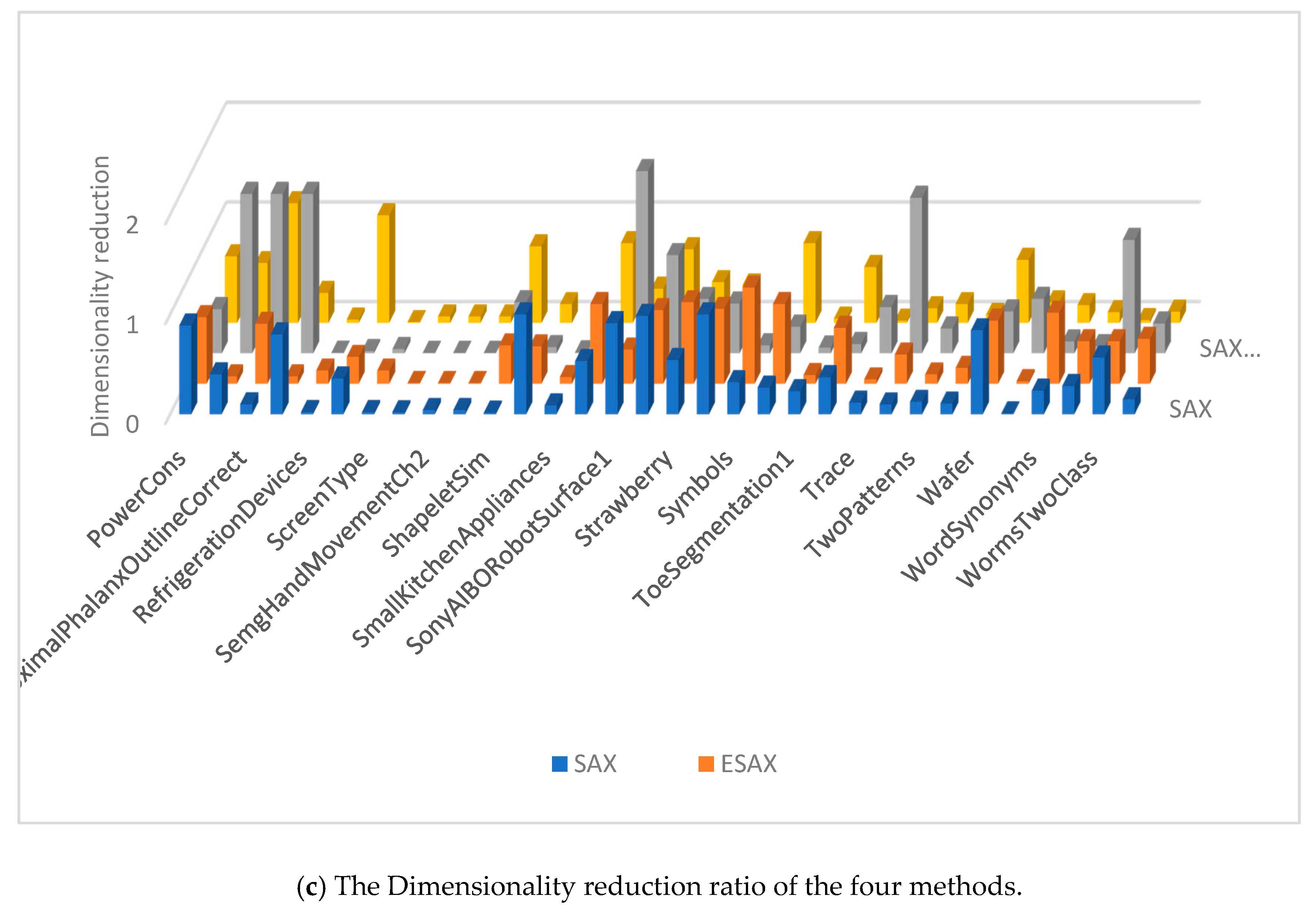
The dimensionality reduction ratios are calculated using the w when the four methods achieve their smallest classification error rates on each data set, shown in Figure 8. The SAX-TD and SAX-BD representation use more values than SAX, SAX-TD use fewer values than ESAX. In fact, our method has a low dimensionality reduction ratio in majority datasets, and even uses fewer values than SAX-TD.

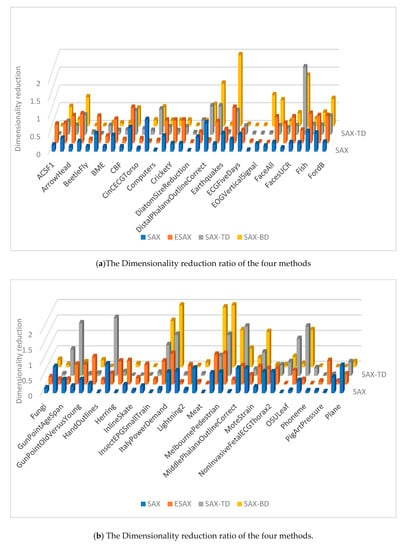
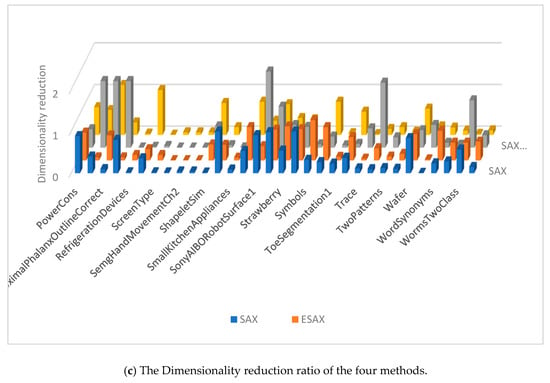
Figure 8. Dimensionality reduction ratio of the four methods.

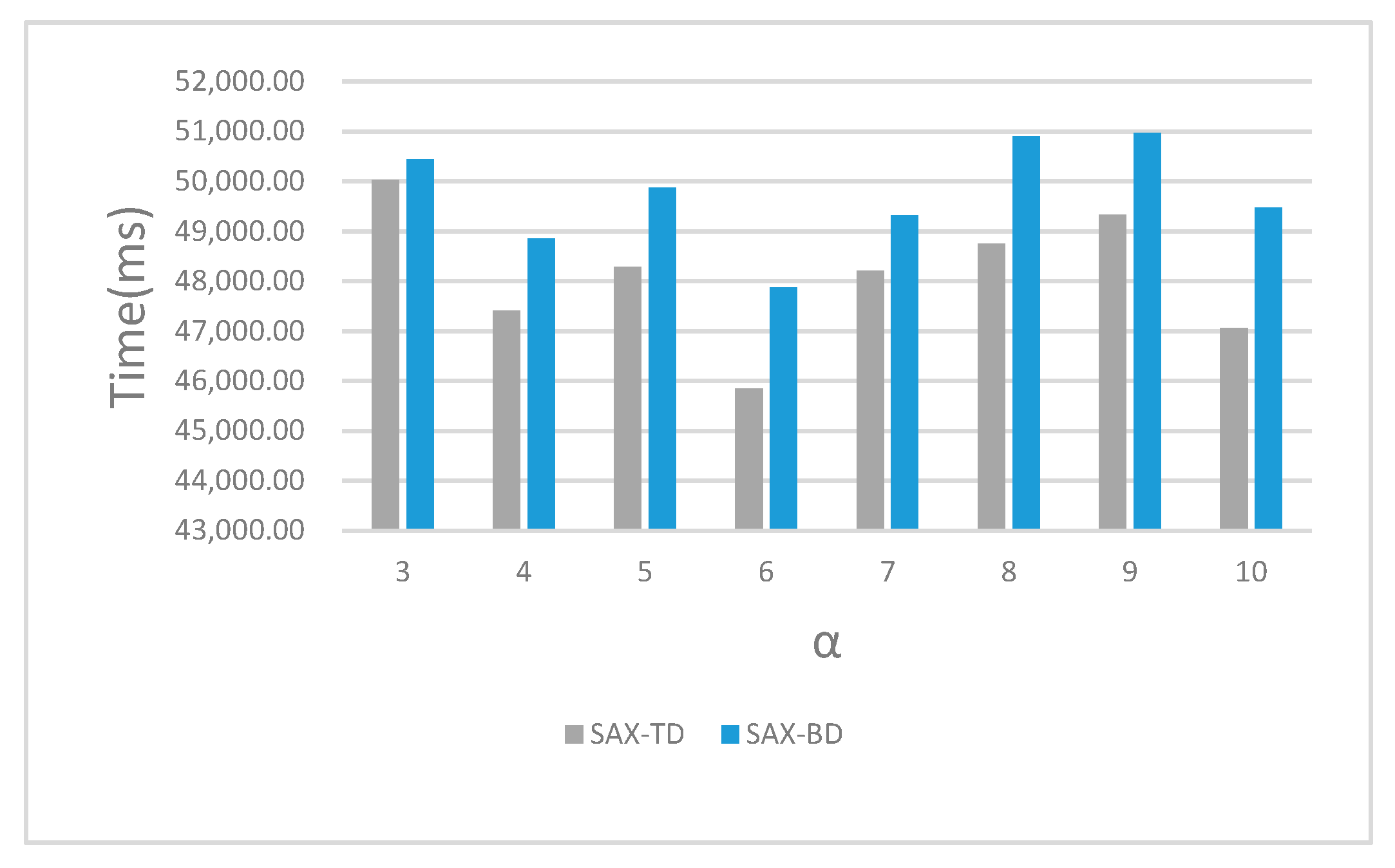
We also recorded the running time of SAX-TD and SAX-BD with different α from 3 to 10 shown in Figure 9. The experimental results indicated that we have made a greater improvement at the cost of only a little time, and that’s well worth it.

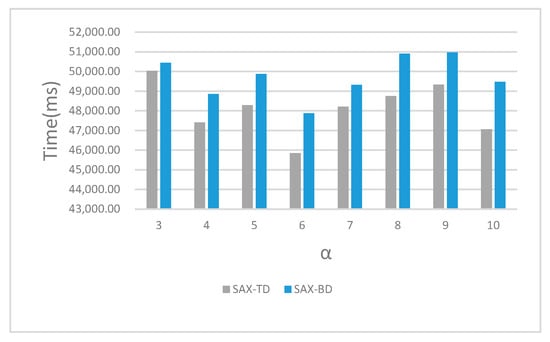
Figure 9. The running time of different methods with different values of α.

5. Conclusions

Our proposed SAX-BD algorithm uses the boundary distance as a new distance metric to obtain a new time series representation. We analyze some cases that ESAX and SAX-TD cannot solve, and it is known that the classification accuracy of ESAX algorithm is not as good as SAX-TD. We combine the advantages of these two methods, analyzing and deriving our method as an extension of these two methods. We also proved that our improved distance measure not only keeps a lower-bound to the Euclidean distance, but also has a low dimensionality reduction ratio in majority datasets. In terms of the expression complexity of time series, our algorithm SAX-BD and ESAX algorithm are three times more than SAX, and two times more than SAX-TD. However, in terms of running time, we spend just a little more. In terms of the classification accuracy, we have improved this a lot, that means a good compromise has made between dimensional reduction and classification accuracy. For future work, we intend to change our original algorithm to make time advantage.