Differential Evolution with Linear Bias Reduction in Parameter Adaptation
Abstract
1. Introduction
2. Materials and Methods
2.1. Differential Evolution Algorithm
2.2. Related Studies on Differential Evolution
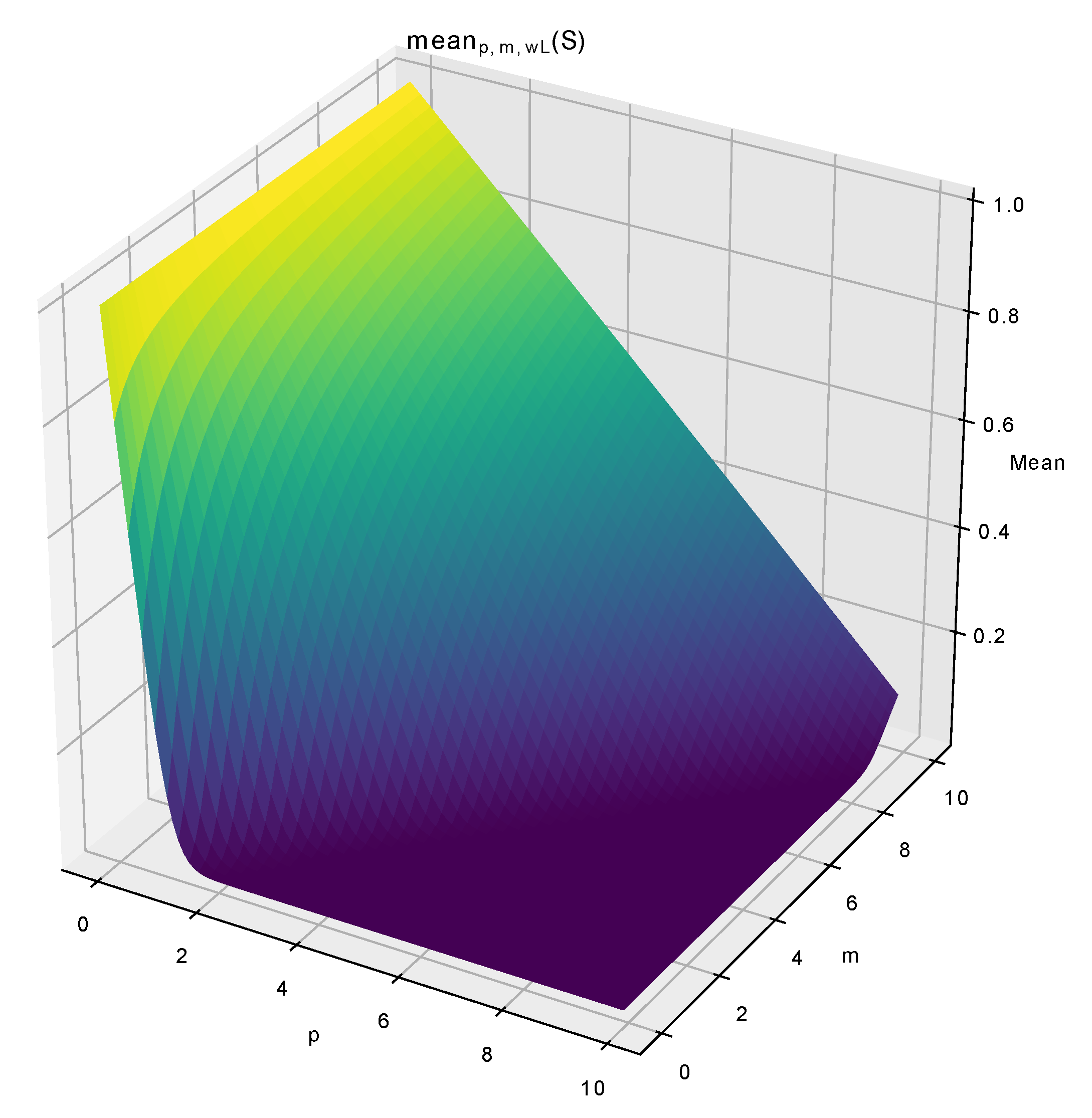
2.3. Proposed Approach: Linear Bias Reduction
| Algorithm 1 L-SHADE-LBR. |
|
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EA | Evolutionary Algorithm |
| DE | Differential Evolution |
| L-SHADE | Linear population size reduction Success History-based Adaptive Differential Evolution |
| LBR | Linear Bias Reduction |
| CEC | Congress on Evolutionary Computation |
References
- Aleti, A.; Moser, I. A Systematic Literature Review of Adaptive Parameter Control Methods for Evolutionary Algorithms. ACM Comput. Surv. 2016, 49, 1–35. [Google Scholar] [CrossRef]
- Eiben, A.E.; Selmar, K.S. Evolutionary Algorithm Parameters and Methods to Tune Them. In Autonomous Search; Springer: Berlin/Heidelberg, Germany, 2012; pp. 15–36. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential Evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization; Technial Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Neri, F.; Tirronen, V. Recent advances in Differential Evolution: A survey and experimental analysis. Artif. Intell. Rev. 2010, 33, 61–106. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in Differential Evolution–an updated survey. Swarm Evol. Comput. 2016, 15, 1–30. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Success-history based parameter adaptation for differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Viktorin, A.; Senkerik, R.; Pluhacek, M.; Kadavy, T.; Zamuda, A. Distance based parameter adaptation for Success-History based Differential Evolution. Swarm Evol. Comput. 2019, 50, 100462. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Brest, J.; Maučec, M.S.; Boškovic, B. Single objective real-parameter optimization algorithm jSO. In Proceedings of the IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 1311–1318. [Google Scholar]
- Stanovov, V.; Akhmedova, S.; Semenkin, E.; Semenkina, M. Generalized Lehmer Mean for Success History based Adaptive Differential Evolution. In Proceedings of the IJCCI 2019: 11th International Joint Conference on Computational Intelligence, Vienna, Austria, 17–19 September 2019; pp. 93–100. [Google Scholar]
- Storn, R.M.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Zhang, J.; Snaderson, A. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. Selective Pressure Strategy in differential evolution: Exploitation improvement in solving global optimization problems. Swarm Evol. Comput. 2019, 50, 100463. [Google Scholar] [CrossRef]
- Zaharie, D. On the explorative power of differential evolution. In Proceedings of the 3rd International Workshop Symbolic Numerical Algorithms Scientific Computing, Timişoara, Romania, 2–5 October 2001. [Google Scholar]
- Zaharie, D. Critical values for the control parameters of differential evolution algorithms. In Proceedings of the 8th International Mendel Conference Soft Computing, Brno, Czech Republic, 8–10 June 2002; pp. 62–67. [Google Scholar]
- Zaharie, D. Parameter adaptation in differential evolution by controlling the population diversity. In Proceedings of the 4th International Workshop Symbolic Numeric Algorithms Scientific Computing, Timisoara, Romania, 9–12 October 2002; pp. 385–397. [Google Scholar]
- Zaharie, D. Statistical properties of differential evolution and related random search algorithms. In Proceedings of the International Conference on Computational Statistics, Kraków, Poland, 23–25 June 2008; pp. 473–485. [Google Scholar]
- Brest, J.; Greiner, S.; Boškovic, B.; Mernik, M.; Žumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Omran, M.G.H.; Salman, A.; Engelbrecht, A.P. Self-adaptive differential evolution. Comput. Intell. Secur. Lect. Notes Artif. Intell. 2005, 3801, 192–199. [Google Scholar]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Neri, F.; Tirronen, V. Scale factor local search in differential evolution. Memet. Comput. 2009, 1, 153–171. [Google Scholar] [CrossRef]
- Das, S.; Konar, A.; Chakraborty, U.K. Two improved differential evolution schemes for faster global search. In Proceedings of the 2005 Conferenceon Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005; pp. 991–998. [Google Scholar]
- Elsayed, S.M.; Sarker, R.A.; Ray, T. Differential evolution with automatic parameter configuration for solving the CEC2013 competition on real-parameter optimization. In Proceedings of the IEEE Congresson Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1932–1937. [Google Scholar]
- Sarker, R.A.; Elsayed, S.M.; Ray, T. Differential evolution with dynamic parameters selection for optimization problems. IEEE Trans. Evol. Comput. 2014, 18, 689–707. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z.; Ling, C.X.; Li, H. Enhanced Differential Evolution With Adaptive Strategies for Numerical Optimization. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2011, 41, 397–413. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Weber, M.; Tirronen, V.; Neri, F. Scale factor inheritance mechanism in distributed differential evolution. Soft Comput. 2010, 14, 1187–1207. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 372–379. [Google Scholar]
- Mohamed, A.W.; Hadi, A.A.; Fattouh, A.M.; Jambi, K.M. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 145–152. [Google Scholar]
- Caraffini, F.; Neri, F.; Cheng, J.; Zhang, G.; Picinali, L.; Iacca, G.; Mininno, E. Super-fit Multicriteria Adaptive Differential Evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013. [Google Scholar]
- Sallam, K.M.; Elsayed, S.M.; Chakrabortty, R.K.; Ryan, M.J. Improved Multi-operator Differential Evolution Algorithm for Solving Unconstrained Problems. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Al-Dabbagh, R.D.; Neri, F.; Idris, N.; Baba, M.S. Algorithmic design issues in adaptive differential evolution schemes: Review and taxonomy. Swarm Evol. Comput. 2018, 44, 284–311. [Google Scholar] [CrossRef]
- Brest, J.; Maučec, M.S.; Boškovic, B. Differential Evolution Algorithm for Single Objective Bound-Constrained Optimization: Algorithm j2020. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Brest, J.; Maučec, M.S.; Boškovic, B. The 100-Digit Challenge: Algorithm jDE100. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 19–26. [Google Scholar]
- Piotrowski, A. Review of Differential Evolution population size. Swarm Evol. Comput. 2019, 32, 1–24. [Google Scholar] [CrossRef]
- Zamuda, A.; Brest, J.; Mezura-Montes, E. Structured Population Size Reduction Differential Evolution with Multiple Mutation Strategies on CEC 2013 real parameter optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1925–1931. [Google Scholar]
- Caraffini, F.; Kononova, A.V.; Corne, D. Infeasibility and structural bias in differential evolution. Inf. Sci. 2019, 496, 161–179. [Google Scholar] [CrossRef]
- Bullen, P.S. Handbook of Means and Their Inequalities; Springer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Yue, C.T.; Price, K.V.; Suganthan, P.N.; Liang, J.J.; Ali, M.Z.; Qu, B.Y.; Awad, N.H.; Biswas, P. Problem Definitions and Evaluation Criteria for the CEC 2020 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization; Technial Report; Nanyang Technological University: Singapore, 2019. [Google Scholar]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. Genetic Algorithm with Success History based Parameter Adaptation. In Proceedings of the IJCCI 2019: 11th International Joint Conference on Computational Intelligence, Vienna, Austria, 17–19 September 2019; pp. 180–187. [Google Scholar]
| L-SHADE vs. L-SHADE-LBR | 0+/27 = /3− | 8+/21 = /1− | 17+/12 = /1− | 16+/10 = /4− |
| jSO vs. jSO-LBR | 0+/29 = /1− | 5+/24 = /1− | 10+/20 = /0− | 12+/16 = /2− |
| DISH vs. DISH-LBR | 0+/30 = /0− | 2+/28 = /0− | 4+/25 = /1− | 9+/16 = /5− |
| Function | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f3 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f4 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f5 | 1.466332 ± 7.966326 | 1.820984 ± 8.296894 | 2.028990 ± 9.021237 |
| f6 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f7 | 1.165531 ± 4.999618 | 1.206354 ± 5.092644 | 1.202930 ± 5.555746 |
| f8 | 1.338034 ± 8.316749 | 1.878932 ± 8.513805 | 1.853360 ± 1.042962 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 2.224059 ± 4.032137 | 1.822742 ± 3.227775 | 3.377682 ± 5.852428 |
| f11 | 1.181580 ± 4.216185 | 1.516416 ± 3.630057 | 0.0 ± 0.0 |
| f12 | 1.526398 ± 3.919816 | 2.734428 ± 1.723809 | 1.673563 ± 4.110506 |
| f13 | 2.441962 ± 2.352857 | 2.474151 ± 2.390764 | 3.043588 ± 2.362332 |
| f14 | 4.638013 ± 1.575738 | 4.747525 ± 1.948063 | 3.902250 ± 1.931283 |
| f15 | 1.346569 ± 1.999631 | 1.225807 ± 1.933628 | 3.401098 ± 2.058195 |
| f16 | 4.510030 ± 1.916985 | 3.580149 ± 1.948515 | 5.429780 ± 3.146415 |
| f17 | 1.572282 ± 1.571081 | 1.409888 ± 1.729228 | 9.310686 ± 2.782305 |
| f18 | 2.218042 ± 1.984943 | 1.422543 ± 1.699201 | 1.992204 ± 1.953476 |
| f19 | 9.994697 ± 1.044910 | 1.164565 ± 1.284938 | 1.266488 ± 1.275577 |
| f20 | 6.121039 ± 4.328228 | 6.121039 ± 4.328228 | 3.672626 ± 1.476685 |
| f21 | 1.450680 ± 5.038353 | 1.506000 ± 5.160565 | 1.302909 ± 4.692892 |
| f22 | 1.000056 ± 3.965344 | 1.000078 ± 5.532071 | 1.000000 ± 0.0 |
| f23 | 3.010949 ± 1.487577 | 3.024831 ± 1.330968 | 3.010731 ± 1.481965 |
| f24 | 2.592233 ± 1.036631 | 2.666515 ± 1.025191 | 2.748786 ± 9.709894 |
| f25 | 4.237633 ± 2.248348 | 4.095063 ± 1.979616 | 4.095055 ± 1.979735 |
| f26 | 3.000000 ± 0.0 | 2.941176 ± 4.159452 | 3.000000 ± 0.0 |
| f27 | 3.893875 ± 2.231327 | 3.892298 ± 5.642233 | 3.894176 ± 2.032786 |
| f28 | 4.231326 ± 1.442053 | 3.578377 ± 1.172708 | 3.294695 ± 8.948919 |
| f29 | 2.332684 ± 2.297889 | 2.334880 ± 1.961177 | 2.347158 ± 3.342209 |
| f30 | 3.244280 ± 1.586213 | 3.945063 ± 2.293938 | 1.641868 ± 1.133010 |
| Function | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f3 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f4 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f5 | 1.931394 ± 8.221626 | 1.833883 ± 8.894004 | 1.775343 ± 6.914080 |
| f6 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f7 | 1.208296 ± 5.567794 | 1.216231 ± 5.829416 | 1.201511 ± 6.008566 |
| f8 | 2.185022 ± 8.815939 | 1.853397 ± 9.033848 | 2.263072 ± 9.046168 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 3.481015 ± 5.336775 | 5.487013 ± 8.016722 | 2.936753 ± 5.244595 |
| f11 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f12 | 7.398462 ± 2.818943 | 1.674478 ± 4.117527 | 2.640647 ± 1.640653 |
| f13 | 2.803025 ± 2.437121 | 2.675462 ± 2.342831 | 3.290499 ± 2.290796 |
| f14 | 1.560720 ± 3.618380 | 1.462447 ± 3.453513 | 1.170540 ± 3.205656 |
| f15 | 2.393091 ± 2.081327 | 2.935211 ± 2.028156 | 2.354370 ± 2.096280 |
| f16 | 7.189243 ± 3.081263 | 5.107098 ± 2.956673 | 5.481845 ± 2.890193 |
| f17 | 4.551964 ± 3.136878 | 5.855833 ± 3.998470 | 5.405732 ± 3.427532 |
| f18 | 2.217356 ± 2.083894 | 5.850836 ± 2.756645 | 2.256478 ± 2.133737 |
| f19 | 1.122558 ± 2.105432 | 1.145965 ± 1.292694 | 8.007165 ± 1.032611 |
| f20 | 8.095347 ± 2.808347 | 3.672626 ± 1.716079 | 3.978678 ± 1.524131 |
| f21 | 1.323348 ± 4.782543 | 1.363186 ± 4.917879 | 1.444566 ± 5.104734 |
| f22 | 1.000079 ± 5.559800 | 1.000068 ± 4.797234 | 1.000268 ± 9.379501 |
| f23 | 3.010237 ± 1.490490 | 2.955855 ± 4.183554 | 3.013980 ± 1.570153 |
| f24 | 3.018687 ± 7.386128 | 2.656853 ± 1.019472 | 2.654399 ± 1.018634 |
| f25 | 4.015055 ± 1.221117 | 4.059703 ± 1.730538 | 4.068576 ± 1.801739 |
| f26 | 3.000000 ± 0.0 | 3.000000 ± 0.0 | 3.000000 ± 0.0 |
| f27 | 3.894635 ± 1.538980 | 3.893975 ± 2.171814 | 3.894477 ± 1.761875 |
| f28 | 3.294695 ± 8.948919 | 3.361344 ± 9.902322 | 3.411471 ± 1.032896 |
| f29 | 2.350070 ± 2.765177 | 2.345793 ± 3.214256 | 2.337357 ± 2.522189 |
| f30 | 3.244093 ± 1.586216 | 1.641771 ± 1.133012 | 3.945173 ± 4.152092 |
| Function | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f3 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f4 | 5.432730 ± 1.761079 | 5.856160 ± 0.0 | 5.856160 ± 0.0 |
| f5 | 7.093248 ± 1.514062 | 5.984748 ± 1.259837 | 8.566069 ± 1.414316 |
| f6 | 1.610282 ± 4.409940 | 2.683804 ± 1.897736 | 1.125136 ± 3.080402 |
| f7 | 3.643252 ± 1.163031 | 3.635001 ± 1.050653 | 3.901514 ± 1.897382 |
| f8 | 7.636827 ± 1.421298 | 5.947331 ± 1.286650 | 8.606066 ± 1.668634 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 1.541919 ± 2.100733 | 1.588640 ± 2.124062 | 1.633723 ± 2.570738 |
| f11 | 1.480573 ± 2.154669 | 1.286354 ± 2.135075 | 6.873639 ± 1.395100 |
| f12 | 9.665733 ± 3.204188 | 2.131759 ± 1.341268 | 2.351108 ± 1.392522 |
| f13 | 1.507205 ± 7.899218 | 1.747101 ± 5.664911 | 1.616138 ± 5.997028 |
| f14 | 2.133530 ± 9.644383 | 2.136757 ± 3.272063 | 2.194751 ± 3.183398 |
| f15 | 2.465098 ± 1.482018 | 1.524179 ± 9.985145 | 1.212446 ± 8.005678 |
| f16 | 6.228463 ± 7.399308 | 3.557114 ± 3.589944 | 4.984834 ± 6.435235 |
| f17 | 3.486476 ± 5.016896 | 3.316091 ± 5.201363 | 3.505441 ± 6.723407 |
| f18 | 2.146325 ± 3.044085 | 2.077898 ± 4.073286 | 2.081425 ± 4.281106 |
| f19 | 5.078805 ± 1.737644 | 5.462701 ± 1.914274 | 5.006098 ± 1.699874 |
| f20 | 3.322552 ± 5.277263 | 3.011395 ± 4.949041 | 2.957005 ± 7.071608 |
| f21 | 2.068744 ± 1.548801 | 2.063994 ± 1.477586 | 2.087112 ± 1.873729 |
| f22 | 1.000000 ± 0.0 | 1.000000 ± 0.0 | 1.000000 ± 0.0 |
| f23 | 3.485940 ± 2.713869 | 3.483330 ± 2.099438 | 3.509930 ± 2.924522 |
| f24 | 4.237707 ± 1.651448 | 4.251463 ± 1.305455 | 4.262602 ± 2.262393 |
| f25 | 3.867463 ± 2.090470 | 3.867043 ± 1.523778 | 3.866993 ± 9.419400 |
| f26 | 9.245550 ± 4.373209 | 9.254841 ± 3.466222 | 9.327218 ± 3.297828 |
| f27 | 5.016845 ± 5.896865 | 4.926597 ± 7.915101 | 4.981355 ± 7.186093 |
| f28 | 3.114948 ± 3.531211 | 3.064948 ± 2.600802 | 3.217193 ± 4.403163 |
| f29 | 4.353955 ± 1.046230 | 4.392384 ± 1.303416 | 4.348371 ± 1.639610 |
| f30 | 1.994910 ± 5.095366 | 1.969638 ± 1.586864 | 1.975658 ± 3.868023 |
| Function | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f3 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f4 | 5.856160 ± 0.0 | 5.867054 ± 7.703027 | 5.856160 ± 0.0 |
| f5 | 7.138668 ± 1.934874 | 8.172221 ± 1.624578 | 7.300936 ± 1.628259 |
| f6 | 5.733510 ± 1.749795 | 2.952184 ± 5.629595 | 5.360755 ± 1.577789 |
| f7 | 3.729442 ± 1.342658 | 3.843567 ± 1.603208 | 3.783948 ± 1.356820 |
| f8 | 7.340093 ± 1.966085 | 8.462537 ± 2.018838 | 7.322912 ± 2.011191 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 1.568173 ± 2.895061 | 1.524144 ± 2.684248 | 1.568425 ± 2.629532 |
| f11 | 4.027302 ± 8.265100 | 4.306909 ± 8.200147 | 7.472353 ± 1.565693 |
| f12 | 8.106433 ± 7.149354 | 9.996226 ± 6.182176 | 6.730995 ± 6.684616 |
| f13 | 1.552083 ± 6.133034 | 1.610696 ± 5.854376 | 1.684447 ± 4.239543 |
| f14 | 2.171615 ± 1.195599 | 2.195247 ± 1.241087 | 2.203156 ± 1.276744 |
| f15 | 1.184498 ± 7.500999 | 1.166798 ± 7.381401 | 1.213596 ± 9.026724 |
| f16 | 5.466729 ± 7.181852 | 3.527649 ± 4.731054 | 3.623068 ± 5.130314 |
| f17 | 3.449224 ± 7.695939 | 3.388604 ± 6.728233 | 3.355475 ± 7.485698 |
| f18 | 2.084219 ± 3.720811 | 2.006454 ± 3.965811 | 2.045489 ± 2.704982 |
| f19 | 4.817716 ± 1.898779 | 4.076852 ± 1.356127 | 4.425025 ± 1.967937 |
| f20 | 2.972537 ± 8.035391 | 2.704956 ± 6.845223 | 2.679755 ± 7.130091 |
| f21 | 2.083516 ± 1.807313 | 2.085552 ± 1.968052 | 2.080673 ± 2.171051 |
| f22 | 1.000000 ± 0.0 | 1.000000 ± 0.0 | 1.000000 ± 0.0 |
| f23 | 3.505319 ± 3.690104 | 3.507215 ± 3.276329 | 3.498206 ± 3.709504 |
| f24 | 4.263549 ± 2.213716 | 4.259219 ± 1.872762 | 4.262288 ± 2.572837 |
| f25 | 3.866960 ± 7.127660 | 3.866957 ± 5.585311 | 3.866962 ± 6.091826 |
| f26 | 9.561221 ± 4.264016 | 9.313090 ± 4.626237 | 9.371625 ± 4.567299 |
| f27 | 4.932655 ± 7.774858 | 4.932667 ± 7.143169 | 4.899617 ± 6.927315 |
| f28 | 3.042600 ± 2.111257 | 3.085200 ± 2.924355 | 3.000000 ± 0.0 |
| f29 | 4.348186 ± 1.955936 | 4.340111 ± 1.408097 | 4.350100 ± 1.643612 |
| f30 | 1.969240 ± 9.962199 | 1.972825 ± 2.132789 | 1.966696 ± 9.911583 |
| Function | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f3 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f4 | 5.235449 ± 4.437343 | 5.987294 ± 4.656380 | 5.533534 ± 4.638192 |
| f5 | 1.858622 ± 2.721102 | 1.090016 ± 2.044454 | 1.643115 ± 2.349557 |
| f6 | 1.826999 ± 9.247796 | 3.321219 ± 7.189487 | 1.159359 ± 1.645192 |
| f7 | 6.474578 ± 1.859098 | 6.125818 ± 1.330959 | 6.533251 ± 2.386148 |
| f8 | 1.786065 ± 2.476184 | 1.059279 ± 1.794339 | 1.642296 ± 2.506320 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 3.145981 ± 3.519306 | 3.289575 ± 3.466515 | 3.287218 ± 3.405172 |
| f11 | 4.479648 ± 7.262966 | 2.847299 ± 3.609160 | 2.765099 ± 3.060072 |
| f12 | 2.211379 ± 5.051756 | 1.791286 ± 4.034954 | 1.688626 ± 4.222375 |
| f13 | 5.887959 ± 3.102544 | 5.325204 ± 2.649015 | 3.130917 ± 1.675635 |
| f14 | 2.896163 ± 3.059013 | 2.516679 ± 1.954335 | 2.528063 ± 2.405140 |
| f15 | 3.628762 ± 8.435876 | 2.536133 ± 3.286879 | 2.407813 ± 2.946462 |
| f16 | 3.678356 ± 8.492899 | 3.514246 ± 1.238785 | 4.255240 ± 1.338552 |
| f17 | 3.210085 ± 8.169067 | 2.288290 ± 7.119400 | 2.673055 ± 7.762843 |
| f18 | 3.657321 ± 9.959862 | 2.552774 ± 2.227834 | 2.530384 ± 1.768854 |
| f19 | 2.229348 ± 5.693372 | 1.598069 ± 3.193897 | 1.473478 ± 2.609984 |
| f20 | 1.403643 ± 6.340770 | 1.545319 ± 5.105286 | 1.195946 ± 5.365881 |
| f21 | 2.167895 ± 2.526317 | 2.112500 ± 2.551442 | 2.176929 ± 2.782886 |
| f22 | 1.090866 ± 1.616684 | 2.492513 ± 1.798316 | 2.005652 ± 1.887346 |
| f23 | 4.306553 ± 5.383210 | 4.292150 ± 5.785777 | 4.311355 ± 6.917497 |
| f24 | 5.070785 ± 3.570835 | 5.065977 ± 3.750386 | 5.083627 ± 4.562561 |
| f25 | 5.403542 ± 2.684350 | 4.823364 ± 6.109998 | 4.811605 ± 3.115865 |
| f26 | 1.222280 ± 5.892037 | 1.137749 ± 5.618732 | 1.127770 ± 5.926815 |
| f27 | 5.254951 ± 1.084758 | 5.098628 ± 9.343850 | 5.120206 ± 1.296607 |
| f28 | 4.901310 ± 2.315774 | 4.625180 ± 1.261646 | 4.598068 ± 6.772419 |
| f29 | 3.695921 ± 2.035753 | 3.693345 ± 1.245696 | 3.660005 ± 1.532970 |
| f30 | 6.485235 ± 6.118087 | 6.093376 ± 3.282382 | 6.120136 ± 4.048972 |
| Function | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f3 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f4 | 6.309933 ± 4.861348 | 5.566785 ± 4.698233 | 4.758795 ± 4.251127 |
| f5 | 1.151320 ± 2.639832 | 1.326464 ± 2.814235 | 1.142791 ± 3.021920 |
| f6 | 8.654442 ± 9.973005 | 3.268284 ± 6.168995 | 1.133130 ± 1.432097 |
| f7 | 6.261671 ± 2.090590 | 6.495951 ± 2.964682 | 6.340675 ± 2.379764 |
| f8 | 1.129984 ± 2.991564 | 1.405517 ± 2.486846 | 1.080723 ± 2.867020 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 3.291896 ± 3.546988 | 3.251439 ± 3.159284 | 3.280655 ± 3.345557 |
| f11 | 2.434579 ± 3.577627 | 2.366605 ± 3.226247 | 2.435336 ± 3.915678 |
| f12 | 1.221989 ± 3.673815 | 1.231565 ± 3.631003 | 1.101802 ± 2.769593 |
| f13 | 2.996118 ± 1.994031 | 2.509417 ± 2.325881 | 2.884285 ± 2.311451 |
| f14 | 2.469884 ± 2.257149 | 2.434175 ± 2.010046 | 2.408265 ± 2.364445 |
| f15 | 2.124024 ± 1.743464 | 2.098253 ± 1.794117 | 2.006068 ± 1.504636 |
| f16 | 3.748420 ± 1.328029 | 4.129801 ± 1.369084 | 3.800765 ± 1.210071 |
| f17 | 2.439444 ± 8.263835 | 2.795374 ± 1.127910 | 2.368689 ± 9.354595 |
| f18 | 2.261803 ± 1.476114 | 2.290233 ± 1.433200 | 2.229708 ± 9.553674 |
| f19 | 1.152990 ± 2.462608 | 1.167486 ± 3.407432 | 1.085855 ± 2.264789 |
| f20 | 1.311696 ± 5.913158 | 1.463096 ± 8.239168 | 1.140987 ± 5.954660 |
| f21 | 2.134822 ± 3.087330 | 2.150670 ± 2.682522 | 2.122163 ± 3.509845 |
| f22 | 2.137994 ± 1.867652 | 1.807509 ± 1.762836 | 1.971311 ± 1.854554 |
| f23 | 4.291962 ± 6.293038 | 4.299165 ± 5.907164 | 4.310311 ± 8.161084 |
| f24 | 5.082245 ± 4.368923 | 5.068221 ± 3.243129 | 5.076325 ± 4.327285 |
| f25 | 4.806366 ± 2.299212 | 4.809218 ± 2.728328 | 4.804641 ± 1.608251 |
| f26 | 1.137797 ± 6.906183 | 1.140350 ± 5.343276 | 1.129101 ± 6.948572 |
| f27 | 5.091280 ± 1.372703 | 5.062935 ± 8.969971 | 5.027209 ± 1.332971 |
| f28 | 4.588490 ± 5.684342 | 4.588490 ± 5.684342 | 4.588490 ± 5.684342 |
| f29 | 3.689658 ± 1.435579 | 3.645692 ± 1.356443 | 3.618460 ± 1.293478 |
| f30 | 6.042557 ± 3.470244 | 6.052686 ± 2.884529 | 6.030053 ± 3.227074 |
| Function | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 2.115272 ± 7.398144 | 3.621475 ± 2.321462 | 2.681979 ± 1.323709 |
| f3 | 2.318827 ± 3.171098 | 1.189379 ± 1.466348 | 1.798921 ± 2.335796 |
| f4 | 1.058027 ± 6.168533 | 1.841503 ± 3.456924 | 1.985144 ± 1.507302 |
| f5 | 6.018822 ± 7.650742 | 2.881188 ± 5.095198 | 3.903405 ± 4.302748 |
| f6 | 2.768146 ± 2.094528 | 6.501323 ± 1.049251 | 1.157600 ± 3.452856 |
| f7 | 1.548649 ± 6.128553 | 1.344337 ± 3.132118 | 1.395379 ± 5.342167 |
| f8 | 5.553710 ± 7.466852 | 2.763175 ± 4.045294 | 3.991552 ± 3.695467 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 9.323340 ± 4.989688 | 9.672592 ± 5.809016 | 9.829538 ± 4.826719 |
| f11 | 4.977651 ± 1.154684 | 1.398680 ± 4.061085 | 1.037060 ± 2.911234 |
| f12 | 2.859917 ± 1.360122 | 1.881319 ± 9.745573 | 1.760383 ± 7.710254 |
| f13 | 4.605786 ± 2.511310 | 1.473008 ± 3.623802 | 1.498773 ± 3.307054 |
| f14 | 2.557099 ± 4.291528 | 7.044519 ± 1.206246 | 6.030425 ± 9.448970 |
| f15 | 2.477823 ± 5.117302 | 2.053792 ± 4.548641 | 1.577945 ± 3.308829 |
| f16 | 1.556113 ± 2.800367 | 1.608918 ± 2.842634 | 1.718316 ± 3.021229 |
| f17 | 1.202785 ± 1.818120 | 1.096731 ± 2.224261 | 1.205546 ± 1.764183 |
| f18 | 2.505036 ± 5.809274 | 2.154752 ± 5.280900 | 1.852876 ± 4.461551 |
| f19 | 1.872595 ± 2.511073 | 1.325648 ± 2.787079 | 9.679019 ± 2.009190 |
| f20 | 1.315492 ± 2.221504 | 1.415311 ± 1.801826 | 1.400301 ± 1.908523 |
| f21 | 2.683218 ± 5.769608 | 2.521659 ± 4.632993 | 2.616113 ± 6.682406 |
| f22 | 1.040296 ± 5.472091 | 1.082725 ± 3.703361 | 1.069680 ± 5.856186 |
| f23 | 5.802729 ± 1.030188 | 5.690771 ± 1.305997 | 5.676531 ± 1.120739 |
| f24 | 9.211472 ± 1.071240 | 9.011854 ± 8.832015 | 9.021128 ± 8.999005 |
| f25 | 7.374379 ± 3.838504 | 7.328269 ± 3.355738 | 7.234544 ± 4.379540 |
| f26 | 3.491742 ± 1.258458 | 3.205070 ± 9.033496 | 3.225848 ± 9.340949 |
| f27 | 6.178230 ± 2.298992 | 5.971925 ± 2.012176 | 5.780971 ± 1.877897 |
| f28 | 5.361838 ± 3.127036 | 5.351704 ± 2.750945 | 5.269297 ± 2.456277 |
| f29 | 1.243196 ± 1.472281 | 1.155445 ± 1.799635 | 1.289836 ± 2.137914 |
| f30 | 2.440230 ± 1.492281 | 2.361227 ± 1.419884 | 2.356999 ± 1.423812 |
| Function | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 5.038721 ± 1.209810 |
| f2 | 1.673566 ± 8.143557 | 2.786236 ± 1.828659 | 1.619229 ± 9.865543 |
| f3 | 2.598700 ± 3.046766 | 5.200551 ± 5.106623 | 1.867233 ± 2.098053 |
| f4 | 2.001814 ± 1.061642 | 2.026510 ± 1.067640 | 1.986945 ± 9.981837 |
| f5 | 2.282564 ± 5.374418 | 2.973385 ± 5.185268 | 2.126504 ± 4.943471 |
| f6 | 4.324963 ± 3.097421 | 1.037825 ± 1.022042 | 2.023262 ± 1.675807 |
| f7 | 1.258454 ± 4.037642 | 1.316895 ± 4.837579 | 1.250752 ± 5.169489 |
| f8 | 2.262054 ± 5.062372 | 2.849150 ± 5.048100 | 2.191965 ± 4.776998 |
| f9 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f10 | 1.003350 ± 5.181942 | 9.919141 ± 5.053399 | 9.883996 ± 5.542053 |
| f11 | 5.681264 ± 2.615972 | 6.601018 ± 3.161370 | 6.454649 ± 3.386242 |
| f12 | 1.084098 ± 4.835960 | 1.171083 ± 5.317012 | 1.629061 ± 7.410286 |
| f13 | 1.252693 ± 2.955466 | 1.221712 ± 3.504948 | 1.239350 ± 3.319592 |
| f14 | 4.026492 ± 4.654467 | 3.953127 ± 4.084129 | 3.520826 ± 3.548234 |
| f15 | 9.450216 ± 3.081027 | 9.918180 ± 3.475378 | 9.316875 ± 3.463347 |
| f16 | 1.762196 ± 2.895494 | 1.653987 ± 3.149891 | 1.610269 ± 3.171456 |
| f17 | 1.177577 ± 2.796055 | 1.214972 ± 2.455955 | 1.195693 ± 2.879482 |
| f18 | 9.865988 ± 2.318114 | 9.849790 ± 2.673075 | 8.753706 ± 1.577905 |
| f19 | 5.375456 ± 6.426384 | 5.332317 ± 6.965122 | 4.849865 ± 6.528906 |
| f20 | 1.361891 ± 2.361198 | 1.382355 ± 1.833415 | 1.440578 ± 2.375126 |
| f21 | 2.498712 ± 4.793399 | 2.528137 ± 6.324763 | 2.474338 ± 4.624437 |
| f22 | 1.089671 ± 5.882543 | 1.056397 ± 5.692429 | 1.064701 ± 6.777621 |
| f23 | 5.685648 ± 1.051014 | 5.673360 ± 9.183117 | 5.682635 ± 9.777963 |
| f24 | 8.976863 ± 8.162956 | 8.979166 ± 6.615433 | 8.970015 ± 7.936307 |
| f25 | 6.981912 ± 4.440744 | 7.117357 ± 4.069772 | 6.780342 ± 4.988064 |
| f26 | 3.120648 ± 8.549825 | 3.144199 ± 9.002875 | 3.076108 ± 9.972924 |
| f27 | 5.746185 ± 2.402400 | 5.729895 ± 1.855867 | 5.600763 ± 2.094522 |
| f28 | 5.161411 ± 1.977592 | 5.203338 ± 2.475601 | 5.205190 ± 2.297309 |
| f29 | 1.268410 ± 2.138615 | 1.240134 ± 1.761199 | 1.265436 ± 1.745885 |
| f30 | 2.301197 ± 1.302743 | 2.257047 ± 1.092659 | 2.254460 ± 1.133409 |
| L-SHADE vs. L-SHADE-LBR | 0+/8 = /1- | 2+/7 = /1- | 2+/6 = /2- | 1+/8 = /1- |
| jSO vs. jSO-LBR | 0+/9 = /0- | 1+/9 = /0- | 3+/7 = /0- | 2+/8 = /0- |
| DISH vs. DISH-LBR | 0+/9 = /0- | 2+/8 = /0- | 2+/7 = /1- | 2+/8 = /0- |
| Func. | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 2.10142 ± 9.06803 | 4.26469 ± 4.06753 | 3.67067 ± 2.07562 |
| f3 | 5.28447 ± 1.11465 | 5.25455 ± 1.00384 | 5.26472 ± 2.30645 |
| f4 | 1.12273 ± 2.46869 | 9.77072 ± 4.59113 | 1.09207 ± 4.67916 |
| f5 | 0.0 ± 0.0 | 0.0 ± 0.0 | 6.24099 ± 1.87230 |
| f6 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f8 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f9 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f10 | 3.42630 ± 1.42101 | 3.39473 ± 1.76526 | 3.39473 ± 1.76526 |
| Func. | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 4.26469 ± 4.06753 | 1.15746 ± 2.03217 | 1.35031 ± 2.35366 |
| f3 | 5.25455 ± 1.00384 | 5.36259 ± 1.81877 | 5.01955 ± 1.19377 |
| f4 | 9.77072 ± 4.59113 | 8.97824 ± 5.08256 | 9.31253 ± 5.43166 |
| f5 | 0.0 ± 0.0 | 6.24099 ± 1.87230 | 0.0 ± 0.0 |
| f6 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f8 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f9 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f10 | 3.39473 ± 1.76526 | 3.36315 ± 2.00340 | 3.19473 ± 8.65478 |
| Func. | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 1.17808 ± 1.45778 | 1.84593 ± 1.83951 | 1.84081 ± 1.86378 |
| f3 | 1.09229 ± 2.57045 | 1.14946 ± 3.42269 | 1.14560 ± 3.15783 |
| f4 | 2.66548 ± 3.96601 | 2.80188 ± 4.31393 | 2.68712 ± 4.43370 |
| f5 | 1.29016 ± 1.31744 | 1.05751 ± 1.28970 | 1.53622 ± 1.78070 |
| f6 | 7.61459 ± 4.86606 | 1.70091 ± 1.63884 | 6.68416 ± 3.85526 |
| f7 | 7.99651 ± 1.71343 | 6.86388 ± 1.52324 | 1.40205 ± 2.24697 |
| f8 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f9 | 2.34825 ± 1.07191 | 2.21541 ± 1.13696 | 2.02562 ± 1.02820 |
| f10 | 4.16120 ± 2.22173 | 3.98009 ± 0.0 | 3.98009 ± 0.0 |
| Func. | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 1.84593 ± 1.83951 | 6.33319 ± 9.86976 | 1.86907 ± 1.69093 |
| f3 | 1.14946 ± 3.42269 | 1.11115 ± 3.65883 | 1.13203 ± 3.67866 |
| f4 | 2.80188 ± 4.31393 | 2.71553 ± 4.90826 | 2.70102 ± 4.86311 |
| f5 | 1.05751 ± 1.28970 | 3.67719 ± 2.19512 | 4.29479 ± 8.28999 |
| f6 | 1.70091 ± 1.63884 | 3.52478 ± 1.48118 | 1.31651 ± 1.05516 |
| f7 | 6.86388 ± 1.52324 | 1.98363 ± 2.13177 | 1.12443 ± 5.56388 |
| f8 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f9 | 2.21541 ± 1.13696 | 2.01274 ± 1.09669 | 2.21412 ± 1.13577 |
| f10 | 3.98009 ± 0.0 | 3.98000 ± 4.77485 | 3.98000 ± 4.77485 |
| Func. | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 1.11444 ± 1.55539 | 1.02993 ± 1.03052 | 3.18849 ± 2.45075 |
| f3 | 1.56548 ± 1.19675 | 1.59237 ± 2.36877 | 1.59270 ± 2.35040 |
| f4 | 3.49454 ± 3.99602 | 3.62932 ± 5.18875 | 3.70914 ± 4.04489 |
| f5 | 2.72357 ± 1.21873 | 8.36060 ± 2.85275 | 2.82653 ± 1.14969 |
| f6 | 1.87866 ± 1.91004 | 7.52602 ± 7.72092 | 7.95332 ± 3.08505 |
| f7 | 5.20809 ± 6.24344 | 5.13873 ± 5.19186 | 7.84397 ± 1.13748 |
| f8 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f9 | 3.81793 ± 2.42286 | 3.88236 ± 2.36353 | 3.89188 ± 1.14562 |
| f10 | 4.00000 ± 0.0 | 4.00000 ± 0.0 | 4.00000 ± 0.0 |
| Func. | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 1.02993 ± 1.03052 | 1.28117 ± 1.36090 | 9.91480 ± 1.03583 |
| f3 | 1.59237 ± 2.36877 | 1.57505 ± 1.53824 | 1.59450 ± 2.06851 |
| f4 | 3.62932 ± 5.18875 | 3.80445 ± 4.43296 | 3.72271 ± 4.30883 |
| f5 | 8.36060 ± 2.85275 | 1.52051 ± 9.02712 | 8.68646 ± 4.30019 |
| f6 | 7.52602 ± 7.72092 | 6.77266 ± 1.30617 | 7.71839 ± 1.49955 |
| f7 | 5.13873 ± 5.19186 | 8.95471 ± 1.24307 | 5.06856 ± 3.73802 |
| f8 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f9 | 3.88236 ± 2.36353 | 3.89321 ± 1.06397 | 3.89540 ± 6.90534 |
| f10 | 4.00000 ± 0.0 | 4.00000 ± 0.0 | 4.00000 ± 0.0 |
| Func. | L-SHADE | jSO | DISH |
|---|---|---|---|
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 1.21924 ± 4.36906 | 2.92990 ± 4.85360 | 2.48343 ± 4.09772 |
| f3 | 2.04116 ± 5.76301 | 2.05948 ± 1.81538 | 2.07393 ± 2.76334 |
| f4 | 4.42784 ± 4.24157 | 4.64267 ± 4.97379 | 4.63768 ± 4.83692 |
| f5 | 1.01366 ± 6.99335 | 2.01814 ± 1.12021 | 6.41469 ± 4.26252 |
| f6 | 2.31513 ± 5.99600 | 2.66587 ± 6.28029 | 9.35968 ± 3.25339 |
| f7 | 9.97161 ± 1.46926 | 6.74912 ± 1.05720 | 6.67590 ± 2.66941 |
| f8 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f9 | 3.97749 ± 1.21733 | 3.97785 ± 1.10925 | 3.97699 ± 2.99098 |
| f10 | 4.13658 ± 3.04777 | 4.13657 ± 1.79505 | 4.13657 ± 1.13687 |
| Func. | L-SHADE-LBR | jSO-LBR | DISH-LBR |
| f1 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| f2 | 2.92990 ± 4.85360 | 2.58541 ± 4.19616 | 2.51160 ± 4.09793 |
| f3 | 2.05948 ± 1.81538 | 2.05692 ± 2.22046 | 2.05423 ± 1.49670 |
| f4 | 4.64267 ± 4.97379 | 4.64425 ± 3.98595 | 4.66623 ± 4.65800 |
| f5 | 2.01814 ± 1.12021 | 3.72641 ± 1.37385 | 2.11216 ± 1.23587 |
| f6 | 2.66587 ± 6.28029 | 3.30280 ± 2.01361 | 2.39600 ± 5.25111 |
| f7 | 6.74912 ± 1.05720 | 8.89405 ± 1.51139 | 6.72319 ± 1.19042 |
| f8 | 1.00000 ± 0.0 | 1.00000 ± 0.0 | 1.00000 ± 0.0 |
| f9 | 3.97785 ± 1.10925 | 3.97576 ± 1.65870 | 3.98260 ± 1.24851 |
| f10 | 4.13657 ± 1.79505 | 4.13657 ± 1.79505 | 4.13657 ± 1.13687 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanovov, V.; Akhmedova, S.; Semenkin, E. Differential Evolution with Linear Bias Reduction in Parameter Adaptation. Algorithms 2020, 13, 283. https://doi.org/10.3390/a13110283
Stanovov V, Akhmedova S, Semenkin E. Differential Evolution with Linear Bias Reduction in Parameter Adaptation. Algorithms. 2020; 13(11):283. https://doi.org/10.3390/a13110283
Chicago/Turabian StyleStanovov, Vladimir, Shakhnaz Akhmedova, and Eugene Semenkin. 2020. "Differential Evolution with Linear Bias Reduction in Parameter Adaptation" Algorithms 13, no. 11: 283. https://doi.org/10.3390/a13110283
APA StyleStanovov, V., Akhmedova, S., & Semenkin, E. (2020). Differential Evolution with Linear Bias Reduction in Parameter Adaptation. Algorithms, 13(11), 283. https://doi.org/10.3390/a13110283






