The Auto-Diagnosis of Granulation of Information Retrieval on the Web
Abstract
1. Introduction
- Determining the auto-diagnosis of the concept ‘I’ for the auto-diagnosis agent,
- Whether the frequency of auto-diagnosis cycles (frequency of updating the auto-diagnosis history) should be consistent with the frequency of 40 Hz of the thalamus–cortex cycles,
- Whether the frequency of synchronization of auto-diagnosis cycles with the stability of auto-diagnosis history should correspond to brain waves: alpha (8–12 Hz), beta (above 12 Hz), theta (4–8 Hz), delta (0.5–4 Hz).
2. Conceiving of Assertions on the Web
- rdfs: Resource—class containing all resources,
- rdfs: Class—class containing all classes and their instances,
- rdf: Property—class containing all properties,
- and other rdfs: Literal, rdfs: Datatype, rdf: langString, rdf: HTML and rdf: XMLLiteral.
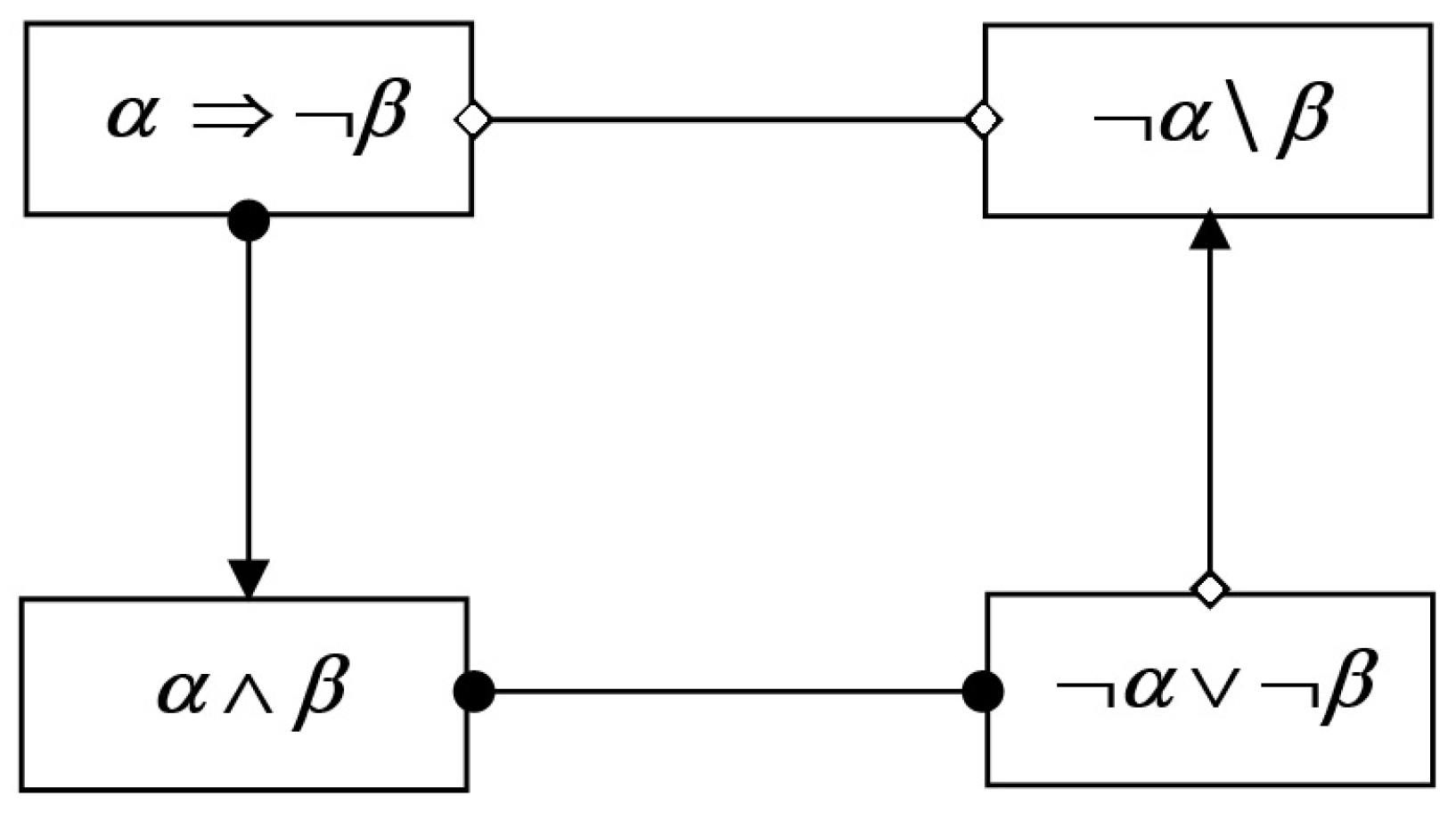
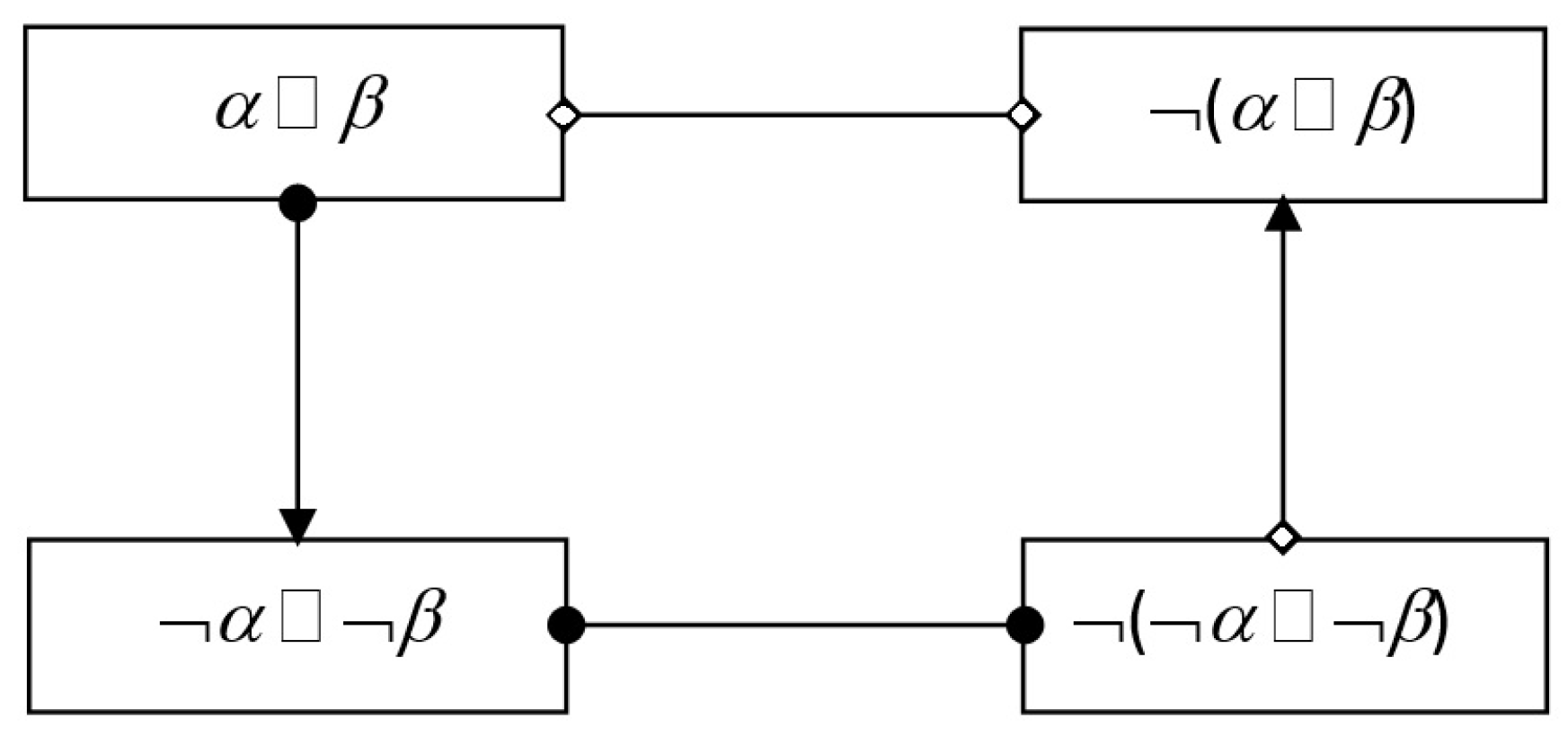
- Positive coupling is satisfied if the consequent is satisfied.
- Negative coupling is satisfied if it is excluded that the antecedent is satisfied, when the consequent is satisfied.
- Positive feedback is satisfied if the consequent is satisfied.
- Negative feedback is satisfied if it is excluded that the antecedent is satisfied, when the consequent is satisfied.
3. Compatibility of the Ontology Expressions with the Thesaurus Expressions
3.1. Algorithm for the Compatibility of Ontology Expressions with Thesaurus Expressions
| Algorithm 1 |
 |
3.2. Deduction
3.3. Analysis
3.4. Reduction
3.5. Synthesis
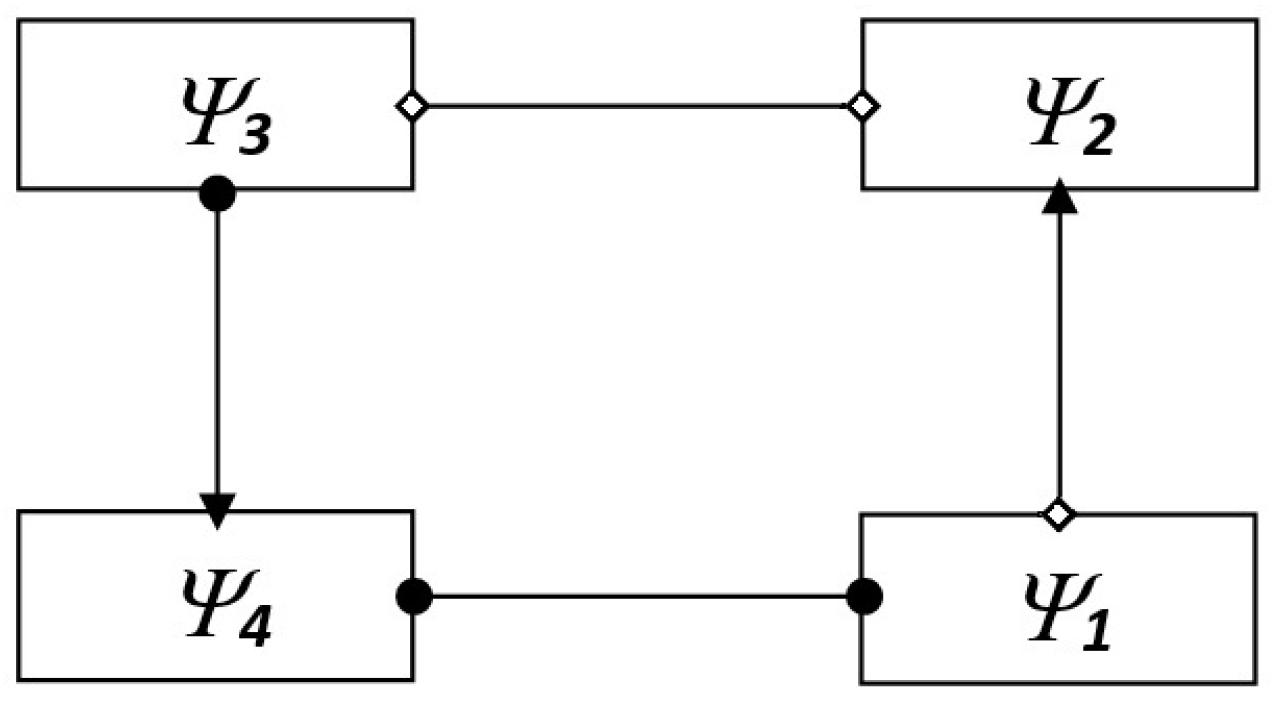
4. Assertion Perception Systems in de Morgan Algebras
4.1. Triangular Norms of Deduction
4.1.1. Deduction Norms
- boundary conditions
- monotonicity
- commutativity
- associativity
- there exists .
- boundary conditions
- monotonicity
- commutativity
- associativity
- there is
4.1.2. Analysis Norms
4.1.3. Reduction Norms
4.1.4. Synthesis Norms
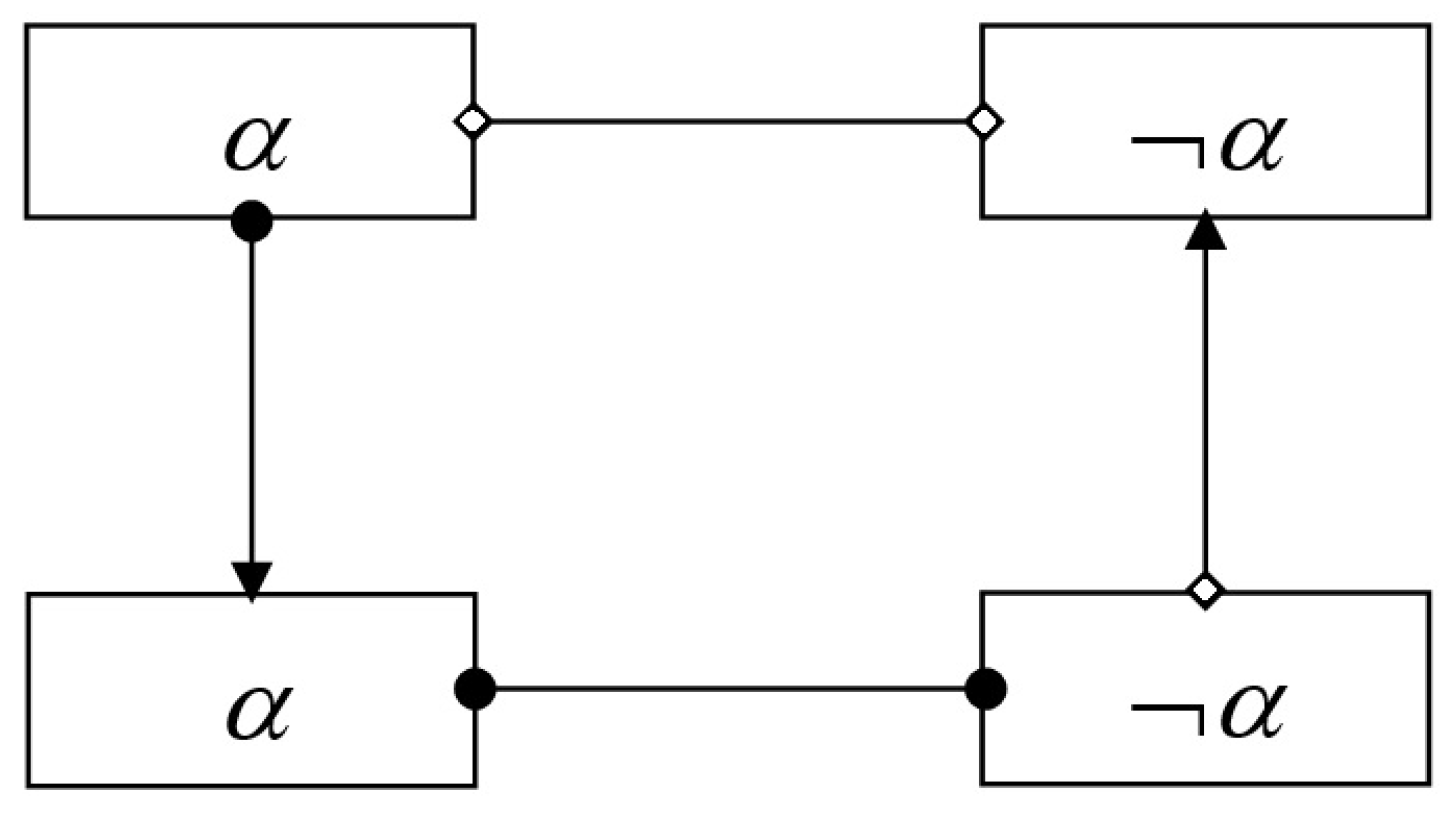
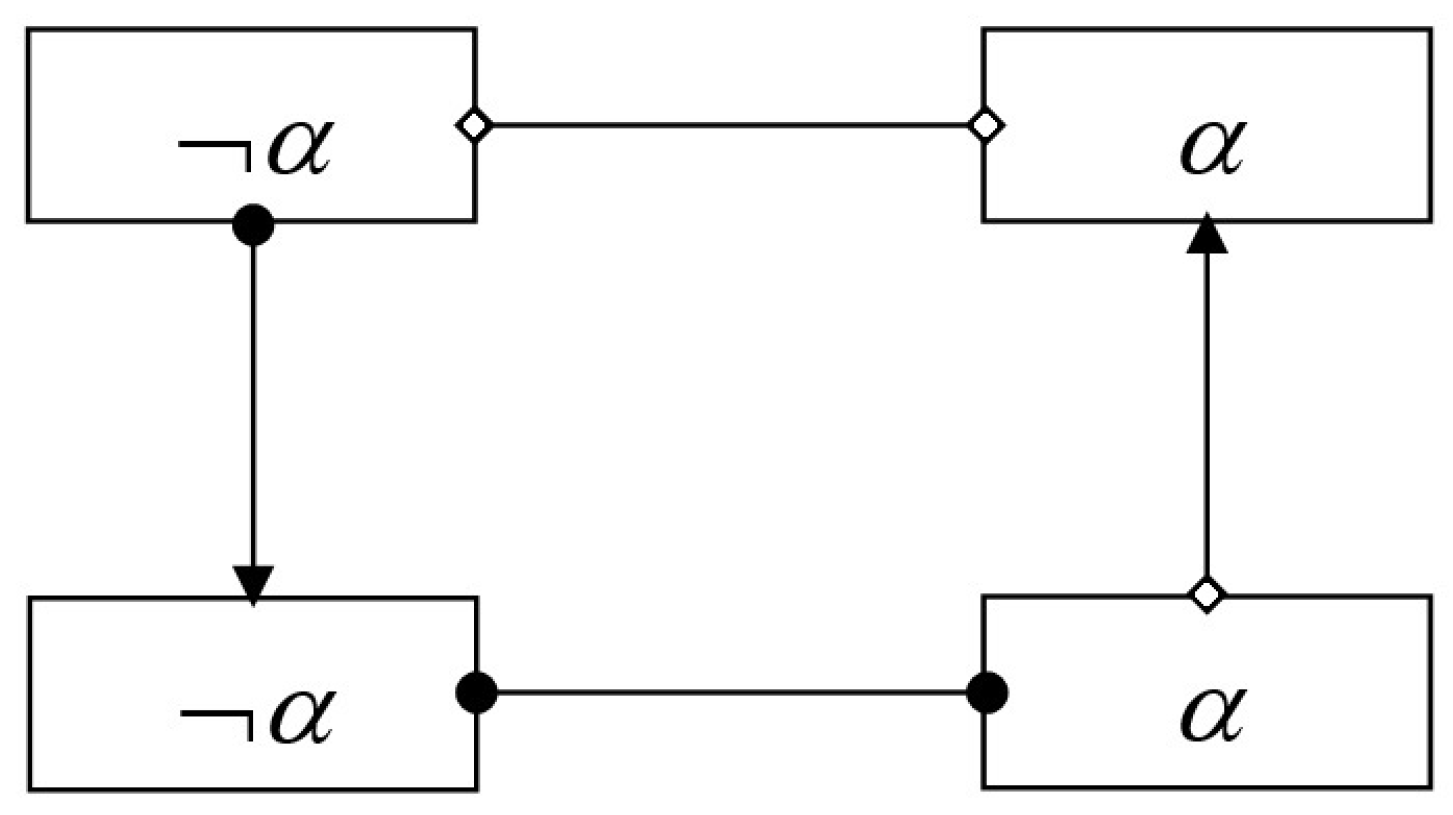
4.1.5. De Morgan Algebra
- the algebra of deduction:
- the algebra of analysis:
- the algebra of reduction:
- the algebra of synthesis:
4.2. Perception Systems
- Let , then ,
- Let , then ,
- Let , then ,
- Let , then ,
- Let , then .
5. Conclusions
Funding
Conflicts of Interest
References
- Bryniarska, A. Autodiagnosis of Information Retrieval on the Web as a Simulation of Selected Processes of Consciousness in the Human Brain. In Biomedical Engineering and Neuroscience; Hunek, W.P., Paszkiel, S., Eds.; Advances in Intelligent Systems and Computing 720; Springer: Berlin/Heidelberg, Germany, 2018; pp. 111–120. [Google Scholar]
- Bryniarska, A. Certain information granule system as a result of sets approximation by fuzzy context. Int. J. Approx. Reason. 2019, 111, 1–20. [Google Scholar] [CrossRef]
- Peters, J.F. Discovery of perceptually near information granules. In Novel Developments in Granular Computing: Applications of Advanced Human Reasoning and Soft Computation; Yao, J.T., Ed.; Information Science Reference: Hersey, NY, USA, 2009. [Google Scholar]
- Peters, J.F.; Ramanna, S. Affinities between perceptual granules: Foundations and Perspectives. In Human-Centric Information Processing Through Granular Modelling; Bargiela, A., Pedrycz, W., Eds.; Springer: Berlin, Germany, 2009; pp. 49–66. [Google Scholar]
- Pedrycz, W. Allocation of information granularity in optimization and decision-making models: Towards building the foundations of Granular Computing. Eur. J. Oper. Res. 2014, 232, 137–145. [Google Scholar] [CrossRef]
- Moore, R. Interval Analysis; Prentice-Hall: Englewood Clifis, NJ, USA, 1966. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–117. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a generalized theory of uncertainty (GTU) an outline. Inf. Sci. 2005, 172, 1–40. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comp. Inform. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets: Theoretical Aspects of Reasoning about Data; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Pawlak, Z.; Skowron, A. Rough membership function. In Advaces in the Dempster-Schafer of Evidence; Yeager, R.E., Fedrizzi, M., Kacprzyk, J., Eds.; Wiley: New York, NY, USA, 1994; pp. 251–271. [Google Scholar]
- Pawlak, Z.; Skowron, A. Rudiments of rough sets. Inf. Sci. 2007, 177, 3–27. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron. A. Rough sets and Boolean reasoning. Inf. Sci. 2007, 177, 41–73. [Google Scholar] [CrossRef]
- Pedrycz, W. Shadowed sets: Representing and processing fuzzy sets. IEEE Trans. Syst. Man Cybern. Part B 1998, 28, 103–109. [Google Scholar] [CrossRef] [PubMed]
- Pedrycz, W. Knowledge-Based Clustering: From Data to Information Granules; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lindsay, P.H.; Norman, D.A. Human Information Processing: An Introduction to Psychology; Academic Press, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Bryniarska, A. The Paradox of the Fuzzy Disambiguation in the Information Retrieval. Int. J. Adv. Res. Artif. Intell. 2013, 2, 55–58. [Google Scholar] [CrossRef][Green Version]
- Manola, F.; Miller, E. RDF Primer. 2004. Available online: http://www.w3.org/TR/rdf-primer/ (accessed on 15 October 2020).
- Resource Description Framework (RDF). RDF Working Group. 2004. Available online: http://www.w3.org/RDF/ (accessed on 15 October 2020).
- Lassila, O.; Swick, R.R. Resource Description Framework (RDF): Model and Syntax Specification. Rekomendacja W3C. 2003. Available online: http://www.w3.org/TR/REC-rdf-syntax/ (accessed on 15 October 2020).
- Michalewicz, Z.; Fogel, D.B. How to Solve It: Modern Heuristic; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Kowalski, R. Logic for Problem Solving; North-Holland: New York, NY, USA; Amsterdam, The Netherlands; Oxford, UK, 1979. [Google Scholar]
- Bobillo, F.; Straccia, U. A Fuzzy Description Logic with Product T-norm. In Proceedings of the 2007 IEEE International Fuzzy Systems Conference, London, UK, 23–26 July 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Sanchez, E. Fuzzy Logic and the Semantic Web; Elsevier: Amsterdam, The Netherlands, 2006; ISBN 13: 978-0-444-51948-1. [Google Scholar]

| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bryniarska, A. The Auto-Diagnosis of Granulation of Information Retrieval on the Web. Algorithms 2020, 13, 264. https://doi.org/10.3390/a13100264
Bryniarska A. The Auto-Diagnosis of Granulation of Information Retrieval on the Web. Algorithms. 2020; 13(10):264. https://doi.org/10.3390/a13100264
Chicago/Turabian StyleBryniarska, Anna. 2020. "The Auto-Diagnosis of Granulation of Information Retrieval on the Web" Algorithms 13, no. 10: 264. https://doi.org/10.3390/a13100264
APA StyleBryniarska, A. (2020). The Auto-Diagnosis of Granulation of Information Retrieval on the Web. Algorithms, 13(10), 264. https://doi.org/10.3390/a13100264





