Application of the Approximate Bayesian Computation Algorithm to Gamma-Ray Spectroscopy
Abstract
1. Introduction
2. Background
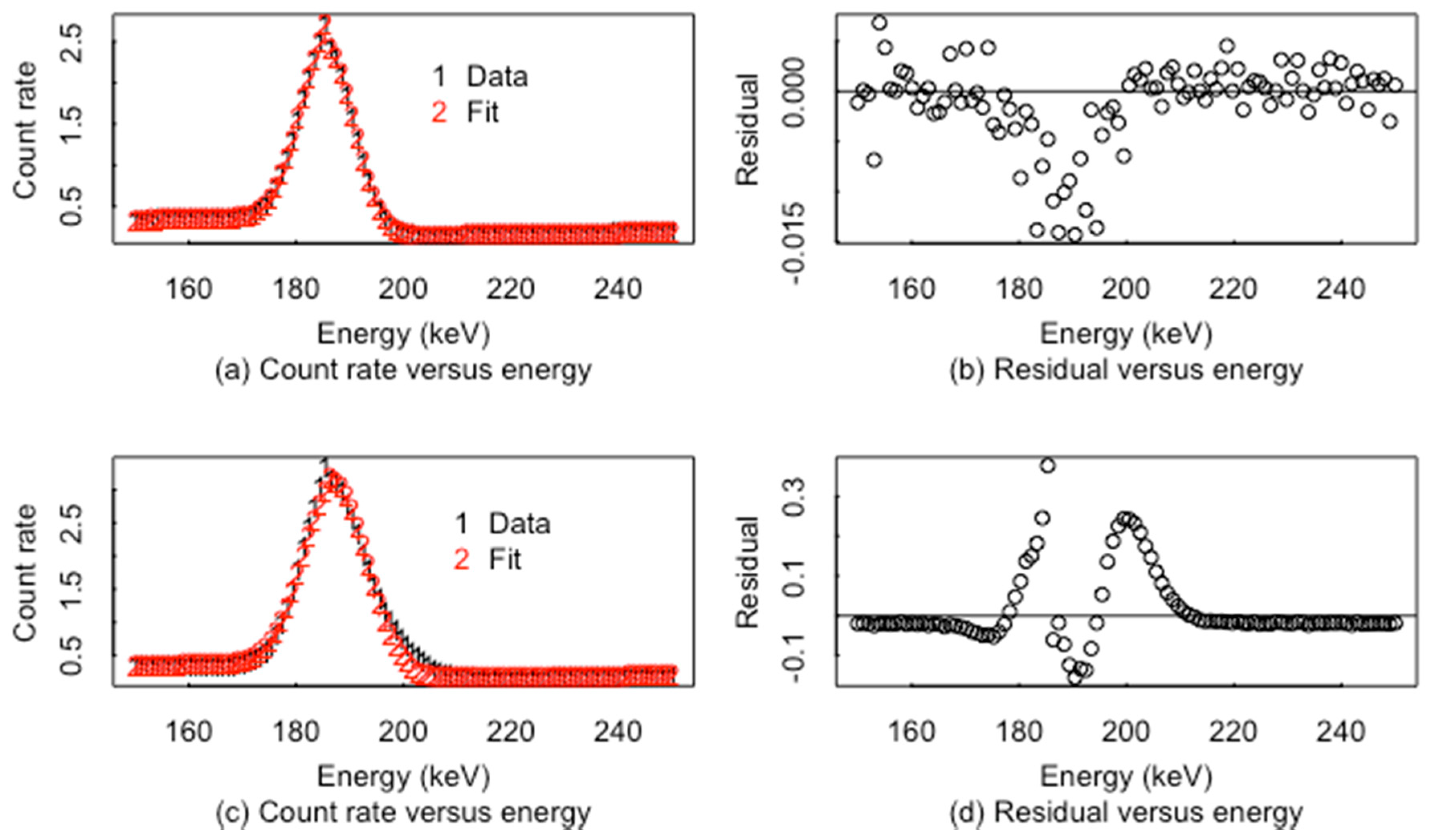
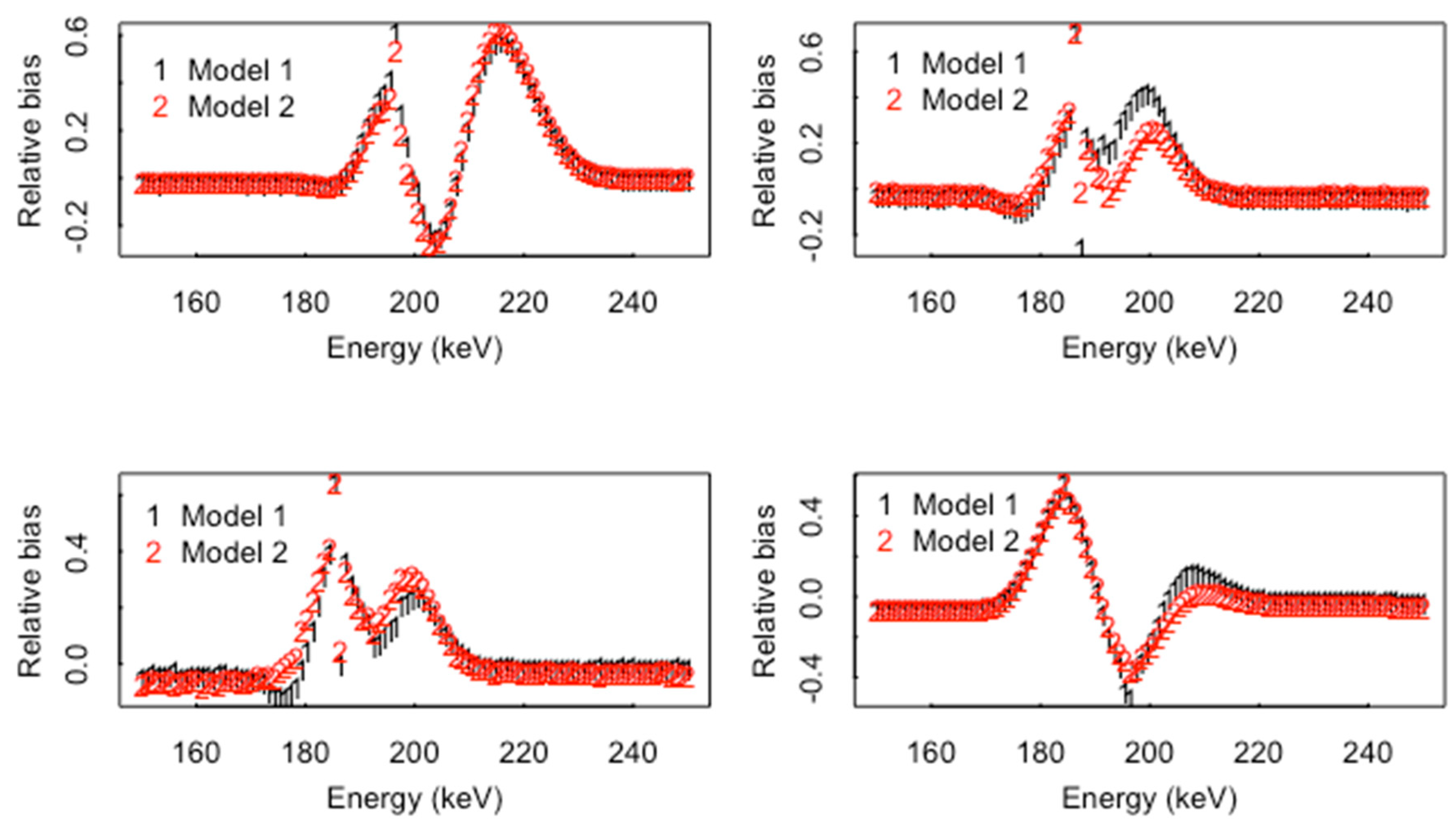
3. Peak Location Algorithms
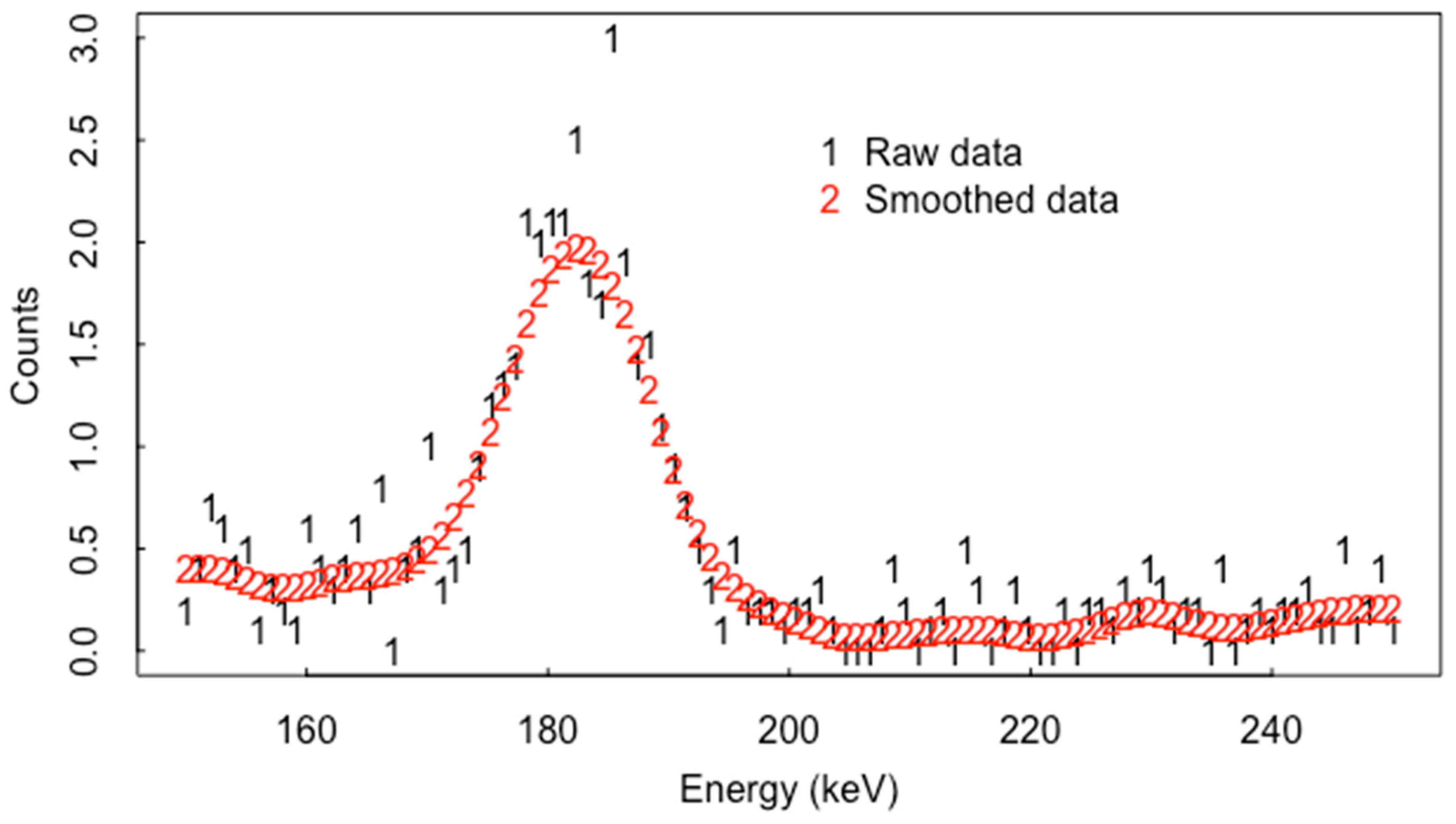
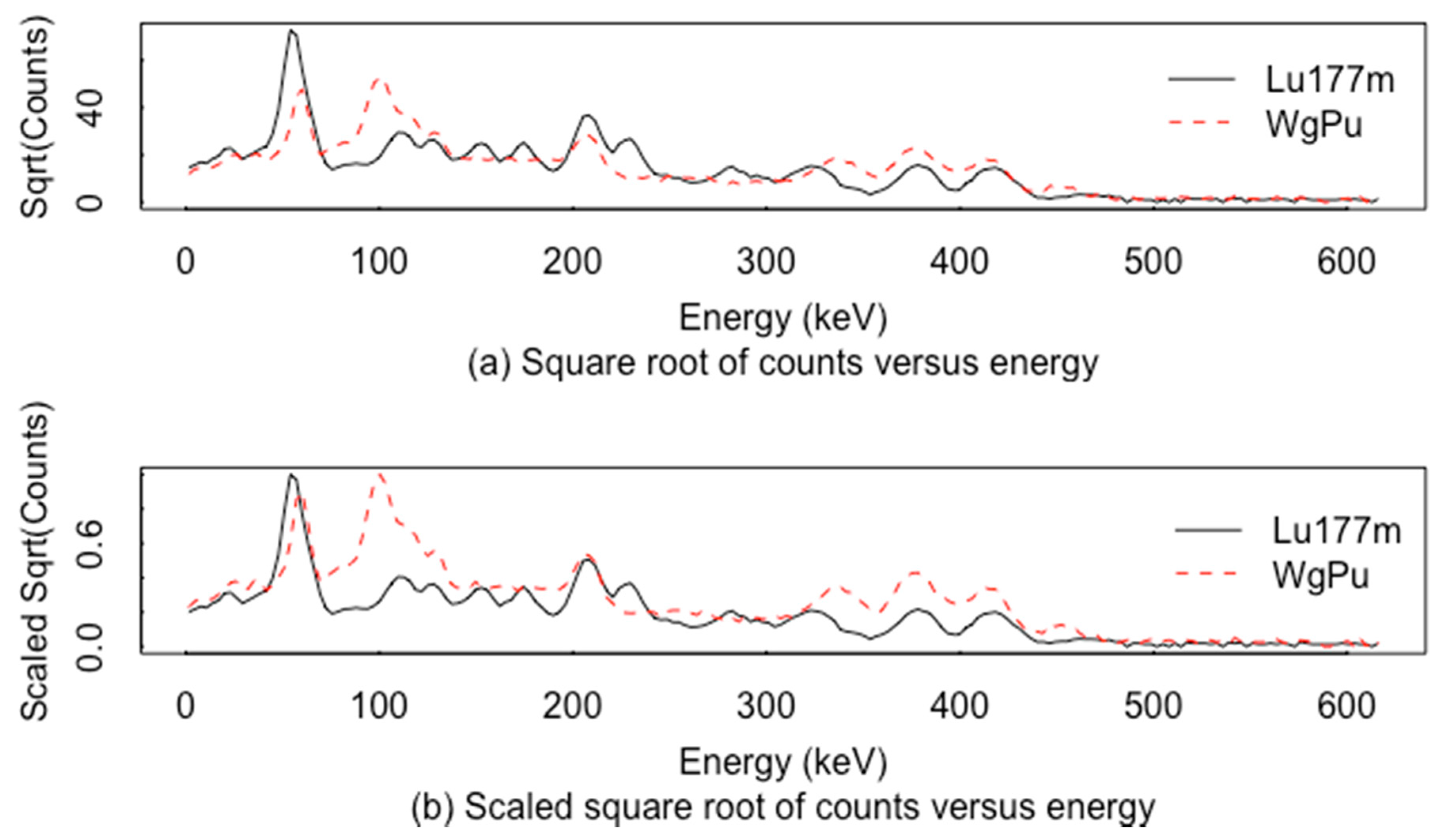
4. Smoothing Algorithms
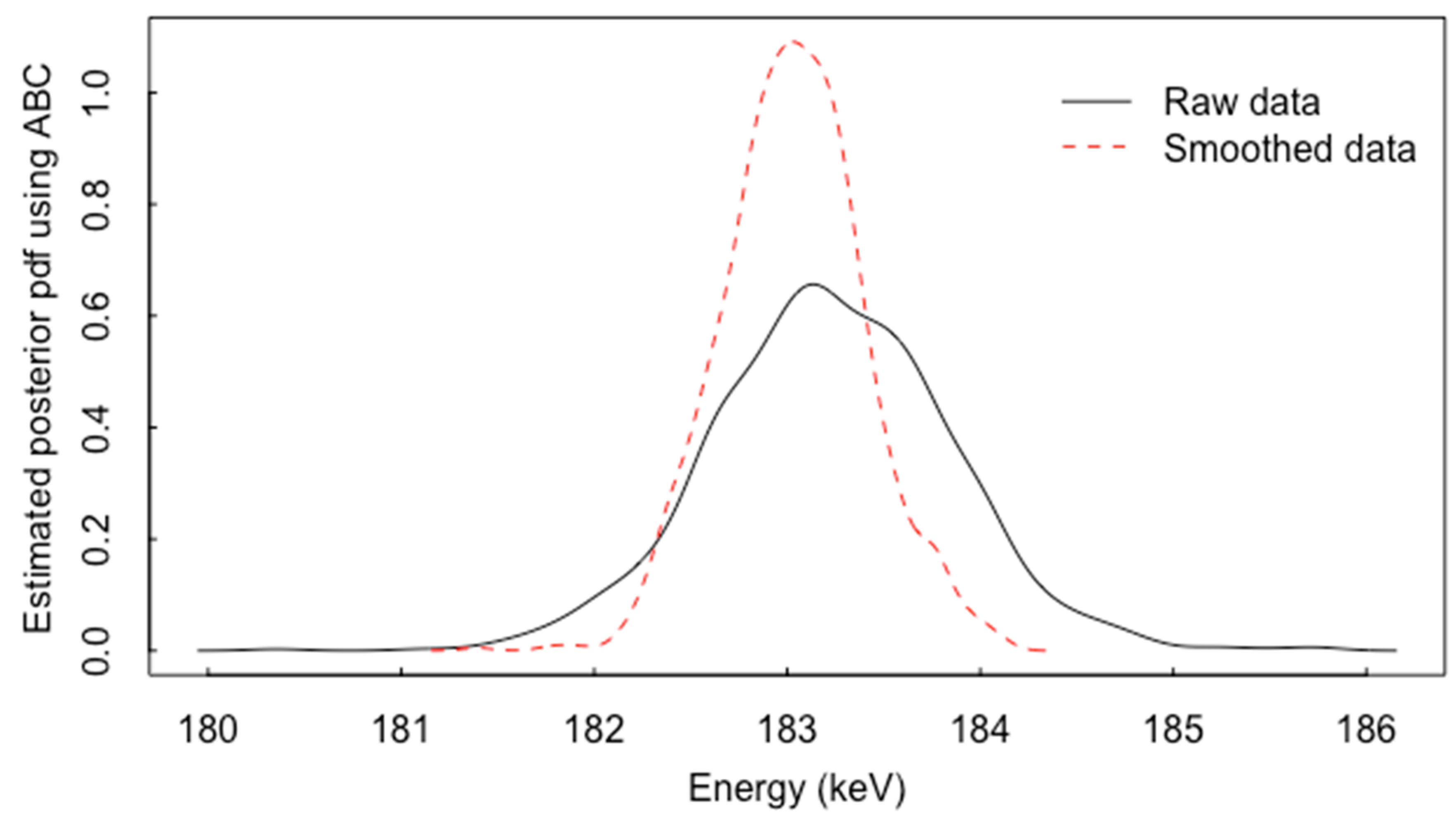
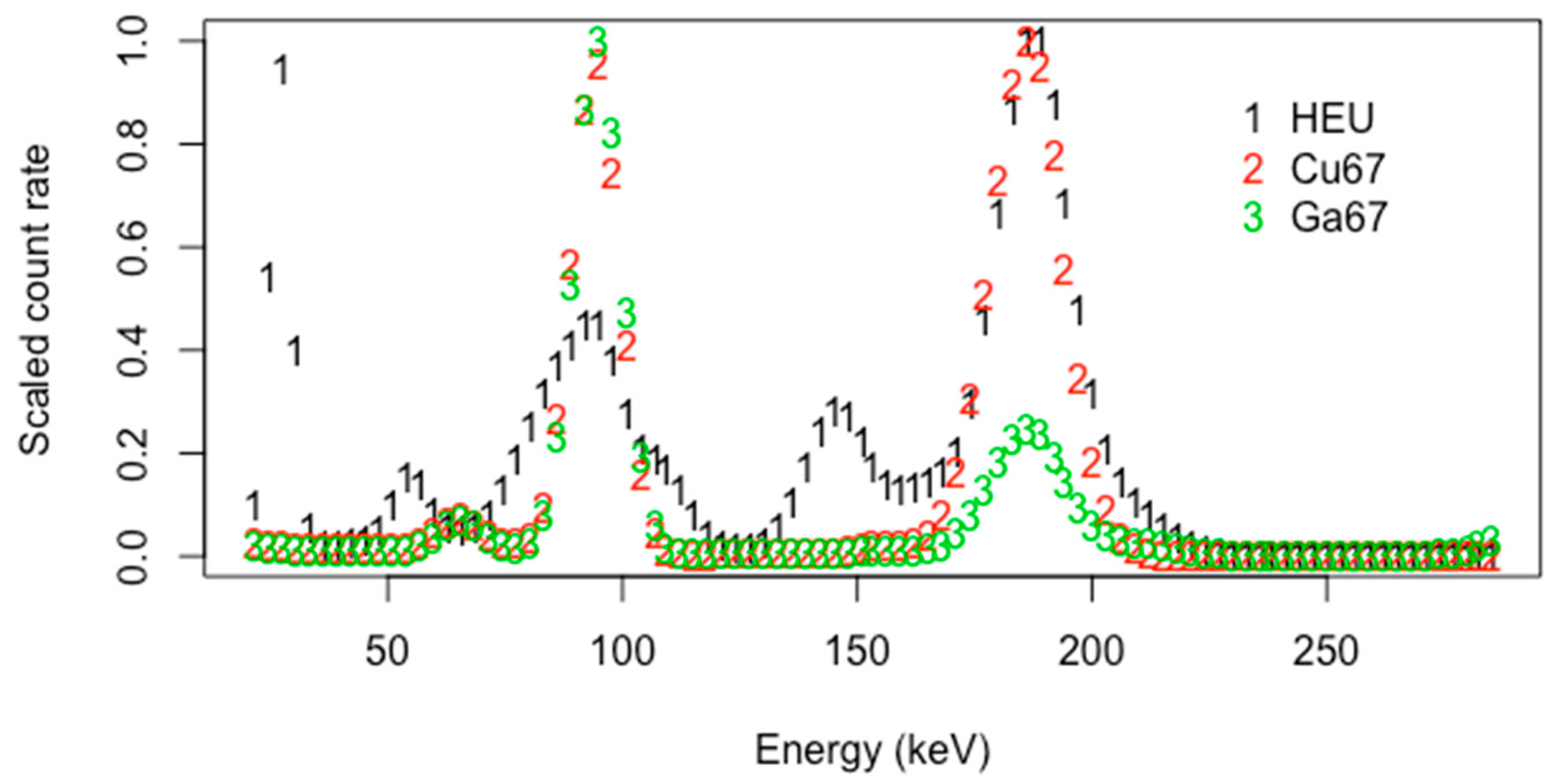
5. Net Peak Area Extraction and ABC
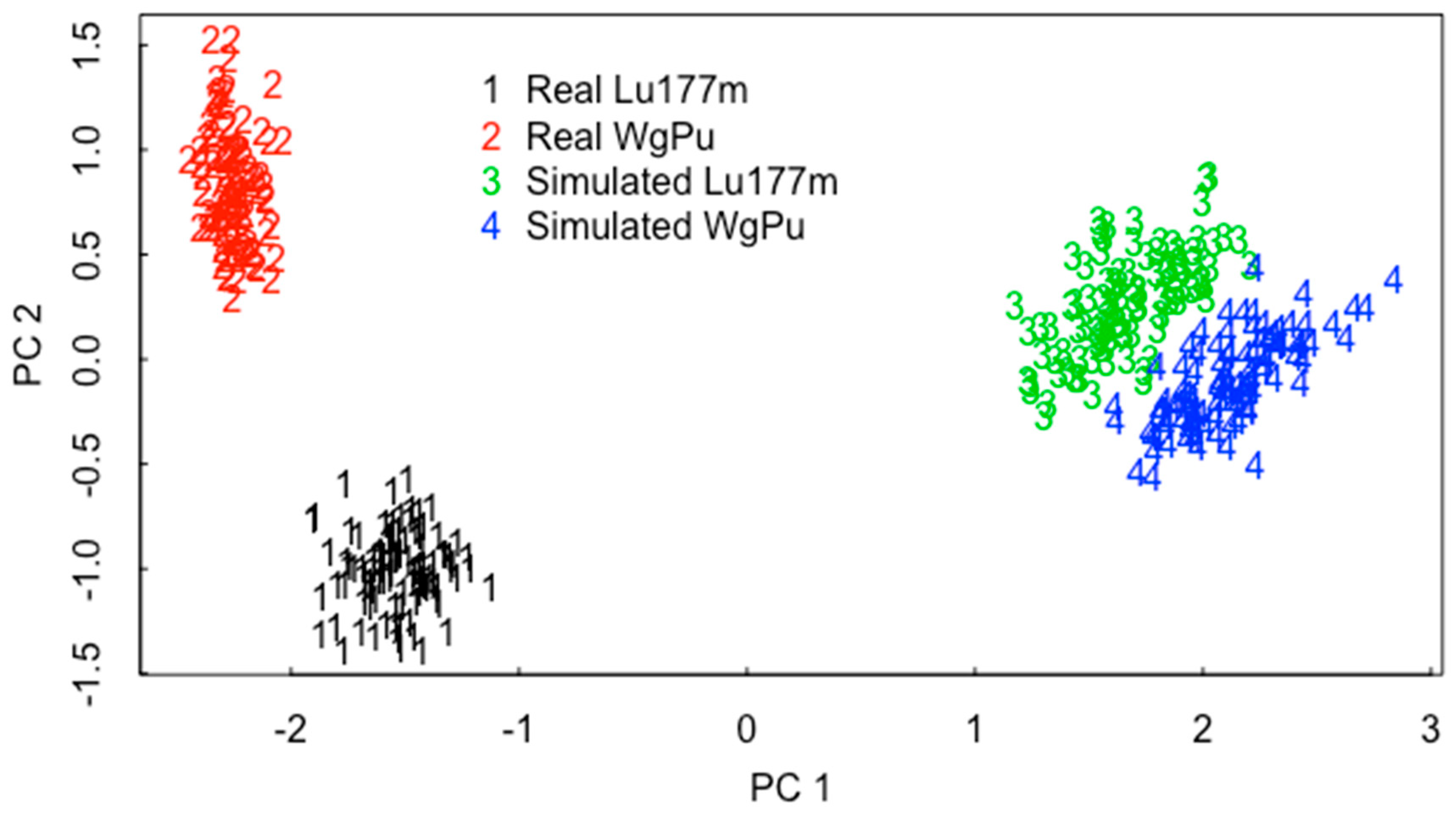
5.1. ABC
ABC Inference
- (1)
- Sample from the prior, ;
- (2)
- Simulate data from the conditional pdf ;
- (3)
- Denote the real data as If the distance then accept as an observation from ;
- (A)
- ABC allows for an easy comparison of the performance of candidate summary statistics such as peak area ratios, off-peak count rates, and goodness-of-fit test results such as scan statistic values near peaks.
- (B)
- ABC allows for easy experimentation with different DRFs.
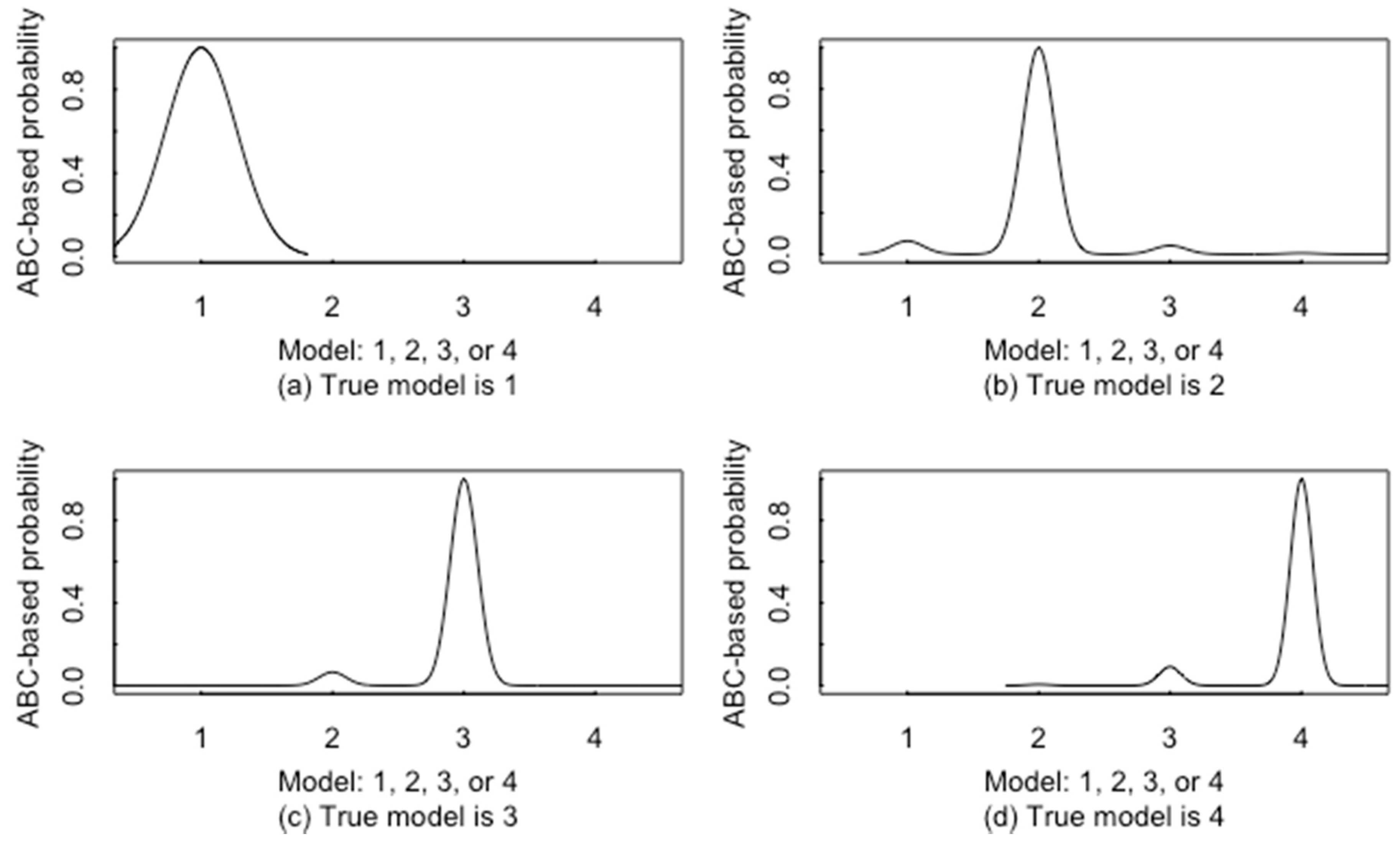
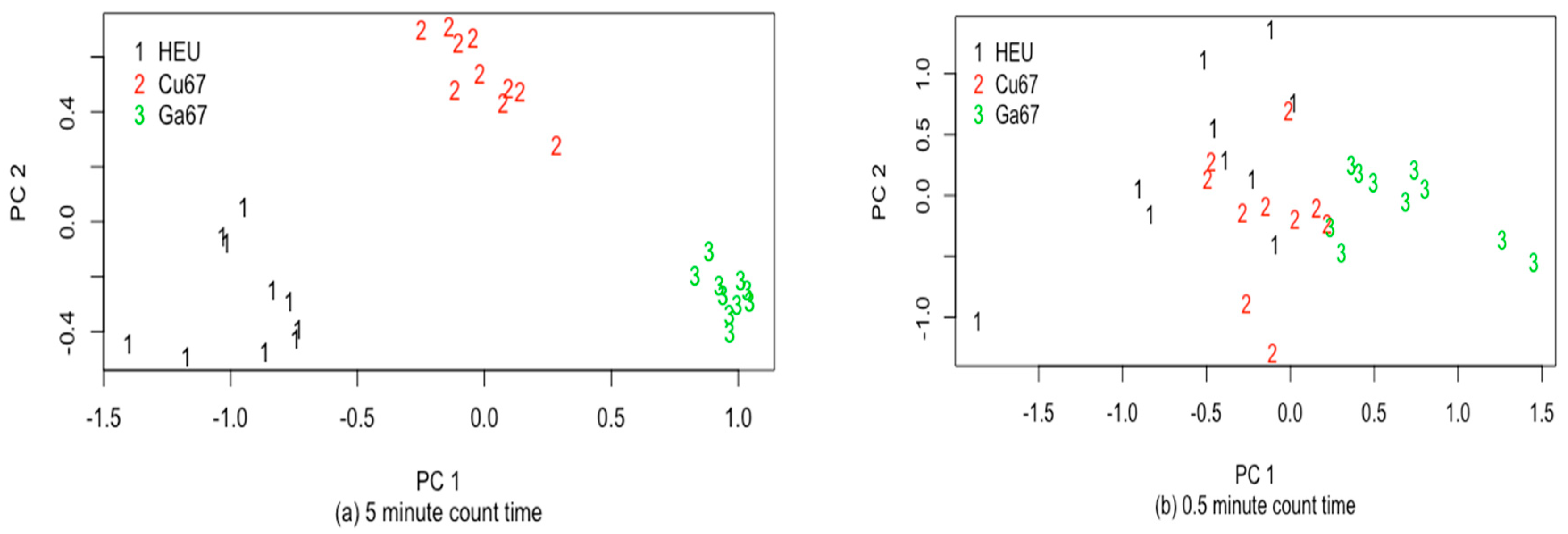
6. A New ABC-Based RIID
7. Discussion and Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stromswold, D.; Carkoch, J.; Ely, J.; Hansen, R.; Kouzes, R.; Milbath, B.; Runkle, R.; Sliger, W.; Smart, J.; Stephens, D.; et al. Field Tests of a NaI(T1)-Based Vehicle Portal Monitor at Border Crossings. In Proceedings of the IEEE Nuclear Science Symposium Conference, Rome, Italy, 16–22 October 2004; Volume 1, pp. 196–200. Available online: http://ieeexplore.ieee.org/iel5/9892/31433/01462180.pdf (accessed on 11 November 2014).
- Sullivan, C.; Garner, S.; Lombardi, M.; Butterfield, K.; Smith-Nelson, M. Evaluation of key detector parameters for isotope identification. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Honolulu, HI, USA, 26 October–3 November 2007; pp. 1181–1184. [Google Scholar]
- Estep, R.; McCluskey, C.; Sapp, B. The multiple isotope material basis set (MIMBS) method for isotope identification with low- and medium-resolution-ray detectors. J. Radioanal. Nucl. Chem. 2008, 276, 737–741. [Google Scholar] [CrossRef]
- Miko, D.; Estep, R.; Rawool-Sullivan, M. An innovative method for extracting isotopic information from low-resolution spectra. Nucl. Instrum. Methods Phys. Res. A 1999, 422, 433–437. [Google Scholar] [CrossRef]
- Estep, R.; Rawool-Sullivan, M.; Miko, D. A Method for correcting NaI spectra for attenuation losses in hand-held instrument applications. IEEE Trans. Nucl. Sci. 1998, 45, 1022–1028. [Google Scholar] [CrossRef]
- Russ, W. Library correlation isotope identification algorithm. Nucl. Instrum. Methods Phys. Res. A 2007, 579, 288–291. [Google Scholar] [CrossRef]
- Burr, T.; Hamada, M. Radio-isotope identification algorithms for NaI gamma spectra. Algorithms 2009, 2, 339–360. [Google Scholar] [CrossRef]
- Sullivan, C.; Stinnett, J. Validation of a Bayesian-based isotope identification algorithm. Nucl. Instrum. Methods Phys. Res. A 2015, 784, 298–305. [Google Scholar] [CrossRef]
- Daniel, G.; Limousin, O.; Maler, D.; Meuris, A. Automatic and real-time identification of radioisotopes in gamma-ray spectra: A new method base on convolutional neural network trained with synthetic data set. IEEE Trans. Nucl. Sci. 2020, 4, 644–653. [Google Scholar] [CrossRef]
- Bai, E.; Chan, K.; Eichinger, W.; Kump, P. Detection of radioisotopes from weak and poorly resolved spectra using Lasso and subsampling techniques. Radiat. Meas. 2011, 46, 1138–1146. [Google Scholar] [CrossRef]
- Li, F.; Gu, Z.; Ge, L.; Li, H.; Tang, X.; Lang, X.; Hu, B. Review of recent gamma spectrum unfolding algorithms and their application. Results Phys. 2019, 13, 102211. [Google Scholar] [CrossRef]
- Mitchell, D. ASEDRA Evaluation Final Report, Sandia National Laboratory Report 2008-6382. 2008. Available online: https://prod-ng.sandia.gov/techlib-noauth/access-control.cgi/2008/086382.pdf (accessed on 3 July 2020).
- LaVigne, E.; Sjoden, G.; Backiak, J.; Detwiler, R. Extraordinary improvement in scintillation detectors via post-processing with ASEDRA-solution to a 50-year-old problem. In Proceedings of the SPIE, Orlando, FL, USA, 18 March 2008. [Google Scholar]
- Zhang, W.; Zahringer, M.; Ungar, K.; Hoffman, I. Statistical analysis of uncertainties of peak identification and area calculation in particulate air-filter environment radioisotope measurements using the results of a comprehensive nuclear-test-ban treaty organization organized intercomparison. Appl. Radiat. Isot. 2008, 66, 1695–1701. [Google Scholar] [CrossRef]
- Robinson, S.; Kiff, S.; Ashbaker, E.; Bender, S.; Flumerfelt, E.; Salvitti, M.; Borgardt, J.; Woodring, M. Effects of high count rate and gain shift on isotope identification algoritms. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Honolulu, HI, USA, 26 October–3 November 2007; Volume 2, pp. 1152–1156. [Google Scholar]
- Blackadar, J. Automatic isotope identifier and their features. IEEE Sens. J. 2005, 5, 589–592. [Google Scholar] [CrossRef]
- Pibida, L.; Unterweger, M.; Karam, L. Evaluation of handheld radioisotope identifiers. J. Res. Natl. Inst. Stand. Technol. 2004, 109, 451–456. [Google Scholar] [CrossRef] [PubMed]
- Sood, A.; Gardner, R. A new Monte Carlo assisted approach to detector response functions. Nucl. Instrum. Methods Phys. Res. B 2004, 213, 100–104. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Sun, S.; Want, B.; Wei, L. A semi-empirical response function for gamma-ray of Scintillation detector based on physical interaction mechanism. arXiv 2019, arXiv:1407.0799. [Google Scholar]
- Meleshenkovskii, L.; Pauly, N.; Labeau, P. Determination of the uranium enrichment without calibration standards using a 500 mm3 CdZnTe room temperature detector with a hybrid methodology based on peak ratios method and Monte Carlo counting efficiency simulations. Appl. Radiat. Isot. 2019, 148, 277–289. [Google Scholar] [CrossRef]
- Mitchell, D. Detector Response and Analysis Software (GADRAS); Sandia Report SAND88-2519; Sandia National Laboratories: Albuquerque, NM, USA, 1988.
- Blum, M.; Nunes, M.; Prangle, D.; Sisson, S. A Comparative review of dimension reduction methods in Approximate Bayesian Computation. Stat. Sci. 2013, 28, 189–208. [Google Scholar] [CrossRef]
- Burr, T.; Hengartner, N.; Matzner-Lober, E.; Myers, S.; Rouviere, L. Smoothing Low Resolution NaI Spectra. IEEE Trans. Nucl. Sci. 2010, 57, 2831–2840. [Google Scholar] [CrossRef]
- Burr, T.; Hamada, M.; Hengartner, N. Impact of spectral smoothing on gamma radiation portal alarm probabilities. Appl. Radiat. Isot. 2011, 69, 1436–1446. [Google Scholar] [CrossRef]
- Burr, T.; Skurikhin, A. Selecting Summary Statistics in Approximate Bayesian Computation for Calibrating Stochastic Models. BioMed Res. Int. 2013, 2013, 210646. [Google Scholar] [CrossRef]
- Burr, T.; Krieger, T.; Norman, C. Approximate Bayesian Computation applied to metrology for nuclear Safeguards. ESARDA Bull. 2018, 57, 50–59. [Google Scholar]
- Talts, S.; Betancourt, M.; Simpson, D.; Vehtari, A.; Gelman, A. Validating Bayesian inference algorithms with simulation-based calibration. arXiv 2018, arXiv:1804.06788. [Google Scholar]
- Burr, T.; Sampson, T.; Vo, D. Statistical evaluation of FRAM-ray isotopic analysis data. Appl. Radiat. Isot. 2005, 62, 931–940. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www.R-project.org/ (accessed on 13 September 2020).
- Mariscotti, M. A Method for automatic identification of peaks in the presence of background and its application to spectrum analysis. Nucl. Instrum. Methods Phys. Res. A 1967, 50, 309. [Google Scholar] [CrossRef]
- Kong, X. Advanced Adaptive Library for Gamma-Ray Spectrometers. Master’s Thesis, University of Illinois, Urbana-Champaign, Urbana, IL, USA, 2014. Available online: www.ideals.illinois.edu/handle/2142/49390 (accessed on 6 January 2020).
- Sullivan, C.; Martinez, M.; Garner, S. Wavelet analysis of NaI spectra. IEEE Trans. Nucl. Sci. 2006, 53, 2916–2922. [Google Scholar] [CrossRef]
- Nunes, M.; Prangle, D. abctools: An R package for Tuning Approximate Bayesian Computation Analyses. R J. 2016, 7, 189–205. [Google Scholar] [CrossRef]
- Carlin, B.; John, B.; Stern, H.; Rubin, D. Bayesian Data Analysis, 1st ed.; Chapman and Hall: London, UK, 1995. [Google Scholar]
- Naus, J. Approximations for distributions of scan statistics. J. Am. Stat. Assoc. 1982, 77, 177–183. [Google Scholar] [CrossRef]
- Croft, S.; Favalli, A.; Weaver, B.; Williams, B.; Burr, T.; Henzlova, D.; McElroy, R. A Critical Examination of Figure of Merit (FOM): Assessing the Goodness-of-Fit in Gamma/X-ray Peak Analysis. Los Alamos National Laboratory Report LAUR 15-27783. 2015. Available online: https://permalink.lanl.gov/object/tr?what=info:lanl-repo/lareport/LA-UR-15-27783 (accessed on 16 October 2020).
- Burr, T.; Croft, S.; Jarman, K.; Nicholson, A.; Norman, C.; Walsh, S. Improved uncertainty quantification in nondestructive assay for nonproliferation. Chemometrics 2016, 159, 164–173. [Google Scholar] [CrossRef]
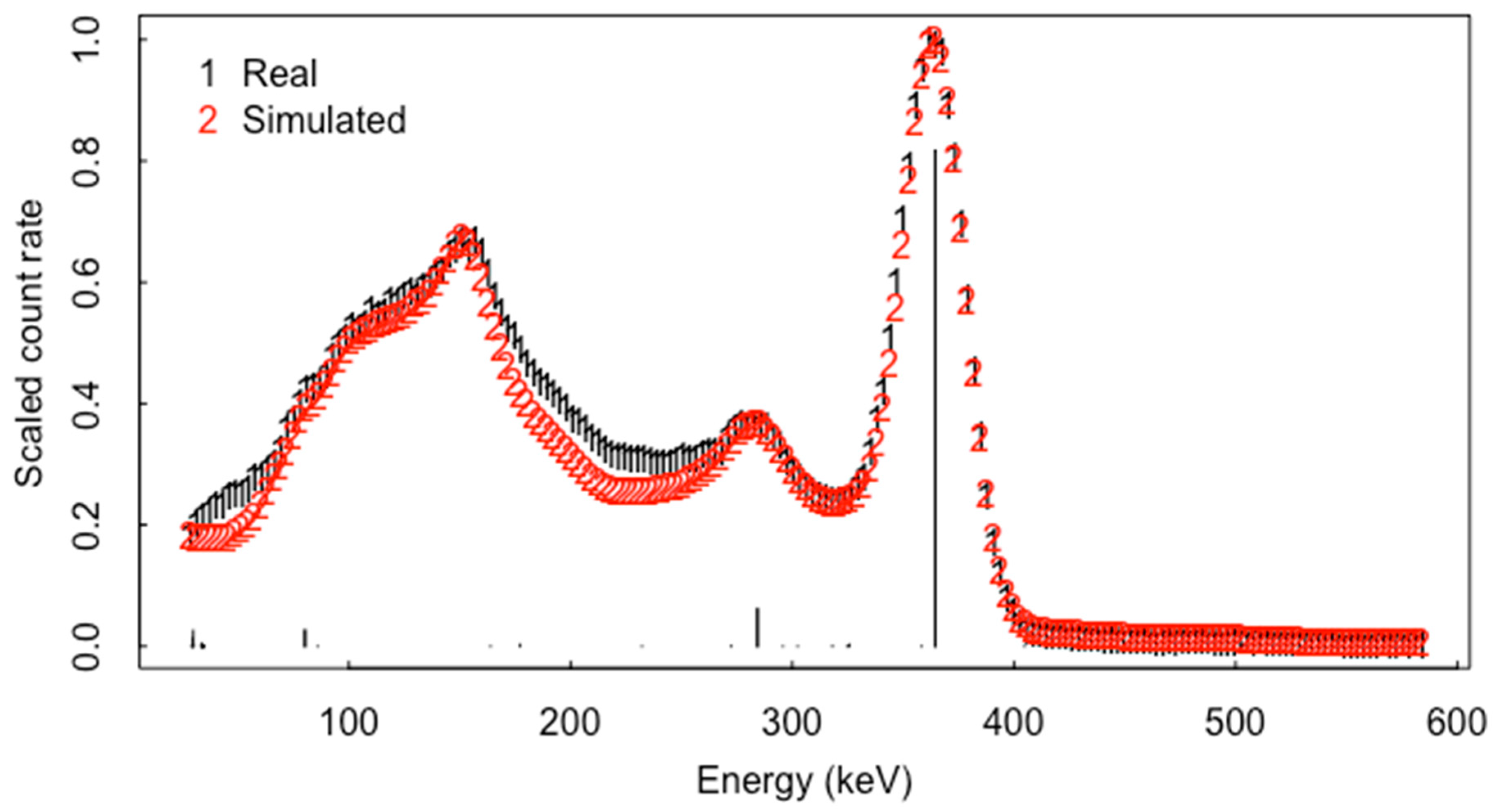
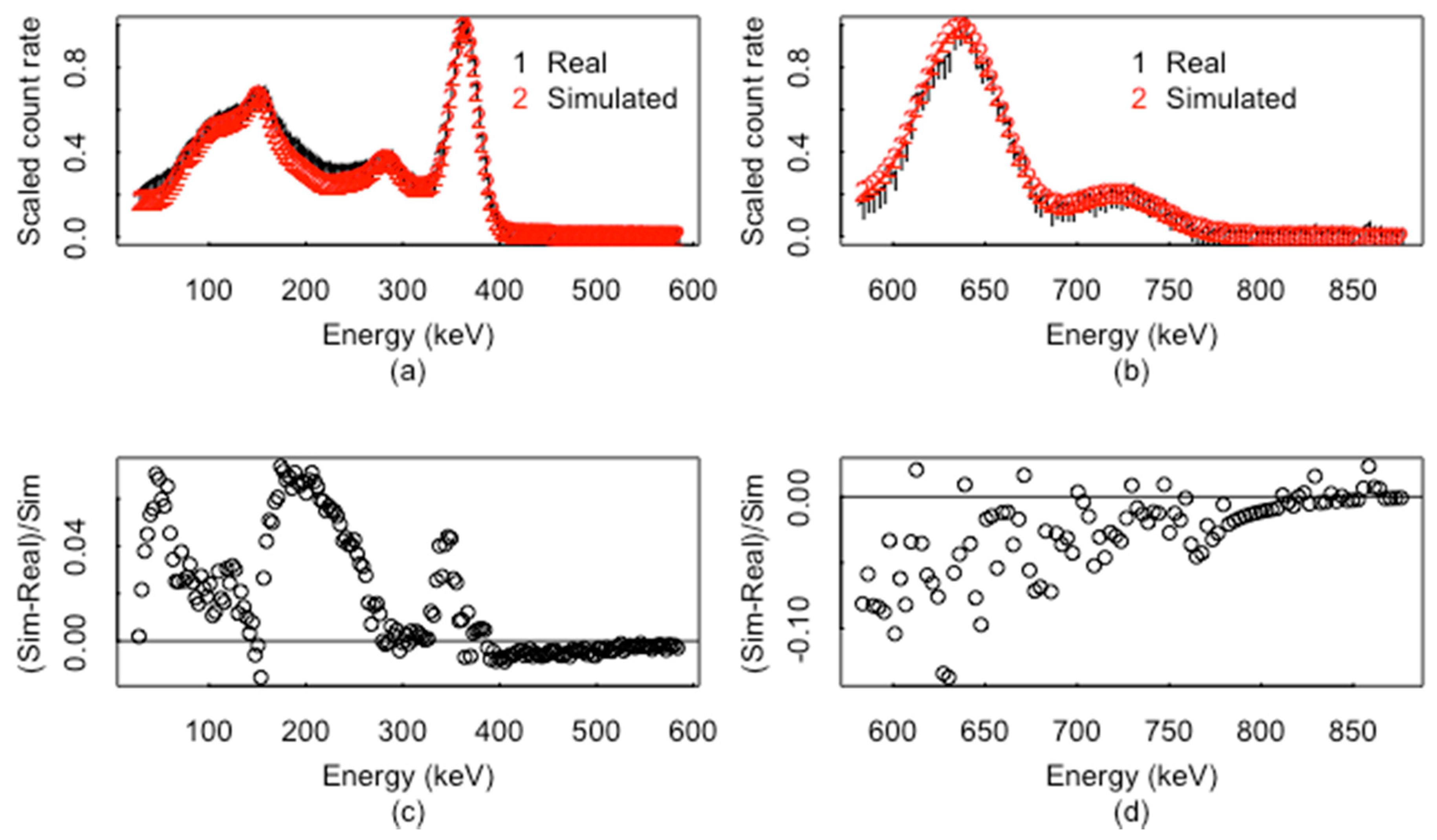
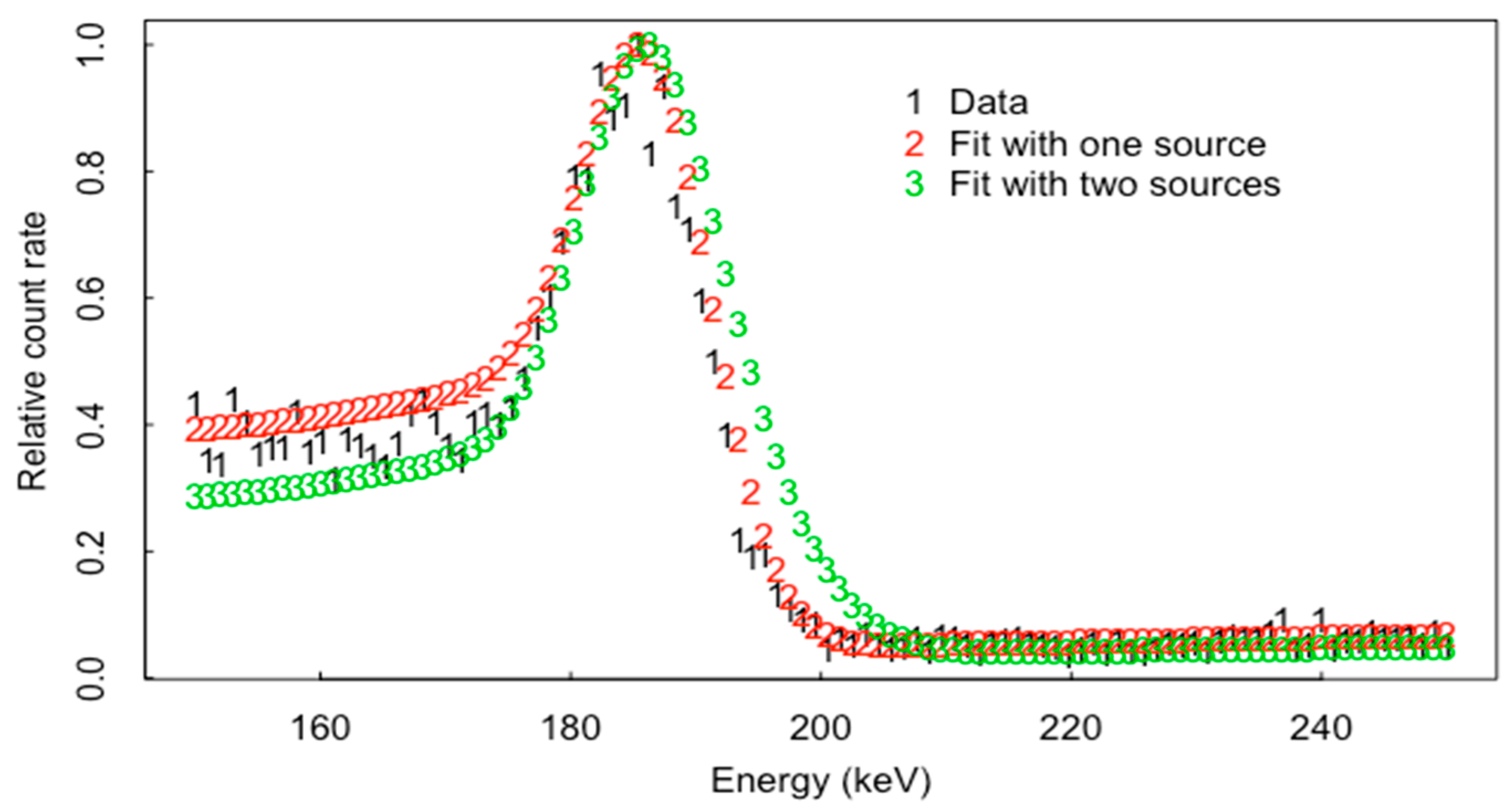
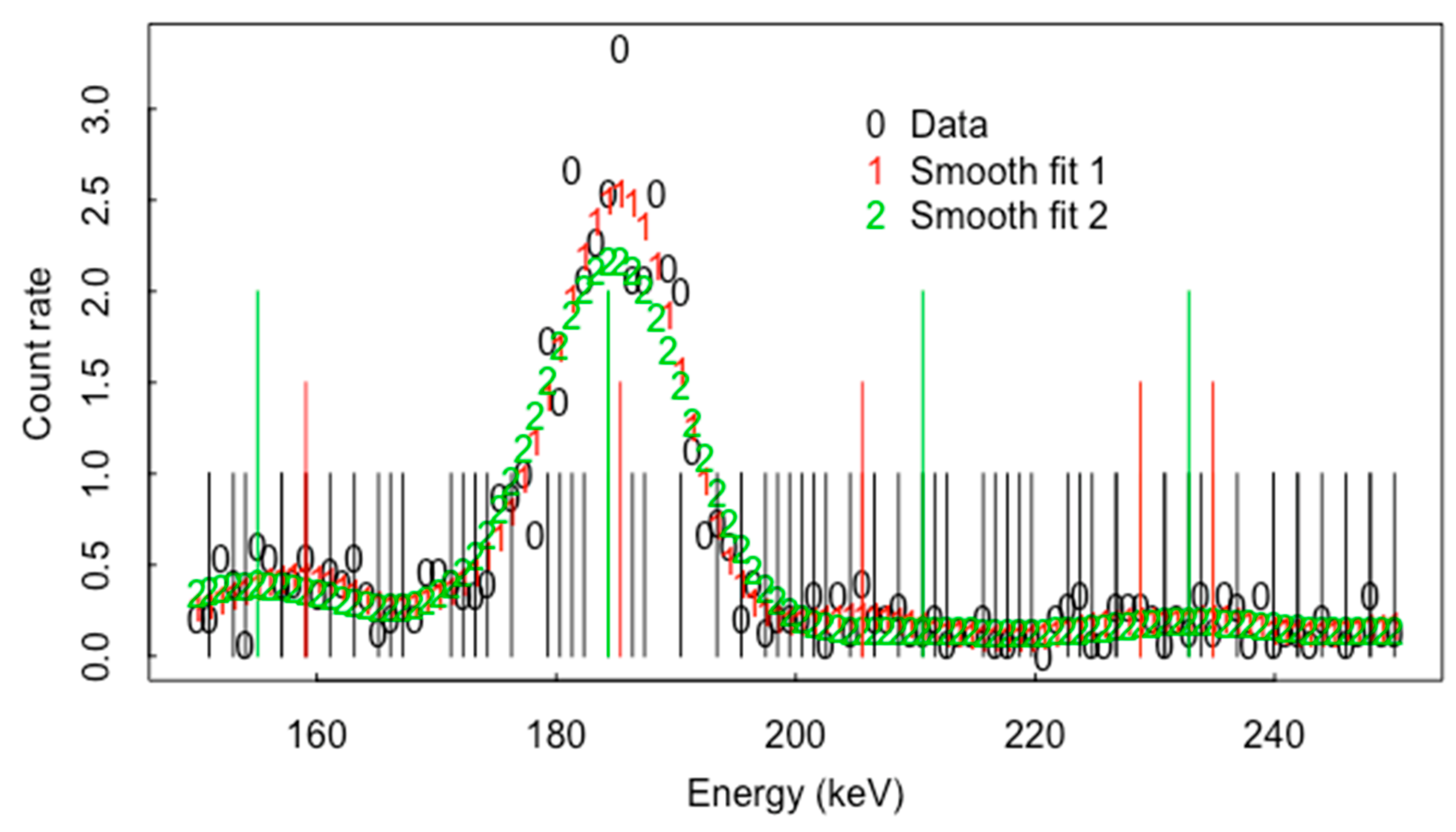
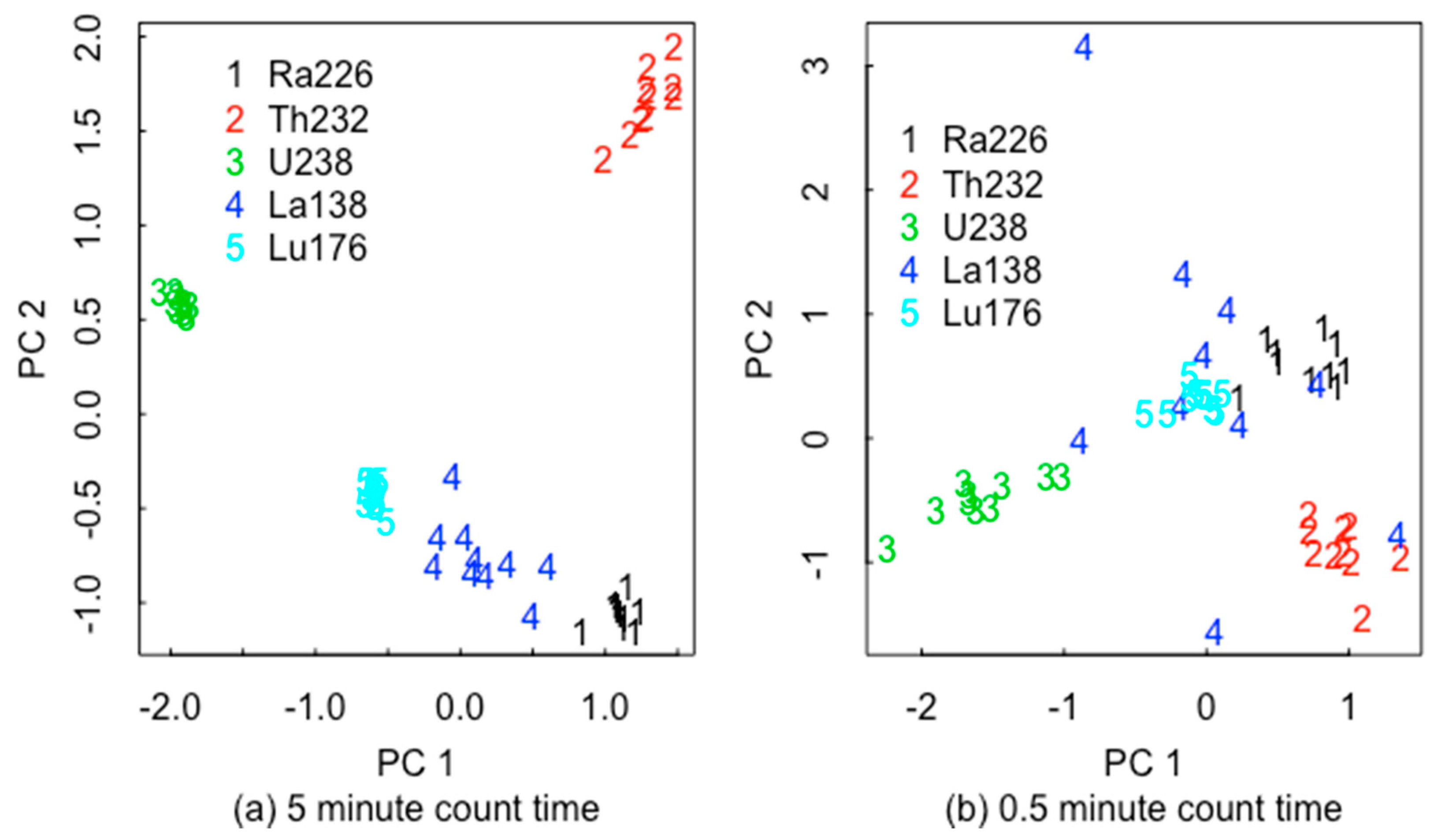
| Inferred/True | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 8927 | 0 | 0 | 1 | 80 |
| 2 | 788 | 10,000 | 0 | 5 | 95 |
| 3 | 272 | 0 | 10,000 | 89 | 387 |
| 4 | 13 | 0 | 0 | 9873 | 1713 |
| 5 | 0 | 0 | 0 | 32 | 7725 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burr, T.; Favalli, A.; Lombardi, M.; Stinnett, J. Application of the Approximate Bayesian Computation Algorithm to Gamma-Ray Spectroscopy. Algorithms 2020, 13, 265. https://doi.org/10.3390/a13100265
Burr T, Favalli A, Lombardi M, Stinnett J. Application of the Approximate Bayesian Computation Algorithm to Gamma-Ray Spectroscopy. Algorithms. 2020; 13(10):265. https://doi.org/10.3390/a13100265
Chicago/Turabian StyleBurr, Tom, Andrea Favalli, Marcie Lombardi, and Jacob Stinnett. 2020. "Application of the Approximate Bayesian Computation Algorithm to Gamma-Ray Spectroscopy" Algorithms 13, no. 10: 265. https://doi.org/10.3390/a13100265
APA StyleBurr, T., Favalli, A., Lombardi, M., & Stinnett, J. (2020). Application of the Approximate Bayesian Computation Algorithm to Gamma-Ray Spectroscopy. Algorithms, 13(10), 265. https://doi.org/10.3390/a13100265





