An Efficient Data Retrieval Parallel Reeb Graph Algorithm
Abstract
1. Introduction
Prior Work and Contribution
- We give an efficient parallel algorithm that computes the Reeb graph of a piece-wise linear function defined on a triangulated 2-manifold with and without a boundary.
- Our method can be used to retrieve the manifold data from the Reeb graph. In other words, given a point in the Reeb graph, we give an efficient method for retrieving the manifold data that correspond to that point. This feature, as well as feature (1), makes our algorithm an augmented Reeb graph algorithm.
- We show how the homological properties of a Reeb graph can be used to extract certain curves on a surface, and we utilize our algorithms to give a mesh segmentation algorithm.
- The algorithms that are presented here are easy to implement and require minimal memory storage.
2. Morse Theory and Reeb Graphs
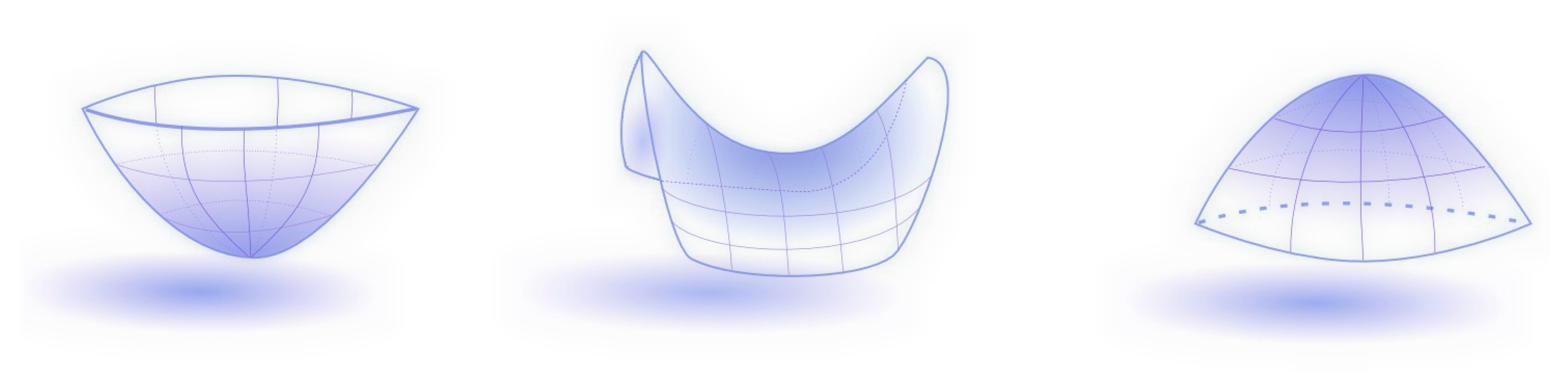
2.1. Morse Theory
- 1.
- Local minimum—
- 2.
- Saddle—
- 3.
- Local maximum—
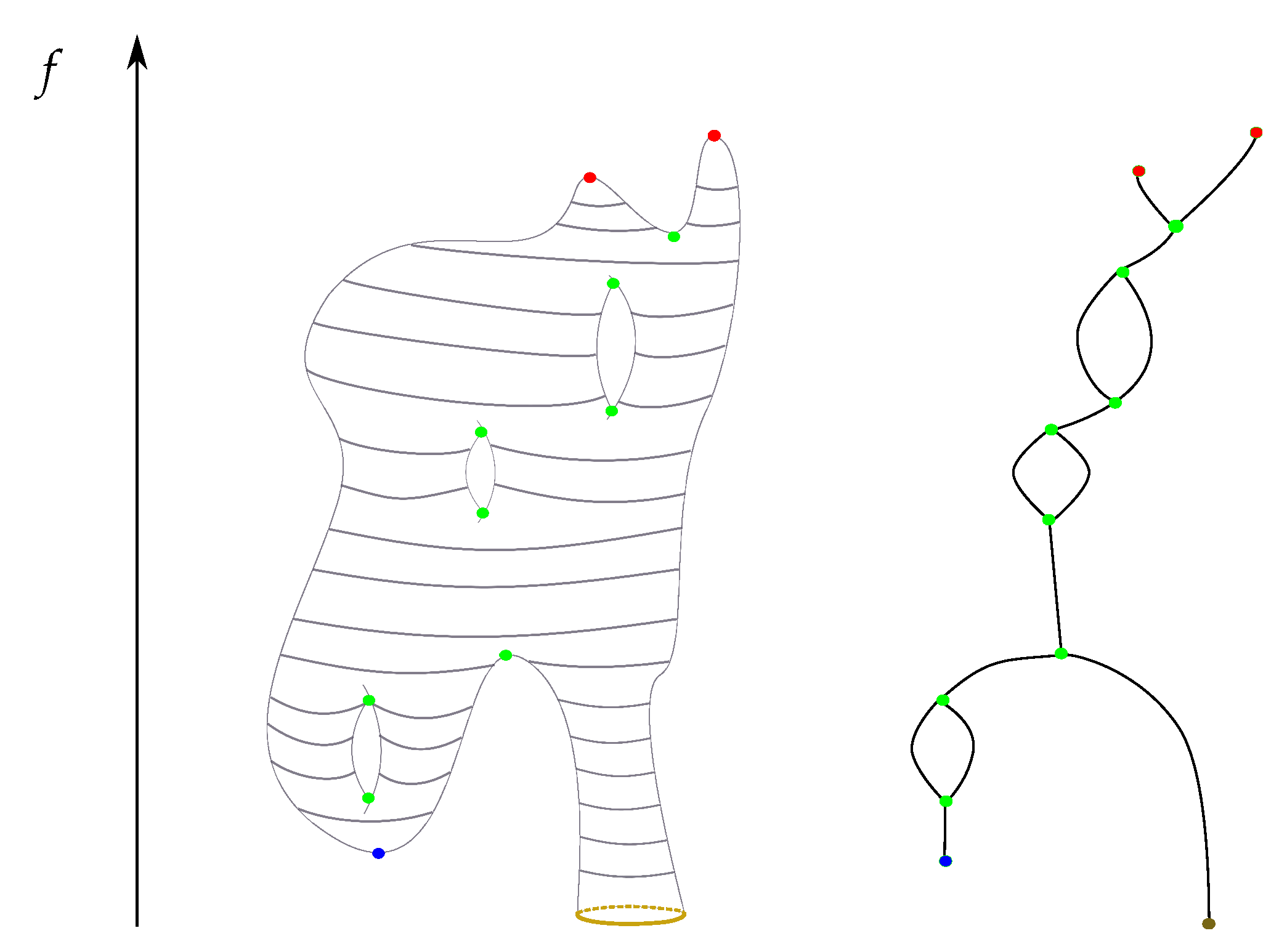
2.2. Reeb Graphs
3. Reeb Graphs on Triangulated Surfaces
3.1. Morse Functions in the Piece-Wise Linear Setting
3.2. Reeb Graphs of General Simplicial Complexes
4. Reeb Graph Sequential Algorithm on Triangulated Surfaces
4.1. Critical Sets and Ascending Paths
4.2. Outline of the Sequential Algorithm
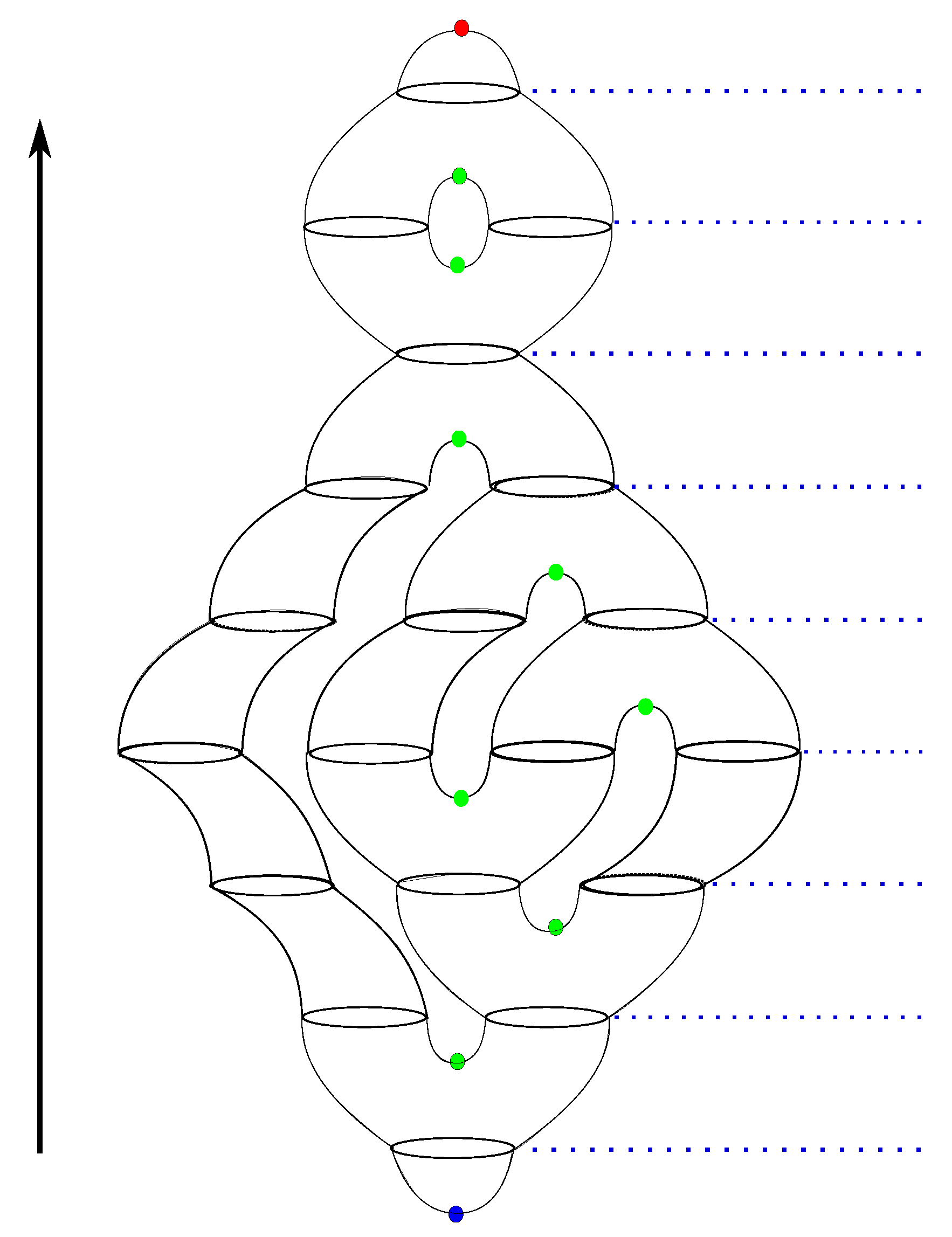
- We start by sorting the critical points of f by their critical values. Let be the set of the sorted critical points of f in an ascending order.
- For each critical point of the function f, we define a node in the Reeb graph . In other words, the node set of the graph precisely corresponds to the set of critical points of the function f defined on M.
- For each critical point v in , we compute the critical set .
- For each saddle or a minimum vertex v in , we associate one or two ascending paths on the mesh: one ascending path if v is a minimum or a merge saddle, and two paths if v is a split saddle. For each ascending path, we march with until this path intersects with the first critical set with a higher critical value than of . At this point, we insert an edge for the Reeb graph between the vertex v and vertex w.
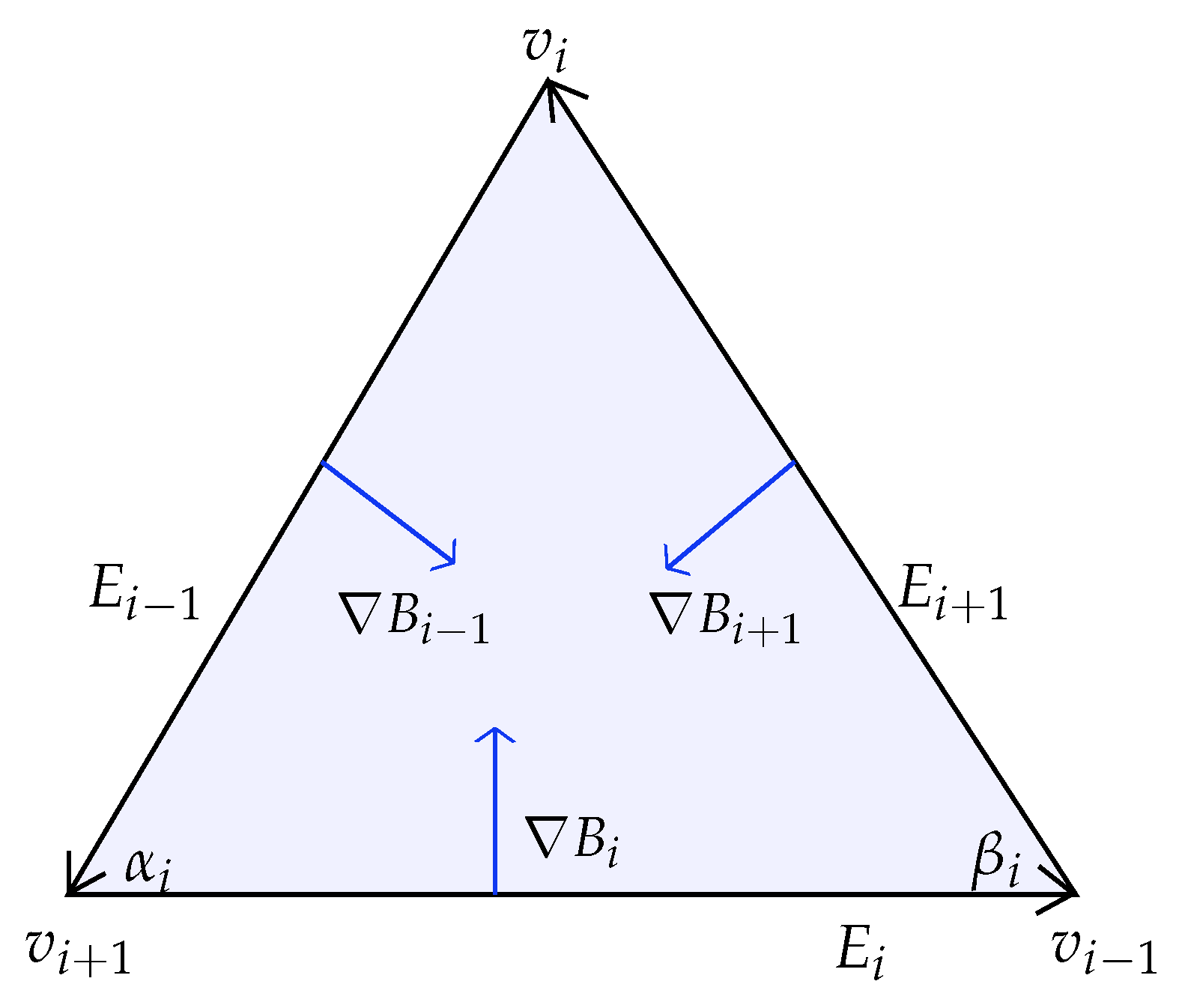
4.2.1. Construction of the Critical Sets
4.2.2. Construction of the Ascending Paths
- If is a merge saddle or a minimum, then we initiate a single ascending path specified, as follows. Let be a vertex in such that . At the kth iteration, consists of with for .
- If is a split saddle, then we start two ascending paths and originating from the point p specified as follows. Divide the set into two disconnected components A and B. Choose the vertex in A, such that for all , and choose the vertex in a similar manner. At the kth iteration, consists of with for (here we assume ). The path is similarly constructed.
4.2.3. Termination of an Ascending Path
4.3. Surfaces with Boundaries
- In step , each connected component in is considered a vertex in the Reeb graph vertex set.
- In step , for each boundary component in , we pick an arbitrary vertex on the boundary and initiate an ascending path that starts from that vertex.
- In step , if an ascending path starting at a vertex v reaches a boundary vertex w in one of the connected components, say , of , then we insert an edge in the Reeb graph between the vertex v and vertex in that corresponds to .
4.4. Correctness of the Sequential Algorithm
- The only topological changes to the level sets of f occur when as pass a critical point. This is formally stated in Theorem 1.
- The structure of the manifold around a critical point is completely determined by the index of that critical point. We give this in Theorem 2.
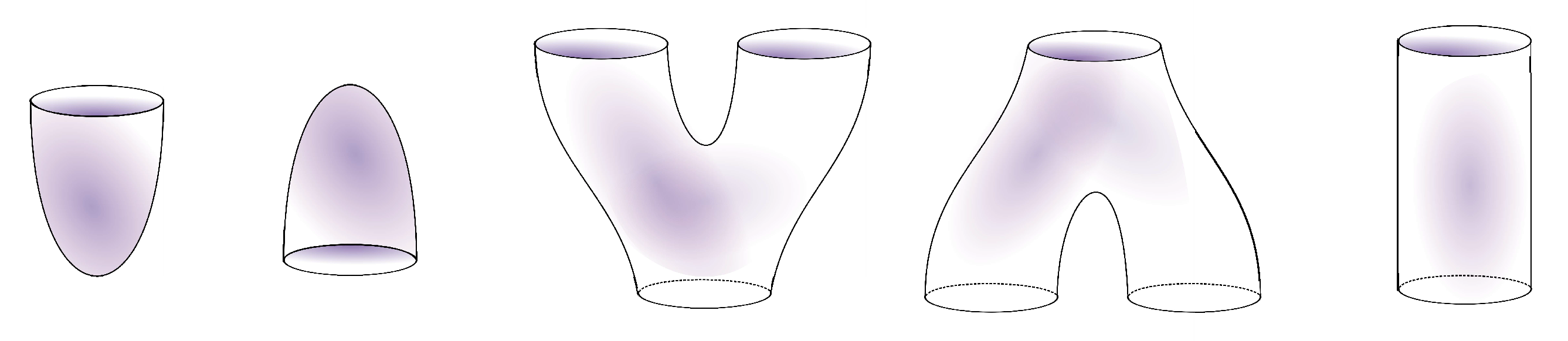
- 1.
- If is equal to 0 or 2, then is homeomorphic to a disjoint union of a disk and a finite number of topological cylinders (that is a genus zero surface with two boundary components).
- 2.
- If , then is homeomorphic to a pair of pants and a finite number of topological cylinders.
4.5. Dealing with Degenerate Cases
- In step (3), we calculate the connected components of the critical set . Here, it is not enough to calculate the critical set . We also need to compute the connected components of this set. Section 4.2.1 explains this.
- We create an ascending path for each connected component in when the multiplicity m of a split saddle p is greater than or equal to 2.
- Sort the critical points of f an in ascending order. Let be this set. This represents the vertex set of the Reeb graph, as we did before.
- For each v in , compute the connected components of and include all of these components in a single container . We will denote, by , the connected component j of the critical set . In this way, we index all of the elements in .
- Declare each set of as not visited.
- For each critical point in and for each component in , we initiate an ascending path P as described in Section 4.2.2. For each such path, we determine the connected component in , which the path terminates, as described in Section 4.2.1. We have two cases:
- (a)
- If the connected component is not visited, then we insert an edge between and and mark the component as visited.
- (b)
- If the connected component is visited, then we do not make any changes to the Reeb graph and terminate the current ascending path. In this case, the ascending path corresponds to an edge that already exists in the Reeb graph. See Remark 2.
5. Parallelization of the Algorithm
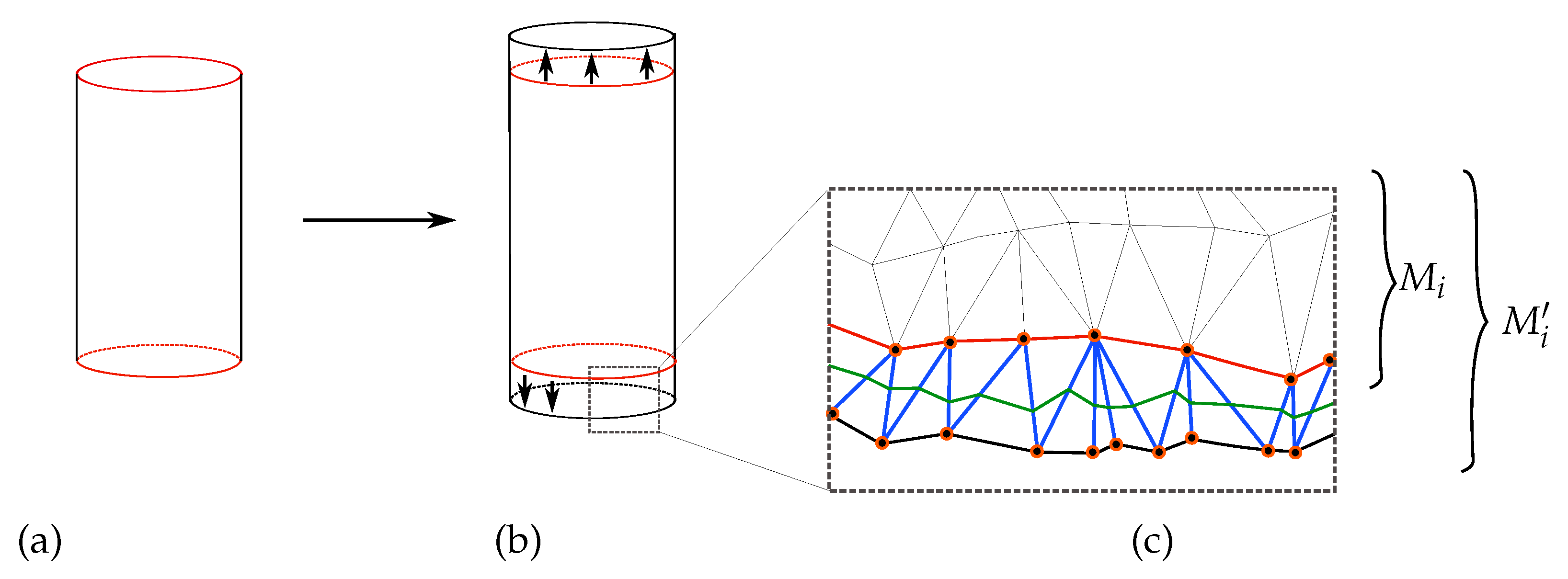
- The Partition Stage. In this stage, we partition the manifold M into submanifolds, such that the vertices counts of each submanifold are approximately equal to each other.
- Computing the Reeb Graph for the Submanifold Stage. Computing the Reeb graphs for each submanifold obtained from stage one concurrently.
- The Gluing Stage. In this step, we glue the Reeb graphs that were obtained from stage 2.
5.1. The Partition Stage
- Compute the critical points of f by assigning a thread to each vertex in M. Let be the list of critical points of f, and let be their corresponding critical values.
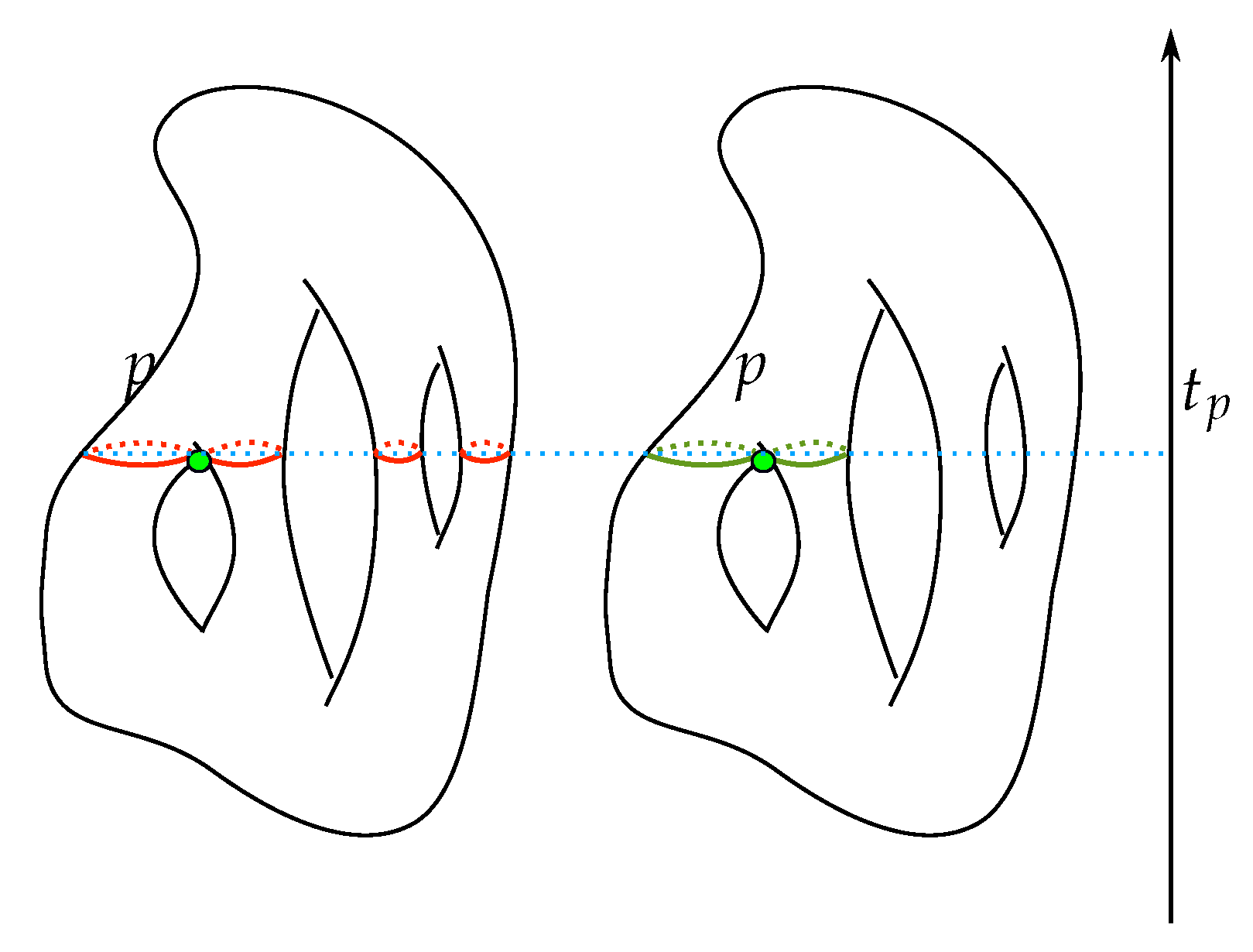
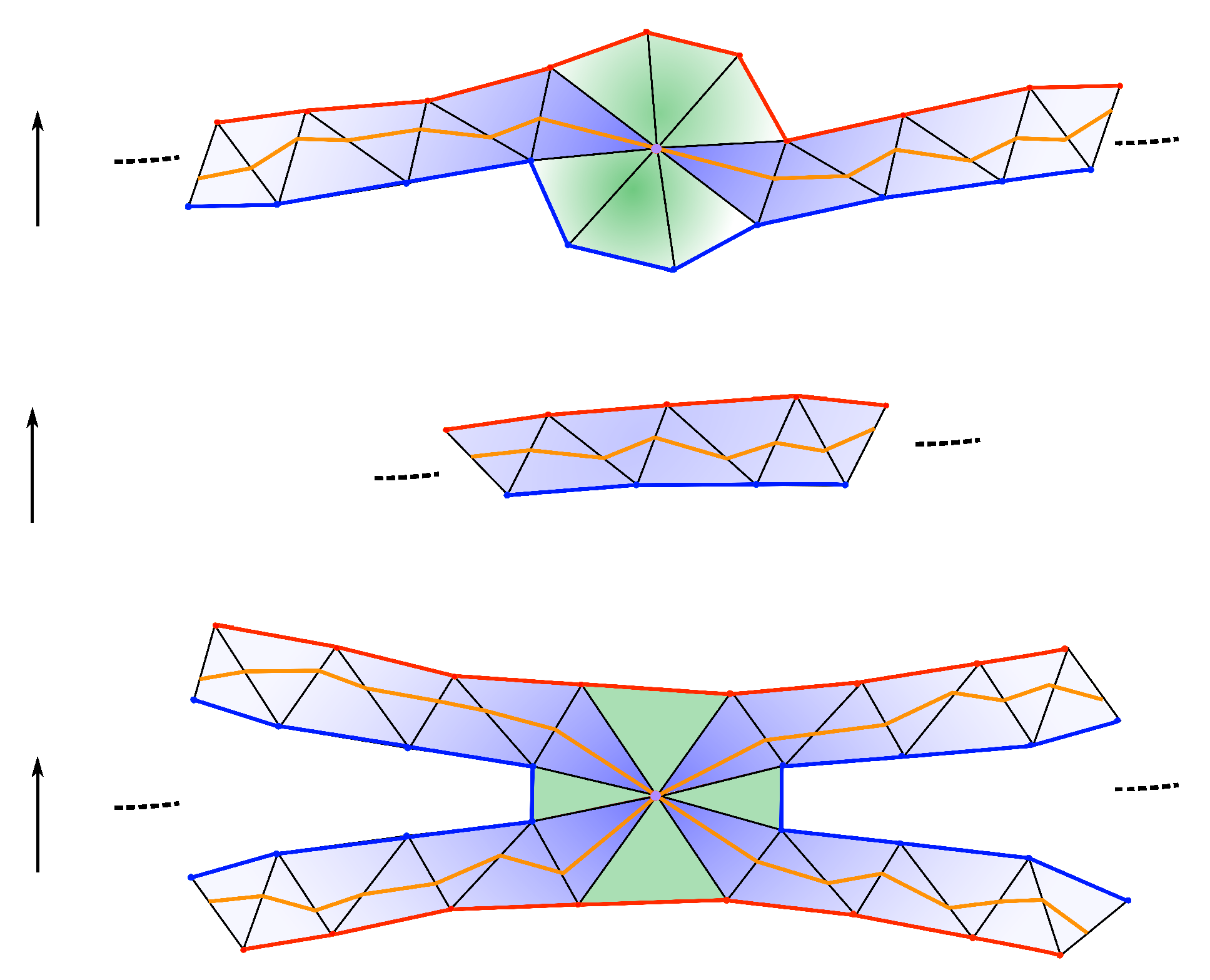
- We choose k regular values of f. These values will be utilized to slice the manifold M into submanifolds , such that the vertex counts of the submanifolds are approximately equal to each other. We also need to determine the connected components for in C. The connected components of the regular value can be computed in linear time with respect to the number of edges in M, as follows. We visit all edges of M and detect if an edge crosses one of the values . If such an edge is found at a level , then we keep rotating around to find all other edges crossing the value within the same connected component of . After visiting all edges, we have also determined the connected components of for each . We will denote the set of all connected components of for by . We also call an edge in M that crosses a crossing edge. See Figure 11 for an illustration.
- Divide the surface M into partitions along the level sets for all . We obtain a list of submanifolds ,…,. Here, we set and . We will denote to by . The set will be denoted by .
- Next, we extend by adding other vertices in M as follows. Let and be the edges in M that intersect with and , respectively. The submanifold is obtained from by adding the vertices from and . We call the edges and the boundary edges of . Note that every two consecutive submanifolds from intersect with each other along their boundary edges. See Figure 12 for an illustration.
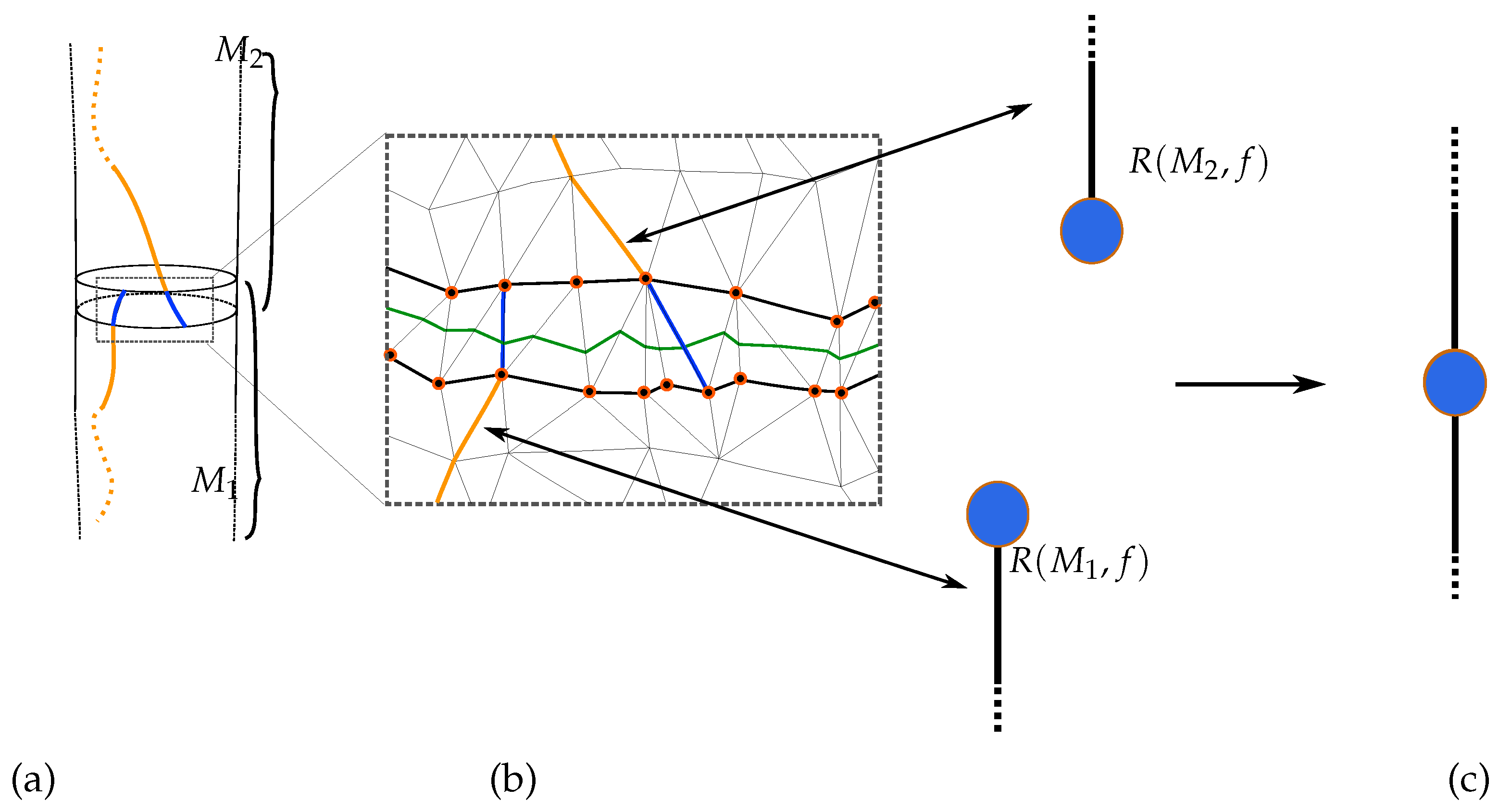
5.2. Computing the Reeb Graph of Each Submanifold
5.3. The Gluing Stage
6. Augmented Reeb Graph Computations: Going from the Reeb Graph to the Manifold
6.1. Building the Augmentation Map
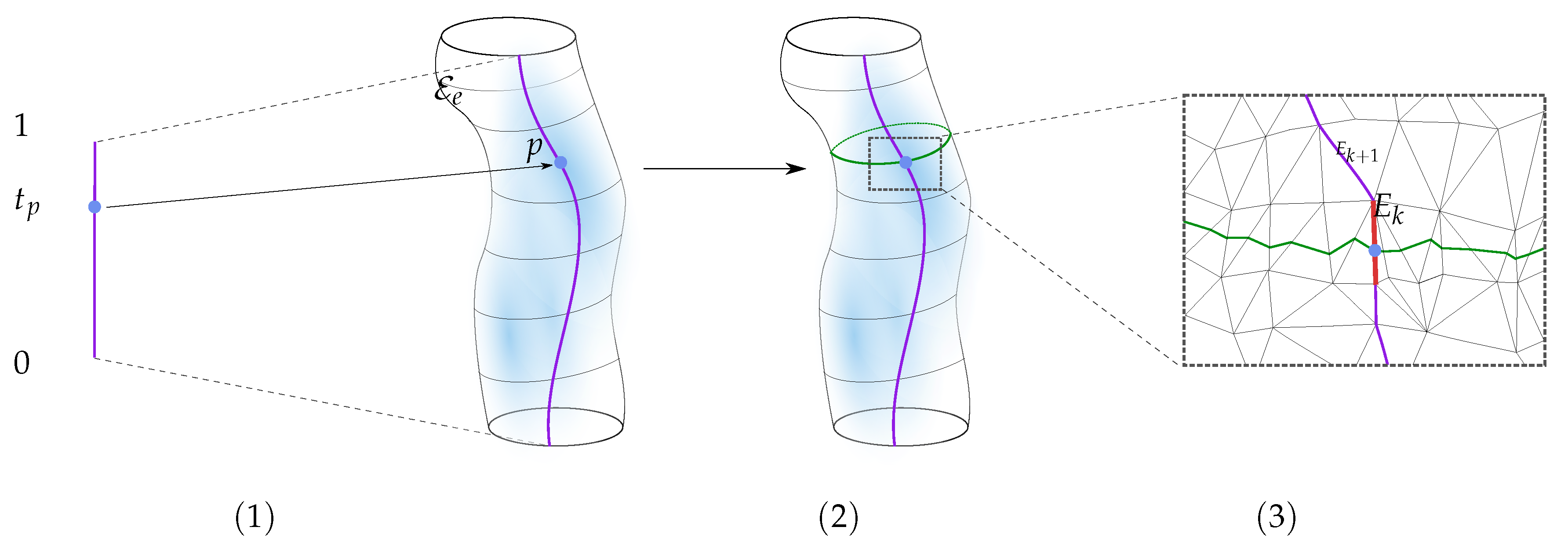
- Map the interval linearly to the interval .
- Use the constructed linear function that is computed in step (1) to map to its corresponding value in .
- Determine the edge in , such that .
- Now, we need to find the value t, in the range of , the range of f, such that contains . We know that this value corresponds to , which lies in the interval . The required t lies in interval . Hence, we map the interval linearly to and determine the value t in that corresponds to .
- The required circle is precisely the connected component of that contains the edge .
6.2. Consistent Parameterization of the Edges of the Reeb Graph
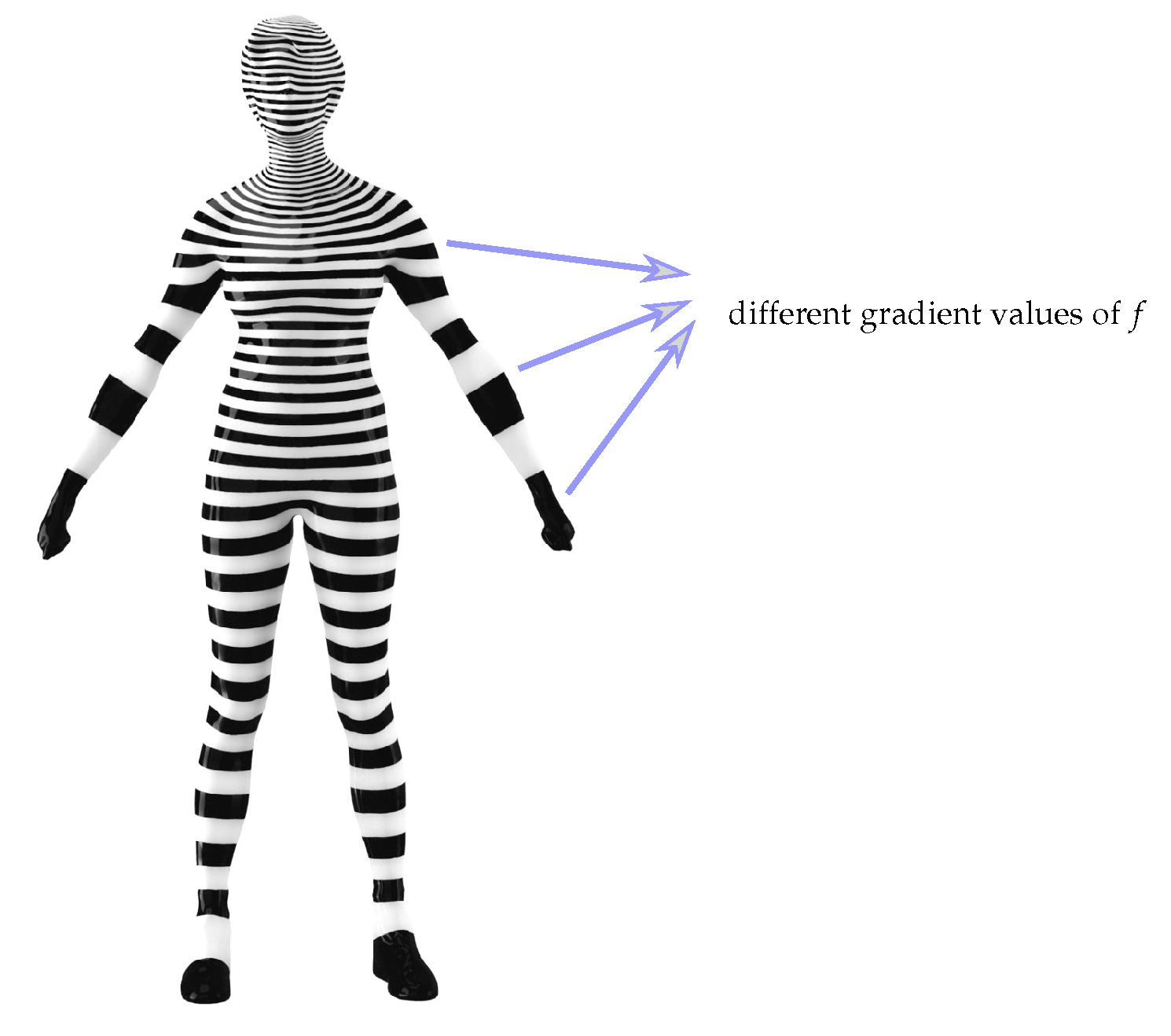
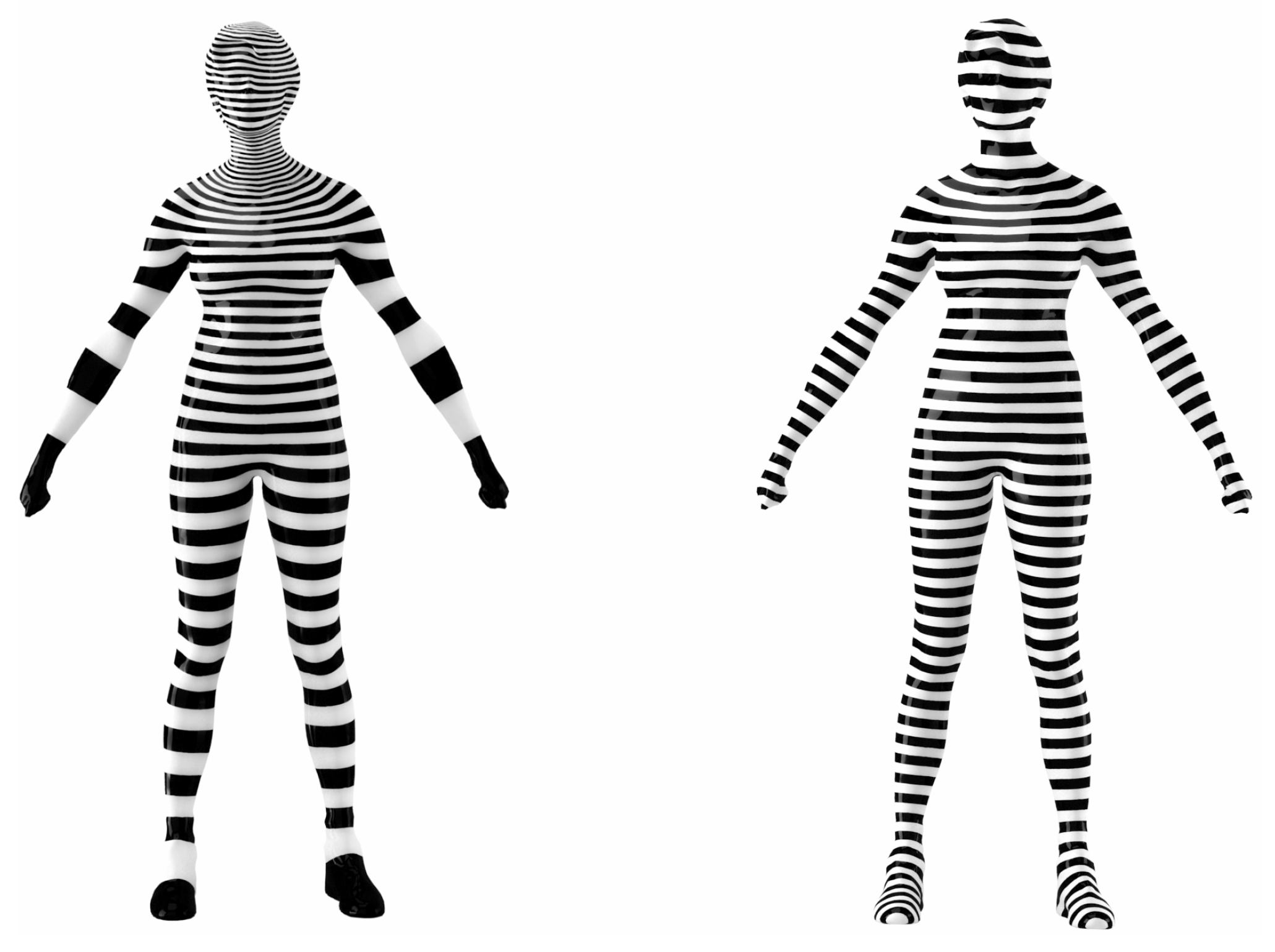
- The levels sets of the function are parallel the level sets of f.
- The function has uniform gradient everywhere.
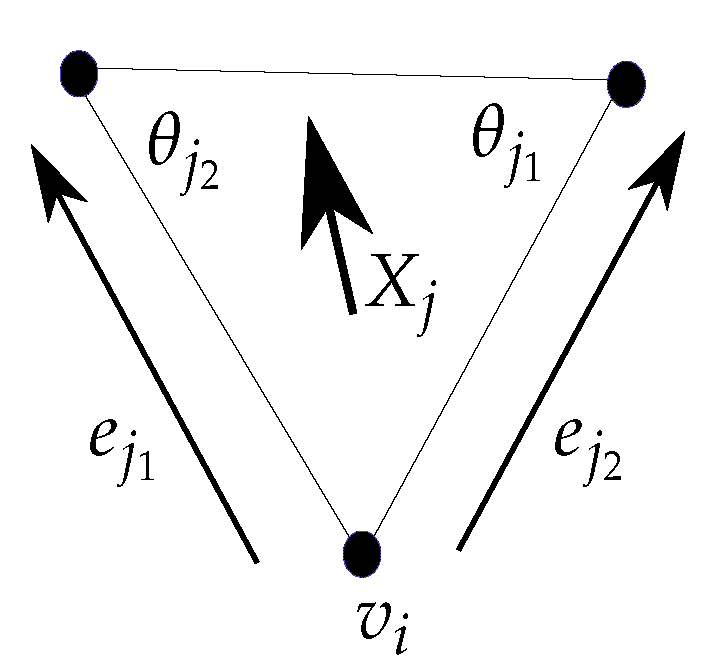
6.2.1. Gradient and Divergence of a PL Function on a Triangulated Mesh
6.2.2. Unit Gradient Scalar Fields
- The levels sets of the function are parallel to the level sets of f.
- The function has uniform gradient everywhere.
- Compute
- Solve the Poisson equation .
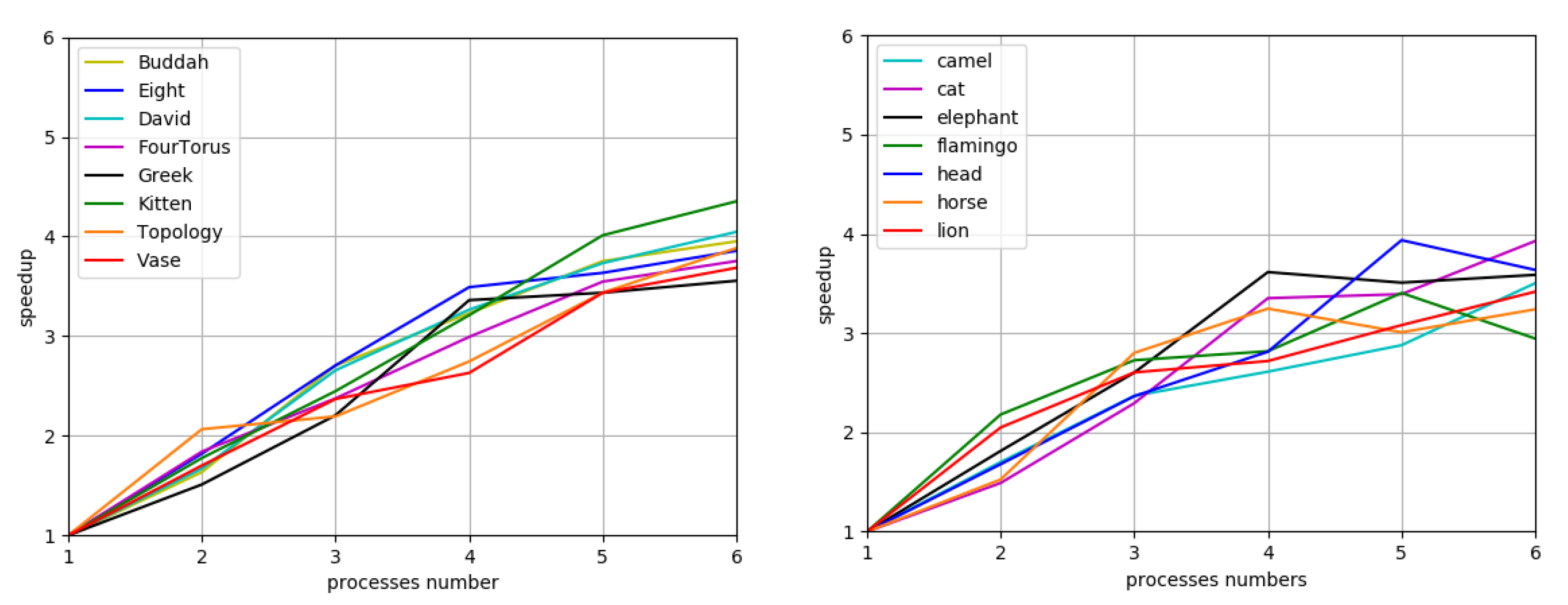
7. Run-Time Analysis and Implementation
8. Applications
- Cutting system curves.
- Pants decomposition curves.
- Branch curves.
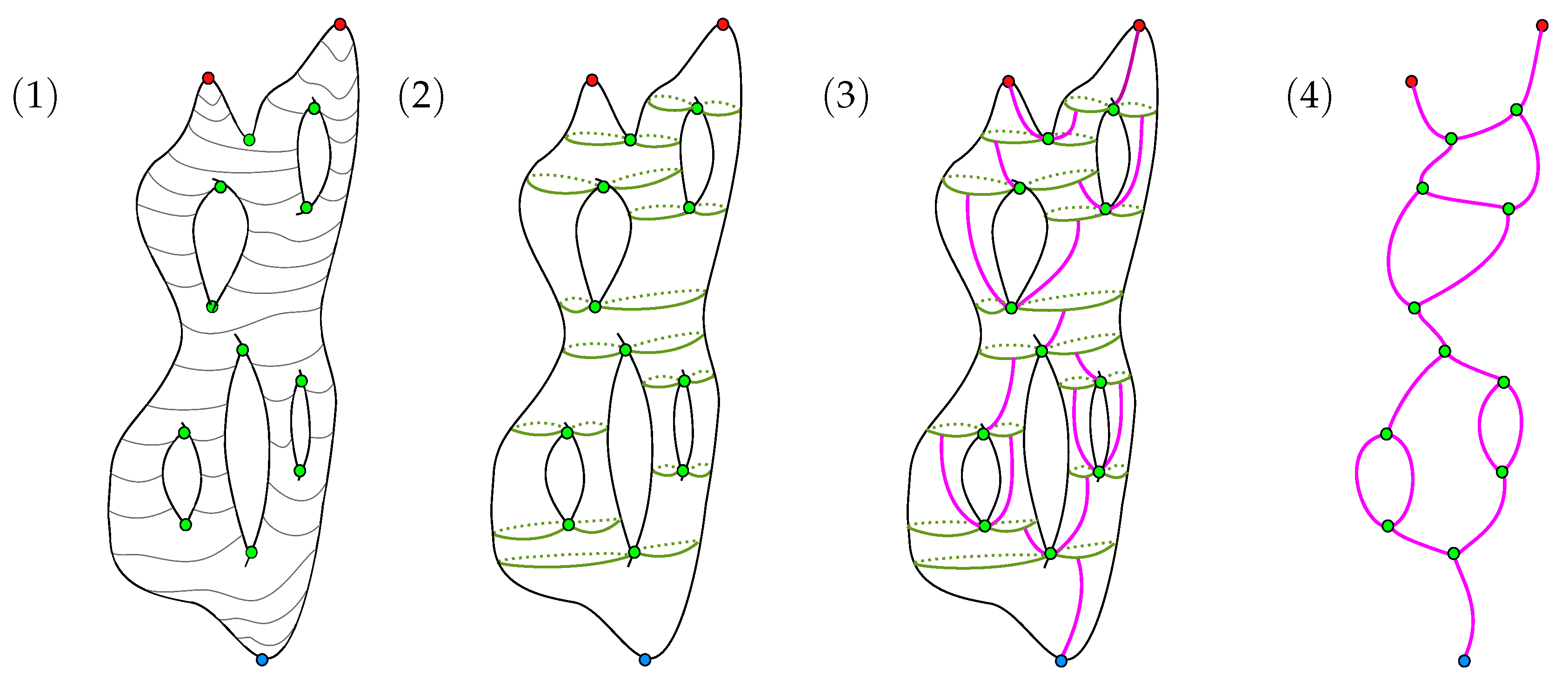
- Let T be a spanning tree of and consider the edges in .
- Select an interior point in , for .
- Each interior point selected in the previous step determines a loop , which can be obtained using the Reeb graph algorithm we described here.
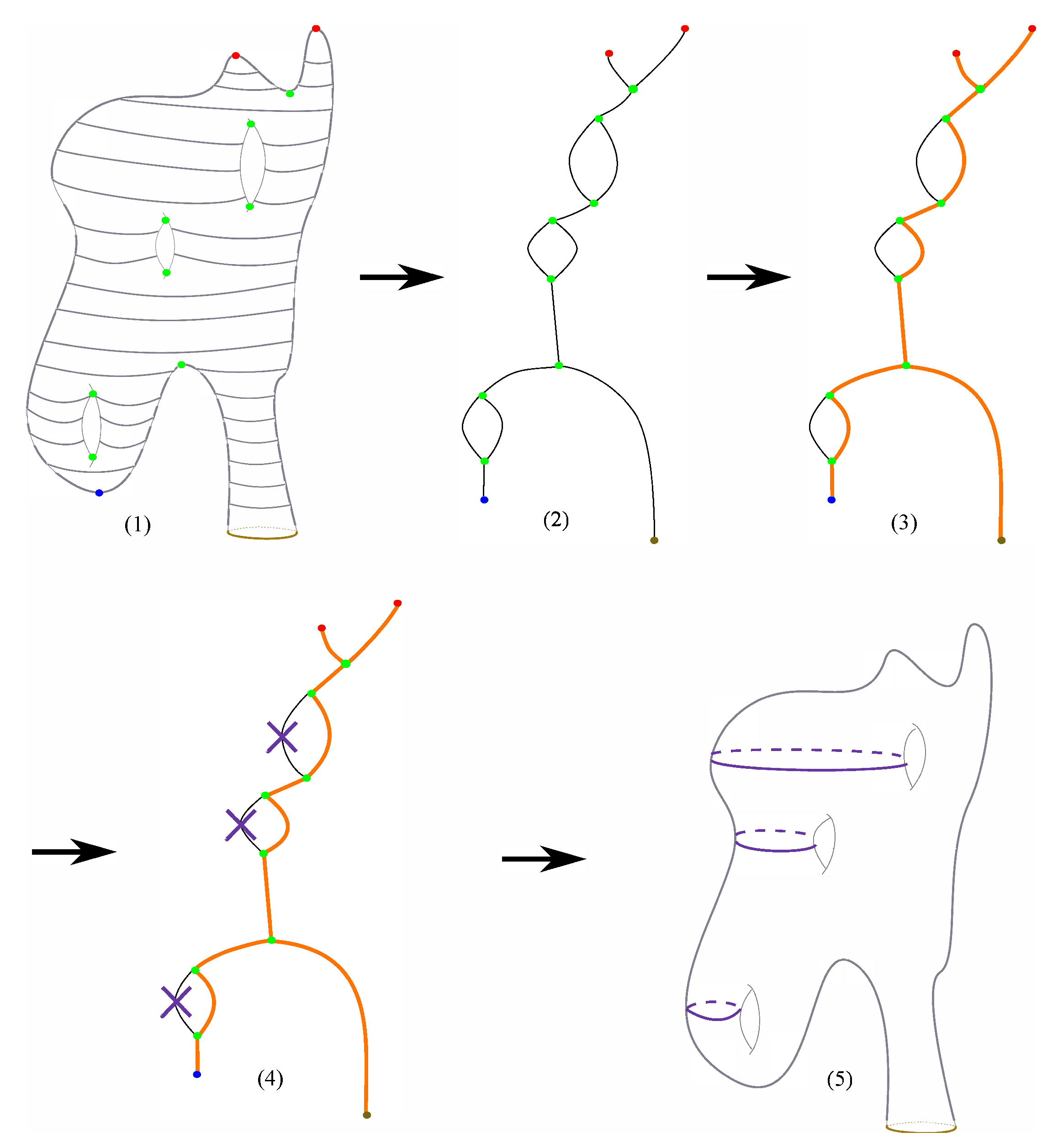
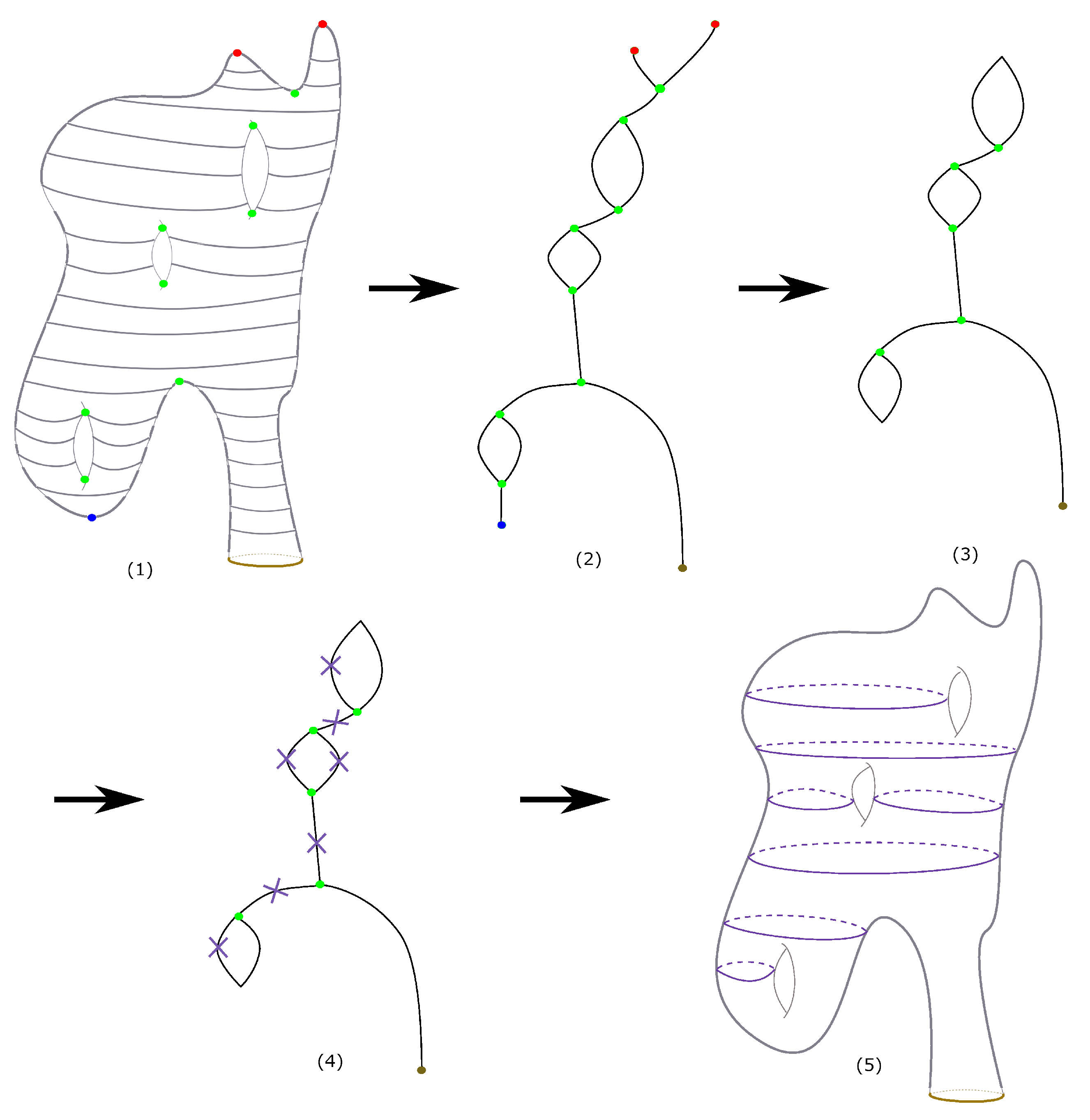
- Let be the deformation retract of . This graph can be obtained by recursively deleting nodes with valency one from and the edge attached to them until no such indices exist. We exclude from this deletion the 1-valence nodes originating from the boundary of M. We also delete all of the nodes with valency 2 and combine the two edges that meet at that node to form a single edge. This step is illustrated in step Figure 23.
- We select one interior point from each edge in , provided that this edge does not have a node of valency one.
- We use our Reeb algorithm to determine the curves on the surface that correspond to the points that we selected on the graph in the previous step.
8.1. Choosing Morse Scalar Functions
- The scalar function has a small number of critical vertices.
- The level sets of the scalar function follow the geometry of the mesh as closely as possible.
- The scalar function requires minimal input from the user.
8.1.1. Harmonic Functions
8.1.2. The Poisson Equation
9. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Carlsson, G. Topology and data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Carlsson, G.; Mémoli, F. Persistent clustering and a theorem of J. Kleinberg. arXiv 2008, arXiv:0808.2241. [Google Scholar]
- Reeb, G. Sur les Points Singuliers d’une Forme de Pfaff Completement Intergrable ou d’une Fonction Numerique (On the Singular Points of a Complete Integral Pfaff Form or of a Numerical Function). C. R. Acad. Sci. Paris 1946, 222, 847–849. [Google Scholar]
- Boyell, R.L.; Ruston, H. Hybrid techniques for real-time radar simulation. In AFIPS ’63 (Fall): Proceedings of the November 12–14, 1963, Fall Joint Computer Conference; Association for Computing Machinery: New York, NY, USA, 1963; pp. 445–458. [Google Scholar]
- Hétroy, F.; Attali, D. Topological quadrangulations of closed triangulated surfaces using the Reeb graph. Graph. Models 2003, 65, 131–148. [Google Scholar] [CrossRef]
- Attene, M.; Biasotti, S.; Spagnuolo, M. Shape understanding by contour-driven retiling. Vis. Comput. 2003, 19, 127–138. [Google Scholar] [CrossRef]
- Biasotti, S.; Falcidieno, B.; Spagnuolo, M. Extended reeb graphs for surface understanding and description. In Discrete Geometry for Computer Imagery; Springer: Berlin/Heidelberg, Germany, 2000; pp. 185–197. [Google Scholar]
- Patane, G.; Spagnuolo, M.; Falcidieno, B. Para-Graph: Graph-Based Parameterization of Triangle Meshes with Arbitrary Genus. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2004; Volume 23, pp. 783–797. [Google Scholar]
- Zhang, E.; Mischaikow, K.; Turk, G. Feature-based surface parameterization and texture mapping. ACM Trans. Graph. 2005, 24, 1–27. [Google Scholar] [CrossRef]
- Werghi, N.; Xiao, Y.; Siebert, J.P. A functional-based segmentation of human body scans in arbitrary postures. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2006, 36, 153–165. [Google Scholar] [CrossRef][Green Version]
- Kanongchaiyos, P.; Shinagawa, Y. Articulated Reeb graphs for interactive skeleton animation. In Multimedia Modeling: Modeling Multimedia Information and Systems; World Scientific: Singapore, 2000; pp. 451–467. [Google Scholar]
- Takahashi, S.; Takeshima, Y.; Fujishiro, I. Topological volume skeletonization and its application to transfer function design. Graph. Models 2004, 66, 24–49. [Google Scholar] [CrossRef]
- Carr, H.; Snoeyink, J.; van de Panne, M. Simplifying flexible isosurfaces using local geometric measures. In Proceedings of the IEEE Visualization, Austin, TX, USA, 10–15 October 2004; pp. 497–504. [Google Scholar]
- Rosen, P.; Wang, B.; Seth, A.; Mills, B.; Ginsburg, A.; Kamenetzky, J.; Kern, J.; Johnson, C.R. Using Contour Trees in the Analysis and Visualization of Radio Astronomy Data Cubes. arXiv 2017, arXiv:1704.04561. [Google Scholar]
- Kweon, I.S.; Kanade, T. Extracting topographic terrain features from elevation maps. CVGIP Image Underst. 1994, 59, 171–182. [Google Scholar] [CrossRef]
- Bajaj, C.; Pascucci, V.; Schikore, D. The contour spectrum. In Proceedings of the IEEE Visualization, Phoenix, AZ, USA, 24–24 October 1997; pp. 167–173. [Google Scholar]
- Harvey, W.; Wang, Y.; Wenger, R. A randomized O (m log m) time algorithm for computing Reeb graphs of arbitrary simplicial complexes. In SoCG ’10: Proceedings of the Twenty-Sixth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 2010; pp. 267–276. [Google Scholar]
- Shinagawa, Y.; Kunii, T.L. Constructing a Reeb graph automatically from cross sections. IEEE Comput. Graph. Appl. 1991, 11, 44–51. [Google Scholar] [CrossRef]
- Cole-McLaughlin, K.; Edelsbrunner, H.; Harer, J.; Natarajan, V.; Pascucci, V. Loops in Reeb graphs of 2-manifolds. In SCG ’03: Proceedings of the Nineteenth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 2003; pp. 344–350. [Google Scholar]
- Tierny, J.; Gyulassy, A.; Simon, E.; Pascucci, V. Loop surgery for volumetric meshes: Reeb graphs reduced to contour trees. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1177–1184. [Google Scholar] [CrossRef]
- Chiang, Y.J.; Lenz, T.; Lu, X.; Rote, G. Simple and optimal output-sensitive construction of contour trees using monotone paths. Comput. Geom. 2005, 30, 165–195. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J.; Mascarenhas, A.; Pascucci, V. Time-varying reeb graphs for continuous space-time data. In SCG ’04: Proceedings of the Twentieth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 2004; pp. 366–372. [Google Scholar]
- Pascucci, V.; Scorzelli, G.; Bremer, P.T.; Mascarenhas, A. Robust on-line computation of Reeb graphs: Simplicity and speed. ACM Trans. Graph. 2007, 26, 58. [Google Scholar] [CrossRef]
- Doraiswamy, H.; Natarajan, V. Efficient algorithms for computing Reeb graphs. Comput. Geom. 2009, 42, 606–616. [Google Scholar] [CrossRef]
- Parsa, S. A deterministic O(m log m) time algorithm for the Reeb graph. In SoCG ’12: Proceedings of the Twenty-Eighth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 2012; pp. 269–276. [Google Scholar]
- Doraiswamy, H.; Natarajan, V. Efficient output-sensitive construction of Reeb graphs. In International Symposium on Algorithms and Computation; Springer: Berlin/Heidelberg, Germany, 2008; pp. 556–567. [Google Scholar]
- Hilaga, M.; Shinagawa, Y.; Kohmura, T.; Kunii, T.L. Topology matching for fully automatic similarity estimation of 3D shapes. In SIGGRAPH ’01: Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 2001; pp. 203–212. [Google Scholar]
- Ge, X.; Safa, I.I.; Belkin, M.; Wang, Y. Data skeletonization via Reeb graphs. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 13–15 December 2011; pp. 837–845. [Google Scholar]
- Tung, T.; Schmitt, F. Augmented reeb graphs for content-based retrieval of 3d mesh models. In Proceedings of the Shape Modeling Applications, Genova, Italy, 7–9 June 2004; pp. 157–166. [Google Scholar]
- Biasotti, S.; Giorgi, D.; Spagnuolo, M.; Falcidieno, B. Reeb graphs for shape analysis and applications. Theor. Comput. Sci. 2008, 392, 5–22. [Google Scholar] [CrossRef]
- Raichel, B.; Seshadhri, C. Avoiding the global sort: A faster contour tree algorithm. arXiv 2014, arXiv:1411.2689. [Google Scholar] [CrossRef]
- Van Kreveld, M.; van Oostrum, R.; Bajaj, C.; Pascucci, V.; Schikore, D. Contour trees and small seed sets for isosurface traversal. In SCG ’97: Proceedings of the Thirteenth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 1997; pp. 212–220. [Google Scholar]
- Tarasov, S.P.; Vyalyi, M.N. Construction of contour trees in 3D in O (n log n) steps. In SSCG ’98: Proceedings of the Fourteenth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 1998; pp. 68–75. [Google Scholar]
- Pascucci, V.; Cole-McLaughlin, K.; Scorzelli, G. Multi-resolution computation and presentation of contour trees. In Proceedings of the IASTED International Conference on Visualization, Imaging, and Image Processing, Marbella, Spain, 6–8 September 2004. [Google Scholar]
- Weber, G.; Scheuermann, G. Topology-based transfer function design. In Proceedings of the IASTED International Conference on Visualization, Imaging, and Image Processing, Marbella, Spain, 3–5 September 2002; pp. 527–532. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor fusion IV: Control paradigms and data structures, Boston, MA, USA, 30 April 1992; pp. 586–606. [Google Scholar]
- Gupta, S.K.; Regli, W.C.; Nau, D.S. Manufacturing feature instances: Which ones to recognize? In SMA ’95: Proceedings of the Third ACM Symposium on Solid Modeling and Applications; ACM: New York, NY, USA, 1995; pp. 141–152. [Google Scholar]
- Gueunet, C.; Fortin, P.; Jomier, J. Contour forests: Fast multi-threaded augmented contour trees. In Proceedings of the IEEE Symposium on Large Data Analysis and Visualization (LDAV), Baltimore, MD, USA, 23–28 October 2016; pp. 85–92. [Google Scholar]
- Carr, H. Topological Manipulation of Isosurfaces. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2004. [Google Scholar]
- Dey, T.K.; Sun, J.; Wang, Y. Approximating cycles in a shortest basis of the first homology group from point data. Inverse Probl. 2011, 27, 124004. [Google Scholar] [CrossRef]
- Chazal, F.; Oudot, S. Towards persistence-based reconstruction in Euclidean spaces. In SCG ’08: Proceedings of the Twenty-Fourth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 2008; pp. 232–241. [Google Scholar]
- Dey, T.K.; Li, K. Cut locus and topology from surface point data. In SCG ’09: Proceedings of the Twenty-Fifth Annual Symposium on Computational Geometry; ACM: New York, NY, USA, 2009; pp. 125–134. [Google Scholar]
- Natali, M.; Biasotti, S.; Patanè, G.; Falcidieno, B. Graph-based representations of point clouds. Graph. Models 2011, 73, 151–164. [Google Scholar] [CrossRef]
- Chazal, F.; Guibas, L.J.; Oudot, S.; Skraba, P. Analysis of scalar fields over point cloud data. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, New York, NY, USA, 4–6 January 2009; pp. 1021–1030. [Google Scholar]
- Singh, G.; Mémoli, F.; Carlsson, G. Topological methods for the analysis of high dimensional data sets and 3d object recognition. In Eurographics/IEEE VGTC Symposium on Point-Based Graphics; The Eurographics Association: Munich, Germany, 2007; pp. 91–100. [Google Scholar]
- Lum, P.; Singh, G.; Lehman, A.; Ishkanov, T.; Vejdemo-Johansson, M.; Alagappan, M.; Carlsson, J.; Carlsson, G. Extracting insights from the shape of complex data using topology. Sci. Rep. 2013, 3, 1236. [Google Scholar] [CrossRef]
- Nicolau, M.; Levine, A.J.; Carlsson, G. Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc. Natl. Acad. Sci. USA 2011, 108, 7265–7270. [Google Scholar] [CrossRef] [PubMed]
- Robles, A.; Hajij, M.; Rosen, P. The Shape of an Image: A Study of Mapper on Images. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP), Funchal, Portugal, 27–29 January 2018. [Google Scholar]
- Rosen, P.; Hajij, M.; Tu, J.; Arafin, T.; Piegl, L. Inferring Quality in Point Cloud-based 3D Printed Objects using Topological Data Analysis. Comput.-Aided Des. Appl. 2019, 16, 519–527. [Google Scholar] [CrossRef]
- Carrière, M.; Oudot, S. Structure and stability of the 1-dimensional mapper. arXiv 2015, arXiv:1511.05823. [Google Scholar]
- Dey, T.K.; Memoli, F.; Wang, Y. Topological Analysis of Nerves, Reeb Spaces, Mappers, and Multiscale Mappers. arXiv 2017, arXiv:1703.07387. [Google Scholar]
- Munch, E.; Wang, B. Convergence between categorical representations of reeb space and mapper. arXiv 2015, arXiv:1512.04108. [Google Scholar]
- Hajij, M.; Wang, B.; Rosen, P. MOG: Mapper on Graphs for Relationship Preserving Clustering. arXiv 2018, arXiv:1804.11242. [Google Scholar]
- Xiao, Y.; Siebert, J.P.; Werghi, N. A discrete Reeb graph approach for the segmentation of human body scans. In Proceedings of the International Conference on 3-D Digital Imaging and Modeling (3DIM), Banff, AB, Canada, 6–10 October 2003; pp. 378–385. [Google Scholar]
- Tung, T.; Schmitt, F. The augmented multiresolution Reeb graph approach for content-based retrieval of 3D shapes. Int. J. Shape Model. 2005, 11, 91–120. [Google Scholar] [CrossRef]
- Mohamed, W.; Hamza, A.B. Reeb graph path dissimilarity for 3D object matching and retrieval. Vis. Comput. 2012, 28, 305–318. [Google Scholar] [CrossRef]
- Biasotti, S.; Mortara, M.; Spagnuolo, M. Surface compression and reconstruction using Reeb graphs and shape analysis. In Proceedings of the Spring Conference on Computer Graphics, Budmerice, Slovakia, 3–6 May 2000; pp. 174–185. [Google Scholar]
- Dey, T.K.; Li, K.; Sun, J.; Cohen-Steiner, D. Computing geometry-aware handle and tunnel loops in 3D models. ACM Trans. Graph. 2008, 27, 45. [Google Scholar] [CrossRef]
- Wood, Z.; Hoppe, H.; Desbrun, M.; Schröder, P. Removing excess topology from isosurfaces. ACM Trans. Graph. 2004, 23, 190–208. [Google Scholar] [CrossRef]
- Lewis, R.H.; Zomorodian, A. Multicore Homology via Mayer Vietoris. arXiv 2014, arXiv:1407.2275. [Google Scholar]
- Lipsky, D.; Skraba, P.; Vejdemo-Johansson, M. A spectral sequence for parallelized persistence. arXiv 2011, arXiv:1112.1245. [Google Scholar]
- Morozov, D.; Weber, G. Distributed contour trees. In Topological Methods in Data Analysis and Visualization III; Springer: Cham, Switzerland, 2012. [Google Scholar]
- Morozov, D.; Weber, G. Distributed merge trees. In Proceedings of the 18th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Shenzhen, China, 23–27 February 2013; Volume 48, pp. 93–102. [Google Scholar]
- Masood, T.B.; Ray, T.; Natarajan, V. Parallel computation of alpha complexes for biomolecules. Comput. Geom. 2020, 90, 101651. [Google Scholar] [CrossRef]
- Hajij, M.; Assiri, B.; Rosen, P. Distributed Mapper. arXiv 2017, arXiv:1712.03660. [Google Scholar]
- Matsumoto, Y. An Introduction to Morse Theory; American Mathematical Society: Providence, RI, USA, 2002; Volume 208. [Google Scholar]
- Banyaga, A.; Hurtubise, D. Lectures on Morse Homology; Springer Science & Business Media: New York, NY, USA, 2013; Volume 29. [Google Scholar]
- Morse, M. The Calculus of Variations in the Large; American Mathematical Society: Providence, RI, USA, 1934; Volume 18. [Google Scholar]
- Milnor, J.W. Morse Theory; Number 51; Princeton University Press: Princeton, NJ, USA, 1963. [Google Scholar]
- Banchoff, T. Critical points and curvature for embedded polyhedra. J. Diff. Geom. 1967, 1, 245–256. [Google Scholar] [CrossRef]
- Guo, X.; Li, X.; Bao, Y.; Gu, X.; Qin, H. Meshless thin-shell simulation based on global conformal parameterization. IEEE Trans. Vis. Comput. Graph. 2006, 12, 375–385. [Google Scholar] [PubMed]
- Ni, X.; Garland, M.; Hart, J.C. Fair morse functions for extracting the topological structure of a surface mesh. ACM Trans. Graph. 2004, 23, 613–622. [Google Scholar] [CrossRef]
- Dong, S.; Bremer, P.T.; Garland, M.; Pascucci, V.; Hart, J.C. Spectral surface quadrangulation. ACM Trans. Graph. 2006, 25, 1057–1066. [Google Scholar] [CrossRef]
- Stander, B.T.; Hart, J.C. Guaranteeing the topology of an implicit surface polygonization for interactive modeling. In SIGGRAPH ’97: Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques; ACM Press: New York, NY, USA, 1997; pp. 279–286. [Google Scholar]
- Yamazaki, I.; Natarajan, V.; Bai, Z.; Hamann, B. Segmenting point sets. In Proceedings of the IEEE International Conference on Shape Modeling and Applications 2006, Matsushima, Japan, 14–16 June 2006; p. 6. [Google Scholar]
- Wang, H.; He, Y.; Li, X.; Gu, X.; Qin, H. Geometry-aware domain decomposition for T-spline-based manifold modeling. Comput. Graph. 2009, 33, 359–368. [Google Scholar] [CrossRef]
- Tsigas, P.; Zhang, Y. A simple, fast parallel implementation of quicksort and its performance evaluation on SUN enterprise 10000. In Proceedings of the Euromicro Conference on Parallel, Distributed, and Network-Based Processing, Genova, Italy, 5–7 February 2003; pp. 372–381. [Google Scholar]
- Singler, J.; Sanders, P.; Putze, F. MCSTL: The multi-core standard template library. In European Conference on Parallel Processing; Springer: Berlin/Heidelberg, Germany, 2007; pp. 682–694. [Google Scholar]
- Pinkall, U.; Polthier, K. Computing discrete minimal surfaces and their conjugates. Exp. Math. 1993, 2, 15–36. [Google Scholar] [CrossRef]
- Polthier, K. Polyhedral Surfaces of Constant Mean Curvature. Ph.D. Thesis, Habilitationsschrift TU, Berlin, Germany, 2002. [Google Scholar]
- Crane, K.; Weischedel, C.; Wardetzky, M. Geodesics in heat: A new approach to computing distance based on heat flow. ACM Trans. Graph. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Sumner, R.W.; Popović, J. Deformation transfer for triangle meshes. ACM Trans. Graph. 2004, 23, 399–405. [Google Scholar] [CrossRef]
- Xiao, Y.; Werghi, N.; Siebert, J.P. A topological approach for segmenting human body shape. In Proceedings of the International Conference on Image Analysis and Processing, Mantova, Italy, 17–19 September 2003; pp. 82–87. [Google Scholar]
- Tierny, J.; Vandeborre, J.P.; Daoudi, M. Topology driven 3D mesh hierarchical segmentation. In Proceedings of the IEEE International Conference on Shape Modeling and Applications 2007 (SMI ’07), Lyon, France, 13–15 June 2007; pp. 215–220. [Google Scholar]
- Hatcher, A.; Thurston, W. A presentation for the mapping class group of a closed orientable surface. Topology 1980, 19, 221–237. [Google Scholar] [CrossRef]
- Zeng, W.; Yin, X.; Zhang, M.; Luo, F.; Gu, X. Generalized Koebe’s method for conformal mapping multiply connected domains. In SIAM/ACM Joint Conference on Geometric and Physical Modeling; ACM: New York, NY, USA, 2009; pp. 89–100. [Google Scholar]
- Hajij, M.; Dey, T.; Li, X. Segmenting a surface mesh into pants using Morse theory. Graph. Models 2016, 88, 12–21. [Google Scholar] [CrossRef]
- Kwok, T.H.; Zhang, Y.; Wang, C.C. Constructing common base domain by cues from Voronoi diagram. Graph. Models 2012, 74, 152–163. [Google Scholar] [CrossRef]
- Li, X.; Gu, X.; Qin, H. Surface mapping using consistent pants decomposition. IEEE Trans. Vis. Comput. Graph. 2009, 15, 558–571. [Google Scholar] [CrossRef]
- Jin, M.; Zeng, W.; Ding, N.; Gu, X. Computing Fenchel-Nielsen coordinates in teichmuller shape space. In Proceedings of the 2009 IEEE International Conference on Shape Modeling and Applications, Beijing, China, 26–28 June 2009; pp. 193–200. [Google Scholar]
- Rosenberg, S. The Laplacian on a Riemannian Manifold: An Introduction to Analysis on Manifolds; Number 31; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Floater, M.S. Mean value coordinates. Comput. Aided Geom. Des. 2003, 20, 19–27. [Google Scholar] [CrossRef]
- Dong, S.; Kircher, S.; Garland, M. Harmonic functions for quadrilateral remeshing of arbitrary manifolds. Comput. Aided Geom. Des. 2005, 22, 392–423. [Google Scholar] [CrossRef]
- Meyer, M.; Desbrun, M.; Schröder, P.; Barr, A.H. Discrete differential-geometry operators for triangulated 2-manifolds. In Visualization and Mathematics III; Springer: Berlin/Heidelberg, Germany, 2003; pp. 35–57. [Google Scholar]
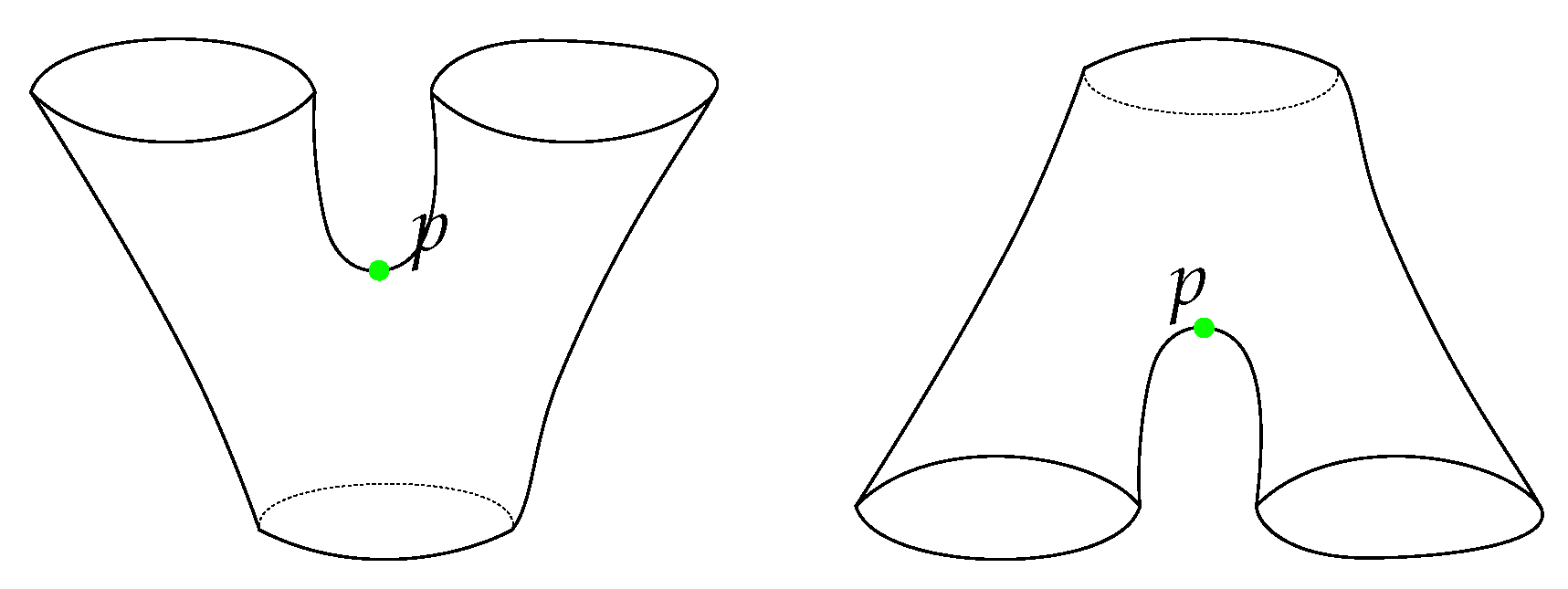



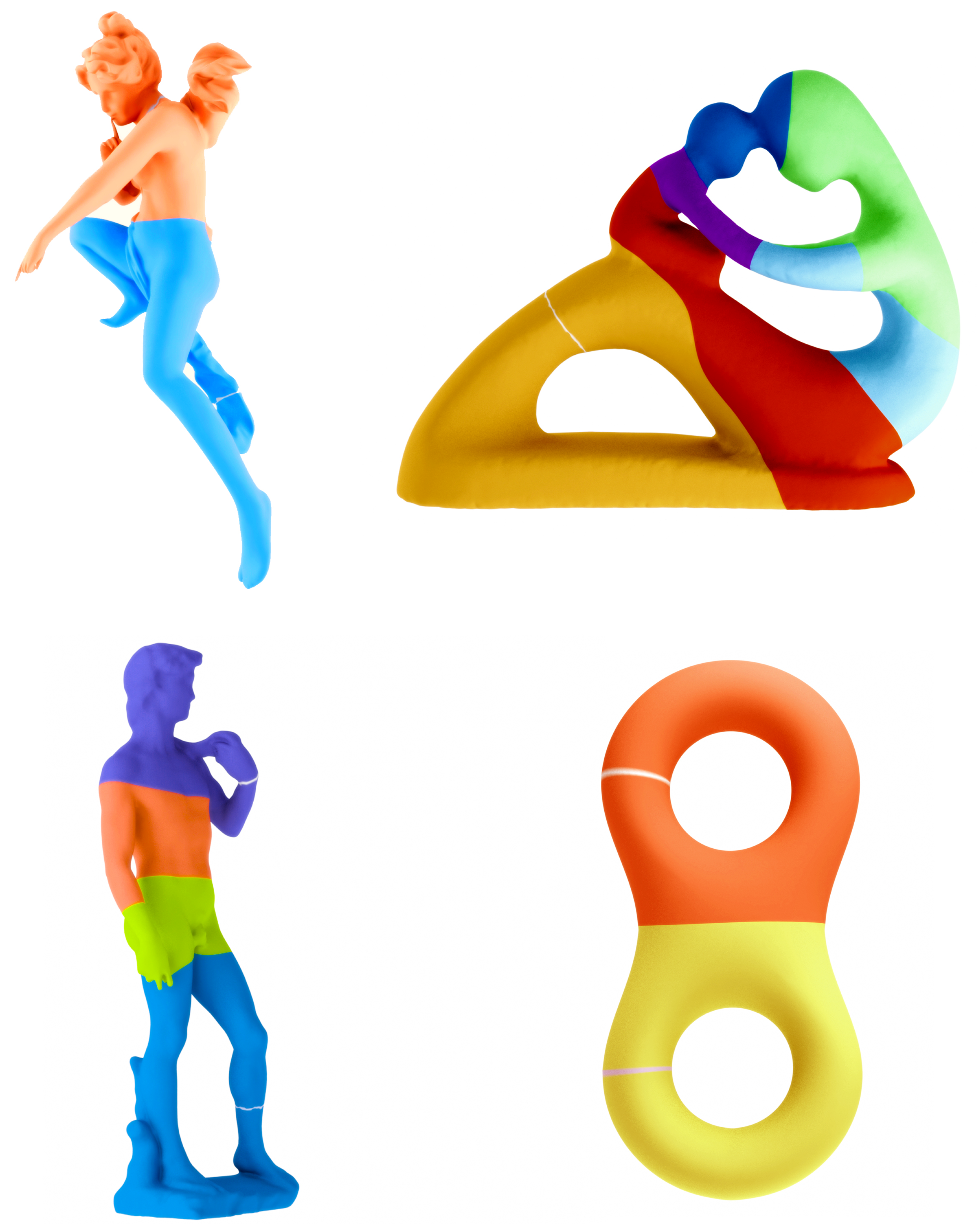

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajij, M.; Rosen, P. An Efficient Data Retrieval Parallel Reeb Graph Algorithm. Algorithms 2020, 13, 258. https://doi.org/10.3390/a13100258
Hajij M, Rosen P. An Efficient Data Retrieval Parallel Reeb Graph Algorithm. Algorithms. 2020; 13(10):258. https://doi.org/10.3390/a13100258
Chicago/Turabian StyleHajij, Mustafa, and Paul Rosen. 2020. "An Efficient Data Retrieval Parallel Reeb Graph Algorithm" Algorithms 13, no. 10: 258. https://doi.org/10.3390/a13100258
APA StyleHajij, M., & Rosen, P. (2020). An Efficient Data Retrieval Parallel Reeb Graph Algorithm. Algorithms, 13(10), 258. https://doi.org/10.3390/a13100258




