Abstract
We introduce a novel methodology for anomaly detection in time-series data. The method uses persistence diagrams and bottleneck distances to identify anomalies. Specifically, we generate multiple predictors by randomly bagging the data (reference bags), then for each data point replacing the data point for a randomly chosen point in each bag (modified bags). The predictors then are the set of bottleneck distances for the reference/modified bag pairs. We prove the stability of the predictors as the number of bags increases. We apply our methodology to traffic data and measure the performance for identifying known incidents.
1. Introduction
Traffic incidents are severely detrimental to society in terms of financial costs which are estimated in the U.S. by the National Highway Traffic Safety Administration [1]. Consequently, an important focus of data analysis concerns detecting incidents from traffic data for the management of response to accidents which can have significant benefits for society [2]. The type of data we consider is a time series of volumetric traffic counts. We propose a novel methodology for analyzing this data for the purpose of identifying traffic incidents.. Our approach is to view the identification of incidents as a problem of anomaly detection within the time-series data. Our method uses tools from statistical analysis–bootstrap aggregation or bagging–and from topological data analysis (TDA)–persistence diagrams–to form an ensemble of predictors to determine whether data points are normal or anomalous. To each data point and random bag, we associate two persistence diagrams, one reference and one modified. The predictors then consist of a score–the bottleneck distance between the diagrams–and for each data point, the set of scores are aggregated into several summary statistics. We then identify data points as being incidents or anomalies by percentile scores of the summary statistics.
Our algorithm using randomized bagging of the data and resultant persistence diagrams as a feature extractor for anomaly detection can be viewed as a semi-supervised learning algorithm. Indeed, our method trains the summary statistics on a small amount of labeled data. Moreover, our algorithm can be applied to any vectorized data and, thus, can be adapted for many other data analytic problems.
1.1. Description of the Data and Challenge Problem
The problem we address is to identify incidents in a data set of volumetric traffic counts obtained from multiple inductive loop road sensors, [3], supplied by the California Department of Transportation. The counts were aggregated over 5 min intervals, and we had access to one full calendar year of traffic counts for each sensor. See Table 1 for a sample from the data. We apply our method to this data set in Section 4.

Table 1.
A sample of the traffic counts from Phase 1-Train.
Our task to identify incidents was part of an anomaly detection problem hosted by the Joint Algorithms for Threat Detection (ATD) and Algorithms for Modern Power Systems (AMPS) Annual Workshop; the challenge problem that we specifically addressed was curated for the ATD program [4]. The challenge problem consisted of two phases: in Phase 1, we were asked to detect incidents within data provided by 10 road sensors that were spatially located to be independent from one another (we were not informed of the locations); in Phase 2, we were asked to repeat Phase 1 provided additional information on the location of the sensors–see Figure 1. For each phase, we were supplied with a training data set and a testing data set with labeled incidents that were hand-selected by the ATD program coordinators. The training data set for Phase 1 contained 9 labeled incidents, and the training data set for Phase 2 contained 10 labeled incidents. There were numerous unlabeled incidents in the training data sets.
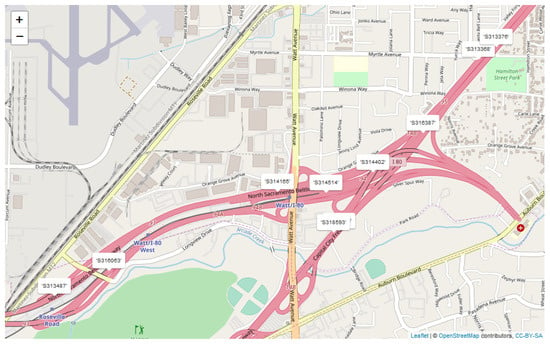
Figure 1.
A map of sensor locations from Phase 2-Train.
The timeline of the challenge problem was as follows:
- Phase 1 training data posted: 15 January 2019
- Phase 1 testing data posted: 22 March 2019
- Phase 1 solution deadline: 2 May 2019
- Phase 2 training data posted: 24 May 2019
- Phase 2 testing data posted: 15 July 2019
- Phase 2 solution deadline: 27 September 2019
Supplementary materials in the form of data sets and code are available at the following repository: https://bitbucket.org/esweber/randomized-persistence-landscapes/src/master/.
Data sets for the challenge problem were originally released as files in MATLAB. We have converted the data to comma-separated values files and all experiments discussed in the paper can be reproduced by executing our code in R-Studio. Our solutions were submitted as a binary output for each 5 min interval with 1 indicating an incident and 0 otherwise. Three evaluation metrics were then used to evaluate the performance of our algorithm: precision, recall, and an F-score.
1.2. Survey of Literature
Detecting incidents in traffic data is important for the safety and welfare of society [2]. Significant efforts have been made to automate incident detection [5,6,7,8]. Traditional automatic incident detection data sources include radar sensors [9], video cameras [10], probes [11]. Loop detectors are also a very common source of traffic data [3,12], which is the source of the traffic data analyzed in our method.
Detecting incidents in traffic data can be formulated as an anomaly detection problem. Approaches in this formulation include: dynamic clustering [13] or Support Vector Machines [14] to detect anomalous trajectories, autoencoders to learn regularity of video sequences [15], motion reconstruction [16], and convolutional neural networks to predict congestion in traffic networks [17]. In this paper, we also view incident detection as an anomaly detection problem, with our approach using TDA to identify outliers. For an overview of anomaly detection, see [18].
Topological data analysis has been used previously in the context of traffic data: [19] uses TDA as a model for tracking vehicles and [20] uses TDA to understand individual travel behaviors. TDA has also been used previously for anomaly detection in [21,22]. TDA provides a framework for studying the “shape” of data in geometric and topological terms rather than a solely statistical framework [23,24,25].
TDA has been an extremely successful tool in applied algebraic topology across a multitude of applications, including analysis of neural networks [26,27], data dimension reduction techniques [28,29], anomaly detection [21,22] biological studies [30], viral evolution [31], the study of blood flow through brain arteries [32], and tracking vehicles [19]. TDA has been applied previously to study time-series data in a variety of settings [33,34]. Existing applications include to financial data [35,36,37], medical signal (EEG) analysis [38,39] and general techniques including sliding-window methods [40,41,42,43]. Most of these methods rely on a Takens-style embedding to transform time-series data into point-cloud data [44,45]. In contrast, our method does not require such an embedding.
Our algorithm is motivated by the intuition that if we take a data set of vectors that represent typical behavior and one of the vectors were replaced with an anomalous observation, the topology of the data set would be significantly altered. This intuition is supported by randomized persistence diagrams [46,47]. For example, [48] finds that samples from a manifold corrupted by noise with a Gaussian distribution will not in general significantly deviate from the persistence diagram of the underlying manifold, but other distributions could. Further results in [49] emphasize this by showing that extending the stability results for noise with a Gaussian distribution in [48] to other noise distributions should not “be expected”.
1.3. Main Contributions
Our main contributions in this paper are two-fold. First, we introduce a novel machine learning algorithm that uses TDA for detecting anomalies in time-series data. This is done by establishing a baseline of typical data distribution to serve as a reference through the method of bagging, and deviations from the reference for various data points are measured using the bottleneck distance from TDA. This procedure is repeated multiple times to reduce the variation that naturally arises from random sampling. The algorithm requires selection of several hyperparameters. Second, we address the problem of identifying incidents in traffic data that consists only of traffic counts. Our data set does not include any functional data, such as velocity, nor does it include video feed which are the most common data sources used in traffic incident detection problems.
1.4. Outline
The rest of the paper is organized as follows. In Section 2 we present the necessary background for understanding persistence diagrams, the fundamental tool from TDA that our algorithm implements. In Section 3 we present the algorithm. In Section 4 we present the results of our algorithm when applied to the traffic data set from the ATD challenge problem.
2. Topological Data Analysis (TDA)
Here, we provide the necessary background for understanding the TDA that our algorithm implements. For more details on the subject, see [50,51]. The appeal of TDA is that it offers techniques from topology to ascertain the "shape" of high-dimensional data sets that is not accessible by other methods. In particular, persistent homology is ubiquitous in TDA for measuring certain topological features of a space (e.g., connectivity, holes, voids). These features are often summarized using Betti numbers or a persistence diagram [23]. Our focus will be on the latter and the bottleneck distance which serves as a metric on a set of those diagrams.
2.1. Persistence Diagrams
Persistence diagrams are computed based on the notion of a simplicial complex. It is natural to think of a simplicial complex in a Euclidean space, but a more abstract definition adequately serves our purposes.
Definition 1
(Abstract Simplicial Complex). A finite collection of sets A is called an abstract simplicial complex if A is closed under subset inclusion, i.e., if whenever and . Furthermore, we call a combinatorial p-simplex if .
In our consideration, each simplex is a subset of data points. There are several useful methods by which to construct simplicial complexes from data. We have chosen the Vietoris–Rips (VR) complex for its computational convenience.
Definition 2
(Vietoris–Rips Complex). Let Y be a finite subset of data points contained in some metric space X. For every , the Vietoris–Rips Complex of Y at scale r is defined as
We note that the VR complex is ascending in the sense that for . Thus, as the radius r increases, we produce a filtration of simplicial complexes on top of the data points in Y. This filtration yields a persistent homology that quantifies the apparent topological features for different dimensions. 0-, 1-, and 2-dimensional features refer to connected components, holes, and voids, respectively. Higher-dimensional features would be the analogues of these features. The persistence diagram quantifies the importance of these features in terms of their persistence over various radii. Persistence gives us a sequence of homology groups for each dimension of the ambient metric space containing the data. By identifying the radii in the sequence when the topological features appear and disappear we obtain a collection of birth and death times for each feature of each dimension.
The birth-death pairs as a multiset in make up the persistence diagram corresponding to Y. The persistence diagrams in our algorithm only contain information on connected components, the zero-dimensional features. We were unable to find a meaningful use for persistence diagrams computed using higher-dimensional features.
2.2. Bottleneck Distance
We use the bottleneck distance to make comparisons between two persistence diagrams. The bottleneck distance can be thought of more generally as a pseudometric on multisets P and Q that quantifies the cost of mapping P to Q. To be precise, suppose P and Q are plain multisets of points in the extended plane . We say is a partial matching between P and Q if it satisfies the following:
- For each , there exists at most one such that .
- For each there exists at most one such that .
We say that is unmatched if there does not exist with or such that . Let . Please note that if , then if satisfies , then
We define the cost function for each matching M to be
Definition 3
(Bottleneck Distance). Let be the set of all partial matchings between P and Q. We define the bottleneck distance between P and Q as
Remark 1.
We refer to the bottleneck distance as a pseudometric because there are multisets P and Q such that yet . Take for example and . Although for every , we find by taking an infimum over . It has been shown that in the case where P and Q are finite multisets in then implies , [52].
3. Description of the Algorithm
Our algorithm is motivated by the intuition that if we take a data set of vectors that represent typical behavior and one of the vectors were replaced with an anomalous observation, the topology of the data set would be significantly altered. The topology of the set is understood by computing persistence diagrams of randomly chosen subsets . When we modify a bag by randomly replacing one of its vectors with we denote the resulting modified bag by . Figure 2 depicts the data points in the reference and modified bags. We then let D and denote the persistence diagrams for vectors in and , respectively. Figure 3 depicts the persistence diagrams for the reference and modified bags for a specfic data point.
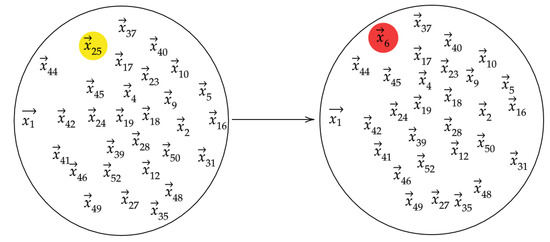
Figure 2.
The left side represents one of the reference bags, while the right side represents the corresponding modified bag for week 6.
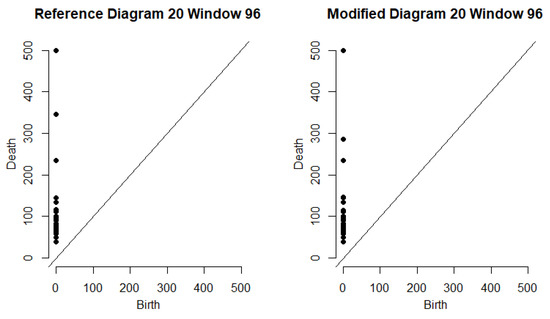
Figure 3.
A plot of the persistence diagram for 20th reference diagram (left) and the modified persistence diagram (right) when week 6 replaces one of the randomly chosen observations in the 7th reference bag. This corresponds to the traffic behavior at sensor on Monday, 6 February 2017 from 7:55–8:55 AM.
The bottleneck distance quantifies how much the topology of a set has changed. We say there is evidence that is anomalous if is relatively large compared to the values in . There are some undesirable cases that may occur due to the random sampling used to form . It may be that the observations contained in do not adequately represent the entire data set, or if the reference bag contains an anomaly, we might replace an anomaly with a non-anomalous vector when forming the modified bag. To mitigate issues such as these, the algorithm uses multiple bags of the same size. We select hyperparameters and repeat N times the process of randomly choosing S vectors to form . This creates a collection of reference bags . For each of the N bags, we form m distinct modified bags by randomly choosing and replacing it with . We calculate the summary statistics mean, median, and standard deviation for the bottleneck distances, and choose a function that identifies anomalies from the summary statistics. The entire algorithm is presented in Algorithm 1.
| Algorithm 1: Anomaly Detection using Persistence Diagrams of Random Subsamples |
 |
The summary statistics of the bottleneck distances can be used in various ways depending on the application. In our application to traffic data, we set thresholds for each summary statistic based on training data. Thus, we set thresholds for the three summary statistics, and we defined if and only if and .
In addition to those previously mentioned, we may also encounter the issue when the modified bag is formed by replacing the same vector . This would make an anomaly look much less anomalous based on our bottleneck distance measurement. Fortunately, if N is chosen to be sufficiently large, then the effect can be very small since the summary statistics converge in probability. Let us formalize the probability distribution here. The sample space consists of ordered pairs
We place the uniform distribution on and denote this by .
Theorem 1.
Let , , and be denote the mean, standard deviation, and median respectively of bottleneck distance associated with as computed in Algorithm 1. Then there exist , and such that
as , and for all ,
Proof.
Define the random variable on by
We have that are i.i.d. random variables. Since and there are no infinite points in , is bounded. The three limits are consequences of the Weak Law of Large Numbers, which requires a sequence of i.i.d. random variables with finite expectation. In particular, let and . Since the are i.i.d. with finite mean , by the Weak Law of Large Numbers,
as . To prove the second limit, we start by writing
Since are i.i.d with , it follows from the Weak Law of Large Numbers that as N tends to infinity. Since we have established as , it follows that as N tends to infinity. Adding up the terms in (1), this means in probability. For the third equation, first define
For any , we have . We can define if , and otherwise. It follows that . Since is the sample median of , it follows that
Since , we apply the Weak Law of Large Numbers to to see that . Similarly, we have , Thus, if we instead define if , we have . Much like what we had in (2), we find
Since , we again have from the Weak Law of Large Numbers applied to that . □
Remark 2.
Since we are sampling from a discrete probability distribution, it is not guaranteed that the distribution producing the has a true median. Hence we must settle for convergence of the sample median to some interval. In the case where there exists η such that , then and the sample median converges in probability to η. We define the sample median the usual way where if , the sample median would be if N is odd or if N is even.
Remark 3.
We note that the values guaranteed in Theorem 1 are data dependent, and that for the purposes of Theorem 1 as well as Algorithm 1, the data are fixed.
4. Results
In this section, we present our contribution to the ATD challenge problem through the application of our method on traffic data collected from major highways in the Sacramento area. The problem was divided into two phases–depending on whether the location information of the sensors was provided–where each phase consisted of a training and testing data set. The objective of each phase of the challenge problem was to predict the time and location of hand-selected traffic incidents in the testing data using the training data which had very few labeled incidents. The data was collected as a count of cars that passed a given sensor during each 5-min interval throughout the 2017 calendar year. An example of this can be seen in Table 1.
The training sets included details on certain incidents reported during the year that include the nearest sensor, the timestamp, and the duration of each incident. In each data set there are a few instances in which a particular sensor was not operating so that there are no counts reported during those five-minute intervals. Table 2 contains additional information on the data sets that were provided.

Table 2.
A summary of the four traffic data sets to which we applied the incident detection algorithm.
To apply the algorithm to the volumetric data, we considered the embedding of the data in as sequences of 12 consecutive 5-min counts from a sensor. This means each vector represents 1 hour’s worth of counts. We index each vector by a 3-tuple . We use p to denote the sensor ID from which the counts were collected. We let , where t denotes the starting time of the five-minute window corresponding to the first of the 12 counts and indicates the day of the week with corresponding to Sunday, corresponding to Monday, etc. We let denote the week in which these counts were collected. (We note that in 2017, there were 53 Sundays, and so for , .) The vectors were then sorted by sensor, starting time, and day of week, meaning the set of all vectors was partitioned into smaller data sets of 52 vectors. We let denote the collection of count vectors from sensor p collected at the time (hour and day of the week) corresponding to . For two different starting times from the same weekday, say and , it is possible that the components of vectors in overlap with those of vectors in . For example, if 8:00 AM, and 8:05 AM, then the vectors in are nearly the same vectors as in , but the entries are shifted left by one component and the final entry is the count from 9:00–9:05 AM. Since there are 288 five-minute intervals throughout the day and we required 12 consecutive counts to form each vector, there are 277 possible vectors of counts each day.
After sorting the vectors, we applied Algorithm 1 to each collection of counts with and . Thus, each vector in , was assigned 30 bottleneck distances. For each time window , we recorded the mean, median, and standard deviation of these bottleneck distances which we denote by , , and , respectively.
As in [53], we expected different periods of the day to exhibit different behavior. Therefore, after obtaining the summary statistics from Algorithm 1, our vectors were classified again according to three factors: day of week, sensor, and time of day. Time of day had 5 levels based on the time of the vector’s first count. The levels were Early Morning, Morning, Mid Day, Evening, and Late Evening, and they corresponded to one-hour windows with start times in the ranges:
- Early Morning 12:00 AM–4:50 AM
- Morning 4:55 AM–7:50 AM
- Mid Day 7:55 AM–3:50 PM
- Evening 3:55 PM–5:50 PM
- Late Evening 5:55 PM–11:55 PM
The windows were ranked by each of their summary statistics within their classification. These rankings were given in the form of a percentile and used as anomaly scores.
We expected that traffic patterns throughout the year should be fairly consistent given a particular sensor, day of the week, and period of the day; however, it is possible that traffic behavior could be unusual for an entire day due to a holiday, road construction, or a weather event. Then, according to this window classification, it cannot be readily ascertained if a particular window with a relatively large mean bottleneck distance is due to something acute, such as a traffic incident, or to something predictable, like Labor Day or a major sporting event. We took this into account by reclassifying the windows by sensor, time of day, and day of the year. We then ranked the windows a second time within each of these treatment groups. Each window was assigned 6 percentile scores, based on three different summary statistics each ranked two different ways.
We describe our procedure using an example from the Phase 2-Train data. To measure the likelihood that there was an incident occurring near sensor on Monday, 6 February 2017, during the window from 7:55 AM to 8:55 AM, we set . We apply our algorithm to . See Figure 3 for an example of the persistence diagrams related to this particular timestamp. If an incident occurred on February 6th, the sixth Monday of 2017 in the time window classification, we would expect that would be large compared to the rest of the collection . When this is done, we find that , which is the second largest of the 52 average bottleneck distances in . Even though this was not the largest average bottleneck distance observed for this sensor, day of week, and time of day, it did rank above the mid-98th percentile among all Mid Day windows according to average bottleneck distance for on a Monday. Similarly, ranked above the 96th percentile and of standard deviations of bottleneck distance, and ranked just above the 99th percentile of median bottleneck distances observed from Mid Day, Monday windows at sensor S314402. If we consider this window among only the observations from Mid Day on February 6th at sensor , then ranks just above the mid-89th percentile, ranks above the mid-90th percentile, and is at least tied as the highest ranking sample median of its class.
After the six rankings are determined for each window in our data set, we are ready to apply selection criteria to determine which windows overlapped with traffic incidents. The selection consists of six thresholds for the six rankings. The thresholds are determined by the rankings of windows near the starting times of the labeled incidents in the training data using the procedure outlined below:
- Identify all windows starting within 30 min of the timestamp of a reported incident at the same sensor where the incident was located.
- For each of the 6 types of rankings, identify a minimum ranking needed to include at least one window corresponding to each labeled incident. If all 6 minimum rankings seem too small, the minimum ranking to include one window from all but one incident could be used instead.
- Set the first threshold, as the largest of the six minimums.
- Identify which of the windows found in step 1 satisfy the threshold of
- For each of the 5 types of rankings that were not used to determine , identify the minimum ranking met by all the windows identified in step 4.
- Set the other 5 thresholds, according to the 5 minimums identified in step 5.
Once the thresholds are set, we classify all windows that have all six rankings each above their respective thresholds as incidents. In the rest of this section, we present the results when this procedure is applied to each of the four data sets. We present the rankings of windows near each incident in the data sets and the thresholds we determined from training data sets. In each phase, we use the thresholds determined by the training data to classify the windows in the corresponding testing data. We measure the performance of these predictions using precision, recall and an F-score.
Remark 4.
Our performance evaluation using Algorithm 1 exclude any incidents detected on Sundays since the training data did not include any reported incidents on Sunday.
To provide some comparison, we also apply a standard normal deviates (SND) algorithm to detect incidents in the phase-1 data. The SND algorithm detects an incident in the kth 5-min time window if the count for that window, , satisfies
We let and respectively denote the mean count and standard deviation of counts from the same treatment group and denotes some threshold that applies across all treatment groups. In this case, a treatment group is made up of all counts belonging to the same sensor, on the same day of week, at the same time of day. For example, in Phase-1, there were 52 counts taken at sensor , on Monday mornings at 8:00 AM, . We can compute the mean and standard deviation of this treatment group,
For a better description of the SND algorithm and its application to incident detection see [11], where incident detection was performed using vehicle velocity rather than traffic flow. The threshold was determined using the Phase 1-Train data by computing the deviates for each window occurring during a labeled incident. For each of the 15 incidents, we computed the 85th percentile of the counts that took place during the incident. We chose to be the second smallest of the 15 percentiles we computed. Thus, for the phase 1 data, we found , meaning any 5-min window where the count exceeded 1.06 standard deviations from the mean was detected as an incident.
4.1. Data without Sensor Locations
In the Phase 1-Train data set, we were able to find windows near the incidents that had very large average bottleneck distances. When sorted by sensor, day of week, and time of day, all of the 15 labeled incidents overlapped with a one-hour window starting within half an hour of some window that was ranked in the 85th percentile. When sorting these sensors further by day of year, the start time of six of the incidents fell within half an hour of the window with the highest average bottleneck distance in their category. Table 3 and Table 4 present the percentile scores of the incidents in the Phase 1-Train dataset.

Table 3.
Percentiles of incidents from the Phase1-Train data when sorted by sensor, day of week, and time of day.

Table 4.
Percentiles of incidents from the Phase 1-Train data when sorted by sensor, day of year, and time of day.
Table 5 contains the 6 thresholds determined using the rankings of windows near the labeled incidents. The quality of the fit is given in Table 6; as a comparison, the quality of fit using the standard normal derivates is given in Table 7. To better describe the quality of the anomaly scores, we provide the receiver operating characteristic (ROC) curve based on the three rankings in Figure 4. We also provide the ROC curve based on the standard normal deviates.

Table 5.
Thresholds used for classifying windows by percentile score in phase 1. * indicates the largest threshold,

Table 6.
Quality of fit for the Phase 1-Train data based on the thresholds determined by the labeled incidents using Algorithm 1.

Table 7.
Quality of fit for the Phase 1-Train data using standard normal deviates.
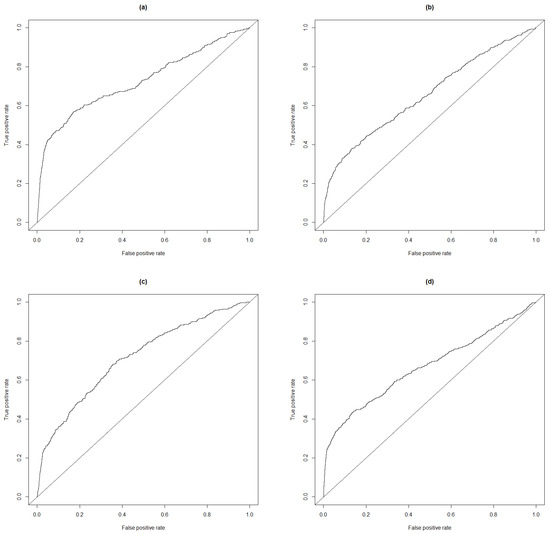
Figure 4.
ROC curves for 4 different anomaly scores: (a) uses average bottleneck distance percentile when sorted by day of week; AUC . (b) uses standard deviation bottleneck distance percentile when sorted by day of week; AUC . (c) uses median bottleneck distance percentile when sorted by day of week; AUC . (d) uses the standard normal deviations; AUC .
Of course, these performance scores say very little about the method since the thresholds were determined using the incidents in the data set. Rather, we apply the thresholds in Table 5 to classify the Phase 1-Test data. Table 8 has the performance scores from this experiment, whereas Table 9 has the performance for the standard normal deviates on this dataset.

Table 8.
Quality of fit for the Phase 1-Test data based on the thresholds determined by the Phase 1-Train incidents using Algorithm 1.

Table 9.
Quality of fit for the Phase 1-Test data using standard normal deviates.
4.2. Data with Sensor Locations
In Phase 2 we were given the locations of the sensors in terms of latitude and longitude. Table 10 and Table 11 display the nine incidents reported in Phase 2-Train and the largest percentile recorded for each summary statistic in windows starting within half an hour of the starting time of each incident at the sensor where the incident was reported.

Table 10.
Percentiles of Phase 2-Train incidents when sorted by sensor, day of week, and time of day.

Table 11.
Percentiles of Phase 2-Train incidents when sorted by sensor, day of year, and time of day.
Depending on the severity of the incident, it is possible that a traffic incident occurring near one sensor will cause some abnormal behavior in the counts of the adjacent sensors. For example, in the network of sensors used in the Phase 2-Train data, traffic flows directly from to . A map of all the sensor locations in this data set is provided in Figure 1. If one of the lanes is obstructed near it is likely to slow down traffic between the two sensors. This might cause the counts from to look fairly large when compared to . On the other hand, if a motorist was able to anticipate this problem in the traffic a mile ahead, they might deviate their route before even passing . If enough cars did this, there would be a lower count at the first sensor, but the count at might still be higher because of all the unfortunate cars that got caught between the sensors at the time of the incident. In either scenario, we would expect some unusual behavior when we compare the counts of both sensors together. Not knowing if the difference should be large or small, we apply the random bagging algorithm to the sequence of differences between the counts, with the intuition that if an incident occurred during a particular hour, especially one with lots of traffic, the mean bottleneck distance for that time window would also be large. We refer to the summary statistics obtained from this procedure as adjacency statistics. In Table 12 and Table 13 we provide the highest rankings near the reported incidents based on the adjacency statistics.

Table 12.
Percentiles of Phase 2-Train incidents when sorted by sensor, day of week, and time of day based on their adjacency statistics.

Table 13.
Percentiles of Phase 2-Train incidents when sorted by sensor, day of year, and time of day based on their adjacency statistics.
The most noticeable difference made by the adjacency statistics can be observed by the percentile of the July incident when windows are sorted by sensor, day of year, and time of day. The highest any window near that time ranks by average bottleneck distance of raw counts is in the 66th percentile of Mid Day counts for that day, but if we consider the differences in counts between the two adjacent sensors, we find the highest ranking Mid Day window for July 24th starts within half an hour of the July incident.
With the addition of the adjacency statistics, we had 12 percentiles to consider for each window. Table 14 presents the 12 thresholds determined from the incidents in the data for Phase 2-Train. The quality of the fit is given in Table 15. We only report the performance statistics for sensors and since those were the only sensors in the data set where incidents were labeled.

Table 14.
Thresholds used for classifying windows by percentile scores in Phase 2. * indicates the largest threshold, .

Table 15.
The quality of fit for the Phase 2-Train data based on the thresholds determined by the labeled incidents.
As in Phase 1, we use the thresholds learned from the training data to classify the windows in the Phase 2-Test data. In this data set, there were 8 sensors. The 8 sensors formed 8 pairs of adjacent sensors, meaning we were able to compute adjacency scores for the windows on every sensor. In Table 16 we present the performance scores for this classification. The data for Phase 2-Test was very different from any of the other data sets. There were 1409 incidents with an average duration of 42 min. Surprisingly, no true incidents were reported at sensor .

Table 16.
The quality of fit for the Phase 2-Test data based on the thresholds determined by the Phase 2-Train incidents.
5. Conclusions
Detecting traffic incidents using volumetric data is challenging, as reflected in our performance scores even though our method performed the best of all ATD challenge problem participants [54]. When compared to the SND algorithm, which is a commonly used method for anomaly detection in traffic data, our TDA approach performed slightly better based on the area under the ROC curve. We think there is much room for improvement in using TDA for traffic incident detection. One possibility is to apply unsupervised learning techniques to the collection of bottleneck distances produced for each vector in Algorithm 1. Another possibility is to use persistence landscapes rather than bottleneck distances.
Supplementary Materials
Data and code are available at the following repository: https://bitbucket.org/esweber/randomized-persistence-landscapes/src/master/.
Author Contributions
Conceptualization, E.S.W.; Methodology, S.N.H., L.P. and E.S.W.; Software, L.P.; Validation, S.N.H., L.P., E.S.W.; Formal Analysis, S.N.H., L.P. and E.S.W.; Investigation, S.N.H., L.P. and E.S.W.; Resources, L.P.; Data Curation, L.P.; Writing—Original Draft Preparation, L.P.; Writing—Review & Editing, S.N.H., E.S.W.; Visualization, L.P.; Supervision, E.S.W.; Project Administration, E.S.W.; Funding Acquisition, E.S.W. All authors have read and agreed to the published version of the manuscript.
Funding
All three authors were supported by the National Science Foundation and the National-Geospatial Intelligence Agency under award #1830254.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blincoe, L.; Seay, A.; Zoloshnja, E.; Miller, T.; Romano, E.; Luchter, S.; Spicer, R. Economic impact of U.S. motor vehicle crashes reaches $230.6 billion, NHTSA reports. Prof. Saf. 2002, 47, 12. [Google Scholar]
- Schrank, D.; Lomax, T. The 2007 Urban Mobility Report. 2007. Available online: https://static.tti.tamu.edu/tti.tamu.edu/documents/umr/archive/mobility-report-2007-wappx.pdf (accessed on 1 June 2020).
- Chen, C.; Petty, K.; Skabardonis, A.; Varaiya, P.; Jia, Z. Freeway Performance Measurement System, Mining Loop Detector Data. Transp. Res. Rec. 2001, 1748, 96–102. [Google Scholar] [CrossRef]
- Truslow, E.; Tsitsopoulos, G.; Manolakis, D. Event Detection in Time Series: A Traffic Data Challenge [Conference Presentation]. In Proceedings of the Algorithms for Threat Detection PI Workshop, Washington, DC, USA, 10–11 October 2018; National Science Foundation: Alexandria, VA, USA, 2018. [Google Scholar]
- Sadeky, S.; Al-Hamadiy, A.; Michaelisy, B.; Sayed, U. Real-time automatic traffic accident recognition using hfg. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3348–3351. [Google Scholar]
- Jiansheng, F.; Hui, Z.; Yaohua, M. Vision-based real-time traffic accident detection. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 1035–1038. [Google Scholar]
- Chakraborty, P.; Hegde, C.; Sharma, A. Trend filtering in network time series with applications to traffic incident detection. In Proceedings of the Time Series Workshop, 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 8 December 2017. [Google Scholar]
- Maaloul, B.; Taleb-Ahmed, A.; Niar, S.; Harb, N.; Valderrama, C. Adaptive video-based algorithm for accident detection on highways. In Proceedings of the 2017 12th IEEE International Symposium on Industrial Embedded Systems (SIES), Toulouse, France, 14–16 June 2017; pp. 1–6. [Google Scholar]
- Shi, Q.; Abdel-Aty, M. Big data applications in real-time traffic operation and safety monitoring and improvement on urban expressways. Transp. Res. Part C Emerg. Technol. 2015, 58, 380–394. [Google Scholar] [CrossRef]
- Zhao, B.; Li, F.-F.; Xing, E.P. Online detection of unusual events in videos via dynamic sparse coding. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 20–25 June 2011; pp. 3313–3320. [Google Scholar]
- Chakraborty, P.; Hess, J.R.; Sharma, A.; Knickerbocker, S. Outlier mining based traffic incident detection using big data analytics. In Proceedings of the Transportation Research Board 96th Annual Meeting Compendium of Papers, Washington DC, WA, USA, 8–12 January 2017; pp. 8–12. [Google Scholar]
- Xu, C.; Liu, P.; Yang, B.; Wang, W. Real-time estimation of secondary crash likelihood on freeways using high-resolution loop detector data. Transp. Res. Part C Emerg. Technol. 2016, 71, 406–418. [Google Scholar] [CrossRef]
- Lou, J.; Liu, Q.; Tan, T.; Hu, W. Semantic interpretation of object activities in a surveillance system. In Proceedings of the Object Recognition Supported by User Interaction for Service Robots, Quebec, Canada, 11–15 August 2002; Volume 3, pp. 777–780. [Google Scholar]
- Piciarelli, C.; Micheloni, C.; Foresti, G.L. Trajectory-based anomalous event detection. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 1544–1554. [Google Scholar] [CrossRef]
- Hasan, M.; Choi, J.; Neumann, J.; Roy-Chowdhury, A.K.; Davis, L.S. Learning temporal regularity in video sequences. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, Nevada, 26 June–1 July 2016; pp. 733–742. [Google Scholar]
- Yuan, Y.; Wang, D.; Wang, Q. Anomaly detection in traffic scenes via spatial-aware motion reconstruction. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1198–1209. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Li, X.; Yao, Y. Representation of Traffic Congestion Data for Urban Road Traffic Networks Based on Pooling Operations. Algorithms 2020, 13, 84. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Bendich, P.; Chin, S.P.; Clark, J.; Desena, J.; Harer, J.; Munch, E.; Newman, A.; Porter, D.; Rouse, D.; Strawn, N.; et al. Topological and statistical behavior classifiers for tracking applications. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2644–2661. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, J.; Ravishanker, N.; Konduri, K. Clustering Activity–Travel Behavior Time Series using Topological Data Analysis. J. Big Data Anal. Transp. 2019, 1, 109–121. [Google Scholar] [CrossRef]
- Islambekov, U.; Yuvaraj, M.; Gel, Y.R. Harnessing the power of topological data analysis to detect change points. Environmetrics 2019, 31, e2612. [Google Scholar] [CrossRef]
- Li, Y.; Islambekov, U.; Akcora, C.; Smirnova, E.; Gel, Y.R.; Kantarcioglu, M. Dissecting Ethereum Blockchain Analytics: What We Learn from Topology and Geometry of the Ethereum Graph? In Proceedings of the 2020 SIAM International Conference on Data Mining, Hilton Cincinnati, OH, USA, 7–9 May 2020; pp. 523–531. [Google Scholar]
- Carlsson, G. Topology and data. Bull. Amer. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Munch, E. A User’s Guide to Topological Data Analysis. J. Learn. Anal. 2017, 4, 47–61. [Google Scholar] [CrossRef]
- Rieck, B.; Togninalli, M.; Bock, C.; Moor, M.; Horn, M.; Gumbsch, T.; Borgwardt, K. Neural Persistence: A Complexity Measure for Deep Neural Networks Using Algebraic Topology. arXiv 2018, arXiv:1812.09764. [Google Scholar]
- Guss, W.H.; Salakhutdinov, R. On Characterizing the Capacity of Neural Networks using Algebraic Topology. arXiv 2018, arXiv:1802.04443. [Google Scholar]
- Biasotti, S.; Falcidieno, B.; Spagnuolo, M. Extended Reeb Graphs for Surface Understanding and Description. In International Conference on Discrete Geometry for Computer Imagery; Discrete Geometry for Computer Imagery; Borgefors, G., Nystrom, I., di Baja, G.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 185–197. [Google Scholar]
- Zhang, E.; Mischaikow, K.; Turk, G. Feature-based Surface Parameterization and Texture Mapping. ACM Trans. Graph. 2005, 24, 1–27. [Google Scholar] [CrossRef]
- Nicolau, M.; Levine, A.J.; Carlsson, G. Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc. Natl. Acad. Sci. USA 2011, 108, 7265–7270. [Google Scholar] [CrossRef]
- Chan, J.M.; Carlsson, G.; Rabadan, R. Topology of viral evolution. Proc. Natl. Acad. Sci. USA 2013, 110, 18566–18571. [Google Scholar] [CrossRef]
- Bendich, P.; Marron, J.S.; Miller, E.; Pieloch, A.; Skwerer, S. Persistent Homology Analysis of Brain Artery Trees. Ann. Appl. Stat. 2016, 10, 198–218. [Google Scholar] [CrossRef]
- Ravishanker, N.; Chen, R. Topological Data Analysis (TDA) for Time Series. arXiv 2019, arXiv:1909.10604. [Google Scholar]
- Robinson, M. Topological Signal Processing; Mathematical Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Truong, P. An Exploration of Topological Properties of High-Frequency One-Dimensional Financial Time Series Data Using TDA. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, December 2019. [Google Scholar]
- Gidea, M. Topological Data Analysis of Critical Transitions in Financial Networks. In NetSci-X 2017. Springer Proceedings in Complexity, Proceedings of the 3rd International Winter School and Conference on Network Science, Indianapolis, IN, USA, 19–23 June 2017; Shmueli, E., Barzel, B., Puzis, R., Eds.; Springer: Cham, Switzerland, 2017; pp. 47–59. [Google Scholar]
- Gidea, M.; Katz, Y. Topological data analysis of financial time series: Landscapes of crashes. Phys. A Stat. Mech. Appl. 2018, 491, 820–834. [Google Scholar] [CrossRef]
- Wang, Y.; Ombao, H.; Chung, M.K. Topological data analysis of single-trial electroencephalographic signals. Ann. Appl. Stat. 2018, 12, 1506–1534. [Google Scholar] [CrossRef] [PubMed]
- Stolz, B.J.; Harrington, H.A.; Porter, M.A. Persistent homology of time-dependent functional networks constructed from coupled time series. Chaos An Interdiscip. J. Nonlinear Sci. 2017, 27, 047410. [Google Scholar] [CrossRef] [PubMed]
- Perea, J.A. Persistent homology of toroidal sliding window embeddings. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal, Shanghai, China, 20–25 March 2016; pp. 6435–6439. [Google Scholar] [CrossRef]
- Tralie, C.J.; Perea, J.A. (Quasi)Periodicity Quantification in Video Data, Using Topology. arXiv 2018, arXiv:1704.08382. [Google Scholar] [CrossRef]
- Perea, J.A.; Harer, J. Sliding Windows and Persistence: An Application of Topological Methods to Signal Analysis. Found. Comput. Math. 2015, 15, 799–838. [Google Scholar] [CrossRef]
- Perea, J.A.; Deckard, A.; Haase, S.B.; Harer, J. SW1PerS: Sliding windows and 1-persistence scoring; discovering periodicity in gene expression time series data. BMC Bioinform. 2015, 16, 257. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.S., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Khasawneh, F.A.; Munch, E. Chatter detection in turning using persistent homology. Mech. Syst. Signal Process. 2016, 70–71, 527–541. [Google Scholar] [CrossRef]
- Kahle, M. Random geometric complexes. Discrete Comput. Geom. 2011, 45, 553–573. [Google Scholar] [CrossRef]
- Bobrowski, O.; Kahle, M. Topology of random geometric complexes: A survey. J. Appl. Comput. Topol. 2018, 1, 331–364. [Google Scholar] [CrossRef]
- Niyogi, P.; Smale, S.; Weinberger, S. A topological view of unsupervised learning from noisy data. SIAM J. Comput. 2011, 40, 646–663. [Google Scholar] [CrossRef]
- Adler, R.J.; Bobrowski, O.; Weinberger, S. Crackle: The homology of noise. Discrete Comput. Geom. 2014, 52, 680–704. [Google Scholar] [CrossRef]
- Bubenik, P. Statistical topological data analysis using persistence landscapes. J. Mach. Learn. Res. 2015, 16, 77–102. [Google Scholar]
- Edelsbrunner, H.; Harer, J. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Oudot, S.Y. Persistence Theory: From Quiver Representations to Data Analysis; American Mathematical Society: Providence, RI, USA, 2015. [Google Scholar]
- Laflamme, E.M.; Ossenbruggen, P.J. Effect of time-of-day and day-of-the-week on congestion duration and breakdown: A case study at a bottleneck in Salem, NH. J. Traff. Transp. Eng. 2017, 4, 31–40. [Google Scholar] [CrossRef]
- Truslow, E.; Tsitsopoulos, G.; Manolakis, D. Traffic Data Challenge Problem Results [Conference Presentation]. In Proceedings of the Algorithms for Threat Detection PI Workshop, Washington, DC, USA, 21–23 October 2019; The George Washington University: Washington, DC, USA. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).