1. Introduction
Access to accurate outbreak prediction models is essential to obtain insights into the likely spread and consequences of infectious diseases. Governments and other legislative bodies rely on insights from prediction models to suggest new policies and to assess the effectiveness of the enforced policies [
1]. The novel coronavirus disease (COVID-19) has been reported to have infected more than 2 million people, with more than 132,000 confirmed deaths worldwide. The recent global COVID-19 pandemic has exhibited a nonlinear and complex nature [
2]. In addition, the outbreak has differences with other recent outbreaks, which brings into question the ability of standard models to deliver accurate results [
3]. In addition to the numerous known and unknown variables involved in the spread, the complexity of population-wide behavior in various geopolitical areas and differences in containment strategies dramatically increased model uncertainty [
4]. Consequently, standard epidemiological models face new challenges to deliver more reliable results. To overcome this challenge, many novel models have emerged which introduce several assumptions to modeling (e.g., adding social distancing in the form of curfews, quarantines, etc.) [
5,
6,
7].
To elaborate on the effectiveness of enforcing such assumptions, understanding standard dynamic epidemiological (e.g., susceptible-infected-recovered, SIR) models is essential [
8]. The modeling strategy is formed around the assumption of transmitting the infectious disease through contacts, considering three different classes of well-mixed populations; susceptible to infection (class
S), infected (class
I), and the removed population (class
R is devoted to those who have recovered, developed immunity, been isolated, or passed away). It is further assumed that the class
I transmits the infection to class
S where the number of probable transmissions is proportional to the total number of contacts [
9,
10,
11]. The number of individuals in the class
S progresses as a time series, often computed using a basic differential equation as follows (Equation (1)):
where
is the infected population, and
is the susceptible population, both as fractions.
represents the daily reproduction rate of the differential equation, regulating the number of susceptible infectious contacts. The value of
in the time series produced by the differential equation gradually declines. Initially, it is assumed that at the early stage of the outbreak
while the number of individuals in class
I is negligible. Thus, the increment
becomes linear and the class
I eventually can be computed as follows (Equation (2)):
where
regulates the daily rate of new infections by quantifying the number of infected individuals competent in the transmission. Furthermore, the class
R, representing individuals excluded from the spread of infection, is computed as follows:
Under the unconstrained conditions of the excluded group, Equation (3), the outbreak exponential growth can be computed as follows (Equation (4)):
The outbreaks of a wide range of infectious diseases have been modeled using Equation (4). However, for the COVID-19 outbreak prediction, due to the strict measures enforced by authorities, the susceptibility to infection has been manipulated dramatically. For example, in China, Italy, France, Hungary, and Spain the SIR model cannot present promising results, as individuals committed voluntarily to quarantine and limited their social interaction. However, for countries where containment measures were delayed (e.g., United States) the model has shown relative accuracy [
12].
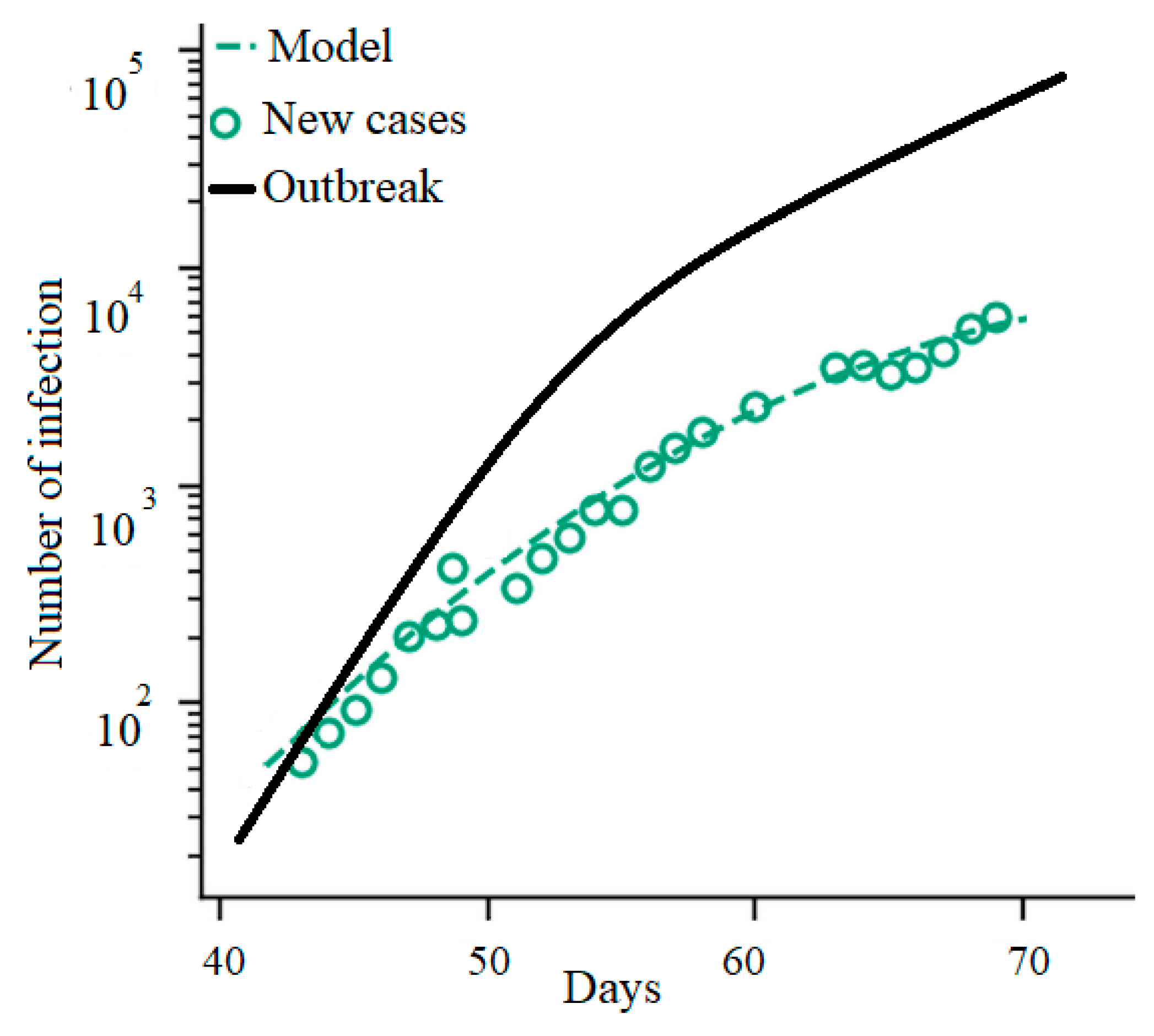
Figure 1 shows the inaccuracy of conventional models applied to the outbreak in Italy by comparing the actual number of confirmed infections and epidemiological model predictions (this trend obviously depends on the approach chosen to model the outbreak; for example, the SEIR model performs usually better than SIR model). SEIR models, by considering the significant incubation period during which individuals are infected, showed increased model accuracy for the Varicella and Zika outbreaks [
13,
14]. SEIR models assume that the incubation period is a random variable and, similarly to the SIR model, there is a disease-free equilibrium [
15,
16]. It should be noted, however, that standard SIR and SEIR models will not fit well where the parameters related to social mixing and, thus, the contact network, are non-stationary through time [
17]. A key cause of non-stationarity is where the social mixing (which determines the contact network) changes through time. Social mixing determines the reproductive number
, which is the number of susceptible individuals that an infected person will infect. When
is less than 1 the epidemic will die out; when it is greater than 1 it will spread.
for COVID-19 prior to lockdown was estimated as a massive 4 [
1], representing a pandemic. It is expected that lockdown measures should bring
down to less than 1. The key reason why SEIR models are difficult to fit for COVID-19 is non-stationarity of mixing, caused by nudging (step-by-step) intervention measures. A further drawback of conventional epidemiological models is the short lead time. To evaluate the performance of the models, the median success of the outbreak prediction presents useful information. The median prediction factor can be calculated as follows (Equation (5)):
As the lead-time increases, the accuracy of the model declines. For instance, for the COVID-19 outbreak in Italy, the accuracy of the model for more than 5 days hence reduces from
for the first five days to
for day 6 [
12]. Overall, the standard epidemiological models can be effective and reliable only if (a) the social interactions are stationary through time (i.e., no changes in interventions or control measures), and (b) there exists a great deal of knowledge of class
R with which to compute Equation (3). To acquire information on class
R, several novel models included data from social media or call data records (CDR), which showed promising results [
18,
19,
20,
21,
22,
23,
24,
25]. However, observation of the behavior of COVID-19 in several countries demonstrates a high degree of uncertainty and complexity [
26]. Thus, for epidemiological models to be able to deliver reliable results, they must be adapted to the local situation based on insights into susceptibility to infection due to changes in public health interventions, and the various states in the SIR/SEIR model [
27]. This imposes a huge limit on the generalization ability and robustness of conventional models. Advancing accurate models with a great generalization ability to be scalable to model both the regional and global pandemic is, thus, essential [
28].
Due to the complexity and the large-scale nature of the problem in developing epidemiological models, machine learning (ML) has recently gained attention for building outbreak prediction models. ML approaches aim at developing models with higher generalization ability and greater prediction reliability for longer lead times [
29,
30,
31,
32,
33].
Although ML methods were used in modeling former pandemics (e.g., Ebola, cholera, swine fever, H1N1 influenza, dengue fever, Zika, oyster norovirus [
8,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43]), there is a gap in the literature for peer-reviewed papers dedicated to COVID-19.
Table 1 represents notable ML methods used for outbreak prediction. These ML methods are limited to the basic methods of random forest, neural networks, Bayesian networks, naïve Bayes, genetic programming, and classification and regression tree (CART). Although ML has long been established as a standard tool for modeling natural disasters and weather forecasting [
44,
45], its application in modeling outbreak is still in the early stages. More sophisticated ML methods (e.g., hybrids, ensembles) are yet to be explored. Consequently, the contribution of this paper is to explore the application of ML for modeling the COVID-19 pandemic. This paper aims to investigate the generalization ability of the proposed ML models and the accuracy of the proposed models for different lead times.
The state-of-the-art machine learning methods for outbreak prediction modeling demonstrate two major research gaps for machine learning to address. Firstly, advancement in time-series prediction of outbreak and, secondly, improvement of SIR and SEIR models. Considering the drawbacks to the existing SIR and SEIR, machine learning can certainly contribute. This paper contributes to the advancement of time-series prediction of COVID-19. Consequently, an initial benchmarking is given to demonstrate the potential of machine learning for future research. The paper further suggests that a genuine novelty in outbreak prediction can be realized by integrating machine learning and SEIR models.
The remainder of this paper is organized as follows.
Section 2 describes the methods and materials. The results are given in
Section 3.
Section 4 and
Section 5 present the discussion and the conclusions, respectively.
2. Materials and Methods
Data were collected from worldometers website [
46] for five countries, namely Italy, Germany, Iran, USA, and China, for total cases over 30 days.
Figure 2 presents the total case number (cumulative statistic) for the considered countries. Currently, to contain the outbreak, the governments have implemented various measures to reduce transmission by inhibiting people’s movements and social activities. Although information on changes in social distancing is essential for advancing the epidemiological models, for modeling with machine learning no assumption is required. As can be seen in
Figure 2, the growth rate in China was greater than that for Italy, Iran, Germany, and the USA in the early weeks of the disease [
46].
The next step is to find the best model for the estimation of the time-series data. Logistic (Equation (6)), linear (Equation (7)), logarithmic (Equation (8)), quadratic (Equation (9)), cubic (Equation (10)), compound (Equation (11)), power (Equation (12)), and exponential (Equation (13)) equations were employed to develop the desired model. These models are generally not good fits for outbreak prediction beyond the available data. In this study, through parameter tuning we aim at finding the optimal performance of these models. The model with the best performance is later used for comparative analysis.
A, B, C, µ, and L are parameters (constants) that characterize the above-mentioned functions. These constants need to be estimated to develop an accurate estimation model. One of the goals of this study was to model time-series data based on the logistic microbial growth model. For this purpose, the modified equation of logistic regression was used to estimate and predict the prevalence (i.e., I/Population at a given time point) of disease as a function of time. Estimation of the parameters was performed using evolutionary algorithms such as the genetic algorithm (GA), particle swarm optimizer, and grey wolf optimizer. These algorithms are discussed in the following.
2.1. Evolutionary Algorithms
Evolutionary algorithms (EA) are powerful tools for solving optimization problems through intelligent methods. These algorithms are often inspired by natural processes to search for all possible answers as an optimization problem [
47,
48,
49]. In the present study, the frequently used algorithms, (i.e., genetic algorithm (GA), particle swarm optimizer (PSO) and grey wolf optimizer (GWO)) were employed to estimate the parameters by solving a cost function.
2.1.1. Genetic Algorithm (GA)
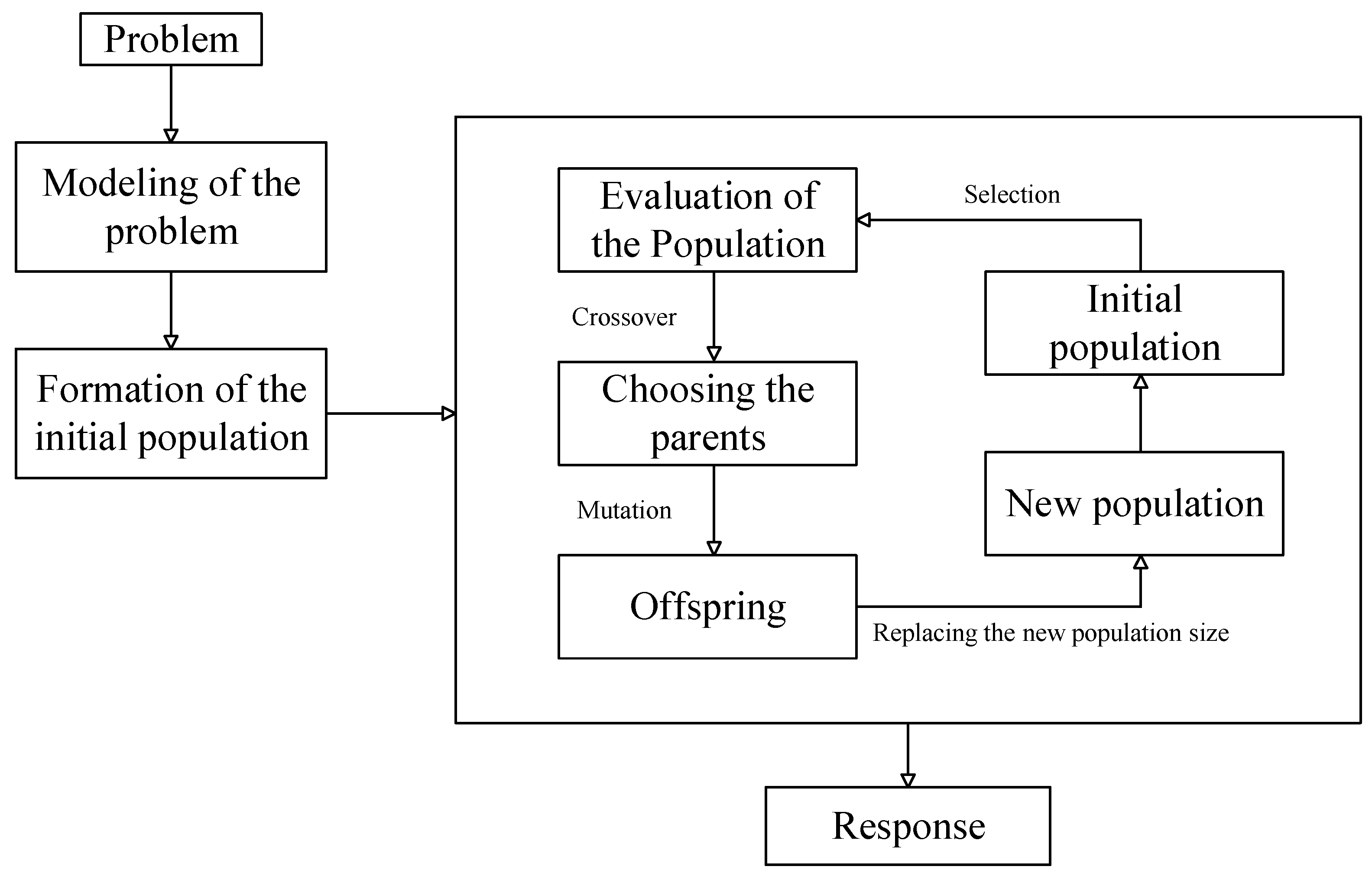
GAs are considered a subset of “computational models” inspired by the concept of evolution [
50]. These algorithms use “Potential Solutions”, “Candidate Solutions”, or “Possible Hypotheses” for a specific problem in a “chromosome-like” data structure. GA maintains vital information stored in these chromosome data structures by applying “Recombination Operators” to chromosome-like data structures [
51,
52,
53,
54]. In many cases, GAs are employed as “Function Optimizer” algorithms, which are algorithms used to optimize “Objective Functions”. Of course, the range of applications that use the GA to solve problems is very wide [
53,
55]. The implementation of the GA usually begins with the production of a population of chromosomes generated randomly, and bound up and down by the variables of the problem. In the next step, the generated data structures (chromosomes) are evaluated, and chromosomes that can better display the optimal solution of the problem are more likely to be used to produce new chromosomes. The degree of “goodness” of an answer is usually measured by the population of the current candidate’s answers [
56,
57,
58,
59,
60]. The main algorithm of a GA process is demonstrated in
Figure 3.
In the present study, GA [
60] was employed for estimation of the parameters of Equations (6) to (13). The population number was selected to be 300 and the maximum generation (as iteration number) was determined to be 500 according to different trial and error processes to reduce the cost function value. The cost function was defined as the mean square error between the target and estimated values according to Equation (14):
where
Es refers to estimated values,
T refers to the target values, and
N refers to the number of data.
2.1.2. Particle Swarm Optimization (PSO)
In 1995, Kennedy and Eberhart [
60] introduced the PSO as an uncertain search method for optimization purposes. The algorithm was inspired by the mass movement of birds looking for food. A group of birds accidentally look for food in a space. There is only one piece of food in the search space. Each solution in PSO is called a particle, which is equivalent to a bird in the bird’s mass movement algorithm. Each particle has a value that is calculated by a competency function which increases as the particle in the search space approaches the target (food in the bird’s movement model). Each particle also has a velocity that guides the motion of the particle. Each particle continues to move in the problem space by tracking the optimal particles in the current state [
61,
62,
63]. The PSO method is rooted in Reynolds’ work, which is an early simulation of the social behavior of birds. The mass of particles in nature represents collective intelligence. Consider the collective movement of fish in water or birds during migration. All members move in perfect harmony with each other, hunt together if they are to be hunted, and escape from the clutches of a predator by moving toward other prey if they are preyed upon [
64,
65,
66]. Particle properties in this algorithm include [
66,
67,
68]:
Each particle independently looks for the optimal point.
Each particle moves at the same speed at each step.
Each particle remembers its best position in the space.
The particles work together to inform each other of the places they are looking for.
Each particle is in contact with its neighboring particles.
Every particle is aware of the particles that are in the neighborhood.
Every particle is known as one of the best particles in its neighborhood.
The PSO implementation steps can be summarized as: the first step establishes and evaluates the primary population. The second step determines the best personal memories and the best collective memories. The third step updates the speed and position. If the conditions for stopping are not met, the cycle will return to the second step.
The PSO algorithm is a population-based algorithm [
69,
70]. This property makes it less likely to be trapped in a local minimum. This algorithm operates according to possible rules, not definite rules. Therefore, PSO is a random optimization algorithm that can search for unspecified and complex areas. This makes PSO more flexible and durable than conventional methods. PSO deals with non-differential target functions because the PSO uses the information result (performance index or target function to guide the search in the problem area). The quality of the proposed route response does not depend on the initial population. Starting from anywhere in the search space, the algorithm ultimately converges on the optimal answer. PSO has great flexibility to control the balance between the local and overall search space. This unique PSO property overcomes the problem of improper convergence and increases the search capacity. All of these features make PSO different from the GA and other innovative algorithms [
62,
66,
68].
In the present study, PSO was employed for estimation of the parameters of Equations (6) to (13). The population number was selected to be 1000 and the iteration number was determined to be 500 according to different trial and error processes to reduce the cost function value. The cost function was defined as the mean square error between the target and estimated values according to Equation (14).
2.1.3. Grey Wolf Optimizer (GWO)
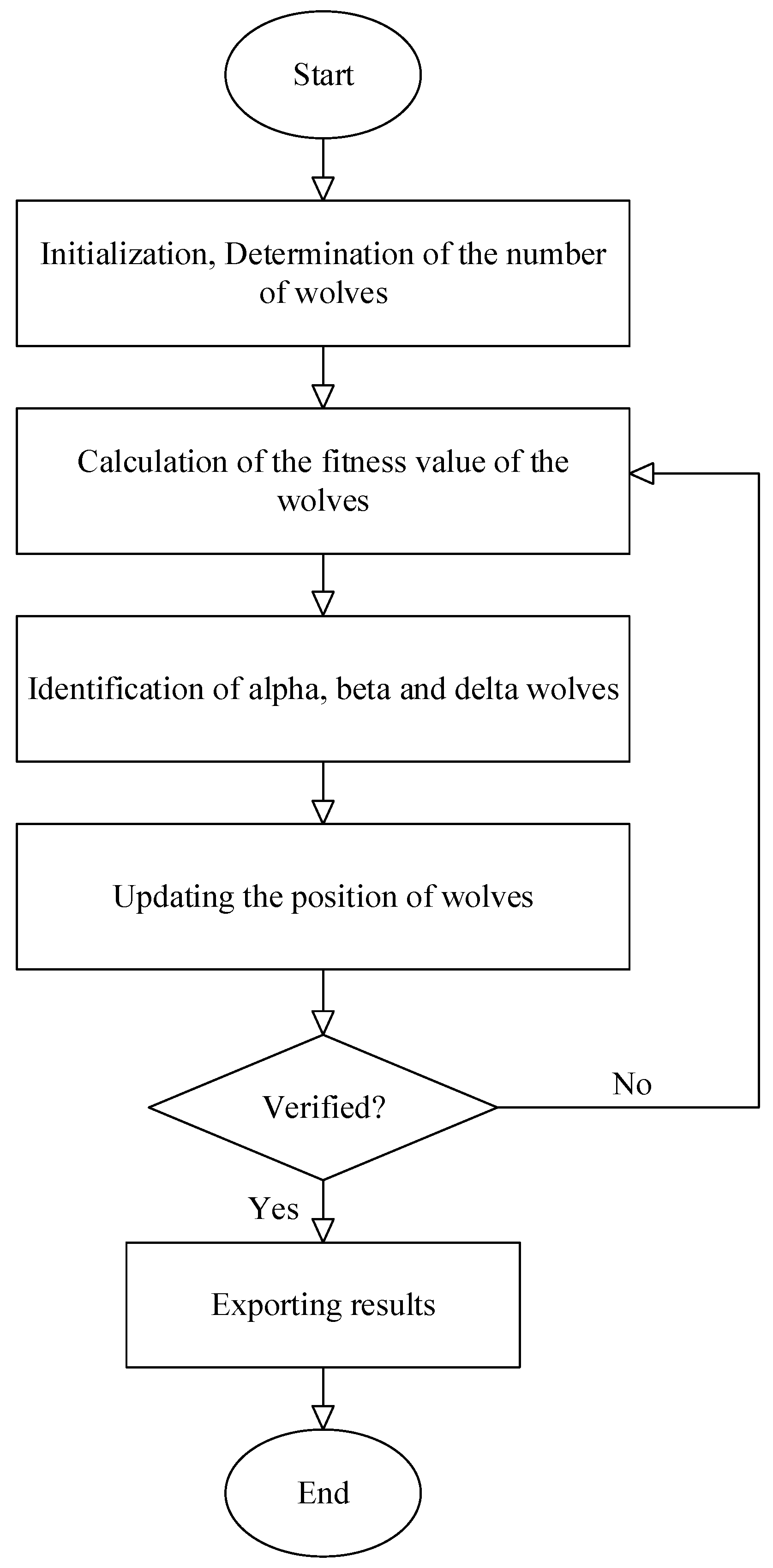
One recently developed smart optimization algorithm that has attracted the attention of many researchers is the grey wolf algorithm. Like most other intelligent algorithms, GWO is inspired by nature. The main idea of the grey wolf algorithm is based on the leadership hierarchy in wolf groups and how they hunt [
71]. In general, there are four categories of wolves among the herd of grey wolves, alpha, beta, delta and omega. Alpha wolves are at the top of the herd’s leadership pyramid; the remainder of the wolves take orders from the alpha group and follow them (usually there is only one alpha wolf in each herd). Beta wolves are in the lower tier, but their superiority over delta and omega wolves allows them to provide advice and help to alpha wolves. Beta wolves are responsible for regulating and orienting the herd based on alpha movement. Delta wolves, which are next in line in the power pyramid of the wolf herd, are usually made up of guards, elderly population, caregivers of damaged wolves, and so on. Omega wolves are the weakest in the power hierarchy [
71]. Equations (15) to (18) are used to model the hunting tool:
where
t represents repetition of the algorithm.
and
are vectors of the prey site and the
vectors represent the locations of the grey wolves.
is linearly reduced from 2 to 0 during the repetition.
and
are random vectors in which each element can take on realizations in the range [0,1]. The GWO algorithm flowchart is shown in
Figure 4.
In the present study, GWO [
71] was employed for estimation of the parameters of Equations (1) to (8). The population number was selected to be 500 and the iteration number was determined to be 1000 according to different trial and error processes to reduce the cost function value. The cost function was defined as the mean square error between the target and estimated values according to Equation (14).
2.2. Machine Learning (ML)
ML is regarded as a subset of Artificial Intelligence (AI). Using ML techniques, the computer learns to use patterns or “training samples” in data (processed information) to predict or make intelligent decisions without overt planning [
72,
73]. In other words, ML is the scientific study of algorithms and statistical models used by computer systems that use patterns and inference to perform tasks instead of using explicit instructions [
74,
75].
Time series are data sequences collected over a period of time [
76], which can be used as inputs to ML algorithms. This type of data reflects the changes that a phenomenon has undergone over time. Let X
t be a time-series vector, in which
xt is the outbreak at time point
t and
T is the set of all equidistant time points. To train ML methods effectively, we defined two scenarios, listed in
Table 2.
As can be seen in
Table 2, scenario 1 employs data for three weeks to predict the outbreak on day
t and scenario 2 employs outbreak data for five days to predict the outbreak for day
t. Both of these scenarios were employed for fitting the ML methods. In the present research, two frequently used ML methods, the multi-layered perceptron (MLP) and adaptive network-based fuzzy inference system (ANFIS), were employed for the prediction of the outbreak in the five countries.
2.2.1. Multi-Layered Perceptron (MLP)
The Artificial Neural Network (ANN) is an idea inspired by the biological nervous system, which processes information in the same way as the brain. The key element of this idea is the new structure of the information processing system [
77,
78,
79]. The system is made up of several highly interconnected processing elements called neurons that work together to solve a problem [
79,
80]. ANNs, like humans, learn by example. The neural network is set up during a learning process to perform specific tasks, such as identifying patterns and categorizing information. In biological systems, learning is regulated by the synaptic connections between nerves. This method is also used in neural networks [
81]. By processing experimental data, ANNs transfer knowledge or a law behind the data to the network structure, which is called learning. Basically, learning ability is the most important feature of such a smart system. A learning system is more flexible and easier to plan, so it can better respond to new issues and changes in processes [
82].
In ANNs, with the help of programming knowledge, a data structure is designed that can act like a neuron. This data structure is called a node [
83,
84]. In this structure, the network between these nodes is trained by applying an educational algorithm to it. In this memory or neural network, the nodes have two active states (on or off) and one inactive state (off or 0), and each edge (synapse or connection between nodes) has a weight. Positive weights stimulate or activate the next inactive node, and negative weights inactivate or inhibit the next connected node (if active) [
79,
85]. In the ANN architecture, for the neural cell
c, the input
bp enters the cell from the previous cell
p (Equation (19)).
wpc is the weight of the input
bp with respect to cell
c and
ac is the sum of the multiplications of the inputs and their weights [
86]:
A non-linear function
θc is applied to
ac. Accordingly,
bc can be calculated as Equation (20) [
85]:
Similarly,
wcn is the weight of the
bcn which is the output of
c to
n.
W is the collection of all of the weights of the neural network in a set. For input
x and output
y,
hw(x) is the output of the neural network. The main goal is to learn these weights to reduce the error values between
y and
hw(x). That is, the goal is to minimize the cost function
Q(W), Equation (21) [
86]:
In the present research, one of the frequently used types of ANN called the MLP [
77] was employed to predict the outbreak. The MLP was trained using a dataset related to both scenarios. For the training of the network, 8, 12, and 16 inner neurons were tried to achieve the best response. Results were evaluated by root mean square error (RMSE) and correlation coefficient to reduce the cost function value.
Figure 5 presents the architecture of the MLP.
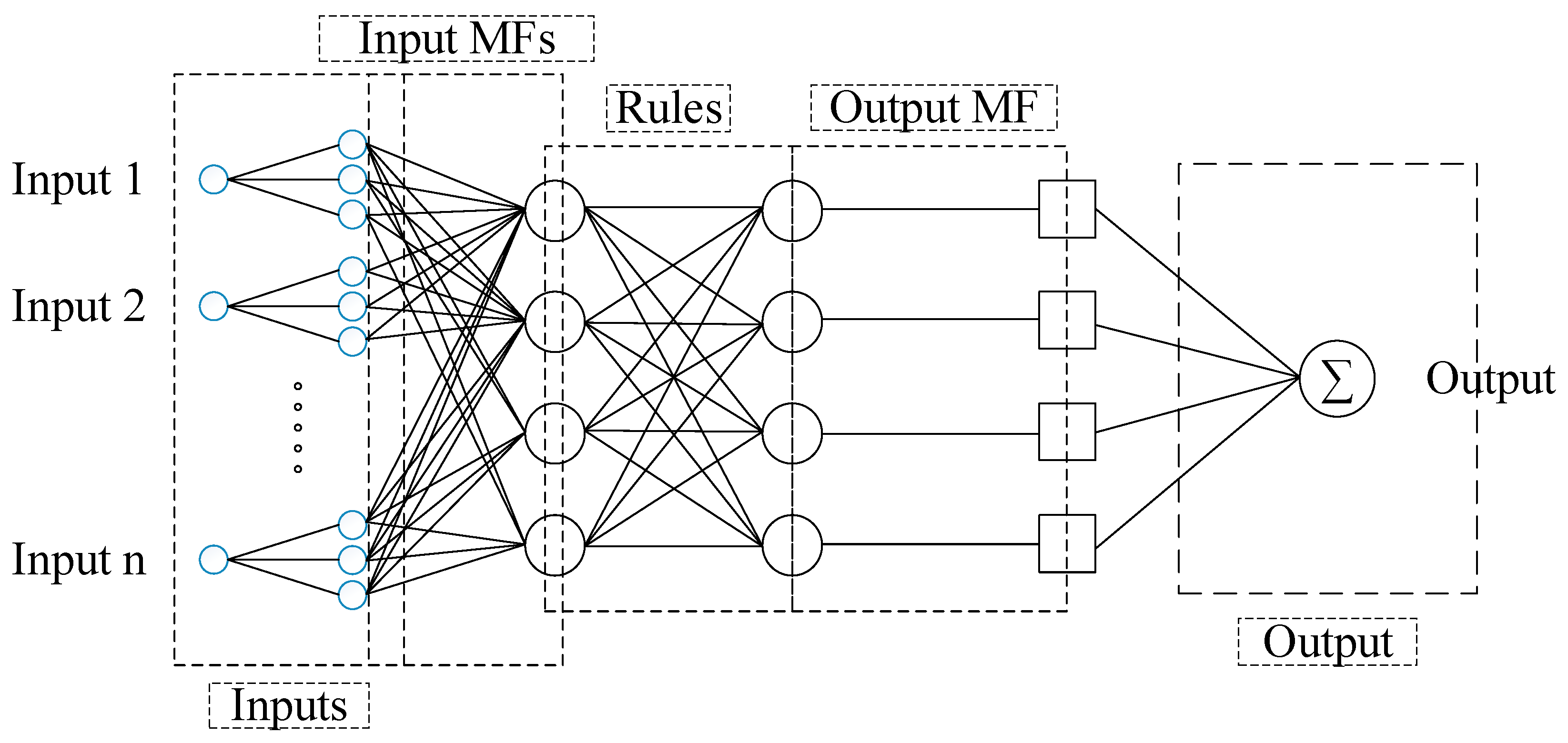
2.2.2. Adaptive Neuro Fuzzy Inference System (ANFIS)
An adaptive neuro fuzzy inference system is a type of ANN based on the Takagi–Sugeno fuzzy system [
87]. This approach was developed in the early 1990s. Because this system integrates the concepts of neural networks and fuzzy logic, it can take advantage of both capabilities in a unified framework. This technique is one of the most frequently used and robust hybrid ML techniques. It is consistent with a set of fuzzy if–then rules that can be learned to approximate nonlinear functions [
88,
89]. Hence, ANFIS was proposed as a universal estimator. An important element of fuzzy systems is the fuzzy partition of the input space [
90,
91]. For input
k, the fuzzy rules in the input space make a
k-faced fuzzy cube. Achieving a flexible partition for nonlinear inversion is non-trivial. The idea of this model is to build a neural network whose outputs are a degree of the input that belongs to each class [
92,
93,
94]. The membership functions (MFs) of this model can be nonlinear, multidimensional and, thus, different to conventional fuzzy systems [
95,
96,
97]. In ANFIS, neural networks are used to increase the efficiency of fuzzy systems. The method used to design neural networks is to employ fuzzy systems or fuzzy-based structures. This model is a kind of division and conquest method. Instead of using one neural network for all the input and output data, several networks are created in this model:
A fuzzy separator to cluster input–output data within multiple classes.
A neural network for each class.
Training neural networks with output–input data in the corresponding classes.
Figure 6 presents a simple architecture for ANFIS.
In the present study, ANFIS is developed to tackle two scenarios described in
Table 2. Each input included by two MFs with the Tri shape, Trap shape, and Gauss shape MFs. The output MF type was selected to be linear with a hybrid optimizer type.
2.2.3. Evaluation Criteria
Evaluation was conducted using the root mean square error (RMSE) (Equation (22)) and correlation coefficient (Equation (23)). These statistics compare the target and output values, and calculate a score as an index for the performance and accuracy of the developed methods [
88,
98]. Presents the evaluation criteria equations.
where
N is the number of data, and
P and
A are, respectively, the predicted (output) and desired (target) values.
3. Results
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10 present the results of the accuracy statistics for the logistic, linear, logarithmic, quadratic, cubic, compound, power, and exponential equations, respectively. The coefficients of each equation were calculated by the three ML optimizers; GA, PSO, and GWO. The table contains country name, model name, population size, number of iterations, processing time, RMSE, and correlation coefficient.
According to
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10, GWO provided the highest accuracy (smallest RMSE and largest correlation coefficient) and smallest processing time compared to PSO and GA for fitting the logistic, linear, logarithmic, quadratic, cubic, power, compound, and exponential equations for all five countries. It can be suggested that GWO is a sustainable optimizer due to its acceptable processing time compared with PSO and GA. Therefore, GWO was selected as the best optimizer by providing the highest accuracy values compared with PSO and GA. In general, it can be claimed that GWO, by suggesting the best parameter values for the functions presented in Equations (6)–(13), increases outbreak prediction accuracy for COVID-19 in comparison with PSO and GA. Therefore, the functions derived by GWO were selected as the best predictors for this research.
Table 11,
Table 12,
Table 13,
Table 14 and
Table 15 present the description and coefficients of the linear, logarithmic, quadratic, cubic, compound, power, exponential, and logistic equations estimated by GWO.
Table 11,
Table 12,
Table 13,
Table 14 and
Table 15 also present the RMSE and
r-square values for each equation fitted to data for China, Italy, Iran, Germany, and USA, respectively.
As is clear from
Table 11,
Table 12,
Table 13,
Table 14 and
Table 15, in general, the logistic equation followed by the quadratic and cubic equations provided the smallest RMSE and the largest
r-square values for the prediction of COVID-19 outbreak. The claim can also be considered from
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
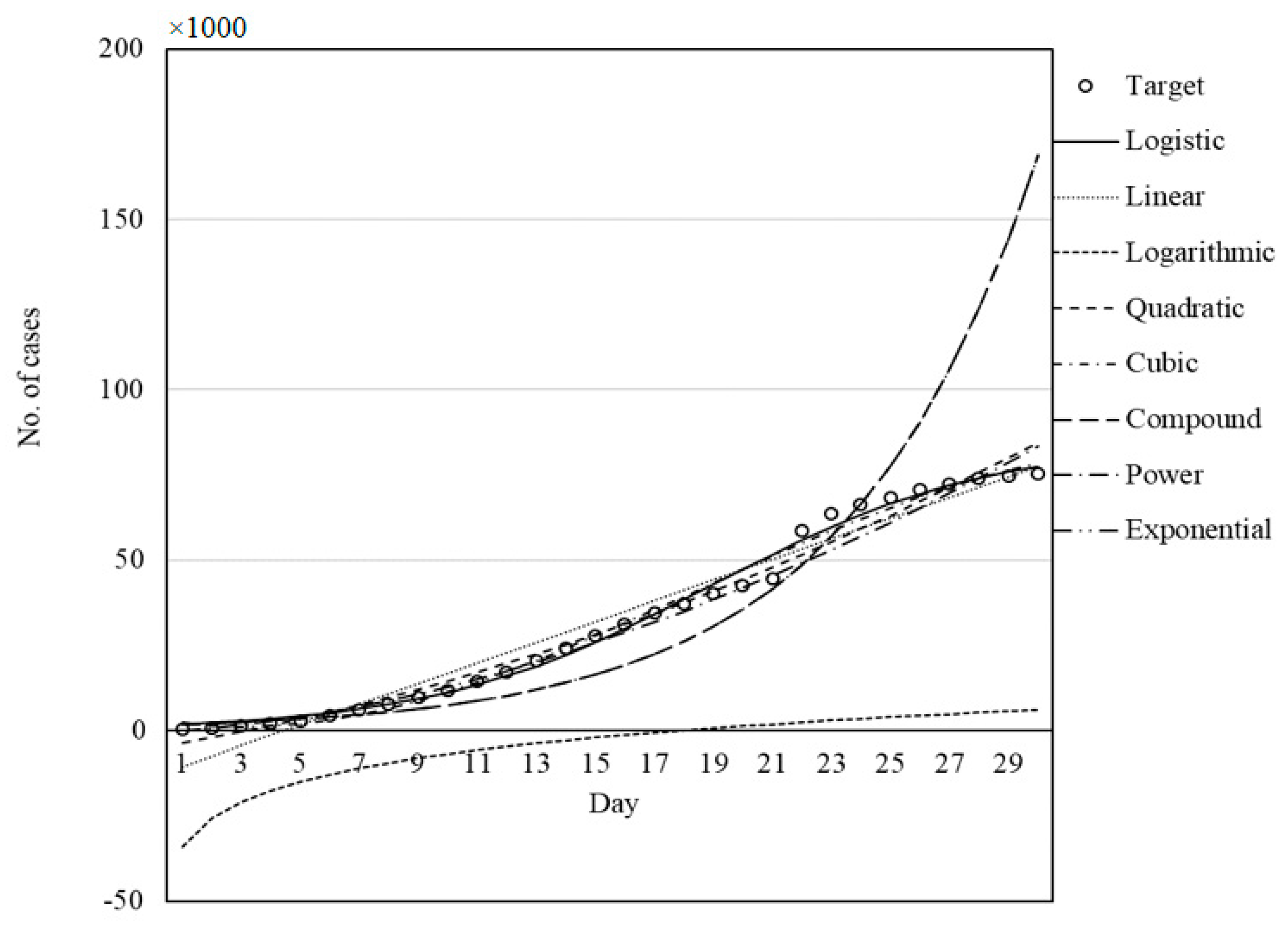
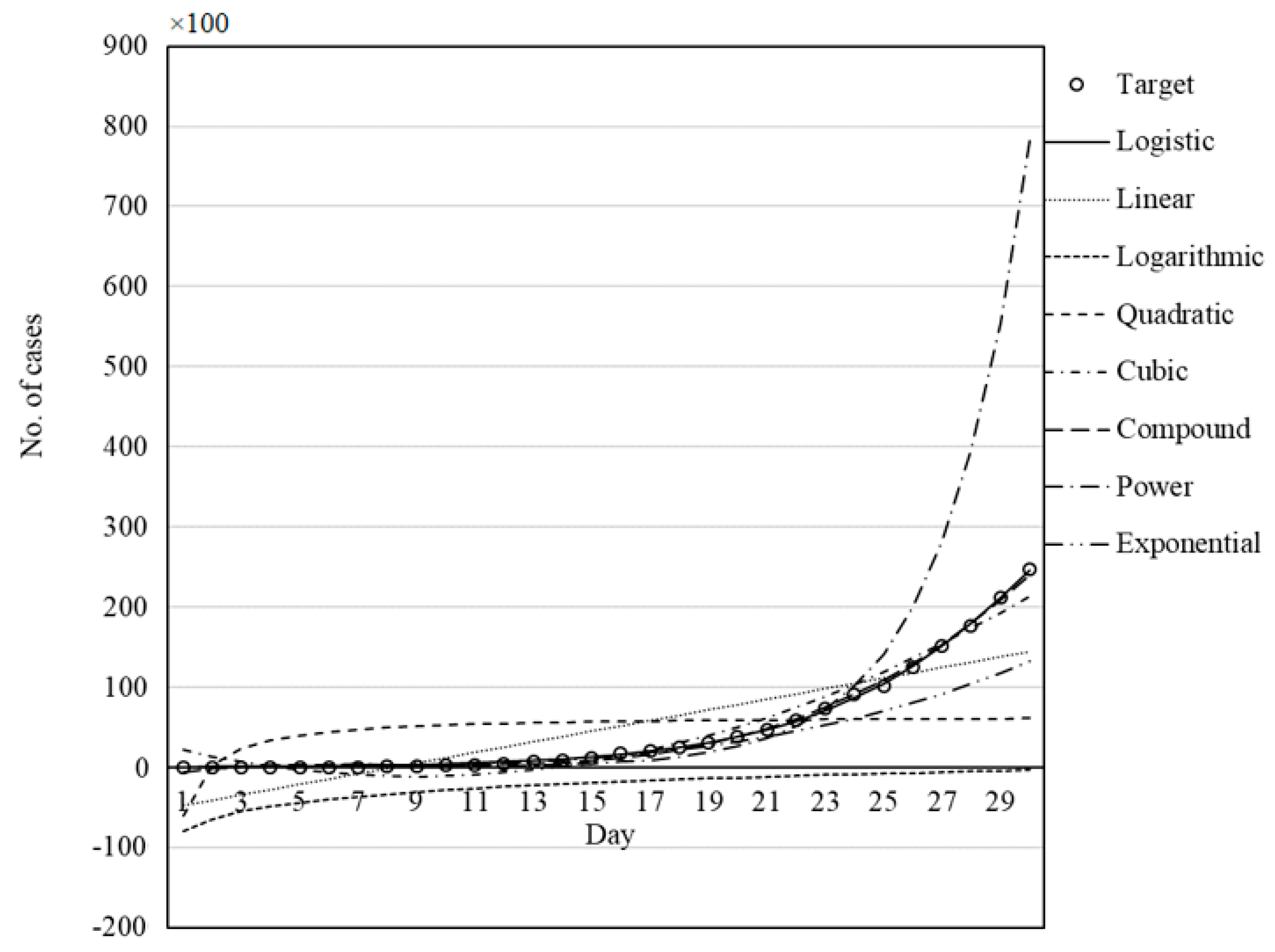
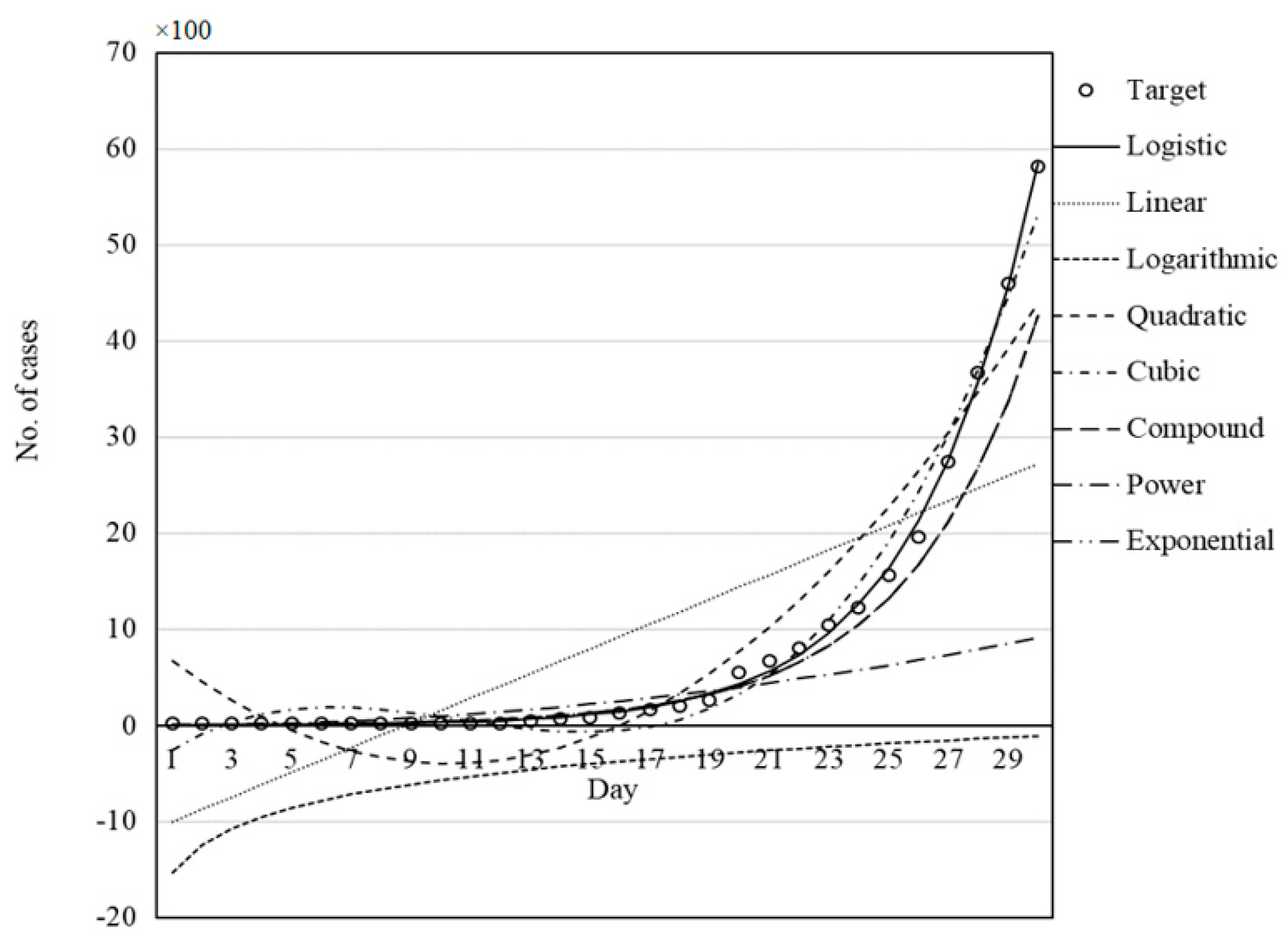
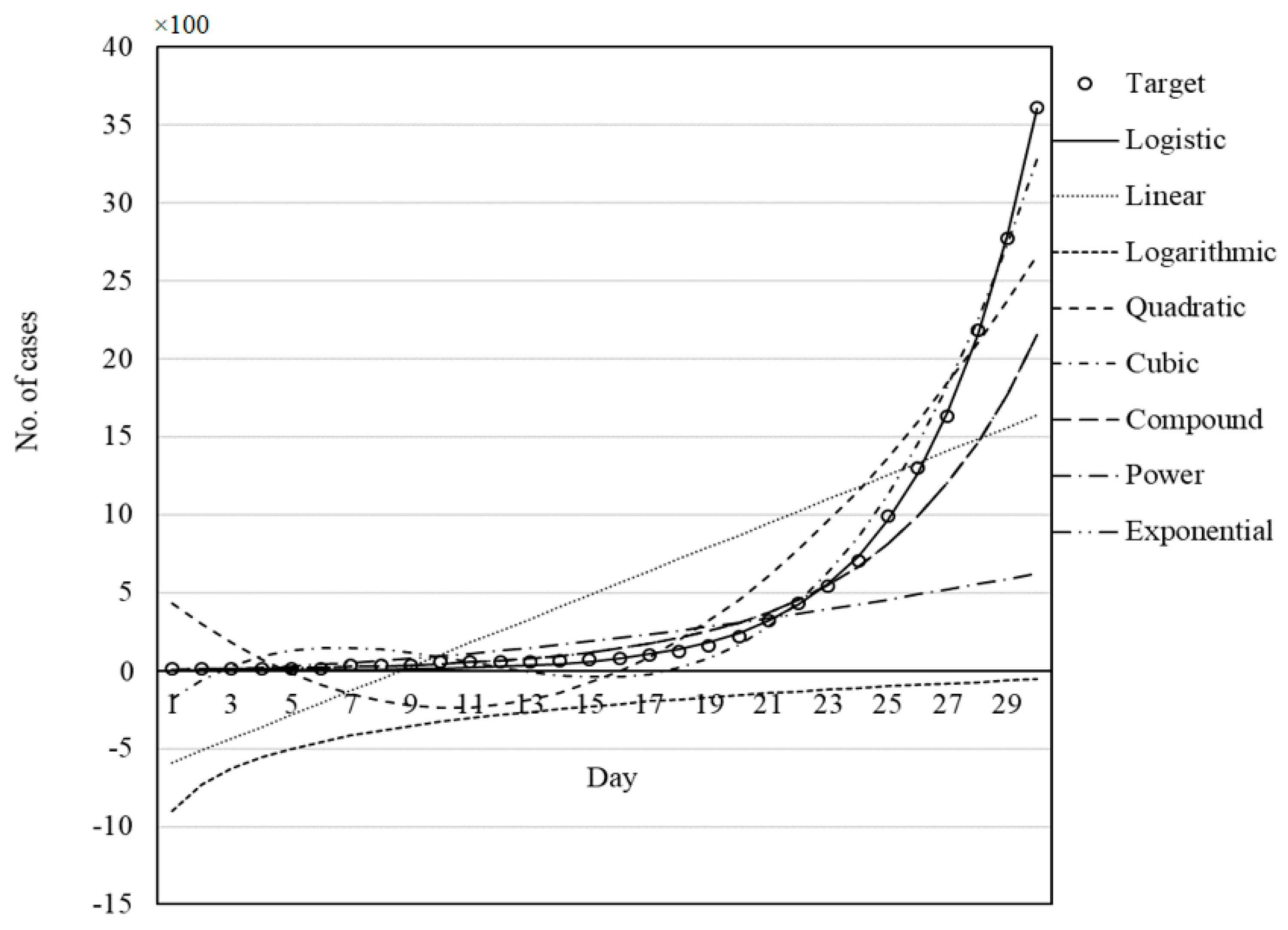
Figure 11, which present the capability and trend of each model derived by GWO in the prediction of COVID-19 cases for China, Italy, Iran, Germany, and the USA, respectively.
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11 illustrate the fit of the models investigated in this paper. The best fit for the prediction of COVID-19 cases was achieved for the logistic model followed by cubic and quadratic models for China (
Figure 7), logistic followed by cubic models for Italy (
Figure 8), cubic followed by logistic and quadratic models for Iran (
Figure 9), the logistic model for Germany (
Figure 10), and logistic model for the USA (
Figure 11).
Machine Learning Results
This section presents the results for the training stage of ML methods. MLP and ANFIS were employed as single and hybrid ML methods, respectively. ML methods were trained using two datasets related to scenario 1 and scenario 2.
Table 16 presents the results of the training phase.
According to
Table 16, the datasets related to scenarios 1 and 2 have different performance values. Accordingly, for Italy, the MLP with 16 neurons provided the highest accuracy for scenario 1 and ANFIS with Tri. MF provided the highest accuracy for scenario 2. By considering the average values of the RMSE and correlation coefficient, it can be concluded that scenario 1 is more suitable for modeling outbreak cases in Italy because it provides higher accuracy (the smallest RMSE and the largest correlation coefficient) than scenario 2.
For the dataset related to China, for both scenarios, MLP with 12 and 16 neurons, respectively for scenarios 1 and 2, provided the highest accuracy compared with the ANFIS model. By considering the average values of RMSE and correlation coefficient, it can be concluded that scenario 2 with a larger average correlation coefficient and smaller average RMSE than scenario 1 is more suitable for modeling the outbreak in China.
For the dataset of Iran, MLP with 12 neurons in the hidden layer for scenario 1 and ANFIS with Gaussian MF type for scenario 2 provided the best performance for the prediction of the outbreak. By considering the average values of the RMSE and correlation coefficient, it can be concluded that scenario 1 provided better performance than scenario 2. In addition, in general, the MLP has higher prediction accuracy compared with the ANFIS method.
In Germany, MLP with 12 neurons in its hidden layer provided the highest accuracy (smallest RMSE and largest correlation coefficient). By considering the average values of the RMSE and correlation coefficient, it can be concluded that scenario 1 is more suitable for the prediction of the outbreak in Germany than scenario 2.
In the USA, the MLP with 8 and 12 neurons, respectively, for scenarios 1 and 2, provided higher accuracy (the smallest RMSE and the largest correlation coefficient values) than the ANFIS model. By considering the average values of the RMSE and correlation coefficient values, it can be concluded that scenario 1 is more suitable than scenario 2, and MLP is more suitable than ANFIS for outbreak prediction.
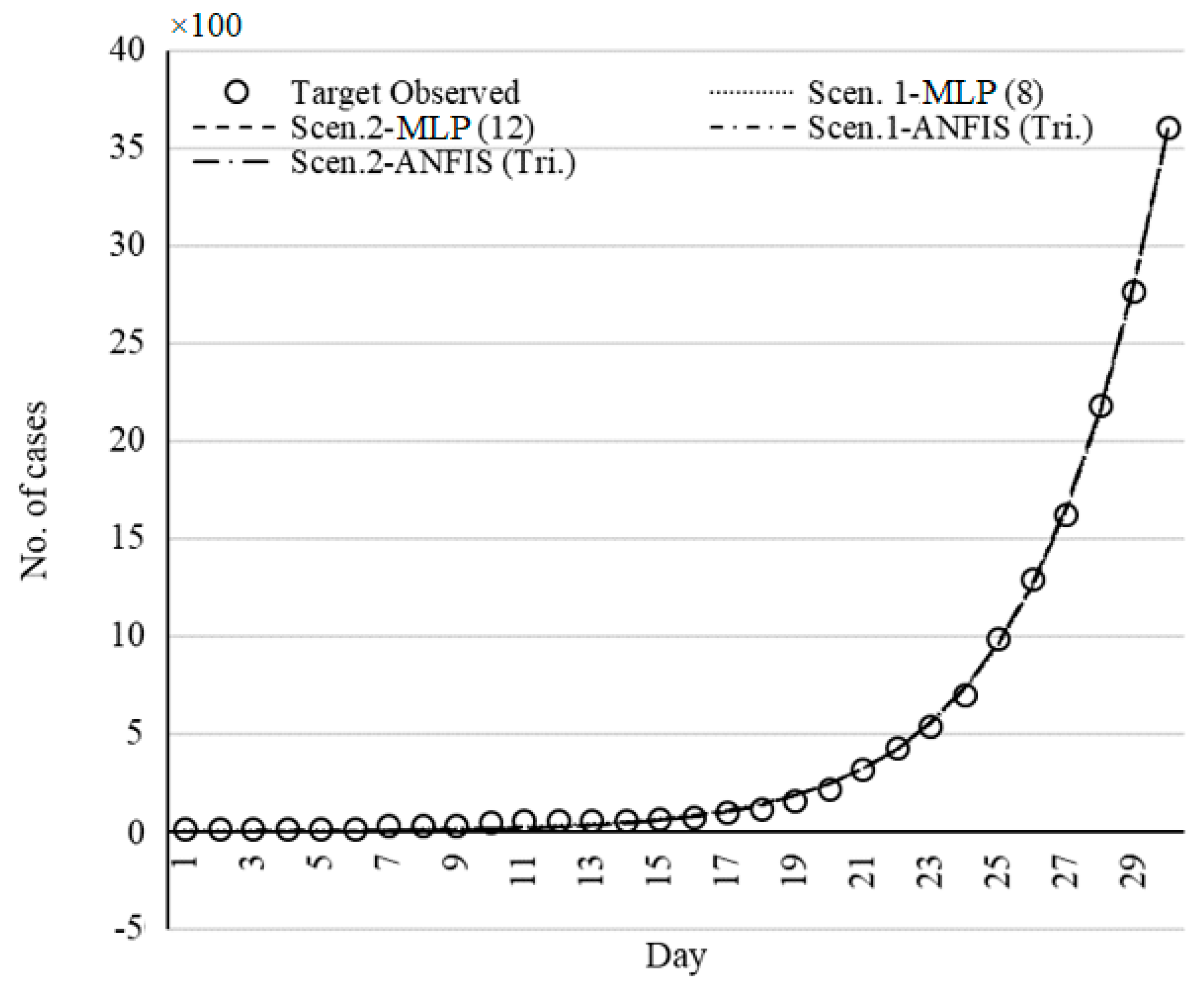
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16 present the model fits for Italy, China, Iran, Germany, and the USA, respectively. By comparing
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16 with
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11, it can be concluded that the MLP and the logistic model fitted by GWO provided a better fit than the other models. In addition, the ML methods provided better performance compared with other models.
Comparing the Fitted Models
This section presents a comparison of the accuracy and performance of the selected models for the prediction of 30 days’ outbreak.
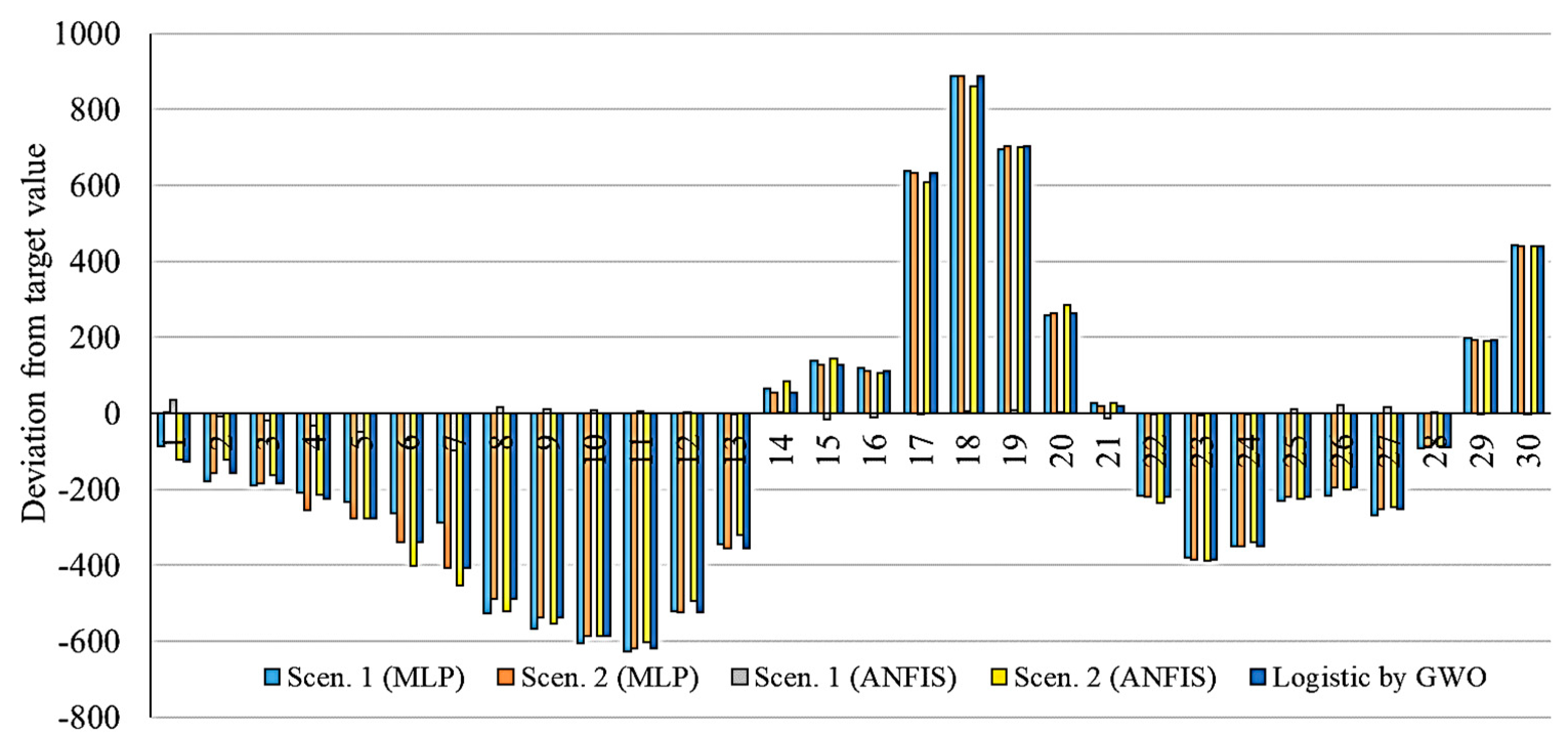
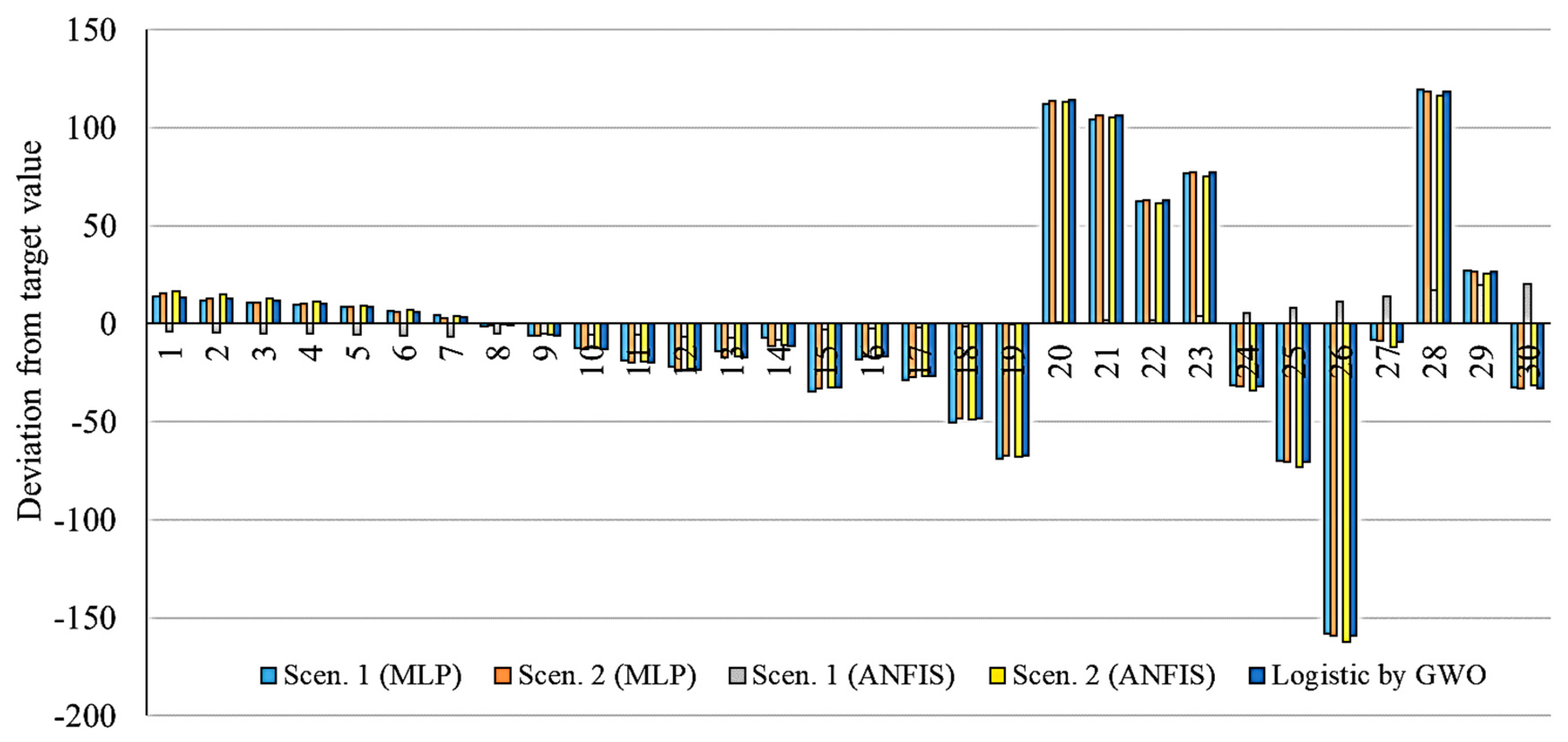
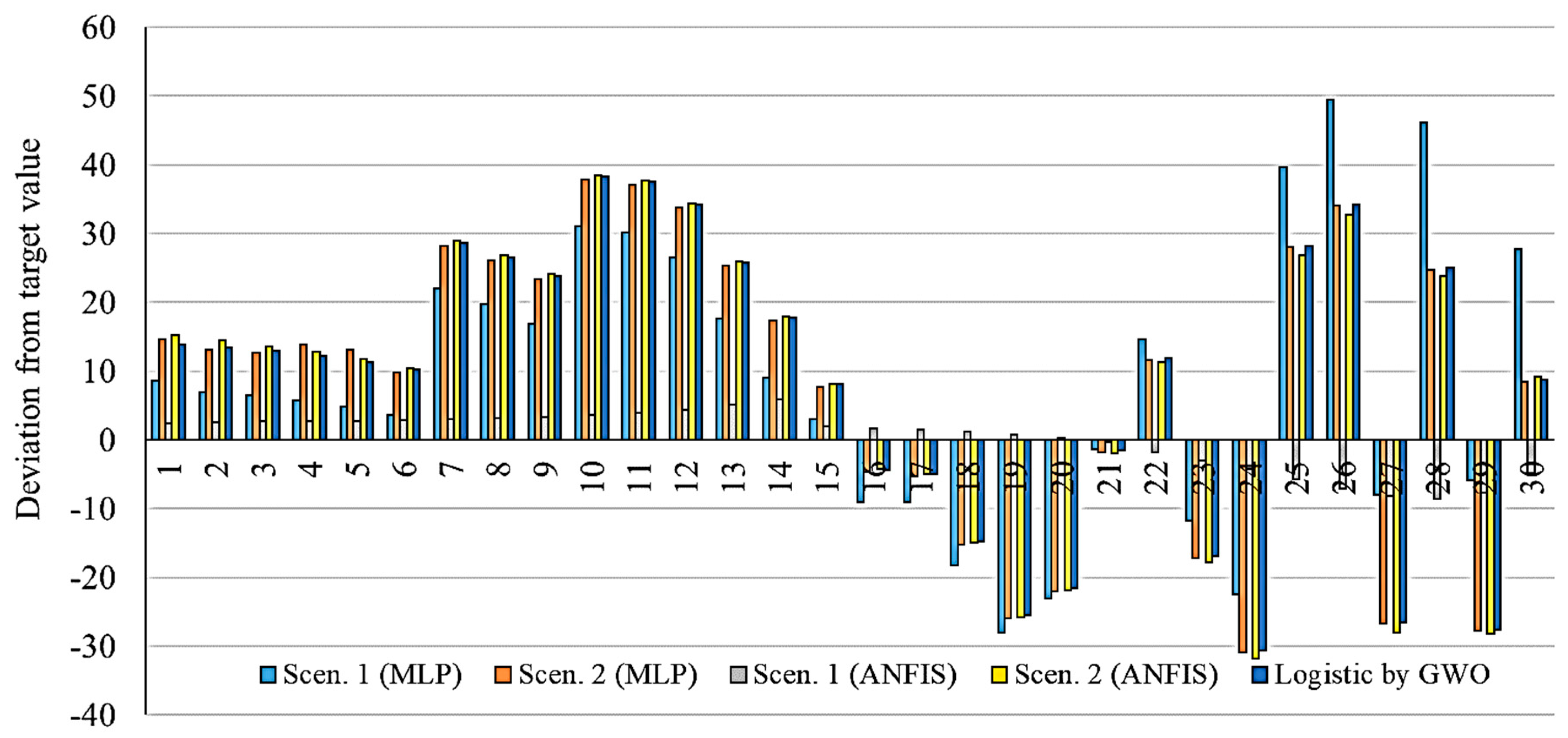
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21 show the deviation from the target values for the selected models.
As is clear from
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21, the smallest deviation from the target values is related to the MLP for scenario 1 followed by MLP for scenario 2. This indicates the highest performance of the MLP method for the prediction of the outbreak.
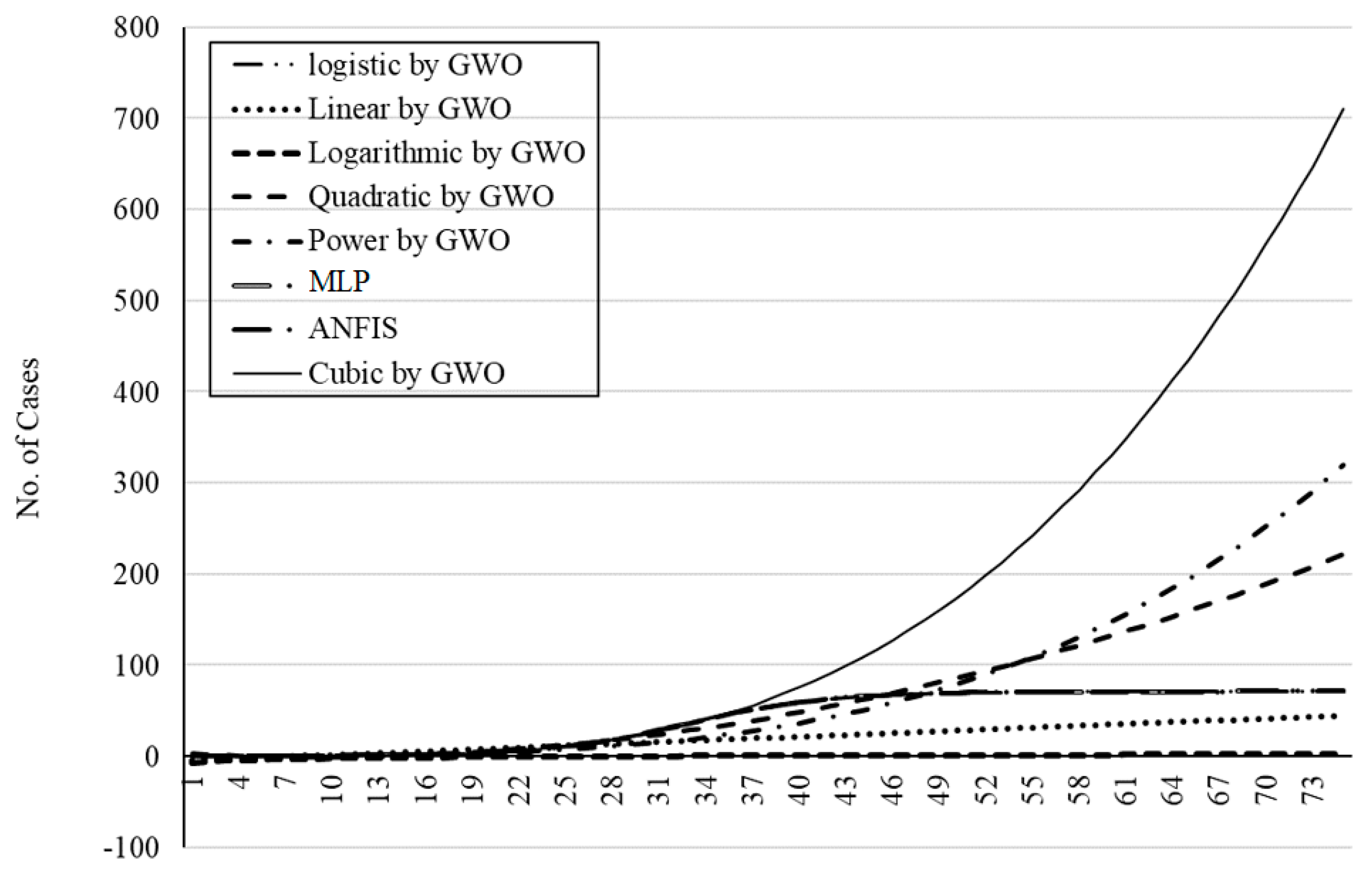
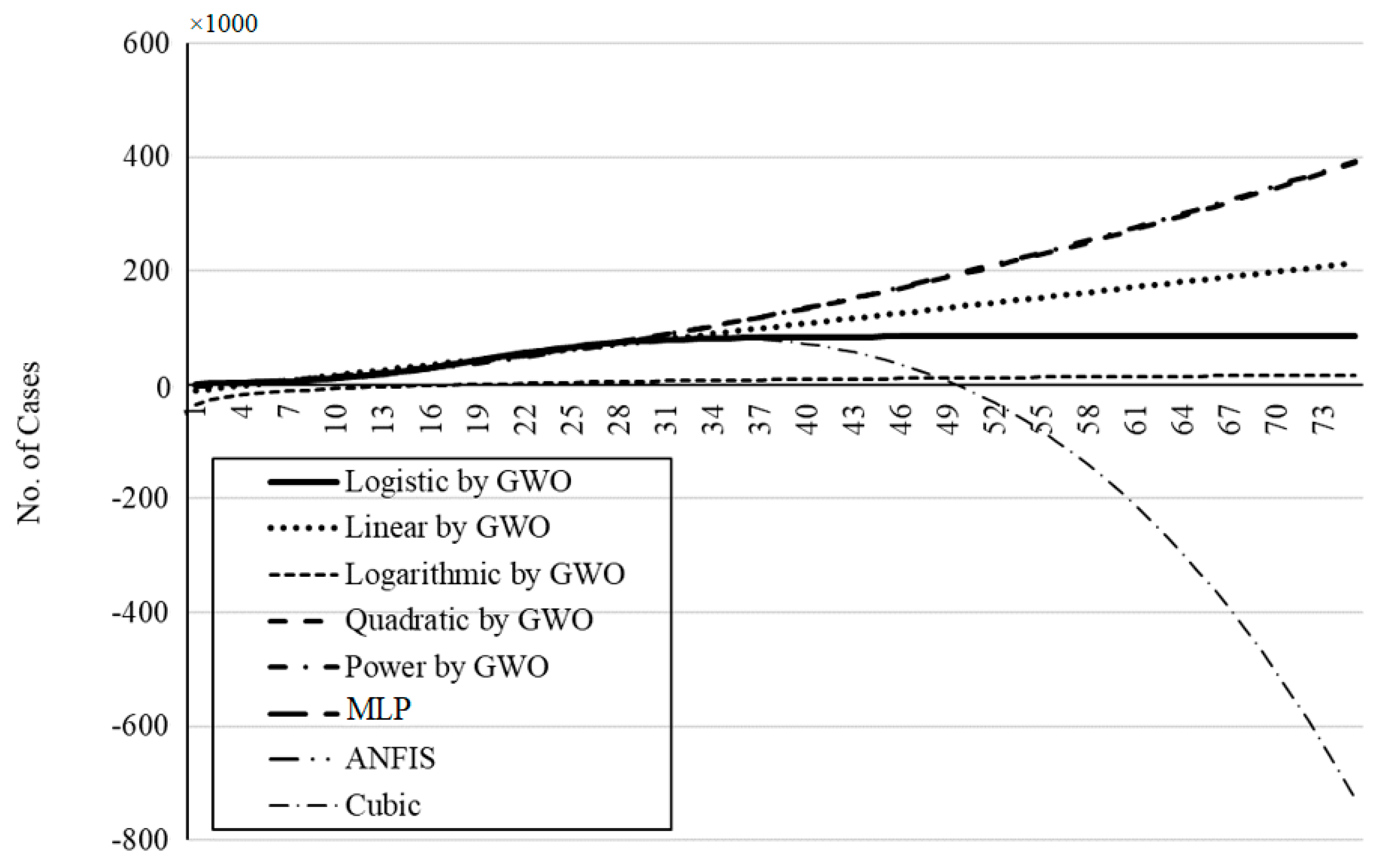
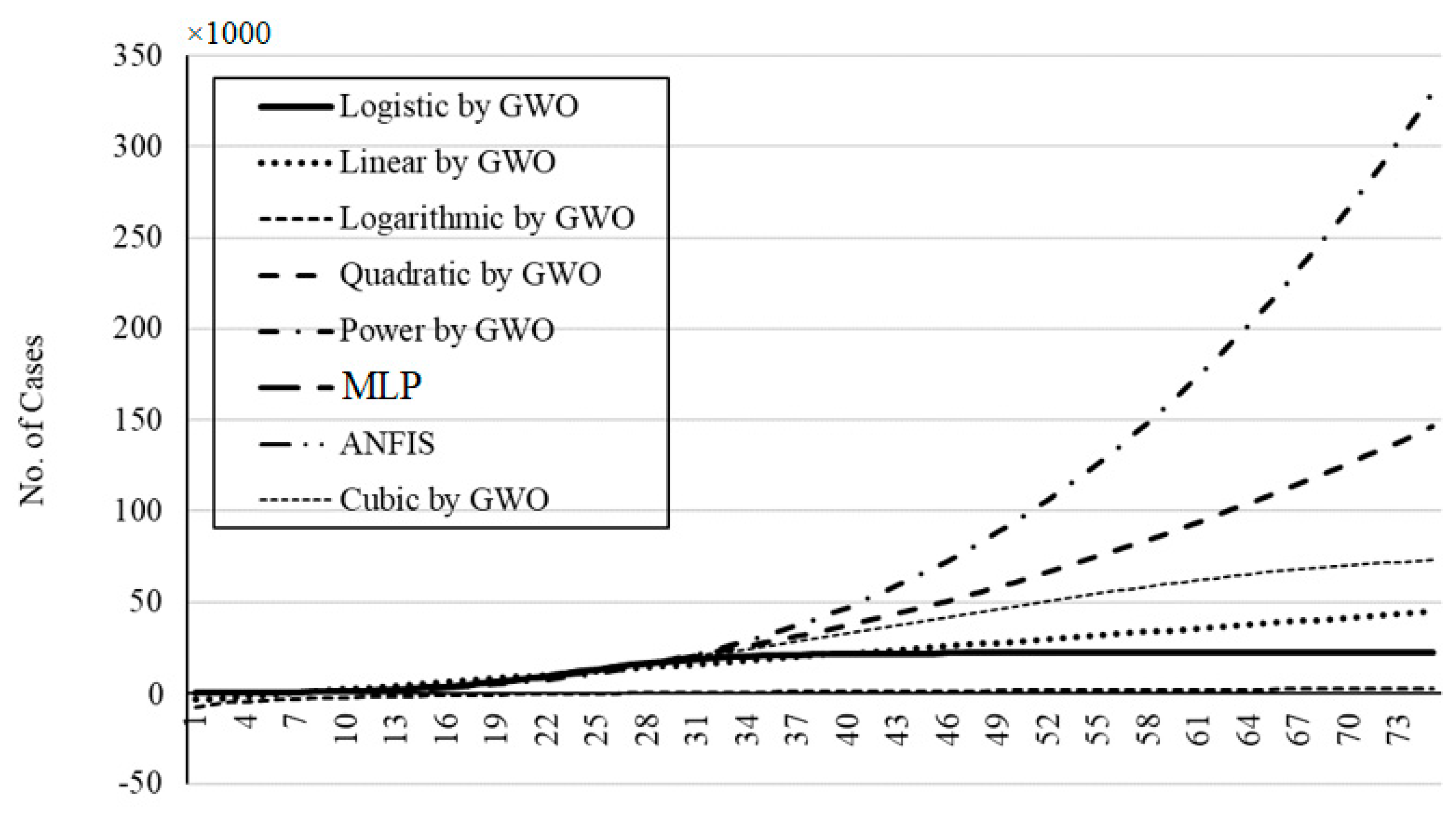
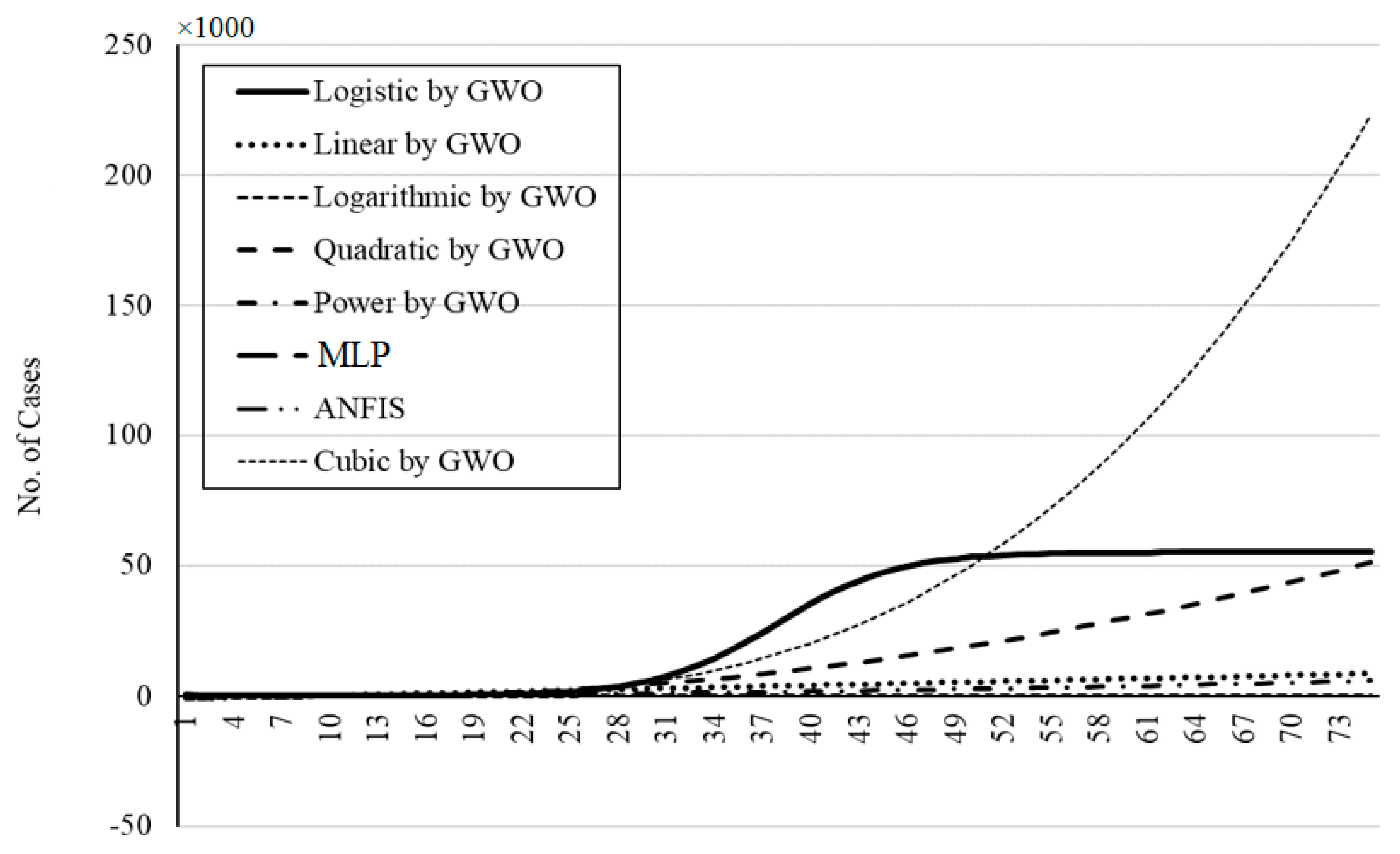
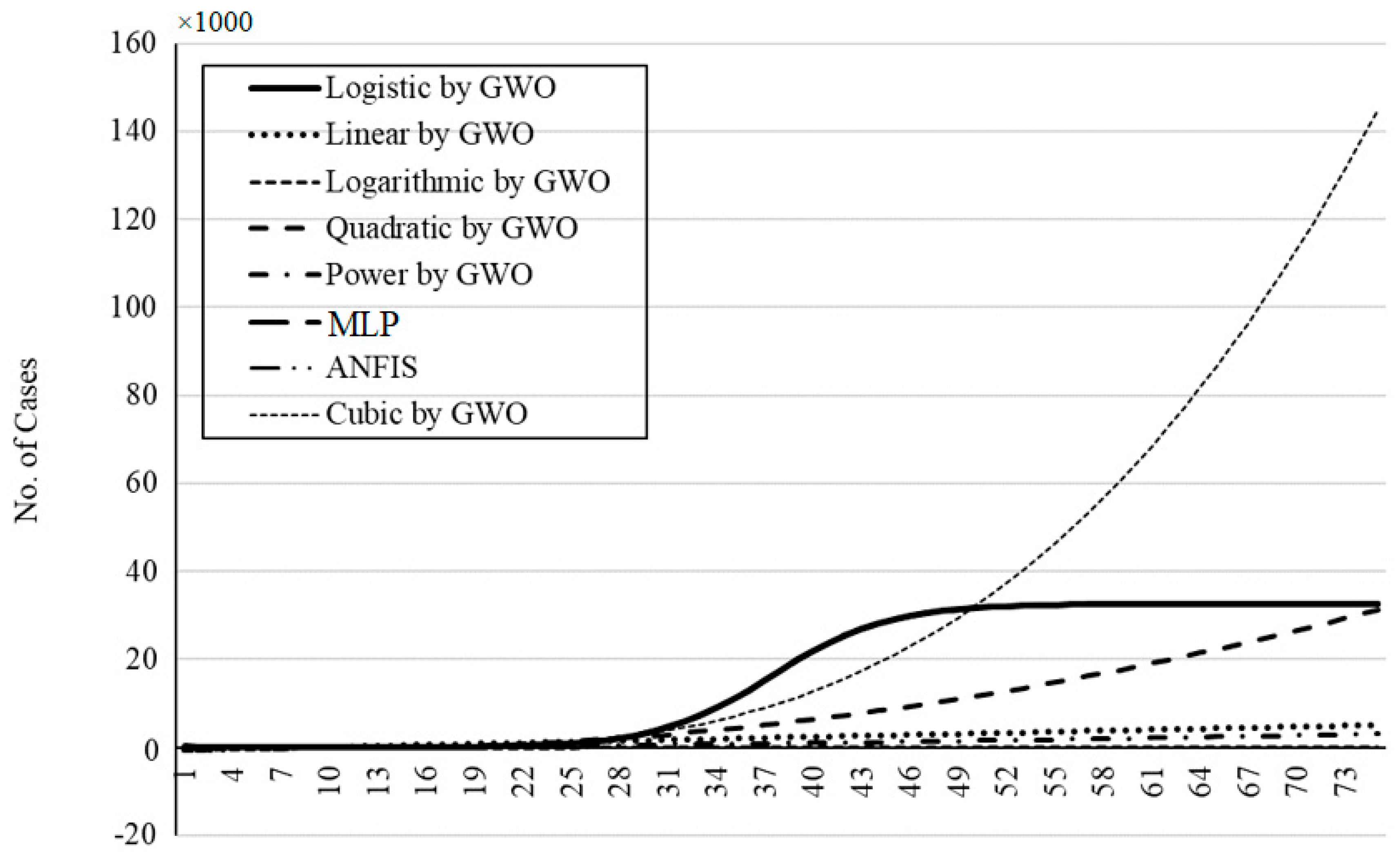
Figure 22,
Figure 23,
Figure 24,
Figure 25 and
Figure 26 present the outbreak prediction for 75 days and
Table 17,
Table 18,
Table 19,
Table 20 and
Table 21 present the outbreak prediction for 150 days.
Figure 27 represents the dispersion of the outbreak for the countries studied in this paper.
4. Discussion
The parameters of several simple mathematical models (i.e., logistic, linear, logarithmic, quadratic, cubic, compound, power, and exponential) were fitted using GA, PSO, and GWO. The logistic model outperformed other methods and showed promising results based on training for 30 days. Extrapolation of the prediction beyond the original observation range of 30 days should not be expected to be realistic considering the new statistics. The fitted models generally showed low accuracy and also weak generalization ability for the five countries. Although the prediction for China was promising, the model was insufficient for extrapolation, as expected. In turn, the logistic GWO outperformed the PSO and GA, and the computational cost for GWO was reported as satisfactory. Consequently, for further assessment of the ML models, the logistic model fitted with GWO was used for comparative analysis.
In the next step, for introducing the machine learning methods for time-series prediction, two scenarios were proposed. Scenario 1 considered four data samples from the progress of the infection from previous days, as reported in
Table 2. The sampling for data processing was done weekly for scenario 1. However, scenario 2 was devoted to daily sampling for all previous consecutive days. Providing these two scenarios expanded the scope of this study. Training and test results for the two machine learning models (MLP and ANFIS) were considered for the two scenarios. A detailed investigation was also carried out to explore the most suitable number of neurons. For the MLP, the performances of using 8, 12, and 16 neurons were analyzed throughout the study. For the ANFIS, the membership function (MF) types of Tri, Trap, and Gauss were analyzed throughout the study. The five counties of Italy, China, Iran, Germany, and USA were considered. The performance of both ML models for these countries varied between the two different scenarios. Given the observed results, it is not possible to select the most suitable scenario. Therefore, both daily and weekly sampling can be used in machine learning modeling. Comparison between analytical and machine learning models using the deviation from the target value (
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21) indicated that the MLP in both scenarios delivered the most accurate results. Extrapolation for long-term prediction of up to 150 days using the ML models was tested. The actual prediction of MLP and ANFIS for the five countries was reported and showed the progression of the outbreak.
This paper evaluated the applicability of two machine learning models, MLP and ANFIS, for predicting the COVID-19 outbreak. The models showed promising results in terms of predicting the time series without the assumptions that epidemiological models require. Machine learning models, as an alternative to epidemiological models, showed potential in predicting COVID-19, as they did for modeling other outbreaks (see
Table 1). Considering the availability of only a small amount of training data, it is expected that machine learning will be developed further as the basis for, or a component of, future outbreak prediction models.
Here, it is worth mentioning that machine learning can also be found useful in dealing with the challenges that SEIR models face for COVID-19. For example, the number of cases reported by worldometer is not the number of infected (E in the SEIR model). For example, the number of cases reported by worldometer for the UK situation is the number of people tested. In addition, data for the number of infectious people (I in SEIR) is a challenging matter because many people who might be infectious may not choose to be for tested if, for example, their symptoms are mild. Although better data exist on the number of people who are admitted to hospital and the number who die, these also do not represent R because it is generally accepted that most people with COVID-19 recover without entering hospital. Considering this data problem, it is extremely difficult to fit SEIR models satisfactorily. Considering such challenges, for future research, the ability of machine learning for estimation of the missing information on the number of exposed E or infected can be evaluated. Furthermore, the temporal non-stationarity data in control measures can also be investigated using machine learning.