Multi-Fidelity Gradient-Based Strategy for Robust Optimization in Computational Fluid Dynamics
Abstract
1. Introduction
2. Problem Definition
2.1. Test Problem: Quasi-1D Supersonic Nozzle
- geometric tolerances on the nozzle shape, modeled by treating the shape parameters as normally distributed random variables, with mean and coefficient of variation , with the standard deviation;
- uncertainties in inlet total pressure described as a uniformly-distributed random variable with imposed lower and upper bounds;
- uncertainties in the gas properties, here represented by the specific heat ratio , which is also assumed as uniformly distributed.
3. Uncertainty Quantification Methods
3.1. Bayesian Kriging and Gradient-Enhanced Kriging
3.1.1. Bayesian Kriging
3.1.2. Gradient Enhanced Kriging
3.2. Method of Moments
3.3. Gradient Calculation
4. Robust Design Optimization Strategy
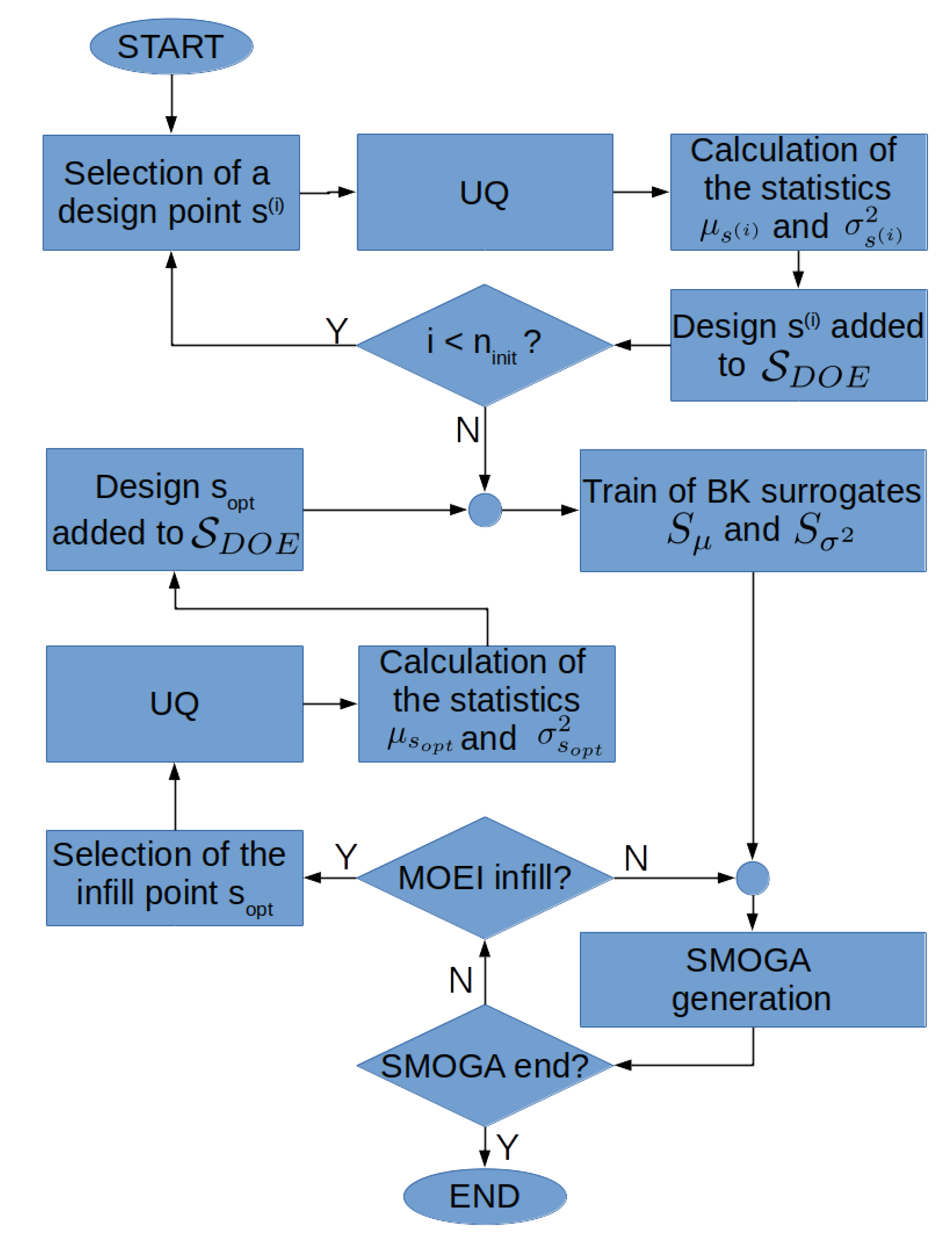
4.1. BK-Based Robust Design Optimization
| Algorithm 1: BK RDO loop with the MOEI adaptation. |
1. Initialization: LHS DOE with samples While Select design in Run UQ solver to compute the statistics , Train surrogates , 2. BK-SMOGA loop While If MOEI infill prescribed: Solve MOEI pbto choose a new sample Run UQ solver to compute , Re-train , by adding |
4.2. Multi-Fidelity Methods for RDO
| Algorithm 2: MF RDO loop with the MOEI adaptation. |
1. Initialization: LHS LF DOE with samples LHS HF DOE with samples While Select design in Run MoM solver to compute the statistics , Train LF surrogates , While Select design in Run GEK solver to compute the statistics , Use Equation (22) to construct MF surrogates: , 2. MF-SMOGA loop While If MOEI infill prescribed: Solve MOEI pb on MF surrogate to choose a new sample If EI>tol: Run MoM solver to compute , Re-train , by adding Else: Run GEK solver to compute , Re-train , by adding |
5. Results
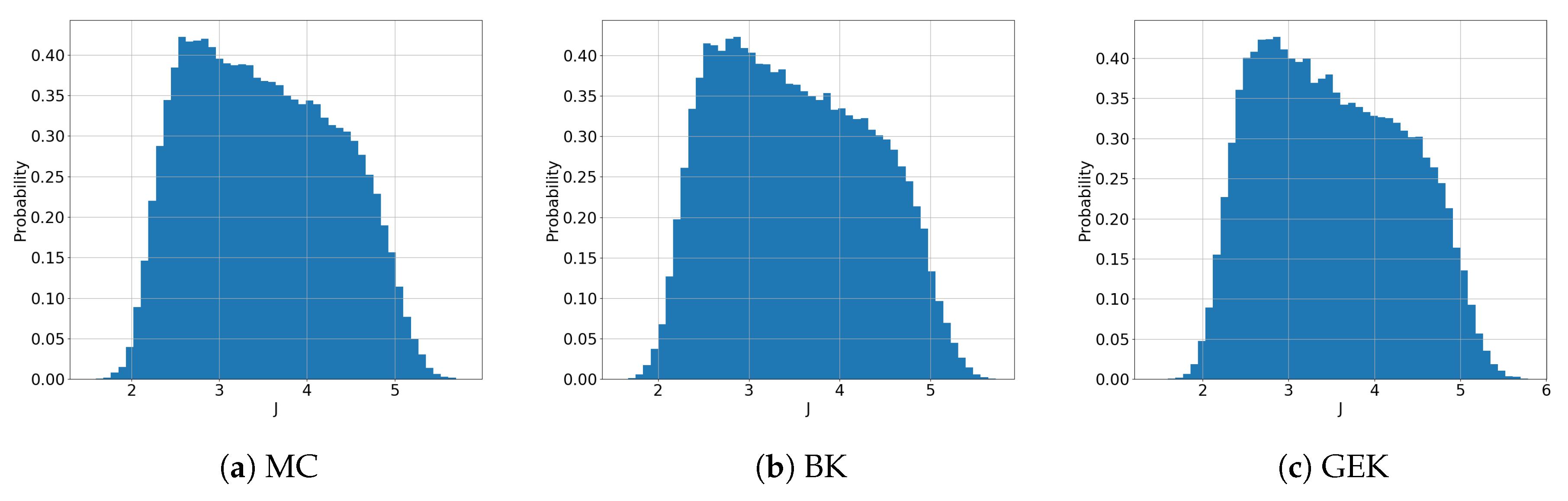
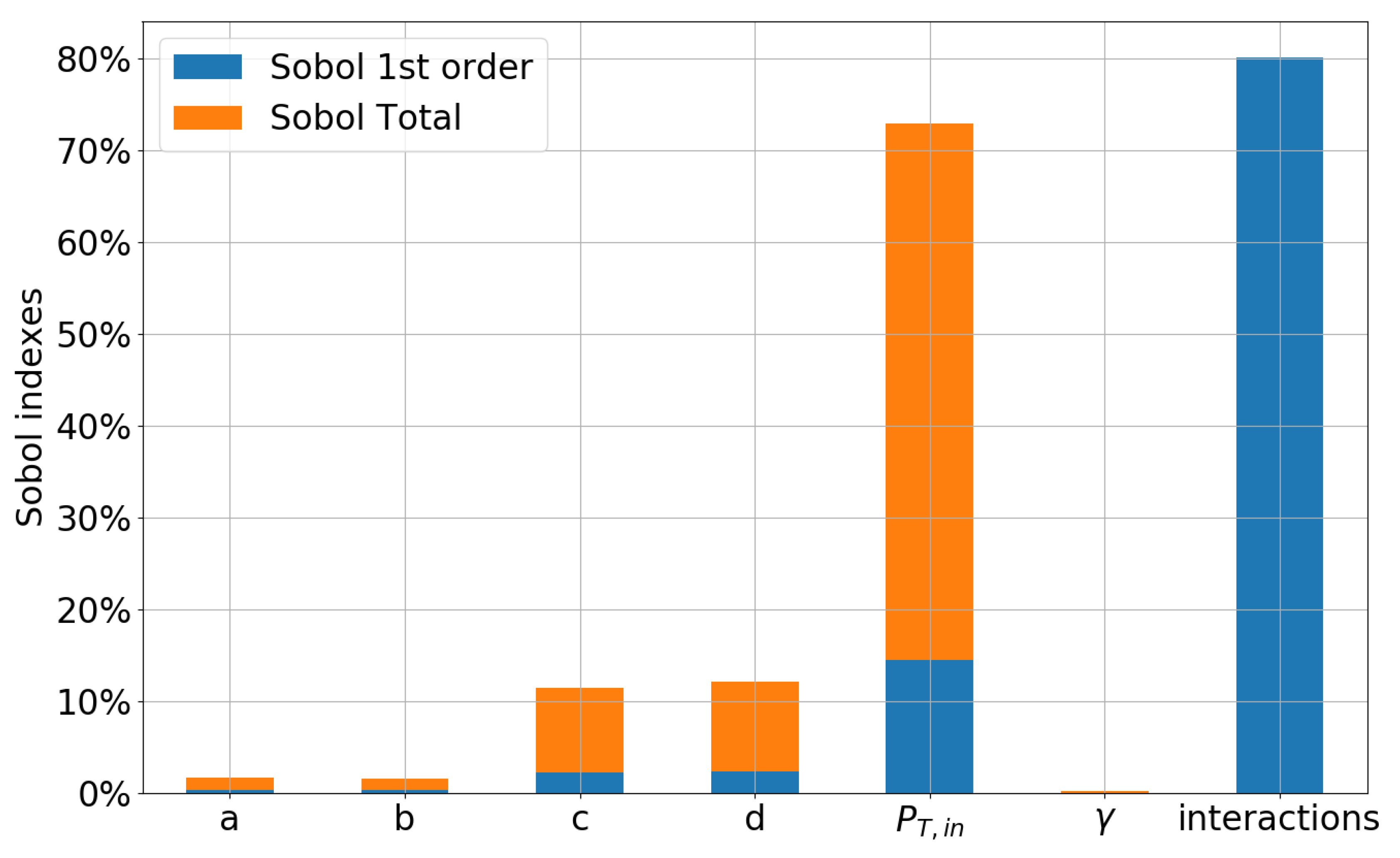
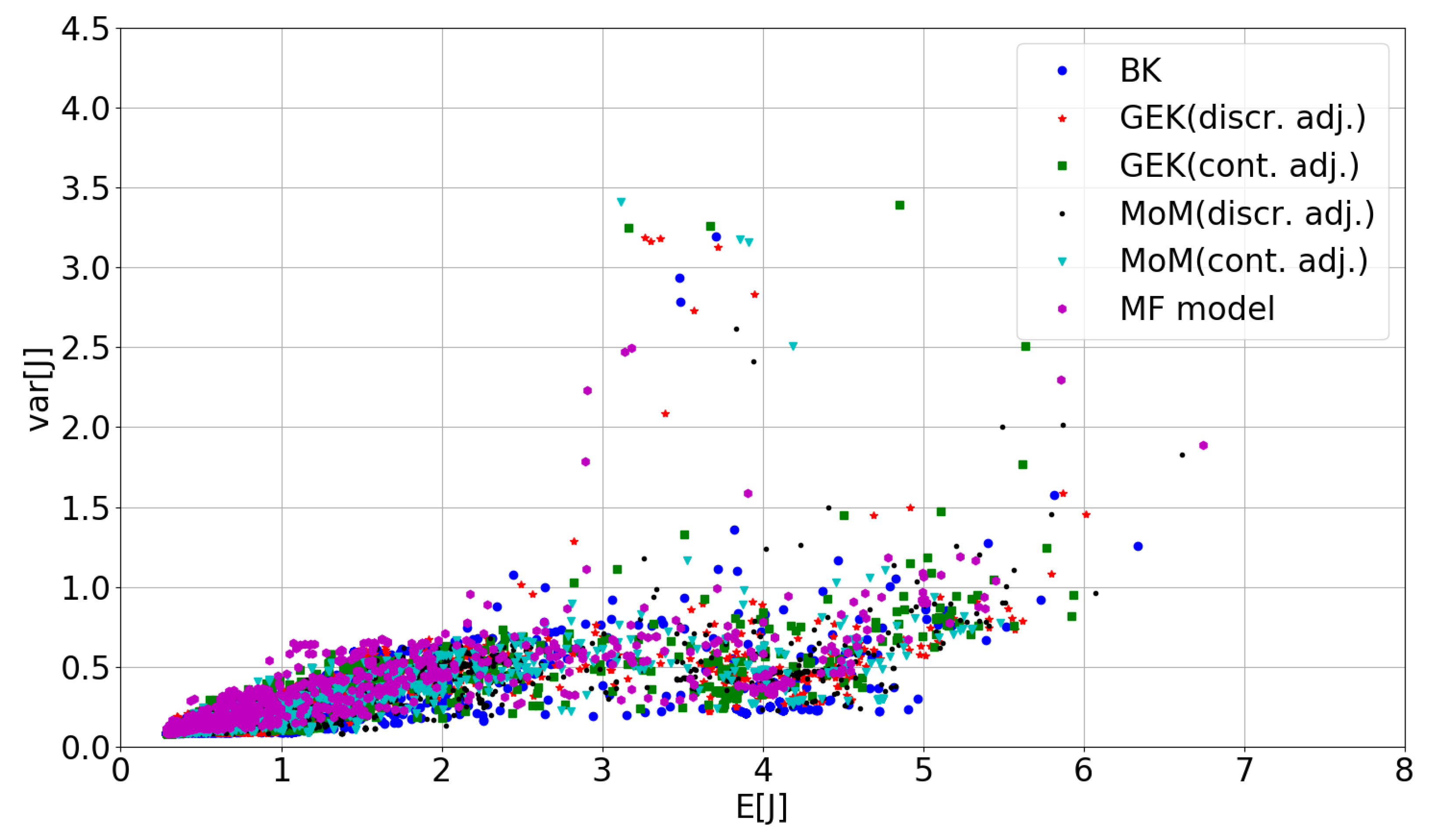
5.1. Preliminary Assessment of the UQ Methods
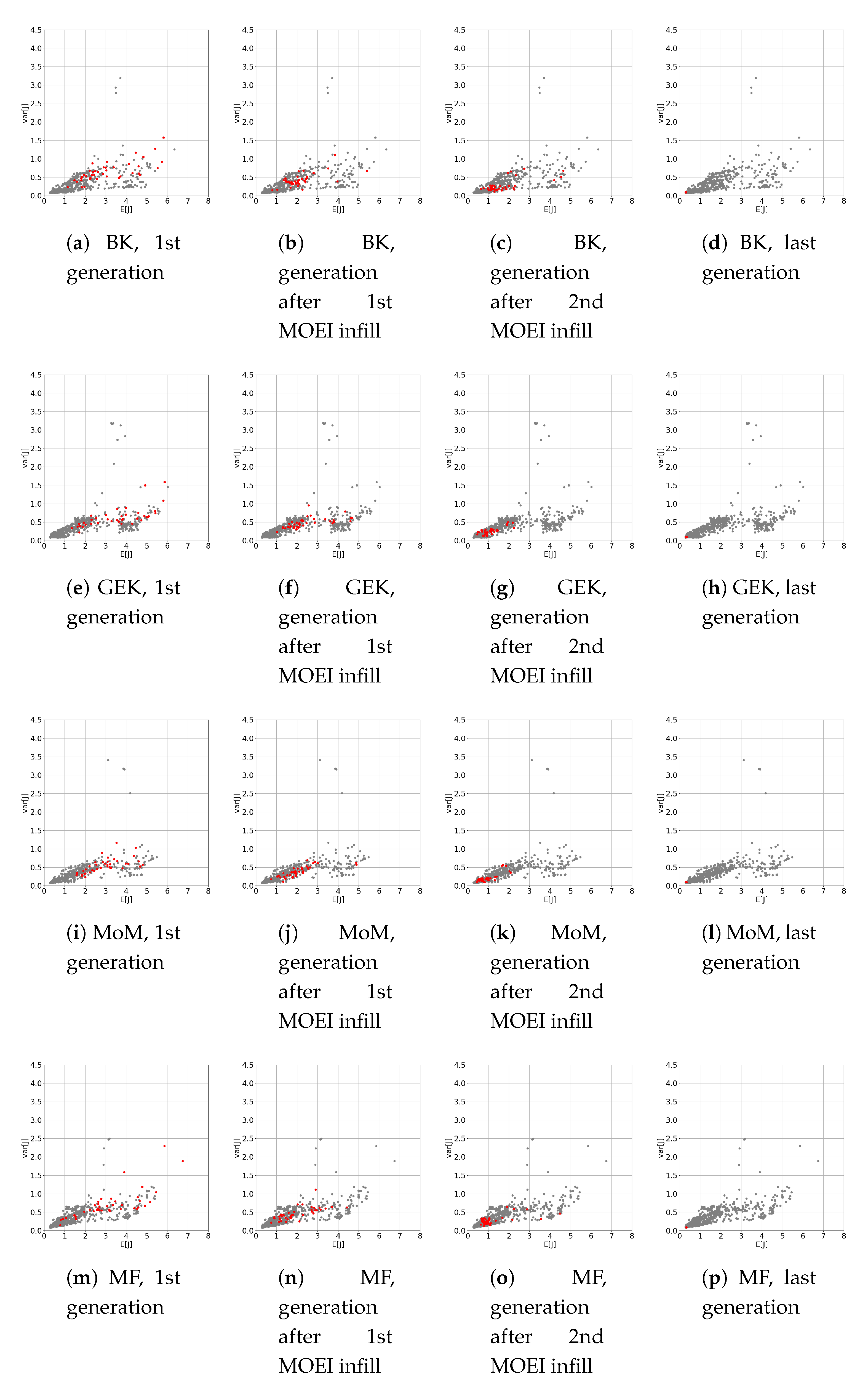
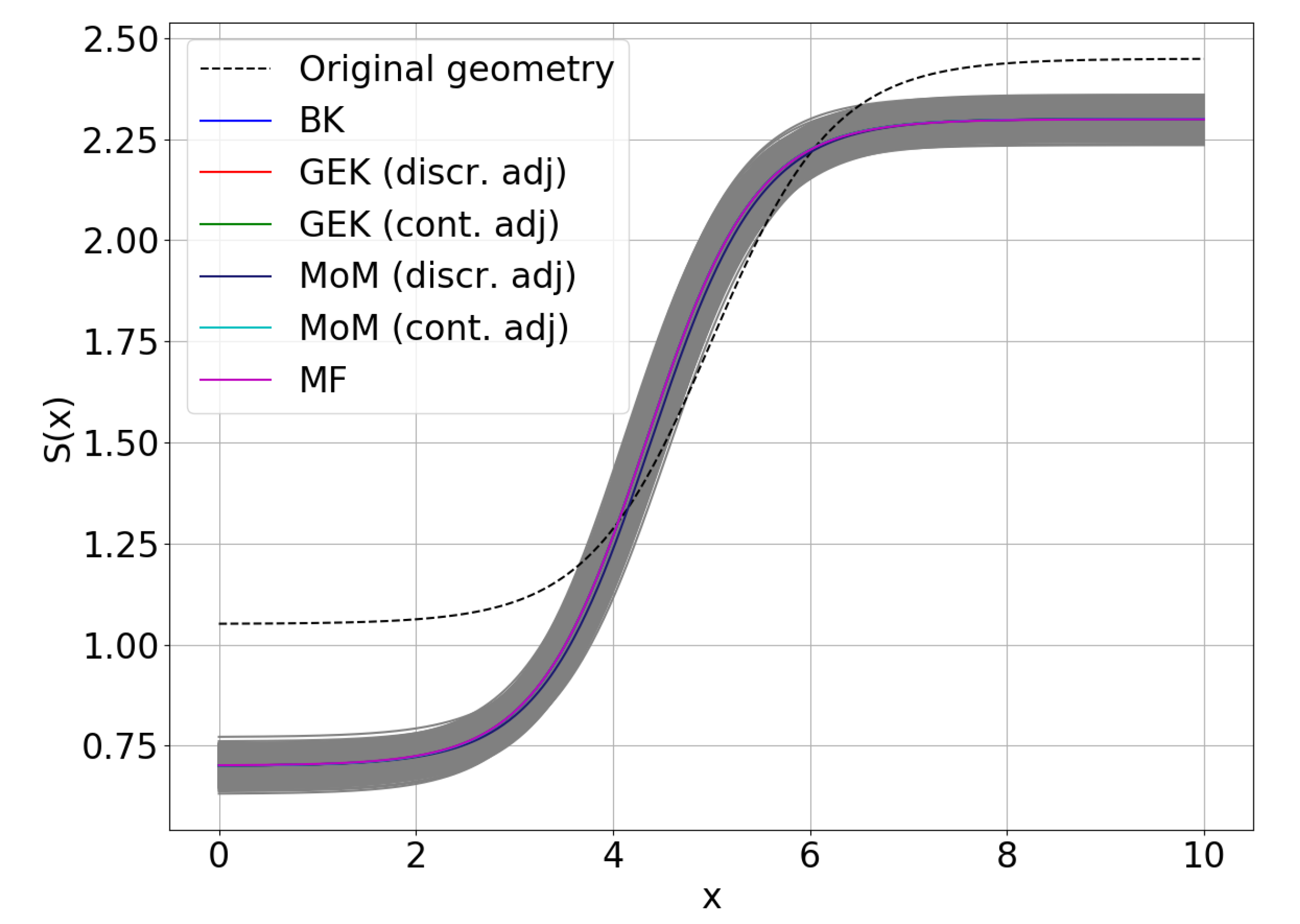
5.2. RDO Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CF(s) | Cost function(s) |
| CFD | Computational fluid dynamics |
| CoV | Coefficient of variation |
| DoE | Design of experiment |
| EI | Expected improvement |
| MOEI | Multi-objective expected improvement |
| BK | Bayesian kriging |
| GEK | Gradient enhanced kriging |
| GP | Gaussian process |
| HF | High fidelity |
| LF | Low fidelity |
| MC | Monte Carlo |
| LHS | Latin hypercube sampling |
| MF | Multi-fidelity |
| MoM | Method of moments |
| NSGAII | Non-dominated sorting genetic algorithm II |
| MOGA | Multi-objective genetic algorithm |
| SMOGA | Surrogate-based multi-objective genetic algorithm |
| QoI(s) | Quantity(ies) of interest |
| RDO | Robust design optimization |
| UQ | Uncertainty quantification |
Appendix A. Calculation of the Gradient from CFD Codes
- is a vector of the control/design variables of dimension , which parametrizes the problem.
- is a vector of state variables depending on with dimension .
Appendix A.1. Discrete Adjoint
Appendix A.2. Continuous Adjoint
Appendix A.3. Discrete and Continuous Adjoint Validation
| Quantity | Finite Differences | Discrete Adjoint | Error % |
|---|---|---|---|
| 341,296 | 341,302 | 0.002% | |
| −854,462 | −854,564 | 0.012% | |
| −2,473,058 | −2,473,429 | 0.015% | |
| 497,319 | 497,371 | 0.010% |
| Quantity | Finite Differences | Continuous Adjoint | Error % |
|---|---|---|---|
| 341,296 | 341,313 | 0.005% | |
| −854,462 | −854,609 | 0.017% | |
| −2,473,058 | −2,473,571 | 0.021% | |
| 497,319 | 497,401 | 0.016% |
References
- Beyer, H.G.; Sendhoff, B. Robust optimization—A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Taguchi, G. System of Experimental Design: Engineering Methods to Optimize Quality and Minimize Costs; UNIPUB/Kraus International Publications: Millwood, NY, USA, 1987. [Google Scholar]
- Maliki, M.; Sudret, B.; Bourinet, J.; Guillaume, B. Quantile-based optimization under uncertainties using adaptive Kriging surrogate models. Struct. Multidiscip. Optim. 2016, 54, 1403–1421. [Google Scholar] [CrossRef]
- Razaaly, N.; Persico, G.; Gori, G.; Congedo, P.M. Quantile-based robust optimization of a supersonic nozzle for organic rankine cycle turbines. Appl. Math. Model. 2020, 82, 802–824. [Google Scholar] [CrossRef]
- Cook, L.; Jarrett, J. Horsetail matching: A flexible approach to optimization under uncertainty. Eng. Optim. 2018, 50, 549–567. [Google Scholar] [CrossRef]
- Deb, K. Optimization for Engineering Design—Algorithms and Examples, 2nd ed.; PHI Learning Private Limited: New Delhi, India, 2012; pp. 1–421. [Google Scholar]
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; The MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Congedo, P.; Hercus, S.J.; Cinnella, P.; Corre, C. Efficient robust optimization techniques for uncertain dense gas flows. In Proceedings of the An ECCOMAS Thematic Conference, Antalya, Turkey, 23–25 May 2011. [Google Scholar]
- Bufi, E.A.; Cinnella, P. Robust optimization of supersonic ORC nozzle guide vanes. J. Phys. Conf. Ser. 2017, 821, 012014. [Google Scholar] [CrossRef]
- Cinnella, P.; Bufi, E. Robust optimization using nested Kriging surrogates: Application to supersonic ORC nozzle guide vanes. Ercoftac Bull. 2017, 110, 89. [Google Scholar]
- Congedo, P.M.; Corre, C.; Martinez, J.M. Shape optimization of an airfoil in a BZT flow with multiple-source uncertainties. Comput. Methods Appl. Mech. Eng. 2011, 200, 216–232. [Google Scholar] [CrossRef]
- Cinnella, P.; Hercus, S.J. Robust optimization of dense gas flows under uncertain operating conditions. Comput. Fluids 2010, 39, 1893–1908. [Google Scholar] [CrossRef]
- Congedo, P.; Corre, C.; Martinez, J.M. A simplex-based numerical framework for simple and efficient robust design optimization. Comput. Optim. Appl. 2013, 56, 231–251. [Google Scholar] [CrossRef]
- Hazelton, M.L. Methods of Moments Estimation. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 816–817. [Google Scholar] [CrossRef]
- Jameson, A.; Martinelli, L.; Pierce, N. Optimum Aerodynamic Design Using the Navier–Stokes Equations. Theor. Comput. Fluid Dyn. 1998, 10, 213–237. [Google Scholar] [CrossRef]
- Giles, M.B.; Pierce, N.A. An Introduction to the Adjoint Approach to Design. Flow Turbul. Combust. 2000, 65, 393–415. [Google Scholar] [CrossRef]
- Cinnella, P.; Pini, M. Hybrid Adjoint-based Robust Optimization Approach for Fluid-Dynamics Problems. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar] [CrossRef]
- Papoutsis-Kiachagias, E.M.; Papadimitriou, D.I.; Giannakoglou, K.C. Robust design in aerodynamics using third-order sensitivity analysis based on discrete adjoint. Application to quasi-1D flows. Int. J. Numer. Methods Fluids 2012, 69, 691–709. [Google Scholar] [CrossRef]
- Papadimitriou, D.I.; Giannakoglou, K.C. Third-order sensitivity analysis for robust aerodynamic design using continuous adjoint. Int. J. Numer. Methods Fluids 2013, 71, 652–670. [Google Scholar] [CrossRef]
- Papadimitriou, D.I.; Papadimitriou, C. Aerodynamic shape optimization for minimum robust drag and lift reliability constraint. Aerosp. Sci. Technol. 2016, 55, 24–33. [Google Scholar] [CrossRef]
- Padulo, M.; Campobasso, S.; Guenov, M.D. Comparative Analysis of Uncertainty Propagation Methods for Robust Engineering Design. In Proceedings of the DS 42: Proceedings of ICED 2007, the 16th International Conference on Engineering Design, Paris, France, 28–31 July 2007; p. DS42_P_158. [Google Scholar]
- Chung, H.S.; Alonso, J.J. Using Gradients to Construct Cokriging Approximation Models for High-Dimensional Design Optimization Problems. In Proceedings of the 40th AIAA Aerospace Sciences Meeting Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Laurenceau, J.; Sagaut, P. Building Efficient Response Surfaces of Aerodynamic Functions with Kriging and Cokriging. AIAA J. 2008, 46, 498–507. [Google Scholar] [CrossRef]
- Dwight, R.P.; Han, Z.H. Efficient Uncertainty Quantification Using Gradient-Enhanced Kriging. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. American Institute of Aeronautics and Astronautics, Structures, Structural Dynamics, and Materials and Co-located Conferences, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar] [CrossRef]
- Hercus, S.J.; Cinnella, P. Robust shape optimization of uncertain dense gas flows through a plane turbine cascade. In Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference, American Society of Mechanical Engineers, Hamamatsu, Japan, 24–29 July 2011; pp. 1739–1749. [Google Scholar]
- Cinnella, P.; Congedo, P. Optimal airfoil shapes for viscous transonic flows of Bethe–Zel’dovich–Thompson fluids. Comput. Fluids 2008, 37, 250–264. [Google Scholar] [CrossRef]
- Wang, X.; Hirsch, C.; Liu, Z.; Kang, S.; Lacor, C. Uncertainty-based robust aerodynamic optimization of rotor blades. Int. J. Numer. Methods Eng. 2013, 94, 111–127. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K.; Gunzburger, M. Survey of Multifidelity Methods in Uncertainty Propagation, Inference, and Optimization. SIAM Rev. 2018, 60, 550–591. [Google Scholar] [CrossRef]
- Giselle Fernández-Godino, M.; Park, C.; Kim, N.H.; Haftka, R.T. Issues in Deciding Whether to Use Multifidelity Surrogates. AIAA J. 2019, 57, 2039–2054. [Google Scholar] [CrossRef]
- Choi, S.; Alonso, J.; Kroo, I. Multi-Fidelity Design Optimization Studies for Supersonic Jets Using Surrogate Management Frame Method. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar] [CrossRef]
- Parussini, L.; Venturi, D.; Perdikaris, P.; Karniadakis, G. Multi-fidelity Gaussian process regression for prediction of random fields. J. Comput. Phys. 2017, 336, 36–50. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Shah, H.; Hosder, S.; Koziel, S.; Tesfahunegn, Y.; Leifsson, L. Multi-fidelity robust aerodynamic design optimization under mixed uncertainty. Aerosp. Sci. Technol. 2015, 45, 17–19. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Rozza, G.; Huynh, D.B.P.; Patera, A.T. Reduced Basis Approximation and a Posteriori Error Estimation for Affinely Parametrized Elliptic Coercive Partial Differential Equations. Arch. Comput. Methods Eng. 2008, 15, 229–275. [Google Scholar] [CrossRef]
- Antoulas, A.C.; Beattie, C.A.; Gugercin, S. Interpolatory Model Reduction of Large-Scale Dynamical Systems. In Efficient Modeling and Control of Large-Scale Systems; Mohammadpour, J., Grigoriadis, K.M., Eds.; Springer: Boston, MA, USA, 2010; pp. 3–58. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Ng, L.W.T.; Willcox, K.E. Multifidelity approaches for optimization under uncertainty. Int. J. Numer. Methods Eng. 2014, 100, 746–772. [Google Scholar] [CrossRef]
- Leusink, D.; Alfano, D.; Cinnella, P. Multi-Fidelity Optimization Strategy for the Industrial Aerodynamic Design of Helicopter Rotor Blades. Aerosp. Sci. Technol. 2015, 42, 136–147. [Google Scholar] [CrossRef]
- Fusi, F.; Guardone, A.; Quaranta, G.; Congedo, P. Multifidelity Physics-Based Method for Robust Optimization Applied to a Hovering Rotor Airfoil. AIAA J. 2015, 53, 3448–3465. [Google Scholar] [CrossRef]
- Lewis, R.; Nash, S. A multigrid approach to the optimization of systems governed by differential equations. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000. [Google Scholar] [CrossRef]
- Meliani, M.; Bartoli, N.; Lefebvre, T.; Bouhlel, M.A.; Martins, J.; Morlier, J. Multi-fidelity efficient global optimization: Methodology and application to airfoil shape design. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Forrester, A.I.; Bressloff, N.W.; Keane, A.J. Optimization using surrogate models and partially converged computational fluid dynamics simulations. Proc. R. Soc. Math. Phys. Eng. Sci. 2006, 462, 2177–2204. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S.; Zimmermann, R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
- Zhang, Y.; Kim, N.H.; Park, C.; Haftka, R.T. Multifidelity Surrogate Based on Single Linear Regression. AIAA J. 2018, 56, 4944–4952. [Google Scholar] [CrossRef]
- Forrester, A.I.; Sóbester, A.; Keane, A.J. Multi-fidelity optimization via surrogate modeling. Proc. R. Soc. Math. Phys. Eng. Sci. 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- March, A.; Willcox, K.; Wang, Q. Gradient-based multifidelity optimisation for aircraft design using Bayesian model calibration. Aeronaut. J. 2011, 115, 729–738. [Google Scholar] [CrossRef]
- Gratiet, L.L.; Cannamela, C. Cokriging-Based Sequential Design Strategies Using Fast Cross-Validation Techniques for Multi-Fidelity Computer Codes. Technometrics 2015, 57, 418–427. [Google Scholar] [CrossRef]
- Park, C.; Haftka, R.T.; Kim, N.H. Remarks on multi-fidelity surrogates. Struct. Multidiscip. Optim. 2017, 55, 1029–1050. [Google Scholar] [CrossRef]
- Gano, S.E.; Renaud, J.E.; Sanders, B. Hybrid Variable Fidelity Optimization by Using a Kriging-Based Scaling Function. AIAA J. 2005, 43, 2422–2433. [Google Scholar] [CrossRef]
- Zheng, J.; Shao, X.; Gao, L.; Jiang, P.; Li, Z. A hybrid variable-fidelity global approximation modeling method combining tuned radial basis function base and kriging correction. J. Eng. Des. 2013, 24, 604–622. [Google Scholar] [CrossRef]
- Fischer, C.C.; Grandhi, R.V.; Beran, P.S. Bayesian Low-Fidelity Correction Approach to Multi-Fidelity Aerospace Design. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Keane, A.J.; Voutchkov, I. Robust design optimization using surrogate models. J. Comput. Des. Eng. 2020, 7, 44–55. [Google Scholar] [CrossRef]
- Serafino, A.; Obert, B.; Hagi, H.; Cinnella, P. Assessment of an Innovative Technique for the Robust Optimization of Organic Rankine Cycles. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Loeppky, J.; Socks, J.; Welch, N. Choosing the sample size of a computer experiment. a practical guide. Technometrics 2009, 137, 366–378. [Google Scholar] [CrossRef]
- De Baar, J.H.S.; Dwight, R.P.; Bijl, H. Improvements to Gradient-Enhanced Kriging Using a Bayesian Interpretation. IJUQ 2014, 4, 205–223. [Google Scholar] [CrossRef]
- Le Gratiet, L. Multi-Fidelity Gaussian Process Regression for Computer Experiments. Ph.D. Thesis, Université Paris-Diderot—Paris VII, Paris, France, 2013. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Wikle, C.K.; Berliner, L.M. A Bayesian tutorial for data assimilation. Phys. Nonlinear Phenom. 2007, 230, 1–16. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Constantinescu, E.M.; Anitescu, M. Physics-Based Covariance Models for Gaussian Processes with Multiple Outputs. Int. J. Uncertain. Quantif. 2013, 3, 47–71. [Google Scholar] [CrossRef]
- De Baar, J.H.S. Stochastic Surrogates for Measurements and Computer Models of Fluids. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Walters, R.; Huyse, L. Uncertainty Analysis for Fluid Mechanics with Applications; NASA Langley Research Center: Hampton, VA, USA, 2002. [Google Scholar]
- Archetti, F.; Candelieri, A. Bayesian Optimization and Data Science; Springer: Berlin, Germany, 2019. [Google Scholar]
- Rojas-Gonzalez, S.; Van Nieuwenhuyse, I. A survey on kriging-based infill algorithms for multiobjective simulation optimization. Comput. Oper. Res. 2020, 116, 104869. [Google Scholar] [CrossRef]
- Močkus, J. On bayesian methods for seeking the extremum. In Optimization Techniques IFIP Technical Conference Novosibirsk, 1–7 July 1974; Marchuk, G.I., Ed.; Springer: Berlin/Heidelberg, Germany, 1975; pp. 400–404. [Google Scholar]
- Dwight, R.; De Baar, J.; Azijli, I. A tutorial on adaptive surrogate modeling. In Introduction to Optimization and Multidisciplinary Design in Aeronautics and Turbomachinery, 7–11 May 2012; Marchuk, G.I., Ed.; Von Karman Institute: Rhode-St-Genèse, Belgium, 2012. [Google Scholar]
- Keane, A.J. Statistical Improvement Criteria for Use in Multiobjective Design Optimization. AIAA J. 2006, 44, 879–891. [Google Scholar] [CrossRef]
- Sobol, I. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Thévenin, D.; Janiga, G. Optimization and Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germnay, 2008. [Google Scholar]
- Hascoët, L.; Pascual, V. The Tapenade Automatic Differentiation tool: Principles, Model, and Specification. ACM Trans. Math. Softw. 2013, 39, 1–43. [Google Scholar] [CrossRef]

| Quantity | pdf Distribution | Distribution Parameters |
|---|---|---|
| a | Gaussian | [1.5–2.0], |
| b | Gaussian | [0.6–0.8], |
| c | Gaussian | [0.7–0.9], |
| d | Gaussian | [3.9–4.1], |
| Uniform | [0.90–1.10] | |
| Uniform | [1.39–1.41] |
| Design Parameter | |
|---|---|
| a | ∼ |
| b | ∼ |
| c | ∼ |
| d | ∼ |
| UQ Method | CFD Solves | Adjoint Solves | err% | err % | Time (s) | ||
|---|---|---|---|---|---|---|---|
| MC | 1.0 × 10 | 0 | 3.508 | 0.6724 | - | 0.0% | 3.0 × 10 |
| BK | 60 | 0 | 3.507 | 0.6724 | −0.03% | 0.0% | 1.8 × 10 |
| GEK (discrete adjoint) | 15 | 15 | 3.506 | 0.6724 | −0.05% | 0.0% | 9.0 × 10 |
| GEK (continuous adjoint) | 15 | 15 | 3.467 | 0.6972 | −1.16% | 3.69% | 6.8 × 10 |
| MoM (discrete adjoint) | 1 | 1 | 3.451 | 0.6464 | −1.63% | −3.87% | 6.0 × 10 |
| MoM (continuous adjoint) | 1 | 1 | 3.451 | 0.6757 | −1.63% | 0.49% | 4.5 × 10 |
| UQ Method | E[a] | E[b] | E[c] | E[d] | E[J] | var[J] | Optimization Time (h) |
|---|---|---|---|---|---|---|---|
| BK | 1.500000 | 0.800000 | 0.900000 | 3.900000 | 0.28509 | 0.08545 | ∼20 |
| GEK (discrete adjoint) | 1.500002 | 0.799998 | 0.900000 | 3.900000 | 0.28771 | 0.08368 | ∼10 |
| GEK (continuous adjoint) | 1.500000 | 0.799999 | 0.900000 | 3.900000 | 0.28743 | 0.08416 | ∼8 |
| MoM (discrete adjoint) | 1.500042 | 0.799961 | 0.898917 | 3.940293 | 0.28514 | 0.08465 | ∼0.7 |
| MoM (continuous adjoint) | 1.500012 | 0.799993 | 0.899999 | 3.900004 | 0.28815 | 0.08502 | ∼0.5 |
| MF model | 1.500000 | 0.799205 | 0.899942 | 3.900006 | 0.28501 | 0.08471 | ∼2.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serafino, A.; Obert, B.; Cinnella, P. Multi-Fidelity Gradient-Based Strategy for Robust Optimization in Computational Fluid Dynamics. Algorithms 2020, 13, 248. https://doi.org/10.3390/a13100248
Serafino A, Obert B, Cinnella P. Multi-Fidelity Gradient-Based Strategy for Robust Optimization in Computational Fluid Dynamics. Algorithms. 2020; 13(10):248. https://doi.org/10.3390/a13100248
Chicago/Turabian StyleSerafino, Aldo, Benoit Obert, and Paola Cinnella. 2020. "Multi-Fidelity Gradient-Based Strategy for Robust Optimization in Computational Fluid Dynamics" Algorithms 13, no. 10: 248. https://doi.org/10.3390/a13100248
APA StyleSerafino, A., Obert, B., & Cinnella, P. (2020). Multi-Fidelity Gradient-Based Strategy for Robust Optimization in Computational Fluid Dynamics. Algorithms, 13(10), 248. https://doi.org/10.3390/a13100248





