A Compact FEM Implementation for Parabolic Integro-Differential Equations in 2D

Abstract

Although two-dimensional (2D) parabolic integro-differential equations (PIDEs) arise in many physical contexts, there is no generally available software that is able to solve them numerically. To remedy this situation, in this article, we provide a compact implementation for solving 2D PIDEs using the finite element method (FEM) on unstructured grids. Piecewise linear finite element spaces on triangles are used for the space discretization, whereas the time discretization is based on the backward-Euler and the Crank–Nicolson methods. The quadrature rules for discretizing the Volterra integral term are chosen so as to be consistent with the time-stepping schemes; a more efficient version of the implementation that uses a vectorization technique in the assembly process is also presented. The compactness of the approach is demonstrated using the software Matrix Laboratory (MATLAB). The efficiency is demonstrated via a numerical example on an L-shaped domain, for which a comparison is possible against the commercially available finite element software COMSOL Multiphysics. Moreover, further consideration indicates that COMSOL Multiphysics cannot be directly applied to 2D PIDEs containing more complex kernels in the Volterra integral term, whereas our method can. Consequently, the subroutines we present constitute a valuable open and validated resource for solving more general 2D PIDEs.

1. Introduction

Parabolic integro-differential equations (PIDEs) arise in various physical contexts, such as heat conduction in materials with memory [1,2,3], the compression of poro-viscoelastic media [4], nuclear reactor dynamics [5], epidemic phenomena in biology [6] and drug absorption/release [7,8]. Existing and unique results from such kinds of problems can be found in [9,10,11,12].

Inevitably, such equations have to be solved numerically and various approaches have been developed for this, such as spectral methods, spline and collocation, the method of lines and finite-element methods [13,14,15,16,17,18,19,20,21]. Amongst these, one of the most attractive is arguably the finite-element method (FEM), since it can be applied to irregularly-shaped domains in higher dimensions; moreover, convergence (both a priori and a posteriori) analysis for such problems is already well-established, and for this one may refer to [9,10,12,22,23,24,25,26,27,28]. As regards existing software platforms which could be used for a finite-element implementation without having to resort to lengthy programming from first principles, the main choices are freefem++ [29], deal.II [30], iFEM [31], FEniCS [32], DUNE [33], FEATool [34], MATLAB’s Partial Differential Equation Toolbox [35] and COMSOL Multiphysics [36]; however, it is not immediately obvious how to solve PIDEs with any of these. This is perhaps surprising in the case of MATLAB, which has become increasingly popular in recent years for the numerical solutions of various partial differential equations (PDEs) in structural mechanics and heat transfer [37,38,39,40,41,42,43,44,45,46,47], and has proven to be an excellent tool for academic education in general [40].

Against that background, the purpose of this article is to provide a compact formulation for solving PIDEs in two spatial dimensions (2D) using FEM on unstructured grids (we made the resulting software, which we programmed in MATLAB, openly available). This is done by extending the already available FEM formulations for PDEs [40,43,44,48,49] to PIDEs. In particular, we:

• Use piecewise linear finite element spaces on triangles for the space discretization;
• Vase the time discretizations on the backward-Euler and the Crank–Nicolson methods;
• Choose the quadrature rules for discretizing the Volterra integral term so as to be consistent with the time-stepping schemes.

In addition, we demonstrate that for PDEs, vectorization techniques can be used to speed up the sets of code for PIDEs. Importantly, these sets of code can be easily extended to more complex geometries, and to PIDEs with different kernels in the Volterra integral term. A comparison with results obtained using COMSOL Multiphysics for a test example shows that our method is competitive. Moreover, further consideration indicates that COMSOL Multiphysics cannot be directly applied to 2D PIDEs containing more complex kernels in the Volterra integral term, whereas our method can.

The rest of the paper is organized as follows. The model problem and its weak formulation are described in Section 2. The discretization is sketched in Section 3. The data representation of the triangulation is described in Section 4, together with the discrete space. The assembly of the stiffness matrix, mass matrix and load vector are presented in Section 5. Improved pseudo-codes using vectorization is presented in Section 6, and an implementation in MATLAB is discussed in Section 7. In Section 8, a comparison of the results obtained using the different sets of code is presented; results obtained using COMSOL Multiphysics are also compared. Conclusions are drawn in Section 9.

2. Model Problem and Weak Formulation

Given a Lebesgue measurable set $\Omega$, we denote by $L^p(\Omega ),1\le p\le \infty$ the Lebesgue spaces. When $p=2$, the space $L^2(\Omega )$ is equipped with an inner product $\langle ·,·\rangle$. For an integer $m>0$, we use the standard notation for Sobolev spaces $W^{m,p}\left(\omega \right)$ with $1\le p\le \infty$. When $p=2$, we denote $W^{m,2}(\Omega )$ by $H^m(\Omega )$. The function space $H_0^1(\Omega )$ consists of elements from $H^1(\Omega )$ that vanish on the boundary of $\Omega$, where the boundary values are to be interpreted in the sense of a trace.

Consider the following initial-boundary value problem for a linear PIDE of the form

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial t}(\mathit{x},t)+\mathcal{A}u(\mathit{x},t)& ={\int }_0^t\mathcal{B}(t,s)u(\mathit{x},s)\mathrm{d}s+f(\mathit{x},t),(\mathit{x},t)\in \Omega \times (0,T],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill u(\mathit{x},t)& =0,(\mathit{x},t)\in \partial \Omega \times [0,T],\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill u(\mathit{x},0)& =u_0\left(\mathit{x}\right),\mathit{x}\in \Omega .\hfill \end{array}$$

(3)

Here, $0<T<\infty$ and $\Omega \subset {\mathbb{R}}^2$ is a bounded Lipschitz domain with boundary $\partial \Omega$. Further, $\mathcal{A}u(\mathit{x},t)=-\Delta u(\mathit{x},t)$ and

$$\mathcal{B}(t,s)u(\mathit{x},s)=-\nabla ·\left(B\right(t,s)\nabla u(\mathit{x},s\left)\right),$$

(4)

where $\Delta$ denotes the Laplacian and ∇ denotes the spatial gradient. We assume that the coefficient matrix $B(t,s)=\left\{b_{ij}(\mathit{x};t,s)\right\}$ is $2\times 2$ in ${L^{\infty }(\Omega )}^{2\times 2}$. If we assume the initial function $u_0\left(\mathit{x}\right)$ to be in $H^2(\Omega )\cap H_0^1(\Omega )$, the source term $f(\mathit{x},t)$ to be in $L^2(0;T;L^2(\Omega ))$ and

$$\underset{\overline{\Omega }\times \{0\le s\le t\le T\}}{max}\left|\frac{\partial }{\partial x}{b}_{i,j}(x;t,s)\right|<\infty ,$$

then the problem (1) admits a unique solution

$$u\in L^2(0,T;H^2(\Omega )\cap H_0^1(\Omega ))\cap H^1(0,T;L^2(\Omega )).$$

The existence results are discussed in detail in Chapter 2 of [9]. For regularity and stability results of such problems, please refer to [10,28].

Let $a(·,·):H_0^1(\Omega )\times H_0^1(\Omega )\to \mathbb{R}$ be the bilinear form corresponding to the operator $\mathcal{A}$ defined by

$$a(\varphi ,\psi ):=\langle \nabla \varphi ,\nabla \psi \rangle \forall \varphi ,\psi \in H_0^1(\Omega ).$$

Similarly, let $b(t,s;·,·)$ be the bilinear form corresponding to the operator $\mathcal{B}(t,s)$ defined on $H_0^1(\Omega )\times H_0^1(\Omega )$ by

$$b(t,s;\varphi \left(s\right),\psi ):=\langle B(t,s)\nabla \varphi \left(s\right),\nabla \psi \rangle \forall \varphi \left(s\right),\psi \in H_0^1(\Omega ).$$

Then, the weak formulation of the problem (1) may be stated as follows: find $u:[0,T]\to H_0^1(\Omega )$ such that, for all $t\in (0,T]$,

$$\begin{array}{cc}\hfill {\int }_{\Omega }\frac{\partial u}{\partial t}\varphi \mathrm{d}{\mathit{x}}^{\prime }+a(u,\varphi )& ={\int }_0^{t}b(t,s;u(s),\varphi )\mathrm{d}s+{\int }_{\Omega }f\varphi \mathrm{d}{\mathit{x}}^{\prime }\forall \varphi \in H_0^1(\Omega ),\hfill \\ \hfill u(·,0)& =u_0.\hfill \end{array}$$

(5)

3. Galerkin Discretizations

Let $\mathcal{T}$ denote a regular partition of the domain $\Omega \in {\mathbb{R}}^2$ into disjoint triangles K of diameter $h_K$ such that:

• ${\cup }_{K_i\in \mathcal{T}}\overline{K_i}=\overline{\Omega }$, and any pair of triangles intersect along a complete edge, at a vertex, or not at all;
• No vertex of any triangle lies on the interior of a side of another triangle.

Let $\mathbb{V}$ be the finite element space defined by

$$\mathbb{V}:=H_0^1(\Omega )\cap \{\varphi \in C\left(\overline{\Omega }\right):\varphi {|}_K\in {\mathbb{P}}_1\forall K\in {\mathcal{T}}_h\},$$

where ${\mathbb{P}}_1$ is the space of polynomials in d variables of degree at most 1.

With $\mathcal{N}=\{z_1,\cdots ,z_M\}$ as the set of nodes of $\mathcal{T}$, we consider the nodal basis $\mathcal{B}=\{{\varphi }_1,\cdots ,{\varphi }_M\}$, where the hat function ${\varphi }_l\in {\mathbb{P}}_1$ is characterized by ${\varphi }_l\left(z_k\right)={\delta }_{kl}$, where ${\delta }_{kl}$ is the Kronecker delta.

Let $0=t_0<t_1<\dots <t_N=T$ be a partition of $[0,T]$ with ${\tau }_n:=t_n-t_{n-1}$. Set $f^n(·)=f(·,t_n)$ for $t=t_n,n\in [0,1,\dots ,N]$. Now, for $n=1,2,\cdots ,N$, we define

$$\partial v^n:=\frac{v^n-v^{n-1}}{{\tau }_n},t_{n-1/2}:=\frac{t_n+t_{n-1}}{2}\mathrm{and}{v}^{n-1/2}:=\frac{v^n+v^{n-1}}{2}.$$

In this article, we consider uniform time steps, i.e., $\tau ={\tau }_1=\dots ={\tau }_N$.

3.1. Backward-Euler Scheme

Let $I_h$ be the Lagrange interpolant corresponding to $\mathbb{V}$. Then, the fully discrete backward-Euler scheme may be stated as follows: given $U^0$, where $U^0=I_h{u}_0$, find $U^n\in \mathbb{V},n\in [1:N]$ such that

$${\int }_{\Omega }\partial U^n\varphi \mathrm{d}{\mathit{x}}^{\prime }+a(U^n,\varphi )={\sigma }^n\left(b(t_n;U,\varphi )\right)+{\int }_{\Omega }{f}^n\varphi \mathrm{d}{\mathit{x}}^{\prime },\forall \varphi \in \mathbb{V},$$

(6)

where

$${\sigma }^n\left(b(t_n;v,\varphi )\right)=\langle \sum _{j=0}^{n-1}{\tau }_{j+1}B(t_n,t_j)\nabla v\left(t_j\right),\nabla \varphi \rangle ,$$

(7)

if the left rectangular rule is used to discretize the integral term, or 

$${\sigma }^n\left(b(t_n;v,\varphi )\right)=\langle \sum _{j=1}^n{\tau }_{j}B(t_n,t_j)\nabla v\left(t_j\right),\nabla \varphi \rangle ,$$

(8)

if the right rectangular rule is used. In any case, both are consistent with the backward-Euler scheme and the order of accuracy is same.

The discrete problem (6) becomes: find ${\mathbf{U}}^n={\sum }_{j=1}^{M}u(z_j,t_n){\varphi }_j\left(\mathit{x}\right)\in {\mathbb{R}}^m$ such that

$$(\mathbf{M}+\tau \mathbf{A}){\mathbf{U}}^n=\mathbf{M}{\mathbf{U}}^{n-1}+{\tau }^2\mathbf{A}(B(t_n,t_0){\mathbf{U}}^0+\dots +B(t_n,t_{n-1}){\mathbf{U}}^{n-1})+\tau {\mathbf{b}}^n,$$

(9)

where the mass matrix $\mathbf{M}$, the stiffness matrix $\mathbf{A}$ and the load vector ${\mathbf{b}}^n$ are given by

$$\begin{array}{cc}\hfill \mathbf{M}& =\left\{M_{i,j}\right\}={\int }_{\Omega }{\varphi }_j{\varphi }_i\mathrm{d}{\mathit{x}}^{\prime },\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \mathbf{A}& =\left\{A_{i,j}\right\}={\int }_{\Omega }\nabla {\varphi }_j·\nabla {\varphi }_i\mathrm{d}{\mathit{x}}^{\prime },\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\mathbf{b}}^n& =\left\{b_i^n\right\}={\int }_{\Omega }{f}^n{\varphi }_i\mathrm{d}{\mathit{x}}^{\prime },\hfill \end{array}$$

(12)

respectively.

3.2. Crank–Nicolson Scheme

We now state the Crank–Nicolson scheme as follows: given $U^0$, where $U^0=I_h{u}_0$, find $U^n\in \mathbb{V},n\in [1:N]$ such that

$${\int }_{\Omega }\partial U^n\varphi \mathrm{d}{\mathit{x}}^{\prime }+a(U^{n-1/2},\varphi )={\sigma }^n\left(b(t_{n-1/2};U,\varphi )\right)+{\int }_{\Omega }{f}^{n-1/2}\varphi \mathrm{d}{\mathit{x}}^{\prime }\forall \varphi \in \mathbb{V},$$

(13)

where

$${\sigma }^n\left(b(t_{n-1/2};v,\varphi )\right):=〈\sum _{j=0}^{n-2}\frac{{\tau }_{j+1}}{2}\left[B(t_{n-1/2},t_j)\nabla v^j+B(t_{n-1/2},t_{j+1})\nabla v^{j+1}\right],\nabla \varphi 〉$$

$$+〈\frac{{\tau }_n}{4}\left[B(t_{n-1/2},t_{n-1})\nabla v^{n-1}+B(t_{n-1/2},t_{n-1/2})\nabla v^{n-1/2}\right],\nabla \varphi 〉.$$

Here, the trapezoidal rule is used to discretize the integral term in order to be consistent with the Crank–Nicolson scheme.

Using (13), we obtain the following matrix equation for the Crank–Nicolson scheme:

$$\begin{array}{cc}\hfill (\mathbf{M}+\frac{\tau }{2}\mathbf{A}-\frac{{\tau }^2}{8}B(t_{\frac{1}{2}},t_1)\mathbf{A}){\mathbf{U}}^1& =(\mathbf{M}-\frac{\tau }{2}\mathbf{A}){\mathbf{U}}^0+\frac{3{\tau }^2}{8}B(t_{\frac{1}{2}},t_0)\mathbf{A}{\mathbf{U}}^0+\tau {\widehat{b}}^1,\hfill \\ \hfill (\mathbf{M}+\frac{\tau }{2}\mathbf{A}-\frac{{\tau }^2}{8}B(t_{n-1/2},t_n)\mathbf{A}){\mathbf{U}}^n& =(\mathbf{M}-\frac{\tau }{2}\mathbf{A}){\mathbf{U}}^{n-1}+\tau {\widehat{b}}^n\hfill \\ \hfill & +\frac{{\tau }^2}{2}\mathbf{A}\left[B(t_{n-1/2},t_0){\mathbf{U}}^0+2{\displaystyle \sum _{i=1}^{n-2}}B(t_{n-1/2},t_i){\mathbf{U}}^i\right]+\frac{7{\tau }^2}{8}B(t_{n-1/2},t_{n-1})A{\mathbf{U}}^{n-1},\hfill \end{array}$$

(14)

for $n>1$ and where $\mathbf{M}$ is the mass matrix, $\mathbf{A}$ is the stiffness matrix and ${\widehat{b}}_n$ is the load vector:

$${\widehat{b}}^n=\left\{b_i\right\}={\int }_{\Omega }\frac{f^n+f^{n-1}}{2}{\varphi }_i\mathrm{d}{\mathit{x}}^{\prime }.$$

(15)

3.3. Remark on More General Boundary Conditions

Problems involving more general boundary conditions can also be addressed in a similar manner. Suppose that the domain boundary is split into two components ${\Gamma }_D$ and ${\Gamma }_N$ such that ${\Gamma }_D\cup {\Gamma }_N=\partial \Omega$ and ${\Gamma }_D\cap {\Gamma }_N=\varnothing$, assuming that ${\Gamma }_D$ is closed and has a nonzero measure. For sufficiently regular Neumann boundary data $g_N$, consider a problem posed with mixed-type boundary conditions:

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial t}(\mathit{x},t)+\mathcal{A}u(\mathit{x},t)& ={\int }_0^t\mathcal{B}(t,s)u(\mathit{x},s)ds+f(\mathit{x},t),(\mathit{x},t)\in \Omega \times (0,T],\hfill \\ \hfill u(\mathit{x},t)& =g\left(\mathit{x}\right),(\mathit{x},t)\in {\Gamma }_D\times [0,T],\hfill \\ \hfill \frac{\partial u}{\partial n}(\mathit{x},t)& =g_N\left(\mathit{x}\right),(\mathit{x},t)\in {\Gamma }_N\times [0,T],\hfill \\ \hfill u(\mathit{x},0)& =u_0\left(\mathit{x}\right),\mathit{x}\in \Omega .\hfill \end{array}$$

(16)

We assume there is a function $u_D(\mathit{x},t)\in H^1(\Omega )\mathrm{for}t\in [0,T]$ such that $u_D(\mathit{x},t)=g\left(\mathit{x}\right)\mathrm{for}\mathit{x}\in \partial \Omega ,t\in [0,T].$ Then, the weak form of this problem reads: find $u=w+u_D:[0,T]\to H_{g,{\Gamma }_D}^1(\Omega ),w\in H_{0,{\Gamma }_D}^1(\Omega )$ such that

$$\begin{array}{cc}\hfill {\int }_{\Omega }\frac{\partial w}{\partial t}\varphi \mathrm{d}{\mathit{x}}^{\prime }+a(w,\varphi )& =-{\int }_{\Omega }\frac{\partial u_D}{\partial t}\varphi \mathrm{d}{\mathit{x}}^{\prime }+{\int }_0^{t}b(t,s;w(s),\varphi )\mathrm{d}s-a(u_D,\varphi )\hfill \\ \hfill & +{\int }_0^{t}b(t,s;u_D\left(s\right),\varphi )\mathrm{d}s+{\int }_{\Omega }f\varphi \mathrm{d}{\mathit{x}}^{\prime }+{\int }_{{\Gamma }_N}{g}_N\varphi \mathrm{d}S\hfill \\ \hfill & -{\int }_0^t\left({\int }_{{\Gamma }_N}B(t,s)g_N\left(s\right)\varphi \mathrm{d}S\right)\mathrm{d}s\forall \varphi \in H_0^1(\Omega ),t\in (0,T],\hfill \\ \hfill u(·,0)& =u_0,\hfill \end{array}$$

where

$$H_{g,{\Gamma }_D}^1(\Omega ):=\{w\in H^1(\Omega ):w=g\mathrm{on}{\Gamma }_D\}$$

and

$$H_{0,{\Gamma }_D}^1(\Omega ):=\{w\in H^1(\Omega ):w=0\mathrm{on}{\Gamma }_D\}.$$

4. Data Representation

To fix ideas ahead of benchmark computations, consider the L-shaped domain $\Omega ={[-1,1]}^2\setminus [-1,0]\times [0,1]$ with a closed polygonal boundary $\Gamma ={\Gamma }_D$, as shown in Figure 1, where nodes are represented as blue squares and the exterior continuous line represents the boundary with Dirichlet boundary condition ${\Gamma }_D$; this domain was chosen as it is often used for benchmarking FEM computations [41,44,50,51].

In order to represent the relationship between node and spatial coordinates, and between elements and nodes, it is necessary to define arrays that store this information. Thus, we define the array c4n, which represents the node-coordinate relation, and the array n4e, which represents the element-node relation to generate the domain; these are given in

Table 1. Arrays c4n, n4e and dir.

c4n
1	-1.0	-1.0
2	0.0	-1.0
3	1.0	-1.0
4	-0.5	-0.5
5	0.5	-0.5
6	-1.0	0.0
7	0.0	0.0
8	1.0	0.0
9	0.5	0.5
10	0.0	1.0
11	1.0	1.0

n4e
1	1	2	4
2	2	3	5
3	3	8	5
4	8	7	5
5	7	2	5
6	7	4	2
7	4	7	6
8	6	1	4
9	6	7	9
10	9	7	11
11	9	11	10
12	9	10	6

dir
1	1	2
2	2	3
3	3	8
4	8	11
5	11	10
6	10	7
7	7	6
8	6	1

. In addition, the Dirichlet boundary conditions are represented by a data structure dir which contains nodal information; this is also given in Table 1. The first columns of the arrays c4n, n4e and dir represent the node number, element number and edge number, respectively.

5. Assembly

In this section, we assemble the stiffness matrix, the mass matrix, the load vector and the initial and boundary conditions. The assembly is standard and builds on the ideas for PDEs presented in [40,44]; however, we include it here for completeness, ensuring that the standard routines and the non-standard ones related to PIDEs are available in one location. In what follows, we take $\mathit{x}=(x,y)$ and let $(x_1,y_1),(x_2,y_2)$ and $(x_3,y_3)$ be the vertices of an element K and ${\varphi }_1,{\varphi }_2$ and ${\varphi }_3$ the corresponding local basis functions in $\mathbb{V}$. The sets of code which make use of the subroutines presented in this section are given in Appendix A.

For the sets of pseudocode that follow, we first need to establish a common notation; this is given in

Table 2. Some common functions and operations.

$\mathit{A}(:)$	All the elements of A, treated as a single column
$A(:,j)$	j-th column of A
$A(i,:)$	i-th row of A
$A==k$	Indices $(i,j)$ where $A(i,j)=k$
$A^T$	Transpose of A
$A(\alpha ,\beta )$	Entry of A at position ($\alpha$, $\beta$)
$a\leftarrow b$	Assignment
$A\ast B$	Matrix multiplication
$A.\ast B$	Element-wise multiplication
$A./B$	Element-wise division
$A\setminus B$	Return, without repeating, elements of A which are not in B
ACCUMARRAY$(x,y,s)$	Return an array with size s (vector containing the dimensions of the output).
	The values in the output are sums of the values in y having identical subscripts in x
DET$\left(A\right)$	Determinant of A
$I_d$	$d\times d$ identity matrix
NCOL$\left(A\right)$	Number of columns in A
INV$\left(A\right)$	Inverse of A
NROW$\left(A\right)$	Number of rows in A
ONES$(m,n)$	$m\times n$ matrix with all entries equal to ones
REPMAT$(A,m,n)$	Returns $m\times n$ block matrix with each block equal to A
RESHAPE$(A,m,n)$	Reshape A into $m\times n$ matrix provided $m\ast n=$ NCOL(A)*NROW$\left(A\right)$
SPARSE$(m,n)$	$m\times n$ sparse matrix of zeros
SUM$(A,k)$	Sum of elements of A along the index k
UNIQUE$\left(A\right)$	Return entries of A without repeating
ZEROS$(m,n)$	$m\times n$ matrix with all entries equal to zero
$[,]$	Horizontal concatenation
$[;]$	Vertical concatenation

.

5.1. Assembling the Stiffness Matrix

Since

$${\varphi }_j(x_k,y_k)={\delta }_{jk},j,k=1,2,3,$$

(17)

a simple calculation reveals

$${\varphi }_j(x,y)=det\left[\begin{array}{ccc}1& x& y\\ 1& x_{j+1}& y_{j+1}\\ 1& x_{j+2}& y_{j+2}\end{array}\right]/det\left[\begin{array}{ccc}1& x_j& y_j\\ 1& x_{j+1}& y_{j+1}\\ 1& x_{j+2}& y_{j+2}\end{array}\right].$$

(18)

Hence, we obtain

$$\nabla {\varphi }_j(x,y)=\frac{1}{\mathcal{K}}\left[\begin{array}{c}{y}_{j+1}-y_{j+2}\\ x_{j+2}-x_{j+1}\end{array}\right].$$

(19)

Here, the indices are to be understood modulo 3, and $\mathcal{K}$ is the area of triangle K. Thus, using (11), the entries of the stiffness matrix can be computed as

$$A_{jk}={\int }_K\nabla {\varphi }_j{(\nabla {\varphi }_k)}^T\mathrm{d}{\mathit{x}}^{\prime }=\frac{1}{\mathcal{K}}(y_{j+1}-y_{j+2},x_{j+2}-x_{j+1})\left[\begin{array}{c}{y}_{k+1}-y_{k+2}\\ x_{k+2}-x_{k+1}\end{array}\right],$$

(20)

with indices modulo 3. This can be written as

$$A=G{G}^T,G:={\left[\begin{array}{ccc}1& 1& 1\\ x_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right]}^{-1}\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 1\end{array}\right].$$

(21)

The pseudocode given in Algorithm 1 computes the local stiffness matrix contributions, based on Equations (17)–(21).

Algorithm 1 Computation of local stiffness matrix contributions.

1: procedurestima($c4n$) 2:     $d\leftarrow \mathrm{NCOL}\left(c4n\right)$ 3:     $M_1\leftarrow [\mathrm{ONES}(1,d+1);c4n^T]$ 4:     $M_2\leftarrow [\mathrm{ZEROS}(1,d);I_d]$ 5:     $G\leftarrow \mathrm{INV}\left(M_1\right)\ast M_2$ 6:     $P_1\leftarrow [\mathrm{ONES}(1,d+1);c4n^T]$ 7:     $S\leftarrow \frac{\mathrm{DET}\left(P_1\right)\ast G\ast G^T}{{\prod }_{j=1}^{d}j}$ 8:     return S 9: end procedure

Using the local contributions, one can compute the global contributions using the pseudocode given in Algorithm 2.

Algorithm 2 Computation of the global contributions.

1: procedureStiffAssemb($n4e,c4n$) 2:     $r\leftarrow \mathrm{NROW}\left(c4n\right)$ 3:     $A\leftarrow \mathrm{SPARSE}(r,r)$ 4:     for $j\leftarrow 1$ to r, do 5:         $A\left(n4e\right(j,:),n4e(j,:\left)\right)\leftarrow A\left(n4e\right(j,:),n4e(j,:\left)\right)+\mathrm{STIMA}\left(c4n\right(n4e(j,:),:\left)\right)$ 6:     end for 7:     return A 8: end procedure

5.2. Assembling the Mass Matrix

The entries of the mass matrix M can be computed as

$$M_{jk}={\int }_K{\varphi }_j{\varphi }_k\mathrm{d}{\mathit{x}}^{\prime }.$$

(22)

For triangular, piecewise affine elements, we obtain

$${\int }_K{\varphi }_j{\varphi }_k\mathrm{d}{\mathit{x}}^{\prime }=\frac{1}{24}det\left[\begin{array}{cc}{x}_2-x_1& x_3-x_1\\ y_2-y_1& y_3-y_1\end{array}\right]\left[\begin{array}{ccc}2& 1& 1\\ 1& 2& 1\\ 1& 1& 2\end{array}\right];$$

(23)

the pseudocode for M, based on Equations (22) and (23), is given in Algorithm 3.

Algorithm 3 Assembling the mass matrix.

1: procedureMassAssemb($n4e,c4n$) 2:     $r\leftarrow \mathrm{NROW}\left(c4n\right)$ 3:     $M\leftarrow \mathrm{SPARSE}(r,r)$ 4:     for $j\leftarrow 1$ to r do 5:         $X_1\leftarrow [\left[111\right];{\left(c4n(n4e(j,:),:)\right)}^T]$ 6:         $X_2\leftarrow [\left[211\right];\left[121\right];\left[112\right]]$ 7:         $M(n4e(j,:),n4e(j,:))\leftarrow M(n4e(j,:),n4e(j,:))+(\frac{1}{24}\ast \mathrm{DET}\left(X_1\right)\ast X_2)$ 8:     end for 9:     return M 10: end procedure

5.3. Assembling the Load Vector

The volume forces, which are calculated using Algorithm 4, are used for assembling the load vector. Using the value of f at the center of gravity $(x_S,y_S)$ of K, the integral ${\int }_{K}f{\varphi }_j\mathrm{d}{\mathit{x}}^{\prime }$ is approximated by

$${\int }_{K}f{\varphi }_j\mathrm{d}{\mathit{x}}^{\prime }\approx \frac{1}{6}det\left[\begin{array}{cc}{x}_2-x_1& x_3-x_1\\ y_2-y_1& y_3-y_1\end{array}\right]f(x_S,y_S).$$

(24)

In addition, the load vector contains a contribution from the integral terms containing the kernel B; this is given in Algorithm 5.

Algorithm 4 Source function.

1: proceduref($\mathit{x},t$) 2:     $VolumeForce\leftarrow (1-2\ast t).\ast {\pi }^2.\ast exp(-{\pi }^2\ast t).\ast sin(\pi .\ast \mathit{x}(:,1)).\ast sin(\pi .\ast \mathit{x}(:,2))$ 3:     return $VolumeForce$ 4: end procedure

Algorithm 5 Coefficient function in the kernel.

1: procedureintgral($t,s$) 2:     $BTS\leftarrow exp(-{\pi }^2\ast (t-s))$ 3:     return $BTS$ 4: end procedure

5.4. Boundary and Initial Conditions

The sets of pseudocode for the boundary and initial conditions given by Equations (2) and (3), respectively, are given in Algorithms 6 and 7, respectively.

Algorithm 6 Boundary conditions.

1: procedureUd($\mathbf{x},\mathbf{t}$) 2:     $DBV\left(\mathbf{x}\right(:,1)==-1)\leftarrow 0$ 3:     $DBV\left(\mathbf{x}\right(:,1)==0)\leftarrow 0$ 4:     $DBV\left(\mathbf{x}\right(:,1)==1)\leftarrow 1$ 5:     $DBV\left(\mathbf{x}\right(:,2)==-1)\leftarrow 0$ 6:     $DBV\left(\mathbf{x}\right(:,2)==0)\leftarrow 0$ 7:     $DBV\left(\mathbf{x}\right(:,2)==1)\leftarrow 0$ 8:     return $DBV$ 9: end procedure

Algorithm 7 Initial conditions.

1: procedureU0($c4n$) 2:     $\mathbf{x}\leftarrow c4n(:,1)$ 3:     $\mathbf{y}\leftarrow c4n(:,2)$ 4:     $u_0\leftarrow sin(\pi \ast \mathbf{x})\ast sin(\pi \ast \mathbf{y})$ 5:     return $u_0$ 6: end procedure

6. Improved Assembly

To improve the implementation, we present in this section an optimization of the algorithm that switches away from a looping approach towards the utilization of vector tools, available in software such as MATLAB. A brief description of these improvements follows. Similar approaches can be found in [40,43], and the sets of code supplied are modified versions of those given in [52]; they are included for completeness. The sets of pseudocode which make use of the subroutines presented in this section are given in Appendix B.

6.1. Assembling the Stiffness Matrix

The vectorization of the code for the stiffness matrix is done by using the commands SPARSE and RESHAPE, which allow us to store in the vectors I and J the indices related to the contributions of each node of each element for building the stiffness matrix A. This provides the possibility to evaluate the stiffness matrix A in one line, i.e., without a loop, as shown in Algorithm 8.

Algorithm 8 Assembling the stiffness matrix with vectorization.

1: procedureStiffAssemb($n4e,nC,area4,d21,d31,nE$) 2:     $I\leftarrow \mathrm{RESHAPE}(n4e{(:,\left[123123123\right])}^T,9\ast nE,1)$ 3:     $J\leftarrow \mathrm{RESHAPE}(n4e{(:,\left[111222333\right])}^T,9\ast nE,1)$ 4:     $a\leftarrow {(\mathrm{SUM}(d21.\ast d31,2)./area4)}^T$ 5:     $b\leftarrow {(\mathrm{SUM}(d31.\ast d31,2)./area4)}^T$ 6:     $c\leftarrow {(\mathrm{SUM}(d21.\ast d21,2)./area4)}^T$ 7:     $A\leftarrow [-2\ast a+b+c;a-b;a-c;a-b;b;-a;a-c;-a;c]$ 8:     $A\leftarrow \mathrm{SPARSE}(I,J,A(:),nC,nC)$ 9:     return A 10: end procedure

6.2. Assembling the Mass Matrix

Similarly to the previous paragraph, we can build the mass matrix M by using the SPARSE command. We remark that, in this case, the evaluation of the matrix is reduced to the calculation of only two vectors, as shown in Algorithm 9.

Algorithm 9 Assembling the mass matrix with vectorization.

1: procedureMassAssemb($nC,n4e,area$) 2:     $I\leftarrow n4e\left(\right[123123123],:)$ 3:     $J\leftarrow n4e\left(\right[111222333],:)$ 4:     $A_6\leftarrow \frac{1}{6}\ast are{a}^T$ 5:     $A_{12}\leftarrow \frac{1}{12}\ast are{a}^T$ 6:     $K_g\leftarrow [A_6;A_{12};A_{12};A_{12};A_6;A_{12};A_{12};A_{12};A_6]$ 7:     $M\leftarrow \mathrm{SPARSE}(I(:),J(:),K_g(:),nC,nC)$ 8:     return M 9: end procedure

6.3. Assembling the Load Vector

In order to assemble the right-hand side, we refer to what we have done in Section 5.3 considering the volume forces and the center of gravity. Here, however, the improvement consists of neglecting the loop by inserting the MATLAB command ACCUMARRAY, which creates an array of given size, where the values are collected through the REPMAT command, which in this case returns a $3\times 1$ array containing copies of the corresponding evaluation of the element.

6.4. Boundary and Initial Conditions

For the vectorized version also, the sets of pseudocode for the boundary and initial conditions are given in Algorithms 6 and 7, respectively.

7. Overview of an Implementation in Matlab

A minimal MATLAB implementation of the presented algorithm is available from Supplementary Materials. There are six zipfiles which contain the necessary MATLAB files therein:

• BE_LRR_unvectorized.zip (backward-Euler, left rectangular rule, unvectorized);
• BE_LRR_vectorized.zip (backward-Euler, left rectangular rule, vectorized);
• BE_RRR_unvectorized.zip (backward-Euler, right rectangular rule, unvectorized);
• BE_RRR_vectorized.zip (backward-Euler, right rectangular rule, vectorized);
• CN_unvectorized.zip (Crank–Nicolson, unvectorized);
• CN_vectorized.zip (Crank–Nicolson, vectorized).

To run the demo program, uncompress the desired zip file and run the Main.m file; this:

• Specifies the geometry;
• Computes the solution;
• Plots the solution.

In particular, the computation of the solution is carried out by SCHEME_NAME_PIDE.m, which sets the initial conditions via U0.m, and assembles the stiffness matrix and the mass matrix via StiffAssemb.m and MassAssemb.m, respectively; thereafter, solve_SCHEME_NAME.mupdates the boundary conditions via Ud.m, assembles the load vector via f.m and obtains the solution at the current time step. Furthermore, note that whilst most of the subroutines are the same in both the vectorized and unvectorized versions of the code, those for StiffAssemb.m and MassAssemb.m are necessarily slightly different, in line with the discussion in Section 5 and Section 6.

8. Numerical Results

In this section, we study a numerical example and compare the results obtained using different versions of the MATLAB-based sets of code; in addition, solutions were obtained using COMSOL Multiphysics. For the example, we consider the L-shaped domain $\Omega ={[-1,1]}^2\setminus [-1,0]\times [0,1]$ mentioned earlier; take

$$f(x,y,t)=(1-2t){\pi }^{2}u(x,y,t)$$

(25)

and

$$B(t,s)=exp(-{\pi }^2(t-s)),$$

(26)

which is a kernel that occurs in different settings in many of the references given earlier, and others [2,3,4,7,14,53,54]; this leads to the following exact solution for u:

$$u(x,y,t)=exp(-{\pi }^{2}t)sin\left(\pi x\right)sin\left(\pi y\right).$$

(27)

Figure 2a shows the exact solution to the problem, whereas Figure 2b corresponds to the backward-Euler approximation, where the left rectangular rule is applied to treat the Volterra integral term. Figure 2c,d show the solutions obtained using the backward-Euler approximation with the right rectangular rule and the Crank–Nicolson approximation with the trapezoidal rule, respectively, to treat the Volterra integral term. 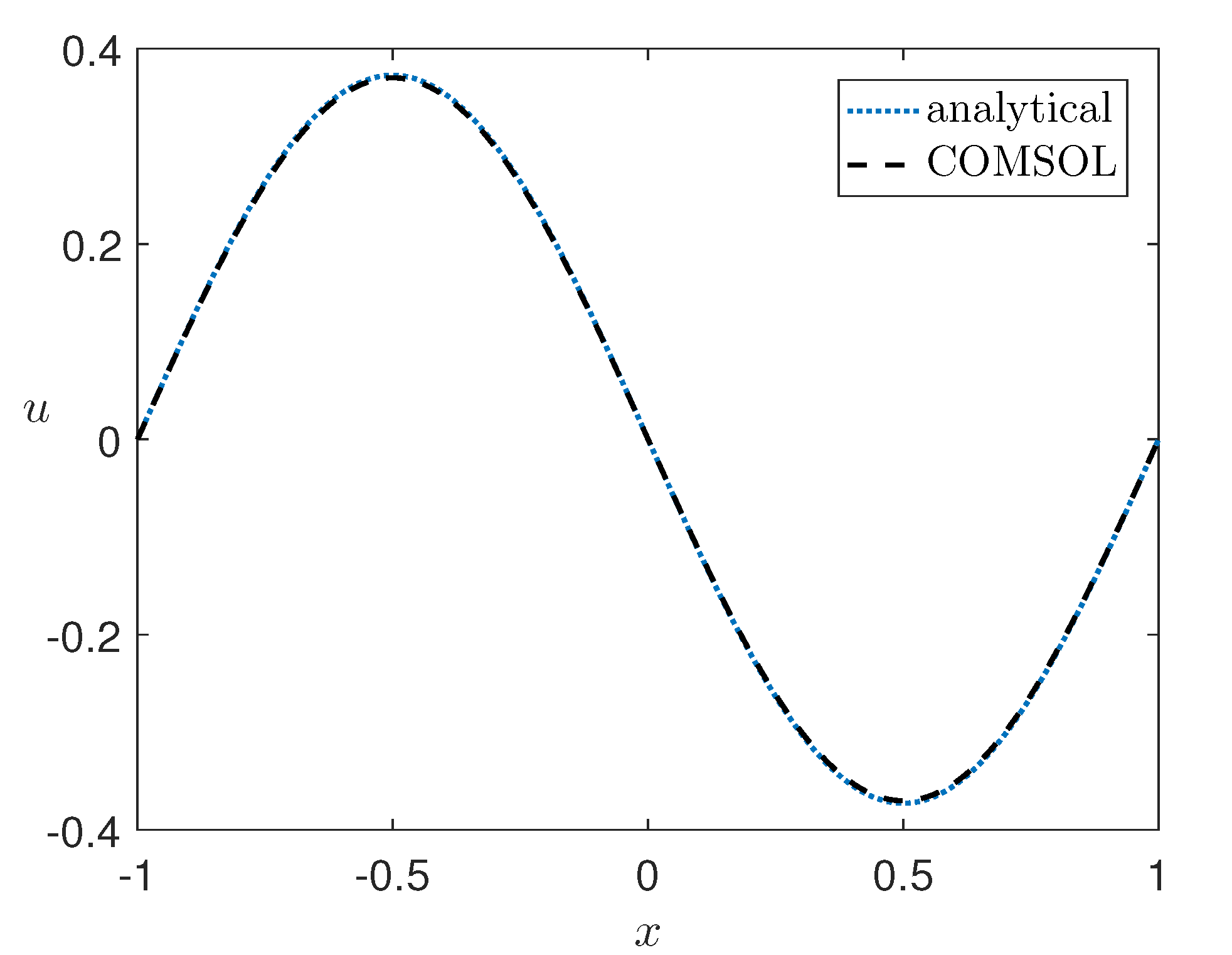In addition, Figure 3 shows a comparison of the analytical solution with the solution computed by COMSOL Multiphysics with 66142 P1 elements for $t=T,y=-0.5$, where $T=0.1$; as expected, the agreement is very good.

To illustrate the advantage of the vectorized code for each numerical scheme over the unvectorized one, which uses for loops for the assembly process, we have presented a comparison of the runtimes with respect to the number of elements, N. This is given in

Table 3. Quantitative information on the runtimes of the unvectorized and vectorized MATLAB sets of code with different numerical schemes, and the same for code from COMSOL Multiphysics, when solving the PIDE. Abbreviations: BELR, backward-Euler scheme with left rectangular rule; BERR, backward-Euler scheme with right rectangular rule; CN, Crank–Nicolson scheme with trapezoidal rule; N, number of elements; $t_{unvec}^{SCHEME}$, runtime of the unvectorized code in seconds involving loops in the assembly process, using a particular method $SCHEME$ (= BELR, BERR or CN); $t_{vec}^{SCHEME}$, runtime of the vectorized code in seconds without loops in the assembly process, using a particular method $SCHEME$; $t_C$, runtime for COMSOL Multiphysics.

h	N	${\mathit{t}}_{\mathbf{unvec}}^{\mathbf{BELR}}$$\left[\mathbf{s}\right]$	${\mathit{t}}_{\mathbf{vec}}^{\mathbf{BELR}}$$\left[\mathbf{s}\right]$	${\mathit{t}}_{\mathbf{unvec}}^{\mathbf{BERR}}$$\left[\mathbf{s}\right]$	${\mathit{t}}_{\mathbf{vec}}^{\mathbf{BERR}}$$\left[\mathbf{s}\right]$	${\mathit{t}}_{\mathbf{unvec}}^{\mathbf{CN}}$$\left[\mathbf{s}\right]$	${\mathit{t}}_{\mathbf{vec}}^{\mathbf{CN}}$$\left[\mathbf{s}\right]$	${\mathit{t}}_{\mathit{C}}$$\left[\mathbf{s}\right]$
0.2	258	0.81	0.77	0.82	0.77	0.83	0.77	0.31
0.1	978	0.98	0.81	1.00	0.81	1.04	0.82	0.55
0.05	4086	2.06	1.08	1.96	1.08	2.13	1.08	1.73
0.025	16,406	10.26	4.36	10.51	4.40	10.93	4.41	6.93
0.0125	66,142	114.40	38.04	112.86	38.24	114.42	38.36	34.13

, which also shows the runtimes for COMSOL Multiphysics. Note that all sets of code were run on an Intel Core i7 Notebook with a 1.7 GHz processor and 8 GB of RAM. We can note from Table 3 that vectorized versions of the MATLAB sets of code presented in this article on the finest mesh get close to COMSOL’s performance. Nevertheless, there are several factors behind the results. On the one hand, in the developed MATLAB sets of code, we discretize the Volterra integral term; as a result, one has to store the memory term values at all of the time discretization points. On the other hand, because of the particular form of the kernel in (26), and as explained in Appendix C, COMSOL Multiphysics does not need to evaluate the integral at all; even so, the difference in computational time is not decisive. However, and as also explained in Appendix C, we would not have been able to use COMSOL Multiphysics at all in this way if the kernel had not had a separable form, whereas the sets of code presented in this article do not have this limitation.

In addition, we define an efficiency factor, $C_{eff}$, given by $C_{eff}=t_{unvec}$/$t_{vec}$, where $t_{unvec}$ is the runtime of the unvectorized code and $t_{vec}$ is the runtime of the vectorized code; the results for this are shown in

Table 4. The efficiency factor, $C_{eff}$, for different MATLAB-based sets of code and different space meshes with a fixed time step $(\tau =0.00125)$.

h	N	${\mathit{C}}_{\mathbf{eff}}^{\mathbf{BELR}}$	${\mathit{C}}_{\mathbf{eff}}^{\mathbf{BERR}}$	${\mathit{C}}_{\mathbf{eff}}^{\mathbf{CN}}$
0.2	258	1.06	1.06	1.07
0.1	978	1.22	1.23	1.27
0.05	4086	1.91	1.82	1.97
0.025	16,406	2.35	2.39	2.48
0.0125	66,142	3.01	2.95	2.98

. From the latter, we observe that refining the mesh increases the efficiency factor $C_{eff}$. This shows that the relative performance of the vectorized code improves significantly as the number of elements is increased.

9. Conclusions

In this paper, we have presented a compact implementation using the finite-element method for solving linear PIDEs in arbitrary 2D geometries, both in terms of sets of pseudocode and in terms of a MATLAB code, which we have made openly available; we note that such a code is not available in other competing FEM software, such as freefem++ or deal.II. In addition, it was found that a vectorized version of the MATLAB code solves the model problem considered around three times more quickly than the unvectorized code on finer meshes. Furthermore, because of the particular form of the kernel in the Volterra integral term, the model problem could be represented in a form that was amenable to solution using the commercial finite-element software COMSOL Multiphysics. For this particular problem, in which the kernel has a separable form, COMSOL Multiphysics slightly outperforms even our vectorized code when using a mesh of around 66,000 elements.

Future development of this work would involve extending the sets of code to handle non-linear integral terms [55] and to three dimensions.