Abstract
Many sharing-economy platforms operate as follows. Owners list the availability of resources, prices, and contract-length limits. Customers propose contract start times and lengths. The owners decide immediately whether to accept or decline each proposal, even if the contract is for a future date. Accepted proposals generate revenue. Declined proposals are lost. At any decision epoch, the owner has no information regarding future proposals. The owner seeks easy-to-implement algorithms that achieve the best competitive ratio (CR). We first derive a lower bound on the CR of any algorithm. We then analyze CRs of all intuitive “greedy” algorithms. We propose two new algorithms that have significantly better CRs than that of any greedy algorithm for certain parameter-value ranges. The key idea behind these algorithms is that owners may reserve some amount of capacity for late-arriving higher-value proposals in an attempt to improve revenue. Our contribution lies in operationalizing this idea with the help of algorithms that utilize thresholds. Moreover, we show that if non-optimal thresholds are chosen, then those may lead to poor CRs. We provide a rigorous method by which an owner can decide the best approach in their context by analyzing the CRs of greedy algorithms and those proposed by us.
1. Introduction
Popular web platforms, such as Airbnb and Turo, provide owners the ability to list resources available for sharing, prices, and contract-length limits. The list of resources that may be shared is long and getting longer, including items such as apartments, tools, clothes, and intangibles such as the owners’ time (e.g., tutoring or handyman services). The sharing/renting process is known by many names such as peer-to-peer renting [1], collaborative consumption [2], and sharing economy [3]. Sharing economy is growing—in mid-2019, there were 1546 sharing-economy start-ups listed on AngelList, a US website for start-ups, with an average valuation of $3M [4]. An individual interested in a listed resource can see its availability and place a request with the owner, indicating the desired contract start time and length. The owner must then decide (either immediately or within a short period of time) whether to accept or decline the request, even if the contract is for a future date. Accepted requests earn a reward that is equal to the product of the posted price and the contract duration. Declined requests are lost and earn nothing. A key trade-off that the owner confronts is the reward he or she earns from the current request and the potential loss of reward from higher-value future requests that may clash with the current one.
We assume that the owner has no information about future requests that may arise, other than the contract-length limits. The minimum contract duration is predetermined either by the platform, e.g., one night on Airbnb, or by the owner, e.g., the number of hours on the car-sharing platform Getaround. The owners usually set the maximum contract duration, e.g., two days for a wedding gown rental [5]. In case of services such as tutoring and handyman work, such a restriction may be a result of limited human capacity. At times, an owner may also place an upper limit on contract length because of local laws. For example, renting an apartment for more than 30 days automatically confers tenant rights to the customer in California [6], and this may not be acceptable to the apartment owner. Finally, market forces may result in a de facto upper bound on the contract length. This may happen on platforms such as Getaround whose competitive advantage comes from offering short-duration contracts that are not offered by conventional rental agencies. Such platforms are more expensive for longer-duration contracts. This naturally limits the length of contracts in practice.
There are many situations in which the owner may not have information about future requests, other than the contract-length limits. This may happen when demand depends on a multitude of frequently changing external factors that are difficult to anticipate. Additionally, the owner may not have access to the web platform data, and the data that he or she observes may be very limited. Because of the lack of information about future requests, the owner’s problem is an online version of a problem that Kolen et al. [7] call the interval scheduling problem with given machines. In the offline version, the entire sequence of requests and their attributes are known upfront. We refer to the owner’s problem as the online reservation problem (ORP) because our motivating application is the reservation of resources on sharing economy platforms.
Even in those instances where the owners have access to some information about future requests, but the information is incomplete, it may be desirable to use an online algorithm because they are robust against forecast errors [8] and distributional misspecifications [9]. Moreover, the decision-maker will not need to customize the algorithm to exploit the type, quantity, and quality of information available. Specifically, for the application that we have in mind, the owner is unlikely to have the expertise and resources to develop customized approaches. Our approach is designed to be easily implementable in practice.
The relative performance of an algorithm for a given problem instance is the ratio of the offline optimal reward to the reward earned by the algorithm. We use worst-case relative performance of an algorithm, also known as competitive ratio (CR), as a measure of its goodness, given that we have no information about future requests. The smaller the CR, the more competitive the algorithm.
1.1. The Problem Statement
An instance L of the ORP is a non-empty finite sequence of requests or jobs. Each job i in L has three attributes: arrival time , start time , and length (or duration) . Let and be the contract-length limits. We constrain L to belong to a set , where . What this means is that, while L can consist of an arbitrary number of jobs with arbitrary arrival and start times, the length of each job must belong to the interval . We also define .
Let n denote the maximum number of concurrently available identical resources or servers, indexed . Each server can only process one job at a time. Jobs in L arrive one at a time and the attributes of each job are revealed only upon its arrival. As soon as a job arrives, the owner must immediately assign the job to one of the servers (resources) or decline it, only knowing that the length of any job that may arrive later will be in . Once assigned, a job cannot be reassigned to other servers or be preempted. Similarly, overlapping (or clashing or conflicting) jobs may not be assigned to the same server, i.e., jobs i and j with and cannot be assigned to the same server. Given job i, we say that server j has no conflicts if no job already assigned to server j clashes with job i. Without a loss of generality, we set the unit rent equal to 1. Therefore, the owner receives a reward that is equal to the duration of the job if it is assigned to one of the n servers and zero otherwise. Declined jobs are lost. We say that job- job-j, i.e., i and j represent the same job, if , , and .
Given L, let denote the total value of jobs in an offline optimal set, which is an optimal set of jobs that would be accepted if L was known entirely in advance. Let A denote an arbitrary algorithm in the set , where is the set of algorithms that, upon arrival of a job, either immediately assign it to one of the servers with no conflicts, or decline it, based only on the characteristics of the previously-arrived jobs, the past assign/decline decisions, the number of servers n, and the set . Given A, let denote the expected total value of jobs accepted by A for the problem instance L. Given this notation, the relative performance of A for instance L is defined as and the competitive ratio (CR) of A is defined as
Given n and , which we will sometimes refer to as the parameters of the problem, our objective is to find an such that for every . Additionally, we say that Algorithm A is c-competitive if . Note that, although , for any L, can possibly be equal to 0 for some A and L. To handle such cases, throughout the paper, we will assume that for any and for any .
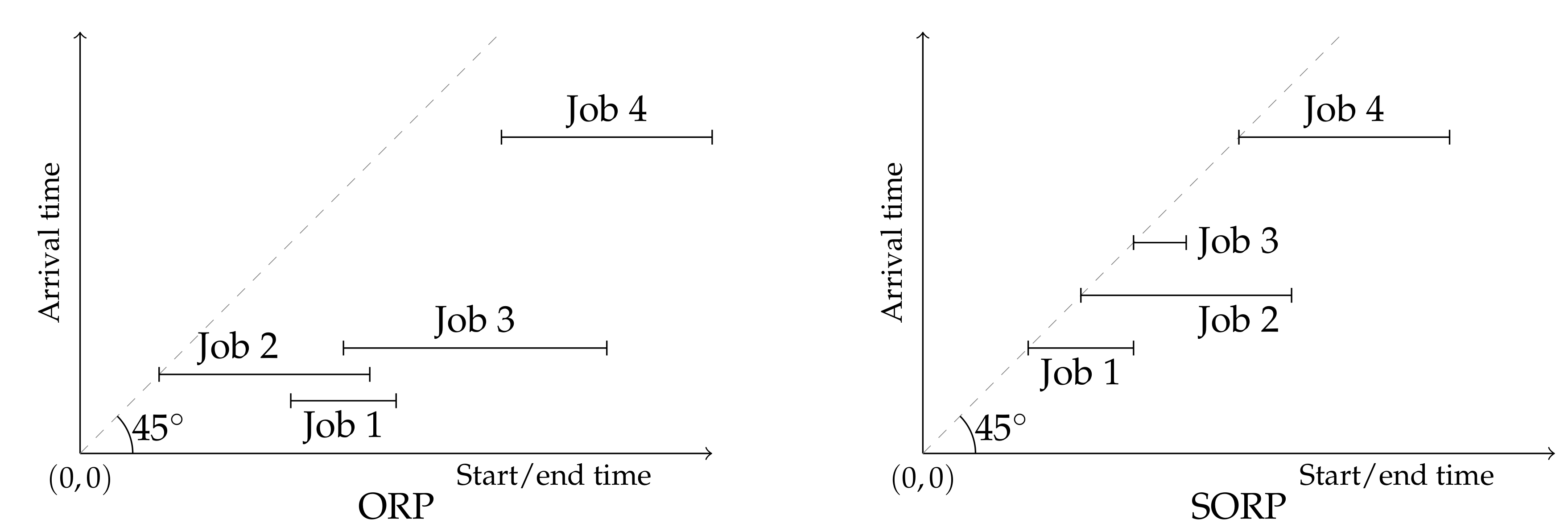
We also study a special case, which is abbreviated as SORP (special ORP). The difference between the ORP and the SORP is that for each i in the latter (see Figure 1). Such scenarios fit operations at platforms such as Uber and Lyft, and in problems that deal with the assignment of open jobs to reserve drivers in transit operations [10]. We use to denote the set of all possible non-empty finite sequences in which jobs arrive at their start times. Subsequently, the CR of an arbitrary for the SORP is defined as
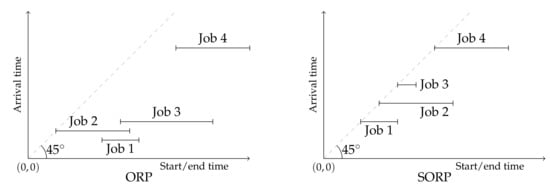
Figure 1.
Examples of problem instances with four jobs each under the online reservation problem (ORP) and the special case of the ORP (SORP) settings.
In the remainder of this paper, we use to denote the set and to denote the set for any . Given sets A and B, and .
1.2. Our Approach
We first find a lower bound on the CR of any algorithm in in Section 2, proving that no algorithm can have a CR better than . Subsequently, in Section 3.1, we analyze the CRs of all greedy algorithms (including those that are randomized), which are those that do not decline a request whenever a server is available. We study greedy algorithms because they are intuitive and have been studied in the context of other problems, such as the bin-packing problem [11]. We prove that any greedy algorithm is -competitive. The gap between the CRs of the greedy algorithms and the best possible CR motivates the need for better algorithms. The linear dependence of the CRs of greedy algorithms on arises because, in some instances, they end up accepting jobs with duration and declining those with duration . Therefore, we design two new algorithms while using the intuition that reserving capacity for higher-value future jobs may help to improve the CR and that this may be operationalized while using thresholds. We first propose a deterministic algorithm, Algorithm D, in Section 3.2, which uses deterministic server-specific admission thresholds. We find the upper bound on the CR of Algorithm D and prove that the algorithm is -competitive in the limit . We also propose a randomized algorithm, Algorithm R, in Section 3.3, which uses a randomized threshold. We prove that Algorithm R is -competitive for any n and , and it is therefore optimal in the sense that no algorithm can be better than -competitive. For the SORP, we follow the same approach as we do for the ORP.
Although we summarized our approach and results in terms of the big notation in the previous paragraph, we actually derive the exact values of all the CR bounds as functions of n and . Being able to design algorithms that are -competitive is important from a theoretical point of view, but our focus while designing Algorithms D and R is to go a step further and achieve CRs that have small numerical values. We do so because this paper is motivated by practical applications and an owner in a real-life setting will choose to use an algorithm for ORP/SORP only if the algorithm’s CR is small for his/her particular n and , regardless of the limiting behavior of the CR.
1.3. Related Literature
Several studies that analyze online scheduling problems that are similar to the ORP assume that some distributional information on job arrivals and/or durations is available [12,13,14]. Because the focus in these studies is on exploiting the distributional information, we do not review them. Instead we focus on those paper related to the ORP that do not assume availability of such information and seek algorithms with the best CR. Amongst these, there are numerous papers that allow for the preemption of already accepted jobs. Papers in this stream propose algorithms for problems with a variety of different features and analyze the CRs of proposed algorithms; see [15,16,17,18,19,20]. Preemption is not allowed in our setting, and therefore, we focus on papers that do not allow preemption. Finally, although Buchbinder and Naor [21] analyze a generic online packing problem that does not allow preemption using the primal-dual framework, it is not possible to express ORP or SORP as their online packing formulation. Therefore, we do not discuss [21] either.
Boyar and Larsen [22] analyze online seat reservations for a train that stops at k stations. They study two scenarios, first where all of the tickets yield the same reward, and second where the reward from a ticket is proportional to the number of stops in the journey. If we think of tickets as jobs and seats as servers, it is easy to see the connection between the latter scenario and the ORP. Boyar and Larsen [22] only consider greedy algorithms. Instead of “greedy”, they use the term “fair” for such algorithms. They prove that CR of any greedy deterministic algorithm is , which means that there exist real numbers and integer such that for all . By plugging in and in the expressions for CRs of greedy algorithms for the ORP, we find that they are indeed -competitive. However, since we do not limit ourselves to greedy algorithms, we are able to achieve smaller CRs. Moreover, Boyar and Larsen [22]’s formulation allows for jobs to have durations only in the integer set , whereas the ORP allows durations to belong to the interval .
Some other papers, e.g., [10,23,24], are similar to the SORP in the sense that they assume that jobs arrive exactly at their start times. We cannot use the algorithms or other results from these papers for the ORP because the set of allowed instances for the SORP is a proper subset of those for the ORP. However, our approach for the ORP can be utilized to solve the SORP. We will show in Section 4 that we can tweak our ORP algorithms to achieve even smaller CRs for the SORP.
Gupta and Li [10] study the multi-processor online fixed job scheduling problem for reserve driver scheduling. Their problem is identical to the SORP, except that the servers in their version are only available for specific time intervals, which model driver shifts. They propose a randomized algorithm for their problem that is -competitive. One of our algorithms is also -competitive. Furthermore, the numerical values of the upper bounds on CRs of our algorithms are much smaller than that of Gupta and Li [10]’s algorithm.
Lipton and Tomkins [23] study a problem that is identical to the SORP with a single server, except that and are not known. They show that no algorithm can have a CR that is or better. They also propose an algorithm that is -competitive, where is any positive real number. This randomized algorithm relies on a specific converging sequence of coin-flip probabilities. Faigle et al. [25] extend these results in two ways. First, they show that multiple different sequences can be used for constructing randomized algorithms for the problem if converges, and that the resulting algorithm will be -competitive. Second, the authors generalize the results to include the multiple server case. Unlike the problems that were studied by Lipton and Tomkins [23] and Faigle et al. [25], and are known in the case of sharing economy platforms. Therefore, we exploit this information to obtain better CRs.
Garofalakis et al. [24] consider the online scheduling of continuous media streams. This is identical to the single server case of the SORP, except that jobs now only demand a portion of the bandwidth of the server. They prove that no algorithm can be better than -competitive, where is the maximum fractional bandwidth that any job can demand. They also propose an algorithm that has CR within a constant factor of if . In the case of rental platforms, the customer must demand at least one unit of resource and, therefore, the fractional bandwidth assumption of [24] does not hold.
One might be tempted to think that the multiple server case of SORP is equivalent to the problem that was studied by Garofalakis et al. [24]. However, in a rental platform setting, the customer must be assigned a unique resource (such as a room or a car) throughout the duration of the contract. The formulation studied by Garofalakis et al. [24] fails to impose such a requirement and, hence, the supposed equivalence does not hold.
Finally, we would like to mention that Ball and Queyranne [26] study an online version of a revenue management problem that has many similarities with the ORP. In their formulation, each job is characterized by a fare and a maximum of n jobs can be accepted. The problem studied by Ball and Queyranne [26] can be thought of as consisting of those instances in which the start times of all the jobs are identical from the perspective of the framework that we established for the ORP in Section 1.1. Therefore, each job in an arbitrary instance of the problem conflicts with every other job in the same instance. Additionally, because of this, only n jobs can be accepted at most. Furthermore, the fares in the formulation by Ball and Queyranne [26] can be thought of as job durations in the ORP. Therefore, the formulation studied in [26] is equivalent to a special case of the ORP where the set of allowed instances is a proper subset of those for the ORP.
Ball and Queyranne [26] study various versions of their problem that differ based on the set of the possible fares and based on whether a job must be completely accepted (discrete version) or partial acceptance is allowed (continuous version). Like the discrete version, jobs must be either accepted or declined entirely in the ORP. However, partial acceptance of jobs in the continuous version studied by [26] can be considered to be equivalent to an owner making accept/decline decisions that are based on weighted coin flips. Ball and Queyranne [26] propose threshold-based algorithms for the various versions that they study and prove optimality for some of of them. Most notably, they prove that no algorithm for the continuous version of their problem that allows jobs to have any fare in the set can have a CR better than . They also present an algorithm that achieves CR that is exactly equal to the lower bound. Note that one cannot directly use the algorithms or other results from [26] for the ORP because the set of allowed instances for the formulation studied in [26] is a proper subset of those for the ORP. We complement the work of Ball and Queyranne [26] by studying the ORP that does not constrain the job start times to be identical. We prove that no algorithm for the ORP can have a CR better than and also present Algorithm R that is -competitive. Finally, while we are unable to close the gap between the exact values of the bounds, we do provide algorithms with CRs that are close to the lower bound.
1.4. Contribution
Our contribution is as follows. We model problem features that many owners face when sharing resources via web platforms. Upon doing so, we obtain an online version of the interval scheduling problem that has not been studied before. Although similar problems have been studied, they do not capture all of the problem features that we do. We prove a lower bound on the CR of any algorithm for the ORP. We also establish CRs or upper bounds on CRs for greedy algorithms in the context of the ORP for the first time. We propose two algorithms that are easy to implement and use intuitively-appealing threshold-criteria for making accept/decline decisions. We show that the CRs of both these algorithms are significantly better than that of any greedy algorithm for specific ranges of parameter values. We modify our algorithms and analyses to apply to the SORP setting, and we show that the CRs of our algorithms are smaller than those of the algorithm that was proposed in [10].
Although we study the asymptotic dependence of CR bounds on , we would like to emphasize that our contribution lies in obtaining exact values of CR bounds. This is so because the paper is motivated by practical use cases where the value of the bounds for particular n and matter more than the asymptotic behavior. In fact, analyzing the limiting behavior may not require the kind of rigorous analysis that is presented in this paper.
2. A Lower Bound on CRs
We use Yao’s principle [27] to derive a lower bound on the CR of any algorithm for the ORP. We start by stating the Yao’s principle, as applicable to the ORP, in Theorem 1 below.
Theorem 1.
Yao’s Principle for the ORP: Let be the set of all algorithms for the ORP, as defined in Section 1.1, and let be the subset of deterministic algorithms in . If is a set of instances and is a probability distribution with as its support, then is a lower bound on the CR of any algorithm in . The expectations are over the probability distribution .
Next, in Theorem 2, we derive a lower bound on CR of any algorithm for the ORP.
Theorem 2.
The CR of any algorithm for the ORP is bounded below by , where .
Sketch of the Proof.
In the detailed proof that is presented in Appendix A, we present a set of instances , a probability distribution over , find a lower bound on , and apply Theorem 1. The key challenge in this exercise is to come up with and , such that a closed-form expression for the lower bound on can be derived. We also want to construct and such that the lower bound is as large as possible.
The lower bound is increasing in because the CR of every algorithm must be increasing in by definition. This lower bound is tight for some parameter values, as we will show later. It is also tight in the sense that we present an algorithm later (Algorithm R) that is -competitive.
3. Algorithms
We begin this section by presenting Lemma 1 that will be the basis for deriving upper bounds on CRs of algorithms in subsequent proofs. Subsequently, in Section 3.1, we analyze CRs of all greedy algorithms for the ORP. In Section 3.2 and Section 3.3, we analyze the CRs of algorithms D and R, respectively. Lemma 1 is based on the notions of allocation scheme and allocation, which we define next.
Definition 1.
Given two sets of jobs, B and C, an allocation scheme from B to C is a function w that maps the Cartesian product to the set of non-negative real numbers such that for any job , is less than or equal to , the duration of job b. Furthermore, is called the allocation from job b to job c.
Lemma 1.
Given Algorithm and an instance L, let be the set of jobs accepted by A and be an offline optimal set. If we are given a positive real number a and if for every instance , we are given an allocation scheme from to such that for any job , holds, then a is an upper bound on the CR of Algorithm A.
Sketch of the Proof.
The proof involves algebraic arguments, which are presented in Appendix B. The intuition behind the lemma is that if for a given instance L, we can allocate the durations of jobs that are accepted by Algorithm A to jobs in the offline optimal set such that each job in the offline optimal set is allocated at least of its duration, then . Furthermore, if we can do the same for every instance , then .
Intuitively, Lemma 1 uses the concept of allocation scheme to check whether the algorithm under consideration accepts jobs with enough duration vis-à-vis the offline optimal set for all possible instances. Hence, if one comes up with appropriate allocation schemes, Lemma 1 implies an upper bound for the algorithm. We use this idea multiple times for proving the various results in the paper.
3.1. Greedy Algorithms
A greedy algorithm is one that assigns a job to a server with no conflicts, whenever at least one such server exists. Otherwise, it declines the job.
Theorem 3.
The following statements regarding the CR of an arbitrary greedy algorithm A are true.
- if .
- if .
- if and .
- if and .
Sketch of the Proof.
The key challenge in establishing an upper bound is to come up with allocation schemes from the sets of jobs tha are accepted by Algorithm A to offline optimal sets such that Lemma 1 can be applied. The detailed proof along with the allocation schemes is given in Appendix C.
The upper bound in the first statement is tight because of a matching lower bound from Theorem 2. The lower bounds in the second and fourth statements are proved by identifying specific instances and calculating the ratio for them. The lower bound so proved is tight for the second statement. □
The statements in theorem above provide results for cases that are based on:
- whether or , and
- whether or .
By separately considering the four cases, we are able to derive more accurate bounds. Note that, for any given , upper bounds are smaller for when compared to those for . Intuitively, this happens because, when , the owner must not only decide whether to accept or decline a job, but he/she must also assign the accepted jobs to one of the multiple servers. This additional level of decision-making causes the CR to deteriorate. Additionally, note that, for any given n, the CR is increasing in . This directly follows from the definition of CR. All of the phenomena discussed in this paragraph also hold true for Theorems 4 and 5 that are presented in the subsequent sections and that contain bounds on CRs of Algorithms D and R, respectively.
It follows from Theorems 2 and 3 that the CR of any greedy algorithm is optimal when . Additionally, just like the lower bound on CR of any online algorithm (Theorem 2), the CR is increasing in . However, the rate of increase is linear instead of logarithmic. This gap motivates the need for algorithms with better CRs. Intuitively, the rate of increase is linear because, in some instances, a greedy algorithm only accepts jobs with duration close to . These decisions prevent it from accepting overlapping jobs with duration that arrive in the future and that would have been accepted instead if we knew the entire instance upfront.
3.2. The Deterministic-Selection Algorithm (Algorithm D)
Job j is said to be admissible to server i if it does not conflict with any previously-accepted job of server i and if the job j’s duration, , is greater than or equal to the admission threshold of server i, (defined subsequently in Definition 2). Algorithm D assigns an incoming job to the smallest-indexed server to which it is admissible, if at least one such server exists. Otherwise, it declines the job. The pseudocode is provided below (Algorithm 1).
| Algorithm 1: Pseudocode for Algorithm D. |
 |
The admission thresholds serve to increase the likelihood that some longer duration jobs will be accepted by turning away small jobs, thereby overcoming a shortcoming of the greedy algorithms.
Definition 2.
- such that
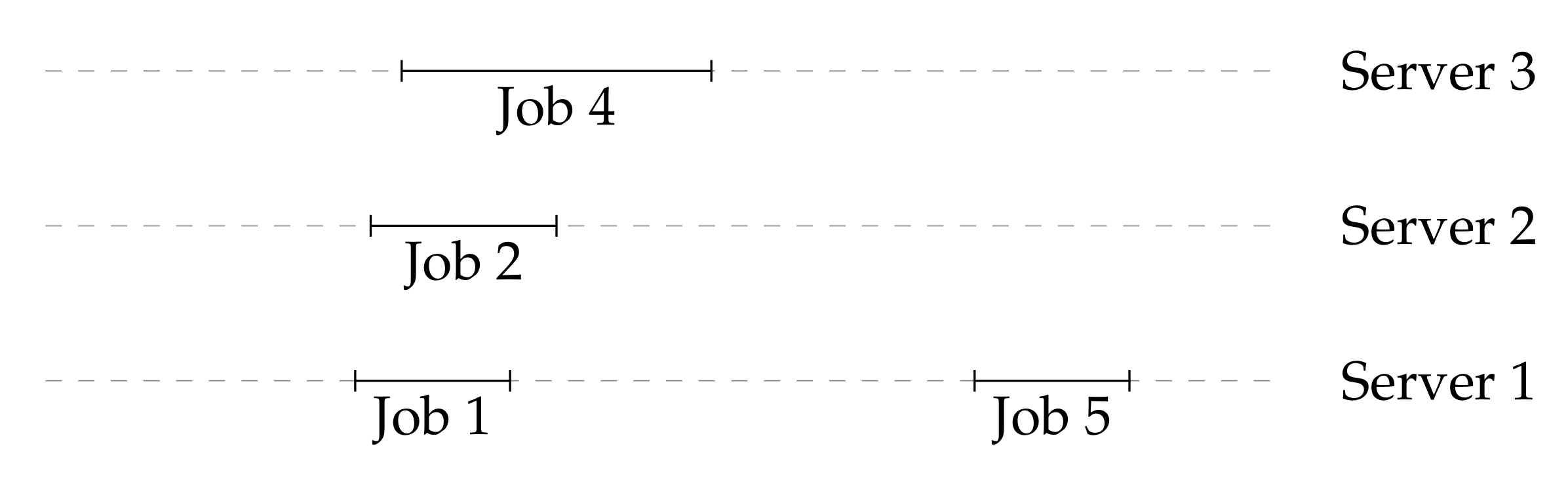
To further illustrate how Algorithm D works, we consider a numerical example where , , and . Therefore, . Additionally, by Definition 2, , , and . Consider the instance with five jobs presented in Table 1, below. The same instance is represented pictorially in Figure 2.

Table 1.
An instance of ORP with five jobs. Jobs arrive in the order of their index j.

Figure 2.
Representation of the instance presented in Table 1.
Note that, in the instance presented in Table 1, the first four jobs overlap with each other. Job 5 does not overlap with any of the other jobs. Algorithm D makes decisions as follows:
- Job 1:
- -
- Job 1 is admissible to server 1 because the duration of job 1 is greater than or equal to admission threshold of server 1 () and because no jobs were previously assigned to server 1.
- -
- Job 1 is admissible to server 2 because duration of job 1 is greater than or equal to the admission threshold of server 2 () and because no jobs were previously assigned to server 2.
- -
- Job 1 is not admissible to server 3 because the duration of job 1 is smaller than the admission threshold of server 3 ().
Because server 1 has the smallest index amongst servers to which job 1 is admissible, Algorithm D assigns the job to server 1. - Job 2:
- -
- Job 2 is not admissible to server 1 because it conflicts with job 1 that was previously assigned to server 1.
- -
- Job 2 is admissible to server 2 because the duration of job 2 is greater than or equal to admission threshold of server 2 () and because no jobs were previously assigned to server 2.
- -
- Job 2 is not admissible to server 3 because the duration of job 2 is smaller than the admission threshold of server 3 ().
Since server 2 is the only server to which job 2 is admissible, Algorithm D assigns the job to server 2. - Job 3:
- -
- Job 3 is not admissible to server 1 because it conflicts with job 1 that was previously assigned to server 1.
- -
- Job 3 is not admissible to server 2 because it conflicts with job 2 that was previously assigned to server 2.
- -
- Job 3 is not admissible to server 3 because duration of job 3 is smaller than the admission threshold of server 3 ().
Since there are no servers to which job 3 is admissible, Algorithm D declines the job. - Job 4:
- -
- Job 4 is not admissible to server 1 because it conflicts with job 1 that was previously assigned to server 1.
- -
- Job 4 is not admissible to server 2 because it conflicts with job 2 that was previously assigned to server 2.
- -
- Job 4 is admissible to server 3 because the duration of job 4 is greater than or equal to the admission threshold of server 3 () and because no jobs were previously assigned to server 3.
Because server 3 has the smallest index amongst servers to which job 4 is admissible, Algorithm D assigns the job to server 3. - Job 5:
- -
- Job 5 is admissible to server 1 because duration of job 5 is greater than or equal to admission threshold of server 1 () and because job 5 does not conflict with job 1 that was previously assigned to server 1.
- -
- Job 5 is admissible to server 2 because the duration of job 5 is greater than or equal to admission threshold of server 2 () and because job 5 does not conflict with job 2 that was previously assigned to server 2.
- -
- Job 5 is not admissible to server 3 because the duration of job 5 is smaller than the admission threshold of server 3 ().
Because server 1 has the smallest index amongst servers to which job 5 is admissible, Algorithm D assigns the job to server 1.
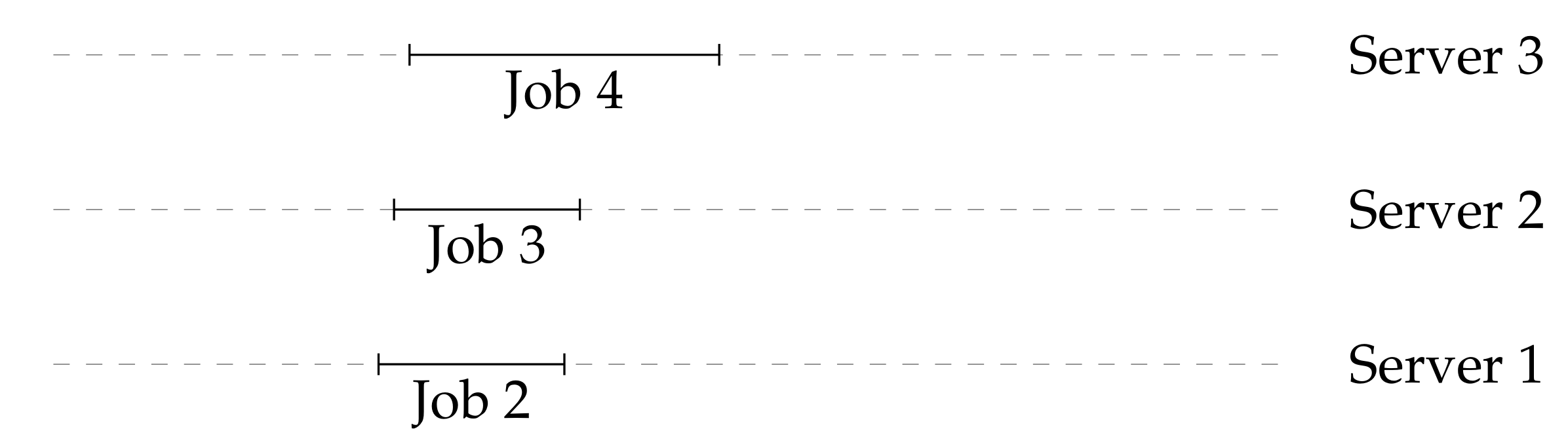
After all of the decisions, the assignment of jobs to servers is represented in Figure 3, below.
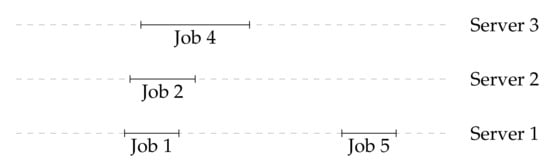
Figure 3.
Assignment of jobs in the instance presented in Table 1 by Algorithm D.
Next, we present a result on CR of Algorithm D in Theorem 4, below.
Theorem 4.
The following statements regarding the CR of Algorithm D are true.
- if .
- if .
- if and .
- if and .
Sketch of the Proof.
The first three statements follow directly from Theorem 3 because for all i, and therefore, Algorithm D is a greedy algorithm for these cases. Proof for the fourth statement is given in Appendix D. Just like Theorem 3, the crux of this proof lies in identifying allocation schemes from the sets of jobs accepted by the algorithm to the offline optimal sets such that Lemma 1 can be applied to prove the proposed upper bound.
Corollary 1.
.
The results in the first three statements of Theorem 4 are identical to those that are presented in the first three statements of Theorem 3 because Algorithm D behaves like a greedy algorithm for those cases. However, by cleverly setting individual thresholds for the servers, Algorithm D achieves a CR that is in the limit . In terms of CR, Algorithm D outperforms any greedy algorithm when n and are sufficiently large. Table 2 is presented in Section 3.3 and it gives values of either the CR or the upper bound on the CR of Algorithm D, as derived in Theorem 4, for some specific n and .

Table 2.
Numerical values of lower bound on competitive ratios (CRs) from Theorems 2 and either CRs or upper bounds on CRs from Theorems 3–5. The formulae for calculating these values can be found in the respective theorem statements. Algorithm A represents any greedy algorithm.
3.3. The Randomized-Selection Algorithm (Algorithm R)
Algorithm R also uses a threshold, but the threshold is sampled from a specified distribution. In the beginning, Algorithm R samples the threshold x from the distribution with CDF (defined subsequently in Definition 3). The same threshold x is then used for all jobs in the instance. Algorithm R declines all incoming jobs with a duration strictly smaller than the threshold x. Any qualifying job is assigned to the smallest-indexed server with no conflicts, if at least one such server exists. Otherwise, the job is declined. The pseudocode is provided below (Algorithm 2).
| Algorithm 2: Pseudocode for Algorithm R. |
 |
The idea behind the threshold in Algorithm R is the same as that in Algorithm D: to increase the likelihood that some longer duration jobs will be accepted by turning away small jobs and thereby overcoming a shortcoming of the greedy algorithms.
Definition 3.
CDF , such that
To further illustrate how Algorithm R works, we consider a numerical example where , , and . Therefore, . We consider the same instance that was presented in Table 1 and Figure 2. Algorithm R first samples threshold x from the distribution with CDF . For the purpose of this example, we will assume that the sampled value is 1.1. Note that the decisions would be different if the sampling resulted in a different value of x. Anyhow, for , Algorithm R makes decisions as follows:
- Job 1: Because the duration of job 1 is less than threshold x, Algorithm R declines the job.
- Job 2: The duration of job 2 is greater than threshold x. Further, none of the servers have any previously-accepted jobs that conflict with job 2. Because server 1 has the smallest index amongst these servers, Algorithm R assigns the job to server 1.
- Job 3: The duration of job 3 is greater than threshold x. Further, only servers 2 and 3 do not have any previously-accepted jobs that conflict with job 3. Because server 2 has the smallest index amongst these servers, Algorithm R assigns the job to server 2.
- Job 4: The duration of job 4 is greater than threshold x. Further, only server 3 does not have any previously-accepted jobs that conflict with job 4. Therefore, Algorithm R assigns the job to server 3.
- Job 5: Because the duration of job 5 is less than threshold x, Algorithm R declines the job.
After all of the decisions, the assignment of jobs to servers is represented in Figure 4, below.
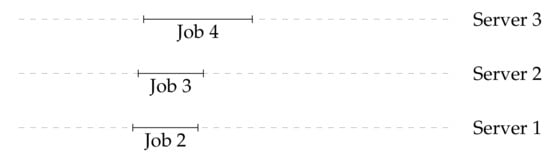
Figure 4.
Assignment of jobs in the instance presented in Table 1 by Algorithm R when sampled threshold is equal to 1.1. Note that the decisions would be different if the sampling resulted in a different value of the threshold.
Next, we present a result on CR of Algorithm R in Theorem 5, below.
Theorem 5.
The following statements regarding the CR of Algorithm R are true.
- if .
- if .
- if and .
- if and .
Sketch of the Proof.
Statements 1 and 3 follow directly from Theorem 3 because the sampled threshold is equal to with probability 1, and therefore, Algorithm R is a greedy algorithm for these cases. For the proof of other two statements, we consider an arbitrary instance, L, and present an allocation scheme. Using this allocation scheme, we derive a lower bound on the total duration of jobs that are accepted by Algorithm R when the sampled threshold is equal to x. We then use this lower bound to show that when , and when . Appendix E provides the details.
The results in statements 1 and 3 of Theorem 5 are identical to those that are presented in the corresponding statements of Theorem 3 because Algorithm R behaves like a greedy algorithm for these cases. However, CR of Algorithm R is , just as the lower bound on CRs derived in Theorem 2, and is therefore optimal in this sense. In terms of CR, Algorithm R outperforms any greedy algorithm when is sufficiently large, and it outperforms Algorithm D when n is sufficiently small and is sufficiently large. Both Algorithm D and Algorithm R use thresholds, and we chose these thresholds in such a way that we were able to derive small upper bounds on CRs using our proof techniques. Although the motivation while designing Algorithm R was to consistently beat Algorithm D, the change in ordering of upper bounds on CRs of these algorithms for different values of n and seems to primarily be an artifact of the chosen thresholds/proof techniques and nothing more.
Table 2 gives numerical values of lower bounds and upper bounds on CRs derived in Section 2 and Section 3. Note that the CRs or the upper bounds on CRs are quite large when compared to the lower bound, , in some cases. This might be happening because may not be tight for these cases. The only case in which the lower bound is provably tight happens to be when . Finding a tight lower bound for every n and and finding an algorithm that achieves a CR equal to the lower bound for every n and are both open problems.
4. Jobs Arrive at Their Start Times (SORP)
In this section, we study the special case of the ORP, abbreviated as SORP, where all of the jobs arrive exactly at their start times, and this fact is known upfront to the decision-maker. Although we apply Algorithm R to the SORP exactly the way we did for the ORP, we modify the server-specific admission thresholds of Algorithm D. This is done to exploit the extra information that is known to the decision-maker that each job will arrive at its start time.
We first derive the lower bound on the CR of any algorithm for the SORP (Theorem 6). Subsequently, we analyze CRs of greedy algorithms and Algorithms D and R for the SORP (Theorems 7–9). The proofs are very similar to the corresponding derivations for the ORP, and therefore, we omit them here (proofs may be found in [28]). The lower bound on CR of any algorithm and the CRs of the studied algorithms are smaller than those for the ORP because the set of allowed instances for the SORP is a proper subset of those for the ORP.
Theorem 6.
The CR of any algorithm for the SORP is bounded below by .
Theorem 7.
The following statements regarding the CR of an arbitrary greedy algorithm A are true.
- if .
- if .
- if and .
- if and .
Gupta and Li [10] also prove Statement 2 in Theorem 7, but they do so while using arguments different from ours. We prove all four statements using the common framework of allocation schemes and Lemma 1.
Algorithm D works the same way for the SORP as it does for the ORP; the only difference is that the server thresholds are given by ’s (defined in Definition 4) instead of ’s.
Definition 4.
- such that
The notation that is defined above differs from that in Definition 2 in that each occurrence of 3 in Definition 2 is replaced by 2 here.
Theorem 8.
The following statements regarding the CR of Algorithm D are true.
- if .
- if .
- if and .
- if and .
Corollary 2.
.
Theorem 9.
The following statements regarding the CR of Algorithm R are true.
- if .
- if .
- if and .
- if and .
Table 3 gives numerical values of lower bounds and CRs or upper bounds on CRs as derived in this section. We also compare our results with Gupta and Li [10], who study a variant of the SORP in which the servers are available only for specific time intervals. By making these time intervals arbitrarily long, we get back the SORP. Gupta and Li [10] only consider cases where and propose an -competitive algorithm for it. The algorithm requires two additional parameters as input (in addition to n and ) that can be tuned as desired by the owner (see Appendix F). We tune the two additional parameters in order to achieve the smallest value of this upper bound, which is presented in the last row of Table 3. Note that the CRs or upper bounds on CRs of our algorithms are significantly smaller than those of the algorithm presented in [10].

Table 3.
Numerical values of lower bound on CRs from Theorem 6 and either CRs or upper bounds on CRs from Theorems 7–9, and [10]. The formulae for calculating values related to results derived in this paper can be found in the respective theorem statements. The formulae for upper bounds on CR for algorithm from [10] are provided in Appendix F. Algorithm A represents any greedy algorithm.
5. Take-Aways
Owners may intuitively realize that using thresholds to reserve capacity for high value jobs that may arrive in the future will help to improve the CR relative to the greedy algorithms. Algorithms D and R use precisely this intuition. However, the choice of thresholds is important. In fact, the CR may deteriorate depending upon the choice of thresholds. For example, if all of the thresholds are strictly greater than , then the CR for that algorithm will be ∞. Because, in general, the owners will not have the technical expertise to set the thresholds optimally by analyzing the relationship between thresholds and the resultant CRs, we provide specific threshold values (see Definitions 2 and 3) and specific ways of applying them in the form of Algorithms D and R, which result in good CRs.
We present a rigorous method to help the owner choose an appropriate algorithm by deriving the CRs of greedy algorithms and the two algorithms proposed by us. Upon knowing the CRs, the owner will be more confident in his or her choice of algorithm, whether it be a greedy algorithm or one of the algorithms that we propose. Our analysis makes it easy to trade off performance and ease of implementation.
Author Contributions
Conceptualization, S.G. and D.G.; methodology, S.G. and D.G.; software, S.G.; validation, S.G. and D.G.; formal analysis, S.G.; investigation, S.G.; resources, S.G. and D.G.; data curation, S.G.; writing–original draft preparation, S.G. and D.G.; writing—review and editing, S.G. and D.G.; visualization, S.G.; supervision, D.G.; project administration, D.G.; funding acquisition, D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported in part by the National Science Foundation under Award No. CMMI-1755254. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Theorem 2
Proof.
We begin by defining some notation. Let an arbitrarily large real number, k and b arbitrary positive integers, , and arbitrarily small. Let for and for . Let and be sequences of jobs, each with n jobs, as shown in Table A1. Each 2-tuple in Table A1 represents a job, with the first value in the tuple being the start time of the job and the second value being the job’s duration. The jobs in the sequences are ordered by their arrival times. Appending these sequences one after another, we define sequences (instances) as described in Table A2. The arrival times of the jobs are such that the jobs in each of are ordered by their arrival times. A specific example of for the case when and is depicted in Figure A1. Define . The probability distribution over the set is shown in the Table A2.

Table A1.
Sequences and . Each sequence has n jobs. Each 2-tuple represents a job, with the first value in the tuple being the start time of the job and the second value being the job’s duration. The jobs in the sequences are ordered by their arrival times.
Table A1.
Sequences and . Each sequence has n jobs. Each 2-tuple represents a job, with the first value in the tuple being the start time of the job and the second value being the job’s duration. The jobs in the sequences are ordered by their arrival times.
| Notation | Sequence of Jobs |
|---|---|
| ⋮ | ⋮ |
| ⋮ | ⋮ |

Table A2.
Probability distribution over . represents a sequence with jobs from placed first, then from , and so on. The arrival times of the jobs are such that the jobs in each of are ordered by their arrival times.
Table A2.
Probability distribution over . represents a sequence with jobs from placed first, then from , and so on. The arrival times of the jobs are such that the jobs in each of are ordered by their arrival times.
| Instance | Probability |
|---|---|
| ⋮ | ⋮ |
| ⋮ | ⋮ |
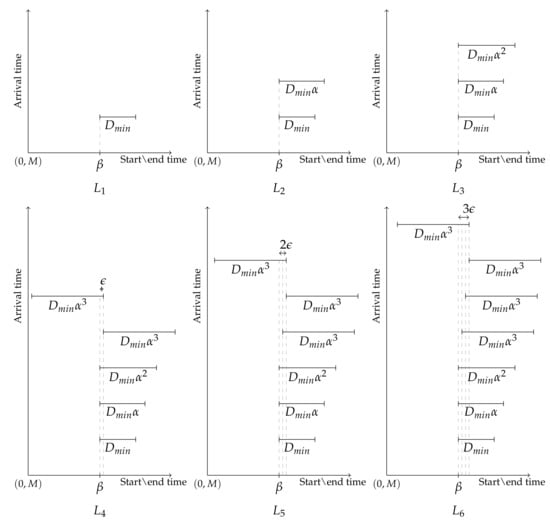
Figure A1.
when and . is a very large real number.
Figure A1.
when and . is a very large real number.
Then, if and if . Therefore,
We next find an upper bound on for any . Consider an arbitrary deterministic Algorithm . When the instance is , let denote the number of jobs accepted by Algorithm A from the subsequence , . holds because each job in the sequence overlaps with every other job in the same sequence and because only non-overlapping jobs can be assigned to the same server. Since A is a deterministic online algorithm, it will accept exactly jobs when faced with the instance . Similarly, when faced with , it will accept jobs from the subsequence and jobs from the subsequence . And so on. Therefore, for . Further, for because is an upper bound on the number of jobs that can be accepted from the last n jobs in instance . is a valid upper bound because every job in the subsequences overlaps with each of the last n jobs in when and because only non-overlapping jobs can be assigned to the same server. Since , we have
Since Algorithm A was arbitrary, Inequality (A2) holds for all algorithms in , and therefore, by Equation (A1) and Theorem 1, for any randomized online Algorithm B for the ORP,
Since Equation (A3) holds for any ,
Since Algorithm B was arbitrary, the result is proved. □
Appendix B. Proof of Lemma 1
Proof.
Let be an arbitrary instance of the ORP. By definition, . By Definition 1, for any job . Therefore,
Since L was arbitrary,. □
Appendix C. Proof of Theorem 3
Before proceeding with the proof for Theorem 3, we present Lemma A1 that we will use to substantiate some intermediate claims in the theorem’s proof.
Lemma A1.
Given an instance L, define be the set of jobs accepted by Algorithm A and be an offline optimal set. Then, following statements hold true:
- If , any job does not overlap with any other job in except itself. Also, any job does not overlap with any other job in except itself.
- If , then any job overlaps with at most jobs in the set .
- If , then for any job , the jobs in that overlap with job b have total duration strictly less than .
Proof of Lemma A1
Statement 1. Follows directly from the fact that set contains only non-overlapping jobs and that the same holds for set .
Statement 2. Set contains jobs that would have been selected if we knew the instance L upfront, and therefore, it can be partitioned into n subsets such that each subset consists only of non-overlapping jobs. Now, any job in can overlap with at most 2 jobs in any one of these subsets. Therefore, any job overlaps with at most jobs in the set .
Statement 3. Set contains jobs that would have been selected if we knew the instance L upfront, and therefore, it can be partitioned into n subsets such that each subset consists only of non-overlapping jobs. Now, for any job , the total duration of jobs that overlap with job b in any one of the subsets must be strictly less than . Therefore, the total duration of jobs in that overlap with a given job is strictly less than . □
Proof of Theorem 3.
We begin by noting that although other well-known arguments may be used to prove the result for some specific values of n and , but we prove all four statements using the common framework of allocation schemes and Lemma 1. Given an instance L, define to be the set of jobs accepted by Algorithm A and to be the offline optimal set. Then, the individual proofs of the four statements are as follows.
Statement 1. Given instance L, define function as follows:
Claim 1: is an allocation scheme from the set to the set .
Proof of Claim 1.
If job , then it does not overlap with any other job in except itself (Lemma A1), and therefore, . Otherwise if job , it cannot overlap with more than 2 jobs in (Lemma A1), and therefore, . Therefore, by Definition 1, is a valid allocation scheme. □
Claim 2: for any job c in .
Proof of Claim 2.
If job , then it does not overlap with any other job in except itself (Lemma A1), and therefore, . Otherwise if job , it must overlap with at least one job in because Algorithm A could not have declined job c otherwise. Therefore, . □
Since instance L was arbitrary, by Lemma 1 and Theorem 2, the result is proved. □
Statement 2. Given instance L, define function as follows:
Claim 3: is an allocation scheme from the set to the set .
Proof of Claim 3.
If job , then it does not overlap with any other job in except itself (Lemma A1), and therefore, . Otherwise if job , the total duration of jobs in that can overlap with it is strictly less than (Lemma A1), and therefore, . Therefore, by Definition 1, is a valid allocation scheme. □
Claim 4: for any job c in .
Proof of Claim 4.
If job , then it does not overlap with any other job in except itself (Lemma A1), and therefore, . Otherwise if job , it must overlap with at least one job in because Algorithm A could not have declined job c otherwise. Therefore, . □
Since instance L was arbitrary, by Lemma 1, . We will now prove a matching lower bound. Let be arbitrarily large and be arbitrarily small. Consider instance L in which the jobs arrive in following sequence: . Each 2-tuple represents a job, with first value being the start time and the second being the duration. Then, . Therefore, . Since was arbitrary, this inequality holds for every , letting gives us the matching lower bound, . □
Statement 3. Given instance L, define function as follows:
Claim 5: is an allocation scheme from the set to the set .
Proof of Claim 5.
For any job b in , at most jobs from can overlap with it (Lemma A1), and therefore, . Further, if , . Therefore, for any job , . Hence, by Definition 1, is an allocation scheme. □
Claim 6: for any job c in .
Proof□of Claim 6.
If job , then . Otherwise if job , it must overlap with at least n jobs in because Algorithm A could not have declined job c otherwise. Therefore, . □
Since instance L was arbitrary, by Lemma 1, the result is proved. □
Statement 4. Given instance L, define function as follows:
Claim 7: is an allocation scheme from the set to the set .
Proof□of Claim 7.
For any job b in , jobs from that overlap with it have total duration strictly less than (Lemma A1), and therefore,
Further, if , . Therefore, for any job , . Hence, by Definition 1, is an allocation scheme. □
Claim 8: for any job c in .
Proof■of Claim 8.
If job , then . Otherwise if job , it must overlap with at least n jobs in because Algorithm A could not have declined job c otherwise. Therefore, . □
Since instance L was arbitrary, by Lemma 1, . We will now prove the lower bound. Let be arbitrarily large and be arbitrarily small. Consider instance L in which the jobs arrive in following sequence:
. Each 2-tuple represents a job, with first value being the start time and the second being the duration. Then, . Therefore, . Since was arbitrary, this inequality holds for every , letting gives us the lower bound, .
Appendix D. Proof of Statement 4 in Theorem 4
Before presenting the proof for Theorem 4, we present Lemma A2 that is required for supporting intermediate claims in the proof for Theorem 4 and other subsequent proofs.
Lemma A2.
Consider job i that overlaps with jobs, none of which overlap with each other. Let a be the duration of the smallest of the jobs under consideration, and let b be the duration of the largest. Then, if and if .
Proof of Lemma A2
If , then all the jobs are of the same duration, and therefore, job i cannot overlap with more than two jobs. Thus, and . Otherwise, . When , . Otherwise, if , then at least jobs start after , the start time of job i, and end before , the end time of job i. Therefore, □
Proof of Statement 4 in Theorem 4.
Given n and , denote by t. Given an instance L, define to be the set of jobs accepted by Algorithm D and to be the offline optimal set. Define function as follows:
Claim 9: is an allocation scheme from the set to the set .
Proof of Claim 9.
For any given job that is placed assigned to server i by Algorithm D, a non-zero allocation from job b was made to jobs in the set that have duration greater than or equal to , and also to job b itself if it belongs to . Set contains jobs that would have been selected if we knew the instance L upfront, and therefore, the sets and can be partitioned into n subsets such that each subset consists only of non-overlapping jobs. Let D denote one of such n subsets of , and let M be the number of jobs in D with duration greater than or equal to . Then, . If , by Lemma A2, . This also holds true if . Since there are n subsets in the partition of , we have . The only other non-zero allocation from job b could have been to itself if job , and this allocation is less than or equal to . Thus, . Therefore, by Definition 1, is an allocation scheme. □
Claim 10: for any job c in .
Proof of Claim 10.
Consider any job c in and let m be the largest integer in such that . By definition of t, . If job c belongs to the set , then it was rejected by Algorithm D. Therefore, it must overlap with at least one job assigned to each one of the servers , where . Therefore, . Otherwise, if job c belongs to the set , . Therefore, for any job c in , . □
Since instance L was arbitrary, by Lemma 1, the result is proved. □
Appendix E. Proof of Statements 2 and 4 in Theorem 5
Proof.
We begin by presenting some notation. L denotes an arbitrary instance, denotes offline optimal set for L, denotes the total number of jobs with duration equal to x in , denotes the sequence of jobs obtained by removing all jobs with duration strictly less than x from L, denotes the subset of jobs obtained by removing all jobs with duration strictly less than x from , denotes the set of jobs accepted by Algorithm R from instance L when sampled threshold is x, denotes the total duration of jobs in the set , and E denotes the set {distinct durations of jobs in such that and . Define and for .
Statement 2. Algorithm R effectively chooses as threshold with probability for . Consider the run of algorithm when R chooses as the threshold. Define function as follows:
Claim 11: is an allocation scheme from the set to the set .
Proof of Claim 11.
If job , then it does not overlap with any other job in except itself (Lemma A1), and therefore, . Otherwise if job , the only non-zero allocations from job b are to jobs in . Let M be the number of jobs in that overlap with job b. Therefore, . If , by Lemma A2, . This also holds true if . Therefore, by Definition 1, is a valid allocation scheme. □
Now, any job either belongs to , in which case , or belongs to , in which case it is rejected because it overlaps with at least one job in and hence, . Therefore, for any job , . Hence,
For any , . Further, . Therefore,
because . Since L was arbitrary, the result is proved. □
Statement 4. Algorithm R effectively chooses as threshold with probability , . Consider the run of algorithm when R chooses as the threshold. Define function as follows:
Claim 12: is an allocation scheme from the set to the set .
Proof of Claim 12.
For any given job , a non-zero allocation from job b was made to jobs in and also to job b itself if it belongs to . Now, the set of jobs in that overlap job b can be partitioned into n subsets such that no two jobs overlap in each subset. This is possible because a valid assignment of jobs in to the n servers must exist by definition of C. Let D denote one of these subsets, and let M be the number of jobs in it. Then . If , by Lemma A2, . This also holds true if . Because there are n subsets in the partition, . Also, if job , . Therefore, . Hence, by Definition 1, is a valid allocation scheme. □
Now, any job either belongs to , in which case , or belongs to , in which case it is rejected because it overlaps with at least n jobs in and hence, . Therefore, for any job , . Hence, We then follow steps similar to those for the proof of Statement 2 to get the desired result. □
Appendix F.
Upper Bound on CR of the Algorithm Presented in [10] The algorithm proposed by Gupta and Li [10] has two additional parameters and that can be tuned as desired by the owner. Note that any value of and is permissible as long as , , and .
Gupta and Li [10] prove that the CR of their algorithm when is bounded from above by the largest value amongst , , and . They further prove that the bound is twice as large when .
References
- Fraiberger, S.P.; Sundararajan, A. Peer-to-Peer Rental Markets in the Sharing Economy. NYU Stern School of Business Research Paper. Available online: https://ssrn.com/abstract=2574337 (accessed on 1 July 2020).
- Hamari, J.; Sjöklint, M.; Ukkonen, A. The sharing economy: Why people participate in collaborative consumption. J. Assoc. Inf. Sci. Technol. 2016, 67, 2047–2059. [Google Scholar] [CrossRef]
- Martin, C.J. The sharing economy: A pathway to sustainability or a nightmarish form of neoliberal capitalism? Ecol. Econ. 2016, 121, 149–159. [Google Scholar]
- AngelList. Sharing Economy Startups. Available online: https://angel.co/sharing-economy-4 (accessed on 1 July 2019).
- Zilok. Rental Wedding Gown. Available online: us.zilok.com/rental/119802-wedding-gown.html (accessed on 1 January 2018).
- DCA. California Tenants: A Guide to Residential Tenants’ and Landlords’ Rights and Responsibilities; California Department of Consumer Affairs: Sacramento, CA, USA, 2012. [Google Scholar]
- Kolen, A.W.; Lenstra, J.K.; Papadimitriou, C.H.; Spieksma, F.C. Interval scheduling: A survey. Naval Res. Logist. (NRL) 2007, 54, 530–543. [Google Scholar] [CrossRef]
- Ma, W.; Simchi-Levi, D. Algorithms for online matching, assortment, and pricing with tight weight-dependent competitive ratios. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Buchbinder, N.; Kimbrel, T.; Levi, R.; Makarychev, K.; Sviridenko, M. Online Make-to-Order Joint Replenishment Model: Primal-Dual Competitive Algorithms. Oper. Res. 2013, 61, 1014–1029. [Google Scholar] [CrossRef]
- Gupta, D.; Li, F. Reserve driver scheduling. IIE Trans. 2016, 48, 193–204. [Google Scholar] [CrossRef]
- Azar, Y.; Boyar, J.; Favrholdt, L.M.; Larsen, K.S.; Nielsen, M.N. Fair versus Unrestricted Bin Packing. In Algorithm Theory—SWAT 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 200–213. [Google Scholar]
- Chen, Y.; Levi, R.; Shi, C. Revenue management of reusable resources with advanced reservations. Prod. Oper. Manag. 2017, 26, 836–859. [Google Scholar] [CrossRef]
- Maillardet, R.; Taylor, P. Queues with advanced reservations: An infinite-server proxy for the bookings diary. Adv. Appl. Probab. 2016, 48, 13–31. [Google Scholar] [CrossRef]
- Van de Vrugt, M.; Litvak, N.; Boucherie, R.J. Blocking probabilities in Erlang loss queues with advance reservation. Stoch. Models 2014, 30, 187–196. [Google Scholar] [CrossRef]
- Miyazawa, H.; Erlebach, T. An Improved Randomized On-Line Algorithm for a Weighted Interval Selection Problem. J. Sched. 2004, 7, 293–311. [Google Scholar] [CrossRef]
- Seiden, S.S. Randomized online interval scheduling. Oper. Res. Lett. 1998, 22, 171–177. [Google Scholar] [CrossRef]
- Faigle, U.; Nawijn, W.M. Note on scheduling intervals on-line. Discret. Appl. Math. 1995, 58, 13–17. [Google Scholar]
- Fung, S.P.Y.; Poon, C.K.; Zheng, F. Online interval scheduling: Randomized and multiprocessor cases. J. Comb. Optim. 2008, 16, 248–262. [Google Scholar] [CrossRef][Green Version]
- Koren, G.; Shasha, D. Dover: An Optimal On-Line Scheduling Algorithm for Overloaded Uniprocessor Real-Time Systems. SIAM J. Comput. 1995, 24, 318–339. [Google Scholar] [CrossRef]
- Baruah, S.; Koren, G.; Mao, D.; Mishra, B.; Raghunathan, A.; Rosier, L.; Shasha, D.; Wang, F. On the competitiveness of on-line real-time task scheduling. Real Time Syst. 1992, 4, 125–144. [Google Scholar] [CrossRef]
- Buchbinder, N.; Naor, J.S. The Design of Competitive Online Algorithms via a Primal–Dual Approach. Found. Trends Theor. Comput. Sci. 2009, 3, 93–263. [Google Scholar] [CrossRef]
- Boyar, J.; Larsen, K.S. The Seat Reservation Problem. Algorithmica 1999, 25, 403–417. [Google Scholar] [CrossRef]
- Lipton, R.J.; Tomkins, A. Online Interval Scheduling. In Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, Arlington, VA, USA, 23–25 January 1994; pp. 302–311. [Google Scholar]
- Garofalakis, M.; Ioannidis, Y.; Özden, B.; Silberschatz, A. Competitive On-line Scheduling of Continuous-Media Streams. J. Comput. Syst. Sci. 2002, 64, 219–248. [Google Scholar] [CrossRef]
- Faigle, U.; Garbe, R.; Kern, W. Randomized online algorithms for maximizing busy time interval scheduling. Computing 1996, 56, 95–104. [Google Scholar] [CrossRef]
- Ball, M.O.; Queyranne, M. Toward Robust Revenue Management: Competitive Analysis of Online Booking. Oper. Res. 2009, 57, 950–963. [Google Scholar] [CrossRef]
- Yao, A.C.C. Probabilistic computations: Toward a unified measure of complexity. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science (SFCS 1977), Providence, RI, USA, 31 October– 2 November 1977; pp. 222–227. [Google Scholar]
- Goyal, S. Essays on The Online Multiple Knapsack Problem & The Online Reservation Problem. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).