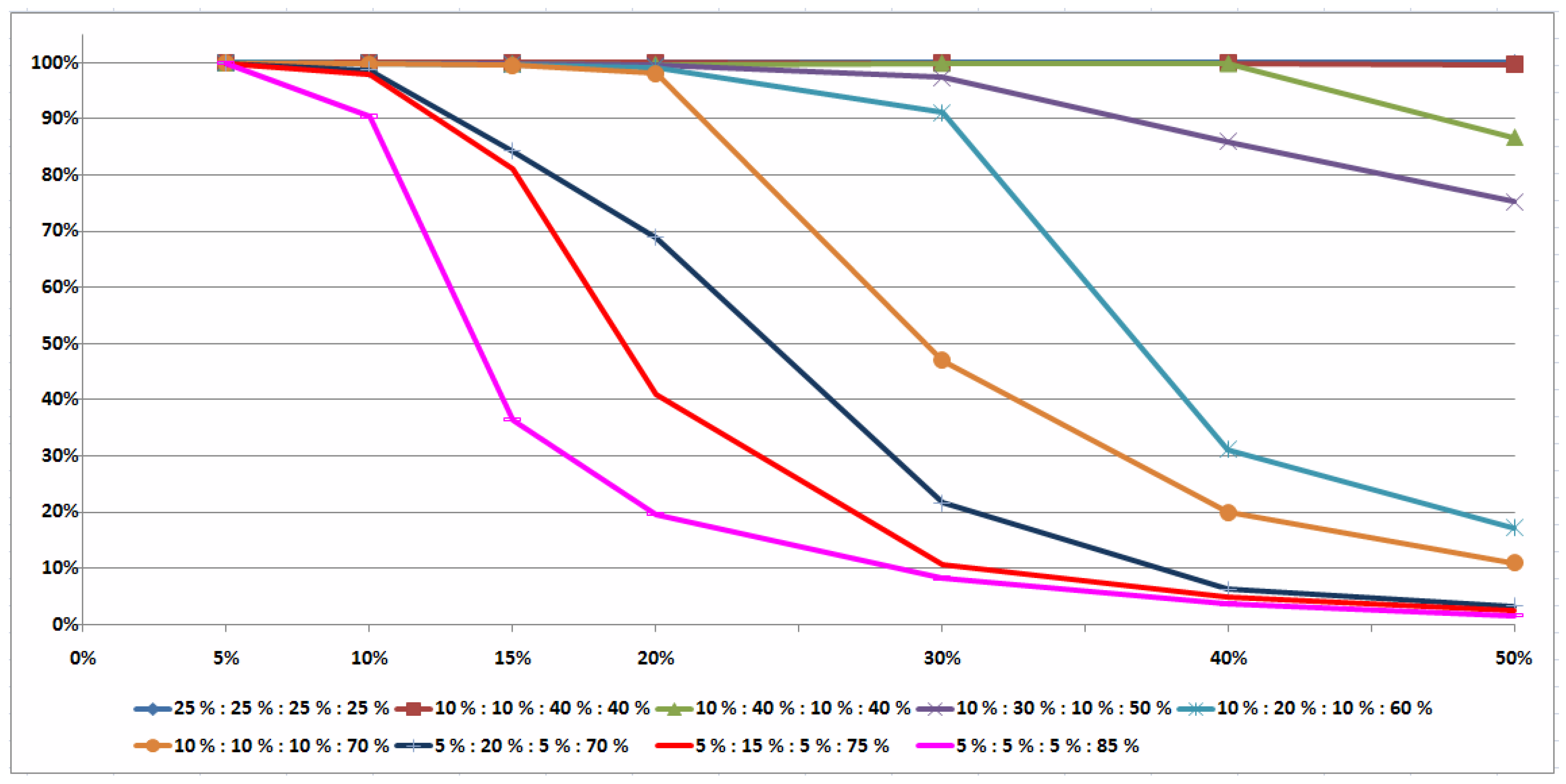
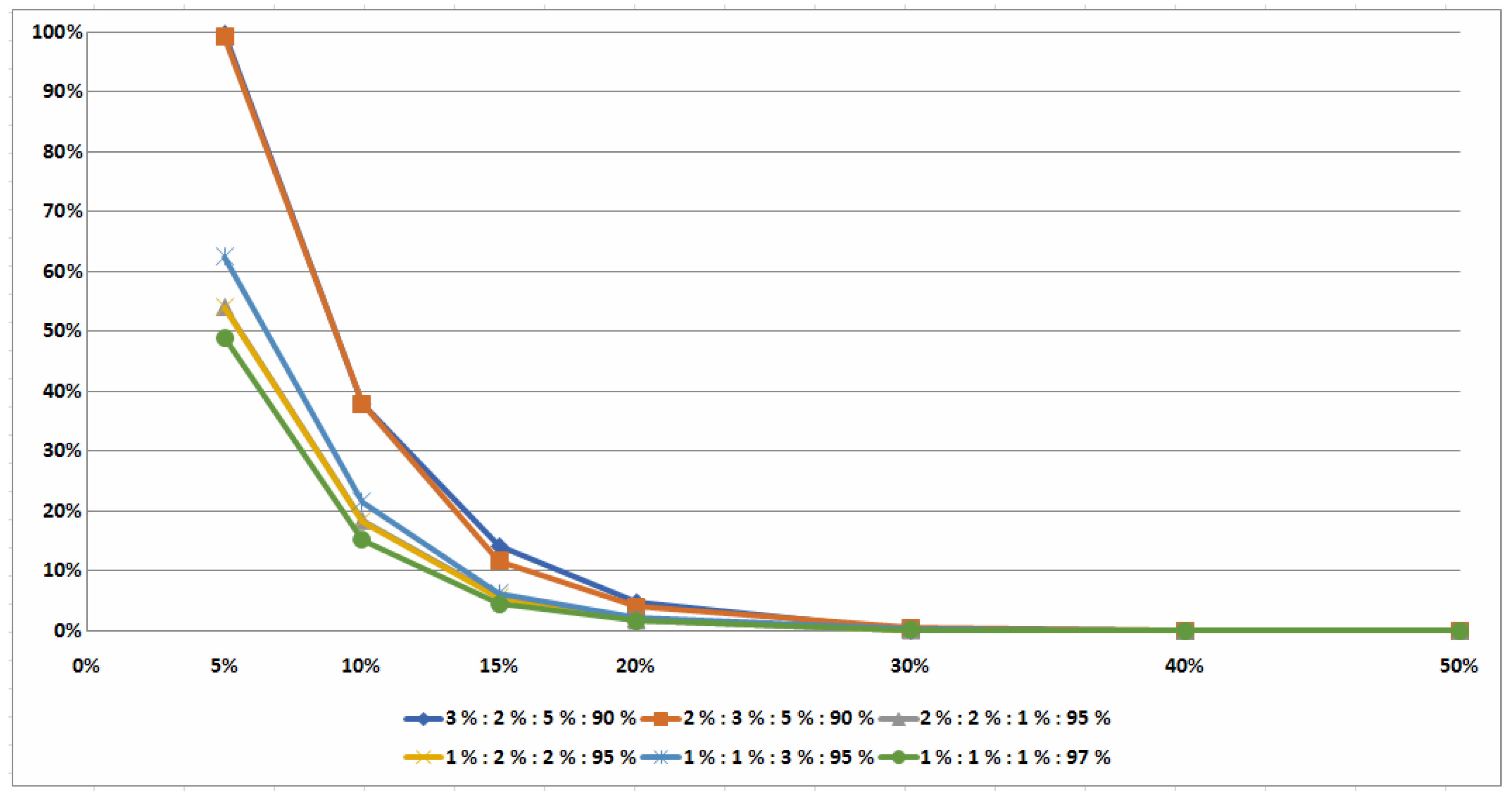
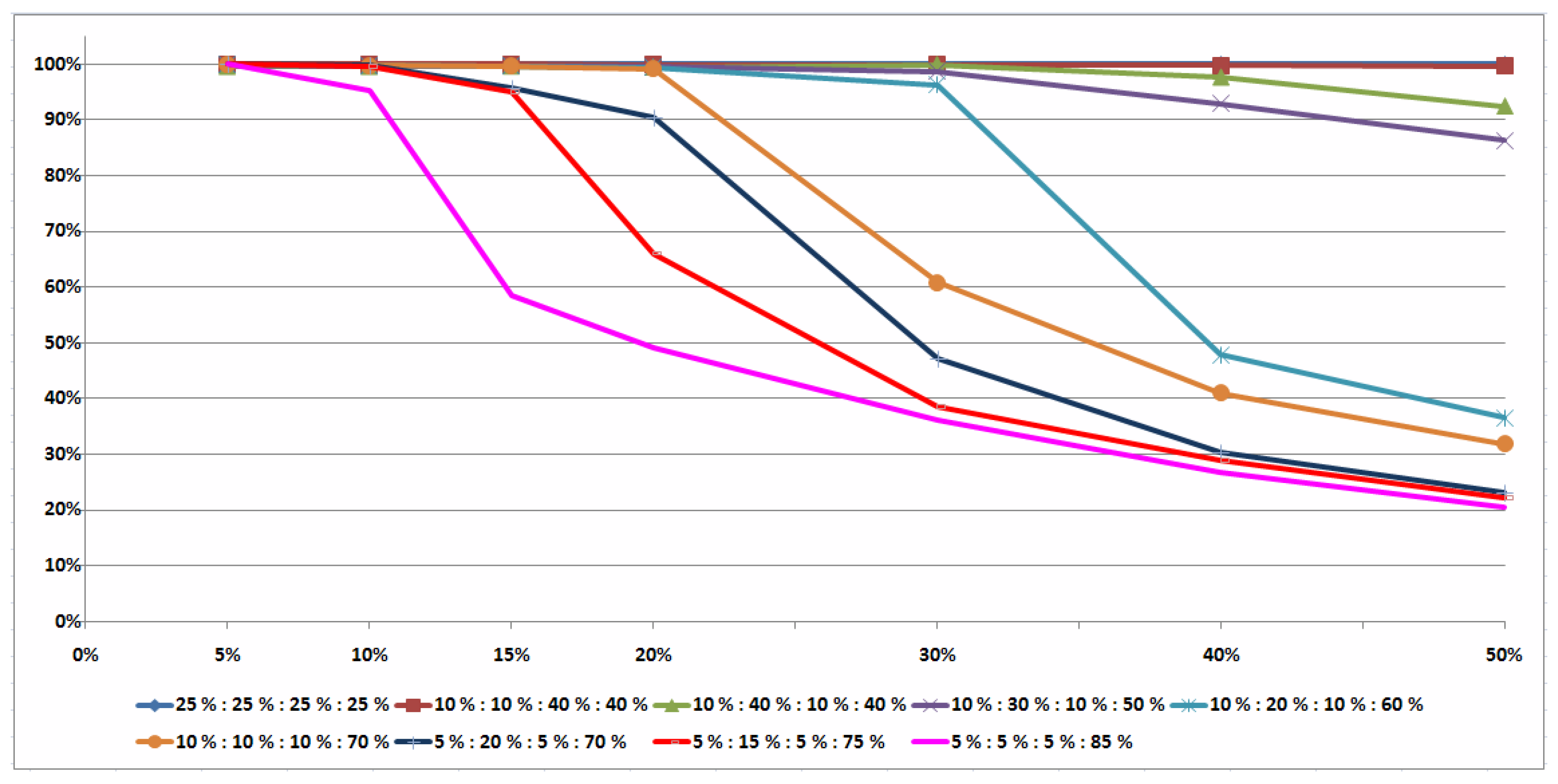
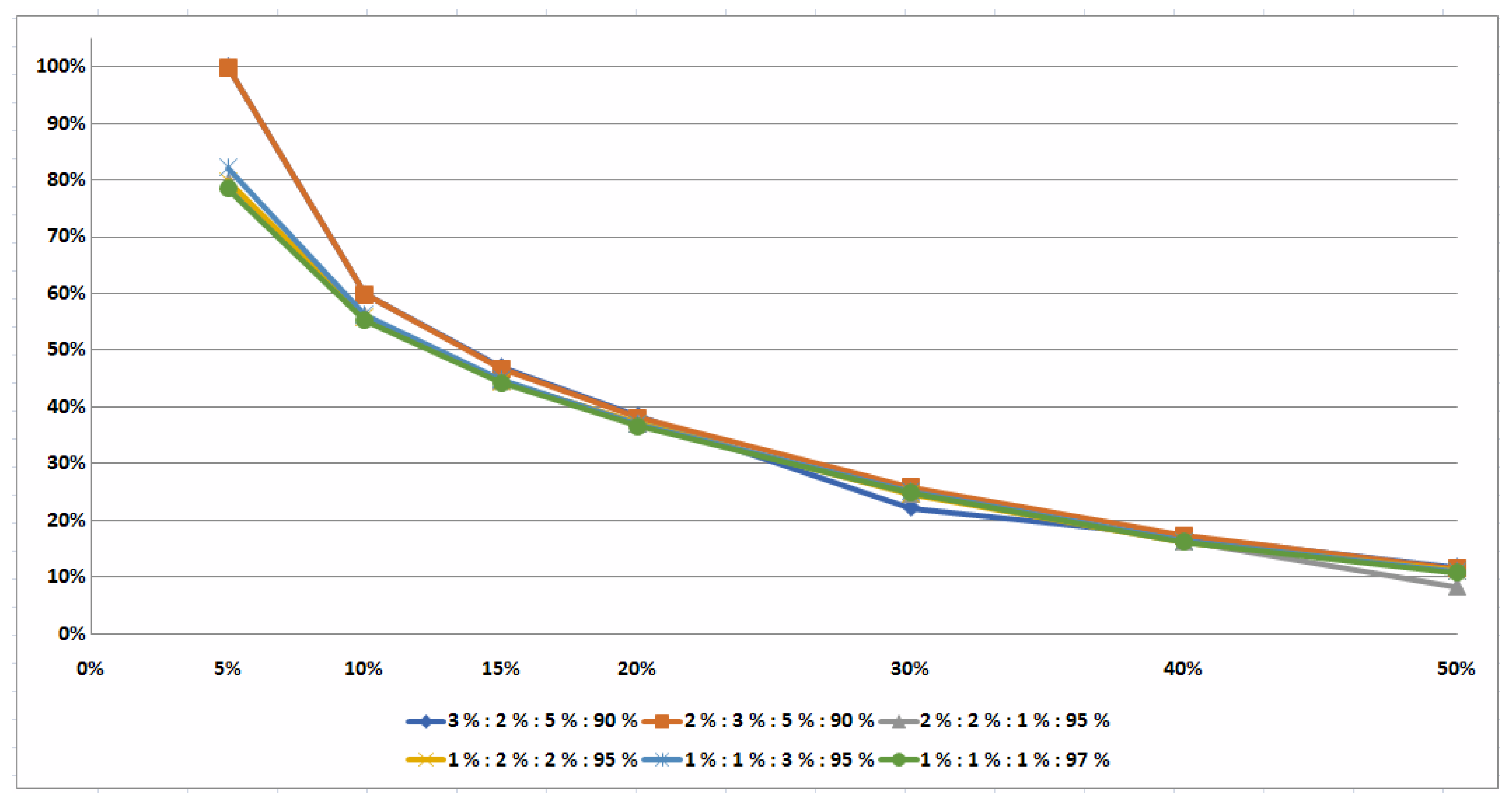
5.1. Sufficient Conditions for an Optimal Pair of Job Permutations
In the proofs of several claims, we use a notion of the main machine, which is introduced within the proof of the following theorem.
Theorem 7. Consider the following conditions in Inequalities (7) or (8): If one of the above conditions holds, then any pair of job permutations is a single-element dominant set for the problem with set of the given jobs.
Proof. Let the condition in Inequalities (
7) hold. Then, we consider an arbitrary pair of job permutations
with any fixed scenario
and show that this pair of job permutations
is optimal for the individual deterministic problem
with scenario
p, i.e.,
.
Let () denote a completion time of all jobs (jobs ) on machine (machine ) in the schedule , where and . For the problem , the maximal completion time of the jobs in schedule may be calculated as follows: .
Machine (machine ) is called a main machine for the schedule if equality holds (equality holds, respectively).
For schedule
, the following equality holds:
where
and
denote total idle times of machine
and machine
in the schedule
, respectively. We next show that, if the condition in Inequalities (
7) holds, then machine
is a main machine for schedule
and machine
has no idle time, i.e., machine
is completely filled in the segment
for processing jobs from the set
. At the initial time
, machine
begins to process jobs from the set
without idle times until the time moment
From the first inequality in (
7), we obtain the following relations:
Therefore, at the time moment , machine begins to process jobs from the set without idle times and we obtain the following equality: where and machine has no idle time. We next show that machine is a main machine for the schedule . To this end, we consider the following two possible cases.
(a) Let machine have no idle time.
By summing Inequalities (
7), we obtain the following inequality:
Thus, the following relations hold:
Hence, machine is a main machine for the schedule .
(b) Let machine have an idle time.
An idle time of machine is only possible if some job from set is processed on machine at the time moment when this job could be processed on machine .
Obviously, after the time moment
when machine
completes all jobs from set
, machine
can process some jobs from set
without an idle time. Therefore, the inequality
holds and we obtain the following relations:
We conclude that, in case
(b), machine
is a main machine for the schedule
. Thus, if the condition in Inequalities (
7) holds, then machine
is a main machine for the schedule
and machine
has no idle time, i.e., equality
holds and machine
is completely filled in the segment
with processing jobs from the set
.
Thus, the pair of permutations is optimal for scenario . Since scenario p was chosen arbitrarily in the set T, we conclude that the pair of job permutations is a singleton for the problem with set of the given jobs. As a pair of permutations is an arbitrary pair of job permutations in the set S, any pair of job permutations is a singleton for the problem with job set .
The case when the condition in Inequalities (
8) holds may be analyzed similarly via replacing machine
by machine
and vice versa. □
If conditions of Theorem 7 hold, then in the optimal pair of job permutations existing for the problem , the orders of jobs from sets and may be chosen arbitrarily. Theorem 7 implies the following two corollaries.
Corollary 3. If the following inequality holds: then set , where is an arbitrary permutation in set , is a dominant set of schedules for the problem with set of the given jobs.
Proof. We consider an arbitrary vector of the job durations and an arbitrary permutation in the set . The set contains at least one Johnson’s permutation for the deterministic problem with job set and scenario (the components of vector are equal to the corresponding components of vector p). We consider a pair of job permutations and show that it is an optimal pair of job permutations for the problem with job set and scenario p. Without loss of generality, both permutations and are ordered in increasing order of the indexes of their jobs.
Similar to the proof of Theorem 7, one can show that, if the condition in Inequalities (
9) holds, then machine
processes jobs without idle times and equality
holds, where the value of
cannot be reduced. If machine
has no idle time, we obtain equalities
On the other hand, an idle time of machine
is only possible if some job
from set
is processed on machine
at the time moment
when job
could be processed on machine
. In such a case, the value of
is equal to the makespan
for the problem
with job set
and scenario
. As the permutation
is a Johnson’s permutation, the value of
cannot be reduced and we obtain the following equalities:
Thus, the pair of job permutation is optimal for the problem with scenario . The optimal pair of job permutations for the problem with scenario belongs to the set . As vector p is an arbitrary vector in the set T, the set contains an optimal pair of job permutations for all scenarios from set T. Due to Definition 4, the set is a dominant set of schedules for the problem with job set . □
Corollary 4. Consider the following inequality: If the above inequality holds, then set , where is an arbitrary permutation in set , is a dominant set of schedules for the problem with set of the given jobs.
This claim may be proven similar to Corollary 3. If the conditions of Corollary 3 (Corollary 4) hold, then the order for processing jobs from set (set , respectively) in the optimal schedule for the problem may be arbitrary. Since the orders of jobs from the sets and are fixed in the optimal schedule (Remark 1), we need to determine only orders for processing jobs from set (set , respectively). To do this, we will consider two uncertain problems with job set and with the machine route and that with job set and with the opposite machine route .
Lemma 2. If is a set of permutations from the dominant set for the problem with job set , then is a dominant set for the problem with job set .
The proof of Lemma 2 and those for other statements in this section are given in
Appendix A.
Lemma 3. Let be a set of permutations from the dominant set for the problem with job set , . Then, is a dominant set for the problem with job set .
The proof of this claim is similar to that for Lemma 2 (see
Appendix A).
Theorem 8. Let be a set of permutations from the dominant set for the problem with job set , and let be a set of permutations from the dominant set for the problem with job set . Then, is a dominant set for the problem with job set .
Theorem 9. Let a pair of identical permutations determine a single-element J-solution for the problem with job set , and let a pair of identical permutations determine a single-element J-solution for the problem with job set . Then, the pairs of permutations are a single-element dominant set for the problem with job set .
The following claim follows directly from Theorem 9.
Corollary 5. If the conditions of Theorem 9 hold, then there exists a single pair of job permutations, which is an optimal pair of job permutations for the problem with job set and any scenario .
Theorem 9 implies also the following corollary proven in
Appendix A.
Corollary 6. If the conditions of Theorem 9 hold, then there exists a single pair of job permutations which is a J-solution for the problem with job set .
Note that the criterion for a single-element J-solution for the problem is given in Theorem 2.
5.2. Precedence Digraphs Determining a Minimal Dominant Set of Schedules
In
Section 4.2, it is assumed that
and
, i.e.,
. Based on the results presented in
Section 4.2, we can determine a binary relation
for the problem
with job set
and a binary relation
for this problem with job set
. For job set
, the binary relation
determines the digraph
with the vertex set
and the arc set
. For job set
, the binary relation
determines the digraph
with the vertex set
and the arc set
.
Let us consider the problem with job set and the corresponding digraph (the same results for the problem with job set can be derived in a similar way).
Definition 5. Two jobs, and , , are called conflict jobs if they are not in the relation , i.e., and .
Due to Definitions 2 and 3, for the conflict jobs
and
,
, Inequalities (
4) and (
5) do not hold either for the case
with
or for the case
with
.
Definition 6. The subset is called a conflict set of jobs if, for any job , either relation or relation holds for each job (provided that any proper subset of the set does not possess such a property).
From Definition 6, it follows that the conflict set
is a minimal set (with respect to the inclusion). Obviously, there may exist several conflict sets in the set
. (A conflict set of the jobs
can be determined similarly.) Let the strict order
for the problem
with job set
be represented as follows:
where all jobs between braces are conflict ones and each of these jobs is in relation
with any job located outside the brackets in Relation (
10). In such a case, an optimal order for processing jobs from the set
is determined as follows:
.
Due to Theorem 5, we obtain that set of the permutations generated by the digraph contains an optimal Johnson’s permutation for each vector of the durations of jobs from the set . Thus, due to Definition 1, the singleton , where , is a J-solution for the problem with job set . Analogously, the singleton , where , is a J-solution for the problem with job set . We can determine a dominant set of schedules for the problem with job set as follows: . The following theorems allow us to reduce a dominant set for the problem . We use the following notation:
Theorem 10. Let the strict order over set be determined as follows: . Consider the following inequality: If the above inequality holds, then set with is a dominant set of schedules for the problem with job set .
Proof. We consider an arbitrary vector of the job durations and an arbitrary permutation from the set . The set contains at least one optimal Johnson’s permutation for the problem with job set and vector of the job durations (components of this vector are equal to the corresponding components of the vector p).
We consider a pair of job permutations
and show that it is an optimal pair of job permutations for the problem
with set
of the jobs and scenario
p. To this end, we show that the value of
cannot be reduced. Indeed, an idle time for machine
is only possible if some job
from the set
is processed on machine
at the same time when job
could be processed on machine
. In such a case,
is equal to the makespan
for the problem
with job set
and vector
of the job durations. As permutation
is a Johnson’s permutation, the value of
cannot be reduced. In the beginning of the permutation
, the jobs of set
are arranged in the Johnson’s order. Thus, if machine
has an idle time while processing these jobs, this idle time cannot be reduced. From Inequality (
11), it follows that machine
has no idle time while processing jobs from the conflict set.
In the end of the permutation , jobs of set are arranged in Johnson’s order. Therefore, if machine has an idle time while processing these jobs, this idle time cannot be reduced. Thus, the value of cannot be reduced by changing the order of jobs in the conflict set.
We obtain the qualities The pair of job permutations is optimal for the problem with scenario . Thus, set contains an optimal pair of job permutations for the problem with scenario . As vector p is an arbitrary vector in set T, set contains an optimal pair of job permutations for each vector from set T. Due to Definition 4, set is a dominant set of schedules for the problem with job set . □
Theorem 11. Let the partial strict order over set be determined as follows: . Consider the following inequality:If the above inequality holds for all then the set , where , is a dominant set for the problem with job set . Proof. We consider an arbitrary scenario and a pair of job permutations , where is a Johnson’s permutation of the jobs from the set with vector of the job durations (components of this vector are equal to the corresponding components of vector p). We next show that this pair of job permutations is optimal for the individual deterministic problem with scenario p, i.e., .
If conditions of Theorem 11 hold, then machine processes jobs from the conflict set without idle times. At the initial time , machine begins to process jobs from the permutation without idle times. Let a time moment be as follows: At the time moment , job is ready for processing on machine .
On the other hand, at the time
, machine
begins to process jobs from the set
without idle times and then jobs from the permutation
. Let
denote the first time moment when machine
is ready for processing job
. Obviously, the following inequality holds:
From the condition in Inequality (
12) with
, we obtain inequality
Therefore, the following relations hold:
Machine processes job without an idle time between job and job .
Analogously, using , one can show that machine processes jobs from the conflict set without idle times between jobs and , between jobs and , and so on to between jobs and . To end this proof, we have to show that the value of cannot be reduced.
An idle time for machine is only possible between some jobs from the set . However, the permutation is a Johnson’s permutation of the jobs from the set for the vector of the job durations. Therefore, the value of cannot be reduced. On the other hand, in the permutation , all jobs and all jobs are arranged in Johnson’s orders. Therefore, if machine has an idle time while processing these jobs, this idle time cannot be reduced. It is clear that machine has no idle time while processing jobs from the conflict set. Thus, the value of cannot be reduced by changing the order of jobs from the conflict set. We obtain the equalities
It is shown that the pair of job permutations is optimal for the problem with vector of job durations. As vector p is an arbitrary one in set T, the set contains an optimal pair of job permutations for each scenario from set T. Due to Definition 4, the set is a dominant set of schedules for the problem with job set . □
The proof of the following theorem is given in
Appendix A.
Theorem 12. Let the partial strict order over set have the form . If inequalitieshold for all indexes , then the set , where , is a dominant set of pairs of permutations for the problem with job set . Similarly, one can prove sufficient conditions for the existence of an optimal job permutation for the problem with job set , when the partial strict order on the set has the following form: .
To apply Theorems 11 and 12, one can construct a job permutation that satisfies the strict order . Then, one can check the conditions of Theorems 11 and 12 for the constructed permutation. If the set of jobs is empty in the constructed permutation, one needs to check conditions of Theorem 12. If the set of jobs is empty, one needs to check the conditions of Theorem 11. It is needed to construct only one permutation to check Theorem 11 and only one permutation to check Theorem 12.
5.3. Two Illustrative Examples
Example 1. We consider the uncertain job-shop scheduling problem with lower and upper bounds of the job durations given in Table 1. These bounds determine the set T of possible scenarios. In Example 1, jobs , , and have the machine route ; jobs , , and have the machine route ; and job (job , respectively) has to be processed only on machine (on machine , respectively). Thus, , , , .
We check the conditions of Theorem 7 for a single pair of job permutations, which is optimal for all scenarios
T. For the given jobs, the condition in Inequalities (
7) of Theorem 7 holds due to the following relations:
Due to Theorem 7, the order of jobs from the set and the order of jobs from the set may be arbitrary in the optimal pair of job permutations for the problem under consideration. Thus, any pair of job permutations is a single-element dominant set for Example 1.
Example 2. Let us now consider the problem with numerical input data given in Table 1 with the following two exceptions: and . We check the condition in Inequalities (
7) of Theorem 7 and obtain
Thus, the condition of Inequalities (
7) does not hold for Example 2. We check the condition of Inequalities (
8) of Theorem 7 and obtain
However, we see that the condition of Equation (
8) does not hold:
From Equation (
14), it follows that the condition of Inequalities (
9) of Corollary 3 does not hold. On the other hand, due to Equation (
15), conditions of Corollary 4 hold. Thus, the order for processing jobs from set
in the optimal schedule
for the problem
may be arbitrary. One can fix permutation
with the increasing order of the indexes of their jobs:
. Since the orders of jobs from the sets
and
are fixed in the optimal schedule (Remark 1), i.e.,
and
, we need to determine the order for processing jobs in set
. To this end, we consider the problem
with job set
. We see that conditions of Theorem 2 do not hold for the jobs in set
since
,
, and
; however the following inequalities hold:
and
.
We next construct the binary relation
over set
based on Definition 3 and Theorem 1. Due to checking Inequalities (
4) and (
5), we conclude that the inequality in Equation (
5) holds for the pair of jobs
and
. We obtain the relation
. Analogously, we obtain the relation
. For the pair of jobs
and
, neither Inequality (
4) nor Inequality (
5) hold. Therefore, the partial strict order
over set
has the following form:
. The job set
is a conflict set of these jobs (Definition 6).
Let us check whether the sufficient conditions given in
Section 5.2 hold.
We check the conditions of Theorem 10 for the jobs from set
. For
and
, we obtain the following equalities:
The condition of Theorem 10 does not hold since the following relations hold:
For checking the conditions of Theorem 11, we need to check both permutations of the jobs from set , which satisfy the partial strict order : , where and .
We consider permutation
. As in the previous case,
,
,
, and we must consider two inequalities in the condition in Equaiton (
12) with
and
. For
, we obtain the following:
However, for
, we obtain
Thus, the conditions of Theorem 11 do not hold for permutation .
We consider permutation
, where
and
. Again, we must test the two inequalities in Equation (
12), where either
or
. For
, we obtain
However, for
, we obtain
Thus, the conditions of Theorem 11 do not hold for permutation .
Note that we do not check the conditions of Theorem 12 since the conflict set of jobs
is located at the end of the partial strict order
. We conclude that none of the proven sufficient conditions are satisfied for a schedule optimality. Thus, there does not exist a pair of permutations of the jobs in set
which is optimal for any scenario
. The
J-solution
for Example 2 consists of the following two pairs of job permutations:
, where
We next show that none of these two pairs of job permutations is optimal for all scenarios using the following two scenarios: and For scenario , only pair of permutations is optimal with since . On the other hand, for scenario , only the pair of permutations is optimal with since .
Note that the whole set S of the semi-active schedules has the cardinality . Thus, for solving Example 2, one needs to consider only two pairs of job permutations instead of 36 semi-active schedules.