Parameterized Optimization in Uncertain Graphs—A Survey and Some Results
Abstract
1. Introduction
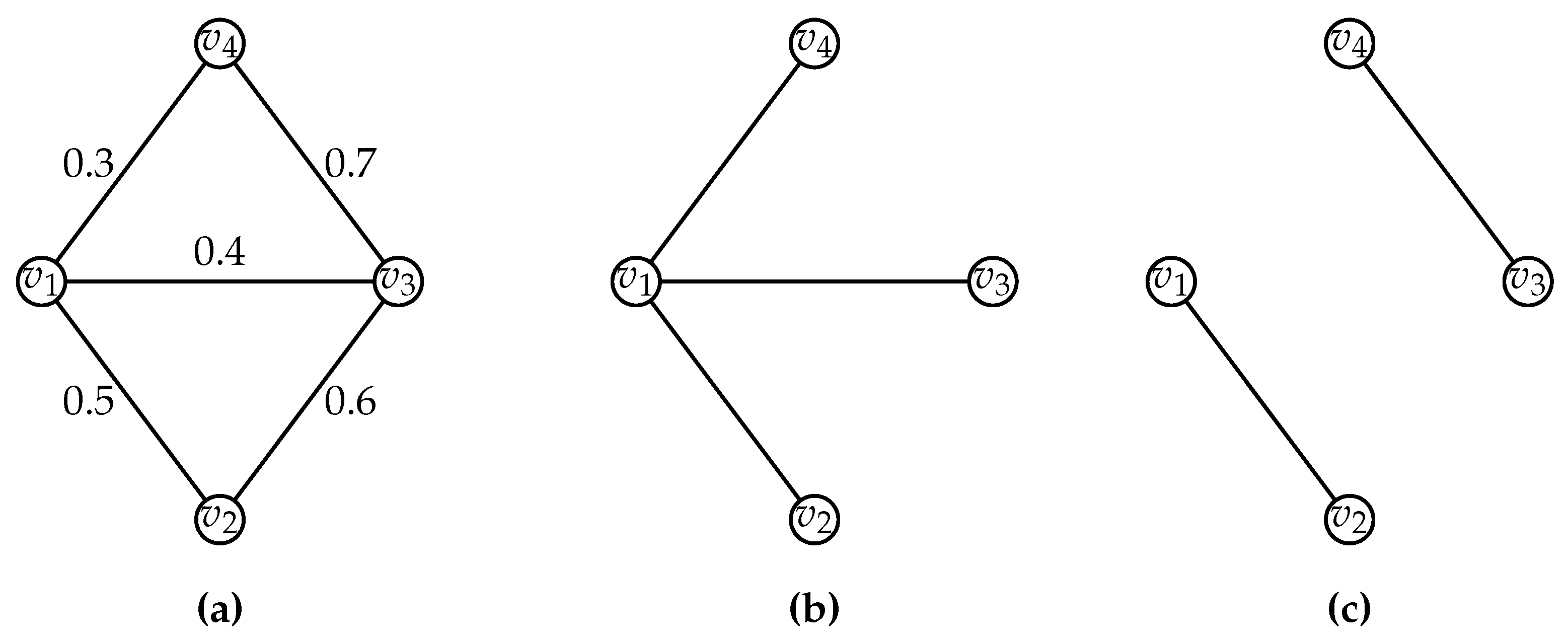
1.1. Uncertain Graphs-Definition and Semantics
1.2. Survey of Optimization Problems in Uncertain Graphs
1.3. Our Questions and Results
2. Distribution Models for Uncertain Graphs
2.1. Random Failure Model
2.2. Independent Cascade Model
2.3. Set-Based Dependency (SBD) Model
2.4. Linear Reliable Ordering (LRO) Model
3. Definitions Related to Graphs
- (a)
- For each vertex , there is a node such that .
- (b)
- For each edge , there is a node such that .
- (c)
- For each vertex , the induced subtree of the nodes in H that contains v is connected.
- 1.
- Leaf node.A node with no child and .
- 2.
- Introduce node.A node with one child j such that for some .
- 3.
- Forget node.A node with one child j such that for some .
- 4.
- Join node.A node with two children j and g such that .
4. Max-Exp-Cover-1-RF Problem is FPT by )
4.1. Recursive Formulation of the Value of a Solution
4.2. Bottom-Up Computation of an Optimal Set
- Case . Define . Let denote the partition of obtained by removing vertex v from the set A of the partition . Let be the SN-function defined as follows:Then,
- Case . Since v is in but not in it follows that . Therefore, the coverage of the vertex v by the vertices that occur only in is zero. Let be the partition of obtained by removing the vertex v from the appropriate set in the partition . The SN-function is defined as follows on the set : For , .
- For each , and .
- For each , and .
- For each , and are defined as follows. For each partition , and .
- Case . Let be the partition of obtained from by removing v from A. Let be the SN-function on such that , if and , otherwise. We know from our claimed optimality of , and that , and the value of , thatTherefore, it follows that . In other words, we have concluded that the value for the row in is not the optimum value. This contradicts our premise at node j, which is of height at most for which, by induction hypothesis, the table maintains the optimal values. Therefore, our assumption that is not optimum is wrong.
- Case . Let be the partition of obtained by removing v from the appropriate set in the partition . Let be the SN-function on such that for each . We know from our claimed optimality of , and that , and the value of that . Therefore, it follows that . In other words, we have concluded that the value for the row in is not the optimum value. This contradicts our premise at node j, which is of height at most for which, by induction hypothesis, the table maintains the optimal values. Therefore, our assumption that is not optimum is wrong.
5. Parameterized Complexity of Probabilistic-Core Problem
5.1. An Exact Algorithm for the Probabilistic-Core-LRO Problem
| Algorithm 1:Probabilistic-Core-LRO |
 |
5.2. Parameterized Complexity of the Probabilistic-Core-RF Problem
5.3. The Probabilistic-Core-RF Problem is FPT by Treewidth
- for each , and , and
- for each , .
5.3.1. Dynamic Programming
5.3.2. Correctness and Running Time
6. Discussion
- Are there efficient reductions between distribution models so that we can classify problems based on the efficiency of algorithms under different distribution models? This question is also of practical significance because the distribution models are specified as sampling algorithms. Consequently, the complexity of expectation computation on uncertain graphs under different distribution models is an interesting new parameterization. Further, one concrete question is whether the LRO model is easier than the RF model for other optimization problems on uncertain graphs. For the two case studies considered in this paper, that is the case.
- While our results do support the natural intuition that a tree decomposition is helpful in expectation computation, it is unclear to us how traditional techniques in parameterized algortihms can be carried over to this setting. In particular, it is unclear to us as to whether for any distribution model, a kernelization based algorithm can give an FPT algorithm on uncertain graphs.
- We have considered the coverage and the core problems on uncertain graphs under the LRO and RF models. However, we have not been able to get an FPT algorithm with the parameter treewidth for Max-Exp-Cover-1-RF. Actually, any approach to avoid the exponential dependence on would be very interesting and would give a significant insight on other approaches to evaluate the expected coverage.
- Even though the Individual-Core-RF problem and Probabilistic-Core-RF problem are similar, we have not been able to get an FPT algorithm for the Individual-Core-RF problem with treewidth as the parameter. Even for other structural parameters such as vertex-cover number and feedback vertex set number, FPT results will give a significant insight on the Individual-Core problem.
Author Contributions
Funding
Conflicts of Interest
References
- Añez, J.; Barra, T.D.L.; Pérez, B. Dual graph representation of transport networks. Trans. Res. Part B Methodol. 1996, 30, 209–216. [Google Scholar] [CrossRef]
- Hua, M.; Pei, J. Probabilistic Path Queries in Road Networks: Traffic Uncertainty Aware Path Selection. In Proceedings of the 13th International Conference on Extending Database Technology (EDBT ’10), Lausanne, Switzerland, 22–26 March 2010; pp. 347–358. [Google Scholar] [CrossRef]
- Asthana, S.; King, O.D.; Gibbons, F.D.; Roth, F.P. Predicting protein complex membership using probabilistic network reliability. Genome Res. 2004, 14, 1170–1175. [Google Scholar] [CrossRef]
- Domingos, P.; Richardson, M. Mining the Network Value of Customers. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’01), San Francisco, CA, USA, 26–29 August 2001; pp. 57–66. [Google Scholar] [CrossRef]
- Frank, H. Shortest Paths in Probabilistic Graphs. Oper. Res. 1969, 17, 583–599. [Google Scholar] [CrossRef]
- Valiant, L.G. The Complexity of Enumeration and Reliability Problems. SIAM J. Comput. 1979, 8, 410–421. [Google Scholar] [CrossRef]
- Hoffmann, M.; Erlebach, T.; Krizanc, D.; Mihalák, M.; Raman, R. Computing Minimum Spanning Trees with Uncertainty. In Proceedings of the 25th Annual Symposium on Theoretical Aspects of Computer Science, Bordeaux, France, 21–23 February 2008; pp. 277–288. [Google Scholar] [CrossRef]
- Focke, J.; Megow, N.; Meißner, J. Minimum Spanning Tree under Explorable Uncertainty in Theory and Experiments. In Proceedings of the 16th International Symposium on Experimental Algorithms (SEA 2017), London, UK, 21–23 June 2017; pp. 22:1–22:14. [Google Scholar] [CrossRef]
- Frank, H.; Hakimi, S. Probabilistic Flows Through a Communication Network. IEEE Trans. Circuit Theory 1965, 12, 413–414. [Google Scholar] [CrossRef]
- Evans, J.R. Maximum flow in probabilistic graphs-the discrete case. Networks 1976, 6, 161–183. [Google Scholar] [CrossRef]
- Hassin, R.; Ravi, R.; Salman, F.S. Tractable Cases of Facility Location on a Network with a Linear Reliability Order of Links. In Algorithms-ESA 2009, Proceedings of the 17th Annual European Symposium, Copenhagen, Denmark, 7–9 September 2009; Springer: Berlin, Germany, 2009; pp. 275–276. [Google Scholar]
- Hassin, R.; Ravi, R.; Salman, F.S. Multiple facility location on a network with linear reliability order of edges. J. Comb. Optim. 2017, 34, 1–25. [Google Scholar] [CrossRef]
- Narayanaswamy, N.S.; Nasre, M.; Vijayaragunathan, R. Facility Location on Planar Graphs with Unreliable Links. In Proceedings of the Computer Science-Theory and Applications-13th International Computer Science Symposium in Russia, CSR 2018, Moscow, Russia, 6–10 June 2018; pp. 269–281. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.M.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar] [CrossRef]
- Bonchi, F.; Gullo, F.; Kaltenbrunner, A.; Volkovich, Y. Core decomposition of uncertain graphs. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’14), New York, NY, USA, 24–27 August 2014; pp. 1316–1325. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Y.; Zhang, W.; Lin, X.; Qin, L. Efficient Probabilistic K-Core Computation on Uncertain Graphs. In Proceedings of the 34th IEEE International Conference on Data Engineering (ICDE), Paris, France, 16–19 April 2018; pp. 1192–1203. [Google Scholar] [CrossRef]
- Ball, M.O.; Provan, J.S. Calculating bounds on reachability and connectedness in stochastic networks. Networks 1983, 13, 253–278. [Google Scholar] [CrossRef]
- Zou, Z.; Li, J. Structural-Context Similarities for Uncertain Graphs. In Proceedings of the 2013 IEEE 13th International Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; pp. 1325–1330. [Google Scholar] [CrossRef]
- Daskin, M.S. A Maximum Expected Covering Location Model: Formulation, Properties and Heuristic Solution. Transp. Sci. 1983, 17, 48–70. [Google Scholar] [CrossRef]
- Ball, M.O. Complexity of network reliability computations. Networks 1980, 10, 153–165. [Google Scholar] [CrossRef]
- Karp, R.M.; Luby, M. Monte-Carlo algorithms for the planar multiterminal network reliability problem. J. Complex. 1985, 1, 45–64. [Google Scholar] [CrossRef][Green Version]
- Provan, J.S.; Ball, M.O. The Complexity of Counting Cuts and of Computing the Probability that a Graph is Connected. SIAM J. Comput. 1983, 12, 777–788. [Google Scholar] [CrossRef]
- Guo, H.; Jerrum, M. A Polynomial-Time Approximation Algorithm for All-Terminal Network Reliability. SIAM J. Comput. 2019, 48, 964–978. [Google Scholar] [CrossRef]
- Ghosh, J.; Ngo, H.Q.; Yoon, S.; Qiao, C. On a Routing Problem Within Probabilistic Graphs and its Application to Intermittently Connected Networks. In Proceedings of the 26th IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies, INFOCOM, Anchorage, AK, USA, 6–12 May 2007; pp. 1721–1729. [Google Scholar] [CrossRef]
- Rubino, G. Network Performance Modeling and Simulation; chapter Network Reliability Evaluation; Gordon and Breach Science Publishers, Inc.: Newark, NJ, USA, 1999; pp. 275–302. [Google Scholar]
- Swamynathan, G.; Wilson, C.; Boe, B.; Almeroth, K.C.; Zhao, B.Y. Do social networks improve e-commerce?: a study on social marketplaces. In Proceedings of the first Workshop on Online Social Networks (WOSN 2008), Seattle, WA, USA, 17–22 August 2008; pp. 1–6. [Google Scholar] [CrossRef]
- White, D.R.; Harary, F. The Cohesiveness of Blocks In Social Networks: Node Connectivity and Conditional Density. Soc. Methodol. 2001, 31, 305–359. [Google Scholar] [CrossRef]
- Papadimitriou, C.H.; Yannakakis, M. Shortest paths without a map. Theor. Comput. Sci. 1991, 84, 127–150. [Google Scholar] [CrossRef]
- Khuller, S.; Moss, A.; Naor, J. The Budgeted Maximum Coverage Problem. Inf. Process. Lett. 1999, 70, 39–45. [Google Scholar] [CrossRef]
- Brown, J.J.; Reingen, P.H. Social Ties and Word-of-Mouth Referral Behavior. J. Consum. Res. 1987, 14, 350–362. [Google Scholar] [CrossRef]
- Richardson, M.; Domingos, P.M. Mining knowledge-sharing sites for viral marketing. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 61–70. [Google Scholar] [CrossRef]
- Bass, F.M. A New Product Growth for Model Consumer Durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Snyder, L.V. Facility location under uncertainty: A review. IIE Trans. 2006, 38, 547–564. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Gendreau, M.; Laporte, G. Location of facilities on a network subject to a single-edge failure. Networks 1992, 22, 231–246. [Google Scholar] [CrossRef]
- Colbourn, C.J.; Xue, G. A linear time algorithm for computing the most reliable source on a series-parallel graph with unreliable edges. Theor. Comput. Sci. 1998, 209, 331–345. [Google Scholar] [CrossRef]
- Ding, W. Computing the Most Reliable Source on Stochastic Ring Networks. In Proceedings of the 2009 WRI World Congress on Software Engineering, Xiamen, China, 19–21 May 2009; Volume 1, pp. 345–347. [Google Scholar] [CrossRef]
- Ding, W.; Xue, G. A linear time algorithm for computing a most reliable source on a tree network with faulty nodes. Theor. Comput. Sci. 2011, 412, 225–232. [Google Scholar] [CrossRef][Green Version]
- Melachrinoudis, E.; Helander, M.E. A single facility location problem on a tree with unreliable edges. Networks 1996, 27, 219–237. [Google Scholar] [CrossRef]
- Nemhauser, G.L.; Wolsey, L.A.; Fisher, M.L. An analysis of approximations for maximizing submodular set functions—I. Math. Program. 1978, 14, 265–294. [Google Scholar] [CrossRef]
- Cygan, M.; Fomin, F.V.; Kowalik, L.; Lokshtanov, D.; Marx, D.; Pilipczuk, M.; Pilipczuk, M.; Saurabh, S. Parameterized Algorithms; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Sigal, C.E.; Pritsker, A.A.B.; Solberg, J.J. The Stochastic Shortest Route Problem. Oper. Res. 1980, 28, 1122–1129. [Google Scholar] [CrossRef]
- Guerin, R.A.; Orda, A. QoS routing in networks with inaccurate information: Theory and algorithms. IEEE/ACM Trans. Netw. 1999, 7, 350–364. [Google Scholar] [CrossRef]
- Günneç, D.; Salman, F.S. Assessing the reliability and the expected performance of a network under disaster risk. In Proceedings of the International Network Optimization Conference (INOC), Spa, Belgium, 22–25 April 2007. [Google Scholar]
- Diestel, R. Graph Theory, 4th ed.; Graduate Texts in Mathematics; Springer: Berlin, Germany, 2012; Volume 173. [Google Scholar]
- Bodlaender, H.L. A Tourist Guide through Treewidth. Acta Cybern. 1993, 11, 1–21. [Google Scholar]
- Kloks, T. Treewidth, Computations and Approximations; Lecture Notes in Computer Science; Springer: Berlin, Germany, 1994; Volume 842. [Google Scholar]
- Downey, R.G.; Fellows, M.R. Fixed-parameter intractability. In Proceedings of the Seventh Annual Structure in Complexity Theory Conference, Boston, MA, USA, 22–25 June 1992. [Google Scholar]
- Koster, A.M.C.A.; Wolle, T.; Bodlaender, H.L. Degree-Based Treewidth Lower Bounds. In Proceedings of the 4th International Workshop, WEA 2005 Experimental and Efficient Algorithms, Santorini Island, Greece, 10–13 May 2005; pp. 101–112. [Google Scholar] [CrossRef]

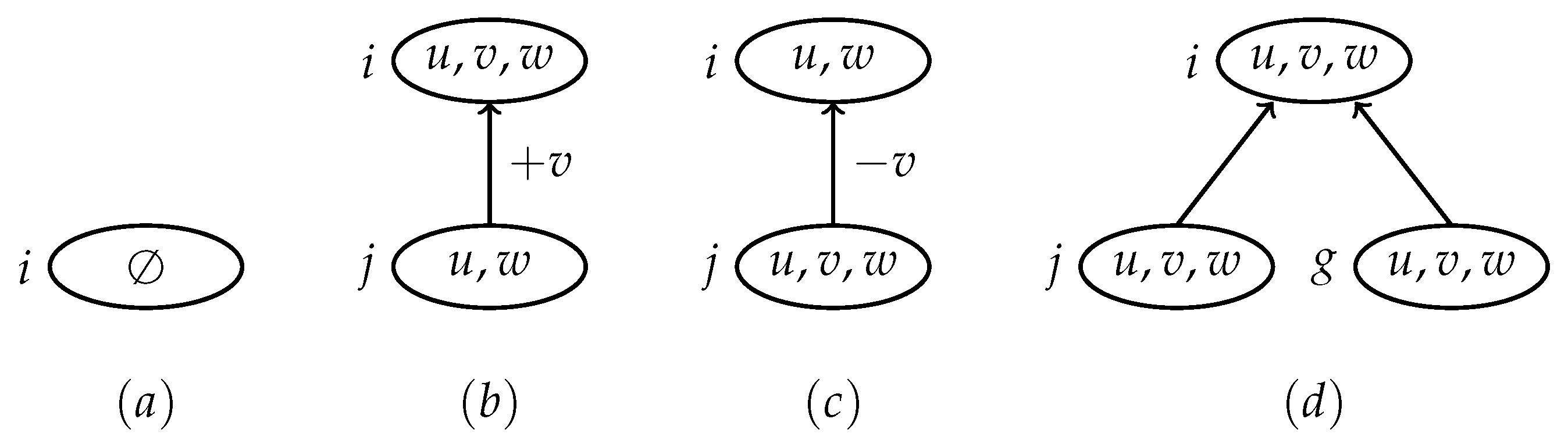
| Work | Optimization Problem | Uncertainty Model |
|---|---|---|
| Frank and Hakimi, 1965 [9] | Probabilistic maximum flow | Capacities on the edges are drawn from an independent continuous distribution. |
| Frank, 1969 [5] | Probabilistic shortest path | Length of the edges are drawn from a continuous distribution. |
| Evans, 1976 [10] | Probabilistic maximum flow | Capacities on the edges are obtained from an arbitrary but unknown discrete probability distribution. |
| Valiant, 1979 [6] | Network reliability | The probability is the same for each edge and failure of every edge is independent. |
| Sigal, Pritsker and Solberg, 1980 [41] | Stochastic shortest path | Edge weights are drawn from a known cumulative distribution function. |
| Daskin, 1983 [19] | Expected coverage | Failure probability is the same for each vertex |
| Papadimitriou Yannakakis, 1991 [28] | Canadian Traveler Problem | Each edge has a survival probability, edge failure is independent and algorithm knows of the failure during execution. |
| Guerin and Orda, 1999 [42] | Most reliable path and flows with bandwidth selection | Each edge e has a survival probability for the availability of bandwidth x. |
| Hassin, Salman and Ravi, 2009 (2017) [11,12] | Expected coverage | Each edge e has a survival probability and edge failure follows LRO model. |
| Bonchi, Gullo, Kaltenbrunner and Volkovich, 2014 [15] | Probabilistic-Core | Each edge e has a survival probability and edge failure follows RF model. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narayanaswamy, N.S.; Vijayaragunathan, R. Parameterized Optimization in Uncertain Graphs—A Survey and Some Results. Algorithms 2020, 13, 3. https://doi.org/10.3390/a13010003
Narayanaswamy NS, Vijayaragunathan R. Parameterized Optimization in Uncertain Graphs—A Survey and Some Results. Algorithms. 2020; 13(1):3. https://doi.org/10.3390/a13010003
Chicago/Turabian StyleNarayanaswamy, N. S., and R. Vijayaragunathan. 2020. "Parameterized Optimization in Uncertain Graphs—A Survey and Some Results" Algorithms 13, no. 1: 3. https://doi.org/10.3390/a13010003
APA StyleNarayanaswamy, N. S., & Vijayaragunathan, R. (2020). Parameterized Optimization in Uncertain Graphs—A Survey and Some Results. Algorithms, 13(1), 3. https://doi.org/10.3390/a13010003





