Abstract
This manuscript will explore and analyze the effects of different paradigms for the control of rigid body motion mechanics. The experimental setup will include deterministic artificial intelligence composed of optimal self-awareness statements together with a novel, optimal learning algorithm, and these will be re-parameterized as ideal nonlinear feedforward and feedback evaluated within a Simulink simulation. Comparison is made to a custom proportional, derivative, integral controller (modified versions of classical proportional-integral-derivative control) implemented as a feedback control with a specific term to account for the nonlinear coupled motion. Consistent proportional, derivative, and integral gains were used throughout the duration of the experiments. The simulation results will show that akin feedforward control, deterministic self-awareness statements lack an error correction mechanism, relying on learning (which stands in place of feedback control), and the proposed combination of optimal self-awareness statements and a newly demonstrated analytically optimal learning yielded the highest accuracy with the lowest execution time. This highlights the potential effectiveness of a learning control system.
1. Introduction
The goal of rotational mechanics control is to have a system that can move to and hold a specific orientation in three-dimensional space, relative to an inertial frame. The term system generically applies to many physical practices, and aerospace systems are emphasized here with extension to maritime systems by description. The goal may be viewed through three different lenses: classical control, modern control, and/or artificial intelligence (either stochastic or deterministic). These lenses explain the same control theory in three different contexts. For all three paradigms, consideration of motion mechanics must include kinetics, kinematics, disturbances, controls, actuators, and estimators that dictate the system’s motion [1]. Specifically, with regard to classical control, both feed-forward and feedback controller are implemented in order to eliminate error between a desired and commanded signal [2]. With regard to modern control, the classical notion of feedforward and feedback is contemplated in terms of an estimation [3] and correction method [4,5,6] implemented using a non-linear control estimator coupled with a nonlinear corrector in order to reduce error. The third context relates control systems to deterministic artificial intelligence and machine learning.
In today’s world, machine learning and artificial intelligence are usually referred as same. But that is not the truth, both are different in so many aspects. Machine learning is one of these aspects. Artificial intelligence is by far divided into two approaches, statistical and deterministic to program a machine to mimic human beings. When a machine is given the data to rely on for its intelligence, it’s called the statistic or probabilistic approach. When a result is derived by the machine through a series of conditions, it’s called deterministic approach [7].
1.1. The Contributions
The contributions to the field described in this manuscript include augmentation of feedback proportional-derivative-integral, PDI control (a modified form of proportional-integral-derivative, PID control) with a nonlinear de-coupling control that seeks to account for the nonlinear coupling of vector cross-products. The nominal PDI controller is tuned with the accepted methodologies [2,4,5,6], and the slightly novel approach is the augmentation. The augmented PDI control is compared to state-optimal feedforward control. A larger contribution is the development of deterministic self-awareness statements in lieu of feedforward control, while another substantial contribution is the development of optimal learning statements resulting from exact reparameterization of the nonlinear forms into a linear diffeomorphism. The proposed systems are all shown to very effectively drive rigid-body systems to desired configurations, while the combination of optimal self-awareness statements and optimal learning comprising deterministic artificial intelligence will be shown to be the most superior approach. Readers wishing to preview the claims before continuing to read the manuscript should refer Figure 8 to see the proposed approaches compared using very small-scale state errors.
1.2. The Literature Review
Ashford proposed a deterministic artificial intelligence approach for cyber information security relying on self-awareness for defense and healing [8]. Significant recent research has investigated the self-awareness of several animals [9,10,11], including elephants [12], magpies [13,14], dolphins [15], chimpanzees [16], ants [17], and humans [18,19], including children [20,21,22,23,24].
Scholars have long pondered the nature of self-awareness [25,26,27] and its neural basis in stochastic, non-deterministic approaches [28]. The emerging research in self-awareness of contexts includes using cross-domain computing environments to automatically identify the context of the user [29]. The environmental impacts on driving styles are predicted using new methods and models [30]. Another recent self-awareness work accounts for predictive capabilities, immersive devices, multimodal interactions, and adaptive displays of multi-system robots to develop interfaces including predictive virtual reality, conventional, and predictive conventional [31]. Assisting people to copy with incurable diseases including chronic obstructive pulmonary disease using context-aware systems has been extensively examined in publications of recent decades [32]. Context-awareness and social computing integrating multiple technologies has spawned a conceptual framework for collaborative context-aware learning activities [33].
Stochastically using both business and information services to monitor hazards while driving helps ensure driving safety [34]. Using large amounts of data sources, including sensors streaming, in manufacturing self-optimizing algorithms approaches context sensitivity [35]. Emotional components may augment context-awareness with the advent of simulations of empathy and emotion [36]. Information on the state and progress of systems of computing systems which can maintain models and learn leads to the ability for the systems to associate their behaviors with reason instantiating computational self-awareness [37]. This key novel work, only three years old, inspires the adoption of self-awareness as a new way of thinking (as a starting point for artificial intelligence), and it has spawned a recent lineage of the growth of the notion in typical stochastic (non-deterministic) approaches to artificial intelligences.
Wireless sensor networks were augmented by Kao, et al. with self-awareness paradigms providing autonomy and fault-tolerant adaptive routing overcoming limits of self-selective and self-healing routing [38]. Adaptive health monitoring was achieved by self-awareness for systems using information from five levels from the configuration level to the level of data connection. [39] Higher personality state variability was addressed by Jauk, et al. [40] using self-awareness seeking to explain contradictory results using the so-called “theory of mind” offered by Wundrack, et al. [41] Jauk’s argument focused on Wundrack’s isolation of the causality direction, and furthermore point out the ability of perspective-taking may be both cause and effect of personality state variability.
Heterogeneous or homogeneous types of potency of multi-robot systems were achieved by Kosak, et al. by integration of algorithms and mechanisms into both simulation and laboratory experiments [42]. Human behavior mimicking by robots with self-awareness and awareness of their environment proved able to autonomously operate in dynamic environments with optimal route planning [43].
Various instantiations of stochastic artificial intelligence (A.I.) described above seek optimality after acceptance of the structure of the system and form of learning. None of these are used in the deterministic artificial intelligence algorithm presented here, instead they serve as a background to highlight the distinction between stochastic and non-stochastic (deterministic) artificial intelligence [2,3,4,5,6,7,8]. Deterministic artificial intelligence instantiated here, stems from a lineage of nonlinear adaptive control [44,45,46] inspired learning augmented by physics-based control methods [47,48] inspired deterministic self-awareness statements. A rigid body’s self-awareness of its own attributes is updated every time-step with new information from learning, noting the generic term “rigid-body” applies to physical systems in many disparate disciplines. The aforementioned lineage of references was applied to aerospace systems (both autonomous jet aircraft and spacecraft), while the novel methods presented here are simultaneously being applied to maritime systems to be revealed in sequel research being prepared for publication. Notice the algorithm presented here disposes of feedback control, replacing it with deterministic self-awareness statements that are parameterized such that learning algorithms use control-error feedback (not state feedback) to learn the proper, time-variant self-awareness statement. Notice the typical control calculation in Figure 1 composed of any number of kinds of feedback control are eliminated in Figure 2 will be replaced. The self-awareness statements necessitate online autonomous trajectory generation, done here in accordance with reference [49]. This self-updating learning mechanism can be viewed akin to the update cycle used by supervised learning algorithms to model a system’s performance. As an example, the updating mechanism is either a linear or non-linear method to update an unknown inertia matrix for a rigid body [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], while new learning methods will be proven here to be optimal.

Figure 1.
The system topology from commanded end-state and time, through autonomously calculated desired roll , pitch , and yaw inputs, through control calculations executed by control moment gyroscope actuators resulting in actual Euler angle outputs of kinematic expressions of kinetic responses. Notice that actual responses are unknown, but sensed and filtered, and then used in state estimators to provide full state feedback.
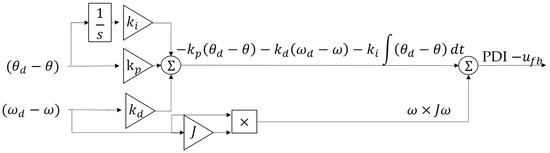
Figure 2.
Nonlinear-enhanced PDI controller with desired ωd input to remove virtual zero reference scaled by Kp, Kd, and Ki gains. Also notice the nonlinear cross product enhancement.
Figure 1 depicts the topology of the computational steps that take desired angle inputs and calculates Euler Angle outputs: roll , pitch , and yaw . The desired angle inputs are processed through the trajectory, controls, actuators, dynamics, and disturbances blocks. Section 2 will explain the theory behind the overall control system. Section 3 will detail the experimental setup and the results, and Section 4 will conclude this manuscript hopefully achieving the objective of this paper: introduce a new paradigm for self-awareness and optimal learning in the category deterministic artificial intelligence.
2. Materials and Methods
The rotation maneuver of a rigid body (representing at least aerospace and maritime systems) from one position to another is measured from the inertial reference frame or to the final position measured in the body reference frame annotated . For the simulations presented here, a model was created to rotate in a user-prescribed maneuver time from an initial arbitrary orientation to a final arbitrary orientation , where the orientations may also be set by the users. The kinetics and kinematics, accounting for motion in the orbital frame, and realistic disturbance calculations are all explained in reference [1]. This section of the manuscript focuses on deterministic artificial intelligence used for the control calculation utilizing an error estimation and correction mechanism. Simulations will be provided in Section 3 utilizing three control moment gyroscopes [50] that are responsible for physically moving the system according to the inputted control signal.
2.1. Rigid Body Mechanics
Rigid bodies rotate in accordance with Euler’s moment equation, and this physics-based governing differential equation will be used later to formulate a control in a feedforward topology that asserts behavior in accordance with the fact the item being controlled is a rigid body. It is desired for the autonomous system to be self-aware that it is (for example) an aerospace or maritime system which will obey Euler’s moment equation. This general notion will utilize the nomenclature self-awareness statement, since the control enforces the self-awareness that the control-item is a rigid body and must obey Euler’s equations, and by this method eliminates the need for learning of the structure of the output data (instantiating a significant improvement over stochastic artificial intelligence methods). Equation (1) is Euler’s moment equation for rigid body mechanics in three dimensions, one equation for each dimension in matrix form.
These governing equations apply to any rotating, rigid body of mass and thus it’s applicability to maritime and aerospace systems ubiquitously. T represents the total resultant torque which is hoped to equal to the optimal control ; represents the change in system angular momentum in the inertial frame; represents the angular velocity of the body; is the inertia matrix for the entire body.
2.2. Luenberger-Like Controllers (i.e., Nonliner-Enhanced Proportional-Derivative-Integral, PDI)
The input torque vector, [Tx, Ty, Tz] is a signal generated by the trajectory block in Figure 1. However, this signal is not tuned to adjust to real world influences, where mechanical hardware can introduce errors due to incorrectly or un-modeled attributes, noise, etc. In order to overcome these losses, either a feed forward controller, a feedback controller, or a combination of both controllers can be used to counter errors. More specifically, proportional, integral, and derivative (PID) gains are correlated only to the position error generated when moving from one position to another position to correct the errors, as displayed in Equation (2). On the other hand, proportional-derivative-integral (PDI) control uses full-state feedback to eliminate virtual-zero references inherent to the cascaded topology of the classical PID form. The modern PDI form is augmented here with a nonlinear term to counter the nonlinear coupling induced by the cross-product operation necessary to account for rigid body motion in moving reference frames, and the combined form is displayed in Equation (3) whose topology is illustrated in Figure 2.
However, using only the position error , its integral , and its derivative results in inaccuracies. This is due in part to noise amplification of the derivative calculation, which is both inefficient and inaccurate as a result of the virtual zero reference created in the cascaded topology of a PID controller. This inaccuracy can be prevented by calculating both the position error and the velocity error, which has been done in this experiment via a nonlinear-enhanced Luenberger proportional, derivative, integral (PDI) controller [15,16,17,18] where the enhanced Luenberger Controller differs from the conventional PID controller which only receives a position error and does not have a nonlinear decoupling term to account for moving reference frames. The result is a controller that outputs a commanded torque to the actuator block in Figure 1. Topologies are shown of the overall feedback controller in Figure 4, and the enhanced Luenberger PDI controller in Figure 5. A further augmentation adds a nonlinear component: accounting for coupled motion.
2.3. Deterministic Artificial Intelligence
Equation (1) is an analytic governing equation of motion substantiates the kinetics in Figure 1 and the nonlinear enhancement in Equation (3). Substituting the desired states and into the classical PID control form makes it difficult to see possible exact solutions: , where is error associated with the angular position state.
Error-Analysis Yields Deterministic Self-Awareness Statement
Equate coefficients of like derivatives of states in Equation (4) and contemplate how they could possibly be analytically equivalent expressions. The comparison is the reason why “???” is placed over the equal sign in the equation. The comparison should lead the reader to replace the equal sign with an unequal sign, since the expression will never be analytically equivalent. The same unfavorable comparison holds true for the nonlinear-enhanced PDI controller, and this inspires the utilization of the exact forms of the governing differential equation of motion in the proposed control as done in Equation (5), the deterministic artificial intelligence self-awareness statement enforcing the rigid body knowledge of its governing equations. Comparison of the methods proposed here will use tracking error analysis in simulations and also computational burden as figures of merit.
Theorem 1.
Deterministic self-awareness statements in a feedforward topology can be optimal (exact) with respect to state tracking error.
Proof of Theorem 1.
Using the deterministic self-awareness statement in a feedforward topology defines the control as the governing equation of motion: .
Corollary stability analysis: As done earlier, equate coefficients of like derivatives of states in Equation (8) and contemplate how they could possibly be analytically equivalent expressions. It is quite easy to see how the deterministic self-awareness statement could lead to analytic solutions. ,. □
A control system is capable of learning by estimating the incremental torque error using any motion observer and using the estimate to learn the erroneous properties that generated the errors. In a learning control system, the control estimator is the feedforward topology defined by Equation (8) and the corrector or learning mechanism is the feedback defined by Equation (9), where and are defined by Equations (6) and (10) (where the * denotes optimality) respectively and where the incremental learning correlating to the incremental error at each time step is in Equation (9).
Theorem 2.
Deterministic learning in a feedback topology are optimal with respect to state tracking error.
Proof of Theorem 2.
Error illustrate the control signal to be incorrect, and the control error may be attributed to the mismodeled self-awareness statement by estimating the incremental torque error and solving the regression formulated problem for the vector of unknowns: . Since the optimal learning expressed in a feedback topology is the 2-norm optimal solution to the standard regression-formulated governing dynamics in Equations (10) and (11), learning is optimal in that sense. □
Corollary stability analysis: When the context of assertion of deterministic self-awareness statements is viewed as a prediction step in a typical Kalman Filter, the subsequent correction-step is stable in accordance with long-held proofs of the stability and optimality of Kalman Filters [51].
Combining Equations (5) and (9) yields a learning system that develops a more accurate time-varying control (12).
Summarizing, replacing the control element of Figure 1 with deterministic artificial intelligence elements of self-awareness statements and learning (as depicted in Figure 3) is accomplished by formulating the term “” in (8) represents the self-awareness statement written in a regression format with states in the matrix of “knowns” and other variables in the vector of “unknowns”. This novel method replaces the feedback control calculation block in Figure 1, and rather than substitute stochastic artificial intelligence in its place, we recommend replacement with self-awareness statements that use feedback to optimally learn. The non-linear state transition matrix was built by knowing the dynamics of the system (embodied in the governing differential equations of rotational mechanics) and is the estimated vector of unknown variables. Another application includes analyzing a changing inertia matrix, where it is assumed that the mass of the system is varying. The vector of unknowns is the learned moment of inertia that is recalculated at every iteration of the model and determining its new mass per Equation (9). This analytically exact and now-proven optimal control should immediately (and at every time step) know the precise correct control and is therefore theorized to approach so-called deadbeat control that is correct at the earliest opportunity (without copious training data required by stochastic methods).

Figure 3.
The system topology of deterministic artificial intelligence.
3. Results
This section of the manuscript documents the implementation of three different control algorithm combinations to induce a yawing motion on a rigid body (e.g., autonomous aerospace and maritime systems) by sending the commanded torque signal to a non-redundant array of control moment gyroscope actuators [52]. The three cases investigated are a non-linear feedforward control (case one), a linear feedback control with nonlinear augmentation (case two), and deterministic artificial intelligence as previously presented in a combined non-linear feedforward plus feedback topology of learning (not feedback control) after asserting self-awareness statement. Case one (nonlinear feedforward) implements Equation (5) without the learning, i.e., Equation (7) is not implemented. Case two implements Equation (3) in a typical feedback control topology which is disposed of in case three’s implementation of Equations (5) and (7), where optimal learning in Equation (9) supports the implementation of Equation (7). The combined form is Equation (14). The gains for the classical controllers used for comparison are found in Table 1. Notice that Table 1 includes the gains from the Luenberger observer used to find the control-error necessary for optimal learning. It will be seen that replacement of typical feedforward and feedback topologies with deterministic A.I. will be the most accurate option simultaneously achieving the lowest computational burden.

Table 1.
Tuned gain values 1 for the PDI controller and observer.
The model of the rigid body in this manuscript was built in Matlab and Simulink, where integrations were calculated using the ode45 with Runge-Kutta solver with a fixed time-step. Euler Angles were resolved using a 3-2-1 rotation sequence with the atan2 trigonometry function to eliminate quadrant ambiguity.
Utilizing the same rigid body model and sinusoidal trajectory generation as reference [1], initialized values include: torque = [0, 0, 0] and quaternion = [0, 0, 0, 1]. The rigid body’s inertia matrix is J = [10, 0.1, 0.1; 0.1, 10, 0.1; 0.1, 0.1, 10]. The realistic disturbance torques are defined in reference [5]. The orbital altitude was set at 150 km with an atmospheric drag coefficient of 2.5. Each simulation utilized a five second quiescent period to validate the model, five second maneuver time, and five second post maneuver observation period, totaling 15 s for a large angle slew.
3.1. Time-Step Analysis
Time-step analysis was completed to determine whether reducing the time-step would help minimize the error deviations between the body frame and the inertial frame. The results of executing a maneuver with deterministic artificial intelligence and two different time-steps is depicted in Figure 4. Expectations were that a smaller time-step would result in more precise results, meaning a smaller deviation between the commanded and executed Euler angles. However, comparing the trajectories within each of the three sub-plots in Figure 4 shows that although some refinement is gained by decreasing the time-step, the gain is minimal. Therefore, a larger time-step (e.g., 0.01 s) can be used with slight degradation.
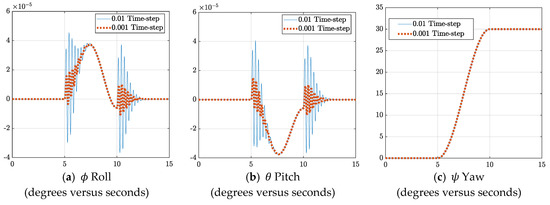
Figure 4.
Time-step analysis for the ϕ, θ, and ψ Euler angles for two disparate time-steps with deterministic artificial intelligence. Pay particular attention to the near coincident performances when viewed in large-scale in Figure 4c, while the smaller-scaled plots reveal differences.
Comparing the θdesired − θactual and ωdesired − ωactual errors for time-steps of 0.01 and 0.001 in Figure 5 yielded a similar result. Therefore, these results confirm that varying the time-step has limited impact on the trajectories. With this knowledge, for the gains in Table 1, a minimum time-step of 0.01 is recommended, since decreasing step-size any further provided slight benefit.
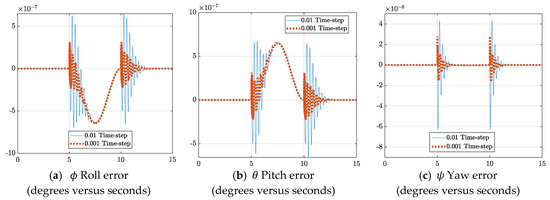
Figure 5.
Time-step analysis comparing θactual − θdesired and ωactual − ωdesired errors.
3.2. Control Implementation
The performance of the three control system implementations is depicted in Figure 6. Comparing the three cases allowed further analysis on the differences between feedforward, feedback, and the combined deterministic artificial intelligence system. The feedforward and the deterministic artificial intelligence systems are more precise than the feedback method. This is because they are based on exact control Equations (9) and (10) respectively. Conversely, the feedback controller is based off a PDI controller that suffers phase lag [53], and is therefore less precise. Additionally, the gains in a PDI or PID controller must be finely tuned with pre-determined gain values, which can be an iterative and time-consuming task because controller performance varies greatly depending on the values. Lastly, the deterministic artificial intelligence configuration represents an error combination of both the feedforward and feedback plots. This allows the analytical accuracy of the feedforward equation to be updated with the responsiveness of the feedback correction by learning. Plot scaling precludes easy visualization of the error, so tabulated numerical results are provided in Table 2.
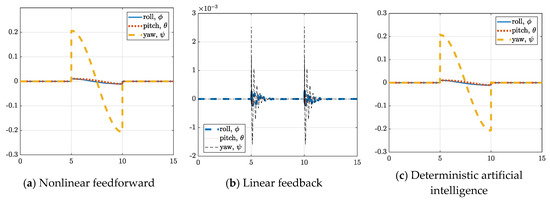
Figure 6.
Control (Newton-meters) versus time in seconds for the three configurations.

Table 2.
Actual desired Euler angle errors and associated run times for the three cases 1.
Figure 7 shows the Euler angle tracking error over time. Figure 7a,b shows that the error is different for each controller. The feedback controller fluctuates initially as it corrects to reduce error over time. The feedforward controller is excellent initially, but slowly deviates as error accrues without correction. Lastly, the deterministic artificial intelligence system is the best, starting with minimal error, and furthermore correcting that error over time.
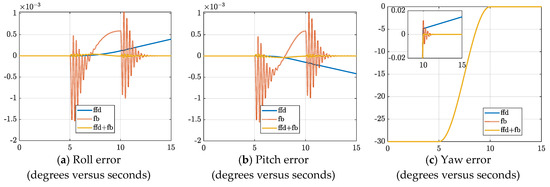
Figure 7.
Euler Angle error for the three controller configurations.
Figure 7c shows the position error in the yaw channel, which is the channel in which a 30-degree maneuver was commanded. The feedforward controller again starts off with minimal error before deviating over time, while the feedback controller starts with the greatest amount of error that is quickly damped, and the deterministic artificial intelligence is the best of both.
Table 2 compares the boundary condition satisfaction at the final time of the maneuver. The results show that the deterministic artificial intelligence system (D.A.I.) has both the least amount of error and the shortest computational runtime. The feedforward controller is the worst in accuracy due to an inability to correct for error, while the feedback controller can correct, but takes longer to do so. The feedback controller is hypothesized to perform worse because Equation (2) tries to model Equation (1), but can only poorly approximate it, yielding inaccuracies.
Figure 8 is a revisualization of the data presented in Figure 7 for clarity of conclusions. This depiction is more intuitive and illustrates the change in angular yaw position over time for each controller, as well as magnifying the post maneuver oscillations and damping (or lack of such, in the case of Figure 8a,b). Commanding , we see that all controller configurations are responsive to this input, with expected differences. The accuracy of the feedforward control in Figure 8a, combined with the lightly damped response of feedback control in Figure 8b, clearly illustrate the superior, dampened response of the deterministic artificial intelligence controller in Figure 8c.
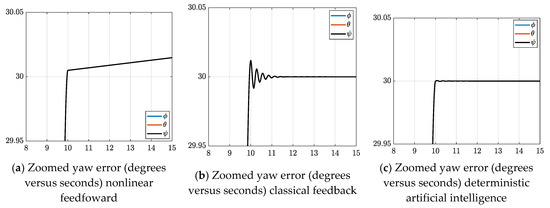
Figure 8.
Change in angular position for all three controller configurations. (degrees versus seconds).
4. Discussion
The implemented experiment compared the effects of a feedforward, feedback, and a deterministic artificial intelligence system. A yaw maneuver was commanded, and the response measured to show that an attitude determination and control system can estimate and then update its control over time, akin to feedforward and feedback (where feedback here is a learning mechanism). The results showed that the feedforward controller lacks a correction mechanism that accrues error, the feedback system requires more time to correct for error that starts in the system, and the deterministic artificial intelligence system combines the best of both systems for superior accuracy in the lower computational burden. Therefore, the deterministic artificial intelligence system is the best choice for its accuracy and adaptability. However, this combined system needs to be further researched by subjecting the system to noise and induced parameter variation (including disturbances) to validate the system’s responsiveness. Future research will implement time-variations in the rigid body’s parameters to simulate damage from inelastic collisions, or alternatively highly energetic elastic collisions that remove significant part of the rigid body. It is theorized that deterministic artificial intelligence could quickly (and optimally) recover.
Readers seeking apply the methods proposed in this manuscript may follow the procedures outlined in the flowchart in Figure 9. System definition acknowledges the first principle governing the rigid body of interest, e.g., spacecraft, aircraft, underwater vehicles, etc.

Figure 9.
Technology development flowchart using the proposed methods.
Future Research
Although the methods proposed here stem from analysis of the errors between the algorithms and the systems being controlled, typical stability analysis for nonlinear learning systems would often include phase portraits and also analytic demonstrations using Lyapunov’s first and second methods. While these were unnecessary here, it remains for future researchers to validate stability demonstrated here with either of these three methods.
Author Contributions
Conceptualization, B.S., A.R., and T.S.; Methodology, T.S.; Software, B.S., A.R., and T.S.; Validation, B.S., A.R., and T.S.; Formal analysis, B.S., A.R., and T.S.; Investigation, B.S., A.R., and T.S.; Resources, T.S.; Data curation, B.S., A.R., and T.S.; Writing—original draft preparation, B.S. and A.R.; Writing—review and editing, B.S., A.R., and T.S.; Visualization, B.S., A.R., and T.S.; Supervision, T.S.; Project administration, B.S. and T.S.; Funding acquisition, T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smeresky, B.; Rizzo, A.; Sands, T. Kinematics in the Information Age. Mathematics 2018, 6, 148. [Google Scholar] [CrossRef]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling Chaos—Forced van der pol equation. Mathematics 2017, 5, 70. [Google Scholar] [CrossRef]
- Sands, T. Nonlinear-Adaptive Mathematical System Identification. Computation 2017, 5, 47. [Google Scholar] [CrossRef]
- Nakatani, S.; Sands, T. Battle-damage tolerant automatic controls. Electr. Electron. Eng. 2018, 8, 10–23. [Google Scholar]
- Nakatani, S.; Sands, T. Simulation of rigid body damage tolerance and adaptive controls. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; pp. 1–16. [Google Scholar]
- Nakatani, S.; Sands, T. Autonomous Damage Recovery in Space. Int. J. Autom. Control Intell. Syst. 2016, 2, 23–36. [Google Scholar]
- EPICA Lastest News Blog. Deterministic Approach to Machine Learning and AI. 2018. Available online: https://www.epica.ai/thinking/blog/deterministic-approach-to-machine-learning-and-ai.html (accessed on 19 November 2019).
- Deterministic Data-based AI Key for Security. Available online: https://www.computerweekly.com/news/252464484/Deterministic-data-based-AI-key-for-security (accessed on 25 November 2019).
- DeGrazia, D. Self-awareness in animals. In The Philosophy of Animal Minds; Lurz, R.W., Ed.; Cambridge University Press: Cambridge, UK, 2009; pp. 201–217. [Google Scholar]
- Bekoff, M. Awareness: Animal reflections. Nature 2002, 419, 255. [Google Scholar] [CrossRef]
- Gallup, G.G., Jr.; Anderson, J.R.; Shillito, D.J. The mirror test. In The Cognitive Animal: Empirical and Theoretical Perspectives on Animal Cognition; Bekoff, M., Allen, C., Burghardt, G.M., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 325–333. [Google Scholar]
- Plotnik, J.M.; De Waal, F.B.; Reiss, D. Self-recognition in an Asian elephant. Proc. Natl. Acad. Sci. USA 2006, 103, 17053–17057. [Google Scholar] [CrossRef]
- Prior, H.; Schwarz, A.; Güntürkün, O. Mirror-Induced Behavior in the Magpie (Pica pica): Evidence of Self-Recognition. PLoS Biol. 2008, 6, e202. [Google Scholar] [CrossRef]
- Alison, M. Mirror Test Shows Magpies Aren’t So Bird-Brained. Available online: https://www.newscientist.com/article/dn14552-mirror-test-shows-magpies-arentso-birdbrained.html#.VHVdHf4tDIV (accessed on 26 November 2014).
- Tennesen, M. Do Dolphins Have a Sense of Self? Natl. Wildl. 2003, 41, 66. [Google Scholar]
- Bard, K. Self-Awareness in Human and Chimpanzee Infants: What is Measured and What is Meant by the Mark and Mirror Test? Infancy 2006, 9, 191–219. [Google Scholar] [CrossRef]
- Cammaerts Tricot, M.C.; Cammaerts, R. Are Ants (Hymenoptera Formicide) Capable of Self Recognition? J. Sci. 2015, 5, 521–532. [Google Scholar]
- Pfeifer, R.; Bongard, J. How the Body Shapes the Way We Think: A New View of Intelligence; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Lieberman, P. The Unpredictable Species: What Makes Humans Unique; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Rochat, P. Five levels of self-awareness as they unfold early in life. Conscious. Cognit. 2003, 12, 717–731. [Google Scholar] [CrossRef]
- Geangu, E. Notes on Self-Awareness Development in Early Infancy. Cognit. Brain Behav. 2008, 12, 103–113. [Google Scholar]
- Yawkey, T.D.; Johnson, J.E. (Eds.) Integrative Processes and Socialization Early to Middle Childhood; Psychology Press: East Sussex, UK, 2013; ISBN 9780203767696. [Google Scholar]
- Rochat, P. Self-Perception and Action in Infancy. Exp. Brain Res. 1998, 123, 102–109. [Google Scholar] [CrossRef]
- Broesch, T.; Callaghan, T.; Henrich, J.; Murphy, C.; Rochat, P. Cultural Variations in Children’s Mirror Self-Recognition. J. Cross Cult. Psychol. 2011, 42, 1018–1029. [Google Scholar] [CrossRef]
- Locke, J. An Essay Concerning Human Understanding; Wentworth Press: Sidney, Australia, 1775; ISBN 0526315180. [Google Scholar]
- Kendra, C. What Is Self-Awareness? Available online: http://psychology.about.com/od/cognitivepsychology/fl/What-Is-Self-Awareness.htm (accessed on 25 November 2014).
- Abraham, S. Goldstein the Insanity Defense; Yale University Press: New Haven, CT, USA, 1967; p. 9. ISBN 978-0-300-00099-3. [Google Scholar]
- Uddin, L.Q.; Davies, M.S.; Scott, A.A.; Zaidel, E.; Bookheimer, S.Y.; Iacoboni, M.; Dapretto, M. Neural Basis of Self and Other Representation in Autism: An fMRI Study of Self-Face Recognition. PLoS ONE 2008, 3, e3526. [Google Scholar] [CrossRef]
- Razzaq, M.A.; Villalonga, C.; Lee, S.; Akhtar, U.; Ali, M.; Kim, E.-S.; Khattak, A.M.; Seung, H.; Hur, T.; Bang, J.; et al. mlCAF: Multi-Level Cross-Domain Semantic Context Fusioning for Behavior Identification. Sensors 2017, 17, 2433. [Google Scholar] [CrossRef]
- Sysoev, M.; Kos, A.; Guna, J.; Pogačnik, M. Estimation of the Driving Style Based on the Users’ Activity and Environment Influence. Sensors 2017, 17, 2404. [Google Scholar] [CrossRef]
- Roldán, J.J.; Peña-Tapia, E.; Martín-Barrio, A.; Olivares-Méndez, M.A.; Del Cerro, J.; Barrientos, A. Multi-Robot Interfaces and Operator Situational Awareness: Study of the Impact of Immersion and Prediction. Sensors 2017, 17, 1720. [Google Scholar] [CrossRef]
- Mcheick, H.; Saleh, L.; Ajami, H.; Mili, H. Context Relevant Prediction Model for COPD Domain Using Bayesian Belief Network. Sensors 2017, 17, 1486. [Google Scholar] [CrossRef]
- García, Ó.; Alonso, R.S.; Prieto, J.; Corchado, J.M. Energy Efficiency in Public Buildings through Context-Aware Social Computing. Sensors 2017, 17, 826. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Yao, W.; Li, X. A Context-Aware S-Health Service System for Drivers. Sensors 2017, 17, 609. [Google Scholar] [CrossRef] [PubMed]
- Scholze, S.; Barata, J.; Stokic, D. Holistic Context-Sensitivity for Run-Time Optimization of Flexible Manufacturing Systems. Sensors 2017, 17, 455. [Google Scholar] [CrossRef]
- Moore, P. Do We Understand the Relationship between Affective Computing, Emotion and Context-Awareness? Machines 2017, 5, 16. [Google Scholar] [CrossRef]
- Lewis, P.R.; Platzner, M.; Rinner, B.; Tørresen, J.; Yao, X. (Eds.) Self-Aware Computing Systems: An Engineering Approach; Springer International Publishing AG: Cham, Switzerland, 2016. [Google Scholar]
- Abba, S.; Lee, J.-A. An Autonomous Self-Aware and Adaptive Fault Tolerant Routing Technique for Wireless Sensor Networks. Sensors 2015, 15, 20316–20354. [Google Scholar] [CrossRef]
- Kao, H.-A.; Jin, W.; Siegel, D.; Lee, J. A Cyber Physical Interface for Automation Systems—Methodology and Examples. Machines 2015, 3, 93–106. [Google Scholar] [CrossRef]
- Jauk, E.; Kanske, P. Perspective Change and Personality State Variability: An Argument for the Role of Self-Awareness and an Outlook on Bidirectionality (Commentary on Wundrack et al., 2018). J. Intell. 2019, 7, 10. [Google Scholar] [CrossRef]
- Wundrack, R.; Prager, J.; Asselmann, E.; O’Connell, G.; Specht, J. Does Intraindividual Variability of Personality States Improve Perspective Taking? An Ecological Approach Integrating Personality and Social Cognition. J. Intell. 2018, 6, 50. [Google Scholar] [CrossRef]
- Kosak, O.; Wanninger, C.; Hoffmann, A.; Ponsar, H.; Reif, W. Multipotent Systems: Combining Planning, Self-Organization, and Reconfiguration in Modular Robot Ensembles. Sensors 2019, 19, 17. [Google Scholar] [CrossRef]
- Van Pham, H.; Moore, P. Robot Coverage Path Planning under Uncertainty Using Knowledge Inference and Hedge Algebras. Machines 2018, 6, 46. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Spacecraft fine tracking pointing using adaptive control. In Proceedings of the 58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007. [Google Scholar]
- Sands, T.; Kim, J.J.; Agrawal, B. Spacecraft Adaptive Control Evaluation. In Proceedings of the Infotech@Aerospace, Garden Grove, CA, USA, 19–21 June 2012. [Google Scholar]
- Sands, T.; Kim, J.J.; Agrawal, B. Improved Hamiltonian adaptive control of spacecraft. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–10. [Google Scholar]
- Sands, T.; Lorenz, R. Physics-Based Automated Control of Spacecraft. In Proceedings of the AIAA Space Conference & Exposition, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar]
- Sands, T. Physics-Based Control Methods. In Advances in Spacecraft Systems and Orbit Determination; InTech Publishers: London, UK, 2012; pp. 29–54. [Google Scholar]
- Sands, T. Improved Magnetic Levitation via Online Disturbance Decoupling. Phys. J. 2015, 1, 272–280. [Google Scholar]
- Baker, K.; Cooper, M.; Heidlauf, P.; Sands, T. Autonomous trajectory generation for deterministic artificial intelligence. Electr. Electron. Eng. 2018, 8, 59–68. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35. [Google Scholar] [CrossRef]
- Sands, T. Control Moment Gyroscope Singularity Reduction via Decoupled Control. In Proceedings of the IEEE SEC Proceedings, Atlanta, GA, USA, 5–8 March 2009. [Google Scholar]
- Sands, T. Phase Lag Elimination at All Frequencies for Full State Estimation of Rigid body Attitude. Phys. J. 2017, 3, 1–12. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).